Mapping Soil Properties in the Haihun River Sub-Watershed, Yangtze River Basin, China, by Integrating Machine Learning and Variable Selection
Abstract
1. Introduction
2. Materials and Methods
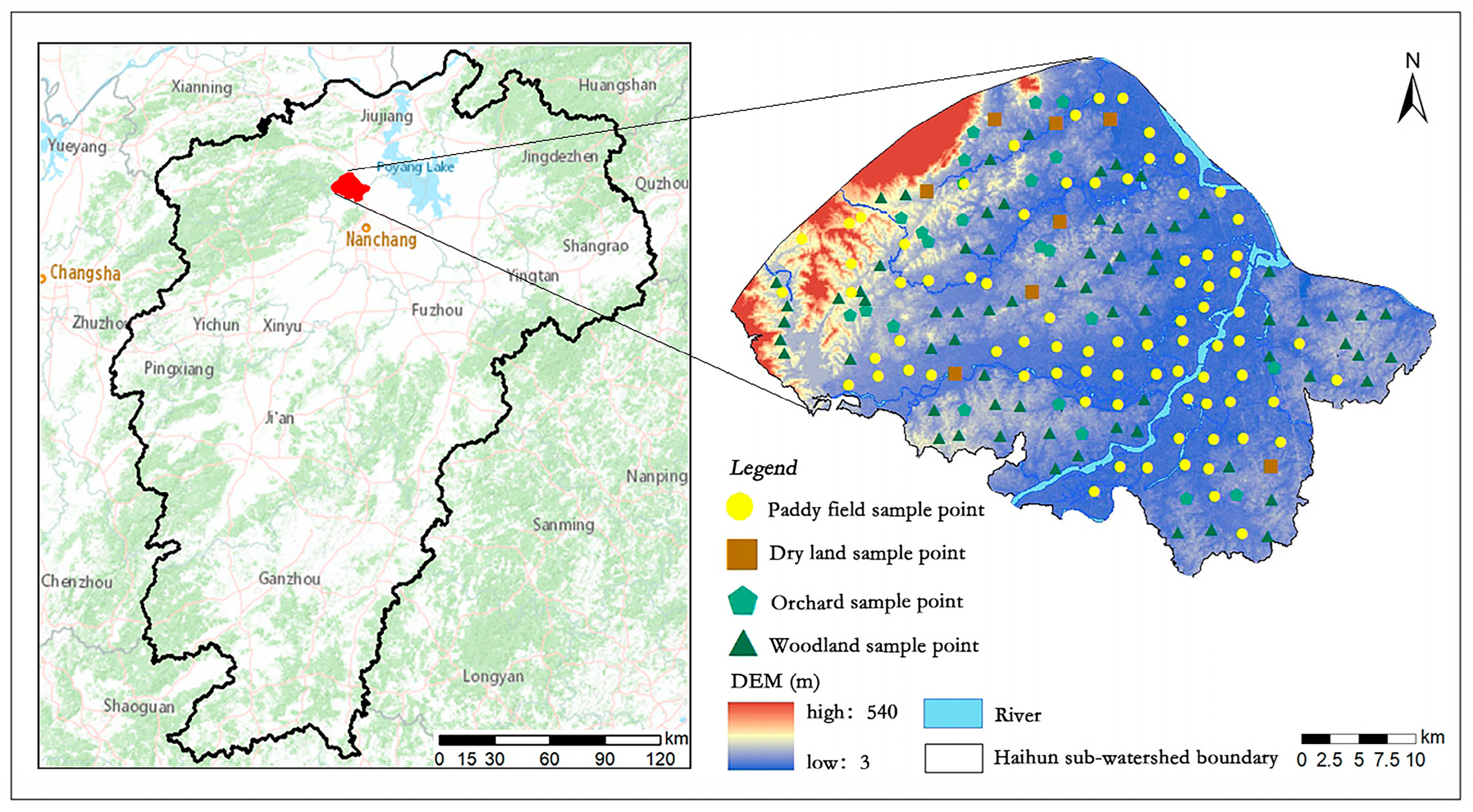
2.1. Study Area
2.2. Soil Sampling and Laboratory Analysis
2.3. Selection of Environmental Covariates
2.3.1. Soil Covariates
2.3.2. Climate Covariates
2.3.3. Remote Sensing Covariates
2.3.4. Organism Covariates
2.3.5. Relief Covariates
2.3.6. Human Activity Covariates
2.4. Modeling Methodology
2.4.1. Recursive Feature Elimination
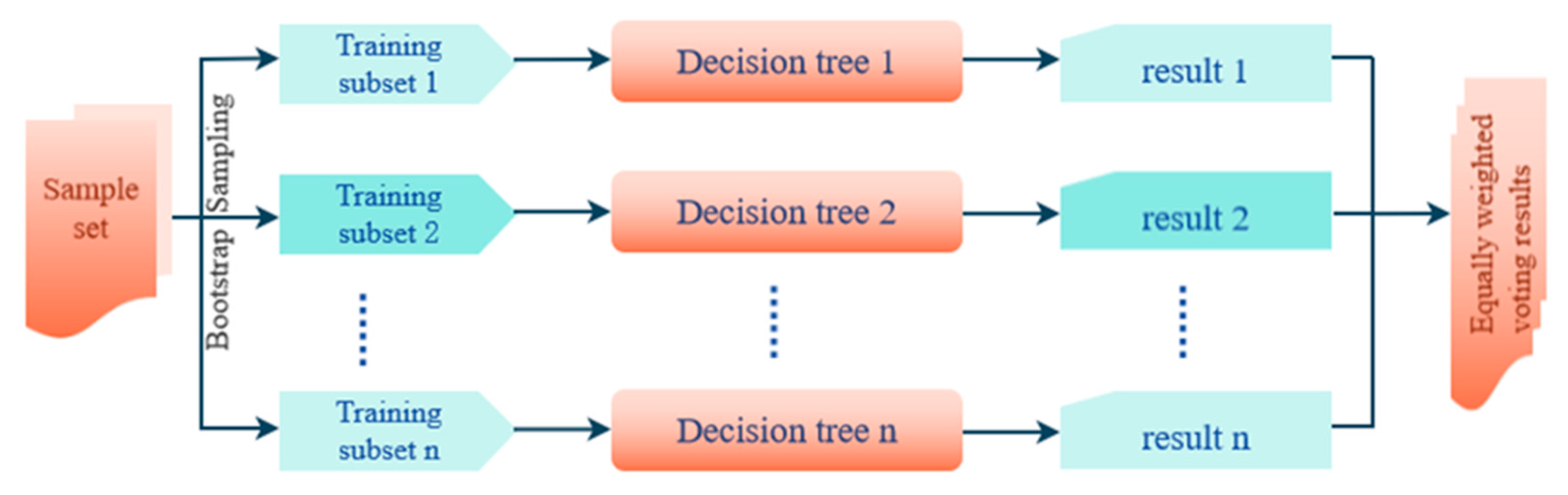
2.4.2. Random Forest
2.4.3. Extreme Gradient Boosting
2.4.4. Model Performance Evaluation
3. Results
3.1. Descriptive Statistics of the Soil Properties
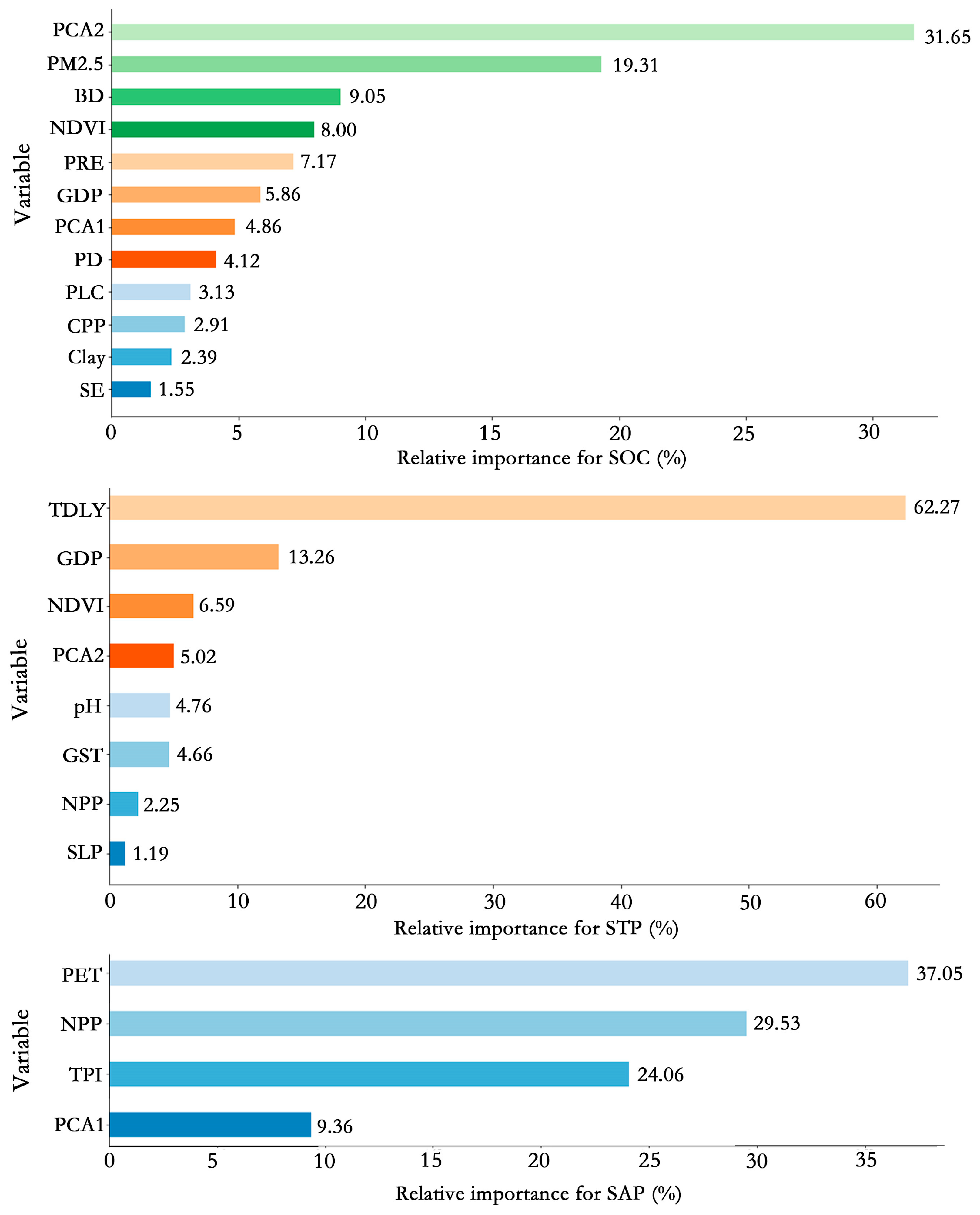
3.2. Variable Selection
3.3. Model Accuracy
3.4. Spatial Distribution of the Soil Properties
3.5. Model Uncertainty
4. Discussion
4.1. Benefits of Variable Selection
4.2. Comparison of Model Performance
4.3. Factors Controlling the Spatial Distribution of the Soil Properties
4.4. Limitations and Deficiencies
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Amundson, R.; Berhe, A.A.; Hopmans, J.W.; Olson, C.; Sztein, A.E.; Sparks, D.L. Soil and human security in the 21st century. Science 2015, 348, 1261071. [Google Scholar] [CrossRef] [PubMed]
- Montanarella, L.; Pennock, D.J.; McKenzie, N.; Badraoui, M.; Chude, V.; Baptista, I.; Mamo, T.; Yemefack, M.; Singh Aulakh, M.; Yagi, K. World’s soils are under threat. Soil 2016, 2, 79–82. [Google Scholar] [CrossRef]
- Crumpton, W. Using wetlands for water quality improvement in agricultural watersheds; the importance of a watershed scale approach. Water Sci. Technol. 2001, 44, 559–564. [Google Scholar] [CrossRef]
- Huang, B.; Sun, W.; Zhao, Y.; Zhu, J.; Yang, R.; Zou, Z.; Ding, F.; Su, J. Temporal and Spatial Variability of Soil organic matter and total nitrogen in an agricultural ecosystem as affected by farming practices. Geoderma 2007, 139, 336–345. [Google Scholar] [CrossRef]
- Reeves, D. The role of soil organic matter in maintaining soil quality in continuous cropping systems. Soil Tillage Res. 1997, 43, 131–167. [Google Scholar] [CrossRef]
- Scull, P.; Franklin, J.; Chadwick, O.A.; McArthur, D. Predictive soil mapping: A review. Prog. Phys. Geogr. 2003, 27, 171–197. [Google Scholar] [CrossRef]
- McBratney, A.B.; Santos, M.M.; Minasny, B. On digital soil mapping. Geoderma 2003, 117, 3–52. [Google Scholar] [CrossRef]
- Brus, D.; Kempen, B.; Heuvelink, G. Sampling for validation of digital soil maps. Eur. J. Soil Sci. 2011, 62, 394–407. [Google Scholar] [CrossRef]
- Chen, S.; Liang, Z.; Webster, R.; Zhang, G.; Zhou, Y.; Teng, H.; Hu, B.; Arrouays, D.; Shi, Z. A high-resolution map of soil pH in China made by hybrid modelling of sparse soil data and environmental covariates and its implications for pollution. Sci. Total Environ. 2019, 655, 273–283. [Google Scholar] [CrossRef]
- Ye, M.; Zhu, L.; Li, X.; Ke, Y.; Huang, Y.; Chen, B.; Yu, H.; Li, H.; Feng, H. Estimation of the soil arsenic concentration using a geographically weighted XGBoost model based on hyperspectral data. Sci. Total Environ. 2023, 858, 159798. [Google Scholar] [CrossRef]
- Estévez, V.; Beucher, A.; Mattbäck, S.; Boman, A.; Auri, J.; Björk, K.-M.; Österholm, P. Machine learning techniques for acid sulfate soil mapping in southeastern Finland. Geoderma 2022, 406, 115446. [Google Scholar] [CrossRef]
- Zhang, Y.; Sui, B.; Shen, H.; Ouyang, L. Mapping stocks of soil total nitrogen using remote sensing data: A comparison of random forest models with different predictors. Comput. Electron. Agric. 2019, 160, 23–30. [Google Scholar] [CrossRef]
- Poggio, L.; De Sousa, L.M.; Batjes, N.H.; Heuvelink, G.B.; Kempen, B.; Ribeiro, E.; Rossiter, D. SoilGrids 2.0: Producing soil information for the globe with quantified spatial uncertainty. Soil 2021, 7, 217–240. [Google Scholar] [CrossRef]
- Safanelli, J.L.; Demattê, J.A.; Chabrillat, S.; Poppiel, R.R.; Rizzo, R.; Dotto, A.C.; Silvero, N.E.; Mendes, W.d.S.; Bonfatti, B.R.; Ruiz, L.F. Leveraging the application of Earth observation data for mapping cropland soils in Brazil. Geoderma 2021, 396, 115042. [Google Scholar] [CrossRef]
- Jia, Y.; Jin, S.; Savi, P.; Gao, Y.; Tang, J.; Chen, Y.; Li, W. GNSS-R soil moisture retrieval based on a XGboost machine learning aided method: Performance and validation. Remote Sens. 2019, 11, 1655. [Google Scholar] [CrossRef]
- Wang, Q.; Le Noë, J.; Li, Q.; Lan, T.; Gao, X.; Deng, O.; Li, Y. Incorporating agricultural practices in digital mapping improves prediction of cropland soil organic carbon content: The case of the Tuojiang River Basin. J. Environ. Manag. 2023, 330, 117203. [Google Scholar] [CrossRef] [PubMed]
- Huang, J.; Fan, G.; Liu, C.; Zhou, D. Predicting soil available cadmium by machine learning based on soil properties. J. Hazard. Mater. 2023, 460, 132327. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.; Arrouays, D.; Mulder, V.L.; Poggio, L.; Minasny, B.; Roudier, P.; Libohova, Z.; Lagacherie, P.; Shi, Z.; Hannam, J. Digital mapping of GlobalSoilMap soil properties at a broad scale: A review. Geoderma 2022, 409, 115567. [Google Scholar] [CrossRef]
- Wadoux, A.M.-C.; Minasny, B.; McBratney, A.B. Machine learning for digital soil mapping: Applications, challenges and suggested solutions. Earth-Sci. Rev. 2020, 210, 103359. [Google Scholar] [CrossRef]
- Brungard, C.W.; Boettinger, J.L.; Duniway, M.C.; Wills, S.A.; Edwards, T.C., Jr. Machine learning for predicting soil classes in three semi-arid landscapes. Geoderma 2015, 239, 68–83. [Google Scholar] [CrossRef]
- Chen, S.; Richer-de-Forges, A.C.; Mulder, V.L.; Martelet, G.; Loiseau, T.; Lehmann, S.; Arrouays, D. Digital mapping of the soil thickness of loess deposits over a calcareous bedrock in central France. Catena 2021, 198, 105062. [Google Scholar] [CrossRef]
- Gomes, L.C.; Faria, R.M.; de Souza, E.; Veloso, G.V.; Schaefer, C.E.G.; Fernandes Filho, E.I. Modelling and mapping soil organic carbon stocks in Brazil. Geoderma 2019, 340, 337–350. [Google Scholar] [CrossRef]
- Nussbaum, M.; Spiess, K.; Baltensweiler, A.; Grob, U.; Keller, A.; Greiner, L.; Schaepman, M.E.; Papritz, A. Evaluation of digital soil mapping approaches with large sets of environmental covariates. Soil 2018, 4, 1–22. [Google Scholar] [CrossRef]
- Yang, R.-M.; Liu, L.-A.; Zhang, X.; He, R.-X.; Zhu, C.-M.; Zhang, Z.-Q.; Li, J.-G. The effectiveness of digital soil mapping with temporal variables in modeling soil organic carbon changes. Geoderma 2022, 405, 115407. [Google Scholar] [CrossRef]
- He, X.; Yang, L.; Li, A.; Zhang, L.; Shen, F.; Cai, Y.; Zhou, C. Soil organic carbon prediction using phenological parameters and remote sensing variables generated from Sentinel-2 images. Catena 2021, 205, 105442. [Google Scholar] [CrossRef]
- Luo, C.; Zhang, X.; Wang, Y.; Men, Z.; Liu, H. Regional soil organic matter mapping models based on the optimal time window, feature selection algorithm and Google Earth Engine. Soil Tillage Res. 2022, 219, 105325. [Google Scholar] [CrossRef]
- Bao, S. Soil Agro-Chemistrical Analysis, 3rd ed.; China Agriculture Press: Beijing, China, 2008; pp. 585–586. [Google Scholar]
- Zhu, A.X.; Lu, G.; Liu, J.; Qin, C.Z.; Zhou, C. Spatial prediction based on Third Law of Geography. Ann. GIS 2018, 24, 225–240. [Google Scholar] [CrossRef]
- Ma, Y.; Minasny, B.; Malone, B.P.; Mcbratney, A.B. Pedology and digital soil mapping (DSM). Eur. J. Soil Sci. 2019, 70, 216–235. [Google Scholar] [CrossRef]
- Renard, K.G.; Foster, G.R.; Weesies, G.A.; Mccool, D.K.; Yoder, D.C. Predicting Soil Erosion by Water: A Guide to Conservation Planning with the Revised Universal Soil Loss Equation (RUSLE); US Department of Agriculture, Agricultural Research Service, Agricultural Handbook No. 703; US Government Printing Office: Washington, DC, USA, 1997. [Google Scholar]
- Muñoz-Sabater, J.; Dutra, E.; Agustí-Panareda, A.; Albergel, C.; Arduini, G.; Balsamo, G.; Boussetta, S.; Choulga, M.; Harrigan, S.; Hersbach, H. ERA5-Land: A state-of-the-art global reanalysis dataset for land applications. Earth Syst. Sci. Data 2021, 13, 4349–4383. [Google Scholar] [CrossRef]
- Ekström, M.; Jones, P.; Fowler, H.; Lenderink, G.; Buishand, T.; Conway, D. Regional climate model data used within the SWURVE project–1: Projected changes in seasonal patterns and estimation of PET. Hydrol. Earth Syst. Sci. 2007, 11, 1069–1083. [Google Scholar] [CrossRef]
- Passy, P.; Théry, S. The use of SAGA GIS modules in QGIS. QGIS Generic Tools 2018, 1, 107–149. [Google Scholar]
- Darst, B.F.; Malecki, K.C.; Engelman, C.D. Using recursive feature elimination in random forest to account for correlated variables in high dimensional data. BMC Genet. 2018, 19, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Hounkpatin, K.O.; Bossa, A.Y.; Yira, Y.; Igue, M.A.; Sinsin, B.A. Assessment of the soil fertility status in Benin (West Africa)—Digital soil mapping using machine learning. Geoderma Reg. 2022, 28, e00444. [Google Scholar] [CrossRef]
- Zhang, X.; Chen, S.; Xue, J.; Wang, N.; Xiao, Y.; Chen, Q.; Hong, Y.; Zhou, Y.; Teng, H.; Hu, B. Improving model parsimony and accuracy by modified greedy feature selection in digital soil mapping. Geoderma 2023, 432, 116383. [Google Scholar] [CrossRef]
- Pilnenskiy, N.; Smetannikov, I. Feature selection algorithms as one of the python data analytical tools. Future Internet 2020, 12, 54. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Pelikan, M.; Pelikan, M. Hierarchical Bayesian Optimization Algorithm.; Springer-Verlag: Berlin, German, 2005; pp. 31–48. [Google Scholar]
- Varoquaux, G.; Buitinck, L.; Louppe, G.; Grisel, O.; Pedregosa, F.; Mueller, A. Scikit-learn: Machine learning without learning the machinery. GetMobile Mob. Comput. Commun. 2015, 19, 29–33. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Truong, Q.; Nguyen, M.; Dang, H.; Mei, B. Housing price prediction via improved machine learning techniques. Procedia Comput. Sci. 2020, 174, 433–442. [Google Scholar] [CrossRef]
- Fushiki, T. Estimation of prediction error by using K-fold cross-validation. Stat. Comput. 2011, 21, 137–146. [Google Scholar] [CrossRef]
- Chai, T.; Draxler, R.R. Root mean square error (RMSE) or mean absolute error (MAE). Geosci. Model Dev. Discuss. 2014, 7, 1525–1534. [Google Scholar]
- Nagelkerke, N.J. A note on a general definition of the coefficient of determination. Biometrika 1991, 78, 691–692. [Google Scholar] [CrossRef]
- Zhou, T.; Geng, Y.; Chen, J.; Pan, J.; Haase, D.; Lausch, A. High-resolution digital mapping of soil organic carbon and soil total nitrogen using DEM derivatives, Sentinel-1 and Sentinel-2 data based on machine learning algorithms. Sci. Total Environ. 2020, 729, 138244. [Google Scholar] [CrossRef] [PubMed]
- Xiong, X.; Grunwald, S.; Myers, D.B.; Kim, J.; Harris, W.G.; Comerford, N.B. Holistic environmental soil-landscape modeling of soil organic carbon. Environ. Model. Softw. 2014, 57, 202–215. [Google Scholar] [CrossRef]
- Nguyen, T.; Yu, X.; Zhang, Z.; Liu, M.; Liu, X. Relationship between types of urban forest and PM2.5 capture at three growth stages of leaves. J. Environ. Sci. 2015, 27, 33–41. [Google Scholar] [CrossRef]
- Zhang, X.; Xue, J.; Chen, S.; Wang, N.; Shi, Z.; Huang, Y.; Zhuo, Z. Digital mapping of soil organic carbon with machine learning in dryland of Northeast and North plain China. Remote Sens. 2022, 14, 2504. [Google Scholar] [CrossRef]
- Guo, B.; Lu, M.; Fan, Y.; Wu, H.; Yang, Y.; Wang, C. A novel remote sensing monitoring index of salinization based on three-dimensional feature space model and its application in the Yellow River Delta of China. Geomat. Nat. Hazards Risk 2023, 14, 95–116. [Google Scholar] [CrossRef]
- Bertalan, L.; Holb, I.; Pataki, A.; Négyesi, G.; Szabó, G.; Szalóki, A.K.; Szabó, S. UAV-based multispectral and thermal cameras to predict soil water content—A machine learning approach. Comput. Electron. Agric. 2022, 200, 107262. [Google Scholar] [CrossRef]
- Luo, C.; Zhang, X.; Meng, X.; Zhu, H.; Ni, C.; Chen, M.; Liu, H. Regional mapping of soil organic matter content using multitemporal synthetic Landsat 8 images in Google Earth Engine. Catena 2022, 209, 105842. [Google Scholar] [CrossRef]
- Zhang, M.; Shi, W.; Xu, Z. Systematic comparison of five machine-learning models in classification and interpolation of soil particle size fractions using different transformed data. Hydrol. Earth Syst. Sci. 2020, 24, 2505–2526. [Google Scholar] [CrossRef]
- Wiesmeier, M.; Urbanski, L.; Hobley, E.; Lang, B.; von Lützow, M.; Marin-Spiotta, E.; van Wesemael, B.; Rabot, E.; Ließ, M.; Garcia-Franco, N. Soil organic carbon storage as a key function of soils—A review of drivers and indicators at various scales. Geoderma 2019, 333, 149–162. [Google Scholar] [CrossRef]
- Liu, F.; Rossiter, D.G.; Zhang, G.-L.; Li, D.-C. A soil colour map of China. Geoderma 2020, 379, 114556. [Google Scholar] [CrossRef]
- Mihelič, R.; Pintarič, S.; Eler, K.; Suhadolc, M. Effects of transitioning from conventional to organic farming on soil organic carbon and microbial community: A comparison of long-term non-inversion minimum tillage and conventional tillage. Biol. Fertil. Soils 2024, 1, 1–15. [Google Scholar] [CrossRef]
- Repasch, M.; Scheingross, J.S.; Hovius, N.; Lupker, M.; Wittmann, H.; Haghipour, N.; Gröcke, D.R.; Orfeo, O.; Eglinton, T.I.; Sachse, D. Fluvial organic carbon cycling regulated by sediment transit time and mineral protection. Nat. Geosci. 2021, 14, 842–848. [Google Scholar] [CrossRef]
- Chen, S.; Feng, X.; Lin, Q.; Liu, C.; Cheng, K.; Zhang, X.; Pan, G. Pool complexity and molecular diversity shaped topsoil organic matter accumulation following decadal forest restoration in a karst terrain. Soil Biol. Biochem. 2022, 166, 108553. [Google Scholar] [CrossRef]
- Liu, J.; Cade-Menun, B.J.; Yang, J.; Hu, Y.; Liu, C.W.; Tremblay, J.; LaForge, K.; Schellenberg, M.; Hamel, C.; Bainard, L.D. Long-term land use affects phosphorus speciation and the composition of phosphorus cycling genes in agricultural soils. Front. Microbiol. 2018, 9, 381167. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Liu, T.; Zhao, C.; Shao, M.; Cheng, J. Land use drives the spatial variability of soil phosphorus in the Hexi Corridor, China. Biogeochemistry 2021, 155, 59–75. [Google Scholar] [CrossRef]
- Maharjan, M.; Maranguit, D.; Kuzyakov, Y. Phosphorus fractions in subtropical soils depending on land use. Eur. J. Soil Biol. 2018, 87, 17–24. [Google Scholar] [CrossRef]
- Milly, P.C.; Dunne, K.A. Potential evapotranspiration and continental drying. Nat. Clim. Chang. 2016, 6, 946–949. [Google Scholar] [CrossRef]
- Luo, C.; Wu, Y.; He, Q.; Wang, J.; Bing, H. Increase of temperature exacerbates the conversion of P fractions in organic horizon. Soil Biol. Biochem. 2024, 192, 109368. [Google Scholar] [CrossRef]
- Zhang, X.; Xue, J.; Chen, S.; Wang, N.; Xie, T.; Xiao, Y.; Chen, X.; Shi, Z.; Huang, Y.; Zhuo, Z. Fine Resolution Mapping of Soil Organic Carbon in Croplands with Feature Selection and Machine Learning in Northeast Plain China. Remote Sens. 2023, 15, 5033. [Google Scholar] [CrossRef]




| Type | Covariate | Abbreviation | Scale | Source |
|---|---|---|---|---|
| Soil (8) | Soil bulk density | BD | 30 m | Calculated from sample data |
| Soil pH | pH | 30 m | Calculated from sample data | |
| Sand content | Sand | 250 m | https://www.geodata.cn/ (accessed on 5 November 2023) | |
| Silt content | Silt | 250 m | https://www.geodata.cn/ (accessed on 5 November 2023) | |
| Clay content | Clay | 250 m | https://www.geodata.cn/ (accessed on 5 November 2023) | |
| Soil erosion | SE | 30 m | [30] | |
| Soil moisture | SM | 1000 m | https://data.tpdc.ac.cn/ (accessed on 12 January 2024) | |
| Bare soil index | BSI | 30 m | Extracted from Landsat 8 data | |
| Climate (7) | Maximum temperature | Tmax | 30 m | [31] |
| Mean temperature | Tmean | 30 m | [31] | |
| Minimum temperature | Tmin | 30 m | [31] | |
| Mean wind speed | WIN | 1000 m | https://www.resdc.cn/ (accessed on 1 November 2023) | |
| Mean ground temperature | GST | 1000 m | https://www.resdc.cn/ (accessed on 1 November 2023) | |
| Mean relative humidity | RHU | 1000 m | https://www.resdc.cn/ (accessed on 1 November 2023) | |
| Precipitation | PRE | 30 m | [31] | |
| Remote sensing (3) | Principal component 1 | PCA1 | 30 m | Extracted from Landsat 8 data |
| Principal component 2 | PCA1 | 30 m | Extracted from Landsat 8 data | |
| Principal component 3 | PCA3 | 30 m | Extracted from Landsat 8 data | |
| Organisms (6) | Normalized difference vegetation index | NDVI | 30 m | https://www.nesdc.org.cn/ (accessed on 19 July 2023) |
| Net primary productivity | NPP | 500 m | https://www.geodata.cn/ (accessed on 1 November 2023) | |
| Net ecosystem productivity | NEP | 1000 m | https://www.geodata.cn/ (accessed on 1 November 2023) | |
| Gross primary productivity | GPP | 1000 m | https://www.geodata.cn/ (accessed on 1 November 2023) | |
| Climate production potential | CPP | 30 m | https://geomodeling.njnu.edu.cn/ (accessed on 28 January 2024) | |
| Potential evapotranspiration | PET | 30 m | [32] | |
| Relief (10) | Elevation | DEM | 30 m | http://www.gscloud.cn/ (accessed on 12 January 2024) |
| Slope | SLP | 30 m | Extracted from DEM data | |
| Aspect | APT | 30 m | Extracted from DEM data | |
| Topographic wetness index | TWI | 30 m | Extracted from DEM data | |
| Plan curvature | PLC | 30 m | Extracted from DEM data | |
| Profile curvature | PRC | 30 m | Extracted from DEM data | |
| Topographic position index | TPI | 30 m | Extracted from DEM data | |
| Topographic ruggedness index | TRI | 30 m | Extracted from DEM data | |
| Multiresolution index of ridge top flatness | MRRTF | 30 m | Extracted from DEM data | |
| Multiresolution index of valley bottom flatness | MRVBF | 30 m | Extracted from DEM data | |
| Human activity (6) | Land use | TDLY | 30 m | Third National Land Survey |
| Nighttime light | NL | 500 m | https://www.geodata.cn/ (accessed on 11 January 2024) | |
| Particulate matter 10 | PM10 | 1000 m | https://www.geodata.cn/ (accessed on 11 January 2024) | |
| Particulate matter 2.5 | PM2.5 | 1000 m | https://www.geodata.cn/ (accessed on 11 January 2024) | |
| Population density | PD | 1000 m | https://data.tpdc.ac.cn/ (accessed on 11 January 2024) | |
| Gross domestic product | GDP | km | https://www.geodata.cn/ (accessed on 11 January 2024) |
| Soil Property * | Min | Max | Mean | Standard Deviation | Coefficient of Variation (%) | Skewness | Kurtosis |
|---|---|---|---|---|---|---|---|
| SOC (g·kg−1) | 0.10 | 2.82 | 1.27 | 0.56 | 44.09 | 0.16 | 2.64 |
| STP (mg·kg−1) | 161.00 | 1103.00 | 505.53 | 192.17 | 38.01 | 0.42 | 2.73 |
| SAP (mg·kg−1) | 0.12 | 59.30 | 10.30 | 11.95 | 116.02 | 0.32 | 3.84 |
| Soil Property | Variables before Selection | Variables after Selection | R2 | |
|---|---|---|---|---|
| Number | Type | Number | ||
| SOC | 40 | Soil | 3 | 0.86 |
| Climate | 1 | |||
| Organisms | 2 | |||
| Relief | 1 | |||
| Remote sensing | 2 | |||
| Human activity | 3 | |||
| STP | 40 | Soil | 1 | 0.89 |
| Climate | 1 | |||
| Organisms | 2 | |||
| Relief | 1 | |||
| Remote sensing | 1 | |||
| Human activity | 2 | |||
| SAP | 40 | Organisms | 2 | 0.91 |
| Relief | 1 | |||
| Remote sensing | 1 | |||
| Soil Property | Model * | RMSE | MAE | R2 |
|---|---|---|---|---|
| SOC | RF_all | 0.41 | 0.33 | 0.45 |
| RF_sel | 0.25 | 0.17 | 0.79 | |
| XG_all | 0.44 | 0.36 | 0.37 | |
| XG_sel | 0.22 | 0.12 | 0.84 | |
| STP | RF_all | 171.91 | 136.82 | 0.20 |
| RF_sel | 71.21 | 50.01 | 0.86 | |
| XG_all | 163.76 | 128.10 | 0.27 | |
| XG_sel | 62.67 | 37.86 | 0.89 | |
| SAP | RF_all | 14.22 | 12.85 | 0.27 |
| RF_sel | 6.54 | 3.94 | 0.70 | |
| XG_all | 11.81 | 9.02 | 0.15 | |
| XG_sel | 5.69 | 3.05 | 0.77 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, J.; Liu, J.; Ye, Y.; Jiang, Y.; Lai, Y.; Qin, X.; Zhang, L.; Jiang, Y. Mapping Soil Properties in the Haihun River Sub-Watershed, Yangtze River Basin, China, by Integrating Machine Learning and Variable Selection. Sensors 2024, 24, 3784. https://doi.org/10.3390/s24123784
Huang J, Liu J, Ye Y, Jiang Y, Lai Y, Qin X, Zhang L, Jiang Y. Mapping Soil Properties in the Haihun River Sub-Watershed, Yangtze River Basin, China, by Integrating Machine Learning and Variable Selection. Sensors. 2024; 24(12):3784. https://doi.org/10.3390/s24123784
Chicago/Turabian StyleHuang, Jun, Jia Liu, Yingcong Ye, Yameng Jiang, Yuying Lai, Xianbing Qin, Lin Zhang, and Yefeng Jiang. 2024. "Mapping Soil Properties in the Haihun River Sub-Watershed, Yangtze River Basin, China, by Integrating Machine Learning and Variable Selection" Sensors 24, no. 12: 3784. https://doi.org/10.3390/s24123784
APA StyleHuang, J., Liu, J., Ye, Y., Jiang, Y., Lai, Y., Qin, X., Zhang, L., & Jiang, Y. (2024). Mapping Soil Properties in the Haihun River Sub-Watershed, Yangtze River Basin, China, by Integrating Machine Learning and Variable Selection. Sensors, 24(12), 3784. https://doi.org/10.3390/s24123784








