Review on Phase Synchronization Methods for Spaceborne Multistatic Synthetic Aperture Radar
Abstract
1. Introduction
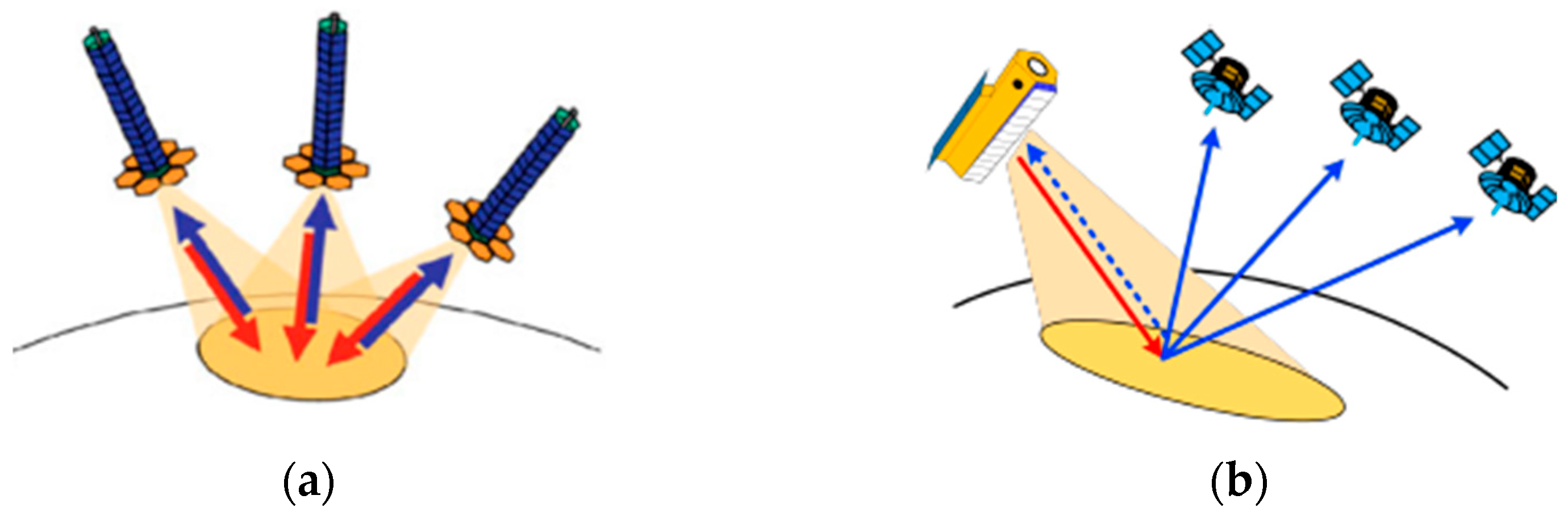
2. Phase Synchronization in Multistatic SAR
3. Phase Synchronization Methods
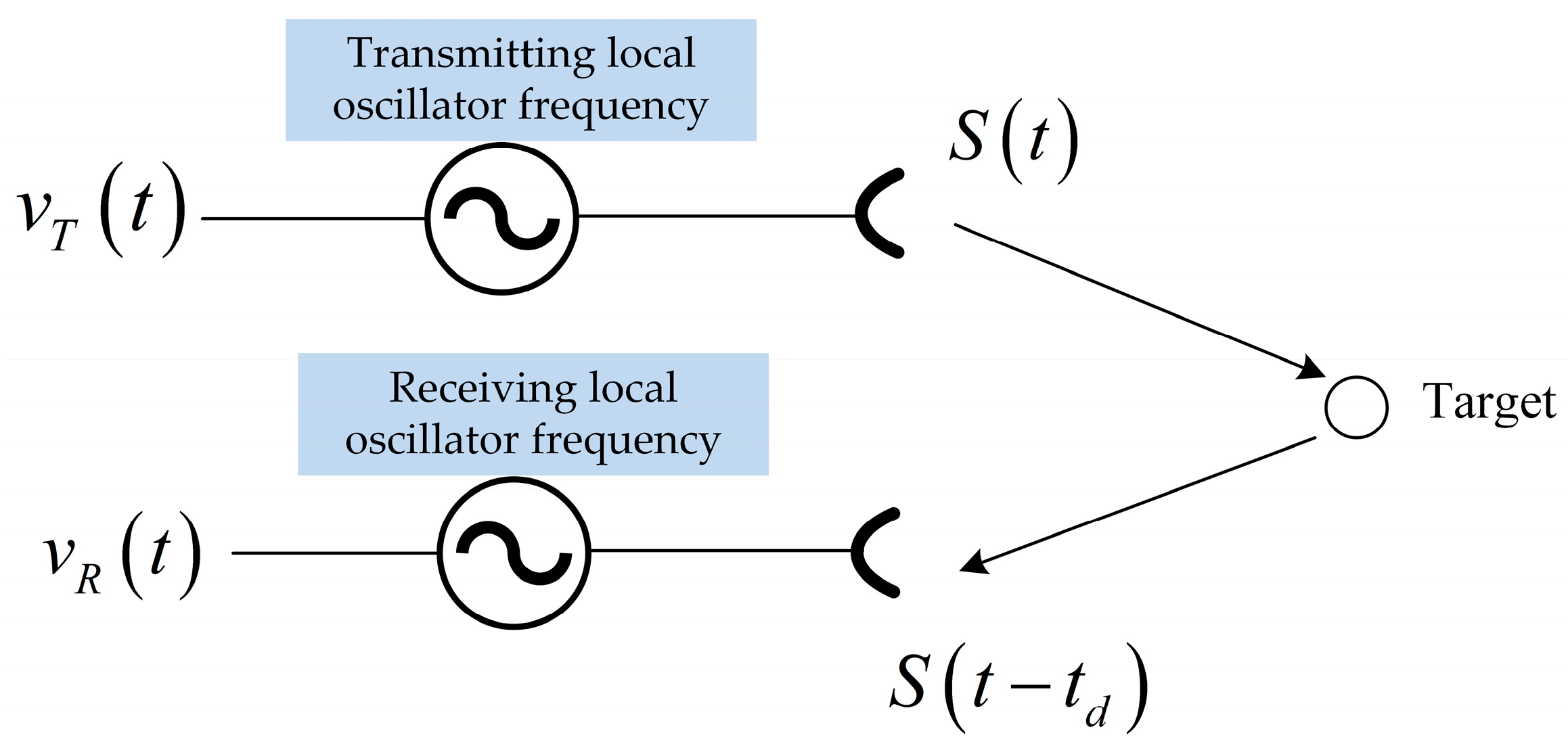
3.1. Synchronization by Direct Microwave Link
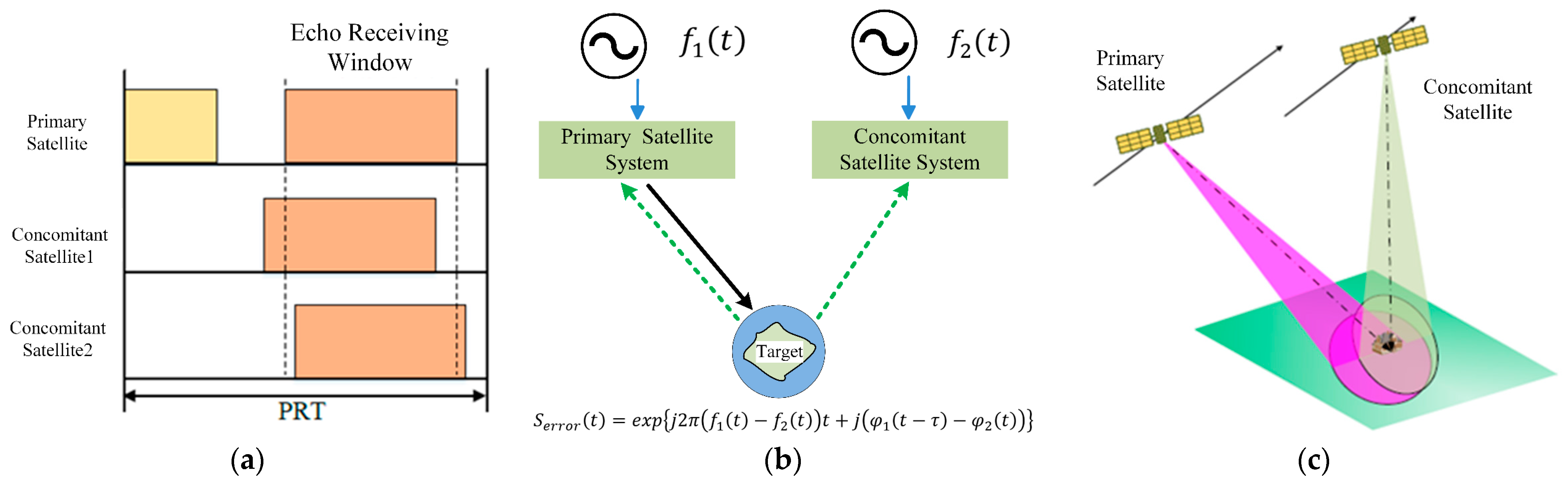
3.2. Synchronization by Data-Based Estimation Algorithm
3.3. Other Phase Synchronization Methods
3.3.1. The Evaluation of Raw Data of the Navigation Receivers
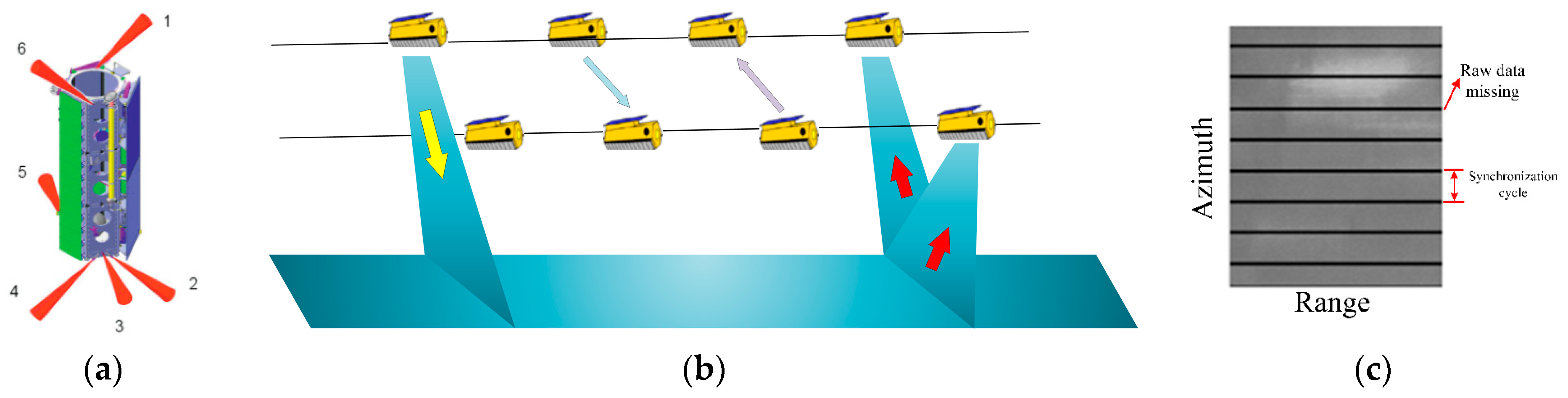
3.3.2. MirrorSAR
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Moreira, A.; Prats-Iraola, P.; Younis, M.; Krieger, G.; Hajnsek, I.; Papathanassiou, K.P. A Tutorial on Synthetic Aperture Radar. IEEE Geosci. Remote Sens. Mag. 2013, 1, 6–43. [Google Scholar] [CrossRef]
- Moccia, A.; Chiacchio, N.; Capone, A. Spaceborne Bistatic Synthetic Aperture Radar for Remote Sensing Applications. Int. J. Remote Sens. 2000, 21, 3395–3414. [Google Scholar] [CrossRef]
- Krieger, G.; Moreira, A.; Fiedler, H.; Hajnsek, I.; Werner, M.; Younis, M.; Zink, M. TanDEM-X: A Satellite Formation for High-Resolution SAR Interferometry. IEEE Trans. Geosci. Remote Sens. 2007, 45, 3317–3341. [Google Scholar] [CrossRef]
- Krieger, G.; Moreira, A. Spaceborne Bi- and Multistatic SAR: Potential and Challenges. IEE Proc.-Radar Sonar Navig. 2006, 153, 184–198. [Google Scholar] [CrossRef]
- Krieger, G.; Hajnsek, I.; Papathanassiou, K.P.; Younis, M.; Moreira, A. Interferometric Synthetic Aperture Radar (SAR) Missions Employing Formation Flying. Proc. IEEE 2010, 98, 816–843. [Google Scholar] [CrossRef]
- Canavan, G.; Thompson, D.; Bekey, I. Distributed Space Systems. In Air and Space Power for the 21st Century; United States Air Force: Washington, DC, USA, 1996. [Google Scholar]
- Winter, J.E.; Anderson, N.C. Distributed Aperture Implementation on the Techsat 21 Satellites. In Proceedings of the 2003 IEEE Aerospace Conference Proceedings, Big Sky, MT, USA, 8–15 March 2003; Volume 2, pp. 815–823. [Google Scholar]
- Massonnet, D. Capabilities and Limitations of the Interferometric Cartwheel. IEEE Trans. Geosci. Remote Sens. 2001, 39, 506–520. [Google Scholar] [CrossRef]
- Massonnet, D. The Interferometric Cartwheel: A Constellation of Passive Satellites to Produce Radar Images to Be Coherently Combined. Int. J. Remote Sens. 2001, 22, 2413–2530. [Google Scholar] [CrossRef]
- Moreira, A.; Krieger, G.; Hajnsek, I.; Hounam, D.; Werner, M.; Riegger, S.; Settelmeyer, E. TanDEM-X: A terraSAR-X Add-on Satellite for Single-Pass SAR Interferometry. In Proceedings of the 2004 IEEE International Geoscience and Remote Sensing Symposium (IGARSS 2004), Anchorage, AK, USA, 20–24 September 2004; Volume 2, pp. 1000–1003. [Google Scholar]
- Lou, L.; Liu, Z. Key Technologies of TH-2 Satellite System. Acta Geod. Cartogr. Sin. 2022, 51, 2403–2416. [Google Scholar] [CrossRef]
- Jin, G.; Liu, K.; Liu, D.; Liang, D.; Zhang, H.; Ou, N.; Zhang, Y.; Deng, Y.; Li, C.; Wang, R. An Advanced Phase Synchronization Scheme for LT-1. IEEE Trans. Geosci. Remote Sens. 2020, 58, 1735–1746. [Google Scholar] [CrossRef]
- Liang, D.; Liu, K.; Zhang, H.; Deng, Y.; Liu, D.; Chen, Y.; Li, C.; Yue, H.; Wang, R. A High-Accuracy Synchronization Phase-Compensation Method Based on Kalman Filter for Bistatic Synthetic Aperture Radar. IEEE Geosci. Remote Sens. Lett. 2020, 17, 1722–1726. [Google Scholar] [CrossRef]
- Jiao, Y.; Liang, D.; Liu, K.; Chen, Y.; Wang, H.; Wang, R. The Synchronization Transceiver Design and Experimental Verification for the LuTan-1 SAR Satellite. Sensors 2020, 20, 1463. [Google Scholar] [CrossRef]
- Moreira, A.; Krieger, G.; Hajnsek, I.; Papathanassiou, K.; Younis, M.; Lopez-Dekker, P.; Huber, S.; Villano, M.; Pardini, M.; Eineder, M.; et al. Tandem-L: A Highly Innovative Bistatic SAR Mission for Global Observation of Dynamic Processes on the Earth’s Surface. IEEE Geosci. Remote Sens. Mag. 2015, 3, 8–23. [Google Scholar] [CrossRef]
- Huber, S.; De Almeida, F.Q.; Villano, M.; Younis, M.; Krieger, G.; Moreira, A. Tandem-L: A Technical Perspective on Future Spaceborne SAR Sensors for Earth Observation. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4792–4807. [Google Scholar] [CrossRef]
- Krieger, G.; Zonno, M.; Rodriguez-Cassola, M.; Lopez-Dekker, P.; Mittermayer, J.; Younis, M.; Huber, S.; Villano, M.; De Almeida, F.Q.; Prats-Iraola, P.; et al. MirrorSAR: A Fractionated Space Radar for Bistatic, Multistatic and High-Resolution Wide-Swath SAR Imaging. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 149–152. [Google Scholar]
- Krieger, G.; Zonno, M.; Mittermayer, J.; Moreira, A.; Huber, S.; Rodriguez-Cassola, M. MirrorSAR: A Fractionated Space Transponder Concept for the Implementation of Low-Cost Multistatic SAR Missions. In Proceedings of the 12th European Conference on Synthetic Aperture Radar (EUSAR 2018), Aachen, Germany, 4–7 June 2018. [Google Scholar]
- Giardino, G.A.; Pasquali, P.; Boncori, J.P.M.; Rosello, J.; Buck, C. Analysis of Bistatic Tomography for SAOCOM-CS and Sentinel-1 CS Missions. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 2480–2482. [Google Scholar]
- Scipal, K.; Davidson, M. The SAOCOM-CS Mission: ESA’s First Bistatic and Tomographic L-Band Mission. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 123–124. [Google Scholar]
- Rott, H.; Lopez-Dekker, P.; Solberg, S.; Ulander, L.; Nagler, T.; Krieger, G.; Prats, P.; Rodriguez, M.; Zonno, M.; Moreira, A. SESAME: A Single-Pass Interferometric SEntinel-1 Companion SAR Mission for Monitoring GEO- and Biosphere Dynamics. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 107–110. [Google Scholar]
- Lopez-Dekker, P.; Rott, H.; Prats-Iraola, P.; Chapron, B.; Scipal, K.; Witte, E.D. Harmony: An Earth Explorer 10 Mission Candidate to Observe Land, Ice, and Ocean Surface Dynamics. In Proceedings of the 2019 IEEE International Geoscience and Remote Sensing Symposium (IGARSS 2019), Yokohama, Japan, 28 July–2 August 2019; pp. 8381–8384. [Google Scholar]
- Shao, Y.F.; Wang, R.; Deng, Y.K.; Liu, Y.; Chen, R.; Liu, G.; Balz, T.; Loffeld, O. Digital Elevation Model Reconstruction in Multichannel Spaceborne/Stationary SAR Interferometry. IEEE Geosci. Remote Sens. Lett. 2014, 11, 2080–2084. [Google Scholar] [CrossRef]
- Wang, R.; Wang, W.; Shao, Y.; Hong, F.; Wang, P.; Deng, Y.; Zhang, Z.; Loffeld, O. First Bistatic Demonstration of Digital Beamforming in Elevation with TerraSAR-X as an Illuminator. IEEE Trans. Geosci. Remote Sens. 2016, 54, 842–849. [Google Scholar] [CrossRef]
- Antoniou, M.; Cherniakov, M. GNSS-Based Bistatic SAR: A Signal Processing View. EURASIP J. Adv. Signal Process. 2013, 2013, 98. [Google Scholar] [CrossRef]
- Santi, F.; Antoniou, M.; Pastina, D. Point Spread Function Analysis for GNSS-Based Multistatic SAR. IEEE Geosci. Remote Sens. Lett. 2015, 12, 304–308. [Google Scholar] [CrossRef]
- Tian, W.; Zhang, T.; Zeng, T.; Hu, C.; Long, T. Space-Surface BiSAR Based on GNSS Signal: Synchronization, Imaging and Experiment Result. In Proceedings of the 2014 IEEE Radar Conference, Cincinnati, OH, USA, 19–23 May 2014; pp. 0512–0516. [Google Scholar]
- Liu, F.; Zhang, L.; Fan, X.; Zhang, T.; Liu, Q. GNSS-Based SAR for Urban Area Imaging: Topology Optimization and Experimental Confirmation. Int. J. Remote Sens. 2019, 40, 4668–4682. [Google Scholar] [CrossRef]
- Younis, M.; Metzig, R.; Krieger, G. Performance Prediction of a Phase Synchronization Link for Bistatic SAR. IEEE Geosci. Remote Sens. Lett. 2006, 3, 429–433. [Google Scholar] [CrossRef]
- Krieger, G.; Cassola, M.R.; Younis, M.; Metzig, R. Impact of Oscillator Noise in Bistatic and Multistatic SAR. In Proceedings of the 2005 IEEE International Geoscience and Remote Sensing Symposium (IGARSS ’05), Seoul, Republic of Korea, 29–29 July 2005; Volume 2, pp. 1043–1046. [Google Scholar]
- Younis, M.; Metzig, R.; Krieger, G.; Bachmann, M.; Klein, R. Performance Prediction and Verification for the Synchronization Link of TanDEM-X. In Proceedings of the 2007 IEEE International Geoscience and Remote Sensing Symposium, Barcelona, Spain, 23–28 July 2007; pp. 5206–5209. [Google Scholar]
- López-Dekker, P.; Mallorquí, J.J.; Serra-Morales, P.; Sanz-Marcos, J. Phase Synchronization and Doppler Centroid Estimation in Fixed Receiver Bistatic SAR Systems. IEEE Trans. Geosci. REMOTE Sens. 2008, 46, 3459–3471. [Google Scholar] [CrossRef]
- Breit, H.; Younis, M.; Balss, U.; Niedermeier, A.; Grigorov, C.; Hueso-Gonzalez, J.; Krieger, G.; Eineder, M.; Fritz, T. Bistatic Synchronization and Processing of TanDEM-X Data. In Proceedings of the 2011 IEEE International Geoscience and Remote Sensing Symposium, Vancouver, BC, Canada, 24–29 July 2011; pp. 2424–2427. [Google Scholar]
- Wang, W.-Q.; Cai, J. Antenna Directing Synchronization for Bistatic Synthetic Aperture Radar Systems. IEEE Antennas Wirel. Propag. Lett. 2010, 9, 307–310. [Google Scholar] [CrossRef]
- Hong, F.; Wang, R.; Zhang, Z.; Lu, P.; Balz, T. Integrated Time and Phase Synchronization Strategy for a Multichannel Spaceborne-Stationary Bistatic SAR System. Remote Sens. 2016, 8, 628. [Google Scholar] [CrossRef]
- Krieger, G.; Younis, M. Impact of Oscillator Noise in Bistatic and Multistatic SAR. IEEE Geosci. Remote Sens. Lett. 2006, 3, 424–428. [Google Scholar] [CrossRef]
- D’Errico, M.; Moccia, A. Attitude and Antenna Pointing Design of Bistatic Radar Formations. IEEE Trans. Aerosp. Electron. Syst. 2003, 39, 949–960. [Google Scholar] [CrossRef]
- Weiss, M. Synchronisation of Bistatic Radar Systems. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS ’04), Anchorage, AK, USA, 20–24 September 2004; Volume 3, pp. 1750–1753. [Google Scholar]
- Eineder, M. Ocillator Clock Drift Compensation in Bistatic Interferometric SAR. In Proceedings of the 2003 IEEE International Geoscience and Remote Sensing Symposium (IGARSS 2003), Toulouse, France, 21–25 July 2003; Volume 3, pp. 1449–1451. [Google Scholar]
- Filho, E.R.S.; Cassola, M.R. Experimental Evaluation of GNSS-Based Frequency Synchronization for SAR Applications. In Proceedings of the 2022 IEEE International Geoscience and Remote Sensing Symposium (IGARSS 2022), Kuala Lumpur, Malaysia, 17–22 July 2022; pp. 7164–7167. [Google Scholar]
- Barnes, J.A.; Chi, A.R.; Cutler, L.S.; Healey, D.J.; Leeson, D.B.; McGunigal, T.E.; Mullen, J.A.; Smith, W.L.; Sydnor, R.L.; Vessot, R.F.C.; et al. Characterization of Frequency Stability. IEEE Trans. Instrum. Meas. 1971, IM–20, 105–120. [Google Scholar] [CrossRef]
- Rutman, J. Characterization of Phase and Frequency Instabilities in Precision Frequency Sources: Fifteen Years of Progress. Proc. IEEE 1978, 66, 1048–1075. [Google Scholar] [CrossRef]
- Schmidt, M.; Schilling, K. Distributed Space Missions for Earth System Monitoring; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Krieger, G.; Zink, M.; Bachmann, M.; Bräutigam, B.; Schulze, D.; Martone, M.; Rizzoli, P.; Steinbrecher, U.; Walter Antony, J.; De Zan, F.; et al. TanDEM-X: A Radar Interferometer with Two Formation-Flying Satellites. Acta Astronaut. 2013, 89, 83–98. [Google Scholar] [CrossRef]
- Brautigam, B.; Gonzalez, J.H.; Schwerdt, M.; Bachmann, M. TerraSAR-X Instrument Calibration Results and Extension for TanDEM-X. IEEE Trans. Geosci. Remote Sens. 2010, 48, 702–715. [Google Scholar] [CrossRef]
- Weigt, M.; Grigorov, C.; Steinbrecher, U.; Schulze, D. TanDEM-X Mission: Long Term in Orbit Synchronisation Link Performance Analysis. In Proceedings of the 10th European Conference on Synthetic Aperture Radar (EUSAR 2014), Berlin, Germany, 3–5 June 2014. [Google Scholar]
- Pinheiro, M.; Rodriguez-Cassola, M.; Prats-Iraola, P.; Krieger, G.; Reigber, A.; Moreira, A. Reconstruction of Missing Data in Interferometric SAR Systems. In Proceedings of the 2013 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Melbourne, Australia, 21–26 July 2013; pp. 2075–2078. [Google Scholar]
- Pinheiro, M.; Rodriguez-Cassola, M.; Prats-Iraola, P.; Reigber, A.; Krieger, G.; Moreira, A. Reconstruction of Coherent Pairs of Synthetic Aperture Radar Data Acquired in Interrupted Mode. IEEE Trans. Geosci. Remote Sens. 2015, 53, 1876–1893. [Google Scholar] [CrossRef]
- Liang, D.; Liu, K.; Yue, H.; Chen, Y.; Deng, Y.; Zhang, H.; Li, C.; Jin, G.; Wang, R. An Advanced Non-Interrupted Synchronization Scheme for Bistatic Synthetic Aperture Radar. In Proceedings of the 2019 IEEE International Geoscience and Remote Sensing Symposium (IGARSS 2019), Yokohama, Japan, 28 July–2 August 2019; pp. 1116–1119. [Google Scholar]
- Liang, D.; Liu, K.; Zhang, H.; Chen, Y.; Yue, H.; Liu, D.; Deng, Y.; Lin, H.; Fang, T.; Li, C.; et al. The Processing Framework and Experimental Verification for the Noninterrupted Synchronization Scheme of LuTan-1. IEEE Trans. Geosci. Remote Sens. 2021, 59, 5740–5750. [Google Scholar] [CrossRef]
- Liang, D.; Zhang, H.; Liu, K.; Wang, R. The Processing Of Synchronization In Bistatic Synthetic Aperture Radar. In Proceedings of the 2020 21st International Radar Symposium (IRS), Warsaw, Poland, 5–8 October 2020; pp. 276–280. [Google Scholar]
- Liang, D.; Liua, K.; Zhang, H.; Liu, D.; Wang, R. An Advanced Non-Interrupted Phase Synchronization Scheme with Internal Calibration for LuTan-1. In Proceedings of the 13th European Conference on Synthetic Aperture Radar (EUSAR 2021), Online, 29 March–1 April 2021; pp. 1–5. [Google Scholar]
- Zhang, Y.; Zhang, H.; Ou, N.; Liu, K.; Liang, D.; Deng, Y.; Wang, R. First Demonstration of Multipath Effects on Phase Synchronization Scheme for LT-1. IEEE Trans. Geosci. Remote Sens. 2020, 58, 2590–2604. [Google Scholar] [CrossRef]
- He, Z.; He, F.; Chen, J.; Huang, H.; Dong, Z.; Liang, D. Echo-Domain Phase Synchronization Algorithm for Bistatic SAR in Alternating Bistatic/Ping–Pong Mode. IEEE Geosci. Remote Sens. Lett. 2012, 9, 604–608. [Google Scholar] [CrossRef]
- He, Z.; He, F.; Chen, J.; Huang, H.; Liang, D. Phase Synchronization Processing Method for Alternating Bistatic Mode in Distributed SAR. J. Syst. Eng. Electron. 2013, 24, 410–416. [Google Scholar] [CrossRef]
- Rodriguez-Cassola, M.; Prats, P.; Lopez-Dekker, P.; Krieger, G.; Moreira, A. General Processing Approach for Bistatic SAR Systems: Description and Performance Analysis. In Proceedings of the 8th European Conference on Synthetic Aperture Radar, Aachen, Germany, 7–10 June 2010; pp. 1–4. [Google Scholar]
- Mancill, C.; Swiger, J. A Map Drift Autofocus Technique for Correcting High Order SAR Phase Error. In Proceedings of the 27th Annual Tri-Service Radar Symposium Record, Monterey, CA, USA, 23–25 June 1981. [Google Scholar]
- Sheen, D.R.; VandenBerg, N.L.; Shackman, S.J.; Wiseman, D.L.; Elenbogen, L.P.; Rawson, R.F. P-3 Ultra-Wideband SAR: Description and Examples. IEEE Aerosp. Electron. Syst. Mag. 1996, 11, 25–30. [Google Scholar] [CrossRef]
- Rosen, P.A.; Hensley, S.; Joughin, I.R.; Li, F.K.; Madsen, S.N.; Rodriguez, E.; Goldstein, R.M. Synthetic Aperture Radar Interferometry. Proc. IEEE 2000, 88, 333–382. [Google Scholar] [CrossRef]
- Wahl, D.E.; Eichel, P.H.; Ghiglia, D.C.; Jakowatz, C.V. Phase Gradient Autofocus-a Robust Tool for High Resolution SAR Phase Correction. IEEE Trans. Aerosp. Electron. Syst. 1994, 30, 827–835. [Google Scholar] [CrossRef]
- Rodriguez-Cassola, M.; Prats-Iraola, P.; López-Dekker, P.; Reigber, A.; Krieger, G.; Moreira, A. Autonomous Time and Phase Calibration of Spaceborne Bistatic SAR Systems. In Proceedings of the 10th European Conference on Synthetic Aperture Radar (EUSAR 2014), Berlin, Germany, 2–6 June 2014. [Google Scholar]
- Prats, P.; Mallorqui, J.J.; Broquetas, A. Calibration of Interferometric Airborne SAR Images Using a Multisquint Processing Approach. In Proceedings of the 2003 IEEE International Geoscience and Remote Sensing Symposium (IGARSS 2003), Toulouse, France, 21–25 July 2003; Volume 7, pp. 4353–4355. [Google Scholar]
- Reigber, A. Correction of Residual Motion Errors in Airborne SAR Interferometry. Electron. Lett. 2001, 37, 1083. [Google Scholar] [CrossRef]
- Prats, P.; Mallorqui, J.J. Estimation of Azimuth Phase Undulations with Multisquint Processing in Airborne Interferometric Sar Images. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1530–1533. [Google Scholar] [CrossRef]
- Prats, P.; Mallorqui, J.J.; Reigber, A.; Broquetas, A. Calibration of Airborne SAR Interferograms Using Multisquint-Processed Image Pairs. In Remote Sensing of Clouds and the Atmosphere VIII: 9–12 September 2003, Barcelona, Spain (Proceedings of Spie); Posa, F., Ed.; SPIE: Barcelona, Spain, 2004; p. 164. [Google Scholar]
- Reigber, A.; Prats, P.; Mallorqui, J.J. Refined Estimation of Time-Varying Baseline Errors in Airborne SAR Interferometry. IEEE Geosci. Remote Sens. Lett. 2006, 3, 145–149. [Google Scholar] [CrossRef]
- Cao, N.; Lee, H.; Zaugg, E.; Shrestha, R.; Carter, W.E.; Glennie, C.; Lu, Z.; Yu, H. Estimation of Residual Motion Errors in Airborne SAR Interferometry Based on Time-Domain Backprojection and Multisquint Techniques. IEEE Trans. Geosci. Remote Sens. 2018, 56, 2397–2407. [Google Scholar] [CrossRef]
- Mendez Dominguez, E.; Meier, E.; Small, D.; Schaepman, M.E.; Bruzzone, L.; Henke, D. A Multisquint Framework for Change Detection in High-Resolution Multitemporal SAR Images. IEEE Trans. Geosci. Remote Sens. 2018, 56, 3611–3623. [Google Scholar] [CrossRef]
- Dominguez, M.; Frioud, M.; Small, D.; Henke, D. Range Adaptive Processing and Multisquint Processing Mode for SAR Image Change Detection. In Proceedings of the 12th European Conference on Synthetic Aperture Radar (EUSAR 2018), Aachen, Germany, 5–7 June 2018; pp. 1–6. [Google Scholar]
- Azcueta, M.; Tebaldini, S. Potential for Absolute Ionosphere and Clock Correction in Noncooperative Bistatic SAR. IEEE Trans. Geosci. Remote Sens. 2020, 58, 363–377. [Google Scholar] [CrossRef]
- Rodriguez-Cassola, M.; Silva Filho, E.R.; Prats, P.; Krieger, G.; Moreira, A. A Robust Data-Based Clock Synchronisation Algorithm for Multi-Channel SAR Systems. In Proceedings of the 2023 IEEE International Geoscience and Remote Sensing Symposium (IGARSS 2023), Pasadena, CA, USA, 16–21 July 2023; pp. 7852–7855. [Google Scholar]
- Cantalloube, H.; Wendler, M.; Giroux, V.; Dubois-Fernandez, P.; Krieger, G. Challenges in SAR Processing for Airborne Bistatic Acquisitions. In Proceedings of the European Conference on Synthetic Aperture Radar (EUSAR), Ulm, Germany, 25–27 May 2004. [Google Scholar]
- Rodriguez-Cassola, M.; Prats, P.; Schulze, D.; Tous-Ramon, N.; Steinbrecher, U.; Marotti, L.; Nannini, M.; Younis, M.; Lopez-Dekker, P.; Zink, M.; et al. First Bistatic Spaceborne SAR Experiments with TanDEM-X. IEEE Geosci. Remote Sens. Lett. 2012, 9, 33–37. [Google Scholar] [CrossRef]
- Rodrigues-Silva, E.; Rodriguez-Cassola, M. Analysis of a POD-Based Approach for Phase and Time Synchronization of Bistatic and Multistatic SAR Systems. In Proceedings of the 13th European Conference on Synthetic Aperture Radar (EUSAR 2021), Online, 29 March–1 April 2021; pp. 1–6. [Google Scholar]
- Mittermayer, J.; Krieger, G.; Bojarski, A.; Zonno, M.; Villano, M.; Pinheiro, M.; Bachmann, M.; Buckreuss, S.; Moreira, A. MirrorSAR: An HRWS Add-On for Single-Pass Multi-Baseline SAR Interferometry. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–18. [Google Scholar] [CrossRef]
- Ustalli, N.; Krieger, G.; Mittermayer, J.; Villano, M.; Waldschmidt, C. MirrorSAR Concept: Phase Synchronization Analysis. In Proceedings of the 2022 Kleinheubach Conference, Miltenberg, Germany, 27–29 September 2022; pp. 1–4. [Google Scholar]
- Ustalli, N.; Villano, M.; Krieger, G.; Mittermayer, J. A Phase Synchronization Technique for Multistatic SAR Systems Based on a Microwave Link. In Proceedings of the 2023 8th Asia-Pacific Conference on Synthetic Aperture Radar (APSAR), Bali Island, Indonesia, 23–27 October 2023; pp. 1–6. [Google Scholar]
- Xiao, P.; Liu, B.; Guo, W. ConGaLSAR: A Constellation of Geostationary and Low Earth Orbit Synthetic Aperture Radar. IEEE Geosci. Remote Sens. Lett. 2020, 17, 2085–2089. [Google Scholar] [CrossRef]




| Synchronization Method | Application in Multistatic SAR | Feasibility | |
|---|---|---|---|
| Direct microwave link | Continuous duplex | Not applied yet | The system hardware for phase synchronization can transmit and receive signals at the same time, and the signals must be sufficiently decoupled. The system design is complex. |
| Pulsed duplex | Not applied yet | The method has the same system hardware and decoupling constraints as continuous duplex. | |
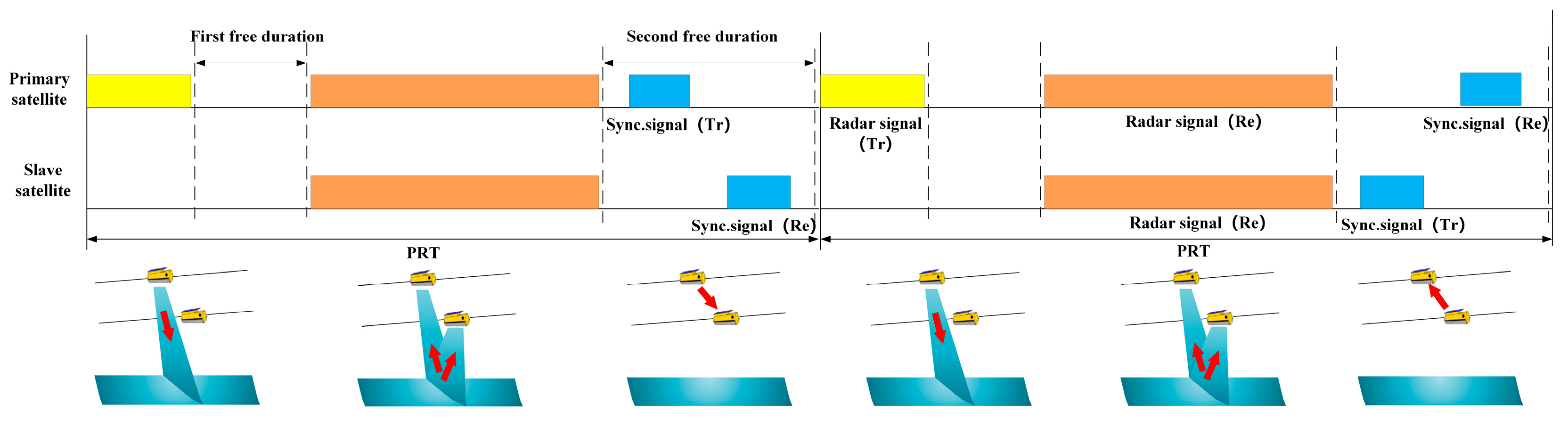
| Pulsed alternate | TandDEM-X, TianHui-2 | The method has been applied in multistatic SAR. In order to transmit synchronization signals, bistatic SAR data acquisition is periodically interrupted, leading to periodic data loss. | |
| Noninterrupted pulsed alternate | LuTan-1 | The method has been applied to the multistatic SAR. The method requires sufficient free time for exchanging synchronization pulses, so PRF design may cause problems in low frequency band multistatic SAR. | |
| Data-based estimation algorithm | Automatic algorithm | TandDEM-X | The quality of the estimate depends on the quality and quantity of available measurements for residual phase errors in the image. |
| Multisquint processing | TandDEM-X | ||
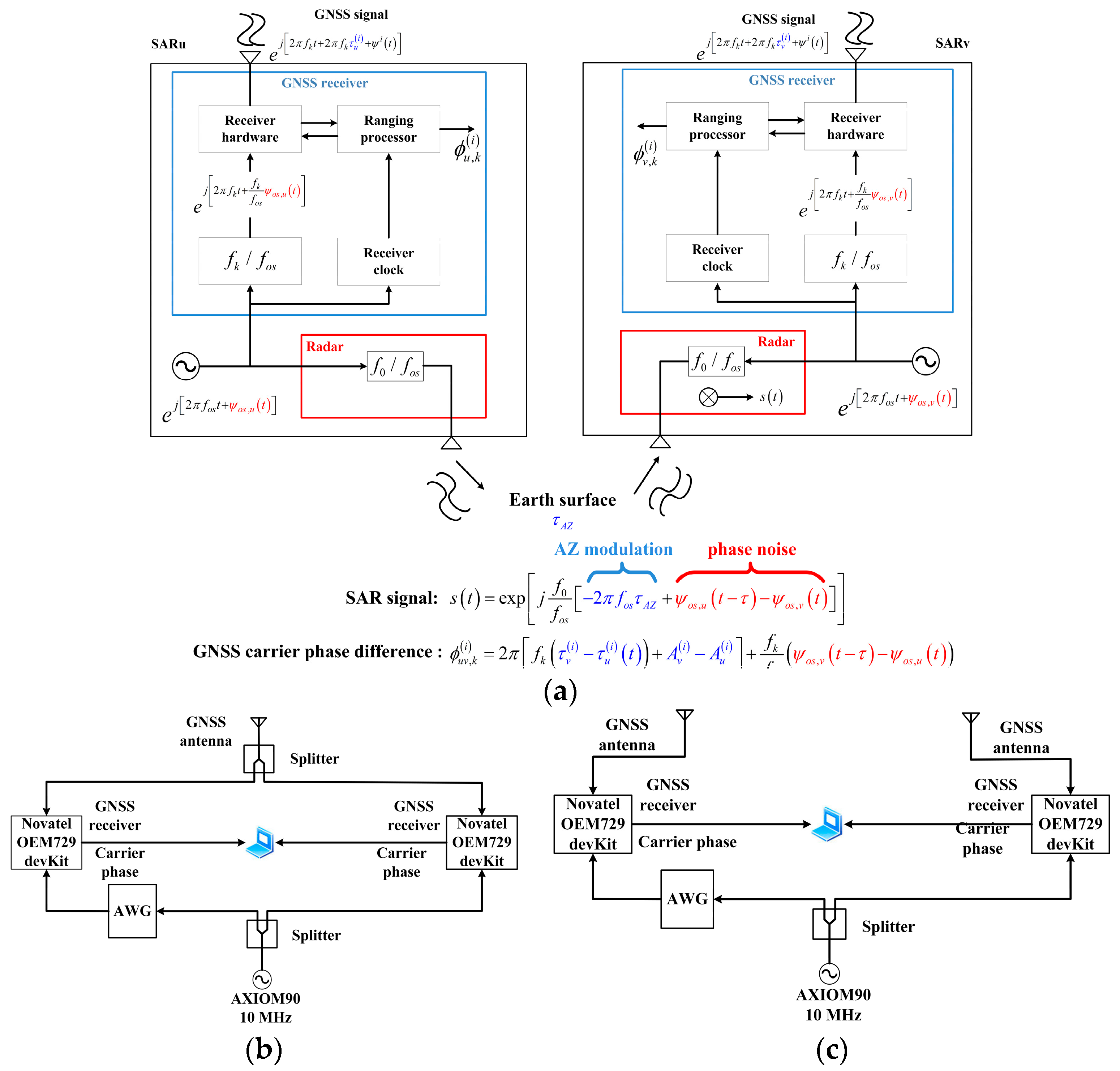
| Evaluation of the raw data from the navigation receivers | GNSS-based phase synchronization | Not applied yet | This method requires accurate relative navigation data, and the GNSS receiver and radar payload share the same oscillator. |
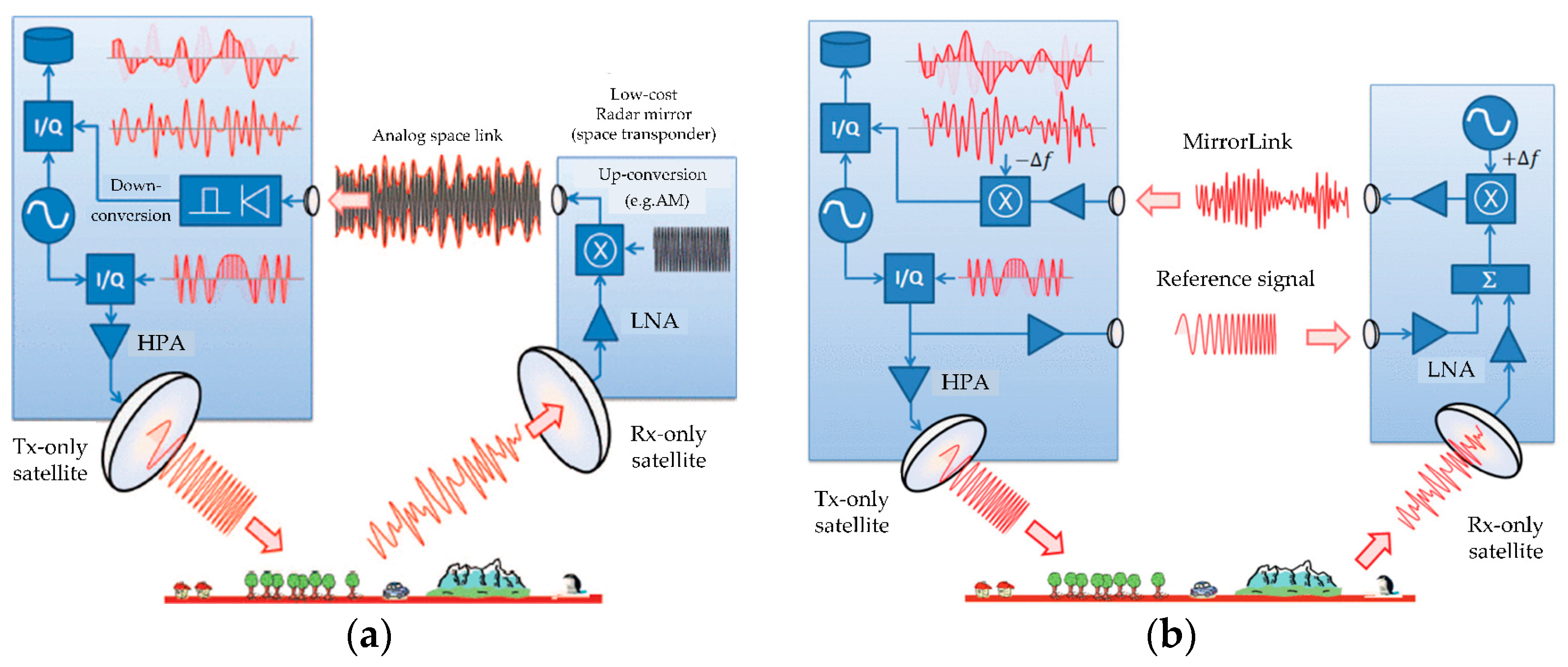
| MirrorSAR | Phase-preserving radar data link | Not applied yet | Radar echoes may be affected by the reference synchronization signal, and the separation of the synchronization signal from the echo signal can be affected by the relative motion between satellites. |
| Double mirror Synchronization | Not applied yet | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, Q.; Li, S.; Yu, W. Review on Phase Synchronization Methods for Spaceborne Multistatic Synthetic Aperture Radar. Sensors 2024, 24, 3122. https://doi.org/10.3390/s24103122
Lin Q, Li S, Yu W. Review on Phase Synchronization Methods for Spaceborne Multistatic Synthetic Aperture Radar. Sensors. 2024; 24(10):3122. https://doi.org/10.3390/s24103122
Chicago/Turabian StyleLin, Qiang, Shiqiang Li, and Weidong Yu. 2024. "Review on Phase Synchronization Methods for Spaceborne Multistatic Synthetic Aperture Radar" Sensors 24, no. 10: 3122. https://doi.org/10.3390/s24103122
APA StyleLin, Q., Li, S., & Yu, W. (2024). Review on Phase Synchronization Methods for Spaceborne Multistatic Synthetic Aperture Radar. Sensors, 24(10), 3122. https://doi.org/10.3390/s24103122






