Abstract
This paper presents a new enhanced coprime array for direction of arrival (DOA) estimation. Coprime arrays are capable of estimating the DOA using coprime properties and outperforming uniform linear arrays. However, the associated algorithms are not directly applicable for estimating the DOA of coherent sources. To overcome this limitation, we propose an enhanced coprime array in this paper. By increasing the number of array sensors in the coprime array, it is feasible to enlarge the aperture of the array and these additional array sensors can be utilized to achieve spatial smoothing, thus enabling estimation of the DOA for coherent sources. Additionally, applying the spatial smoothing technique to the signal subspace, instead of the conventional spatial smoothing method, can further improve the ability to reduce noise interference and enhance the overall estimation result. Finally, DOA estimation is accomplished using the MUSIC algorithm. The simulation results demonstrate improved performance compared to traditional algorithms, confirming its feasibility.
1. Introduction
Extensive research has been conducted on the topic of direction of arrival (DOA) estimation in many array processing areas [1,2,3,4]. Antenna arrays are frequently used in these sectors to receive incoming signals. For instance, DOA estimation that impinges on an array with unknown mutual coupling is important in the area of navigation [5,6]. Scholars have proposed various DOA estimation algorithms using uniform linear arrays (ULAs), such as the ROOT-MUSIC technique [7], propagator method (PM) [8], CAPON [9], multiple signal classification (MUSIC) [10], and estimation of signal parameters via rotational invariance techniques (ESPRIT) [11]. Nevertheless, it is important to recognize that these techniques are predicated on the idea that the signals are independent of one another. Multipath propagation actually contributes to the coherent reception of signals. Because of this coherence, there is a rank deficiency in the covariance matrix of the received signals, which prevents these approaches from accurately estimating the DOA.
To solve the rank deficiency in the covariance matrix of received signals, a lot of approaches have been designed. One such approach is the generalized MUSIC algorithm, introduced in [12]. Another method involves the subspace adaptation technique, as presented in [13]. However, it is important to note that these methods entail multidimensional searching, making them computationally complex and impractical for real-world applications. The spatial smoothing technique [14] has undergone improvements in subsequent research (commonly referred to as MSSP), as documented in [15,16,17]. By combining the covariance matrices of each overlapping subarray, the rank of the covariance matrix is recovered by treating the entire array as a set of overlapping subarrays. Spatial smoothing-based approaches have been widely used and have undergone further enhancements [18,19].
Several alternative approaches have been developed for reconstructing the covariance matrix of coherent signals apart from spatial smoothing. Notably, novel matrix construction methods proposed in [20,21] do not require the signals to be independent. To recover the rank, the Toeplitz matrix construction is presented in [20], whereby the array aperture is sacrificed. On the other hand, ref. [21] presents a non-Toeplitz matrix approach that can manage scenarios involving coherent and incoherent signals. Improved spatial smoothing (ISS) is another noteworthy method that has attracted a lot of interest [22,23]. To improve the effectiveness of DOA estimation, these techniques make use of both the cross-covariance matrix between subarrays and the covariance matrix of each subarray. Additionally, ref. [24] presents an improved spatial smoothing method that is robust to noise and further utilizes information concerning signal subspace.
However, it is crucial to remember that current methods are made for uniform linear arrays (ULAs) and might not work well with sparse arrays, including coprime arrays (CA) [25,26,27] and nested arrays (NA) [28]. Sparse arrays have bigger aperture arrays than ULAs, and the inter-sensor spacing is not limited to half a wavelength. These sparse arrays therefore offer improved performance and create new opportunities for DOA estimation.
The virtual array faces limitations when it comes to processing DOA estimation for coherent sources with sparse arrays, thereby constraining the potential advantages of increased DOA design flexibility. Nevertheless, there are compressed sensing algorithms available for the direct estimation of coherent signals. A sparsity-aware algorithm is presented in [29] for reconstructing the covariance matrix using cyclic rank minimization. The nuclear norm is employed in the construction of the covariance matrix [30], leveraging its positive semi-definite (PSD) structure. A gridless algorithm, utilizing nuclear norm minimization (NNM) for interpolation, is introduced in [31]. Ref. [32] proposes an array interpolation algorithm that utilizes atomic norm minimization (ANM). Sparse Bayesian learning (SBL) [33] provides an efficient method for estimating a sparse signal, which determines the set of DOAs that have non-zero source power from a larger set of potential DOAs. While these algorithms offer high DOA estimation accuracy, it is important to note that they demand a substantial number of sensors and entail relatively high computational complexity.
Although the above compressed sensing algorithms can be directly used for the DOA estimation of coherent sources in sparse arrays, they cannot take full advantage of some characteristics of sparse arrays, such as the ambiguity resolution property of coprime linear arrays, and the performance of DOA estimation needs to be improved. In this paper, an enhanced coprime array is proposed by expanding sensors of the coprime array, combining the enhanced spatial smoothing algorithm and the characteristics of the mutual prime array to eliminate angle ambiguity. The enhanced spatial smoothing is performed on each subarray, and the DOA is estimated using the MUSIC algorithm. Finally, the angle ambiguity is eliminated via the mutual prime characteristics. The computation complexity is lower than compressed sensing algorithms, and the estimation accuracy of DOA is higher than compressed sensing algorithms, which is more suitable for practical application. Specifically, the following succinctly describes our primary contributions:
- We designed an enhanced coprime array with a larger array aperture that can be used to estimate the DOA of coherent sources;
- We utilized an enhanced spatial smoothing technique to effectively smooth the signal subspace rather than directly smoothing the received signal. This technique enhances the capability to resist noise interference and greatly improves the performance of DOA estimation.
- We conducted the performance comparison between the proposed algorithms and classical compressive sensing algorithms for DOA estimation of coherent sources, which demonstrated the superior performance of the proposed algorithms, along with significantly lower computational complexity compared to compressive sensing algorithms.
The remainder of this paper is provided below: Section 2 presents how to design the enhanced coprime array. Section 3 analyzes how the spatial smoothing algorithm and enhanced spatial smoothing algorithm perform the decorrelation step, demonstrating how coprime arrays are utilized to eliminate angle ambiguity. Section 4 analyzes the complexity of the proposed algorithm and the Cramer-Rao Bound (CRB). Section 5 is dedicated to conducting simulation analyses. This paper is concluded in Section 6.
Notations: Lowercase letters , lowercase letters in boldface , uppercase letters in boldface , and letters in blackboard boldface are used to represent scalars, vectors, matrices, and sets, respectively. represents an R-dimensional vector , where is the coordinate. The transpose, complex conjugate, and complex conjugate transpose of are , , and . denotes the trace operator for a matrix. represents the matrix formed by the diagonal elements of the matrix. denotes the entry of .
2. Mathematical Model
The mathematical model of the coprime array is shown in Figure 1, which consists of two sparsely uniform linear arrays (SULAs) with and sensors, respectively, where the inter-sensor spacings are and ( and are coprime, is half a wavelength, ). The reference sensor is the leftmost sensor, and the reference sensors of both SULAs coincide. The location of the array can be denoted as [26]
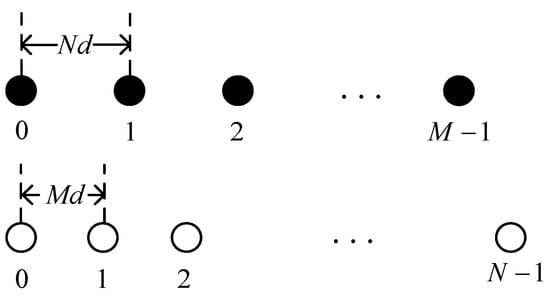
Figure 1.
Coprime array.
In this paper, the enhanced coprime array (Figure 2) is obtained by increasing the number of sensors of each SULA within the coprime array. The number of sensors of the two SULAs is and , respectively. The other settings are consistent with the coprime linear array, and the location of the enhanced coprime array can be written as [27]
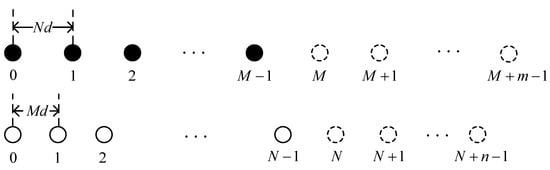
Figure 2.
Enhanced coprime array.
Denote as the th sensor in the enhanced coprime array and .
Given an additive white Gaussian noise model with zero mean for the noise produced by the array upon receiving the signal, far-field narrowband coherent signals, each coming from a different direction, are represented by and impinge on the aforementioned array. We can express the signal received from the array as [1]
where represents the direction matrix of the enhanced coprime array with . stands for the wavelength of the signal. is the waveform of the signal. The vector of the nonzero coherence coefficient is denoted by . Additive white Gaussian noise is known as .
Supposing that the enhanced coprime array receives the signal of snapshots, the model of the received signal can be written as [1]
where the signal waveform vector is denoted by . represents the additive white Gaussian noise.
3. Proposed Algorithm
This section begins by presenting the spatial smoothing technique and the enhanced spatial smoothing technique. It then demonstrates the utilization of the prime characteristic to obtain the DOA without angle ambiguity. Finally, it explores the combination of the aforementioned methods to resolve the DOA of coherent signals received by the enhanced coprime array.
3.1. Spatial Smoothing Technique
The spatial smoothing technique [15] is capable of performing decorrelation processing by reducing the array aperture. By extending the coprime array, the impact of array aperture loss can be minimized. For the th SULA of the extended mutual prime linear array, the received signal model can be expressed as
where and correspond to the direction matrix of the th SULA and the corresponding additive Gaussian white noise, respectively. Spatial smoothing techniques treat this SULA as consisting of multiple overlapping sub-arrays, as shown in Figure 3.

Figure 3.
Spatial smoothing technique.
Denote the direction matrix of the th subarray as . According to the characteristics of the SULA, the relation between the direction matrix of the th subarray and the th subarray can be written as
where , is the sensor spacing of the th SULA. Then, the received signal of the th subarray can be modeled as
where represents the direction matrix of subarray 1, and is the additive Gaussian white noise corresponding to the received signal of the th subarray.
If the received signals are coherent, the rank of the covariance matrix of the received signal will be lower than the number of sources. Consequently, subspace algorithms such as MUSIC will fail to accurately estimate the DOA. To address this issue, we can apply the spatial smoothing technique to the covariance matrix, which restores the rank of the covariance matrix by averaging the covariance matrix of each subarray. The specific formulas of spatial smoothing technique can be modeled by
where . means the average power of the Gaussian white noise. represents the unit matrix.
According to [15], the number of sensors of the subarray needs to be larger than the number of coherent sources; that is, . In the enhanced coprime array proposed in this paper, we can set and choose the smoothing number as . In this case, we can estimate, at most, sources. After that, we can estimate the DOAs in Equation (8) using the MUSIC algorithm.
3.2. Enhanced Spatial Smoothing Technique
The proposed approach in this section is enhanced spatial smoothing [24], which recovers the rank of the covariance matrix by making use of the signal subspace. Taking the example of the SULA with sensors, the corresponding covariance matrix can be modeled as
where . is the direction matrix of , and denotes the corresponding white noise.
By performing eigenvalue decomposition on Equation (9), we derive [20]
where is the maximum eigenvalue of , and denotes the corresponding eigenvector. represents a diagonal matrix including the rest of the smaller eigenvalues, and means the matrix consisting of the corresponding eigenvectors of these eigenvalues.
For [4]:
by applying Equation (11) to Equation (10), we derive
where is the unit matrix and .
Then, can be written as
where .
Denote consecutive elements as
where means the direction matrix. Therefore, we can consider as the sub-array of spatial smoothing. Denote
Regard as the covariance matrix, and the direction matrix is . Performing a similar step as for spatial smoothing leads to
We can expand to obtain
where .
Then the DOA of the coherent signals can be estimated by applying the MUSIC algorithm to Equation (17).
3.3. Eliminating Angle Ambiguity Using Coprime Characteristics
DOA estimation using a SULA can result in angle ambiguity if the sensor spacing exceeds half a wavelength. In such scenarios, when only one source is present, multiple angle estimates for the arrival angles may be generated. To resolve this issue and obtain accurate angle estimates, it is crucial to perform angle ambiguity resolution. When angle ambiguity exists in the SULA, we can obtain [4]
where represents the direction vector corresponding to the actual incident angle , and represents the direction vector corresponding to the ambiguous angle.
Assuming a SULA with a reference sensor located at the origin and its sensors arranged along the positive x-axis, the direction vector can be represented as follows [24]
Then we obtain
where . Denote , and the above equation can be written as
Since the range of incident signal angles is , then we can obtain , which means
By solving the above equation, we obtain
When there is no angle ambiguity (), it corresponds to . When , as indicated by the equation above, has different values. This implies that within the range of , there exist ambiguous angles, including the angle of the original signal of interest. Therefore, when using techniques like MUSIC and peak searching in the spectrum, you will obtain peaks, and it is necessary to discard ambiguous angles.
Assuming that the receiving array is a non-uniform linear array with sensors positioned along the x-axis, and represents the positions of the elements on the x-axis, where is a non-negative integer, then its direction vector can be represented as
The angle ambiguity is
where .
If the array does not have angle ambiguity, we must have
Denote , then over all possible values of , we can obtain
When is prime, its greatest common divisor can only be 1, which means
Equation (28) demonstrates that if the array positions are mutually prime, we can obtain , i.e., . This indicates that there is no issue of angle ambiguity in the estimation of DOA. Consequently, by ensuring that the sensor spacing satisfies the coprime relationships among them, it becomes possible to effectively overcome the problem of angle ambiguity that arises when the sensor spacing exceeds a half-wavelength.
The enhanced coprime array enhanced spatial smoothing MUSIC algorithm (ENSS-MUSIC), as demonstrated in Algorithm 1 of this paper, can be summarized as follows.
| Algorithm 1: Enhanced spatial smoothing MUSIC algorithm |
| Step 1: Calculate the covariance matrix of each SULA according to Equation (4); |
| Step 2: Perform the eigenvalue decomposition of the covariance matrix according to Equation (10); |
| ; |
| Step 4: Calculate the new covariance matrix according to Equations (15) and (16); |
| Step 5: Use the MUSIC algorithm to estimate the DOAs; |
| Step 6: Compare the spectral peaks of subarray1 and subarray2 to find the angle corresponding to the common spectral peak, which is the true angle. |
4. Performance Analysis
4.1. Computation Complexity Analysis
In this section, we undertake a comparison of the complexity of the proposed algorithm, along with several compressive sensing algorithms. This comparison includes the evaluation of algorithms, such as SBL and NNM. The complexity of SS-MUSIC is divided into two parts: SULA 1 and SULA 2. For SULA 1, the covariance matrix is calculated times, and the number of multiplications is . The total number of multiplications using the MUSIC algorithm is , and denotes the number of searches. Similarly, for SULA 2, the total number of multiplications is . Therefore, the computation complexity of SS-MUSIC is
The computation complexity of ENSS-MUSIC is similar to that of SS-MUSIC, which is
The selected algorithms for comparison are compressive sensing algorithms, known for their iterative convergence. Hence, their complexity is dependent on the number of iterations. Determining the appropriate number of iterations based on the desired error introduces complexity in calculating the overall complexity. To assess this, we compared the runtime for various numbers of iterations, as presented in the table. We conducted analyses using 1, 20, 100, and 1000 iterations to evaluate the time required for different iteration counts. See Table 1.

Table 1.
Comparison of runtime of different algorithms.
4.2. Cramer-Rao Bound (CRB)
According to [34], the Cramer-Rao Bound (CRB) matrix can be modeled as
where represents the manifold matrix of the array, , , denotes the average power of signal source, and can be written as
where denotes steering vector.
4.3. The Advantages of the Proposed Array and Algorithm
We propose an enhanced coprime array for the DOA estimation of coherent signals. Our design offers several advantages:
- By employing enhanced spatial smoothing techniques, the DOA can be estimated using subspace-based algorithms like MUSIC accurately. The enhanced coprime array can estimate coherent signals at most;
- The enhanced spatial smoothing technique effectively utilizes all the signal subspace, leading to improved accuracy in DOA estimation and enhanced resistance to noise interference;
- The designed enhanced spatial smoothing MUSIC algorithm offers lower computational complexity compared with the compressed sensing algorithm. Additionally, it provides higher DOA estimation accuracy, improving its suitability for real-world applications.
5. Simulation Results
In this study, we have carefully chosen several widely recognized compressive sensing algorithms, including SBL and NNM. These algorithms were thoroughly evaluated and compared to our own proposed algorithm, with a detailed analysis of their respective performances. For this evaluation, the parameters of the proposed array are fixed as , , . In this setup, two far-field narrowband coherent signals impinge on the proposed array from angles of 9.55° and 25.15°. To quantify the accuracy of the direction of arrival (DOA) estimates, we defined the root mean square error (RMSE) as
where and stand for the total number of coherent sources and Monte Carlo trials, respectively. The estimate of the actual angle is denoted by . We have as the number of Monte Carlo simulations in the following simulations.
In Figure 4, we present a comparison of the spectral peak outcomes obtained from the MUSIC algorithm after applying enhanced spatial smoothing to the two subarrays. The SNR is set as 10 dB, and the number of snapshots is set as 500. Evidently, only the peaks aligning with the true DOA of the coherent signals are observed, consistent with our previous analysis. Figure 5 illustrates a scatter plot of the DOA estimation results across 100 iterations. The SNR is set as 0 dB and the number of snapshots is set as 500. It is apparent that the estimation results consistently form a straight line with minimal variability, suggesting that the proposed algorithm yields highly stable DOA estimates for coherent sources.
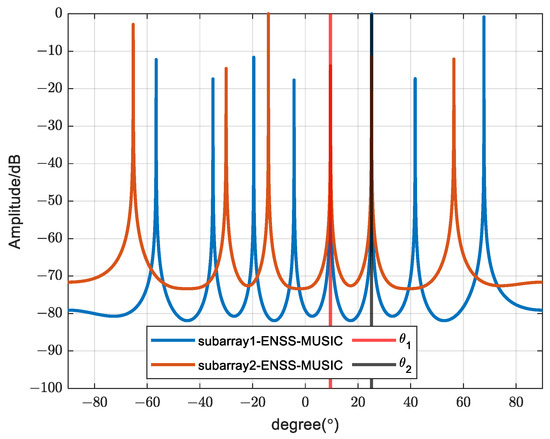
Figure 4.
Spectrum peak comparison of different subarrays.
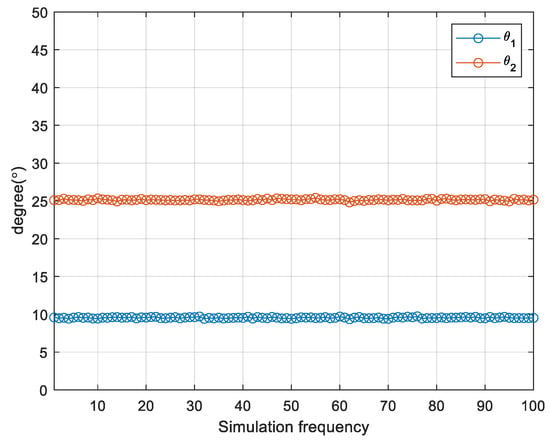
Figure 5.
Scatter plot of DOA estimation results for 100 iterations.
A comparison of the RMSE curves for the various algorithms, with differing SNRs, is shown in Figure 6. The simulation was conducted using 200 snapshots. Notably, the proposed algorithm outperforms other algorithms even under low SNR conditions. This superiority can be attributed to the effective utilization of an enhanced spatial smoothing technique, which incorporates information from the signal subspace, resulting in improved performance. As a result, the performance of the enhanced spatial smoothing technique surpasses that of the spatial smoothing technique. In Figure 7, we evaluate the RMSE of different algorithms with a varying number of snapshots while maintaining an SNR of 5 dB. It is evident that the RMSE of the proposed algorithm is smaller compared to that of other algorithms, indicating a lower estimation error and superior performance.
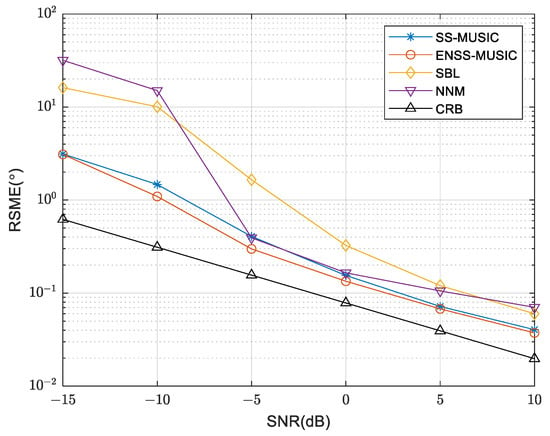
Figure 6.
RMSE comparison of various methods using different SNRs.
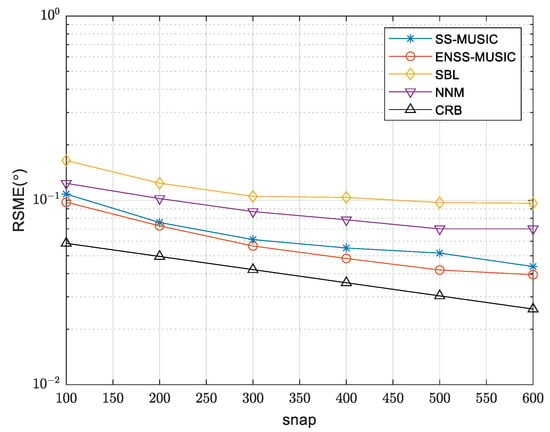
Figure 7.
RMSE comparison of various methods with different numbers of snapshots.
The curves of RMSE are compared in Figure 8 as the SNR varies for different numbers of array sensors. The simulation settings remain unchanged, except for the variation in the number of sensors. It is evident that as the SNR increases, the RMSE consistently decreases, indicating enhanced DOA estimation performance. Furthermore, increasing the number of array sensors also leads to a decrease in RMSE, suggesting that the performance of the proposed algorithm is enhanced by increasing the number of sensors.
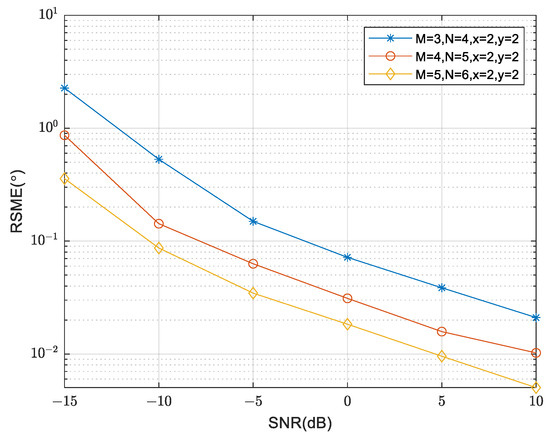
Figure 8.
Comparison of RMSE under different numbers of array sensors.
The curves of RMSE are compared in Figure 9, as the SNR varies for different numbers of sources. The array parameter is fixed at , , , . It is evident that as the number of sources increases, there is a consistent rise in RMSE, implying a decrease in DOA estimation performance. Conversely, an improvement in SNR results in a decrease in RMSE, indicating an enhanced DOA estimation performance.
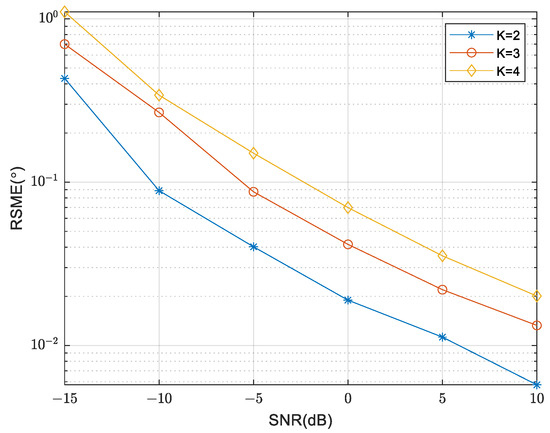
Figure 9.
Comparison of RMSE under different numbers of sources.
6. Conclusions
This paper introduces a novel enhanced coprime array designed for the DOA estimation of coherent signals. Additionally, it presents the DOA estimation algorithm tailored specifically for this array. The algorithm incorporates advanced spatial smoothing techniques to effectively handle coherent signals and exploit the signal subspace of received signals, resulting in enhanced DOA estimation performance and noise robustness. The complexity analysis of the proposed algorithm has been demonstrated to be lower than that of the compressed sensing algorithm. Numerous simulation experiments have been conducted to confirm that the proposed array effectively achieves the estimation of DOA for coherent sources. Furthermore, the performance of the proposed algorithm surpasses that of both the spatial smoothing MUSIC algorithm and the compressed sensing algorithm.
Author Contributions
Methodology, X.H.; Software, X.Z.; Formal analysis, X.H. and X.Z.; Writing—original draft, X.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Gu, Y.; Goodman, N.A.; Hong, S.; Li, Y. Robust adaptive beamforming based on interference covariance matrix sparse reconstruction. Signal Process. 2014, 96, 375–381. [Google Scholar] [CrossRef]
- Johnson, D.H.; Dudgeon, D.E. Array Signal Processing: Concepts and Techniques; Prentice Hall: Hoboken, NJ, USA, 1993. [Google Scholar]
- Cadzow, J.A.; Kim, Y.S.; Shiue, D.C. General direction-of-arrival estimation: A signal subspace approach. IEEE Trans. Aerosp. Electron. Syst. 1989, 25, 31–47. [Google Scholar] [CrossRef]
- Krim, H.; Viberg, M. Two decades of array signal processing research: The parametric approach. IEEE Signal Process. Mag. 1996, 13, 67–94. [Google Scholar] [CrossRef]
- Famoriji, O.J.; Shongwe, T. Deep Learning Approach to Source Localization of Electromagnetic Waves in the Presence of Various Sources and Noise. Symmetry 2023, 15, 1534. [Google Scholar] [CrossRef]
- Famoriji, O.J.; Shongwe, T. Spherical atomic norm-inspired approach for direction-of-arrival estimation of EM waves impinging on spherical antenna array with undefined mutual coupling. Appl. Sci. 2023, 13, 3067. [Google Scholar] [CrossRef]
- Auger, F.; Flandrin, P. Improving the readability of time-frequency and time-scale representations by the reassignment method. IEEE Trans. Signal Process. 1995, 43, 1068–1089. [Google Scholar] [CrossRef]
- Marcos, S.; Marsal, A.; Benidir, M. The propagator method for source bearing estimation. Signal Process. 1995, 42, 121–138. [Google Scholar] [CrossRef]
- Stoica, P.; Wang, Z.; Li, J. Robust capon beamforming. In Proceedings of the Thirty-Sixth Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 3–6 November 2002; Volume 1, pp. 876–880. [Google Scholar]
- Schmidt, R. Multiple emitter location and signal parameter estimation. IEEE Trans. Antennas Propag. 1986, 34, 276–280. [Google Scholar] [CrossRef]
- Roy, R.; Kailath, T. ESPRIT-estimation of signal parameters via rotational invariance techniques. IEEE Trans. Acoust. Speech Signal Process. 1989, 37, 984–995. [Google Scholar] [CrossRef]
- Zoltowski, M.; Haber, F. A vector space approach to direction finding in a coherent multipath environment. IEEE Trans. Antennas Propag. 1986, 34, 1069–1079. [Google Scholar] [CrossRef]
- Viberg, M.; Ottersten, B. Sensor array processing based on subspace fitting. IEEE Trans. Signal Process. 1991, 39, 1110–1121. [Google Scholar] [CrossRef]
- Armstrong, C.V.W.; Ahmed, H.M.; Brans, N.A.; Fathi, E. An adaptive multimicroprocessor array computing structure for radar signal processing applications. In Proceedings of the 6th Annual Symposium on Computer Architecture, New York, NY, USA, 23–25 April 1979; pp. 68–74. [Google Scholar]
- Shan, T.J.; Wax, M.; Kailath, T. On spatial smoothing for direction-of-arrival estimation of coherent signals. IEEE Trans. Acoust. Speech Signal Process. 1985, 33, 806–811. [Google Scholar] [CrossRef]
- Pillai, S.U.; Kwon, B.H. Forward/backward spatial smoothing techniques for coherent signal identification. IEEE Trans. Acoust. Speech Signal Process. 1989, 37, 8–15. [Google Scholar] [CrossRef]
- Ge, F.X.; Shen, D.; Peng, Y.; Li, V.O. Super-resolution time delay estimation in multipath environments. IEEE Trans. Circuits Syst. I: Regul. Pap. 2007, 54, 1977–1986. [Google Scholar] [CrossRef]
- Williams, R.T.; Prasad, S.; Mahalanabis, A.K.; Sibul, L.H. An improved spatial smoothing technique for bearing estimation in a multipath environment. IEEE Trans. Acoust. Speech Signal Process. 1988, 36, 425–432. [Google Scholar] [CrossRef]
- Mestre, X.; Lagunas, M.Á. Modified subspace algorithms for DoA estimation with large arrays. IEEE Trans. Signal Process. 2008, 56, 598–614. [Google Scholar] [CrossRef]
- Han, F.M.; Zhang, X.D. An ESPRIT-like algorithm for coherent DOA estimation. IEEE Antennas Wirel. Propag. Lett. 2005, 4, 443–446. [Google Scholar]
- Wang, N.; Agathoklis, P.; Antoniou, A. A new DOA estimation technique based on subarray beamforming. IEEE Trans. Signal Process. 2006, 54, 3279–3290. [Google Scholar] [CrossRef]
- Chen, Y.M. On spatial smoothing for two-dimensional direction-of-arrival estimation of coherent signals. IEEE Trans. Signal Process. 1997, 45, 1689–1696. [Google Scholar] [CrossRef]
- Wang, B.-H.; Wang, Y.-L.; Chen, H. Weighted spatial smoothing for direction-of-arrival estimation of coherent signals. In Proceedings of the IEEE Antennas and Propagation Society International Symposium, San Antonio, TX, USA, 16–21 June 2002; Volume 2, pp. 668–671. [Google Scholar]
- Pan, J.; Sun, M.; Wang, Y.; Zhang, X. An enhanced spatial smoothing technique with ESPRIT algorithm for direction of arrival estimation in coherent scenarios. IEEE Trans. Signal Process. 2020, 68, 3635–3643. [Google Scholar] [CrossRef]
- Vaidyanathan, P.P.; Pal, P. Sparse sensing with co-prime samplers and arrays. IEEE Trans. Signal Process. 2010, 59, 573–586. [Google Scholar] [CrossRef]
- Qin, S.; Zhang, Y.D.; Amin, M.G. Generalized Coprime Array Configurations for Direction-of-Arrival Estimation. IEEE Trans. Signal Process. 2015, 63, 1377–1390. [Google Scholar] [CrossRef]
- Zheng, W.; Zhang, X.; Wang, Y.; Zhou, M.; Wu, Q. Extended Coprime Array Configuration Generating Large-Scale Antenna Co-Array in Massive MIMO System. IEEE Trans. Veh. Technol. 2019, 68, 7841–7853. [Google Scholar] [CrossRef]
- Pal, P.; Vaidyanathan, P.P. Nested arrays: A novel approach to array processing with enhanced degrees of freedom. IEEE Trans. Signal Process. 2010, 58, 4167–4181. [Google Scholar] [CrossRef]
- Liu, S.; Mao, Z.; Zhang, Y.D.; Huang, Y. Rank minimization-based Toeplitz reconstruction for DoA estimation using coprime array. IEEE Commun. Lett. 2021, 25, 2265–2269. [Google Scholar] [CrossRef]
- Qiao, H.; Pal, P. Unified analysis of co-array interpolation for direction-of-arrival estimation. In Proceedings of the 2017 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), New Orleans, LA, USA, 5–9 March 2017; pp. 3056–3060. [Google Scholar]
- Zhou, C.; Gu, Y.; Shi, Z.; Zhang, Y.D. Off-grid direction-of-arrival estimation using coprime array interpolation. IEEE Signal Process. Lett. 2018, 25, 1710–1714. [Google Scholar] [CrossRef]
- Zhou, C.; Gu, Y.; Fan, X.; Shi, Z.; Mao, G.; Zhang, Y.D. Direction-of-arrival estimation for coprime array via virtual array interpolation. IEEE Trans. Signal Process. 2018, 66, 5956–5971. [Google Scholar] [CrossRef]
- Gerstoft, P.; Mecklenbräuker, C.F.; Xenaki, A.; Nannuru, S. Multisnapshot sparse Bayesian learning for DOA. IEEE Signal Process. Lett. 2016, 23, 1469–1473. [Google Scholar] [CrossRef]
- Lai, X.; Chen, W.; Li, B.; Zeng, H. Improved DFT method for DOA estimation with enhanced coprime array: Based on large difference coarray. Int. J. Electron. 2022, 109, 733–747. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).