Multimodal Early Birth Weight Prediction Using Multiple Kernel Learning
Abstract
:1. Introduction
State of the Art
2. Materials and Methods
2.1. Data Description and Analysis
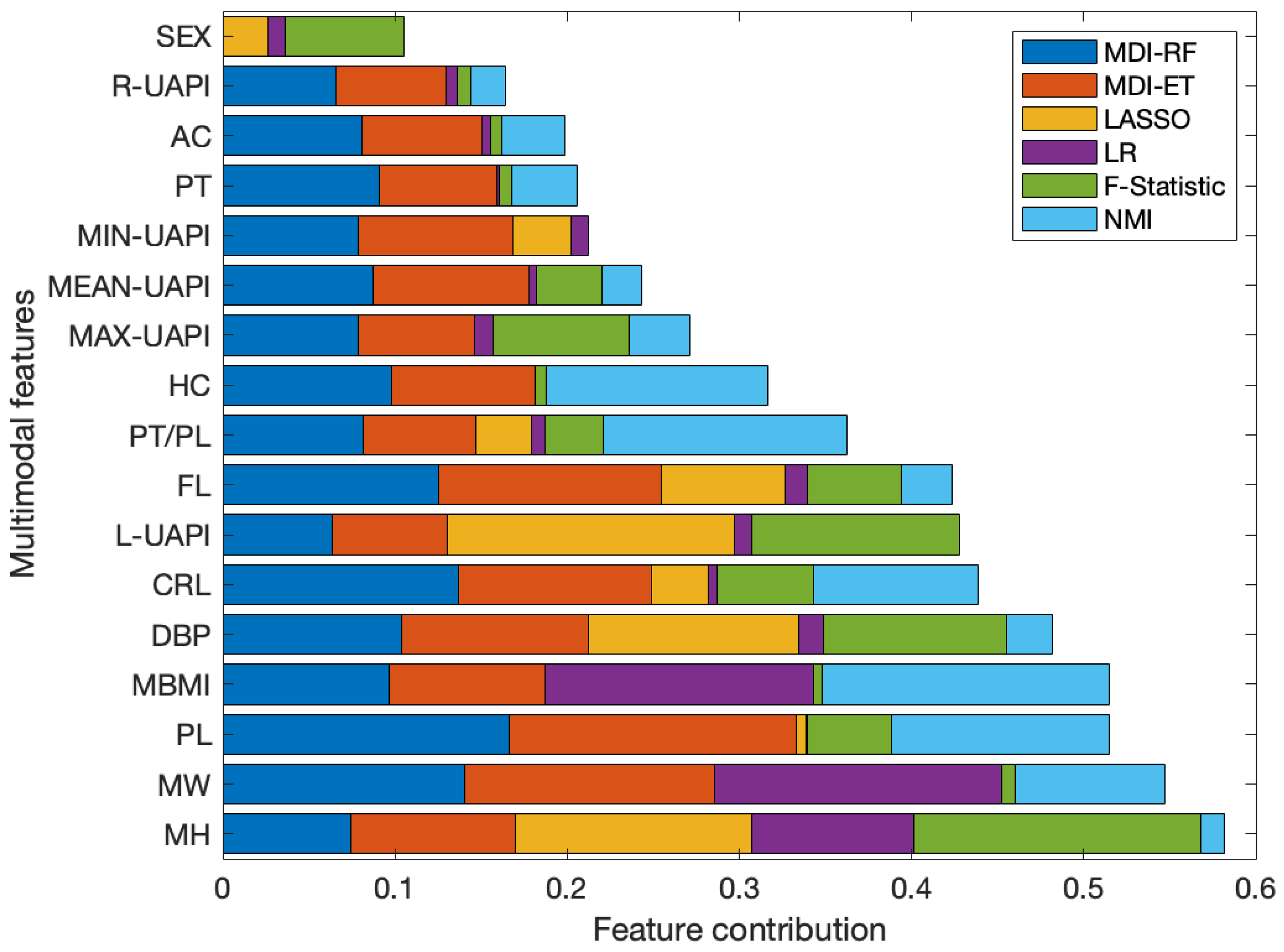
2.2. Ensemble Feature Selection
- Normalized Mutual Information (NMI): is a measure used to assess the similarity between two sets of data, considering the joint and individual information of each set [27]. For this work, the NMI metric is utilized to measure the descriptive capability of each feature versus the BW in a univariate approach.
- F-Statistic: is a statistical measure used to determine the significance of a regression model. It assesses whether at least one of the independent variables in the model has a significant impact on the dependent variable [28].
- Least Absolute Shrinkage and Selection Operator (LASSO): is a linear model with restrictions that allows for variable selection, given that after an iterative selection of the alpha parameter, the weights associated with non-relevant variables become exactly zero [29].
- Multiple Linear Regression (LR): is an algorithm that fits a linear model to minimize the quadratic error between multiple independent variables and the outcome variable [30]. Upon the assumption that all input variables are scaled to the same intervals, the absolute values of the weights derived from the LR model may be interpreted as indicators of the relative importance of each variable.
- Mean Decrease in Impurity (MDI): is a feature selection algorithm, based on an ensemble of decision trees. This algorithm quantifies the importance of individual variables within the regression model process, employing mean squared error as the criterion for impurity assessment [31]. In the computation of MDI, two variants were contemplated: Random Forest (MDI-RF) and Extra Trees (MDI-ET), each comprising 500 estimators and utilizing the conventional impurity criterion.
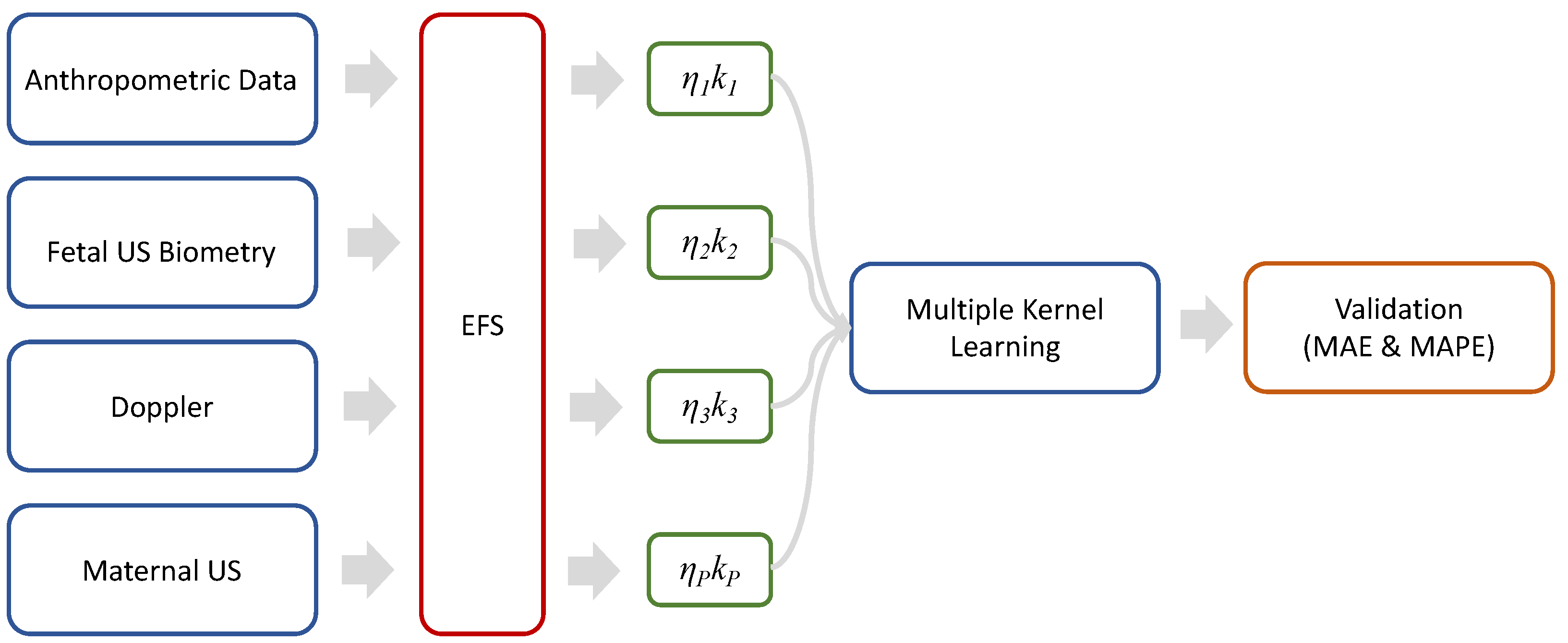
2.3. Multiple Kernel Learning
2.4. Validation
- Random Forest Regressor (RF): is a supervised algorithm based on the ensemble of decision trees [39]. For its implementation, the number of estimators, the criterion (mean squared error, mean absolute error, Friedman squared error or Poisson criterion) and the tree’s depth were optimized.
- Artificial Neuronal Network (ANN): is an algorithm based on multi-layer perceptrons [40]. For this model, the activation function (identity, logistic, tanh or ReLU), the solver (LBFGS, SGD or Adam), the L2 regularization term, batch size, learning rate and the number of neurons in the hidden layers were optimized.
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gjessing, H.K.; Grøttum, P.; Økland, I.; Eik-Nes, S.H. Fetal size monitoring and birth-weight prediction: A new population-based approach. Ultrasound Obstet. Gynecol. 2017, 49, 500–507. [Google Scholar] [CrossRef] [PubMed]
- Barker, D. Adult Consequences of Fetal Growth Restriction. Clin. Obstet. Gynecol. 2006, 49, 270–283. [Google Scholar] [CrossRef] [PubMed]
- World Health Organization. Newborns: Improving Survival and Well-Being. 2020. Available online: https://www.who.int/news-room/fact-sheets/detail/newborns-reducing-mortality (accessed on 19 May 2023).
- Kurmanavicius, J.; Burkhardt, T.; Wisser, J.; Huch, R. Ultrasonographic fetal weight estimation: Accuracy of formulas and accuracy of examiners by birth weight from 500 to 5000 g. J. Perinat. Med. 2004, 32, 155–161. [Google Scholar] [CrossRef] [PubMed]
- Esinler, D.; Bircan, O.; Esin, S.; Sahin, E.G.; Kandemir, O.; Yalvac, S. Finding the Best Formula to Predict the Fetal Weight: Comparison of 18 Formulas. Gynecol. Obstet. Investig. 2015, 80, 78–84. [Google Scholar] [CrossRef] [PubMed]
- Desiani, A.; Primartha, R.; Arhami, M.; Orsalan, O. Naive Bayes classifier for infant weight prediction of hypertension mother. J. Phys. Conf. Ser. 2019, 1282, 012005. [Google Scholar] [CrossRef]
- Faruk, A.; Cahyono, E.S. Prediction and Classification of Low Birth Weight Data Using Machine Learning Techniques. Indones. J. Sci. Technol. 2018, 3, 18. [Google Scholar] [CrossRef]
- Moreira, M.W.L.; Rodrigues, J.J.P.C.; Furtado, V.; Mavromoustakis, C.X.; Kumar, N.; Woungang, I. Fetal Birth Weight Estimation in High-Risk Pregnancies Through Machine Learning Techniques. In Proceedings of the ICC 2019-2019 IEEE International Conference on Communications (ICC), Shanghai, China, 20–24 May 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Jezewski, M.; Czabanski, R.; Roj, D.; Wrobel, J.; Jezewski, J. Application of RBF Neural Networks for Predicting Low Birth Weight Using Features Extracted from Fetal Monitoring Signals. In Proceedings of the World Congress on Medical Physics and Biomedical Engineering, Munich, Germany, 7–12 September 2009; Dössel, O., Schlegel, W.C., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 374–377. [Google Scholar]
- Feng, M.; Wan, L.; Li, Z.; Qing, L.; Qi, X. Fetal Weight Estimation via Ultrasound Using Machine Learning. IEEE Access 2019, 7, 87783–87791. [Google Scholar] [CrossRef]
- Khan, W.; Zaki, N.; Masud, M.M.; Ahmad, A.; Ali, L.; Ali, N.; Ahmed, L.A. Infant birth weight estimation and low birth weight classification in United Arab Emirates using machine learning algorithms. Sci. Rep. 2022, 12, 12110. [Google Scholar] [CrossRef]
- Alzubaidi, M.; Agus, M.; Shah, U.; Makhlouf, M.; Alyafei, K.; Househ, M. Ensemble Transfer Learning for Fetal Head Analysis: From Segmentation to Gestational Age and Weight Prediction. Diagnostics 2022, 12, 2229. [Google Scholar] [CrossRef]
- Tao, J.; Yuan, Z.; Sun, L.; Yu, K.; Zhang, Z. Fetal birthweight prediction with measured data by a temporal machine learning method. BMC Med. Inform. Decis. Mak. 2021, 21, 26. [Google Scholar] [CrossRef]
- Lu, Y.; Fu, X.; Chen, F.; Wong, K.K. Prediction of fetal weight at varying gestational age in the absence of ultrasound examination using ensemble learning. Artif. Intell. Med. 2020, 102, 101748. [Google Scholar] [CrossRef] [PubMed]
- Płotka, S.; Grzeszczyk, M.K.; Brawura-Biskupski-Samaha, R.; Gutaj, P.; Lipa, M.; Trzciński, T.; Sitek, A. BabyNet: Residual Transformer Module for Birth Weight Prediction on Fetal Ultrasound Video. In Proceedings of the Medical Image Computing and Computer Assisted Intervention–MICCAI 2022, Singapore, 18–22 September 2022; Springer: Cham, Switzerland, 2022; pp. 350–359. [Google Scholar]
- Płotka, S.; Grzeszczyk, M.K.; Brawura-Biskupski-Samaha, R.; Gutaj, P.; Lipa, M.; Trzciński, T.; Išgum, I.; Sánchez, C.I.; Sitek, A. BabyNet++: Fetal birth weight prediction using biometry multimodal data acquired less than 24 h before delivery. Comput. Biol. Med. 2023, 167, 107602. [Google Scholar] [CrossRef] [PubMed]
- Sereno, F.; Marques de Sa, P.; Matos, A.; Bernardes, J. Support vector regression applied to foetal weight estimation. In Proceedings of the IJCNN’01, International Joint Conference on Neural Networks, Washington, DC, USA, 15–19 July 2001; Volume 2, pp. 1455–1458. [Google Scholar] [CrossRef]
- Yu, J.H.; Wang, Y.Y.; Chen, P.; Song, Y.H. Ultrasound Estimation of Fetal Weight with Fuzzy Support Vector Regression. In Proceedings of the Advances in Neural Networks–ISNN 2007, Nanjing, China, 3–7 June 2007; Liu, D., Fei, S., Hou, Z., Zhang, H., Sun, C., Eds.; Springer: Berlin/Heidelberg, Germany, 2007; pp. 426–433. [Google Scholar]
- Yu, J.; Wang, Y.; Chen, P. Fetal Weight Estimation Using the Evolutionary Fuzzy Support Vector Regression for Low-Birth-Weight Fetuses. IEEE Trans. Inf. Technol. Biomed. 2009, 13, 57–66. [Google Scholar] [CrossRef] [PubMed]
- Trujillo, O.C.; Perez-Gonzalez, J.; Medina-Bañuelos, V. Early Prediction of Weight at Birth Using Support Vector Regression. In IFMBE Proceedings; Springer: Berlin/Heidelberg, Germany, 2019; pp. 37–41. [Google Scholar] [CrossRef]
- Hoque, N.; Singh, M.; Bhattacharyya, D.K. EFS-MI: An ensemble feature selection method for classification. Complex Intell. Syst. 2018, 4, 105–118. [Google Scholar] [CrossRef]
- Mera-Gaona, M.; López, D.M.; Vargas-Canas, R.; Neumann, U. Framework for the Ensemble of Feature Selection Methods. Appl. Sci. 2021, 11, 8122. [Google Scholar] [CrossRef]
- Bolón-Canedo, V.; Alonso-Betanzos, A. Ensembles for feature selection: A review and future trends. Inf. Fusion 2019, 52, 1–12. [Google Scholar] [CrossRef]
- Li, X.; Chen, X.; Rezaeipanah, A. Automatic breast cancer diagnosis based on hybrid dimensionality reduction technique and ensemble classification. J. Cancer Res. Clin. Oncol. 2023, 149, 7609–7627. [Google Scholar] [CrossRef] [PubMed]
- Hameed, Z.; Rehman, W.U.; Khan, W.; Ullah, N.; Albogamy, F.R. Weighted Hybrid Feature Reduction Embedded with Ensemble Learning for Speech Data of Parkinson’s Disease. Mathematics 2021, 9, 3172. [Google Scholar] [CrossRef]
- Kaluri, R.; Kar, B.; Sarkar, B.K. A Hybrid Feature Reduction Approach for Medical Decision Support System. Math. Probl. Eng. 2022, 2022, 3984082. [Google Scholar] [CrossRef]
- Ross, B.C. Mutual Information between Discrete and Continuous Data Sets. PLoS ONE 2014, 9, e87357. [Google Scholar] [CrossRef]
- Peng, G.; Nourani, M.; Harvey, J.; Dave, H. Feature Selection Using F-statistic Values for EEG Signal Analysis. In Proceedings of the 2020 42nd Annual International Conference of the IEEE Engineering in Medicine & Biology Society (EMBC), Montreal, QC, Canada, 20–24 July 2020; pp. 5963–5966. [Google Scholar] [CrossRef]
- Muthukrishnan, R.; Rohini, R. LASSO: A feature selection technique in predictive modeling for machine learning. In Proceedings of the 2016 IEEE International Conference on Advances in Computer Applications (ICACA), Coimbatore, India, 24 October 2016; pp. 18–20. [Google Scholar] [CrossRef]
- Abid Hasan, M.; Hasan, M.K.; Abdul Mottalib, M. Linear regression-based feature selection for microarray data classification. Int. J. Data Min. Bioinform. 2015, 11, 167–179. [Google Scholar] [CrossRef] [PubMed]
- Nembrini, S.; König, I.R.; Wright, M.N. The revival of the Gini importance? Bioinformatics 2018, 34, 3711–3718. [Google Scholar] [CrossRef] [PubMed]
- Sonnenburg, S.; Rätsch, G.; Schäfer, C.; Schölkopf, B. Large Scale Multiple Kernel Learning. J. Mach. Learn. Res. 2006, 7, 1531–1565. [Google Scholar]
- Gupta, Y.; Kim, J.I.; Kim, B.C.; Kwon, G.R. Classification and Graphical Analysis of Alzheimer’s Disease and Its Prodromal Stage Using Multimodal Features From Structural, Diffusion, and Functional Neuroimaging Data and the APOE Genotype. Front. Aging Neurosci. 2020, 12, 238. [Google Scholar] [CrossRef] [PubMed]
- Wilson, C.M.; Li, K.; Yu, X.; Kuan, P.F.; Wang, X. Multiple-kernel learning for genomic data mining and prediction. BMC Bioinform. 2019, 20, 426. [Google Scholar] [CrossRef] [PubMed]
- Shi, J.; Liu, X.; Li, Y.; Zhang, Q.; Li, Y.; Ying, S. Multi-channel EEG-based sleep stage classification with joint collaborative representation and multiple kernel learning. J. Neurosci. Methods 2015, 254, 94–101. [Google Scholar] [CrossRef]
- Vapnik, V.; Golowich, S.; Smola, A. Support Vector Method for Function Approximation, Regression Estimation and Signal Processing. In Advances in Neural Information Processing Systems; Mozer, M., Jordan, M., Petsche, T., Eds.; MIT Press: Cambridge, MA, USA, 1996; Volume 9. [Google Scholar]
- Genton, M.G. Classes of Kernels for Machine Learning: A Statistics Perspective. J. Mach. Learn. Res. 2002, 2, 299–312. [Google Scholar]
- Martínez Acevedo, M.G.; Sánchez Paz, J.; Pérez Gonzélez, J. Aprendizaje Computacional Para La Estimación Automática Del Peso Al Nacimiento Usando Variables Multimodales Materno-Fetales. Mem. Congr. Nac. Ing. Bioméd. 2021, 8, 61–64. [Google Scholar]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Glorot, X.; Bengio, Y. Understanding the difficulty of training deep feedforward neural networks. In Proceedings of the Thirteenth International Conference on Artificial Intelligence and Statistics, Chia Laguna Resort, Sardinia, Italy, 13–15 May 2010; Teh, Y.W., Titterington, M., Eds.; Proceedings of Machine Learning Research: Albion, NY, USA, 2010; Volume 9, pp. 249–256. [Google Scholar]
- Lauriola, I.; Aiolli, F. MKLpy: A python-based framework for Multiple Kernel Learning. arXiv 2020, arXiv:2007.09982. [Google Scholar]

| Feature | Statistical Description |
|---|---|
| Anthropometric data | |
| Maternal Height (MH) | 155.60 ± 5.96 cm |
| Maternal Weight (MW) | 63.67 ± 11.05 kg |
| Maternal Body Mass Index (MBMI) | 26.28 ± 4.22 kg/m2 |
| Sex | 284/294 (F/M) |
| Fetal US Biometry | |
| Crown–Rump Length (CRL) | 66.72 ± 9.91 mm |
| Biparietal Diameter (BPD) | 21.34 ± 5.90 mm |
| Head Circumference (HC) | 75.10 ± 16.62 mm |
| Femur Length (FL) | 13.27 ± 16.86 mm |
| Abdominal Circumference (AC) | 64.78 ± 12.16 mm |
| Doppler | |
| Right Uterine Artery Pulsatility Index (R-UAPI) | 1.51 ± 0.70 |
| Left Uterine Artery Pulsatility Index (L-UAPI) | 1.61 ± 0.92 |
| Minimum Uterine Artery Pulsatility Index (MIN-UAPI) | 1.26 ± 0.52 |
| Maximum Uterine Artery Pulsatility Index (MAX-UAPI) | 1.86 ± 0.95 |
| Mean Uterine Artery Pulsatility Index (MEAN-UAPI) | 1.56 ± 0.65 |
| Maternal US | |
| Placental Thickness (PT) | 2.05 ± 1.09 |
| Placental Length (PL) | 7.37 ± 1.72 |
| Placental Thickness/Length Ratio (PT/PL) | 4.15 ± 1.48 |
| Target | |
| Birth Weight (BW) | 2868.95 ± 333.68 g |
| Regressor | Anthropometric Data | Fetal US Biometry | Doppler | Maternal US | ||||
|---|---|---|---|---|---|---|---|---|
| MAE (g) | MAPE (%) | MAE (g) | MAPE (%) | MAE (g) | MAPE (%) | MAE (g) | MAPE (%) | |
| MKL | 264.1 ± 23 | 9.81 ± 0.9 | 262.4 ± 19 | 9.54 ± 0.9 | 338.7 ± 20 | 11.26 ± 0.9 | 264.5 ± 21 | 9.81 ± 0.8 |
| RF | 262.4 ± 20 | 9.57 ± 0.9 | 265.7 ± 16 | 9.66 ± 0.8 | 340.1 ± 23 | 11.32 ± 0.9 | 270.4 ± 24 | 9.83 ± 0.8 |
| SVR | 263.1 ± 22 | 9.78 ± 0.9 | 264.1 ± 21 | 9.80 ± 0.9 | 332.2 ± 21 | 11.06 ± 0.9 | 264.1 ± 22 | 9.80 ± 0.9 |
| ANN | 305.1 ± 24 | 11.14 ± 1.3 | 347.3 ± 25 | 12.43 ± 1.0 | 398.2 ± 23 | 13.27 ± 1.3 | 327.5 ± 25 | 11.71 ± 1.0 |
| Regressor | Anthropometric Data | Feta US Biometry | Doppler | Maternal US | ||||
|---|---|---|---|---|---|---|---|---|
| MAE (g) | MAPE (%) | MAE (g) | MAPE (%) | MAE (g) | MAPE (%) | MAE (g) | MAPE (%) | |
| MKL | 286.5 | 10.32 | 283.7 | 10.25 | 352.7 | 12.19 | 292.4 | 10.40 |
| RF | 297.1 | 10.60 | 295.9 | 12.11 | 367.7 | 12.72 | 292.1 | 10.39 |
| SVR | 285.4 | 10.31 | 285.3 | 10.31 | 350.4 | 12.13 | 293.7 | 10.45 |
| ANN | 314.7 | 11.42 | 361.5 | 12.63 | 402.4 | 13.92 | 350.9 | 12.39 |
| Regressor | All Features | Automatic Feature Selection by EFS | ||
|---|---|---|---|---|
| MAE (g) | MAPE (%) | MAE (g) | MAPE (%) | |
| MKL | 255.3 ± 20 | 9.31 ± 0.4 | 233.4 ± 18 | 8.48 ± 0.7 |
| RF | 264.7 ± 21 | 9.65 ± 0.8 | 256.4 ± 21 | 9.54 ± 0.9 |
| SVR | 261.3 ± 22 | 9.52 ± 1.1 | 242.9 ± 19 | 8.84 ± 0.8 |
| ANN | 262.8 ± 20 | 9.58 ± 0.9 | 258.4 ± 20 | 9.39 ± 0.7 |
| Regressor | All Features | Automatic Feature Selection by ESF | ||
|---|---|---|---|---|
| MAE (g) | MAPE (%) | MAE (g) | MAPE (%) | |
| MKL | 265.4 | 9.59 | 234.7 | 8.32 |
| RF | 276.7 | 9.99 | 245.7 | 8.73 |
| SVR | 272.3 | 9.84 | 250.2 | 8.89 |
| ANN | 280.1 | 10.11 | 242.3 | 8.62 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Camargo-Marín, L.; Guzmán-Huerta, M.; Piña-Ramirez, O.; Perez-Gonzalez, J. Multimodal Early Birth Weight Prediction Using Multiple Kernel Learning. Sensors 2024, 24, 2. https://doi.org/10.3390/s24010002
Camargo-Marín L, Guzmán-Huerta M, Piña-Ramirez O, Perez-Gonzalez J. Multimodal Early Birth Weight Prediction Using Multiple Kernel Learning. Sensors. 2024; 24(1):2. https://doi.org/10.3390/s24010002
Chicago/Turabian StyleCamargo-Marín, Lisbeth, Mario Guzmán-Huerta, Omar Piña-Ramirez, and Jorge Perez-Gonzalez. 2024. "Multimodal Early Birth Weight Prediction Using Multiple Kernel Learning" Sensors 24, no. 1: 2. https://doi.org/10.3390/s24010002
APA StyleCamargo-Marín, L., Guzmán-Huerta, M., Piña-Ramirez, O., & Perez-Gonzalez, J. (2024). Multimodal Early Birth Weight Prediction Using Multiple Kernel Learning. Sensors, 24(1), 2. https://doi.org/10.3390/s24010002







