Design of a High Q-Factor Label-Free Optical Biosensor Based on a Photonic Crystal Coupled Cavity Waveguide
Abstract
:1. Introduction
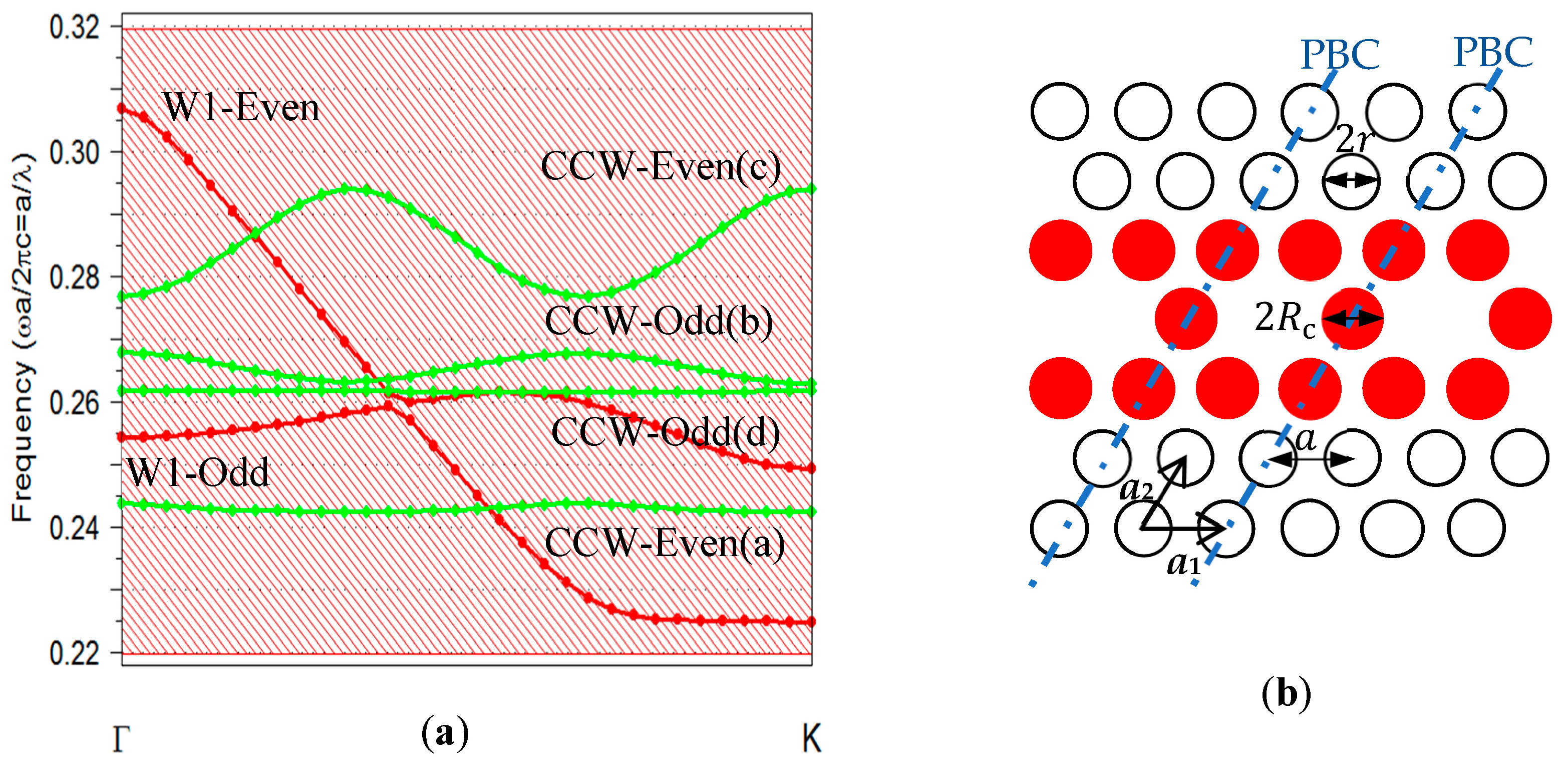
2. Photonic Crystal and Coupled Cavity Waveguide Structure
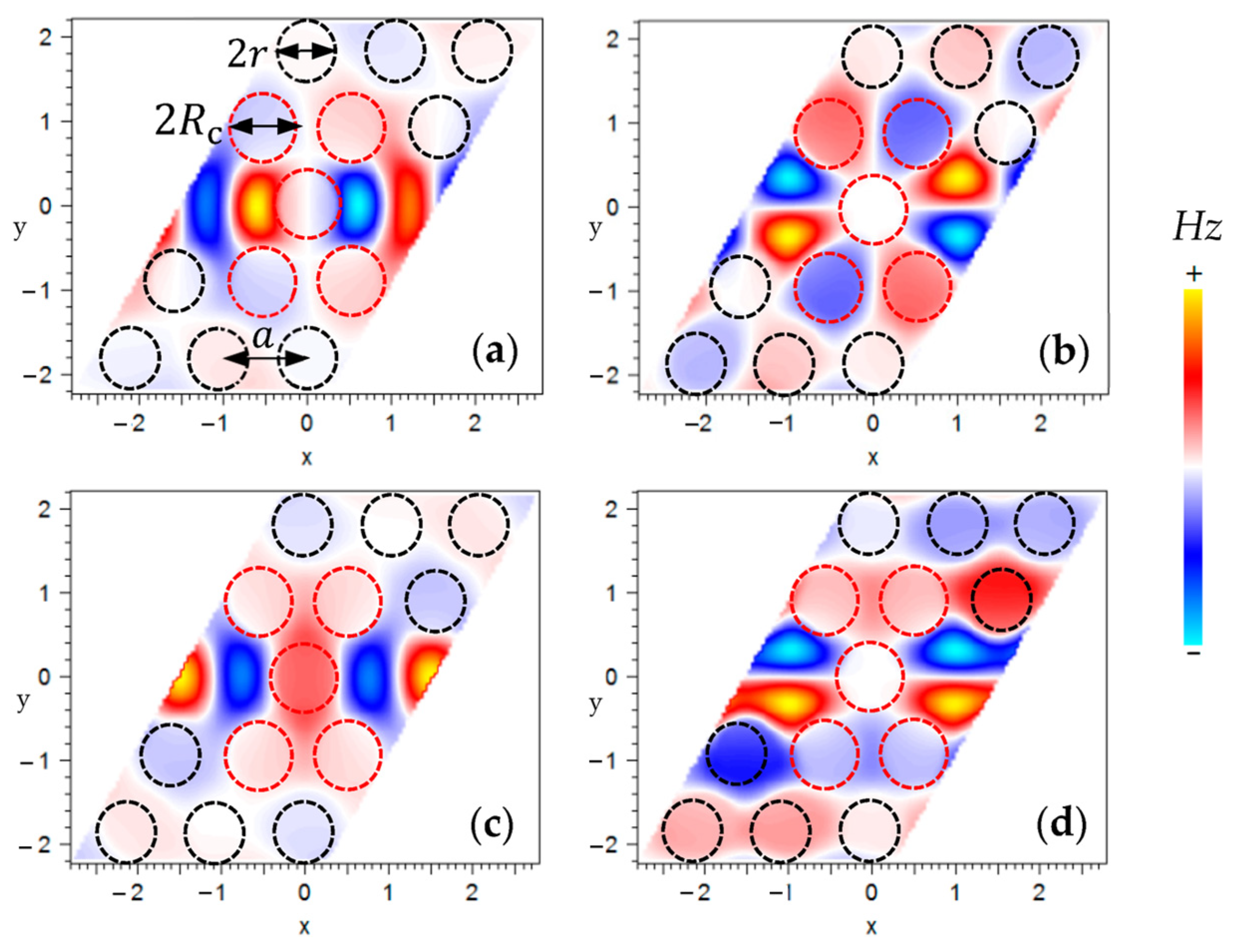
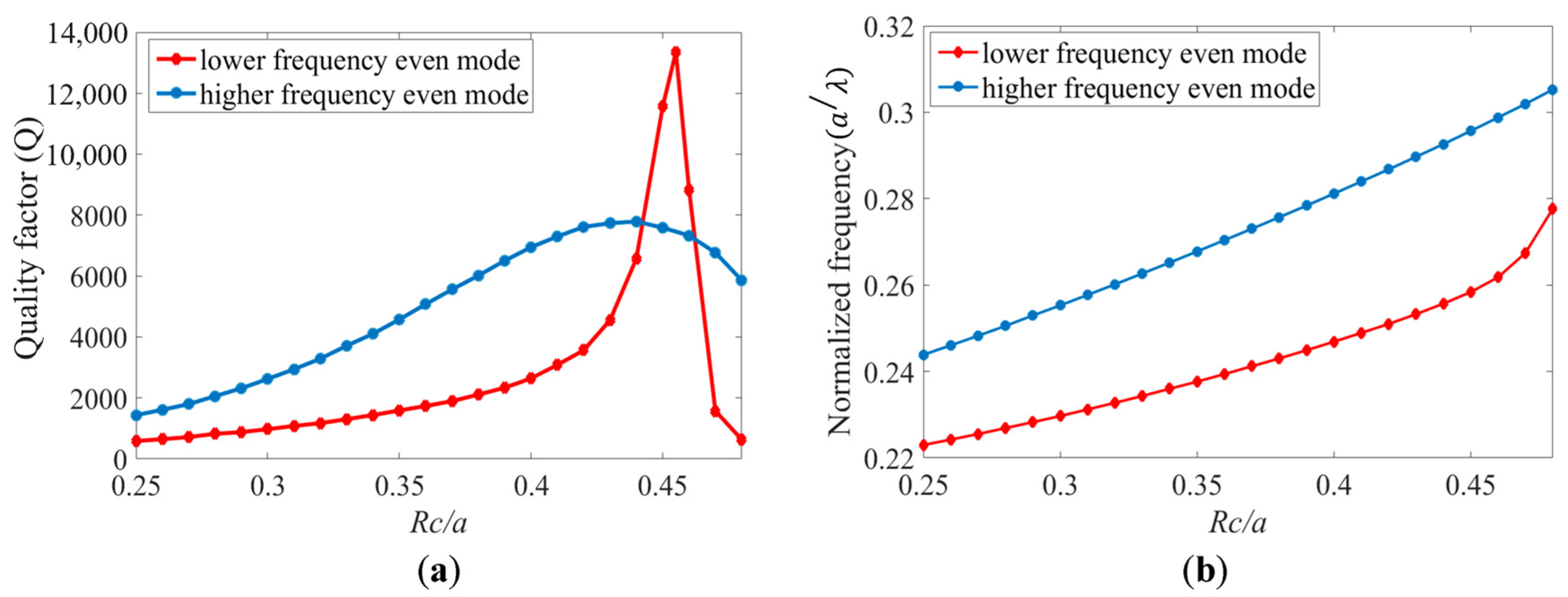
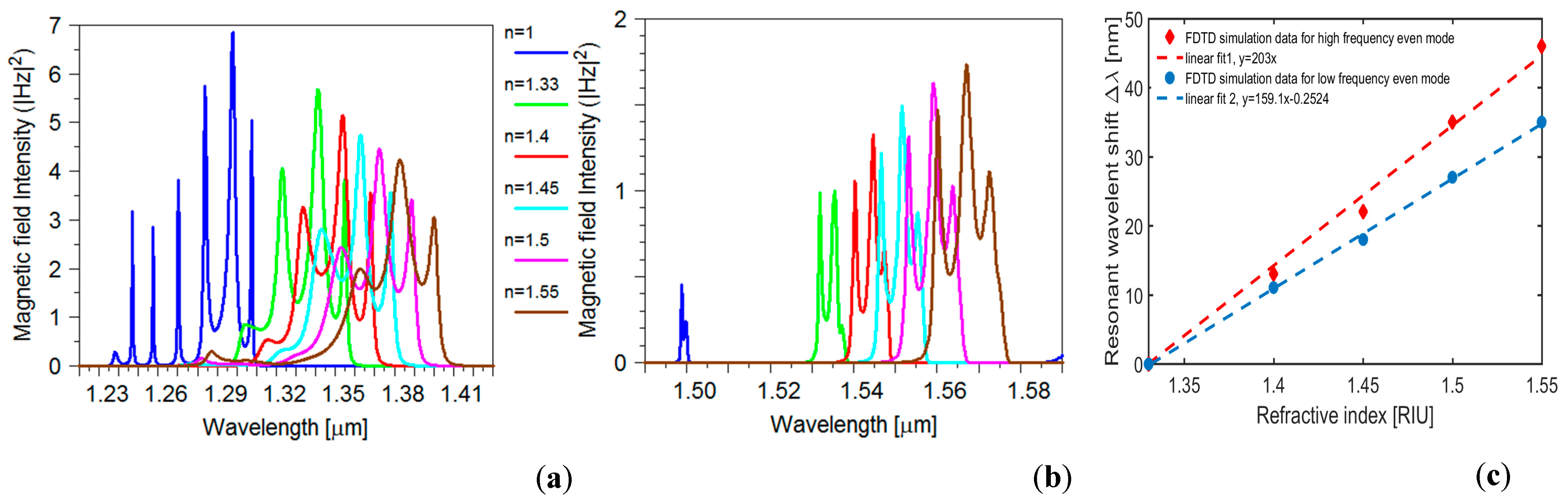
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kozma, P.; Kehl, F.; Ehrentreich-Förster, E.; Stamm, C.; Bier, F.F. Integrated planar optical waveguide interferometer biosensors: A comparative review. Biosens. Bioelectron. 2014, 58, 287–307. [Google Scholar] [CrossRef] [PubMed]
- Pergande, D.; Geppert, T.M.; Von Rhein, A.; Schweizer, S.L.; Wehrspohn, R.B.; Moretton, S.; Lambrecht, A. Miniature infrared gas sensors using photonic crystals. J. Appl. Phys. 2011, 109, 083117. [Google Scholar] [CrossRef]
- Liu, W.; Liu, X.; Zhou, J.; Xu, C.; Dong, B.; Lee, C. Larger-Than-Unity External Optical Field Con fi nement Enabled by Metamaterial-Assisted Comb Waveguide for Ultrasensitive Long-Wave Infrared Gas Spectroscopy. Nano Lett. 2022, 22, 6112–6120. [Google Scholar] [CrossRef] [PubMed]
- Zadeh, F.R.; Kaatuzian, H.; Danaie, M. Hybrid Photonic Crystal Cavity as a Sensitive Label-Free Biosensor. In Proceedings of the 2019 27th Iranian Conference on Electrical Engineering (ICEE), Yazd, Iran, 30 April–2 May 2019. [Google Scholar]
- Li, J. A review: Development of novel fiber-optic platforms for bulk and surface refractive index sensing applications. Sens. Actuators Rep. 2020, 2, 100018. [Google Scholar] [CrossRef]
- Parandin, F.; Heidari, F.; Rahimi, Z.; Olyaee, S. Two-Dimensional photonic crystal Biosensors: A review. Opt. Laser Technol. 2021, 144, 107397. [Google Scholar] [CrossRef]
- Pühringer, G.; Consani, C.; Jakoby, B. Impact of Different Metals on the Performance of Slab Tamm Plasmon Resonators. Sensors 2020, 20, 6804. [Google Scholar] [CrossRef] [PubMed]
- Saeidi, P.; Jakoby, B.; Pühringer, G.; Tortschanoff, A.; Stocker, G.; Dubois, F.; Spettel, J.; Grille, T.; Jannesari, R. Designing Mid-Infrared Gold-Based Plasmonic Slot Waveguides for CO2-Sensing Applications. Sensors 2021, 21, 2669. [Google Scholar] [CrossRef] [PubMed]
- Kita, S.; Hachuda, S.; Otsuka, S.; Endo, T.; Imai, Y.; Nishijima, Y.; Misawa, H.; Baba, T. Super-sensitivity in label-free protein sensing using a nanoslot nanolaser. Opt. Express 2011, 19, 17683. [Google Scholar] [CrossRef]
- Vasilantonakis, N.; Wurtz, G.A.; Podolskiy, V.A.; Zayats, A.V. Refractive index sensing with hyperbolic metamaterials: Strategies for biosensing and nonlinearity enhancement. Opt. Express 2015, 23, 14329. [Google Scholar] [CrossRef]
- He, L.; Yi, Y.; Zhang, J.; Xu, X.; Tang, B.; Li, G.; Zeng, L.; Chen, J.; Sun, T.; Yi, Z. A four-narrowband terahertz tunable absorber with perfect absorption and high sensitivity. Mater. Res. Bull. 2023, 170, 112572. [Google Scholar] [CrossRef]
- Lai, R.; Chen, H.; Zhou, Z.; Yi, Z.; Tang, B.; Chen, J.; Yi, Y.; Tang, C.; Zhang, J.; Sun, T. Design of a Penta-Band Graphene-Based Terahertz Metamaterial Absorber with Fine Sensing Performance. Micromachines 2023, 14, 1802. [Google Scholar] [CrossRef] [PubMed]
- Wu, F.; Chen, M.; Xiao, S. Wide-angle polarization selectivity based on anomalous defect mode in photonic crystal containing hyperbolic metamaterials. Opt. Lett. 2022, 47, 2153–2156. [Google Scholar] [CrossRef]
- Kar, C.; Jena, S.; Udupa, D.V.; Rao, K.D. Tamm plasmon polariton in planar structures: A brief overview and applications. Opt. Laser Technol. 2023, 159, 108928. [Google Scholar] [CrossRef]
- Wu, F.; Liu, T.; Xiao, S. Polarization-sensitive photonic bandgaps in hybrid one-dimensional photonic crystals composed of all-dielectric elliptical metamaterials and isotropic dielectrics. Appl. Opt. 2023, 62, 706–713. [Google Scholar] [CrossRef] [PubMed]
- Bikbaev, R.G.; Vetrov, S.Y.; Timofeev, I.V. Epsilon-Near-Zero Absorber by Tamm Plasmon Polariton. Photonics 2019, 6, 28. [Google Scholar] [CrossRef]
- Baghdouche, L.K.; Cassan, E. Mid-infrared refractive index sensing using optimized slotted photonic crystal waveguides. Photonics Nanostruct. Fundam. Appl. 2018, 28, 32–36. [Google Scholar] [CrossRef]
- Painam, B.; Kaler, R.S.; Kumar, M. Photonic Crystal Waveguide Biochemical Sensor for the Approximation of Chemical Components Concentrations. Plasmonics 2016, 12, 899–904. [Google Scholar] [CrossRef]
- Saker, K.; Bouchemat, T.; Lahoubi, M.; Bouchemat, M.; Pu, S. Magnetic field sensor based on a magnetic-fluid-infiltrated photonic crystal L4 nanocavity and broadband W1 waveguide. J. Comput. Electron. 2019, 18, 619–627. [Google Scholar] [CrossRef]
- Jannesari, R.; Grille, T. Gas sensing with a high-quality-factor photonic crystal ring resonator. In Proceedings of the SPIE—The International Society for Optical Engineering, Barcelona, Spain, 8–10 May 2017. [Google Scholar]
- Jannesari, R.; Pühringer, G.; Grille, T.; Jakoby, B. Design and Analysis of a Slot Photonic Crystal Waveguide for Highly Sensitive Evanescent Field Absorption Sensing in Fluids. Micromachines 2020, 11, 781. [Google Scholar] [CrossRef]
- Karle, T.J.; Chai, Y.J.; Morgan, C.N.; White, I.H.; Krauss, T.F. Observation of pulse compression in photonic crystal coupled cavity waveguides. J. Light. Technol. 2004, 22, 514–519. [Google Scholar] [CrossRef]
- Sanchis, P.; García, J.; Martínez, A.; Martí, J. Pulse propagation in adiabatically coupled photonic crystal coupled cavity waveguides. J. Appl. Phys. 2005, 97, 013101. [Google Scholar] [CrossRef]
- Danaie, M.; Geravand, A.; Mohammadi, S. Photonic crystal double-coupled cavity waveguides and their application in design of slow-light delay lines. Photonics Nanostruct. Fundam. Appl. 2018, 28, 61–69. [Google Scholar] [CrossRef]
- Huang, L.; Tian, H.; Zhou, J.; Liu, Q.; Zhang, P.; Ji, Y. Label-free optical sensor by designing a high-Q photonic crystal ring-slot structure. Opt. Commun. 2015, 335, 73–77. [Google Scholar] [CrossRef]
- Jannesari, R.; Grille, T.; Consani, C.; Stocker, G.; Tortschanoff, A.; Jakoby, B. Design of a Curved Shape Photonic Crystal Taper for Highly Efficient Mode Coupling. Sensors 2021, 21, 585. [Google Scholar] [CrossRef] [PubMed]
- Johnson, S.G.; Bienstman, P.; Skorobogatiy, M.A.; Ibanescu, M.; Lidorikis, E.; Joannopoulos, J.D. Adiabatic theorem and continuous coupled-mode theory for efficient taper transitions in photonic crystals. Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Top. 2002, 66, 066608. [Google Scholar] [CrossRef]
- “RSoft’s Photonic Design Suite. Version Synopsys RSoft 2019.09”, RSoft’s Photonic Design Suite. [Online]. Available online: https://www.synopsys.com/photonic-solutions.html (accessed on 1 January 2022).
- Sakoda, K.; Kawai, N.; Ito, T.; Chutinan, A.; Noda, S.; Mitsuyu, T.; Hirao, K. Photonic bands of metallic systems. I. Principle of calculation and accuracy. Phys. Rev. B Condens. Matter Mater. Phys. 2001, 64, 045116. [Google Scholar] [CrossRef]
- Pergande, D.; Von Rhein, A.; Geppert, T.M.; Wehrspohn, R.B. Coupling schemes for low-group velocity photonic crystal devices. J. Comput. Theor. Nanosci. 2009, 6, 1993–2000. [Google Scholar] [CrossRef]
- Vikas; Saccomandi, P. Antimonene-Coated Uniform-Waist Tapered Fiber Optic Surface Plasmon Resonance Biosensor for the Detection of Cancerous Cells: Design and Optimization. ACS Omega 2023, 8, 4627–4638. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jannesari, R.; Pühringer, G.; Stocker, G.; Grille, T.; Jakoby, B. Design of a High Q-Factor Label-Free Optical Biosensor Based on a Photonic Crystal Coupled Cavity Waveguide. Sensors 2024, 24, 193. https://doi.org/10.3390/s24010193
Jannesari R, Pühringer G, Stocker G, Grille T, Jakoby B. Design of a High Q-Factor Label-Free Optical Biosensor Based on a Photonic Crystal Coupled Cavity Waveguide. Sensors. 2024; 24(1):193. https://doi.org/10.3390/s24010193
Chicago/Turabian StyleJannesari, Reyhaneh, Gerald Pühringer, Gerald Stocker, Thomas Grille, and Bernhard Jakoby. 2024. "Design of a High Q-Factor Label-Free Optical Biosensor Based on a Photonic Crystal Coupled Cavity Waveguide" Sensors 24, no. 1: 193. https://doi.org/10.3390/s24010193
APA StyleJannesari, R., Pühringer, G., Stocker, G., Grille, T., & Jakoby, B. (2024). Design of a High Q-Factor Label-Free Optical Biosensor Based on a Photonic Crystal Coupled Cavity Waveguide. Sensors, 24(1), 193. https://doi.org/10.3390/s24010193





