Angularly Cascaded Long-Period Fiber Grating for Curvature and Temperature Detection
Abstract
:1. Introduction
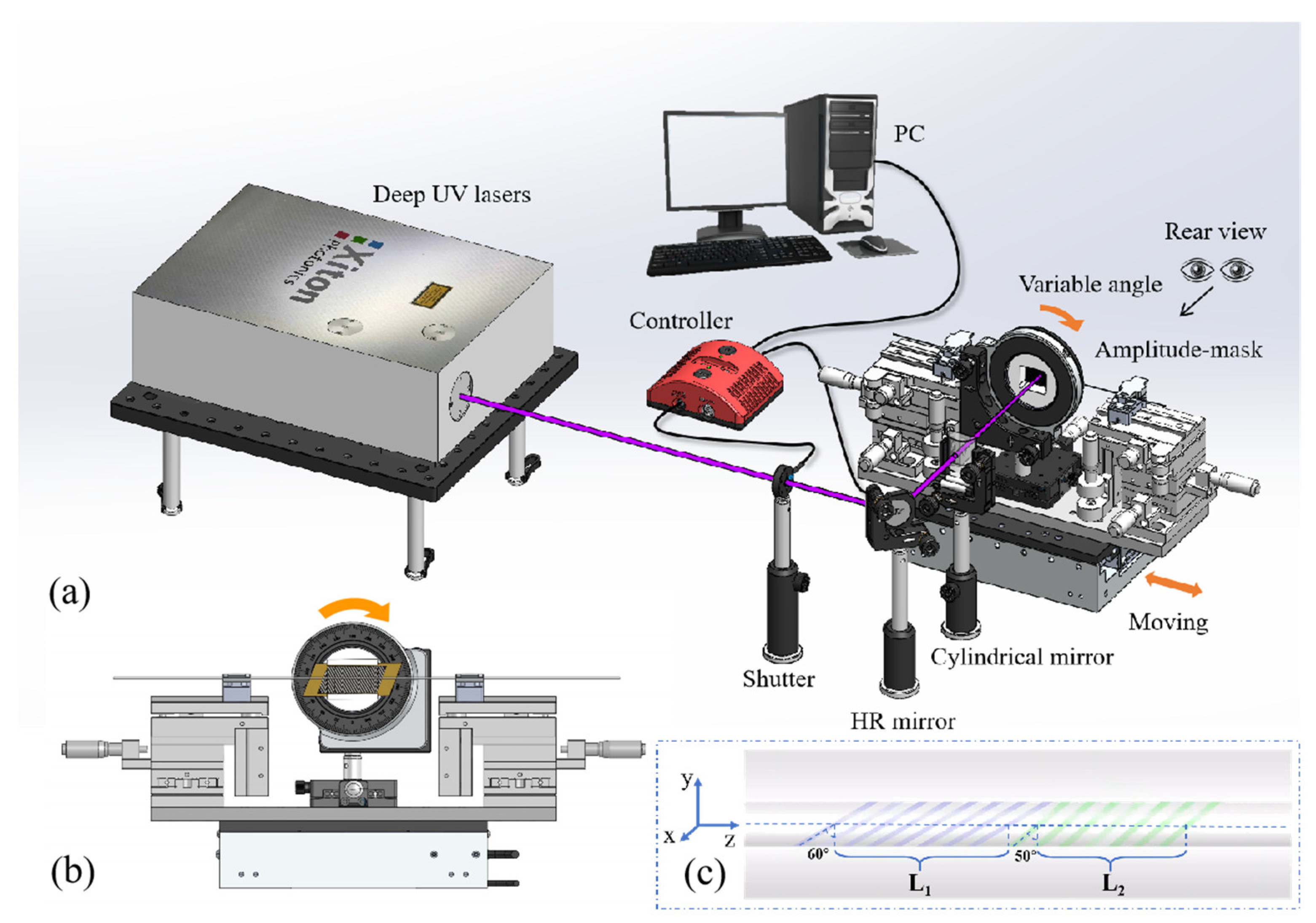
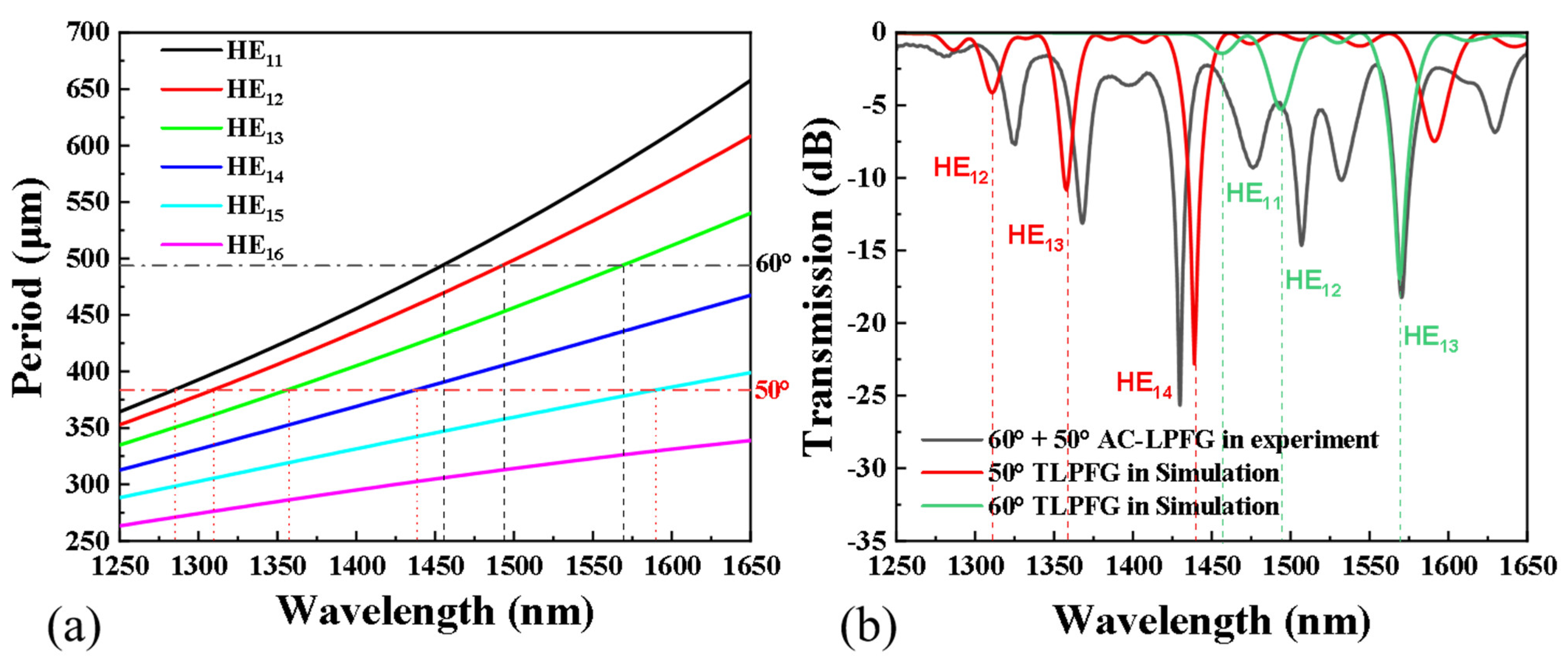
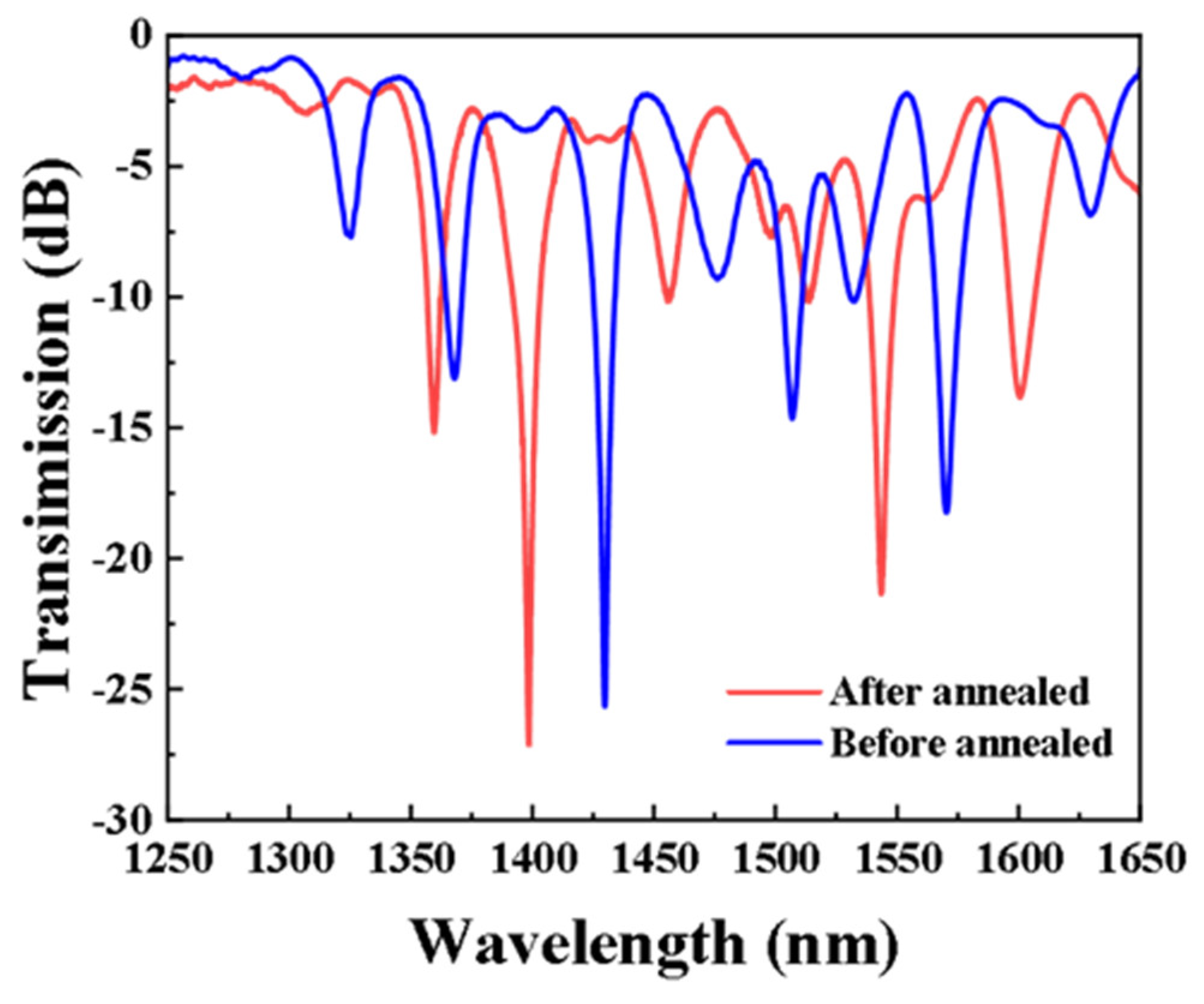
2. Fabrication and Principle
3. Experimental Results
3.1. Experimental Setup
3.2. Curvature Sensitivity
3.3. Temperature Sensitivity
3.4. Dual-Parameter Sensing
4. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, T.; Tong, Z.; Yang, C. Real-time monitoring and decoupling of multi parameters in vascular intervention using a cascaded LPFG-FBG sensor. Sens. Actuators A Phys. 2023, 359, 114463. [Google Scholar] [CrossRef]
- Saputro, J.M.W.; Kim, J.; Bae, M.; Lee, Y.W. Strain-Insensitive Simultaneous Measurements of Torsion and Temperature Using Long-Period Fiber Grating Inscribed on Twisted Double-Clad Fiber. IEEE Sens. J. 2023, 23, 6910–6918. [Google Scholar] [CrossRef]
- Lu, K.; Jiang, C.; Mou, C.; Liu, Y.; Wang, H.; Zhu, Y. High-Sensitivity Magnetic Field Sensor Based on Long-Period Grating Near the Dispersion Turning Point. IEEE Sens. J. 2022, 22, 14109–14117. [Google Scholar] [CrossRef]
- Li, Y.; Liu, T.; Ge, K.; Gan, W.; Dai, S.; Xu, T.; Zhang, P. Detection of copper ions in an aqueous solution by a dual-peak long period fiber grating functionalized with a polypyrrole-chitosan composite. Opt. Express 2023, 31, 6590–6600. [Google Scholar] [CrossRef]
- Fu, X.; Huang, Z.; Zhou, J.; Zhang, W.; Jin, W.; Fu, G.; Liu, F.; Bi, W.; Luo, Y.; Peng, G.-D. A dual-parameter sensing system for temperature and curvature based on Nano-EYDF and in-line cascaded Mach-Zehnder interferometer. Opt. Laser Technol. 2023, 163, 109353. [Google Scholar] [CrossRef]
- Zhao, R.; Shu, X. Curvature sensor based on femtosecond laser-inscribed straight waveguide in FMF. Opt. Laser Technol. 2022, 152, 108154. [Google Scholar] [CrossRef]
- Shao, M.; Liang, J.; Gao, H.; Wang, C.; Liu, Y. Seven-core fiber based in-fiber Mach–Zehnder interferometer for temperature-immune curvature sensing. Opt. Commun. 2023, 528, 128989. [Google Scholar] [CrossRef]
- Rong, Z.; Shu, X.; Xu, Z. Compact Fiber Curvature and Temperature Sensor Inscribed by Femtosecond Laser Through the Coating. J. Light. Technol. 2021, 39, 3981–3990. [Google Scholar] [CrossRef]
- Oliveira, R.; Cardoso, M.; Rocha, A.M. Two-dimensional vector bending sensor based on Fabry-Perot cavities in a multicore fiber. Opt. Express 2022, 30, 2230–2246. [Google Scholar] [CrossRef]
- Silva, S.; Pachon, E.G.P.; Franco, M.A.R.; Jorge, P.; Santos, J.L.; Malcata, F.X.; Cordeiro, C.M.B.; Frazao, O. Curvature and Temperature Discrimination Using Multimode Interference Fiber Optic Structures—A Proof of Concept. J. Light. Technol. 2012, 30, 3569–3575. [Google Scholar] [CrossRef]
- Yuan, W.; Zhao, Q.; Li, L.; Wang, Y.; Yu, C. Simultaneous measurement of temperature and curvature using ring-core fiber-based Mach-Zehnder interferometer. Opt. Express 2021, 29, 17915–17925. [Google Scholar] [CrossRef] [PubMed]
- Zhang, F.; Su, B.; Zhong, L.; Qi, B.; Xu, O.; Qin, Y. Ring core few-mode fiber sensor for curvature measurement. Appl. Opt. 2022, 61, 2598–2603. [Google Scholar] [CrossRef] [PubMed]
- Pereira, D.; Bierlich, J.; Kobelke, J.; Ferreira, M.S. Simultaneous measurement of strain, curvature, and temperature using a hollow square core fiber. Opt. Laser Technol. 2022, 156, 108540. [Google Scholar] [CrossRef]
- Zhao, M.; Li, X.; Li, Y.; Ma, Y.; Sun, J.; Su, C.; Yu, Z.; Qiao, Y.; Geng, T. A single-mode-deformed multimode-single-mode fiber structure for simultaneous measurement of curvature and temperature. Sens. Actuators A Phys. 2022, 347, 113927. [Google Scholar] [CrossRef]
- Li, Z.; Liu, S.; Bai, Z.; Fu, C.; Zhang, Y.; Sun, Z.; Liu, X.; Wang, Y. Residual-stress-induced helical long period fiber gratings for sensing applications. Opt. Express 2018, 26, 24114–24123. [Google Scholar] [CrossRef] [PubMed]
- Zhou, J.; He, X.; Chen, H.; Xiong, Z.; Yang, J.; Guan, C.; Yuan, L. Vector bending sensor based on chirped long-period grating with off-axis micro-helix taper. Chin. Opt. Lett. 2023, 21, 060604. [Google Scholar] [CrossRef]
- Lu, C.; Wang, J.; Xu, X.; Rui, Z.; Xiang, Z.; Yan, Q.; Geng, T.; Yuan, L. Arc-remodified long period fiber grating for monitoring absolute bending condition. J. Opt. 2022, 24, 055801. [Google Scholar] [CrossRef]
- Li, X.; Zhang, L.; Geng, T.; Qiao, Y. Highly Sensitive Bending Sensor Based on C-Shaped-Core Long-Period Fiber Gratings. IEEE Sens. J. 2022, 22, 23968–23974. [Google Scholar] [CrossRef]
- Barrera, D.; Madrigal, J.; Sales, S. Long Period Gratings in Multicore Optical Fibers for Directional Curvature Sensor Implementation. J. Light. Technol. 2018, 36, 1063–1068. [Google Scholar] [CrossRef]
- Dong, X.-R.; Sun, X.-Y.; Li, H.-T.; Hu, Y.-W.; Duan, J.-A.; Zhou, J.-Y.; Wang, C. Femtosecond laser fabrication of long period fiber gratings by a transversal-scanning inscription method and the research of its orientational bending characteristics. Opt. Laser Technol. 2015, 71, 68–72. [Google Scholar] [CrossRef]
- Ling, Q.; Gu, Z.; Guan, T. Theoretical analysis of dual-mode long period fiber grating sensor based on dual-peak resonance for dual-parameter measurement. OSA Contin. 2021, 4, 1041–1048. [Google Scholar] [CrossRef]
- Xu, M.; Liu, J.; Ghulam Abbas, L.; Zhou, A. High-sensitivity two-axis vector bending sensor based on side-grooved long period grating in eccentric core fiber. Opt. Laser Technol. 2022, 153, 108218. [Google Scholar] [CrossRef]
- Elgeneidy, K.; Lohse, N.; Jackson, M. Bending angle prediction and control of soft pneumatic actuators with embedded flex sensors—A data-driven approach. Mechatronics 2018, 50, 234–247. [Google Scholar] [CrossRef]
- Liu, J.; Liao, F.; Chen, Z.; Zhou, R.; Zhong, X.; Liu, B.; Wang, Z.; He, M.; Lin, H.; Zhang, Z.; et al. Digitizing Human Motion via Bending Sensors toward Humanoid Robot. Adv. Intell. Syst. 2023, 5, 2200337. [Google Scholar] [CrossRef]
- Meng, L.; Xu, H.; Huang, Y.; Zhuang, Y.; Wang, L.; Pang, C.; Zhang, M.; Guo, H.; Zhang, J.; Guo, F.; et al. High-Accuracy 3D Shape Sensor Based on Anti-Twist Packaged High Uniform Multicore Fiber FBGs. Adv. Fiber Mater. 2023, 5, 1467–1477. [Google Scholar] [CrossRef]
- Ding, L.; Yu, L.; Hu, G.; Xie, Q.; Zhu, L. Knee Joint Curvature Detection System Based on Fiber Optic Mach-Zendler Interferometric Curvature Sensor. IEEE Sens. J. 2021, 21, 28017–28024. [Google Scholar] [CrossRef]



| Configuration | Max Curvature Sensitivity (nm/m−1) | Range (m−1) | Temperature Sensitivity (pm/°C) | Two-Parameter Measurement Ability | Ref. |
|---|---|---|---|---|---|
| MCF-based FPI | 0.40 | 0–6.4 | 176 ± 4 | No | [9] |
| FMF-based MZI | 2 | 0–10 | 2.34 | No | [6] |
| RCF-based MZI | −3.68 | 1.3856–3.6661 | 72 | Yes | [11] |
| Cascaded MZI based on Nano-EYDF | −9.48 | 0–1.03 | 94.70 | Yes | [5] |
| Deformed-MMF-based MZI | −23.3 | 0–1.1733 | −52.1 | Yes | [14] |
| HLPFG | 1.94 | 0–9.06 | 132.8 | No | [15] |
| AR-LPFG | −17.02 | 0–1.96 | 92.8 | No | [17] |
| CLPFG | 14.08 | 0.128–1.28 | 75.6 | Yes | [16] |
| AC-LPFG | 16.392 | 0–0.9125 | 51 | Yes | Our work |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, A.; Du, J.; Ling, Q.; Chen, Y.; Gu, Z.; Chen, H.; Yu, Z.; Mao, B.-M.; Guan, Z.; Chen, D. Angularly Cascaded Long-Period Fiber Grating for Curvature and Temperature Detection. Sensors 2024, 24, 184. https://doi.org/10.3390/s24010184
Xiao A, Du J, Ling Q, Chen Y, Gu Z, Chen H, Yu Z, Mao B-M, Guan Z, Chen D. Angularly Cascaded Long-Period Fiber Grating for Curvature and Temperature Detection. Sensors. 2024; 24(1):184. https://doi.org/10.3390/s24010184
Chicago/Turabian StyleXiao, Anping, Jie Du, Qiang Ling, Yao Chen, Zhengtian Gu, Haiyun Chen, Zhangwei Yu, Barerem-Melgueba Mao, Zuguang Guan, and Daru Chen. 2024. "Angularly Cascaded Long-Period Fiber Grating for Curvature and Temperature Detection" Sensors 24, no. 1: 184. https://doi.org/10.3390/s24010184
APA StyleXiao, A., Du, J., Ling, Q., Chen, Y., Gu, Z., Chen, H., Yu, Z., Mao, B.-M., Guan, Z., & Chen, D. (2024). Angularly Cascaded Long-Period Fiber Grating for Curvature and Temperature Detection. Sensors, 24(1), 184. https://doi.org/10.3390/s24010184








