EVOAC-HP: An Efficient and Verifiable Outsourced Access Control Scheme with Hidden Policy
Abstract
1. Introduction
- We designed an efficient and secure fine-grained access control scheme named EVOAC-HP for privacy preserving in the medical data scenario, which supports a large universe, adaptive security and flexible access control structure. This scheme uses the attribute bloom filter to achieve policy hiding, which effectively protects data users’ attribute information.
- We adopted outsourcing decryption technology to outsource complex computation to the CSP and support the verification of the outsourcing results, which largely reduces the computation overhead of data users.
- According to security analysis and performance analysis, EVOAC-HP demonstrated enhanced security and efficiency, which is appropriate for medical data-sharing application scenarios with high privacy requirements.
2. Related Work
3. Preliminary
3.1. CP-ABE Definition
- : This algorithm takes the security parameter and attribute universe description U as input, and it outputs a master public key and a master key .
- : This algorithm takes the master key and a set of attributes S, and it outputs a secret decryption key .
- : This algorithm takes the master public key , an access structure over the universe of attributes and a message M, and it outputs a ciphertext .
- : This algorithm takes the master public key , a ciphertext and a secret decryption key , and it outputs a message M or a special symbol ⊥.
3.2. Security Model for CP-ABE
- : defines the challenge access structure and gives it to .
- : runs to obtain the master public key and returns it to .
- : has the ability to request secret keys corresponding to collections of user attributes , . For each , runs and returns to . The queried sets must not meet the access structure requirements of the challenge phase above each query, i.e., .
- : submits two messages, and , with equal length and returns them to . chooses random number and invokes to obtain , which is given to .
- : Phase 1 is reiterated under the same constraint. can continue to query the secret keys for the sets , .
- : outputs his guess value for b.
3.3. Commitment
- : This algorithm takes a security parameter as input and outputs the public commitment key .
- : This algorithm takes a message M and an additional random number r as input and outputs a commitment .
- : This algorithm takes a message M, an additional random number r and a commitment as input and outputs a bit value . If , it indicates that is a valid commitment to M; otherwise, it indicates that is not a commitment to M.
3.4. Attribute Bloom Filter
- : This algorithm takes as input an access policy . The attributes and their corresponding row number i involved in access matrix are concatenated, where each row i maps to attribute according to the mapping function , and they are left-padded with zeros to achieve a maximum bit length. The resulting set of elements is used as input in the garbled BF building algorithm to create , as described in [31].When an element needs to be inserted into , this algorithm randomly produces -bit strings and adopts the XOR-based secret sharing scheme to distribute element . It then assigns . Afterward, x independent and uniform hash functions are used to hash attribute to obtain for , where represents the specific index position in . The i-th share of the element is then stored in at the position indicated by the hash function . When adding more elements to , it is possible that a location has already been filled by an element added earlier. In this case, we can repurpose the existing share assigned as a share for the new element.
- : This algorithm takes as input the master public key , an attribute set S and the attribute bloom filter . For each attribute within the attribute set S, the algorithm calculates the position index in with x hash functions. The value stored in the corresponding position can then be retrieved.Once the element shares the that have been stored in , element can be reconstructed using the formula , where is represented as and attribute is derived from the rightmost bits of element . If there are redundant zeros in , they are removed. When matches the attribute specified in the access policy, this implies that attribute exists in the access control policy. Otherwise, attribute is not present in the access policy. Similarly, the row number i is derived from the leftmost L bits of element , and redundant zeros are removed if present. Once and i have been obtained, the attribute mapping can be rebuilt as .
3.5. Decisional Linear Assumption
4. Access Control System
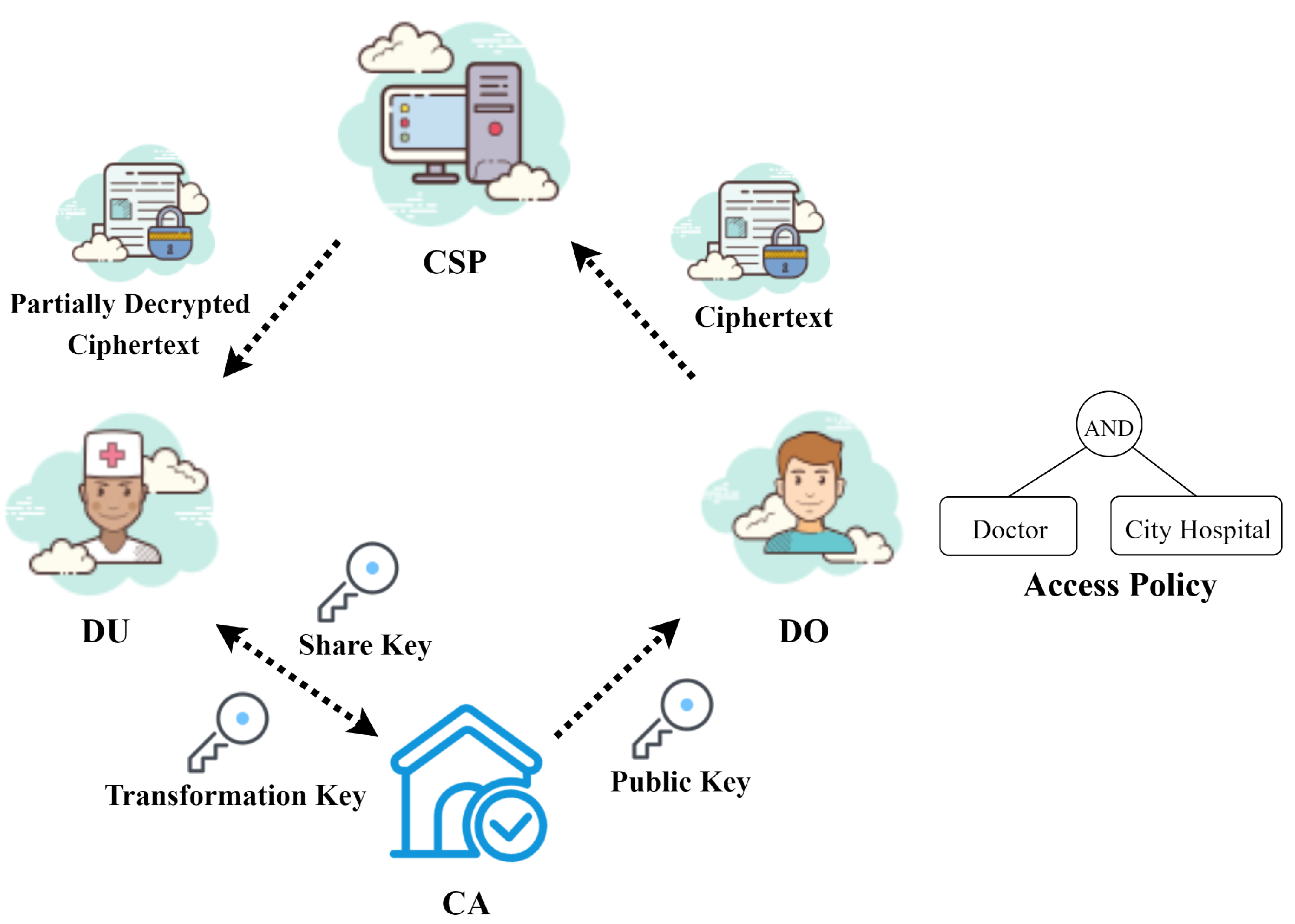
4.1. System Model
- Certificate authority (CA): The central component of the entire system is the CA, which is in charge of the initialization of the system. The CA is responsible for creating the master private key and public parameters. Additionally, the CA generates transformation keys for users based on their attribute set when requested. It is assumed that the CA is a trusted entity.
- Data owners (DOs): DOs are the producers of medical data. When they need to share their data, they first establish a custom access policy that allows users to access and encrypt the data using our proposed encryption scheme. The resulting ciphertext is then uploaded to the CSP. It is worth noting that the access policy in the ciphertext does not reveal the sensitive attributes of the data owner. In a medical scenario, the data owners are the patients.
- Data users (DUs): In the healthcare scenario, the DUs play the role of a doctor or a nurse. They need to retrieve the corresponding ciphertext from the CSP and request it to assist in the transformation of the ciphertext. When obtaining the transformed decrypted ciphertext from the CSP, the data user locally decrypts it to access the EHR data and checks whether the transformation result is correct. Considering that the data user is likely to use resource-limited devices such as conventional desktop computers, the decryption operation is delegated to simplify the computation.
- Cloud service provider (CSP): The CSP is a powerful server with storage and computing services. Its main responsibilities include storing ciphertext corresponding to medical data and providing ciphertext transformation service. It should be noted that the CSP is honest but curious, which means that it may attempt to extract useful information from the ciphertext.
4.2. The Proposed Scheme
| Algorithm 1 Setup (Invoked by CA). |
| Input Security parameter , attribute universe description U Output: The master public key , the master key
|
| Algorithm 2 TkGen (Invoked by CA). |
| Input The master key , attribute set S, a shared public key Output: Transformation key
|
| Algorithm 3 Encrypt (Invoked by DO). |
| Input Master public key , the combination of the message and random number , access structure , attribute set S Output: Encrypted message
|
| Algorithm 4 Transform (Invoked by CSP). |
| Input Ciphertext , transformation key Output: Partially-decrypted ciphertext
|
5. Security Analysis
- System initialization: Adversary sends the access structure that needs to be challenged to algorithm . Algorithm gives to challenger . Challenger generates public parameter with the algorithm in FAME and sends to algorithm . Algorithm calls the algorithm in EVOAC-HP to complete public parameter and send it to adversary .
- Query phase 1: Algorithm receives the decryption key query request submitted by adversary . Let adversary ask for the decryption key of the attribute set , and let algorithm forward this query request to challenger . Challenger calls the algorithm in the FAME scheme to output the decryption key given to algorithm , and algorithm forwards its key to adversary .
- Challenge phase: Adversary submits two equal-length plaintexts, and , to algorithm . Algorithm sends them to challenger and asks for the challenge ciphertext. Challenger randomly selects and calls the algorithm in the FAME scheme to encrypt the message . Finally, challenger sends the ciphertext to algorithm . After receiving the challenge ciphertext , algorithm completes according to the ciphertext form of EVOAC-HP and then sends it to adversary .
- Query phase 2: This phase is the same as Query phase 1.
- Guess phase: If adversary outputs a bit , then algorithm also outputs .
6. Performance Analysis
6.1. Functional Analysis
6.2. Theoretical Analysis
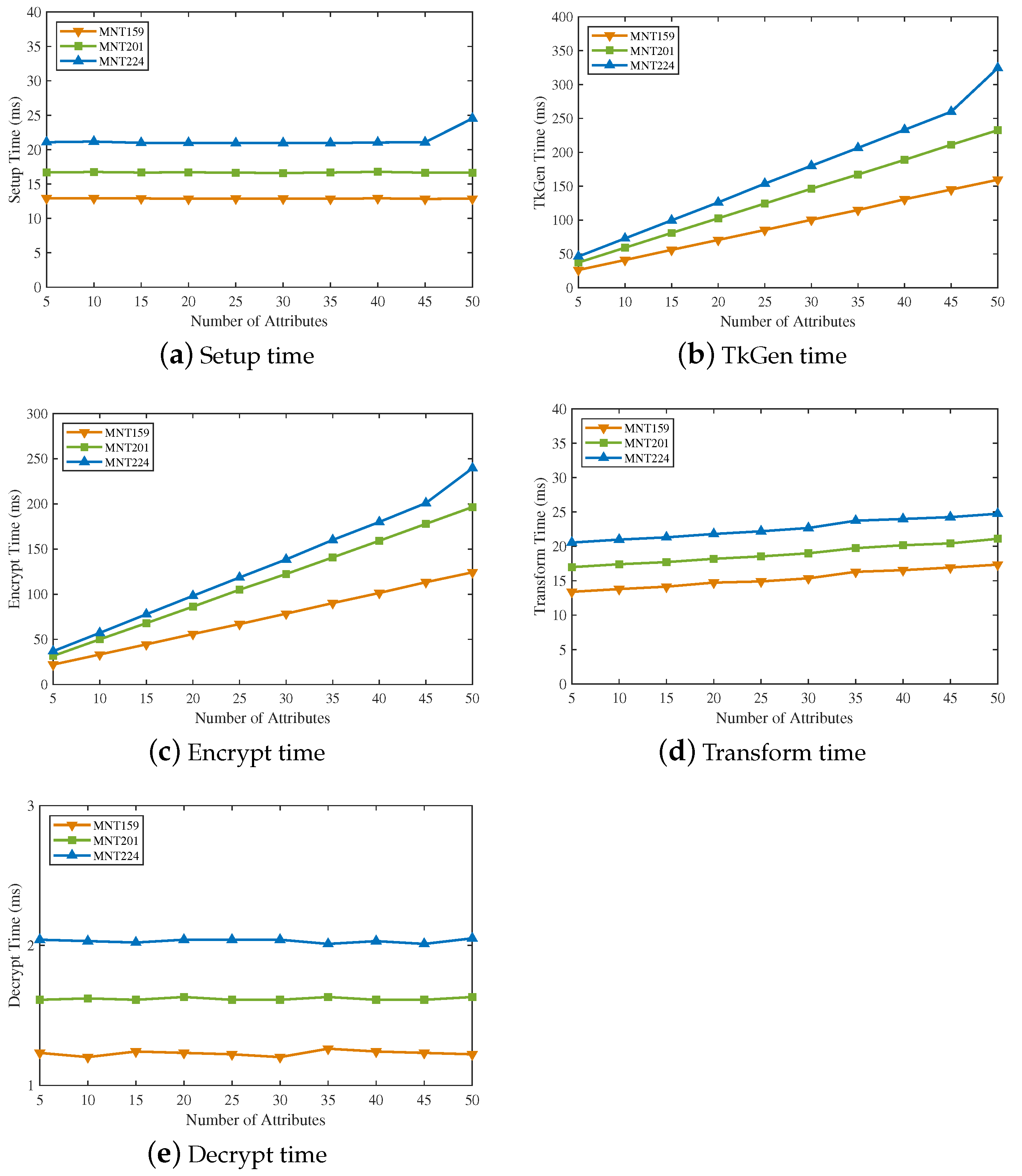
6.3. Experimental Analysis
7. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, M.; Guo, Y.; Zhang, C.; Wang, C.; Huang, H.; Jia, X. MedShare: A privacy-preserving medical data sharing system by using blockchain. IEEE Trans. Serv. Comput. 2021, 16, 438–451. [Google Scholar] [CrossRef]
- Li, F.; Liu, K.; Zhang, L.; Huang, S.; Wu, Q. EHRChain: A blockchain-based ehr system using attribute-based and homomorphic cryptosystem. IEEE Trans. Serv. Comput. 2021, 15, 2755–2765. [Google Scholar] [CrossRef]
- Huang, J.; Kong, L.; Cheng, L.; Dai, H.N.; Qiu, M.; Chen, G.; Liu, X.; Huang, G. BlockSense: Towards Trustworthy Mobile Crowdsensing via Proof-of-Data Blockchain. IEEE Trans. Mob. Comput. 2022, 1–17. [Google Scholar] [CrossRef]
- Sahai, A.; Waters, B. Fuzzy identity-based encryption. In Proceedings of the Annual International Conference on the Theory and Applications of Cryptographic Techniques, Aarhus, Denmark, 22–26 May 2005; Springer: Berlin/Heidelberg, Germany, 2005; pp. 457–473. [Google Scholar] [CrossRef]
- Bethencourt, J.; Sahai, A.; Waters, B. Ciphertext-policy attribute-based encryption. In Proceedings of the 2007 IEEE Symposium on Security and Privacy (SP’07), Berkeley, CA, USA, 20–23 May 2007; pp. 321–334. [Google Scholar] [CrossRef]
- Lewko, A.; Waters, B. New proof methods for attribute-based encryption: Achieving full security through selective techniques. In Proceedings of the Advances in Cryptology–CRYPTO 2012: 32nd Annual Cryptology Conference, Santa Barbara, CA, USA, 19–23 August 2012; pp. 180–198. [Google Scholar] [CrossRef]
- Rouselakis, Y.; Waters, B. Practical constructions and new proof methods for large universe attribute-based encryption. In Proceedings of the 2013 ACM SIGSAC Conference on Computer & Communications Security, Berlin, Germany, 4–8 November 2013; pp. 463–474. [Google Scholar] [CrossRef]
- Nishide, T.; Yoneyama, K.; Ohta, K. Attribute-based encryption with partially hidden encryptor-specified access structures. In Proceedings of the International Conference on Applied Cryptography and Network Security, New York, NY, USA, 3–6 June 2008; Springer: Berlin/Heidelberg, Germany, 2008; pp. 111–129. [Google Scholar] [CrossRef]
- Green, M.; Hohenberger, S.; Waters, B. Outsourcing the Decryption of ABE Ciphertexts. In Proceedings of the 20th USENIX Security Symposium (USENIX Security 11), San Francisco, CA, USA, 8–12 August 2011. [Google Scholar]
- Lai, J.; Deng, R.H.; Guan, C.; Weng, J. Attribute-based encryption with verifiable outsourced decryption. IEEE Trans. Inf. Forensics Secur. 2013, 8, 1343–1354. [Google Scholar] [CrossRef]
- Mao, X.; Lai, J.; Mei, Q.; Chen, K.; Weng, J. Generic and efficient constructions of attribute-based encryption with verifiable outsourced decryption. IEEE Trans. Dependable Secur. Comput. 2015, 13, 533–546. [Google Scholar] [CrossRef]
- Liu, X.; Wang, H.; Zhang, B.; Zhang, B. An efficient fine-grained data access control system with a bounded service number. Inf. Sci. 2022, 584, 536–563. [Google Scholar] [CrossRef]
- Lai, J.; Deng, R.H.; Li, Y. Fully secure cipertext-policy hiding CP-ABE. In Proceedings of the Information Security Practice and Experience: 7th International Conference, ISPEC 2011, Guangzhou, China, 30 May–1 June 2011; Springer: Berlin/Heidelberg, Germany, 2011; pp. 24–39. [Google Scholar] [CrossRef]
- Hur, J. Attribute-based secure data sharing with hidden policies in smart grid. IEEE Trans. Parallel Distrib. Syst. 2013, 24, 2171–2180. [Google Scholar] [CrossRef]
- Agrawal, S.; Chase, M. FAME: Fast attribute-based message encryption. In Proceedings of the 2017 ACM SIGSAC Conference on Computer and Communications Security, Dallas, TX, USA, 30 October–3 November 2017; pp. 665–682. [Google Scholar] [CrossRef]
- Shamir, A. Identity-based cryptosystems and signature schemes. In Proceedings of the Advances in Cryptology: Proceedings of CRYPTO ’84, Santa Barbara, California, USA, 19–22 August 1984; Springer: Berlin/Heidelberg, Germany, 1985; pp. 47–53. [Google Scholar] [CrossRef]
- Goyal, V.; Pandey, O.; Sahai, A.; Waters, B. Attribute-based encryption for fine-grained access control of encrypted data. In Proceedings of the 13th ACM Conference on Computer and Communications Security, Alexandria, VA, USA, 30 October–3 November 2006; pp. 89–98. [Google Scholar] [CrossRef]
- Waters, B. Ciphertext-policy attribute-based encryption: An expressive, efficient, and provably secure realization. In International Workshop on Public Key Cryptography; Springer: Berlin/Heidelberg, Germany, 2011; pp. 53–70. [Google Scholar] [CrossRef]
- Li, J.; Chen, X.; Li, J.; Jia, C.; Ma, J.; Lou, W. Fine-grained access control system based on outsourced attribute-based encryption. In Proceedings of the European Symposium on Research in Computer Security, Egham, UK, 9–13 September 2013; Springer: Berlin/Heidelberg, Germany, 2013; pp. 592–609. [Google Scholar] [CrossRef]
- Li, J.; Huang, X.; Li, J.; Chen, X.; Xiang, Y. Securely outsourcing attribute-based encryption with checkability. IEEE Trans. Parallel Distrib. Syst. 2013, 25, 2201–2210. [Google Scholar] [CrossRef]
- Lin, S.; Zhang, R.; Ma, H.; Wang, M. Revisiting attribute-based encryption with verifiable outsourced decryption. IEEE Trans. Inf. Forensics Secur. 2015, 10, 2119–2130. [Google Scholar] [CrossRef]
- Cui, H.; Wan, Z.; Wei, X.; Nepal, S.; Yi, X. Pay as you decrypt: Decryption outsourcing for functional encryption using blockchain. IEEE Trans. Inf. Forensics Secur. 2020, 15, 3227–3238. [Google Scholar] [CrossRef]
- Qin, X.; Huang, Y.; Yang, Z.; Li, X. LBAC: A lightweight blockchain-based access control scheme for the internet of things. Inf. Sci. 2021, 554, 222–235. [Google Scholar] [CrossRef]
- Qin, X.; Yang, Z.; Li, Q.; Pan, H.; Yang, Z.; Huang, Y. Attribute-based encryption with outsourced computation for access control in IoTs. In Proceedings of the 2022 3rd Asia Service Sciences and Software Engineering Conference, Macao, 24–26 February 2022; pp. 66–73. [Google Scholar] [CrossRef]
- Lai, J.; Deng, R.H.; Li, Y. Expressive CP-ABE with partially hidden access structures. In Proceedings of the 7th ACM Symposium on Information, Computer and Communications Security, Seoul, Republic of Korea, 2–4 May 2012; pp. 18–19. [Google Scholar] [CrossRef]
- Cui, H.; Deng, R.H.; Wu, G.; Lai, J. An efficient and expressive ciphertext-policy attribute-based encryption scheme with partially hidden access structures. In Proceedings of the International Conference on Provable Security, Nanjing, China, 10–11 November 2016; Springer: Berlin/Heidelberg, Germany, 2016; pp. 19–38. [Google Scholar] [CrossRef]
- Zhang, Y.; Zheng, D.; Deng, R.H. Security and privacy in smart health: Efficient policy-hiding attribute-based access control. IEEE Internet Things J. 2018, 5, 2130–2145. [Google Scholar] [CrossRef]
- Cui, H.; Deng, R.H.; Lai, J.; Yi, X.; Nepal, S. An efficient and expressive ciphertext-policy attribute-based encryption scheme with partially hidden access structures, revisited. Comput. Netw. 2018, 133, 157–165. [Google Scholar] [CrossRef]
- Zhang, L.; Hu, G.; Mu, Y.; Rezaeibagha, F. Hidden ciphertext policy attribute-based encryption with fast decryption for personal health record system. IEEE Access 2019, 7, 33202–33213. [Google Scholar] [CrossRef]
- Saidi, A.; Nouali, O.; Amira, A. SHARE-ABE: An efficient and secure data sharing framework based on ciphertext-policy attribute-based encryption and Fog computing. Clust. Comput. 2022, 25, 167–185. [Google Scholar] [CrossRef]
- Dong, C.; Chen, L.; Wen, Z. When private set intersection meets big data: An efficient and scalable protocol. In Proceedings of the 2013 ACM SIGSAC Conference on Computer & Communications Security, Berlin, Germany, 4–8 November 2013; pp. 789–800. [Google Scholar] [CrossRef]
- Yang, K.; Han, Q.; Li, H.; Zheng, K.; Su, Z.; Shen, X. An efficient and fine-grained big data access control scheme with privacy-preserving policy. IEEE Internet Things J. 2016, 4, 563–571. [Google Scholar] [CrossRef]
- Han, Q.; Zhang, Y.; Li, H. Efficient and robust attribute-based encryption supporting access policy hiding in Internet of Things. Future Gener. Comput. Syst. 2018, 83, 269–277. [Google Scholar] [CrossRef]
- Hao, J.; Huang, C.; Ni, J.; Rong, H.; Xian, M.; Shen, X.S. Fine-grained data access control with attribute-hiding policy for cloud-based IoT. Comput. Netw. 2019, 153, 1–10. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, J.; Mu, Y. Privacy-Preserving Flexible Access Control for Encrypted Data in Internet of Things. IEEE Internet Things J. 2021, 8, 14731–14745. [Google Scholar] [CrossRef]
- Deng, W.; Xiang, T.; Liao, X. STEAC: Towards secure, traceable, and efficient cryptographic access control scheme in smart healthcare. Multimed. Tools Appl. 2022, 81, 30069–30092. [Google Scholar] [CrossRef]
- Akinyele, J.A.; Garman, C.; Miers, I.; Pagano, M.W.; Rushanan, M.; Green, M.; Rubin, A.D. Charm: A framework for rapidly prototyping cryptosystems. J. Cryptogr. Eng. 2013, 3, 111–128. [Google Scholar] [CrossRef]
- Bradford, P.G.; Katehakis, M.N. A probabilistic study on combinatorial expanders and hashing. SIAM J. Comput. 2007, 37, 83–111. [Google Scholar] [CrossRef]


| Scheme | Security Model | Large Universe | Hidden Policy | Outsourced Decryption | Verifiability |
|---|---|---|---|---|---|
| [8] | Selective security | ✘ | ✔ | ✘ | ✘ |
| [18] | Selective security | ✔ | ✘ | ✘ | ✘ |
| [9] | Selective security | ✔ | ✘ | ✔ | ✘ |
| [25] | Adaptive security | ✘ | ✔ | ✘ | ✘ |
| [10] | Selective security | ✔ | ✘ | ✔ | ✔ |
| [11] | Selective security | ✔ | ✘ | ✔ | ✔ |
| [32] | Selective security | ✔ | ✔ | ✘ | ✘ |
| [15] | Adaptive security | ✔ | ✘ | ✘ | ✘ |
| EVOAC-HP | Adaptive security | ✔ | ✔ | ✔ | ✔ |
| Scheme | Encryption | Decryption |
|---|---|---|
| [18] | ||
| [32] | ||
| [15] | ||
| EVOAC-HP |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, H.; Zhou, D.; Li, P.; Wang, X. EVOAC-HP: An Efficient and Verifiable Outsourced Access Control Scheme with Hidden Policy. Sensors 2023, 23, 4384. https://doi.org/10.3390/s23094384
Ma H, Zhou D, Li P, Wang X. EVOAC-HP: An Efficient and Verifiable Outsourced Access Control Scheme with Hidden Policy. Sensors. 2023; 23(9):4384. https://doi.org/10.3390/s23094384
Chicago/Turabian StyleMa, Haobin, Dehua Zhou, Peng Li, and Xiaoming Wang. 2023. "EVOAC-HP: An Efficient and Verifiable Outsourced Access Control Scheme with Hidden Policy" Sensors 23, no. 9: 4384. https://doi.org/10.3390/s23094384
APA StyleMa, H., Zhou, D., Li, P., & Wang, X. (2023). EVOAC-HP: An Efficient and Verifiable Outsourced Access Control Scheme with Hidden Policy. Sensors, 23(9), 4384. https://doi.org/10.3390/s23094384





