A Novel Method for Bearing Fault Diagnosis under Variable Speed Based on Envelope Spectrum Fault Characteristic Frequency Band Identification
Abstract
1. Introduction
- There are few in-depth studies on the characteristics of the bearing vibration signal envelope spectrum under VS;
- 3.
- To investigate and reveal the envelope spectrum characteristics of bearing vibration signals under VS;
- 4.
- To attempt to diagnose bearing faults under VS directly through envelope spectrum analysis to overcome shortcomings existing in traditional OT- and TFA-based methods.
2. Envelope Spectrum Characteristics of Bearing Fault Vibration Signals under VS
2.1. Bearing Vibration Signal Model under VS
2.2. Characteristic Analysis of the Envelope Spectrum Based on Simulation Signals
2.2.1. Analysis under Different RF Variation Modes
2.2.2. Analysis under Different RF Variation Ranges
2.2.3. Analysis under Different Fault Types
2.3. Formula Derivation of the Envelope Spectrum under VS
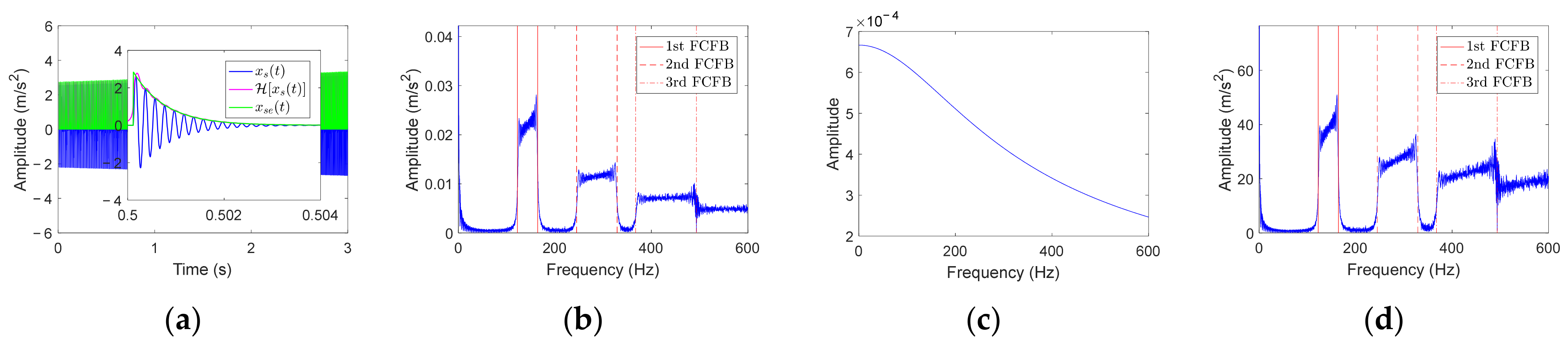
- Conclusion 1: Regular FCFBs appear in the low frequency band of the envelope spectrum of the bearing vibration signal under VS. The range of the nth FCFB is nFCC × [min(fr(t)),max(fr(t))]. The amplitude of FCFB shows a decaying trend from the 1st to the nth FCFB. MFBs exist in the inner race and rolling element fault envelope spectrum, and their ranges around the nth FCFB are n(FCCi ± 1) × [min(fr(t)), max(fr(t))] and n(FCCr ± FCCc) × [min(fr(t)), max(fr(t))], respectively. At the same time, RFB and CFB exist in the inner race and rolling element fault envelope spectrum, and their ranges are equal to the range of RF and the cage frequency, respectively.
- Conclusion 2: The fundamental reason why FCFB in the envelope spectrum lies in the fault impulse is the unequal time interval in the time domain under VS. The range of FCFB is related to the fault type and RF range rather than the variation mode of RF, which affects only the amplitude inside the FCFB.
- Conclusion 3: FCFB, as an important characteristic of the bearing fault vibration signal envelope spectrum under VS, can be utilized for fault diagnosis.
3. The Proposed FCFBI Bearing Fault Diagnosis Method under VS
3.1. Correlation Coefficient-Based FCFBI
3.2. FCFB Feature Enhancement
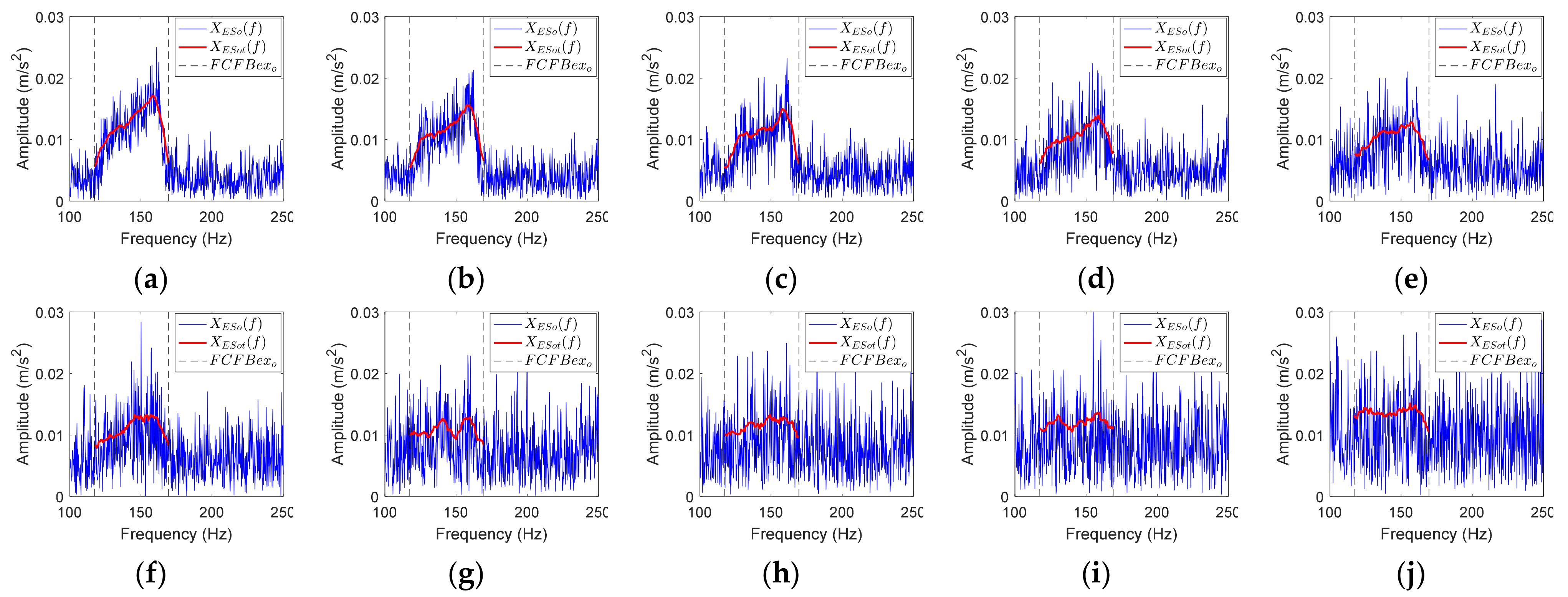
3.2.1. Envelope Spectrum FCFB Trend Fitting
- Denote the envelope spectrum of the bearing vibration signal as XES(f); the corresponding inner race, outer race, and rolling element fault signal envelope spectra are denoted as XESi(f), XESo(f), and XESr(f), respectively. Assuming that XES(f) contains m data points, remove the DC component to obtain the centered envelope spectrum: Xc(f) = XES(f) − mean(XES(f));
- For the ith data point Xc(f)i (i = 1, …, m), calculate the RMS value of this point and the previous wl − 1 points to obtain ;
- Intercept XRMS(f) in FCFBex to obtain the trend of XES(f), which is denoted as XESt(f). Similarly, the trends of the envelope spectra under different faults are denoted as XESti(f), XESto(f), and XEStr(f).
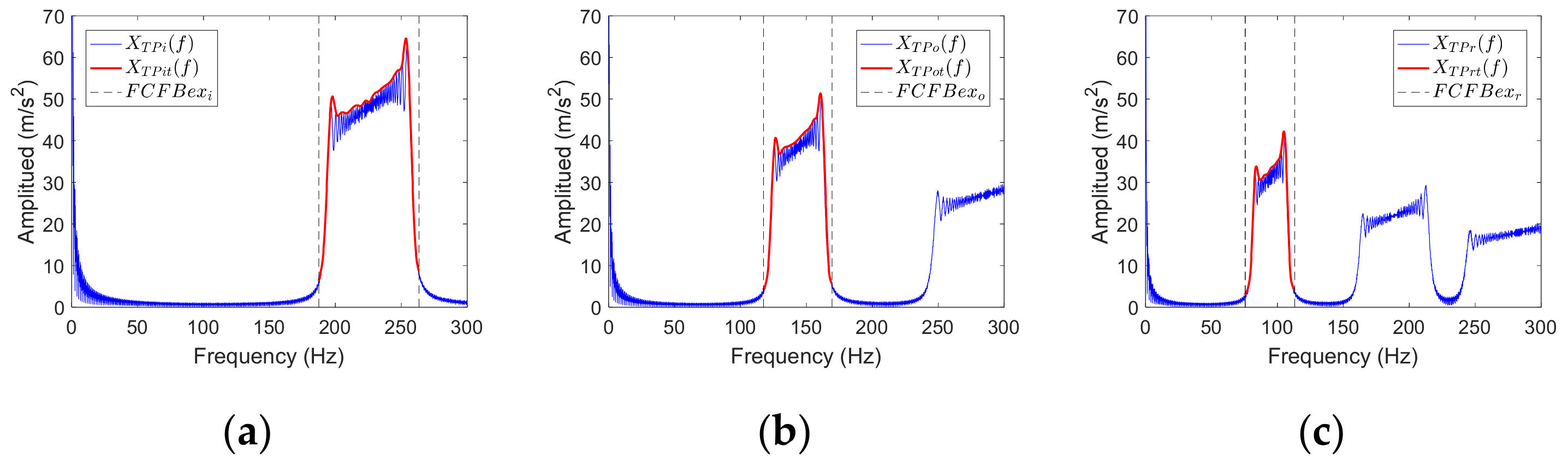
3.2.2. Template FCFB Trend Fitting
- Denote fault template as XTP(f); the corresponding inner race, outer race, and rolling element fault templates are denoted as XTPi(f), XTPo(f), and XTPr(f), respectively. Find all local extreme points of XTP(f) in FCFBex; record these values as set {mk (k = 1, …, n)}, with the corresponding location in FCFBex as {Lock (k = 1, …, n)};
- Let l = 0, and denote the minimum peak distance between local extreme points as mpd;
- Find the maximum value in {mk}, i.e., mkmax = max(mk), and its corresponding location Lockmax;
- Ignore the local extreme points located in [Lockmax − mpd, Lockmax + mpd] and update the remaining set of extreme points as {mk (k = 1, …, nupdate)};
- If nupdate > 1, let l = l + 1, repeat steps 2–4;
- Obtain all of the updated sets of the extreme points {mkmax (kmax = 1, …, l)} and the corresponding location set {Lockmax (kmax = 1, …, l)}. Treat (Lockmax, mkmax) as original values and use cubic spline interpolation to obtain the value of other locations in FCFBex.
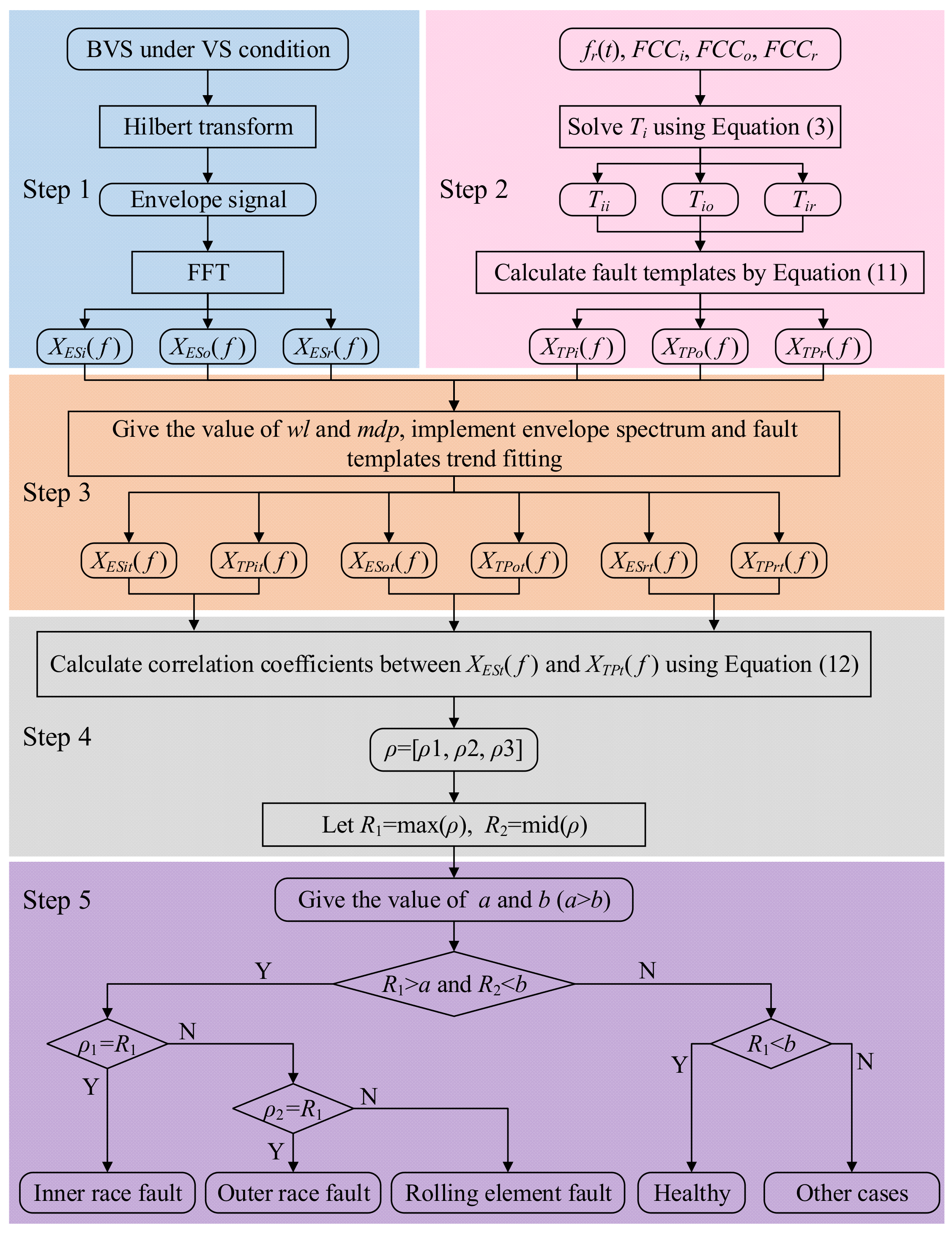
3.3. Procedure of the FCFBI Method
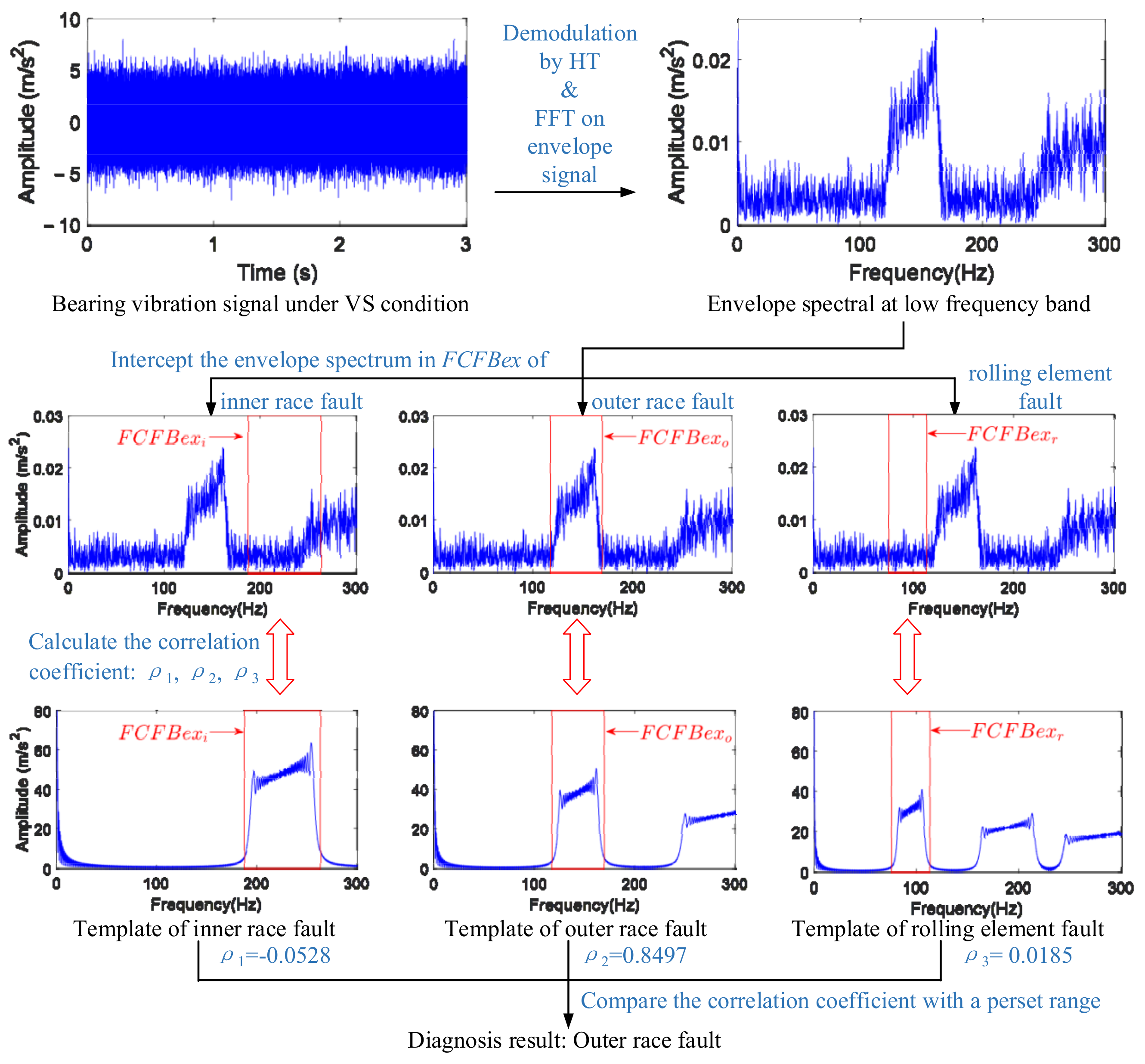
- Perform HT on the bearing vibration signal (BVS) under VS to obtain the envelope signal. Then, carry out FFT on the envelope signal to determine the envelope spectrum. Intercept the envelope spectrum in FCFBex to obtain XESi(f), XESo(f), and XESr(f);
- Insert fr(t), FCCi, FCCo, and FCCr into Equation (3), and then the impulse occurrence time Ti of the inner race, outer race, and rolling element fault can be solved, i.e., Tii, Tio, and Tir. Bring them intoto obtain different fault templates;
- Find the value of wl, fit the envelope spectrum in FCFBs by the sliding window RMS method to obtain XESit(f), XESot(f), and XESrt(f) in the corresponding FCFBex. At the same time, XTPit(f), XTPot(f), and XTPrt(f) can be calculated using the local extreme point interpolation method with given mpd;
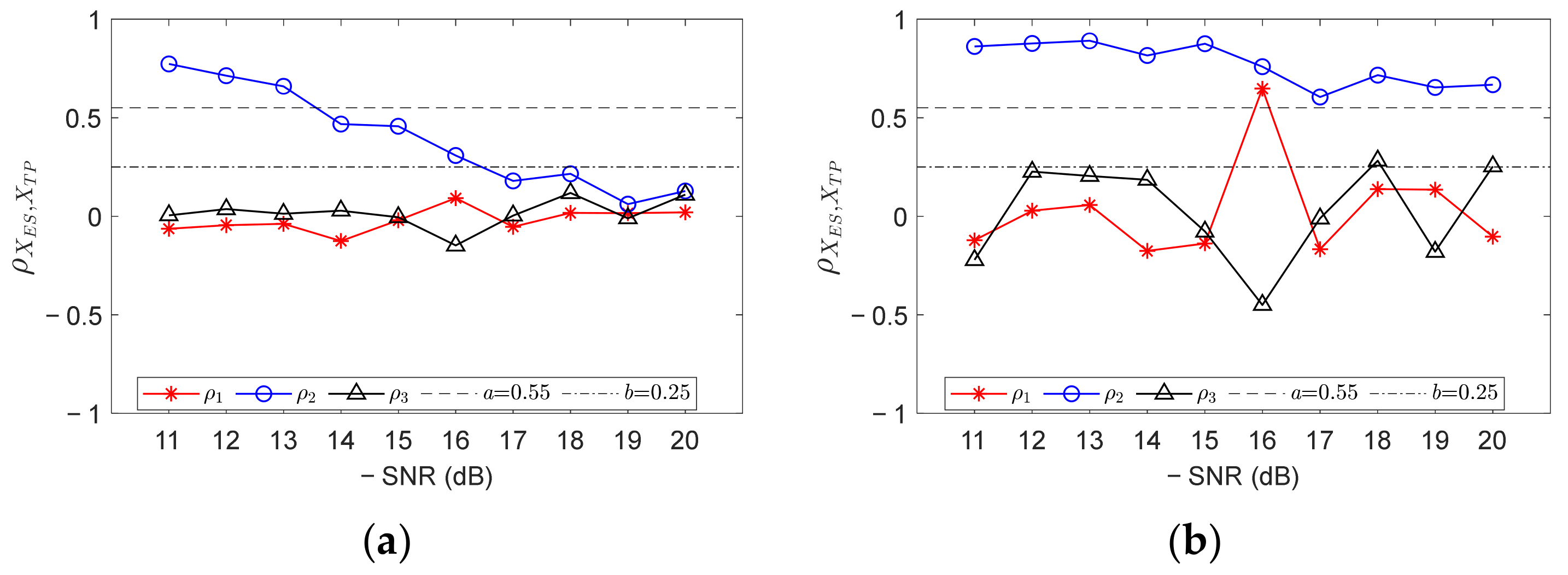
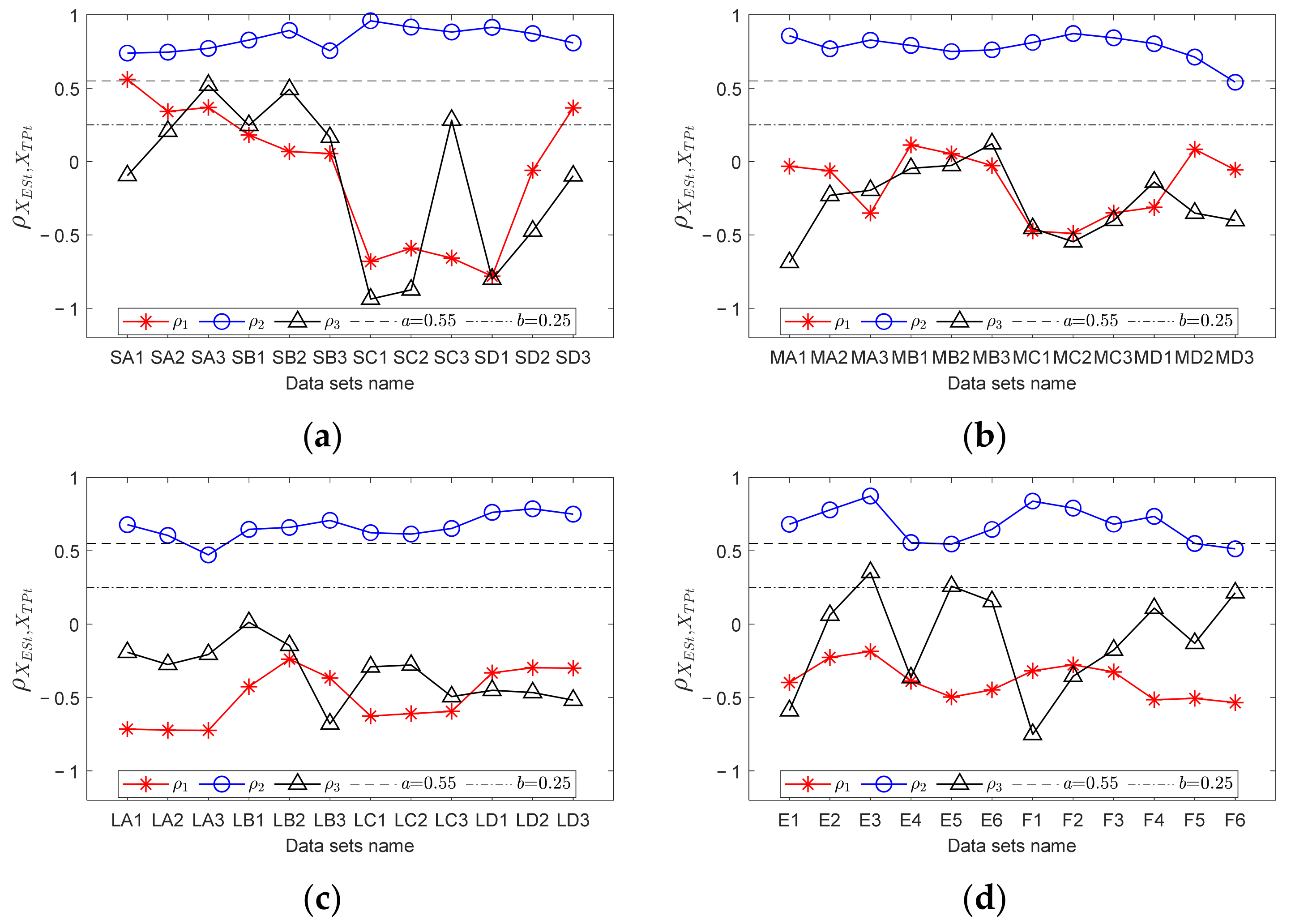
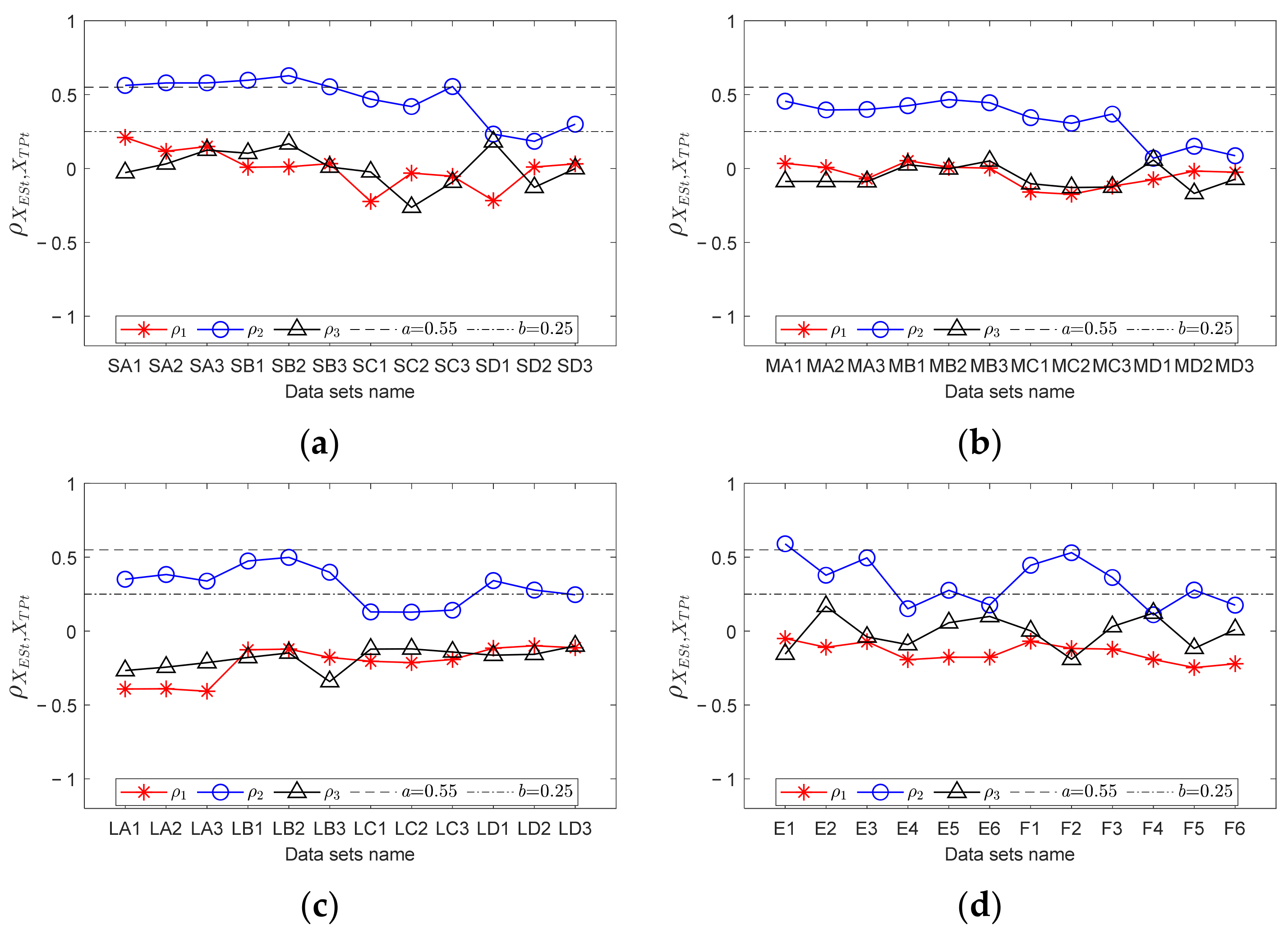
- In FCFBex, utilizeto calculate the correlation coefficients between XESit(f) and XTPit(f), XESot(f) and XTPot(f), and XESrt(f) and XTPrt(f), i.e., ρ1, ρ2, and ρ3. In Equation (12), E, μ, and σ indicate the calculated expectation, mean value, and variance, respectively. Let ρ = [ρ1, ρ2, ρ3], R1 = max(ρ), R2 = mid(ρ);
- Preset a and b (a,b ∈ [−1,1], a > b) as the upper and lower limits of the correlation coefficients. The values of a and b can be determined with trial and error when bearing fault signal samples can be obtained in advance. Output the diagnostic result according to the judgment rule at the bottom side of Figure 10. Other cases may include compound faults, which will not be studied in this paper.
4. Experiment Validation
4.1. Experiment One: Inner Race Fault
4.2. Experiment Two: Outer Race Faults
5. Comparison Verification and Discussion
5.1. Comparison Method One: COT
5.2. Comparison Method Two: MTFCE
5.3. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| RF Range | RF Variation Mode | |||
|---|---|---|---|---|
| Increasing | Decreasing | Increasing then Decreasing | Decreasing then Increasing | |
| Small | S-A-1 (12.5–15.0) S-A-2 (12.9–15.5) S-A-3 (13.4–16.2) | S-B-1 (12.1–10.1) S-B-2 (15.8–13.2) S-B-3 (14.4–12.0) | S-C-1 (20.0–24.0–20.0) S-C-2 (19.3–26.1–19.3) S-C-3 (17.8–21.4–17.8) | S-D-1 (18.8–15.2–18.2) S-D-2 (18.4–15.4–18.4) S-D-3 (19.4–16.2–19.4) |
| Medium | M-A-1 (12.5–18.7) M-A-2 (12.9–19.4) M-A-3 (13.5–20.2) | M-B-1 (15.2–10.1) M-B-2 (19.7–13.2) M-B-3 (18.0–12.0) | M-C-1 (16–24–18.5) M-C-2 (15.4–23.1–17.9) M-C-3 (14.8–21.4–14.3) | M-D-1 (22.8–15.2–19.4) M-D-2 (23.1–15.4–19.8) M-D-3 (23.0–16.2–23.6) |
| Large | L-A-1 (12.5–27.8) L-A-3 (13.5–28.5) | L-B-1 (24.3–9.9) L-B-3 (25.8–12.0) | - | - |
| RF Range | RF Variation Mode | |||
|---|---|---|---|---|
| Increasing | Decreasing | Increasing then Decreasing | Decreasing then Increasing | |
| Small | 25.0–30.0 Hz S-A-1 (3.60 s) S-A-2 (4.80 s) S-A-3 (6.01 s) | 32.0–26.7 Hz S-B-1 (3.86 s) S-B-2 (5.14 s) S-B-3 (6.44 s) | 6.7–8.00–6.7 Hz S-C-1 (2.20 s) S-C-2 (3.00 s) S-C-3 (4.00 s) | S-D-1 (16.8–14.0–16.8 Hz, 2.76 s) S-D-2 (16.6–13.8–16.6 Hz, 3.43 s) S-D-3 (16.5–13.7–16.5 Hz, 4.38 s) |
| Medium | 13.3–20.0 Hz M-A-1 (4.80 s) M-A-2 (6.41 s) M-A-3 (8.01 s) | 25.0–16.7 Hz M-B-1 (6.01 s) M-B-2 (8.02 s) M-B-3 (10.02 s) | 8.8–13.2–8.8 Hz M-C-1 (7.54 s) M-C-2 (10.31 s) M-C-3 (13.77 s) | M-D-1 (21.1–14.0–21.1 Hz, 6.06 s) M-D-2 (20.8–13.8–20.8 Hz, 7.88 s) M-D-3 (20.6–13.7–20.6 Hz, 10.26 s) |
| Large | 5.0–11.0 Hz L-A-1 (4.32 s) L-A-2 (5.76 s) L-A-3 (12.00 s) | 7.3–3.3 Hz L-B-1 (2.88 s) L-B-2 (3.84 s) L-B-3 (4.80 s) | 6.0–13.2–6.0 Hz L-C-1 (12.15 s) L-C-2 (16.60 s) L-C-3 (22.14 s) | L-D-1 (7.9–3.6–7.9 Hz, 10.08 s) L-D-2 (7.7–3.5–7.7 Hz, 13.11 s) L-D-3 (7.8–3.6–7.8 Hz, 17.84 s) |
| Increasing from 0 Hz | 0–5 Hz E-1 (3.60 s) E-2 (4.82 s) E-3 (6.01 s) 0–10 Hz E-4 (7.20 s) E-5 (9.62 s) E-6 (12.01 s) | |||
| Decreasing to 0 Hz | 5–0 Hz F-1 (3.60 s) F-2 (4.81 s) F-3 (6.01 s) 10–0 Hz F-4 (7.20 s) F-5 (9.61 s) F-6 (12.02 s) | |||
References
- Randall, R.B.; Antoni, J. Rolling element bearing diagnostics—A tutorial. Mech. Syst. Signal Process. 2011, 25, 485–520. [Google Scholar] [CrossRef]
- Antoni, J. Fast computation of the kurtogram for the detection of transient faults. Mech. Syst. Signal Process. 2007, 21, 108–124. [Google Scholar] [CrossRef]
- Wodecki, J. Time-Varying Spectral Kurtosis: Generalization of Spectral Kurtosis for Local Damage Detection in Rotating Machines under Time-Varying Operating Conditions. Sensors 2021, 21, 3590. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.-C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. London. Ser. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, N.E. Ensemble empirical mode decomposition: A noise-assisted data analysis method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Yeh, J.-R.; Shieh, J.-S.; Huang, N.E. Complementary Ensemble Empirical Mode Decomposition: A Novel Noise Enhanced Data Analysis Method. Adv. Adapt. Data Anal. 2011, 2, 135–156. [Google Scholar] [CrossRef]
- Torres, M.E.; Colominas, M.A.; Schlotthauer, G.; Flandrin, P. A Complete Ensemble Empirical Mode Decomposition with Adaptive Noise. In Proceedings of the 2011 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Prague, Czech Republic, 22–27 May 2011; pp. 4144–4147. [Google Scholar]
- Sawalhi, N.; Randall, R.; Endo, H. The enhancement of fault detection and diagnosis in rolling element bearings using minimum entropy deconvolution combined with spectral kurtosis. Mech. Syst. Signal Process. 2007, 21, 2616–2633. [Google Scholar] [CrossRef]
- McDonald, G.L.; Zhao, Q.; Zuo, M.J. Maximum correlated Kurtosis deconvolution and application on gear tooth chip fault detection. Mech. Syst. Signal Process. 2012, 33, 237–255. [Google Scholar] [CrossRef]
- McDonald, G.L.; Zhao, Q. Multipoint Optimal Minimum Entropy Deconvolution and Convolution Fix: Application to vibration fault detection. Mech. Syst. Signal Process. 2017, 82, 461–477. [Google Scholar] [CrossRef]
- Lin, J.; Zhao, M. A Review and Strategy for the Diagnosis of Speed-Varying Machinery. In Proceedings of the 2014 International Conference on Prognostics and Health Management, Cheney, WA, USA, 22–25 June 2014; pp. 1–9. [Google Scholar]
- Fyfe, K.; Munck, E. Analysis of Computed Order Tracking. Mech. Syst. Signal Process. 1997, 11, 187–205. [Google Scholar] [CrossRef]
- Ming, A.; Zhang, W.; Qin, Z.; Chu, F. Fault feature extraction and enhancement of rolling element bearing in varying speed condition. Mech. Syst. Signal Process. 2016, 76–77, 367–379. [Google Scholar] [CrossRef]
- Randall, R.B.; Smith, W.A. Bearing Diagnostics Under Widely Varying Speed Conditions. In Proceedings of the 4th International Conference on Condition Monitoring of Machinery in Non-Stationary Operations, Lyon, France, 15–16 December 2014; pp. 15–16. [Google Scholar]
- Zhao, M.; Lin, J.; Xu, X.; Lei, Y. Tacholess Envelope Order Analysis and Its Application to Fault Detection of Rolling Element Bearings with Varying Speeds. Sensors 2013, 13, 10856–10875. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Yang, C.; Zhuang, X.; Liu, H.; Wang, Z. Unknown bearing fault diagnosis under time-varying speed conditions and strong noise background. Nonlinear Dyn. 2022, 107, 2177–2193. [Google Scholar] [CrossRef]
- Borghesani, P.; Ricci, R.; Chatterton, S.; Pennacchi, P. A new procedure for using envelope analysis for rolling element bearing diagnostics in variable operating conditions. Mech. Syst. Signal Process. 2013, 38, 23–35. [Google Scholar] [CrossRef]
- Li, Y.; Zhao, H.; Fan, W.; Shen, C. Generalized Autocorrelation Method for Fault Detection Under Varying-Speed Working Conditions. IEEE Trans. Instrum. Meas. 2021, 70, 1–11. [Google Scholar] [CrossRef]
- Cheng, W.; Gao, R.X.; Wang, J.; Wang, T.; Wen, W.; Li, J. Envelope deformation in computed order tracking and error in order analysis. Mech. Syst. Signal Process. 2014, 48, 92–102. [Google Scholar] [CrossRef]
- Lu, S.; Yan, R.; Liu, Y.; Wang, Q. Tacholess Speed Estimation in Order Tracking: A Review with Application to Rotating Machine Fault Diagnosis. IEEE Trans. Instrum. Meas. 2019, 68, 2315–2332. [Google Scholar] [CrossRef]
- Zhu, H.; He, Z.; Wei, J.; Wang, J.; Zhou, H. Bearing Fault Feature Extraction and Fault Diagnosis Method Based on Feature Fusion. Sensors 2021, 21, 2524. [Google Scholar] [CrossRef]
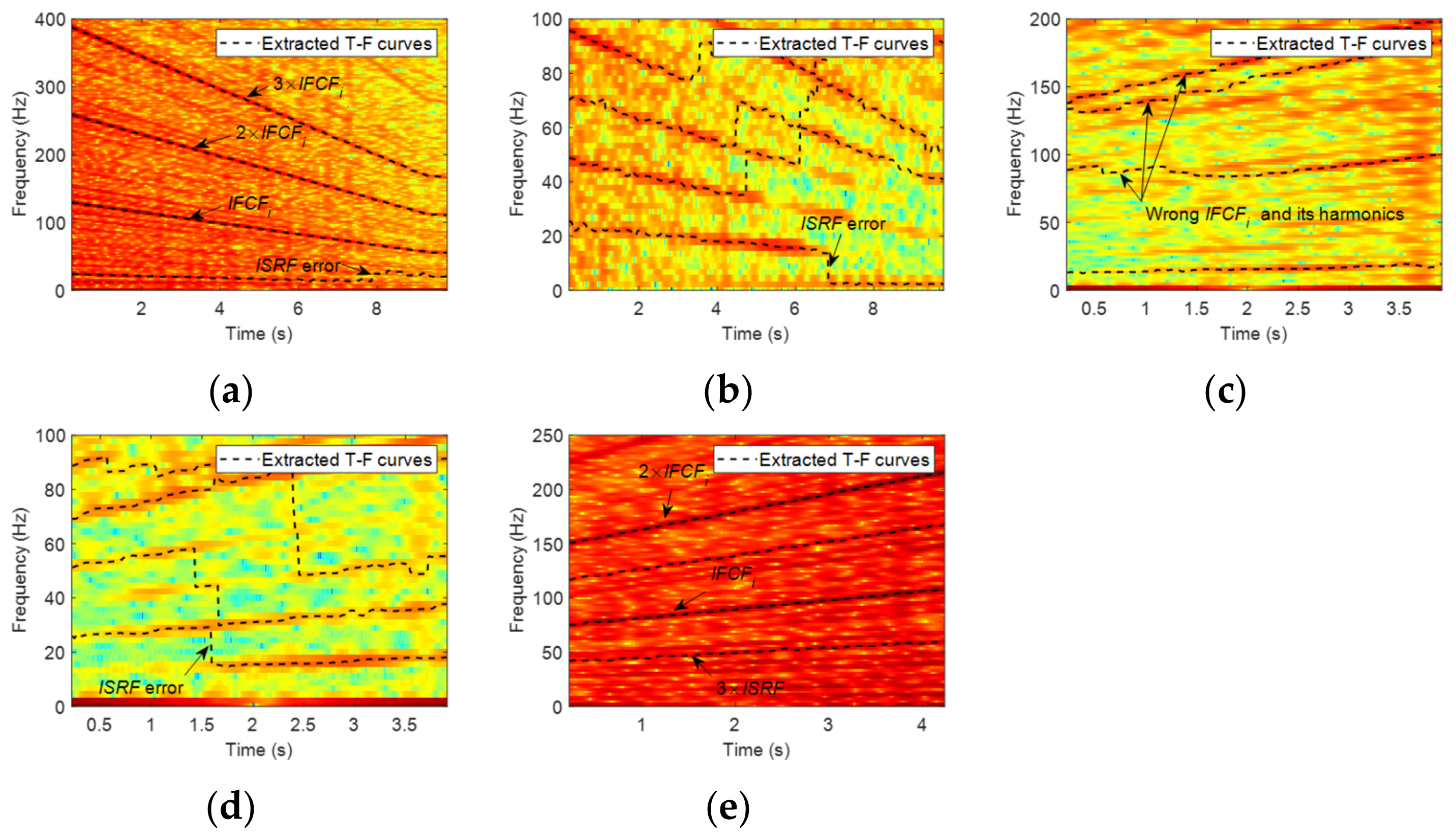
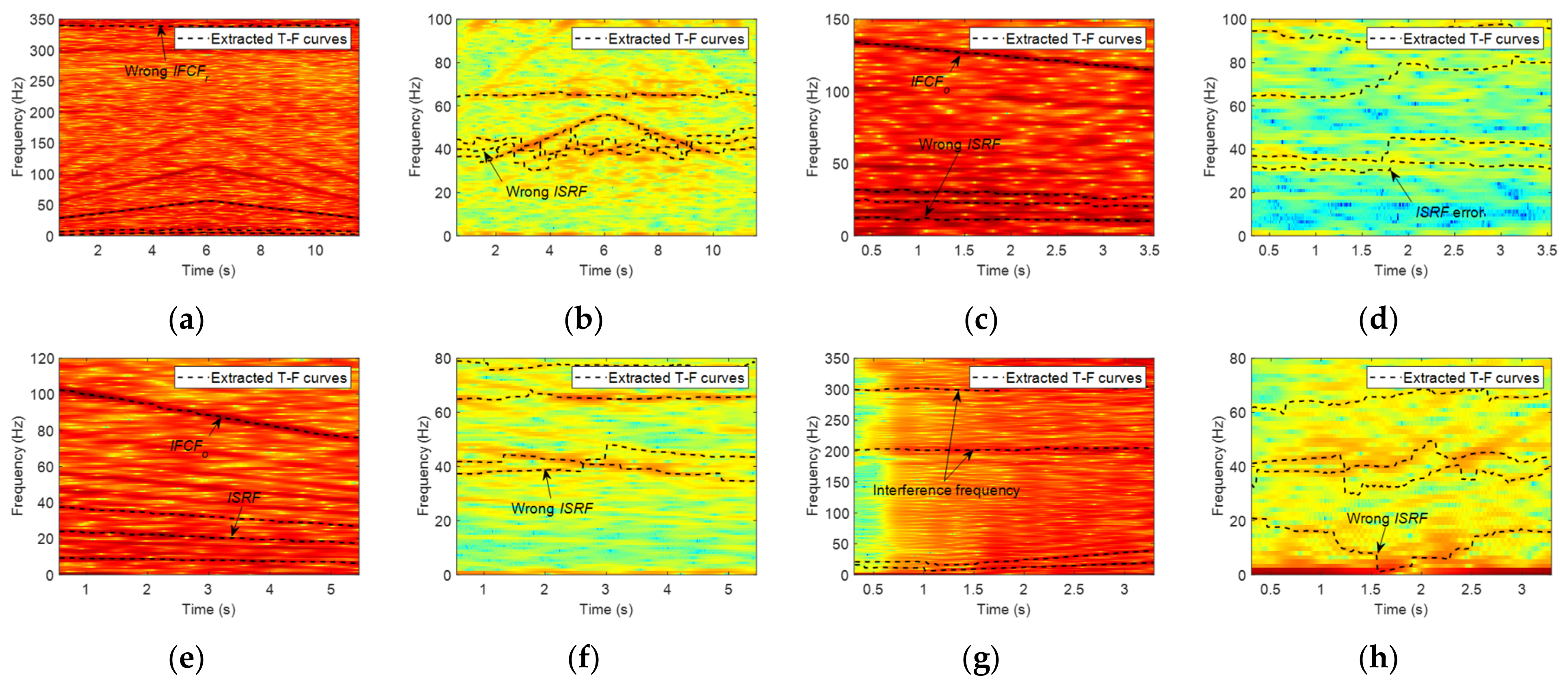
- Huang, H.; Baddour, N.; Liang, M. Multiple time-frequency curve extraction Matlab code and its application to automatic bearing fault diagnosis under time-varying speed conditions. MethodsX 2019, 6, 1415–1432. [Google Scholar] [CrossRef]
- Huang, H.; Baddour, N.; Liang, M. A method for tachometer-free and resampling-free bearing fault diagnostics under time-varying speed conditions. Measurement 2018, 134, 101–117. [Google Scholar] [CrossRef]
- Huang, H.; Baddour, N.; Liang, M. Bearing fault diagnosis under unknown time-varying rotational speed conditions via multiple time-frequency curve extraction. J. Sound Vib. 2018, 414, 43–60. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, X.; Chen, Z.; Yang, Y.; Geng, C.; Zuo, M.J. Time-frequency ridge estimation: An effective tool for gear and bearing fault diagnosis at time-varying speeds. Mech. Syst. Signal Process. 2023, 189, 110108. [Google Scholar] [CrossRef]
- Tang, G.; Wang, Y.; Huang, Y.; Wang, H. Multiple Time-Frequency Curve Classification for Tacho-Less and Resampling-Less Compound Bearing Fault Detection Under Time-Varying Speed Conditions. IEEE Sensors J. 2020, 21, 5091–5101. [Google Scholar] [CrossRef]
- Hou, F.; Selesnick, I.; Chen, J.; Dong, G. Fault diagnosis for rolling bearings under unknown time-varying speed conditions with sparse representation. J. Sound Vib. 2021, 494, 115854. [Google Scholar] [CrossRef]
- Feng, Z.; Chen, X.; Wang, T. Time-varying demodulation analysis for rolling bearing fault diagnosis under variable speed conditions. J. Sound Vib. 2017, 400, 71–85. [Google Scholar] [CrossRef]
- Liu, Q.; Wang, Y.; Xu, Y. Synchrosqueezing extracting transform and its application in bearing fault diagnosis under non-stationary conditions. Measurement 2020, 173, 108569. [Google Scholar] [CrossRef]
- Wang, T.; Liang, M.; Li, J.; Cheng, W. Rolling element bearing fault diagnosis via fault characteristic order (FCO) analysis. Mech. Syst. Signal Process. 2014, 45, 139–153. [Google Scholar] [CrossRef]
- Urbanek, J.; Barszcz, T.; Antoni, J. A two-step procedure for estimation of instantaneous rotational speed with large fluctuations. Mech. Syst. Signal Process. 2013, 38, 96–102. [Google Scholar] [CrossRef]
- Schmidt, S.; Heyns, P.; de Villiers, J. A tacholess order tracking methodology based on a probabilistic approach to incorporate angular acceleration information into the maxima tracking process. Mech. Syst. Signal Process. 2018, 100, 630–646. [Google Scholar] [CrossRef]
- Zhao, M.; Lin, J.; Wang, X.; Lei, Y.; Cao, J. A tacho-less order tracking technique for large speed variations. Mech. Syst. Signal Process. 2013, 40, 76–90. [Google Scholar] [CrossRef]
- Chen, Y.; Zuo, M.J. A sparse multivariate time series model-based fault detection method for gearboxes under variable speed condition. Mech. Syst. Signal Process. 2022, 167, 108539. [Google Scholar] [CrossRef]
- Chen, Y.; Schmidt, S.; Heyns, P.S.; Zuo, M.J. A time series model-based method for gear tooth crack detection and severity assessment under random speed variation. Mech. Syst. Signal Process. 2021, 156, 107605. [Google Scholar] [CrossRef]
- Wang, K.S.; Heyns, P.S. Application of computed order tracking, Vold-Kalman filtering and EMD in rotating machine vibration. Mech. Syst. Sig. Process. 2011, 25, 416–430. [Google Scholar] [CrossRef]
- Huang, H.; Baddour, N. Bearing vibration data collected under time-varying rotational speed conditions. Data Brief 2018, 21, 1745–1749. [Google Scholar] [CrossRef] [PubMed]
- Smith, W.A.; Randall, R.B. Rolling element bearing diagnostics using the Case Western Reserve University data: A benchmark study. Mech. Syst. Signal Process. 2015, 64–65, 100–131. [Google Scholar] [CrossRef]
- Iatsenko, D.; McClintock, P.; Stefanovska, A. Extraction of instantaneous frequencies from ridges in time–frequency representations of signals. Signal Process. 2016, 125, 290–303. [Google Scholar] [CrossRef]
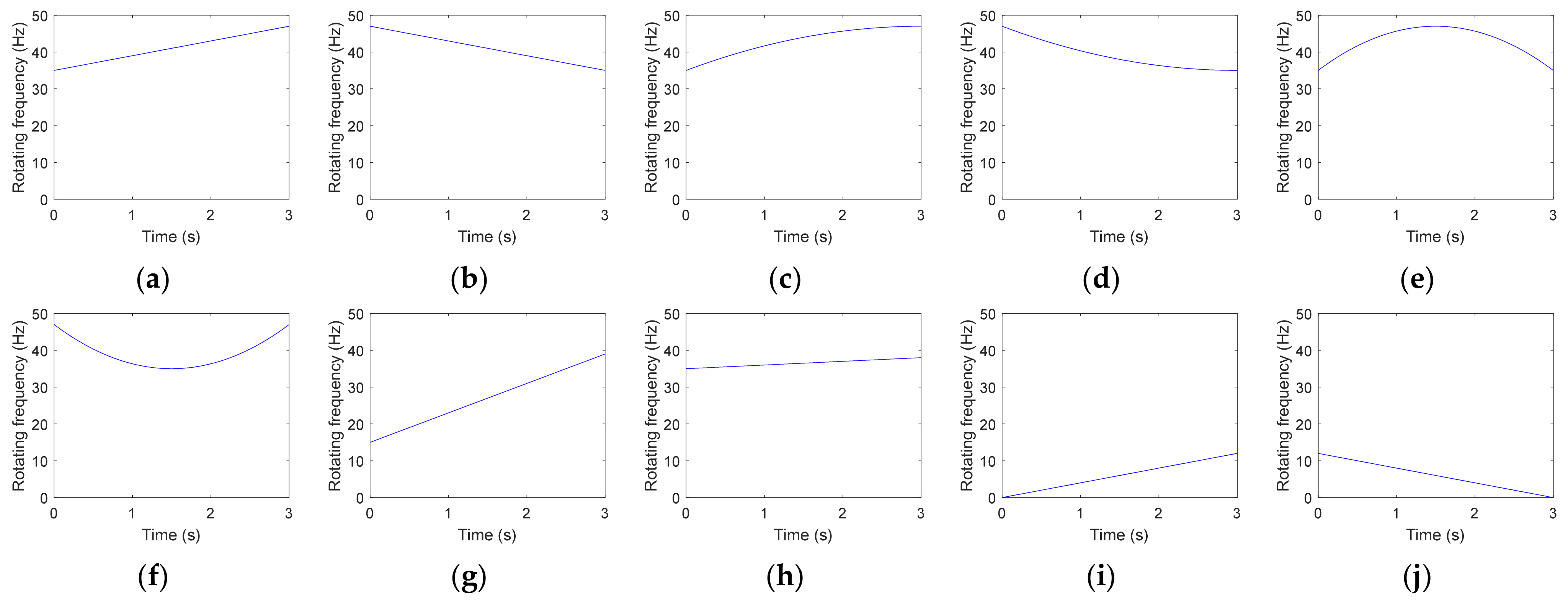
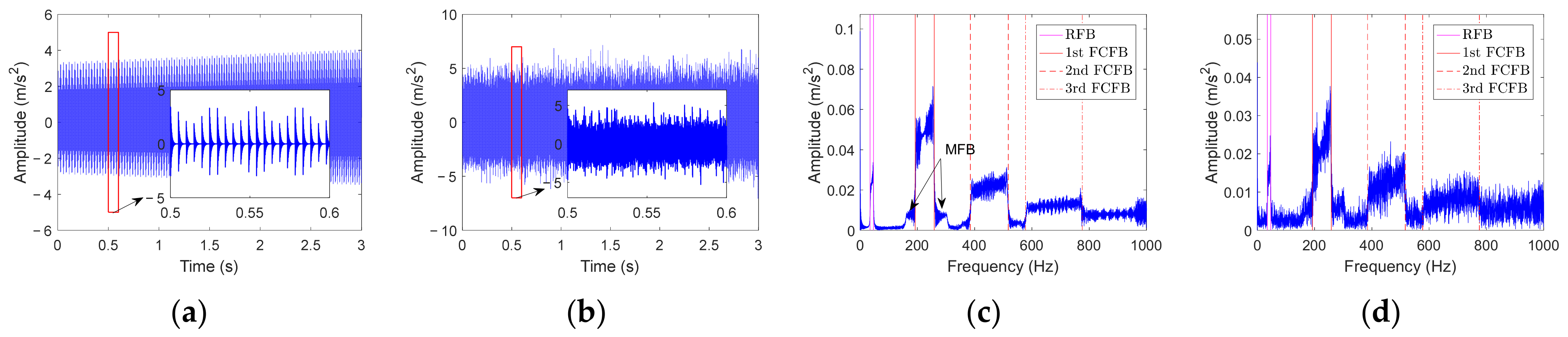
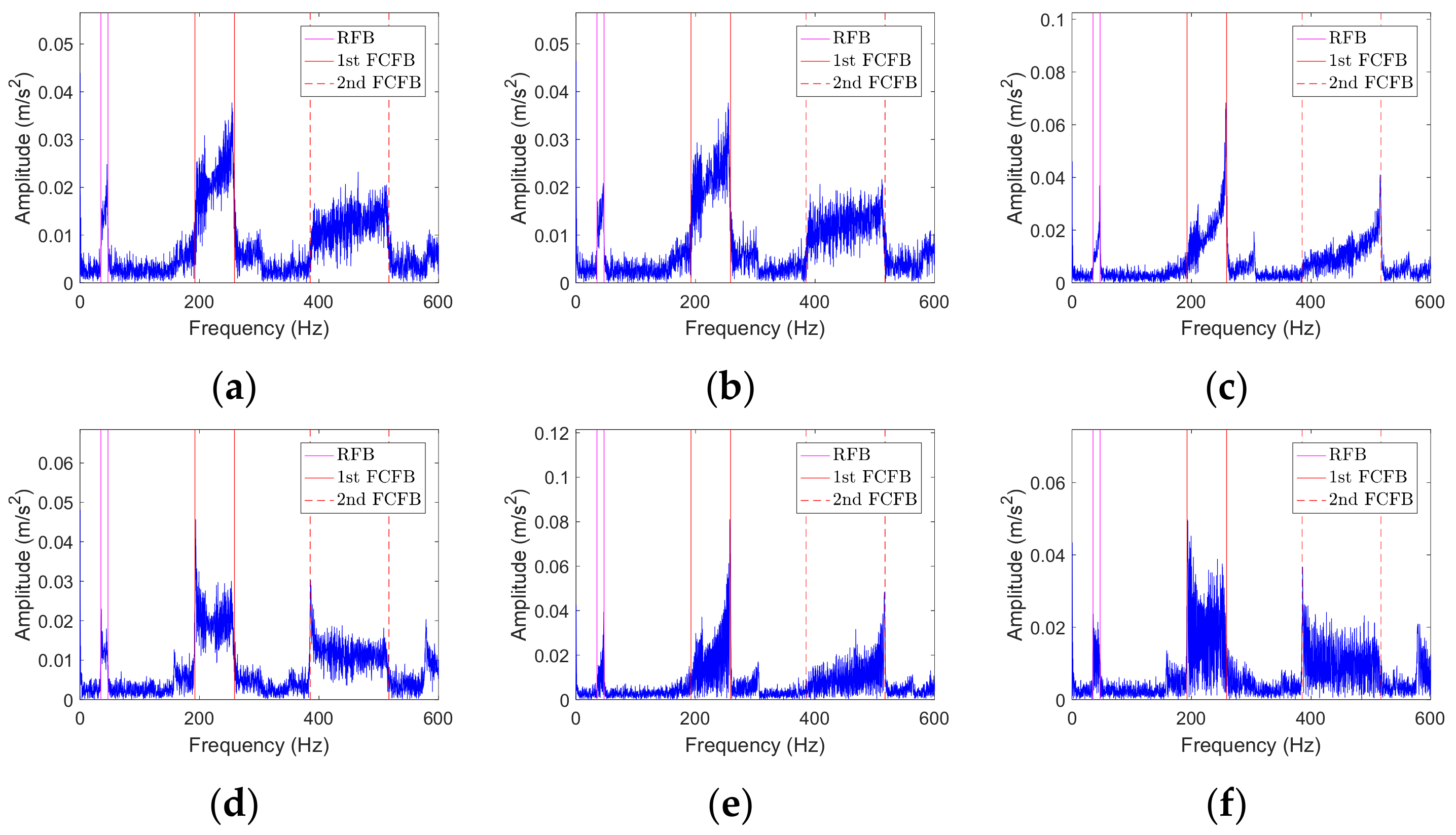

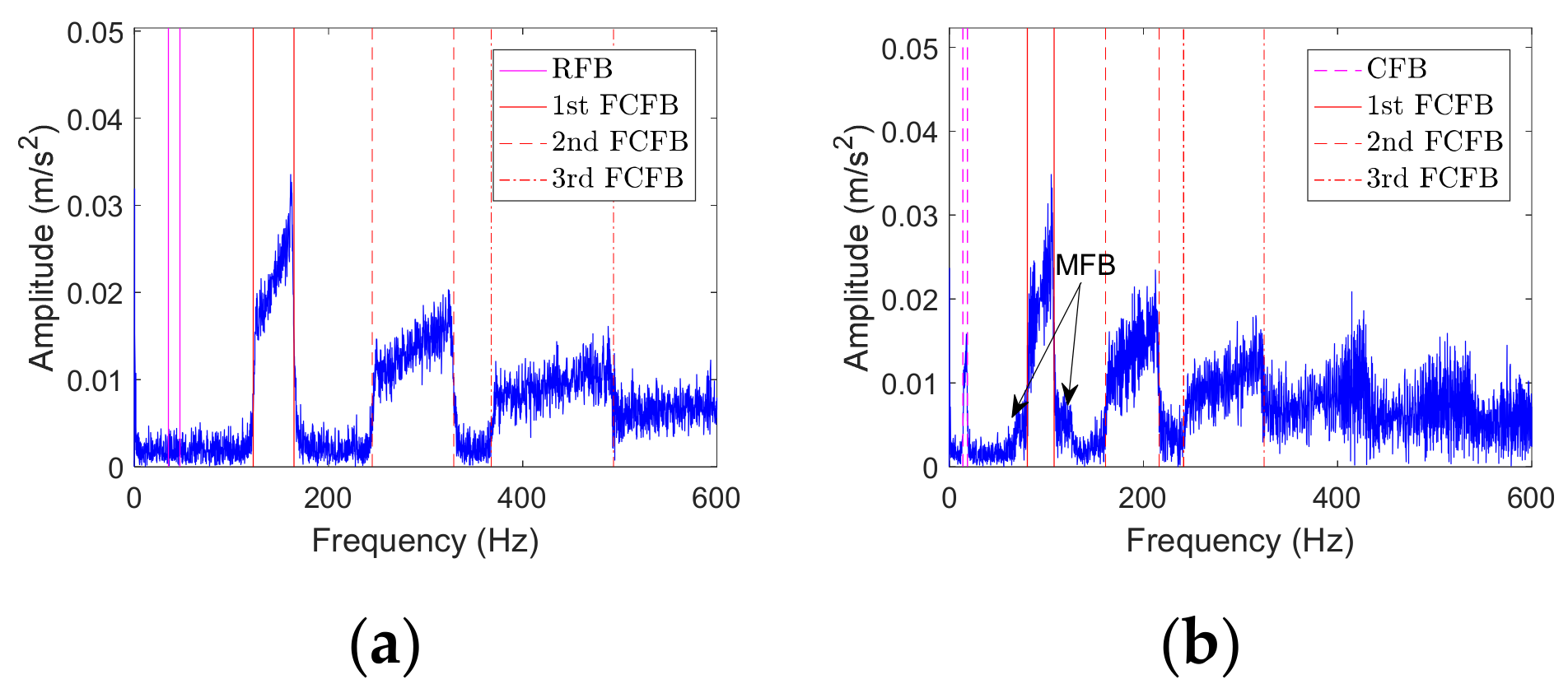









| α | A0 | η | β | ωr | Tt | SNR | FCCi | FCCo | FCCr |
|---|---|---|---|---|---|---|---|---|---|
| 0.3 | 1 | 0.05 | 1500 | 5000 Hz | 3 s | −5 dB | 5.5 | 3.5 | 2.3 |
| RF Variation Modes | Formula |
|---|---|
| Linear increasing | |
| Linear decreasing | |
| Non-linear increasing | |
| Non-linear decreasing | |
| Non-linear increasing then decreasing | |
| Non-linear decreasing then increasing | |
| RF ranges | Formula |
| Large variation range | |
| Small variation range | |
| Increasing from 0 Hz | |
| Decreasing to 0 Hz |
| D/mm | d/mm | z | ϕ/° | FCCi | FCCo | FCCr |
|---|---|---|---|---|---|---|
| 34 | 7.5 | 11 | 0 | 6.71 | 4.29 | 2.16 |
| Type | Peak Amplitude at | Data Sets | Diagnostic Results | ||
|---|---|---|---|---|---|
| 2 × FCCo | 3 × FCCo | 3 × FCCr | |||
| 1 | N | N | Y | S-A-1, S-A-2, S-A-3, S-B-1, S-B-2, S-B-3 | Outer race, rolling element or compound faults (6 data) |
| 2 | Y | N | Y | S-D-1, S-D-2, S-D-3, M-A-1, M-A-3, M-D-1, M-D-2, M-D-3 | Outer race, rolling element or compound faults (8 data) |
| 3 | Y | Y | Y | M-A-2, M-B-1, M-B-2, M-B-3 | Outer race, rolling element or compound faults (4 data) |
| 4 | Y | Y | N | S-C-1, S-C-2, S-C-3, M-C-1, M-C-2, M-C-3, all data under L, E, and F | Outer race fault (30 data) |
| Diagnostic Results | Data Sets |
|---|---|
| Inner race fault (15 data sets) | S-A-1, S-A-3, S-B-2, S-C-1, S-C-2, S-C-3, M-A-2, M-C-1, M-C-2, M-C-3, M-D-1, M-D-2, M-D-3, L-A-3, L-B-3 |
| Healthy (11 data sets) | S-A-2, S-B-1, S-B-3, S-D-1, S-D-2, S-D-3, M-A-1, M-B-2, M-B-3, L-A-1, L-B-1 |
| Outer race fault (2 data sets) | M-A-3, M-B-1 |
| Diagnostic Results | Data Sets |
|---|---|
| Outer race fault (4 data) | S-B-2, S-C-1, L-A-2, L-A-3 |
| Outer race fault by coincidence (3 data sets) | L-C-1, F-1, F-4 |
| Rolling element fault (3 data sets) | S-A-1, M-D-1, M-D-2 |
| Healthy (38 data sets) | Others |
| Method | Theoretical Basis | Diagnostic Accuracy (Inner|Outer Race Fault, %) | Diagnostic Time (Inner|Outer Race Fault|Total Time, s) | Tachometer Dependence | Automatic Degree | |
|---|---|---|---|---|---|---|
| Preset Parameters | Automatic Diagnosis | |||||
| COT | Pseudo-stationary vibration signal in angular domain | 96.4|62.5 | - | High | ΔΦ, k | No |
| MTFCE | TFA of the non-stationary signal and ridge extraction | 53.6|8.3 | 85.6|218.5|304.1 | No | m, w, ol, er_i, er_o, er_r, var_i, var_o, var_r | Yes |
| FCFBI | FCFB in the envelope spectrum | 78.6|77.1 | 187.8|87.2|275 | Low | wl, mdp, ex, a, b | Yes |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pei, D.; Yue, J.; Jiao, J. A Novel Method for Bearing Fault Diagnosis under Variable Speed Based on Envelope Spectrum Fault Characteristic Frequency Band Identification. Sensors 2023, 23, 4338. https://doi.org/10.3390/s23094338
Pei D, Yue J, Jiao J. A Novel Method for Bearing Fault Diagnosis under Variable Speed Based on Envelope Spectrum Fault Characteristic Frequency Band Identification. Sensors. 2023; 23(9):4338. https://doi.org/10.3390/s23094338
Chicago/Turabian StylePei, Di, Jianhai Yue, and Jing Jiao. 2023. "A Novel Method for Bearing Fault Diagnosis under Variable Speed Based on Envelope Spectrum Fault Characteristic Frequency Band Identification" Sensors 23, no. 9: 4338. https://doi.org/10.3390/s23094338
APA StylePei, D., Yue, J., & Jiao, J. (2023). A Novel Method for Bearing Fault Diagnosis under Variable Speed Based on Envelope Spectrum Fault Characteristic Frequency Band Identification. Sensors, 23(9), 4338. https://doi.org/10.3390/s23094338







