A Liquid Metal Temperature Detection System Based on Multi-Node Sapphire Fiber Sensor
Abstract
1. Introduction
2. System Design
3. Sensor Design and Preparation
3.1. Sensitive Area Parameters Design
3.2. Sapphire Fiber Preparation
4. Multi-Node Sensing Simulation Analysis
4.1. Model Construction and Meshing
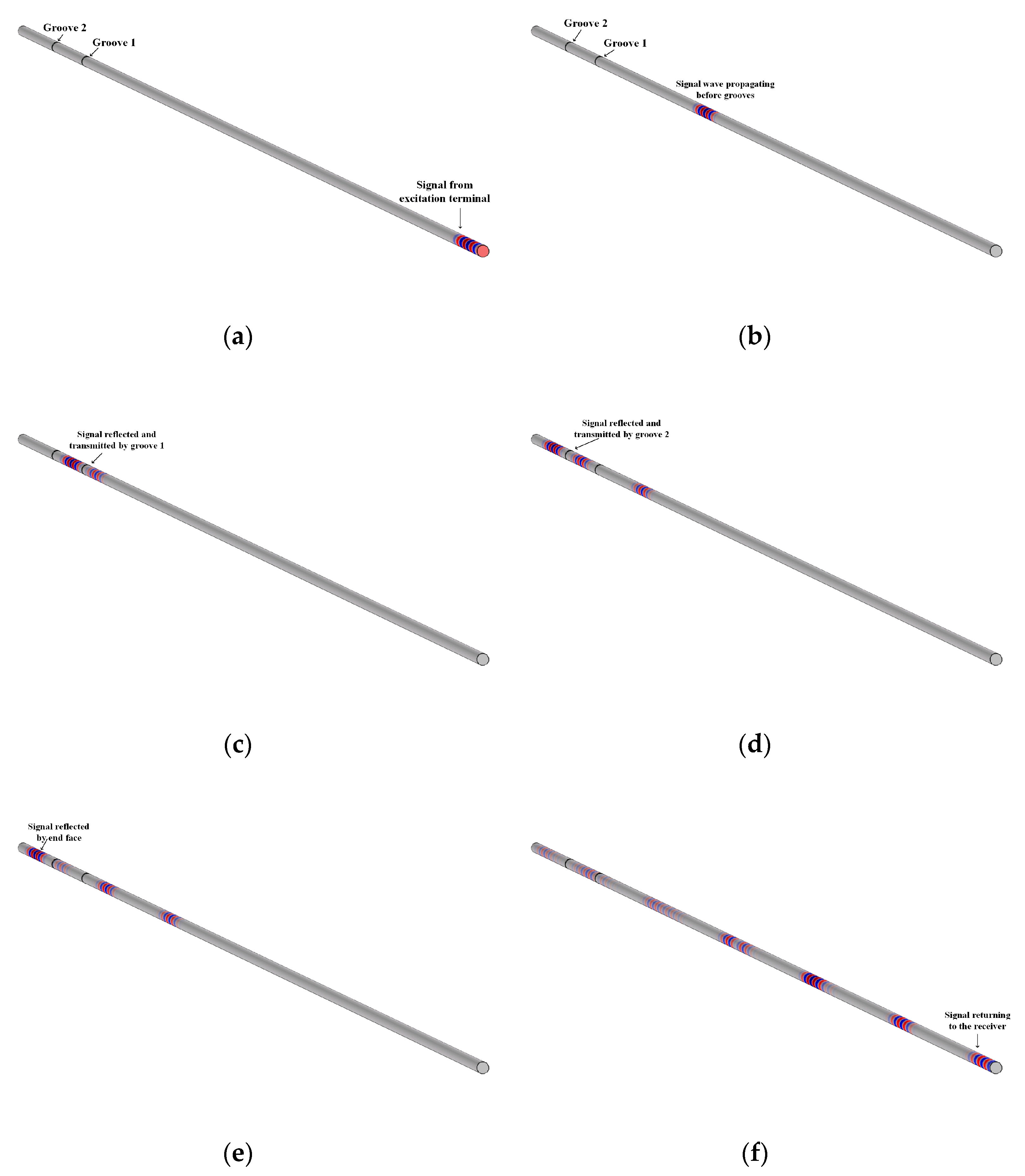
4.2. Simulation and Analysis of Ultrasonic Transmission Characteristics
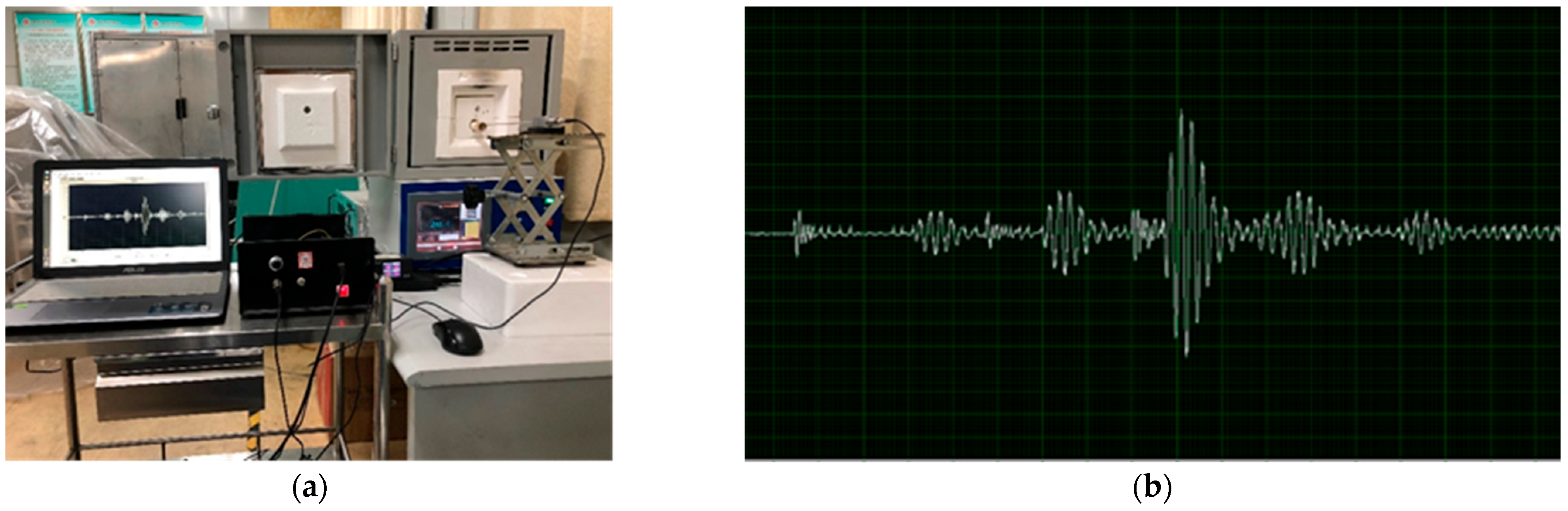
5. Experiments
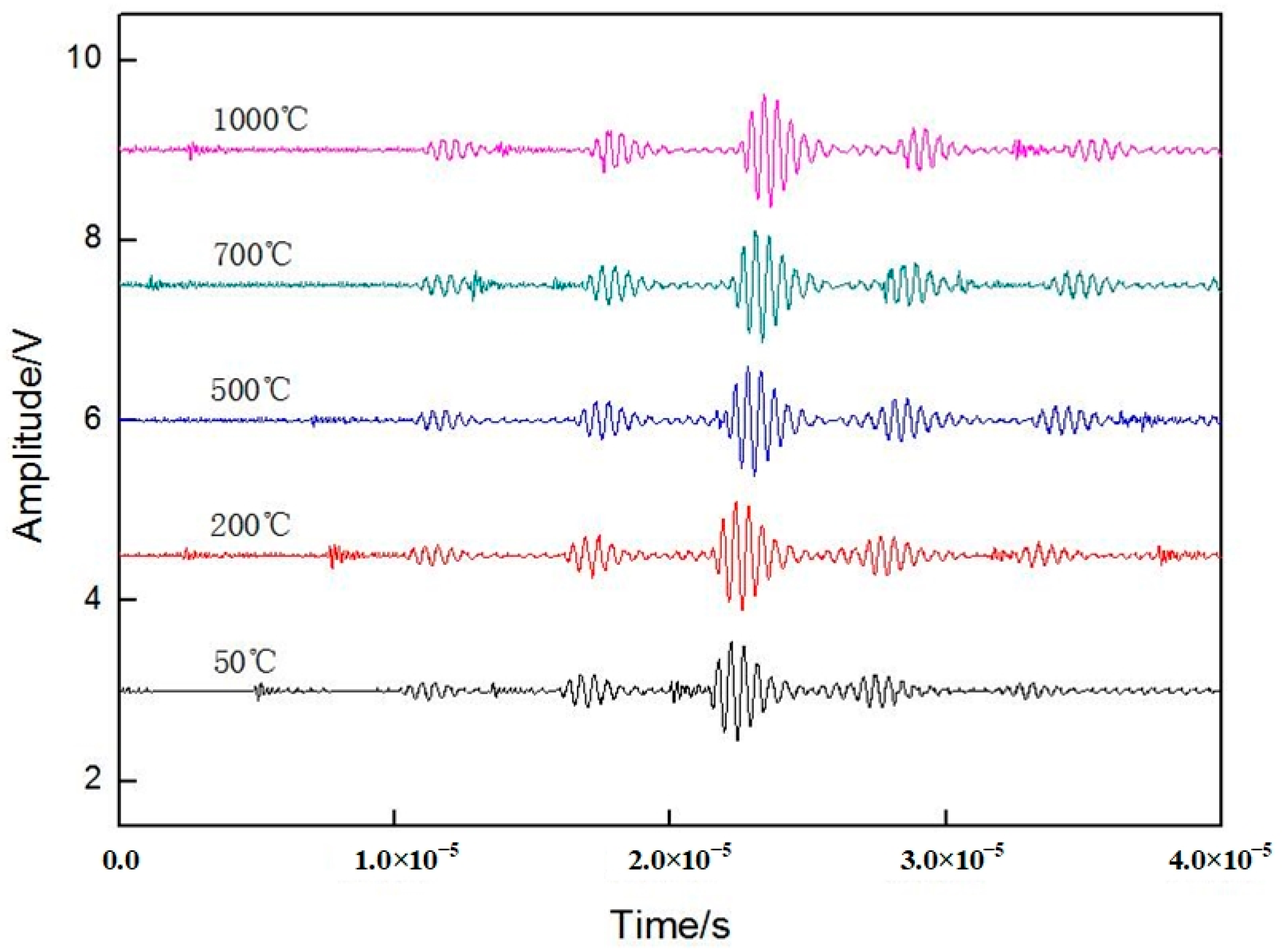
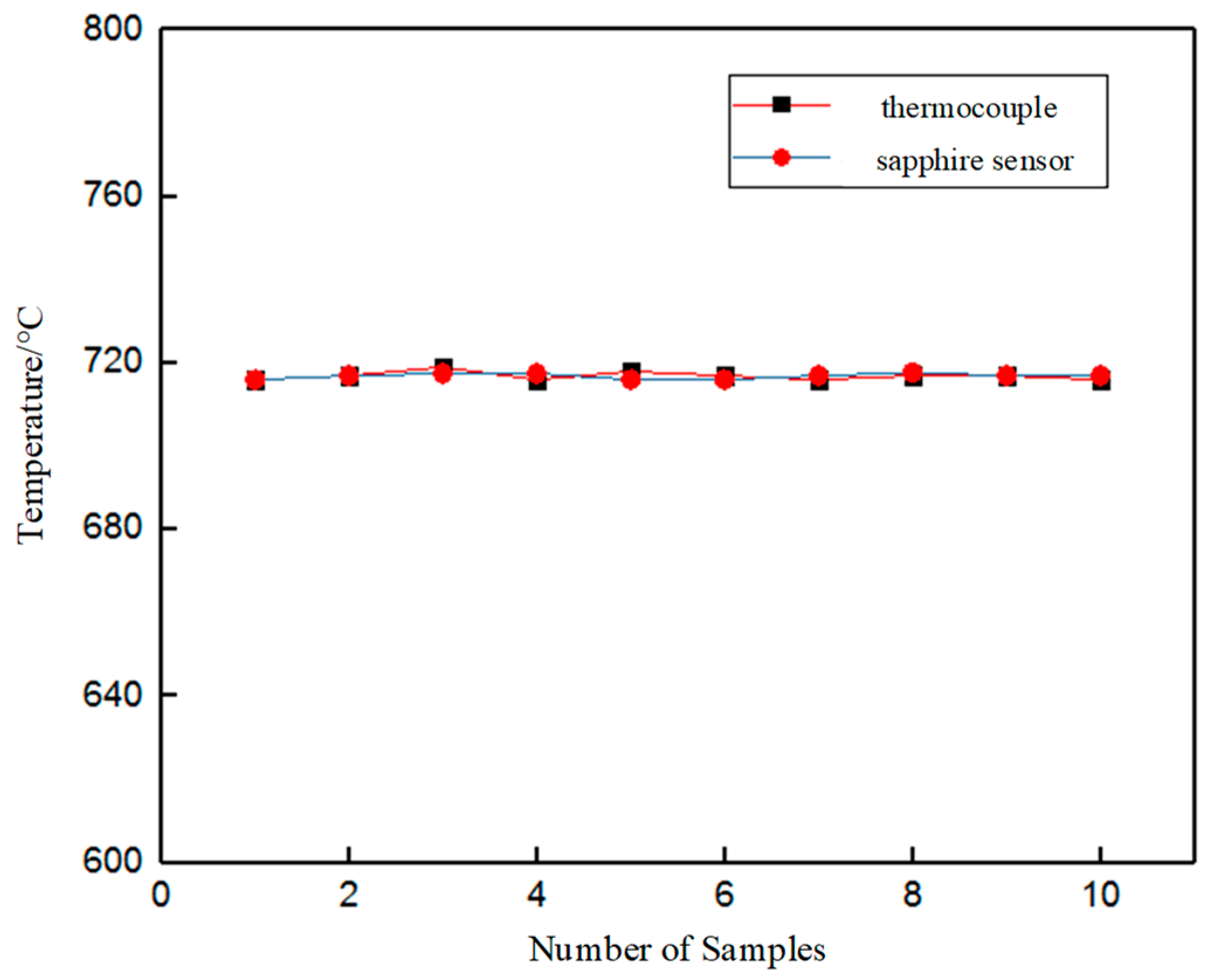
5.1. Static Calibration Experiment
5.2. Temperature Measurement Experiment of Molten Aluminum
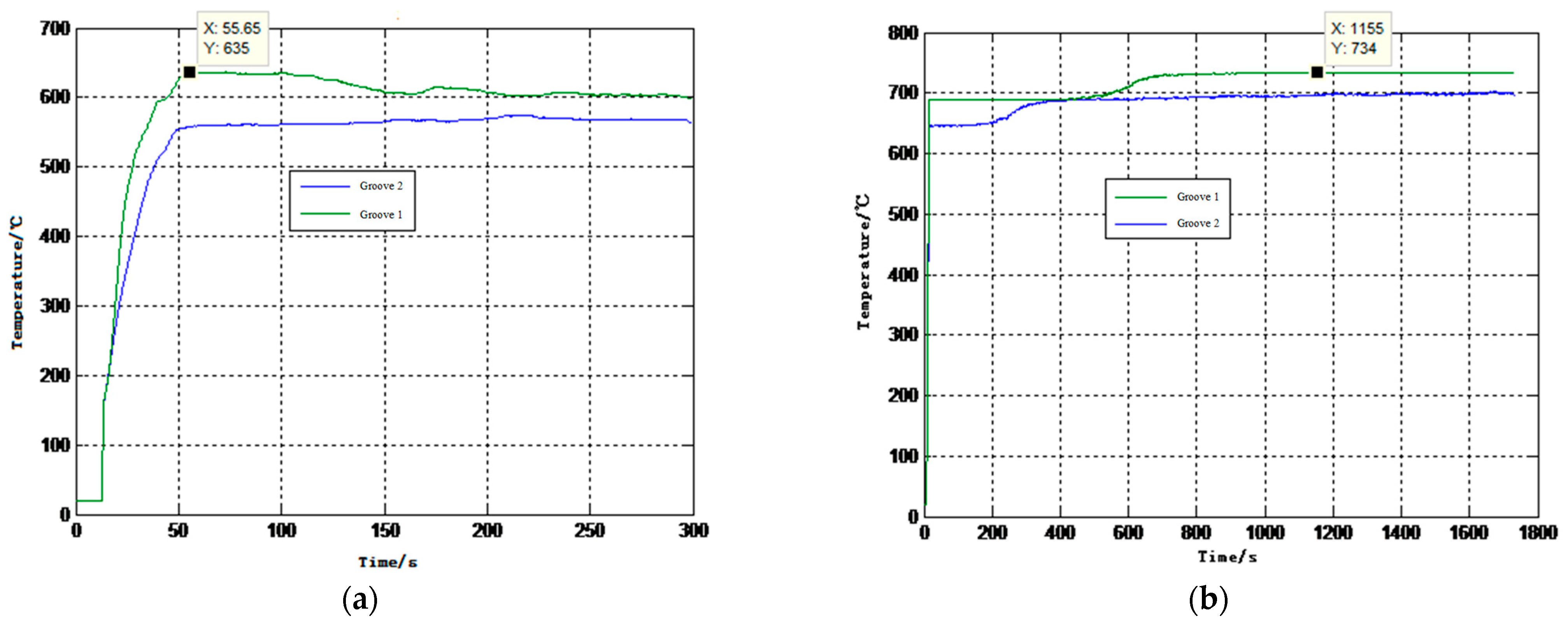
- Process 1: The sensor was inserted into liquid aluminum in the lowest molten state to achieve thermal balance, and the data were continuously collected to obtain the time response curve of the sensor.
- Process 2: The temperature value was set to the upper threshold through the control cabinet, and continuous data collection was conducted during the heating process of the molten aluminum liquid. Since this process was heated by means of a furnace wall-air-dry pot heat exchange, the heating process was relatively slow, and long-term continuous data acquisition was required to obtain the heating curve of the temperature over time.
5.3. Discussions
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bate, C.; King, P.; Sim, J.; Manogharan, G. A Novel Approach to Visualize Liquid Aluminum Flow to Advance Casting Science. Materials 2023, 16, 756. [Google Scholar] [CrossRef] [PubMed]
- Joshi, T.C.; Prakash, U.; Dabhade, V.V. Microstructural development during hot forging of Al 7075 powder. J. Alloys Compd. 2015, 639, 123–130. [Google Scholar] [CrossRef]
- Abdulhadi, H.A.; Ahmad, S.N.A.S.; Ismail, I.; Ishak, M.; Mohammed, G.R. Thermally-Induced Crack Evaluation in H13 Tool Steel. Metals 2017, 7, 475. [Google Scholar] [CrossRef]
- Zhou, W.; Lin, J.; Dean, T.A.; Wang, L. Analysis and modelling of a novel process for extruding curved metal alloy profiles. Int. J. Mech. Sci. 2018, 138–139, 524–536. [Google Scholar] [CrossRef]
- Brough, D.; Jouhara, H. The aluminium industry: A review on state-of-the-art technologies, environmental impacts and possibilities for waste heat recovery. Int. J. Thermofluids 2020, 1–2, 100007. [Google Scholar] [CrossRef]
- Chun, S.-Y.; Lee, G.; Kim, S.-J.; Jeong, B.; Shin, J.; Cho, I.; Kim, H.-D.; Lee, H.; Kim, T. Effects of Post-Treatment to Improve the Surface Quality of 3D Printing Cement Mold Casting. Appl. Sci. 2021, 11, 11824. [Google Scholar] [CrossRef]
- Bai, Z.; Su, N.; Yang, H.; Wu, X. Research on the Corrosion Behaviors of Austenitic Steel in Molten Aluminum Alloy. Coatings 2022, 12, 551. [Google Scholar] [CrossRef]
- Kukharova, T.V.; Ilyushin, Y.V.; Asadulagi, M.-A.M. Investigation of the OA-300M Electrolysis Cell Temperature Field of Metallurgical Production. Energies 2022, 15, 9001. [Google Scholar] [CrossRef]
- Zhang, X.; Friedrich, S.; Friedrich, B. Characterization and Interpretation of the Aluminum Zone Refining through Infrared Thermographic Analysis. Materials 2018, 11, 2039. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Xu, X.; Liu, W.; Huang, L.; Li, H.; Wu, C.; Mu, W.; Li, X. Study on the Influence of Surface Temperature Field of Aluminum Alloy Etched by Laser Water Jet Composite Machining. Materials 2020, 13, 3206. [Google Scholar] [CrossRef] [PubMed]
- Kim, M.-J.; Yun, J.P.; Yang, J.-B.-R.; Choi, S.-J.; Kim, D. Prediction of the Temperature of Liquid Aluminum and the Dissolved Hydrogen Content in Liquid Aluminum with a Machine Learning Approach. Metals 2020, 10, 330. [Google Scholar] [CrossRef]
- Heeley, A.D.; Hobbs, M.J.; Laalej, H.; Willmott, J.R. Miniature Uncooled and Unchopped Fiber Optic Infrared Thermometer for Application to Cutting Tool Temperature Measurement. Sensors 2018, 18, 3188. [Google Scholar] [CrossRef] [PubMed]
- Leonidas, E.; Ayvar-Soberanis, S.; Laalej, H.; Fitzpatrick, S.; Willmott, J.R. A Comparative Review of Thermocouple and Infrared Radiation Temperature Measurement Methods during the Machining of Metals. Sensors 2022, 22, 4693. [Google Scholar] [CrossRef] [PubMed]
- Bramanti, M.; Salerno, E.A.; Tonazzini, A.; Pasini, S.; Gray, A. An acoustic pyrometer system for tomographic thermal imaging in power plant boilers. IEEE Trans. Instrum. Meas. 1996, 45, 159–167. [Google Scholar] [CrossRef]
- Young, K.J.; Ireland, S.N.; Melendez-Cervates, M.C.; Stones, R. On the systematic error associated with the measurement of temperature using acoustic pyrometry in combustion products of unknown mixture. Meas. Sci. Technol. 1998, 9, 1. [Google Scholar] [CrossRef]
- Lu, J.; Wakai, K.; Takahashi, S.; Shimizu, S. Acoustic computer tomographic pyrometry for two-dimensional measurement of gases taking into account the effect of refraction of sound wave paths. Meas. Sci. Technol. 2000, 11, 692. [Google Scholar] [CrossRef]
- Qiwei, H.; Zhengqian, Y.; Yanqin, L.; Guoyin, T.; Huaichun, Z. Acoustic measurement device of furnace velocity field. Autom. Instrum. 2003, 3, 42–45. [Google Scholar]
- Guoyin, T. Experimental Research on Reconstruction of Velocity Field in Furnace Using Acoustic Measurement; Huazhong University of Science & Technology: Wuhan, China, 2004. [Google Scholar]
- Kobayashi, M.; Jen, C.K.; Bussiere, J.F.; Wu, K.T. High-temperature integrated and flexible ultrasonic transducers for nondestructive testing. NDT E Int. 2009, 42, 157–161. [Google Scholar] [CrossRef]
- Bufetova, G.A.; Rusanov, S.Y.; Seregin, V.F.; Pyrkov, Y.N.; Kamynin, V.A.; Tsvetkov, V.B. Temperature distribution across the growth zone of sapphire (Al2O3) and yttrium–aluminum garnet (YAG) single crystal fibers. J. Cryst. Growth 2016, 433, 54–58. [Google Scholar] [CrossRef]
- Bufetova, G.A.; Rusanov, S.Y.; Seregin, V.F.; Pyrkov, Y.N.; Tsvetkov, V.B. Temperature and emissivity measurements at the sapphire single crystal fiber growth process. J. Cryst. Growth 2017, 480, 85–89. [Google Scholar] [CrossRef]
- Carlson, G.A.; Sullivan, W.H.; Plein, H.G.; Kerley, T.M. Ultrasonic Thermometry System for Measuring Very High Temperatures in Reactor Safety Experiments; United States. 1979. Available online: https://www.osti.gov/servlets/purl/12177640 (accessed on 14 April 2023).







Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, G.; Qian, C.; Sun, P.; Li, Z.; Chen, G.; Wang, B.; Zhou, H.; Yu, J. A Liquid Metal Temperature Detection System Based on Multi-Node Sapphire Fiber Sensor. Sensors 2023, 23, 4318. https://doi.org/10.3390/s23094318
Wang G, Qian C, Sun P, Li Z, Chen G, Wang B, Zhou H, Yu J. A Liquid Metal Temperature Detection System Based on Multi-Node Sapphire Fiber Sensor. Sensors. 2023; 23(9):4318. https://doi.org/10.3390/s23094318
Chicago/Turabian StyleWang, Gao, Chengyuan Qian, Peng Sun, Zhiling Li, Guofeng Chen, Bingyin Wang, Hanchang Zhou, and Junzhi Yu. 2023. "A Liquid Metal Temperature Detection System Based on Multi-Node Sapphire Fiber Sensor" Sensors 23, no. 9: 4318. https://doi.org/10.3390/s23094318
APA StyleWang, G., Qian, C., Sun, P., Li, Z., Chen, G., Wang, B., Zhou, H., & Yu, J. (2023). A Liquid Metal Temperature Detection System Based on Multi-Node Sapphire Fiber Sensor. Sensors, 23(9), 4318. https://doi.org/10.3390/s23094318





