A Magnetic Levitation System for Range/Sensitivity-Tunable Measurement of Density
Abstract
1. Introduction
2. Materials and Methods
2.1. Design of M-MagLev System
2.2. Theoretical Method
2.3. Materials
3. Results
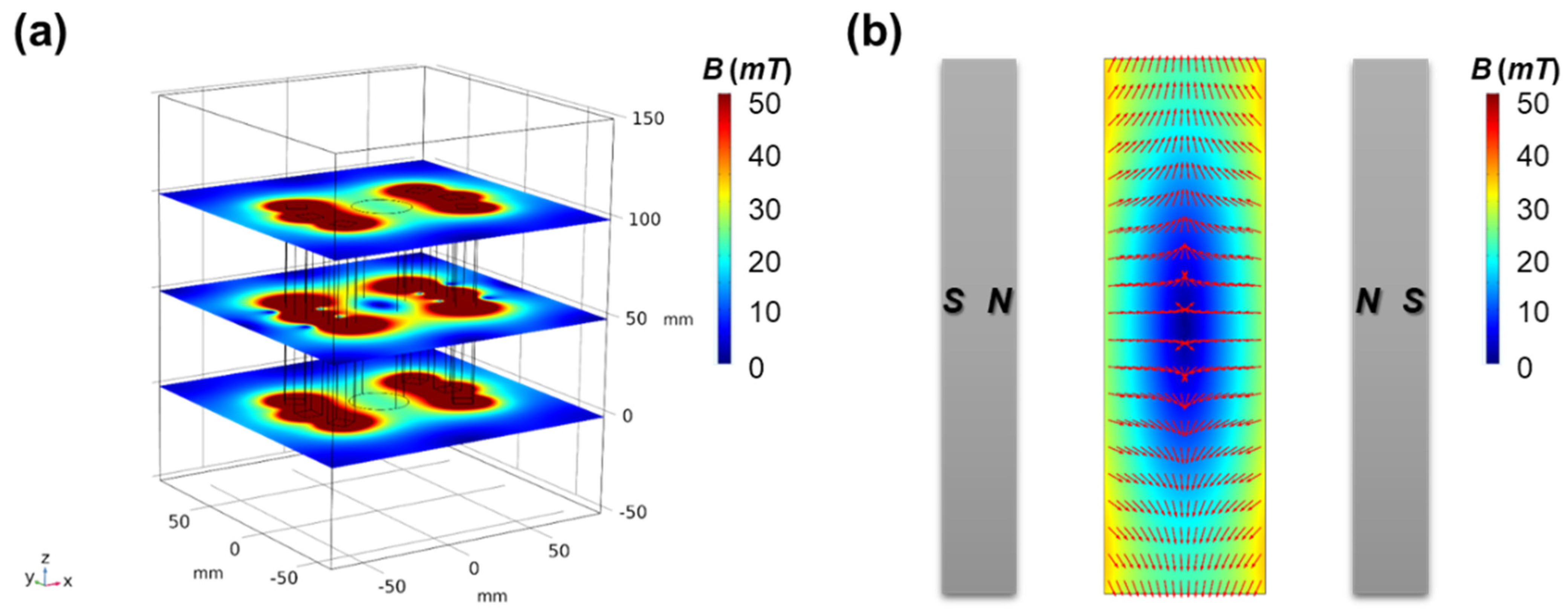
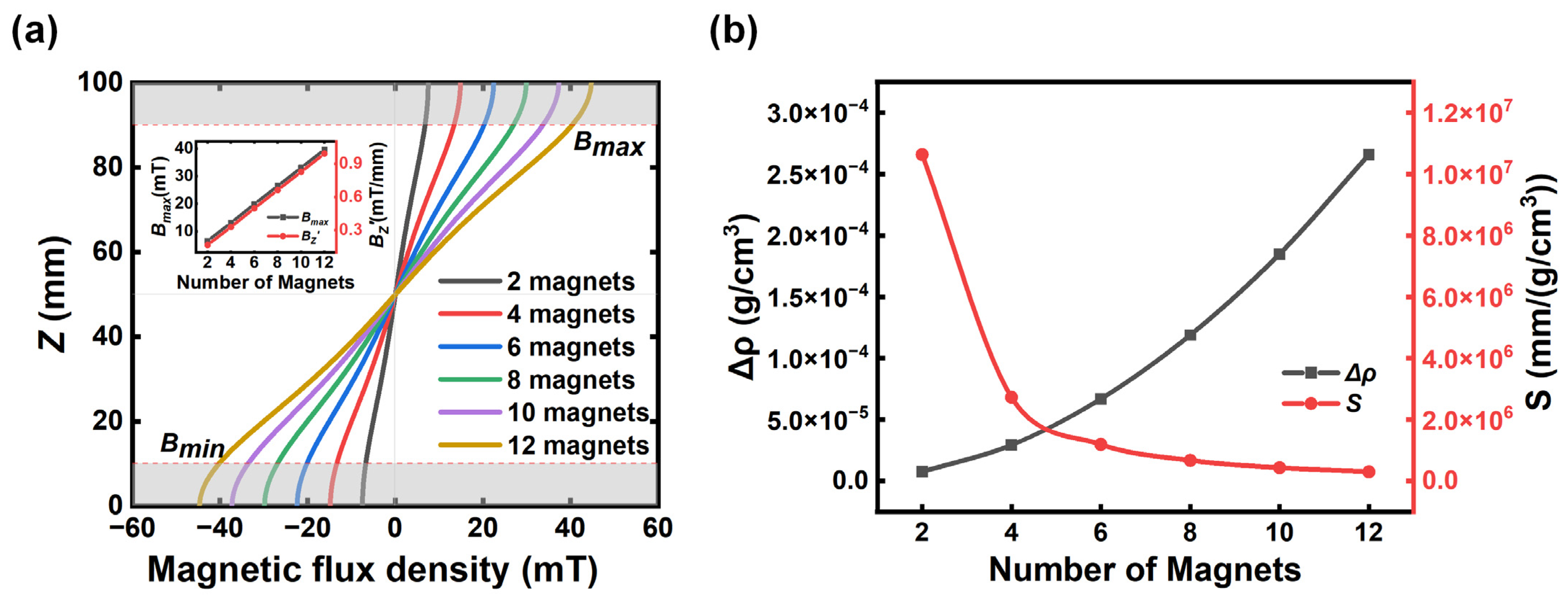
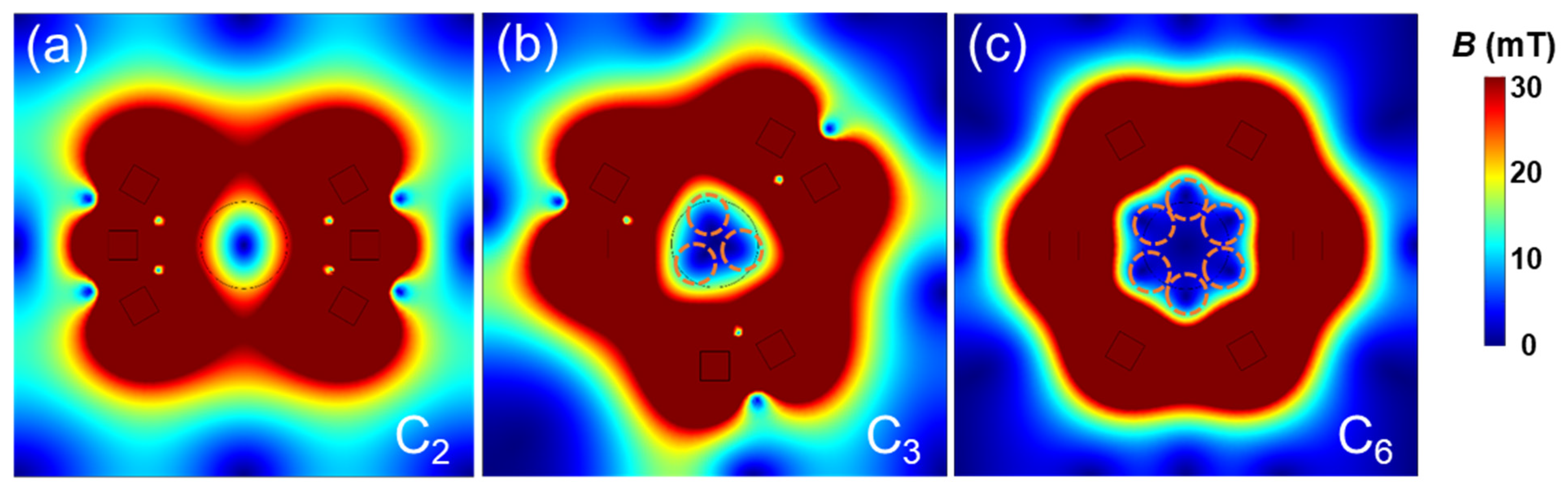
3.1. Simulation Results
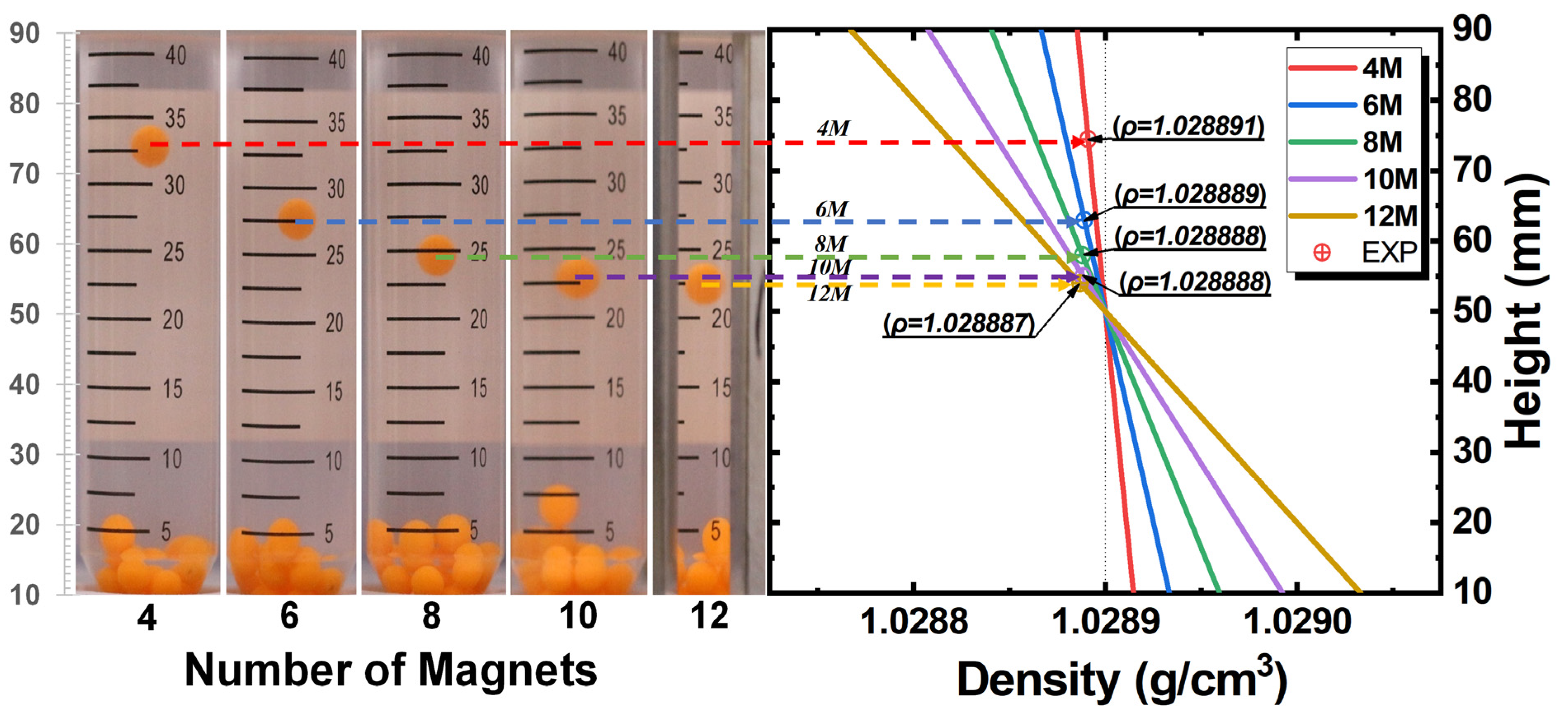
3.2. Experimental Results
4. Discussion
4.1. The Linear Distribution of Magnetic Flux Density
4.2. Measurement Stability
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Aasland, S.; McMillan, P.F. Density-driven liquid–liquid phase separation in the system AI2O3–Y2O3. Nature 1994, 369, 633–636. [Google Scholar] [CrossRef]
- Atkinson, M.B.J.; Bwambok, D.K.; Chen, J.; Chopade, P.D.; Thuo, M.M.; Mace, C.R.; Mirica, K.A.; Kumar, A.A.; Myerson, A.S.; Whitesides, G.M. Using Magnetic Levitation to Separate Mixtures of Crystal Polymorphs. Angew. Chem. Int. Ed. 2013, 52, 10208–10211. [Google Scholar] [CrossRef]
- Yang, X.; Wong, S.Y.; Bwambok, D.K.; Atkinson, M.B.J.; Zhang, X.; Whitesides, G.M.; Myerson, A.S. Separation and enrichment of enantiopure from racemic compounds using magnetic levitation. Chem. Commun. 2014, 50, 7548–7551. [Google Scholar] [CrossRef]
- Hurley, A.C.; Lennard-Jones, J.E. The electrostatic calculation of molecular energies—I. Methods of calculating molecular energies. Proc. R. Soc. London. Ser. A. Math. Phys. Sci. 1997, 226, 170–178. [Google Scholar]
- Kontturi, E.; Lankinen, A. Following the Kinetics of a Chemical Reaction in Ultrathin Supported Polymer Films by Reliable Mass Density Determination with X-ray Reflectivity. J. Am. Chem. Soc. 2010, 132, 3678–3679. [Google Scholar] [CrossRef]
- Klumpp, S.; Lefèvre, C.T.; Bennet, M.; Faivre, D. Swimming with magnets: From biological organisms to synthetic devices. Phys. Rep. 2019, 789, 1–54. [Google Scholar] [CrossRef]
- Ashkarran, A.A.; Mahmoudi, M. Magnetic levitation: A physical tool to measure the density of unknown diamagnetic materials. Phys. Educ. 2021, 56, 055020. [Google Scholar] [CrossRef]
- Hennek, J.W.; Nemiroski, A.; Subramaniam, A.B.; Bwambok, D.K.; Yang, D.; Harburg, D.V.; Tricard, S.; Ellerbee, A.K.; Whitesides, G.M. Using Magnetic Levitation for Non-Destructive Quality Control of Plastic Parts. Adv. Mater. 2015, 27, 1587–1592. [Google Scholar] [CrossRef]
- Ashkarran, A.A.; Mahmoudi, M. Magnetic Levitation Systems for Disease Diagnostics. Trends Biotechnol. 2021, 39, 311–321. [Google Scholar] [CrossRef]
- De Chiffre, L.; Carmignato, S.; Kruth, J.P.; Schmitt, R.; Weckenmann, A. Industrial applications of computed tomography. CIRP Ann. 2014, 63, 655–677. [Google Scholar] [CrossRef]
- Yoo, J.; Tang, S.; Gao, W. Micro- and nanorobots for biomedical applications in the brain. Nat. Rev. Bioeng. 2023. [Google Scholar] [CrossRef]
- von Muhlen, M.G.; Brault, N.D.; Knudsen, S.M.; Jiang, S.; Manalis, S.R. Label-Free Biomarker Sensing in Undiluted Serum with Suspended Microchannel Resonators. Anal. Chem. 2010, 82, 1905–1910. [Google Scholar] [CrossRef] [PubMed]
- Lockett, M.R.; Mirica, K.A.; Mace, C.R.; Blackledge, R.D.; Whitesides, G.M. Analyzing Forensic Evidence Based on Density with Magnetic Levitation. J. Forensic Sci. 2013, 58, 40–45. [Google Scholar] [CrossRef] [PubMed]
- Shapiro, N.D.; Mirica, K.A.; Soh, S.; Phillips, S.T.; Taran, O.; Mace, C.R.; Shevkoplyas, S.S.; Whitesides, G.M. Measuring Binding of Protein to Gel-Bound Ligands Using Magnetic Levitation. J. Am. Chem. Soc. 2012, 134, 5637–5646. [Google Scholar] [CrossRef]
- Tasoglu, S.; Khoory, J.A.; Tekin, H.C.; Thomas, C.; Karnoub, A.E.; Ghiran, I.C.; Demirci, U. Levitational Image Cytometry with Temporal Resolution. Adv. Mater. 2015, 27, 3901–3908. [Google Scholar] [CrossRef]
- Wolfrum, E.J.; Nagle, N.J.; Ness, R.M.; Peterson, D.J.; Ray, A.E.; Stevens, D.M. The Effect of Biomass Densification on Structural Sugar Release and Yield in Biofuel Feedstock and Feedstock Blends. BioEnergy Res. 2017, 10, 478–487. [Google Scholar] [CrossRef]
- Ashcroft, S.J.; Booker, D.R.; Turner, J.C.R. Density measurement by oscillating tube. Effects of viscosity, temperature, calibration and signal processing. J. Chem. Soc. Faraday Trans. 1990, 86, 145–149. [Google Scholar] [CrossRef]
- Burg, T.P.; Godin, M.; Knudsen, S.M.; Shen, W.; Carlson, G.; Foster, J.S.; Babcock, K.; Manalis, S.R. Weighing of biomolecules, single cells and single nanoparticles in fluid. Nature 2007, 446, 1066–1069. [Google Scholar] [CrossRef]
- Rabier, F.; Temmerman, M.; Böhm, T.; Hartmann, H.; Daugbjerg Jensen, P.; Rathbauer, J.; Carrasco, J.; Fernández, M. Particle density determination of pellets and briquettes. Biomass Bioenergy 2006, 30, 954–963. [Google Scholar] [CrossRef]
- Burg, T.P.; Manalis, S.R. Suspended microchannel resonators for biomolecular detection. Appl. Phys. Lett. 2003, 83, 2698–2700. [Google Scholar] [CrossRef]
- Dreisbach, F.; Lösch, H.W. Magnetic Suspension Balance For Simultaneous Measurement of a Sample and the Density of the Measuring Fluid. J. Therm. Anal. Calorim. 2000, 62, 515–521. [Google Scholar] [CrossRef]
- Doan-Nguyen, T.P.; Crespy, D. Advanced density-based methods for the characterization of materials, binding events, and kinetics. Chem. Soc. Rev. 2022, 51, 8612–8651. [Google Scholar] [CrossRef] [PubMed]
- Nemiroski, A.; Soh, S.; Kwok, S.W.; Yu, H.-D.; Whitesides, G.M. Tilted Magnetic Levitation Enables Measurement of the Complete Range of Densities of Materials with Low Magnetic Permeability. J. Am. Chem. Soc. 2016, 138, 1252–1257. [Google Scholar] [CrossRef] [PubMed]
- Abrahamsson, C.K.; Ge, S.; Bell, J.G.; Blackledge, R.D.; Whitesides, G.M. Density Determination and Separation via Magnetic Levitation. In Leading Edge Techniques in Forensic Trace Evidence Analysis; Blackledge, R.D., Ed.; Wiley: Honoken, NJ, USA, 2022; pp. 103–147. [Google Scholar]
- Ge, S.; Nemiroski, A.; Mirica, K.A.; Mace, C.R.; Hennek, J.W.; Kumar, A.A.; Whitesides, G.M. Magnetic Levitation in Chemistry, Materials Science, and Biochemistry. Angew. Chem. Int. Ed. 2020, 59, 17810–17855. [Google Scholar] [CrossRef]
- Moon, F.C. Introduction to Magnetic Levitation. In Superconducting Levitation; Moon, F.C., Ed.; Wiley-VCH: Mörlenbach, Germany, 1995; pp. 1–31. [Google Scholar]
- Mirica, K.A.; Shevkoplyas, S.S.; Phillips, S.T.; Gupta, M.; Whitesides, G.M. Measuring Densities of Solids and Liquids Using Magnetic Levitation: Fundamentals. J. Am. Chem. Soc. 2009, 131, 10049–10058. [Google Scholar] [CrossRef] [PubMed]
- Mirica, K.A.; Phillips, S.T.; Shevkoplyas, S.S.; Whitesides, G.M. Using Magnetic Levitation To Distinguish Atomic-Level Differences in Chemical Composition of Polymers, and To Monitor Chemical Reactions on Solid Supports. J. Am. Chem. Soc. 2008, 130, 17678–17680. [Google Scholar] [CrossRef]
- Nemiroski, A.; Kumar, A.A.; Soh, S.; Harburg, D.V.; Yu, H.-D.; Whitesides, G.M. High-Sensitivity Measurement of Density by Magnetic Levitation. Anal. Chem. 2016, 88, 2666–2674. [Google Scholar] [CrossRef]
- Digiacomo, L.; Quagliarini, E.; Marmiroli, B.; Sartori, B.; Perini, G.; Papi, M.; Capriotti, A.L.; Montone, C.M.; Cerrato, A.; Caracciolo, G.; et al. Magnetic Levitation Patterns of Microfluidic-Generated Nanoparticle–Protein Complexes. Nanomaterials 2022, 12, 2376. [Google Scholar] [CrossRef]
- Zhang, C.; Zhao, P.; Gu, F.; Xie, J.; Xia, N.; He, Y.; Fu, J. Single-Ring Magnetic Levitation Configuration for Object Manipulation and Density-Based Measurement. Anal. Chem. 2018, 90, 9226–9233. [Google Scholar] [CrossRef]
- Ge, S.; Whitesides, G.M. “Axial” Magnetic Levitation Using Ring Magnets Enables Simple Density-Based Analysis, Separation, and Manipulation. Anal. Chem. 2018, 90, 12239–12245. [Google Scholar] [CrossRef]
- Winkleman, A.; Perez-Castillejos, R.; Gudiksen, K.L.; Phillips, S.T.; Prentiss, M.; Whitesides, G.M. Density-Based Diamagnetic Separation: Devices for Detecting Binding Events and for Collecting Unlabeled Diamagnetic Particles in Paramagnetic Solutions. Anal. Chem. 2007, 79, 6542–6550. [Google Scholar] [CrossRef] [PubMed]
- Mirica, K.A.; Ilievski, F.; Ellerbee, A.K.; Shevkoplyas, S.S.; Whitesides, G.M. Using Magnetic Levitation for Three Dimensional Self-Assembly. Adv. Mater. 2011, 23, 4134–4140. [Google Scholar] [CrossRef] [PubMed]
- Tasoglu, S.; Yu, C.H.; Liaudanskaya, V.; Guven, S.; Migliaresi, C.; Demirci, U. Magnetic Levitational Assembly for Living Material Fabrication. Adv. Healthc. Mater. 2015, 4, 1469–1476. [Google Scholar] [CrossRef] [PubMed]
- Huang, G.; Li, M.; Yang, Q.; Li, Y.; Liu, H.; Yang, H.; Xu, F. Magnetically Actuated Droplet Manipulation and Its Potential Biomedical Applications. ACS Appl. Mater. Interfaces 2017, 9, 1155–1166. [Google Scholar] [CrossRef] [PubMed]
- Gao, Q.-H.; Wen, B.; Kang, Y.; Zhang, W.-M. Pump-free microfluidic magnetic levitation approach for density-based cell characterization. Biosens. Bioelectron. 2022, 204, 114052. [Google Scholar] [CrossRef] [PubMed]
- Dabbagh, S.R.; Alseed, M.M.; Saadat, M.; Sitti, M.; Tasoglu, S. Biomedical Applications of Magnetic Levitation. Adv. NanoBiomed Res. 2022, 2, 2100103. [Google Scholar] [CrossRef]
- Quagliarini, E.; Caputo, D.; Cammarata, R.; Caracciolo, G.; Pozzi, D. Coupling magnetic levitation of graphene oxide–protein complexes with blood levels of glucose for early detection of pancreatic adenocarcinoma. Cancer Nanotechnol. 2023, 14, 16. [Google Scholar] [CrossRef]
- Quagliarini, E.; Digiacomo, L.; Caputo, D.; Coppola, A.; Amenitsch, H.; Caracciolo, G.; Pozzi, D. Magnetic Levitation of Personalized Nanoparticle–Protein Corona as an Effective Tool for Cancer Detection. Nanomaterials 2022, 12, 1397. [Google Scholar] [CrossRef]
- Sözmen, A.B.; Arslan-Yıldız, A. Sensitive and rapid protein assay via magnetic levitation. Biosens. Bioelectron. X 2022, 10, 100137. [Google Scholar] [CrossRef]
- Goreke, U.; Bode, A.; Yaman, S.; Gurkan, U.A.; Durmus, N.G. Size and density measurements of single sickle red blood cells using microfluidic magnetic levitation. Lab A Chip 2022, 22, 683–696. [Google Scholar] [CrossRef]
- Ren, X.; Breadmore, M.C.; Maya, F. Biphasic Magnetic Levitation to Detect Organic Pollutants on Microplastics. Anal. Chem. 2022, 94, 9033–9039. [Google Scholar] [CrossRef] [PubMed]
- Ren, X.; Breadmore, M.C.; Maya, F. Magnetism-Assisted Density Gradient Separation of Microplastics. Anal. Chem. 2022, 94, 17947–17955. [Google Scholar] [CrossRef] [PubMed]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, J.; Li, D.; Zhu, C.; Ouyang, Q.; Miao, C.; Yu, H. A Magnetic Levitation System for Range/Sensitivity-Tunable Measurement of Density. Sensors 2023, 23, 3955. https://doi.org/10.3390/s23083955
Yu J, Li D, Zhu C, Ouyang Q, Miao C, Yu H. A Magnetic Levitation System for Range/Sensitivity-Tunable Measurement of Density. Sensors. 2023; 23(8):3955. https://doi.org/10.3390/s23083955
Chicago/Turabian StyleYu, Junhui, Donghai Li, Chengxian Zhu, Qiran Ouyang, Chunyang Miao, and Haidong Yu. 2023. "A Magnetic Levitation System for Range/Sensitivity-Tunable Measurement of Density" Sensors 23, no. 8: 3955. https://doi.org/10.3390/s23083955
APA StyleYu, J., Li, D., Zhu, C., Ouyang, Q., Miao, C., & Yu, H. (2023). A Magnetic Levitation System for Range/Sensitivity-Tunable Measurement of Density. Sensors, 23(8), 3955. https://doi.org/10.3390/s23083955





