Development of a Novel Spherical Light-Based Positioning Sensor in Solar Tracking
Abstract
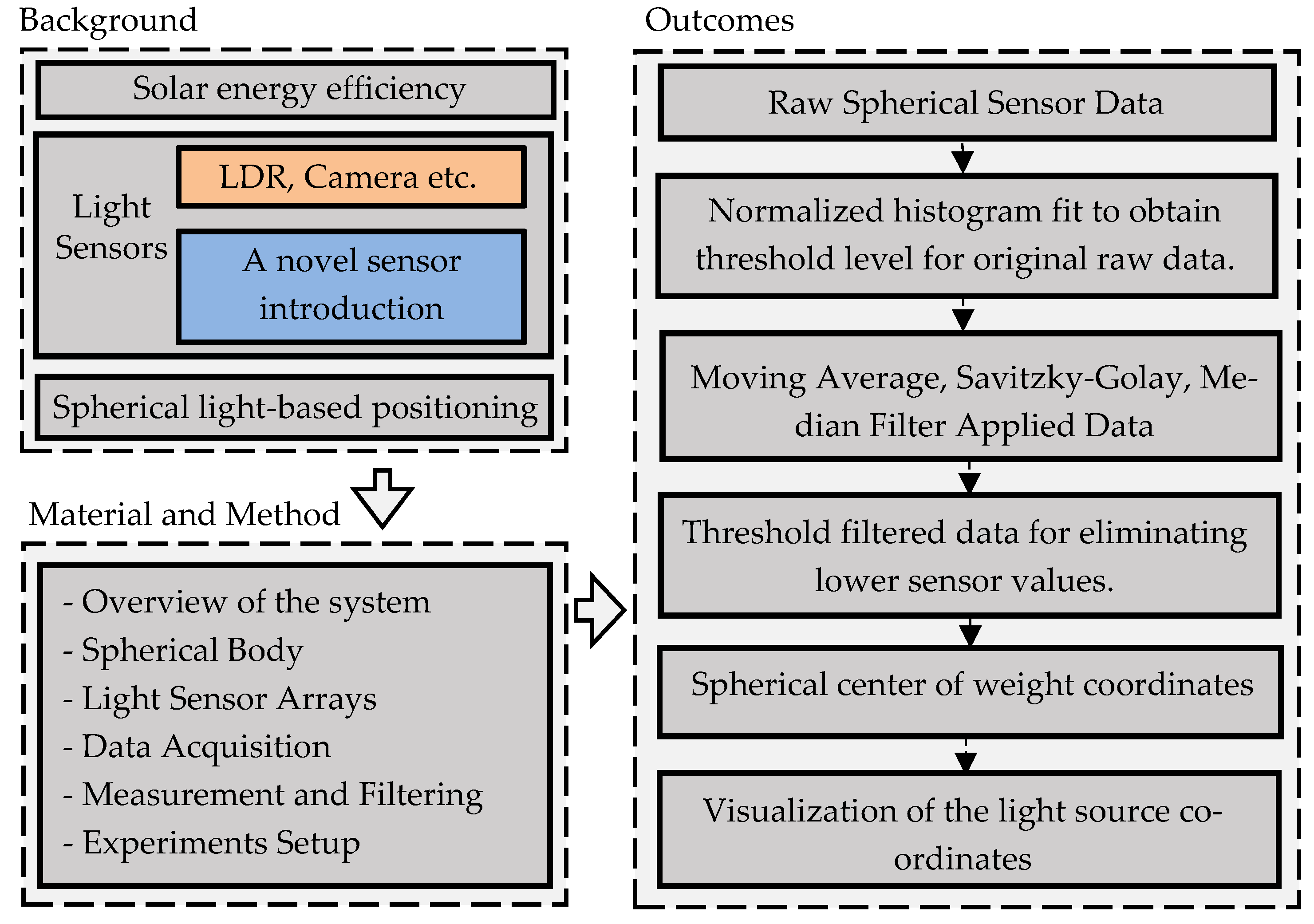
1. Introduction
2. Material and Method
2.1. Overview of Spherical Measurement System
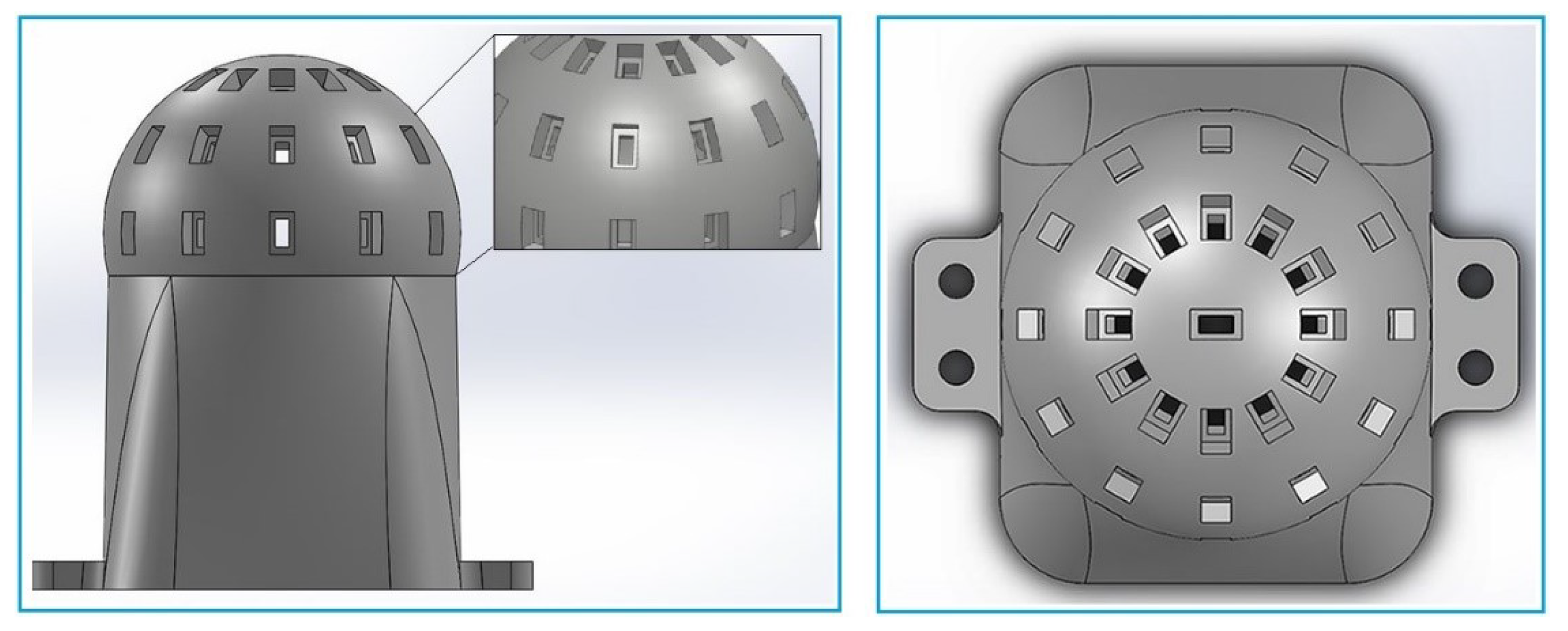
2.1.1. Spherical Body
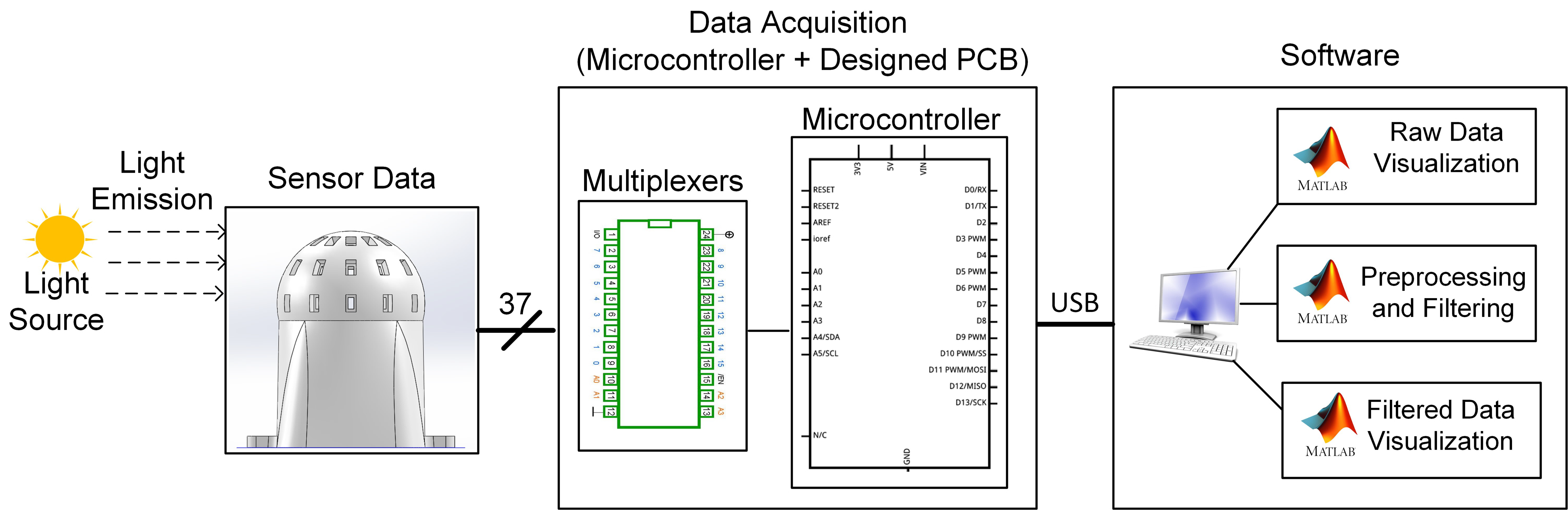
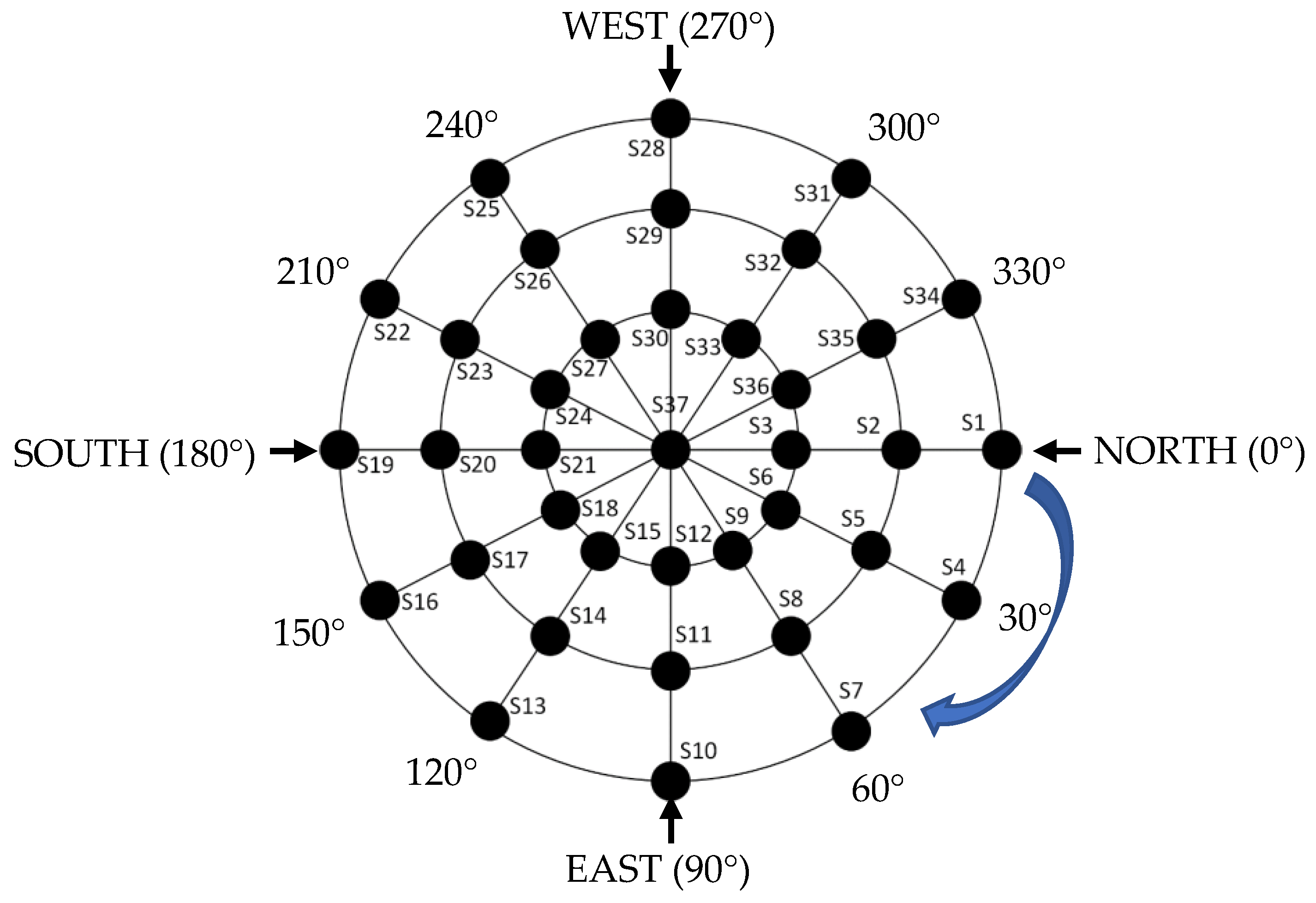
2.1.2. Light Sensor Arrays and Their Placement
2.1.3. Data Acquisition
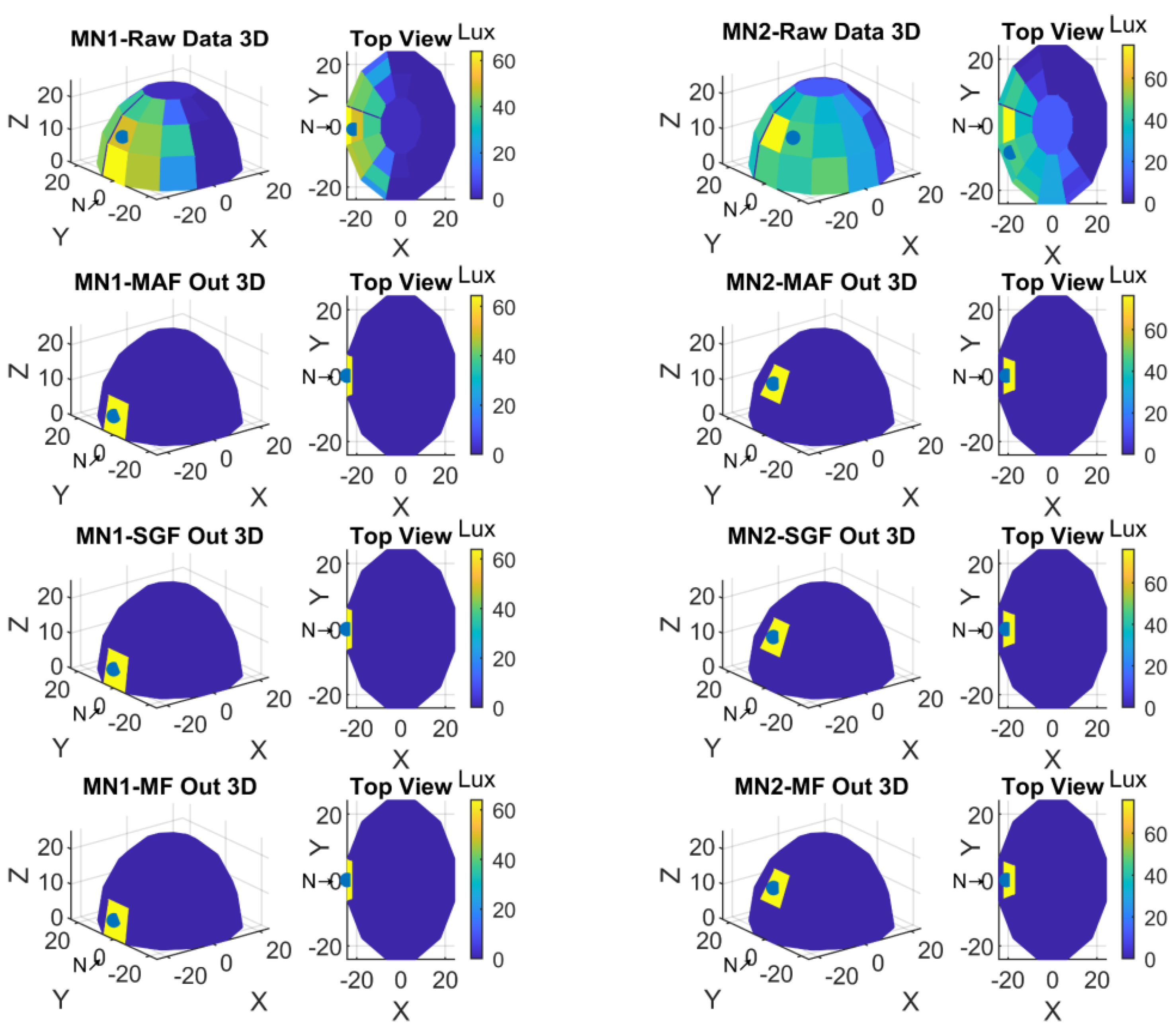
2.1.4. Data Filtering
| Algorithm 1: 40 Points—Moving Average Filter Algorithm |
| 1: Define A[] = 0, sum = 0, i = 1 2: for each sensor_value do 3: do until i = 40 4: Measure Si 5: sum = sum + Si, i = i + 1 6: For i = 40, A[] = sum/40 7: end 8: repeat for next 40 sensor_value 9: end for sensor_value |
| Algorithm 2: Savitzky-Golay Filter Algorithm |
| 1: Define data, data_length, window_length 2: for i in range data_length 3: window = data[integer(i—data_length/2): integer(i + data_length/2 + 1)] 4: coeffs = polynomial fit in range of window_length 5: poly = define polynom using coeffs 6: y[i] = poly(integer (data_length/2)) 7: end |
| Algorithm 3: Order = 5 Median Filter Algorithm |
| 1: Define Y[] = 0, i = 1 2: Measure light sensors array S[] 3: for each 5 light_sensor_values (Si, Si+1, Si+2, Si+3, Si+4) do 4: Sort light_sensor_values 5: Select median 6: Assign Yi to median value, i = i + 1 7: end for 5 light_sensor_values 8: repeat for next light_sensor_values |
| Algorithm 4: Threshold algorithm |
| 1: Define sensor_data[], mu, sigma 2: total = mu + sigma 3: maxvalue = find max (sensor_data[]) 4: thrvalue = total / maxvalue |
2.2. Experiments Setup
- On condition that the measurement system remains at the fixed position, the measurements were made by moving the used light source in azimuth and elevation angles and with 30° angular distance. The measurements were made for 37 different locations in total.
- The distance between the measurement system and the light source (d) was fixed at 40 cm value. The reason is that h and d values increase more than necessary depending on the elevation θ angle value.
- Required h, d, and R parameters were calculated with the trigonometric features in the measurements, and they were determined by using a laser meter in each measurement. The direction of the light source was controlled with a laser. Thus, erroneous measurements were avoided even though the light source was manually placed at the elevation and azimuth angles.
- Spherical body and the electronic box used in the measurement system were placed in a way to enable independent movement in azimuth direction. By designing the experimental setup in this way, angular rotation of the measurement system was ensured without needing the movement of the light source in different azimuth angles.
- Experimental environment was isolated from interfering and external light sources during the experiments.
3. Results
3.1. Raw Data Measurements for Experiment 1
3.2. Preprocessed and Filtered Data Measurements for Experiment 2
3.3. Visualization of Measurements for Experiment 2
4. Conclusions
- The sensor test was done with a manually adjusted mechanical testbed. The sensor orientation was also adjusted with hands. For more accurate tests an automatic motor driven testbed can be built.
- This study can be made more compact and standalone and can be turned into a smart sensor that can be used directly at the point where it is positioned with appropriate processing capacity and can be directly integrated into solar tracking systems. Several smart sensors can be deployed in an internet of things (IoT) environment for the smart interconnected applications.
- The studies that can be done on the production technology of the sensor computer aided model can be transformed into a more advanced sensor where more light sensors can be used together and can be optimized in terms of sensor placements. Thus, the resolution of the sensor can be increased.
- The spherical sensor structure will be able to find new areas of use in indoor environments with light sensors that will operate at different wavelengths. For example, it can be used for location coordination of mobile robots working in dark factories which yields energy saving.
- Fuzzy logic, neural network, or deep learning algorithms can be used to increase the performance of the sensor in the light source localization or light source tracking process.
5. Patents
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kober, T.; Schiffer, H.-W.; Densing, M.; Panos, E. Global Energy Perspectives to 2060—WEC’s World Energy Scenarios 2019. Energy Strateg. Rev. 2020, 31, 100523. [Google Scholar] [CrossRef]
- Luan, C.; Sun, X.; Wang, Y. Driving Forces of Solar Energy Technology Innovation and Evolution. J. Clean. Prod. 2020, 287, 125019. [Google Scholar] [CrossRef]
- Sayigh, A. Solar and Wind Energy Will Supply More Than 50% of World Electricity by 2030. In Green Buildings and Renewable Energy; Springer: Cham, Switzerland, 2020; pp. 385–399. [Google Scholar]
- Yu, J.; Tang, Y.M.; Chau, K.Y.; Nazar, R.; Ali, S.; Iqbal, W. Role of Solar-Based Renewable Energy in Mitigating CO2 Emissions: Evidence from Quantile-on-Quantile Estimation. Renew. Energy 2022, 182, 216–226. [Google Scholar] [CrossRef]
- Moraga-Contreras, C.; Cornejo-Ponce, L.; Vilca-Salinas, P.; Estupiñan, E.; Zuñiga, A.; Palma-Behnke, R.; Tapia-Caroca, H. Evolution of Solar Energy in Chile: Residential Opportunities in Arica and Parinacota. Energies 2022, 15, 551. [Google Scholar] [CrossRef]
- Salimi, M.; Hosseinpour, M.; Borhani, T.N. Analysis of Solar Energy Development Strategies for a Successful Energy Transition in the UAE. Processes 2022, 10, 1338. [Google Scholar] [CrossRef]
- Ghadami, N.; Gheibi, M.; Kian, Z.; Faramarz, M.G.; Naghedi, R.; Eftekhari, M.; Fathollahi-Fard, A.M.; Dulebenets, M.A.; Tian, G. Implementation of Solar Energy in Smart Cities Using an Integration of Artificial Neural Network, Photovoltaic System and Classical Delphi Methods. Sustain. Cities Soc. 2021, 74, 103149. [Google Scholar] [CrossRef]
- Gorjian, S.; Calise, F.; Kant, K.; Ahamed, M.S.; Copertaro, B.; Najafi, G.; Zhang, X.; Aghaei, M.; Shamshiri, R.R. A Review on Opportunities for Implementation of Solar Energy Technologies in Agricultural Greenhouses. J. Clean. Prod. 2021, 285, 124807. [Google Scholar] [CrossRef]
- Pandey, A.K.; Reji Kumar, R.; Kalidasan, B.; Laghari, I.A.; Samykano, M.; Kothari, R.; Abusorrah, A.M.; Sharma, K.; Tyagi, V.V. Utilization of Solar Energy for Wastewater Treatment: Challenges and Progressive Research Trends. J. Environ. Manag. 2021, 297, 113300. [Google Scholar] [CrossRef]
- AL-Rousan, N.; Isa, N.A.M.; Desa, M.K.M. Advances in Solar Photovoltaic Tracking Systems: A Review. Renew. Sustain. Energy Rev. 2018, 82, 2548–2569. [Google Scholar] [CrossRef]
- Hafez, A.Z.; Yousef, A.M.; Harag, N.M. Solar Tracking Systems: Technologies and Trackers Drive Types—A Review. Renew. Sustain. Energy Rev. 2018, 91, 754–782. [Google Scholar] [CrossRef]
- Kumar, K.; Varshney, L.; Ambikapathy, A.; Saket, R.K.; Mekhilef, S. Solar Tracker Transcript—A Review. Int. Trans. Electr. Energy Syst. 2021, 31, e13250. [Google Scholar] [CrossRef]
- Krishan, R.; Naik, K.A.; Raj, R.D.A. Solar Tracking Technology to Harness the Green Energy. In Artificial Intelligence for Solar Photovoltaic Systems; CRC Press: Boca Raton, FL, USA, 2022; pp. 189–212. [Google Scholar]
- Adrian, W.Y.W.; Durairajah, V.; Gobee, S. Autonomous Dual Axis Solar Tracking System Using Optical Sensor and Sun Trajectory. In Proceedings of the 8th International Conference on Robotic, Vision, Signal Processing & Power Applications, Penang, Malaysia, 10–12 November 2013; Lecture Notes in Electrical Engineering. Springer: Singapore, 2014; Volume 291, pp. 507–520. [Google Scholar] [CrossRef]
- Bentaher, H.; Kaich, H.; Ayadi, N.; Ben Hmouda, M.; Maalej, A.; Lemmer, U. A Simple Tracking System to Monitor Solar PV Panels. Energy Convers. Manag. 2014, 78, 872–875. [Google Scholar] [CrossRef]
- Jeong, B.-H.; Park, J.-H.; Kim, S.-D.; Kang, J.-H. Performance Evaluation of Dual Axis Solar Tracking System with Photo Diodes. In Proceedings of the 2013 International Conference on Electrical Machines and Systems (ICEMS), Busan, Republic of Korea, 26–29 October 2013; pp. 414–417. [Google Scholar] [CrossRef]
- Othman, N.; Manan, M.I.A.; Othman, Z.; Al. Junid, S.A.M. Performance Analysis of Dual-Axis Solar Tracking System. In Proceedings of the 2013 IEEE International Conference on Control System, Computing and Engineering, Penang, Malaysia, 29 November–1 December 2013; pp. 370–375. [Google Scholar] [CrossRef]
- Robles Algarin, C.A.; Ospino Castro, A.J.; Naranjo Casas, J. Dual-Axis Solar Tracker for Using in Photovoltaic Systems. Int. J. Renew. Energy Res. 2017. [Google Scholar] [CrossRef]
- Tina, G.M.; Arcidiacono, F.; Gagliano, A. Intelligent Sun-Tracking System Based on Multiple Photodiode Sensors for Maximisation of Photovoltaic Energy Production. Math. Comput. Simul. 2013, 91, 16–28. [Google Scholar] [CrossRef]
- Saeedi, M.; Effatnejad, R. A New Design of Dual-Axis Solar Tracking System With LDR Sensors by Using the Wheatstone Bridge Circuit. IEEE Sens. J. 2021, 21, 14915–14922. [Google Scholar] [CrossRef]
- Hawibowo, S.; Ala, I.; Lestari, R.B.C.; Saputri, F.R. Stepper Motor Driven Solar Tracker System for Solar Panel. In Proceedings of the 2018 4th International Conference on Science and Technology (ICST), Yogyakarta, Indonesia, 7–8 August 2018; pp. 1–4. [Google Scholar] [CrossRef]
- Jaanaki, S.M.; Mandal, D.; Hullikeri, H.H.; Shreenidhi, V.; Arshiya Sultana, A. Performance Enhancement of Solar Panel Using Dual Axis Solar Tracker. In Proceedings of the 2021 International Conference on Design Innovations for 3Cs Compute Communicate Control (ICDI3C), Bangalore, India, 10–11 June 2021; pp. 98–102. [Google Scholar] [CrossRef]
- Beily, M.D.E.; Sinaga, R.; Syarif, Z.; Pae, M.G.; Rochani, R. Design and Construction of a Low Cost of Solar Tracker Two Degree of Freedom (DOF) Based On Arduino. In Proceedings of the 2020 International Conference on Applied Science and Technology (iCAST), Padang, Indonesia, 24 October 2020; pp. 384–388. [Google Scholar] [CrossRef]
- El Hammoumi, A.; Motahhir, S.; El Ghzizal, A.; Chalh, A.; Derouich, A. A Simple and Low-Cost Active Dual-Axis Solar Tracker. Energy Sci. Eng. 2018, 6, 607–620. [Google Scholar] [CrossRef]
- Sawant, A.; Bondre, D.; Joshi, A.; Tambavekar, P.; Deshmukh, A. Design and Analysis of Automated Dual Axis Solar Tracker Based on Light Sensors. In Proceedings of the 2018 2nd International Conference on I-SMAC (IoT in Social, Mobile, Analytics and Cloud) (I-SMAC)I-SMAC (IoT in Social, Mobile, Analytics and Cloud) (I-SMAC), 2018 2nd International Conference on, Palladam, India, 30–31 August 2018; pp. 454–459. [Google Scholar] [CrossRef]
- Kuttybay, N.; Saymbetov, A.; Mekhilef, S.; Nurgaliyev, M.; Tukymbekov, D.; Dosymbetova, G.; Meiirkhanov, A.; Svanbayev, Y. Optimized Single-Axis Schedule Solar Tracker in Different Weather Conditions. Energies 2020, 13, 5226. [Google Scholar] [CrossRef]
- Carballo, J.A.; Bonilla, J.; Berenguel, M.; Fernández-Reche, J.; García, G. New Approach for Solar Tracking Systems Based on Computer Vision, Low Cost Hardware and Deep Learning. Renew. Energy 2019, 133, 1158–1166. [Google Scholar] [CrossRef]
- Abdollahpour, M.; Golzarian, M.R.; Rohani, A.; Abootorabi Zarchi, H. Development of a Machine Vision Dual-Axis Solar Tracking System. Sol. Energy 2018, 169, 136–143. [Google Scholar] [CrossRef]
- Lee, C.D.; Huang, H.C.; Yeh, H.Y. The Development of Sun-Tracking System Using Image Processing. Sensors 2013, 13, 5448–5459. [Google Scholar] [CrossRef]
- Garcia-Gil, G.; Ramirez, J.M. Fish-Eye Camera and Image Processing for Commanding a Solar Tracker. Heliyon 2019, 5, e01398. [Google Scholar] [CrossRef] [PubMed]
- Delgado, F.J.; Quero, J.M.; Garcia, J.; Tarrida, C.L.; Ortega, P.R.; Bermejo, S. Accurate and Wide-Field-of-View MEMS-Based Sun Sensor for Industrial Applications. IEEE Trans. Ind. Electron. 2012, 59, 4871–4880. [Google Scholar] [CrossRef]
- Chen, F.; Feng, J.; Hong, Z. Digital Sun Sensor Based on the Optical Vernier Measuring Principle. Meas. Sci. Technol. 2006, 17, 2494–2498. [Google Scholar] [CrossRef]
- Wei, M.-S.; Xing, F.; Li, B.; You, Z. Investigation of Digital Sun Sensor Technology with an N-Shaped Slit Mask. Sensors 2011, 11, 9764–9777. [Google Scholar] [CrossRef] [PubMed]
- Vaezi, M.; Seitz, H.; Yang, S. A Review on 3D Micro-Additive Manufacturing Technologies. Int. J. Adv. Manuf. Technol. 2013, 67, 1721–1754. [Google Scholar] [CrossRef]
- Gräbner, D.; Dödtmann, S.; Dumstorff, G.; Lucklum, F. 3-D-Printed Smart Screw: Functionalization during Additive Fabrication. J. Sens. Sens. Syst. 2018, 7, 143–151. [Google Scholar] [CrossRef]
- Dijkshoorn, A.; Werkman, P.; Welleweerd, M.; Wolterink, G.; Eijking, B.; Delamare, J.; Sanders, R.; Krijnen, G.J.M. Embedded Sensing: Integrating Sensors in 3-D Printed Structures. J. Sens. Sens. Syst. 2018, 7, 169–181. [Google Scholar] [CrossRef]
- Lucklum, F.; Dumstorff, G. 3D Printed Pressure Sensor with Screen-Printed Resistive Read-Out. In Proceedings of the 2016 IEEE SENSORS, Orlando, FL, USA, 30 October–3 November 2017; pp. 5–7. [Google Scholar] [CrossRef]
- Miner, G.L.; Ham, J.M.; Kluitenberg, G.J. A Heat-Pulse Method for Measuring Sap Flow in Corn and Sunflower Using 3D-Printed Sensor Bodies and Low-Cost Electronics. Agric. For. Meteorol. 2017, 246, 86–97. [Google Scholar] [CrossRef]
- Saari, M.; Xia, B.; Cox, B.; Krueger, P.S.; Cohen, A.L.; Richer, E. Fabrication and Analysis of a Composite 3D Printed Capacitive Force Sensor. 3D Print. Addit. Manuf. 2016, 3, 137–141. [Google Scholar] [CrossRef]
- Vishay. TEMT6000. Vishay Semiconductors 2004. pp. 1–6. Available online: https://www.vishay.com/docs/81579/temt6000.pdf (accessed on 4 January 2023).
- Messenger, R.; Abtahi, H.A. Photovoltaic Systems Engineering: Fourth Edition; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar] [CrossRef]
- Bachi, L.; Billeci, L.; Varanini, M. QRS Detection Based on Medical Knowledge and Cascades of Moving Average Filters. Appl. Sci. 2021, 11, 6995. [Google Scholar] [CrossRef]
- Tanji, A.K.; de Brito, M.A.G.; Alves, M.G.; Garcia, R.C.; Chen, G.-L.; Ama, N.R.N. Improved Noise Cancelling Algorithm for Electrocardiogram Based on Moving Average Adaptive Filter. Electronics 2021, 10, 2366. [Google Scholar] [CrossRef]
- Savitzky, A.; Golay, M.J.E. Smoothing and Differentiation of Data by Simplified Least Squares Procedures. Anal. Chem. 1964, 36, 1627–1639. [Google Scholar] [CrossRef]
- Press, W.H.; Teukolsky, S.A. Savitzky-Golay Smoothing Filters. Comput. Phys. 1990, 4, 669–672. [Google Scholar] [CrossRef]
- Zhang, G.; Hao, H.; Wang, Y.; Jiang, Y.; Shi, J.; Yu, J.; Cui, X.; Li, J.; Zhou, S.; Yu, B. Optimized Adaptive Savitzky-Golay Filtering Algorithm Based on Deep Learning Network for Absorption Spectroscopy. Spectrochim. Acta A Mol. Biomol. Spectrosc. 2021, 263, 120187. [Google Scholar] [CrossRef]
- Oroutzoglou, I.; Kokkinis, A.; Ferikoglou, A.; Danopoulos, D.; Masouros, D.; Siozios, K. Optimizing Savitzky-Golay Filter on GPU and FPGA Accelerators for Financial Applications. In Proceedings of the 2022 11th International Conference on Modern Circuits and Systems Technologies (MOCAST), Bremen, Germany, 8–10 June 2022; pp. 1–4. [Google Scholar] [CrossRef]
- Shukla, P.K.; Roy, V.; Shukla, P.K.; Chaturvedi, A.K.; Saxena, A.K.; Maheshwari, M.; Pal, P.R. An Advanced EEG Motion Artifacts Eradication Algorithm. Comput. J. 2023, 66, 429–440. [Google Scholar] [CrossRef]
- Zhu, R.; Wang, Y. Application of Improved Median Filter on Image Processing. J. Comput. 2012, 7, 838–841. [Google Scholar] [CrossRef]
- Wang, M.; Zhang, X.; Tang, W.; Wang, J. A Structure for Accurately Determining the Mass and Center of Gravity of Rigid Bodies. Appl. Sci. 2019, 9, 2532. [Google Scholar] [CrossRef]








| Experiment 1 Measurement Number (MN) | d (cm) | R (cm) | h (cm) | Corresponded Reference Light Sensor | Elevation Angle (θ) | Azimuth Angle (φ) |
|---|---|---|---|---|---|---|
| 1 | 20 | 20 | 0 | S18 | 60° | 150° |
| 2 | 20 | 23.09 | 11.54 | S17 | 30° | 150° |
| 3 | 20 | 40 | 34.64 | S16 | 0° | 150° |
| 4 | 20 | - | - | S36 | 60° | 330° |
| 5 | 20 | 23.09 | 11.54 | S35 | 30° | 330° |
| 6 | 20 | 23.09 | 11.54 | S34 | 0° | 330° |
| Experiment 2 Measurement Number (MN) | d (cm) | R (cm) | h (cm) | Corresponded Reference Light Sensor | Elevation Angle (θ) | Azimuth Angle (φ) |
|---|---|---|---|---|---|---|
| 1 | 40 | 40 | 0 | S1 | 0° | 0° |
| 2 | 40 | 46.19 | 23.09 | S2 | 30° | 0° |
| 3 | 40 | 80 | 69.28 | S3 | 60° | 0° |
| 4 | 40 | - | - | S37 | 90° | - |
| 5 | 40 | 46.19 | 23.09 | S35 | 30° | 330° |
| 6 | 40 | 46.19 | 23.09 | S32 | 30° | 300° |
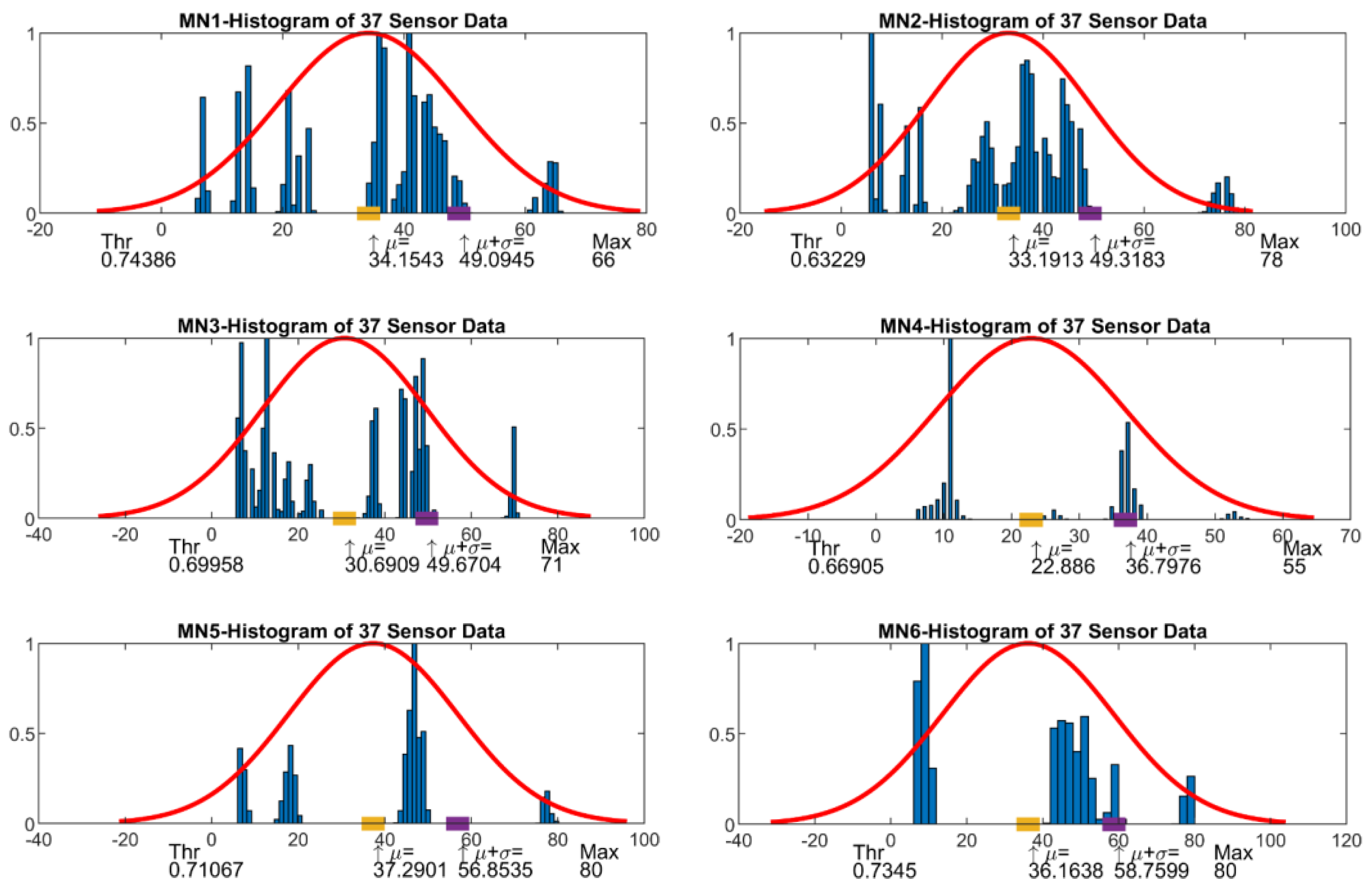
| Experiment 2 Measurement Number | μ | μ + σ | Maximum Value | Normalized Threshold Value |
|---|---|---|---|---|
| MN1 | 34.153 | 49.0945 | 66 | 0.74386 |
| MN2 | 33.1913 | 49.3183 | 78 | 0.63229 |
| MN3 | 30.6909 | 49.6704 | 71 | 0.69958 |
| MN4 | 22.886 | 39.7976 | 55 | 0.66905 |
| MN5 | 37.2901 | 56.8535 | 80 | 0.71067 |
| MN6 | 33.1913 | 49.3183 | 78 | 0.63229 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gora, O.; Akkan, T. Development of a Novel Spherical Light-Based Positioning Sensor in Solar Tracking. Sensors 2023, 23, 3838. https://doi.org/10.3390/s23083838
Gora O, Akkan T. Development of a Novel Spherical Light-Based Positioning Sensor in Solar Tracking. Sensors. 2023; 23(8):3838. https://doi.org/10.3390/s23083838
Chicago/Turabian StyleGora, Oğuz, and Taner Akkan. 2023. "Development of a Novel Spherical Light-Based Positioning Sensor in Solar Tracking" Sensors 23, no. 8: 3838. https://doi.org/10.3390/s23083838
APA StyleGora, O., & Akkan, T. (2023). Development of a Novel Spherical Light-Based Positioning Sensor in Solar Tracking. Sensors, 23(8), 3838. https://doi.org/10.3390/s23083838






