Research on Underdetermined DOA Estimation Method with Unknown Number of Sources Based on Improved CNN
Abstract
1. Introduction
2. Signal Model
3. Convolutional Neural Network Model
3.1. Convolutional Layers
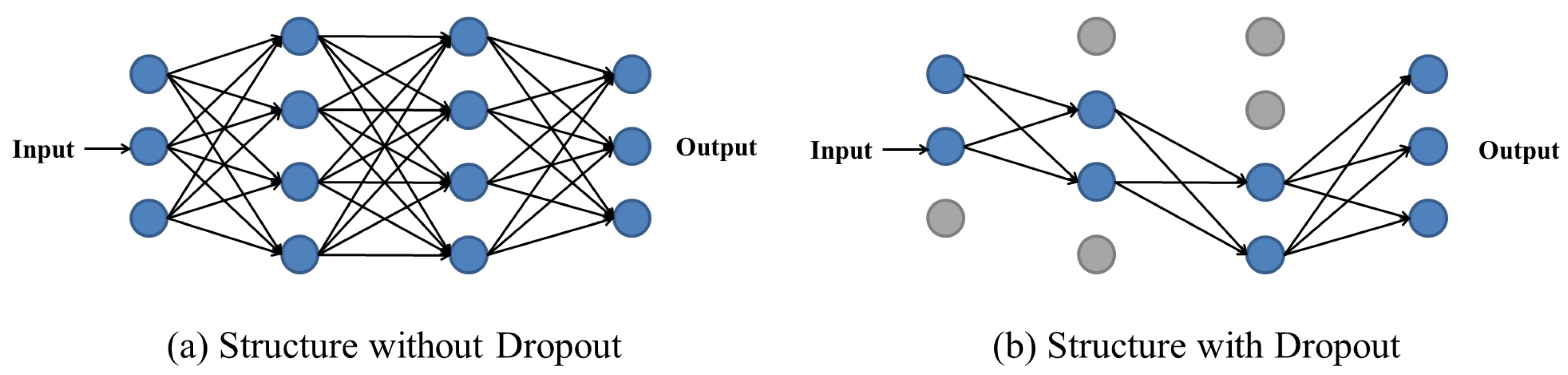
3.2. Fully Connected Layers
4. Simulation Experiments and Analysis of Results
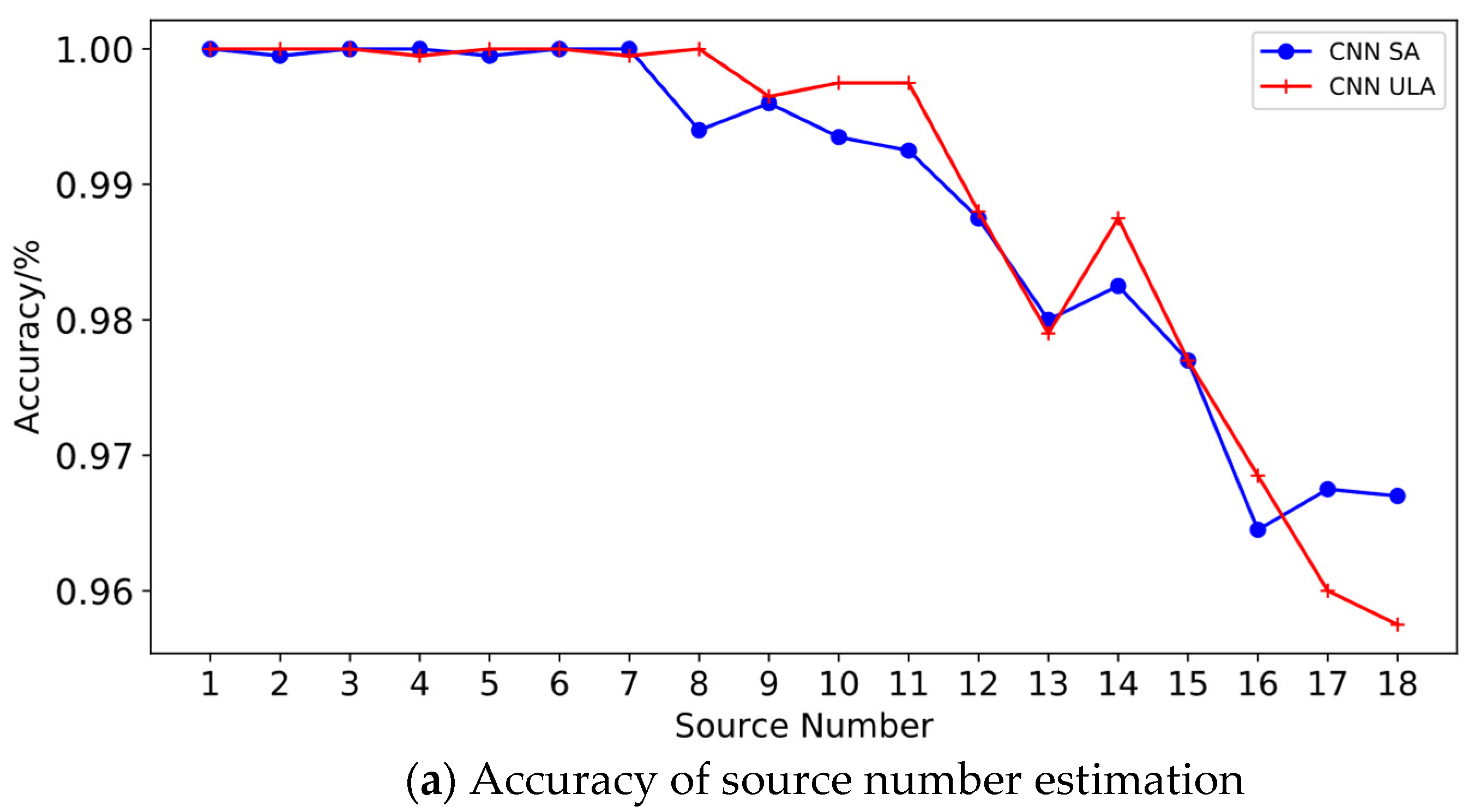
4.1. Performance of Source Number Estimation
4.2. Performance of DOA Estimation
4.2.1. DOA Estimation Performance at Different SNRs
4.2.2. DOA Estimation Performance at Different Snapshots
4.2.3. Performance at Small Snapshots and Low SNR
5. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Reinaldo, P.; Ana, C. An Overview of Deep Learning in Big Data, Image, And Signal Processing in the Modern Digital Age. In Trends in Deep Learning Methodologies; Vincenzo, P., Sandeep, R., Eds.; Academic Press: New York, NY, USA, 2021; pp. 63–87. [Google Scholar]
- Wang, J.; Li, R.; Wang, J. Artificial intelligence and wireless communications. Front. Inform. Technol. Electron. Eng. 2020, 21, 1413–1425. [Google Scholar] [CrossRef]
- Akaike, H. A new look at the statistical identification model. IEEE Trans. Autom. Contr. 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Veen, A.; Romme, J.; Ye, C. Rank Detection Thresholds for Hankel or Toeplitz Data Matrices. In Proceedings of the 2020 28th European Signal Processing Conference (EUSIPCO), Amsterdam, The Netherlands, 18–21 January 2021. [Google Scholar]
- Xu, J.; Wang, C. Research on Source Number Estimation based on Geschgorin Disk Estimator Theorem and Minimum Description Length Criterion. J. Signal Process. 2017, 33, 53–57. [Google Scholar]
- Chu, D.; Chen, H.; Cai, X. An Improved Source Number Estimation Algorithm Based on Geschgorin Disk Estimator Criterion. J. Detect. Control. 2018, 40, 109–115. [Google Scholar]
- Dong, F.; Jiang, Y. Experimental study on the performance of DOA estimation algorithm using a coprime acoustic sensor array without a priori knowledge of the source number. Appl. Acoust. 2022, 186, 108502. [Google Scholar] [CrossRef]
- Izedi, F.; Karimi, M.; Derakhtian, M. Joint DOA estimation and source number detection for arrays with arbitrary geometry. Signal Process. 2017, 140, 149–160. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, D. An Underdetermined Source Number Estimation Method for Non-Circular Targets Based on Sparse Array. IEEE Access 2019, 7, 77944–77950. [Google Scholar] [CrossRef]
- Li, J.; Wang, Y.; Ren, Z. DOA and Range Estimation Using a Uniform Linear Antenna Array Without A Priori Knowledge of the Source Number. IEEE Trans. Antennas Propag. 2021, 69, 2929–2939. [Google Scholar] [CrossRef]
- Matter, F.; Fischer, T.; Pesavento, M. Ambiguities in DOA Estimation with Linear Arrays. IEEE Trans. Signal Process. 2022, 70, 4395–4407. [Google Scholar] [CrossRef]
- Yu, W.; He, P. DOA Estimation Ambiguity Resolution Method for Near Field Distributed Array. In Proceedings of the 2021 6th International Conference on Intelligent Computing and Signal Processing (ICSP), Xi’an, China, 9–11 April 2021. [Google Scholar]
- Pal, P.; Vaidyanathan, P. Multiple level nested array: An efficient geometry for 2qth order cumulant based array processing. IEEE Trans. Signal Process. 2012, 60, 1253–1269. [Google Scholar] [CrossRef]
- Pal, P.; Vaidyanathan, P. Nested arrays: A novel approach to array processing with enhanced degrees of freedom. IEEE Trans. Signal Process. 2010, 58, 4167–4181. [Google Scholar] [CrossRef]
- Ge, S.; Li, K.; Rum, S. Deep Learning Approach in DOA Estimation: A Systematic Literature Review. Mob. Inf. Syst. 2021, 2021, 6392875. [Google Scholar] [CrossRef]
- Luo, F.; Li, Y. Real-time neural computation of the noise subspace for the MUSIC algorithm. In Proceedings of the IEEE International Conference on Acoustics, Minneapolis, MN, USA, 27–30 April 1993. [Google Scholar]
- Gohil, R.; Routray, G. Learning Based Method for Robust DOA Estimation using Co-prime Circular Conformal Microphone Array. In Proceedings of the 2021 National Conference on Communications (NCC), Kanpur, India, 27–30 July 2021. [Google Scholar]
- Liu, Z.; Zhang, C. Direction-of-Arrival Estimation Based on Deep Neural Networks with Robustness to Array Imperfections. IEEE Trans. Antennas Propag. 2018, 66, 7315–7327. [Google Scholar] [CrossRef]
- Ge, X.; Hu, X. DOA Estimation for Coherent Sources Using Deep Learning Method. J. Signal Process. 2019, 8, 98–106. [Google Scholar]
- Chen, F.; Yang, D.; Wu, D. A Novel Direction-of-Arrival Estimation Algorithm Without Knowing the Source Number. IEEE Commun. Lett. 2020, 99, 9215006. [Google Scholar] [CrossRef]
- Huang, H.; Yang, J. Deep Learning for Super-Resolution Channel Estimation and DOA Estimation Based Massive MIMO System. IEEE Trans. Veh. Technol. 2018, 67, 8549–8560. [Google Scholar] [CrossRef]
- Cheng, T.; Wang, B.; Wang, Z. Lightweight CNNs-Based Interleaved Sparse Array Design of Phased-MIMO Radar. IEEE Sens. J. 2021, 21, 13200–13214. [Google Scholar] [CrossRef]
- Zhou, J.; Zhang, Q. Fuzzy Graph Subspace Convolutional Network. IEEE Trans. Neural Networks Learn. Syst. 2022, 99, 1–15. [Google Scholar] [CrossRef]
- Umberto, M. Advanced Applied Deep Learning: Convolutional Neural Networks and Object Detection; Apress: Berkely, CA, USA, 2019; pp. 20–55. [Google Scholar]
- Krówczyńska, M.; Raczko, E. Asbestos–Cement Roofing Identification Using Remote Sensing and Convolutional Neural Networks (CNNs). Remote Sens. 2020, 12, 408. [Google Scholar] [CrossRef]
- Zhao, F.; Hu, G. DOA Estimation Method Based on Improved Deep Convolutional Neural Network. Sensors 2021, 22, 1305. [Google Scholar] [CrossRef]
- Sun, B.; Ruan, H. Underdetermined Direction of Arrival Estimation for coprime array in the presence of nonuniform noise. J. Electron. Inf. Technol. 2021, 43, 3687–3694. [Google Scholar]
- Zuo, M.; Xie, S. DOA Estimation Based on Weighted l1-norm Sparse Representation for Low SNR Scenarios. Sensors 2021, 21, 4614. [Google Scholar] [CrossRef] [PubMed]
- Wang, G.; Li, H. Underdetermined DOA estimation of optimal redundancy array via double reconstruction. Syst. Eng. Electron. 2023, 45, 49–55. [Google Scholar]
- Yan, F.; Jin, M. Low-degree root-MUSIC algorithm for fast DOA estimation based on variable substitution technique. Sci. China Inf. Sci. 2020, 63, 218–220. [Google Scholar] [CrossRef]
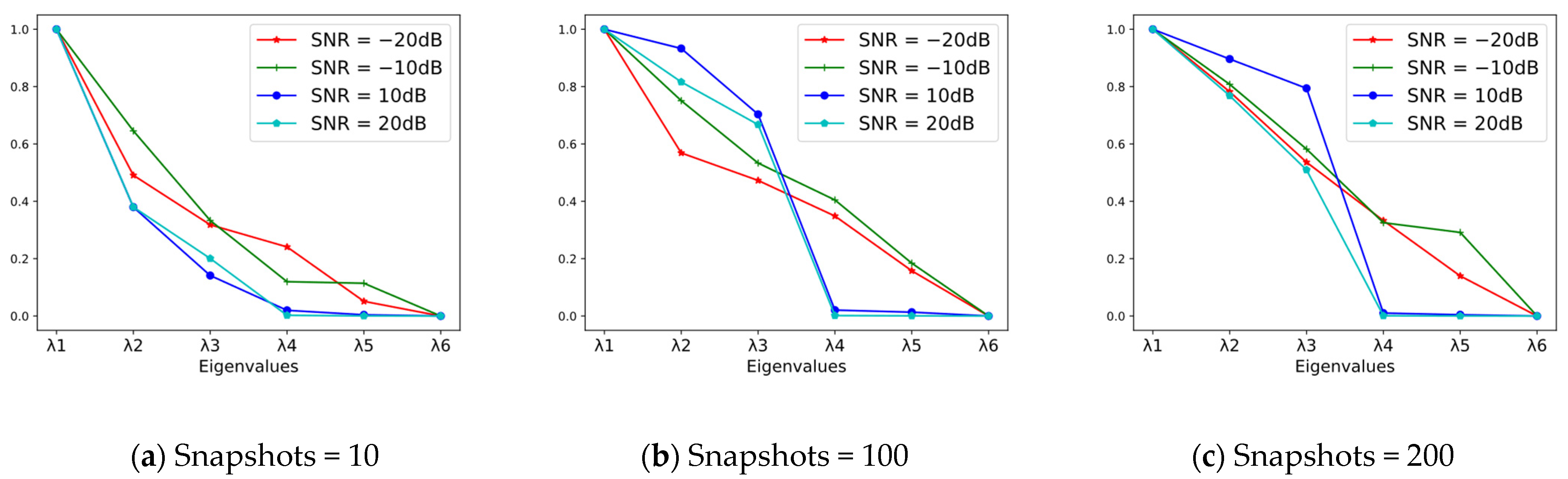

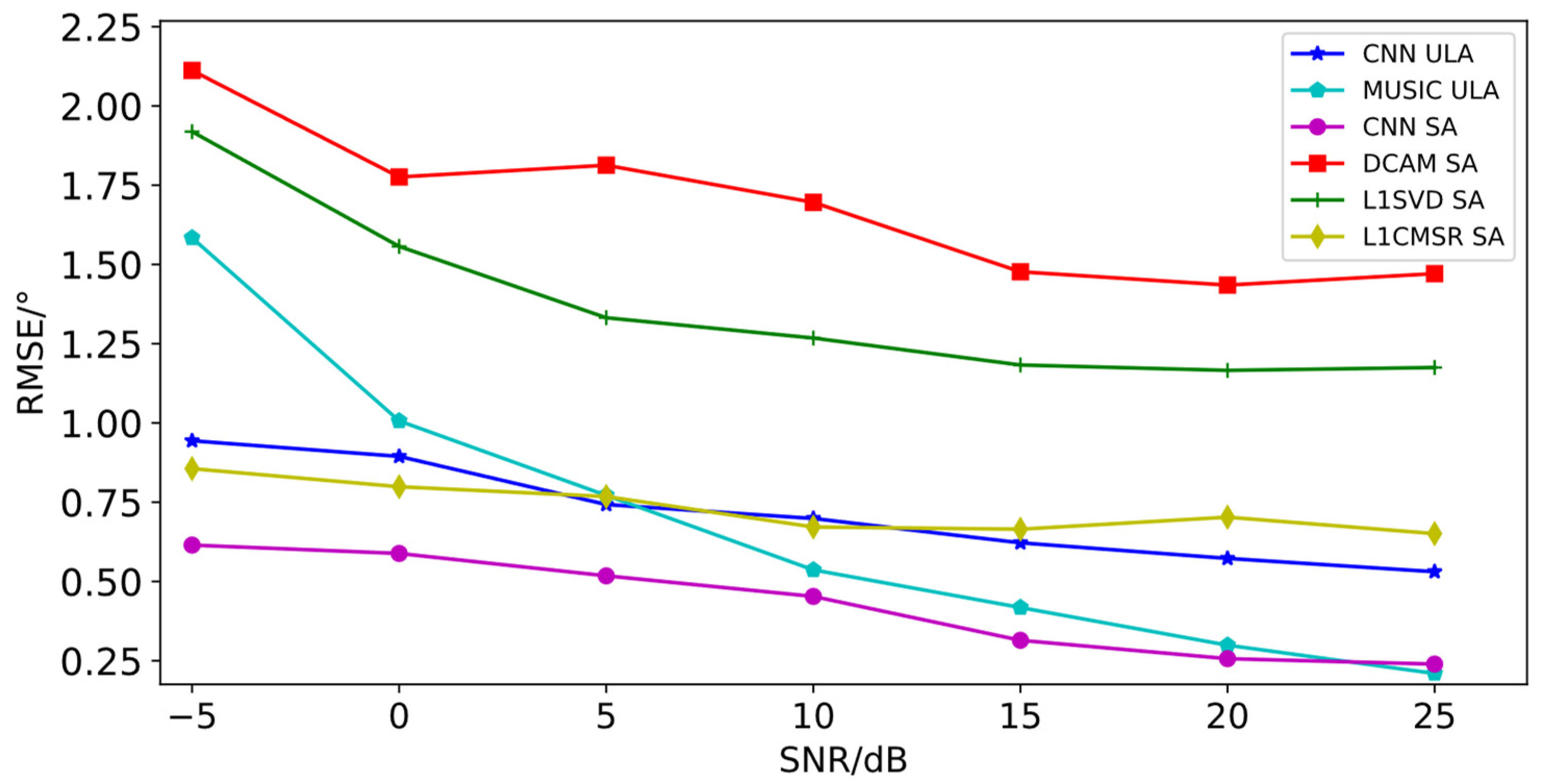
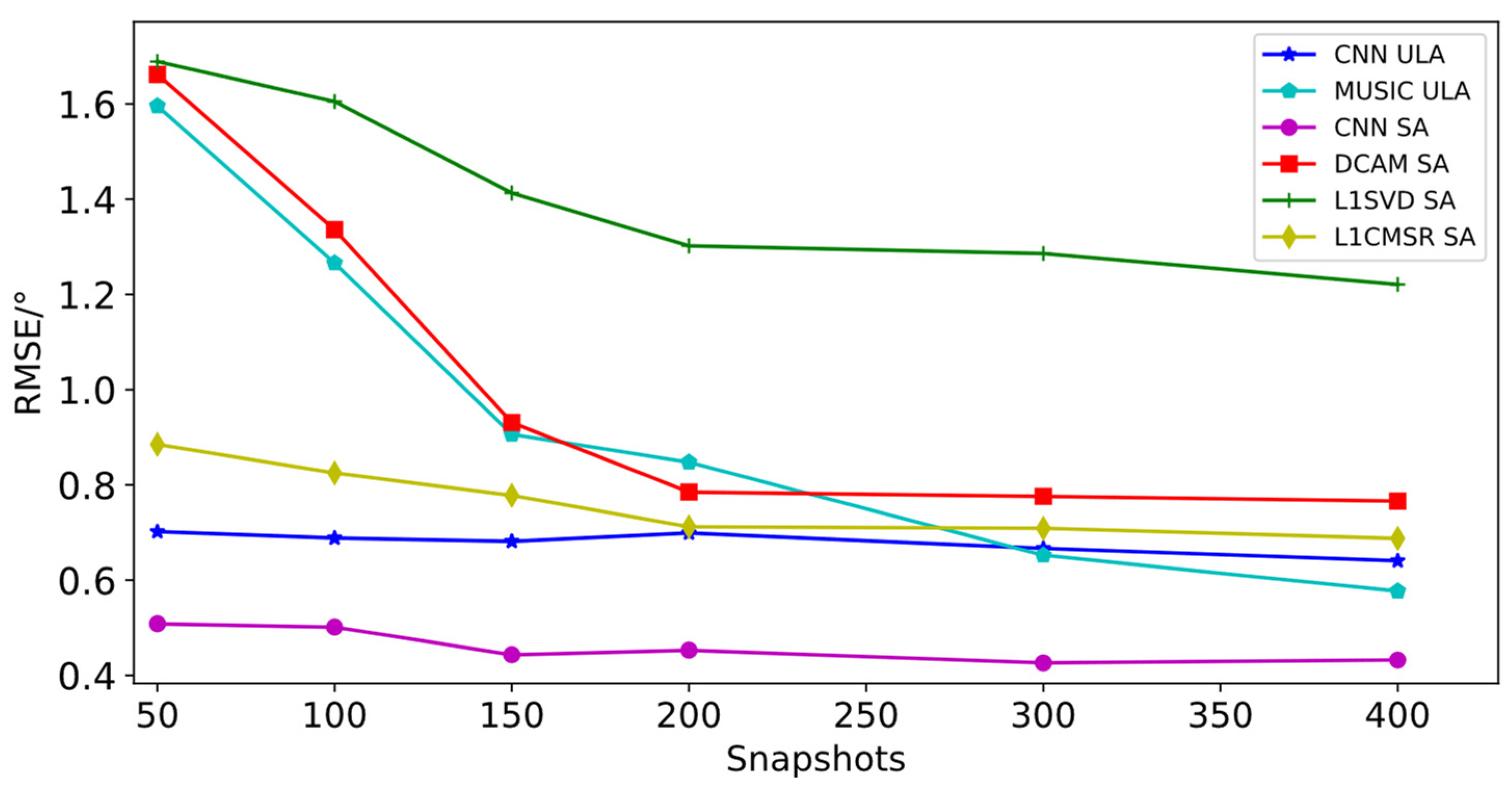

| Snapshots | 10 | 100 | 200 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SNR/dB | −20 | −10 | 10 | 20 | −20 | −10 | 10 | 20 | −20 | −10 | 10 | 20 |
| 954.39 | 74.69 | 11.19 | 8.54 | 392.34 | 40.62 | 7.56 | 7.21 | 376.96 | 41.73 | 6.42 | 8.53 | |
| 504.65 | 49.74 | 4.27 | 3.25 | 307.01 | 34.66 | 7.07 | 5.89 | 345.08 | 37.99 | 5.78 | 6.56 | |
| 352.02 | 27.73 | 1.61 | 1.72 | 288.04 | 29.45 | 5.39 | 4.82 | 309.06 | 33.59 | 5.15 | 4.36 | |
| 283.77 | 12.69 | 0.255 | 0.029 | 263.47 | 26.37 | 0.393 | 0.033 | 279.27 | 28.59 | 0.314 | 0.034 | |
| 116.21 | 12.31 | 0.081 | 0.012 | 225.69 | 21.09 | 0.340 | 0.027 | 251.00 | 27.93 | 0.278 | 0.028 | |
| 70.92 | 4.26 | 0.034 | 0.008 | 194.48 | 16.68 | 0.242 | 0.022 | 230.54 | 22.25 | 0.251 | 0.026 | |
| SNR/dB | −5 | 0 | 5 | 10 | 15 | 20 | 25 | |
|---|---|---|---|---|---|---|---|---|
| Source Number | 1–6 | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
| 7 | 100 | 99.85 | 100 | 100 | 100 | 100 | 100 | |
| 8 | 99.55 | 100 | 99.80 | 100 | 99.95 | 100 | 100 | |
| 9 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | |
| 10 | 99.80 | 100 | 98.50 | 100 | 100 | 100 | 100 | |
| 11 | 100 | 100 | 100 | 99.90 | 100 | 99.85 | 99.95 | |
| 12 | 99.50 | 98.65 | 100 | 100 | 100 | 100 | 99.90 | |
| 13 | 99.80 | 100 | 100 | 99.95 | 99.75 | 99.95 | 100 | |
| 14 | 98.95 | 99.85 | 99.90 | 99.75 | 99.50 | 99.85 | 99.95 | |
| 15 | 97.90 | 98.65 | 98.45 | 99.50 | 99.80 | 99.70 | 99.60 | |
| 16 | 96.10 | 96.15 | 97.20 | 98.50 | 98.60 | 99.45 | 98.75 | |
| 17 | 95.10 | 96.20 | 95.80 | 97.45 | 97.20 | 96.15 | 97.00 | |
| 18 | 94.15 | 95.55 | 95.75 | 97.65 | 97.95 | 98.80 | 98.50 | |
| SNR/dB | −5 | 0 | 5 | 10 | 15 | 20 | 25 | |
|---|---|---|---|---|---|---|---|---|
| Source Number | 1–12 | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
| 13 | 99.55 | 98.70 | 99.75 | 98.90 | 100 | 98.95 | 100 | |
| 14 | 98.75 | 99.45 | 99.85 | 98.45 | 99.65 | 99.70 | 100 | |
| 15 | 99.10 | 100 | 99.35 | 100 | 98.90 | 99.45 | 97.70 | |
| 16 | 97.85 | 99.05 | 99.60 | 99.85 | 98.75 | 100 | 99.05 | |
| 17 | 97.50 | 99.45 | 99.10 | 97.5 | 99.60 | 98.30 | 97.55 | |
| 18 | 96.35 | 97.80 | 98.50 | 97.65 | 98.30 | 99.20 | 99.25 | |
| SNR/dB | −5 | 0 | 5 | 10 | 15 | 20 | 25 | |
|---|---|---|---|---|---|---|---|---|
| Source Number | 1–6 | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
| 7 | 99.95 | 99.85 | 100 | 99.90 | 100 | 99.95 | 100 | |
| 8 | 99.50 | 100 | 99.70 | 100 | 99.85 | 100 | 99.95 | |
| 9 | 99.85 | 99.5 | 99.75 | 99.95 | 100 | 99.9 | 100 | |
| 10 | 99.75 | 100 | 98.25 | 100 | 99.80 | 100 | 99.90 | |
| 11 | 98.95 | 99.85 | 100 | 99.90 | 100 | 99.85 | 99.85 | |
| 12 | 99.50 | 98.65 | 99.80 | 100 | 99.85 | 100 | 99.90 | |
| 13 | 99.35 | 98.95 | 99.25 | 99.95 | 99.75 | 99.95 | 100 | |
| 14 | 98.75 | 99.85 | 99.90 | 99.70 | 99.35 | 99.25 | 99.65 | |
| 15 | 97.40 | 98.60 | 98.45 | 99.35 | 99.70 | 99.15 | 98.95 | |
| 16 | 95.85 | 96.15 | 97.20 | 98.45 | 98.50 | 99.05 | 98.55 | |
| 17 | 94.35 | 96.15 | 95.25 | 96.35 | 96.80 | 95.95 | 96.75 | |
| 18 | 94.05 | 93.95 | 94.25 | 97.35 | 97.95 | 97.80 | 98.50 | |
| SNR/dB | −5 | 0 | 5 | 10 | 15 | 20 | 25 | |
|---|---|---|---|---|---|---|---|---|
| Source Number | 1–4 | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
| 5 | 99.95 | 100 | 100 | 100 | 100 | 100 | 100 | |
| 6 | 100 | 100 | 100 | 100 | 99.95 | 100 | 100 | |
| 7 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | |
| 8 | 99.80 | 100 | 99.95 | 100 | 100 | 100 | 100 | |
| 9–11 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | |
| 12 | 100 | 99.95 | 100 | 100 | 99.90 | 99.85 | 100 | |
| 13 | 99.30 | 98.65 | 99.75 | 98.90 | 100 | 98.95 | 99.95 | |
| 14 | 98.65 | 99.40 | 99.65 | 98.45 | 99.60 | 99.65 | 100 | |
| 15 | 99.05 | 99.85 | 99.35 | 99.80 | 98.75 | 99.25 | 97.70 | |
| 16 | 97.45 | 98.65 | 99.55 | 99.55 | 98.70 | 99.80 | 99.00 | |
| 17 | 96.95 | 98.85 | 98.55 | 96.75 | 99.55 | 98.20 | 97.55 | |
| 18 | 96.35 | 97.65 | 98.35 | 96.35 | 98.25 | 99.10 | 98.75 | |
| SNR/dB | −5 | 0 | 5 | 10 | 15 | 20 | 25 | |
|---|---|---|---|---|---|---|---|---|
| Source Number | 1 | 0.6425 | 0.4169 | 0.3302 | 0.2185 | 0.1674 | 0.1127 | 0.0907 |
| 2 | 0.5209 | 0.4912 | 0.3750 | 0.3220 | 0.3163 | 0.2006 | 0.1740 | |
| 3 | 0.5391 | 0.4136 | 0.4128 | 0.3718 | 0.3293 | 0.3215 | 0.2043 | |
| 4 | 0.5270 | 0.4096 | 0.3521 | 0.3649 | 0.2546 | 0.2500 | 0.1748 | |
| 5 | 0.5446 | 0.5384 | 0.3675 | 0.3661 | 0.3545 | 0.3299 | 0.2709 | |
| 6 | 0.6138 | 0.5912 | 0.4588 | 0.4214 | 0.3454 | 0.3189 | 0.3024 | |
| 7 | 0.6939 | 0.6600 | 0.6225 | 0.5676 | 0.4491 | 0.3357 | 0.3012 | |
| 8 | 0.6884 | 0.6841 | 0.6407 | 0.6945 | 0.5704 | 0.4837 | 0.4021 | |
| 9 | 0.7293 | 0.7011 | 0.6564 | 0.6316 | 0.5584 | 0.5528 | 0.5328 | |
| 10 | 0.7980 | 0.7077 | 0.6559 | 0.6423 | 0.5883 | 0.5705 | 0.5547 | |
| 11 | 0.7724 | 0.7637 | 0.6968 | 0.6171 | 0.5878 | 0.5720 | 0.5702 | |
| 12 | 0.7685 | 0.7960 | 0.7530 | 0.6335 | 0.5889 | 0.5708 | 0.5671 | |
| 13 | 0.8914 | 0.7206 | 0.7452 | 0.6205 | 0.6179 | 0.6024 | 0.5157 | |
| 14 | 1.0573 | 1.0718 | 0.6138 | 0.6543 | 0.6381 | 0.6778 | 0.5631 | |
| 15 | 1.0854 | 1.0813 | 0.8528 | 0.7369 | 0.6540 | 0.5817 | 0.5232 | |
| 16 | 1.1623 | 1.0831 | 0.8521 | 0.9402 | 0.7909 | 0.6080 | 0.6010 | |
| 17 | 1.1949 | 1.1353 | 0.8200 | 0.7391 | 0.6403 | 0.6120 | 0.5941 | |
| 18 | 1.2056 | 1.1018 | 1.0360 | 0.9461 | 0.8307 | 0.7500 | 0.6928 | |
| SNR/dB | −5 | 0 | 5 | 10 | 15 | 20 | 25 | |
|---|---|---|---|---|---|---|---|---|
| Number of Sources | 1 | 0.6138 | 0.3341 | 0.2283 | 0.1974 | 0.1127 | 0.0905 | 0.0378 |
| 2 | 0.5446 | 0.3735 | 0.2211 | 0.1740 | 0.2032 | 0.0985 | 0.0780 | |
| 3 | 0.5270 | 0.3634 | 0.3451 | 0.2895 | 0.2325 | 0.0963 | 0.0907 | |
| 4 | 0.4281 | 0.5442 | 0.4516 | 0.3850 | 0.2207 | 0.1067 | 0.1253 | |
| 5 | 0.4505 | 0.6416 | 0.2404 | 0.2404 | 0.2695 | 0.1716 | 0.0929 | |
| 6 | 0.4196 | 0.3619 | 0.3619 | 0.1439 | 0.2688 | 0.1622 | 0.0781 | |
| 7 | 0.6338 | 0.5979 | 0.5026 | 0.3474 | 0.3101 | 0.2426 | 0.1674 | |
| 8 | 0.7169 | 0.7145 | 0.6007 | 0.3091 | 0.2309 | 0.2050 | 0.1644 | |
| 9 | 0.4597 | 0.5659 | 0.5016 | 0.3904 | 0.3407 | 0.2031 | 0.1804 | |
| 10 | 0.6451 | 0.5151 | 0.3921 | 0.3471 | 0.2517 | 0.2266 | 0.2051 | |
| 11 | 0.4934 | 0.5270 | 0.3187 | 0.3044 | 0.2613 | 0.2319 | 0.2259 | |
| 12 | 0.4799 | 0.4779 | 0.3742 | 0.3304 | 0.2599 | 0.2250 | 0.2161 | |
| 13 | 0.6254 | 0.4938 | 0.4790 | 0.4500 | 0.3632 | 0.2493 | 0.2251 | |
| 14 | 0.6504 | 0.6287 | 0.6230 | 0.5788 | 0.3454 | 0.3189 | 0.3024 | |
| 15 | 0.5746 | 0.5077 | 0.4919 | 0.4609 | 0.3567 | 0.2625 | 0.3061 | |
| 16 | 0.6453 | 0.6357 | 0.5637 | 0.4944 | 0.3596 | 0.2990 | 0.2886 | |
| 17 | 0.8004 | 0.7737 | 0.7045 | 0.6517 | 0.3620 | 0.3094 | 0.2753 | |
| 18 | 0.6888 | 0.6501 | 0.6284 | 0.5805 | 0.3204 | 0.3177 | 0.2917 | |
| Snapshots | 50 | 100 | 150 | 200 | 300 | 400 | |
|---|---|---|---|---|---|---|---|
| Source Number | 1 | 0.3241 | 0.3016 | 0.2740 | 0.2185 | 0.2302 | 0.2035 |
| 2 | 0.3776 | 0.3444 | 0.3090 | 0.3220 | 0.3131 | 0.3326 | |
| 3 | 0.4087 | 0.3746 | 0.3209 | 0.3718 | 0.3379 | 0.3269 | |
| 4 | 0.4552 | 0.4055 | 0.3492 | 0.3649 | 0.3017 | 0.3006 | |
| 5 | 0.4259 | 0.4569 | 0.4079 | 0.3661 | 0.3621 | 0.3421 | |
| 6 | 0.4706 | 0.4745 | 0.4889 | 0.4214 | 0.4023 | 0.4128 | |
| 7 | 0.5822 | 0.5809 | 0.5811 | 0.5676 | 0.5255 | 0.5490 | |
| 8 | 0.6359 | 0.6272 | 0.5445 | 0.6945 | 0.6260 | 0.5650 | |
| 9 | 0.5962 | 0.6572 | 0.6175 | 0.6316 | 0.6604 | 0.5792 | |
| 10 | 0.6271 | 0.6019 | 0.6524 | 0.6423 | 0.5948 | 0.6110 | |
| 11 | 0.6485 | 0.6231 | 0.6450 | 0.6171 | 0.6055 | 0.5781 | |
| 12 | 0.6705 | 0.6606 | 0.6437 | 0.6335 | 0.6403 | 0.6071 | |
| 13 | 0.6687 | 0.6577 | 0.6477 | 0.6205 | 0.6490 | 0.6139 | |
| 14 | 0.6891 | 0.6757 | 0.6524 | 0.6543 | 0.6313 | 0.5903 | |
| 15 | 0.7057 | 0.7652 | 0.7573 | 0.7369 | 0.6696 | 0.6470 | |
| 16 | 0.7625 | 0.7913 | 0.8045 | 0.9402 | 0.7633 | 0.8027 | |
| 17 | 0.8431 | 0.8096 | 0.7924 | 0.7391 | 0.7916 | 0.7405 | |
| 18 | 0.9738 | 0.8668 | 0.8786 | 0.9461 | 0.9148 | 0.8556 | |
| Snapshots | 50 | 100 | 150 | 200 | 300 | 400 | |
|---|---|---|---|---|---|---|---|
| Source Number | 1 | 0.2295 | 0.2051 | 0.1416 | 0.1974 | 0.1907 | 0.2127 |
| 2 | 0.2303 | 0.3010 | 0.2298 | 0.1740 | 0.1569 | 0.1860 | |
| 3 | 0.3520 | 0.3996 | 0.3238 | 0.2895 | 0.3013 | 0.2170 | |
| 4 | 0.3321 | 0.3458 | 0.3102 | 0.3850 | 0.3552 | 0.3108 | |
| 5 | 0.3790 | 0.3649 | 0.3001 | 0.2404 | 0.3125 | 0.2375 | |
| 6 | 0.3376 | 0.2582 | 0.2765 | 0.1439 | 0.1710 | 0.2067 | |
| 7 | 0.3757 | 0.2327 | 0.3300 | 0.3474 | 0.3232 | 0.2814 | |
| 8 | 0.3548 | 0.3405 | 0.3365 | 0.3091 | 0.2810 | 0.2613 | |
| 9 | 0.3734 | 0.4020 | 0.3892 | 0.3904 | 0.3365 | 0.3647 | |
| 10 | 0.3813 | 0.4181 | 0.3363 | 0.3471 | 0.3300 | 0.3010 | |
| 11 | 0.3893 | 0.3517 | 0.3188 | 0.3044 | 0.3087 | 0.2824 | |
| 12 | 0.4166 | 0.4048 | 0.3494 | 0.3304 | 0.3255 | 0.4014 | |
| 13 | 0.4615 | 0.5273 | 0.4631 | 0.4500 | 0.4117 | 0.3801 | |
| 14 | 0.5974 | 0.5716 | 0.4605 | 0.5788 | 0.5314 | 0.4662 | |
| 15 | 0.5608 | 0.5760 | 0.4901 | 0.4609 | 0.4586 | 0.4866 | |
| 16 | 0.5742 | 0.5578 | 0.4844 | 0.4944 | 0.4786 | 0.5428 | |
| 17 | 0.6907 | 0.6767 | 0.6005 | 0.6517 | 0.5466 | 0.5711 | |
| 18 | 0.6717 | 0.6486 | 0.5933 | 0.5805 | 0.5816 | 0.6027 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, F.; Hu, G.; Zhou, H.; Guo, S. Research on Underdetermined DOA Estimation Method with Unknown Number of Sources Based on Improved CNN. Sensors 2023, 23, 3100. https://doi.org/10.3390/s23063100
Zhao F, Hu G, Zhou H, Guo S. Research on Underdetermined DOA Estimation Method with Unknown Number of Sources Based on Improved CNN. Sensors. 2023; 23(6):3100. https://doi.org/10.3390/s23063100
Chicago/Turabian StyleZhao, Fangzheng, Guoping Hu, Hao Zhou, and Shuhan Guo. 2023. "Research on Underdetermined DOA Estimation Method with Unknown Number of Sources Based on Improved CNN" Sensors 23, no. 6: 3100. https://doi.org/10.3390/s23063100
APA StyleZhao, F., Hu, G., Zhou, H., & Guo, S. (2023). Research on Underdetermined DOA Estimation Method with Unknown Number of Sources Based on Improved CNN. Sensors, 23(6), 3100. https://doi.org/10.3390/s23063100





