Unsupervised Single-Channel Singing Voice Separation with Weighted Robust Principal Component Analysis Based on Gammatone Auditory Filterbank and Vocal Activity Detection
Abstract
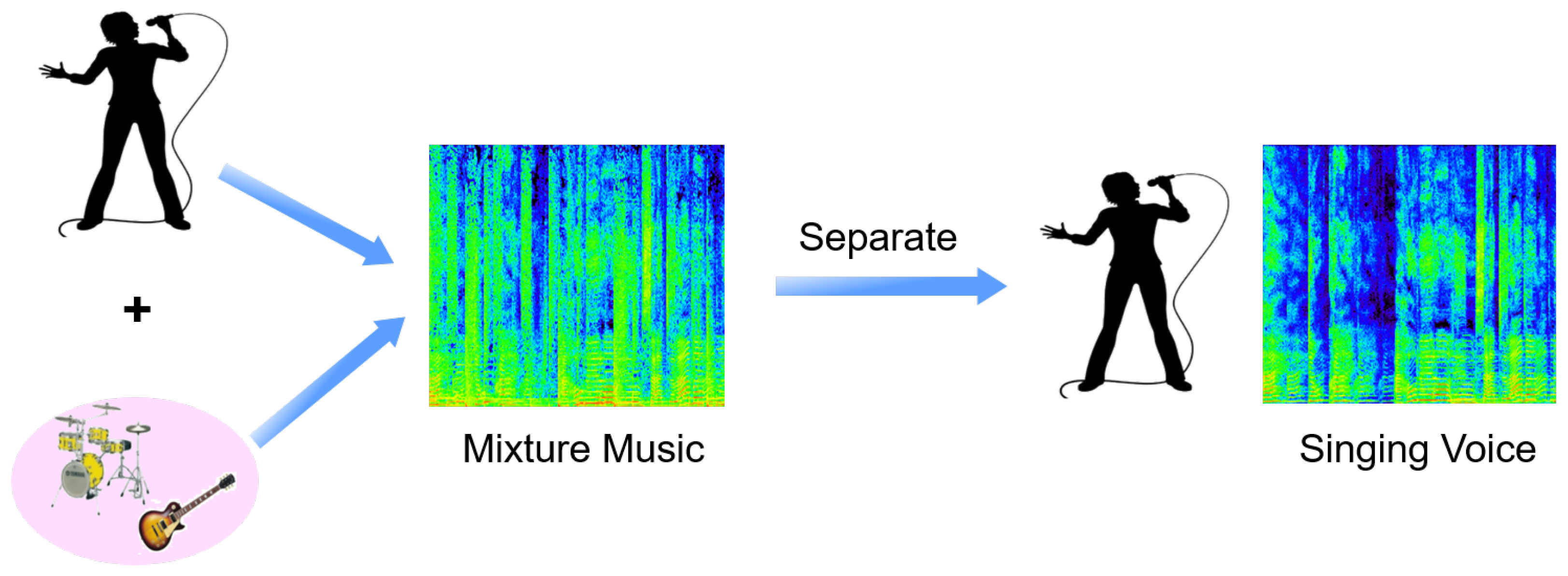
1. Introduction
- We offer the WRPCA addition to RPCA, which uses various weighted RPCA to achieve the improved separation performance.
- We combine gammatone auditory filterbank with vocal activity detection for SVS. Gammatone filterbanks are designed to imitate the human auditory system.
- We build the coalescent masking by fusing the harmonic masking and T-F masking, which can remove nonseparated background music. Additionally, we restrict the temporal segments that can include the singing voice part by using VAD.
- The extensive monaural SVS experiments reveal that the proposed approach can achieve greater separation performance than the RPCA method.
2. Related Work
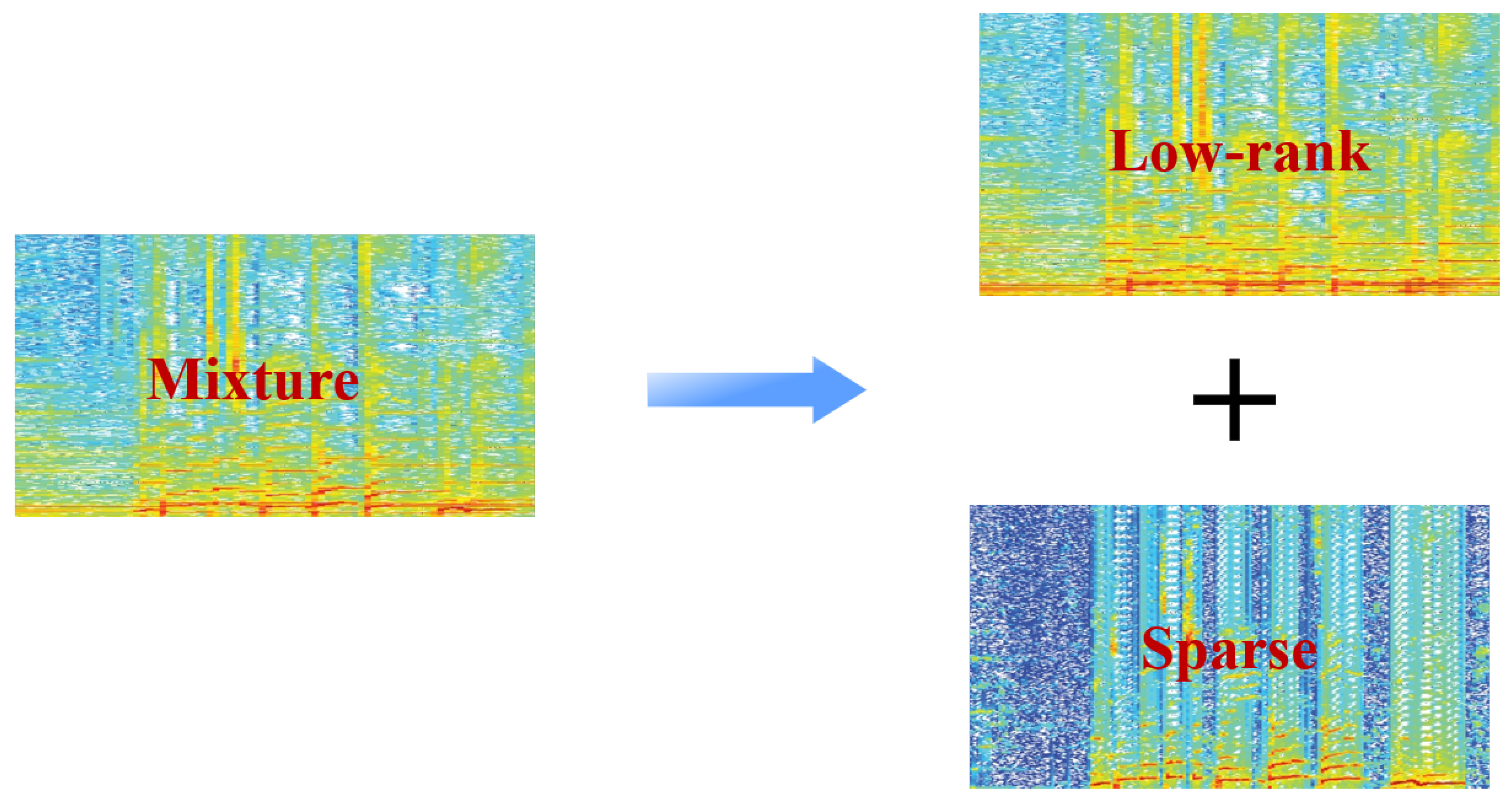
2.1. Overview of RPCA
2.2. RPCA for SVS
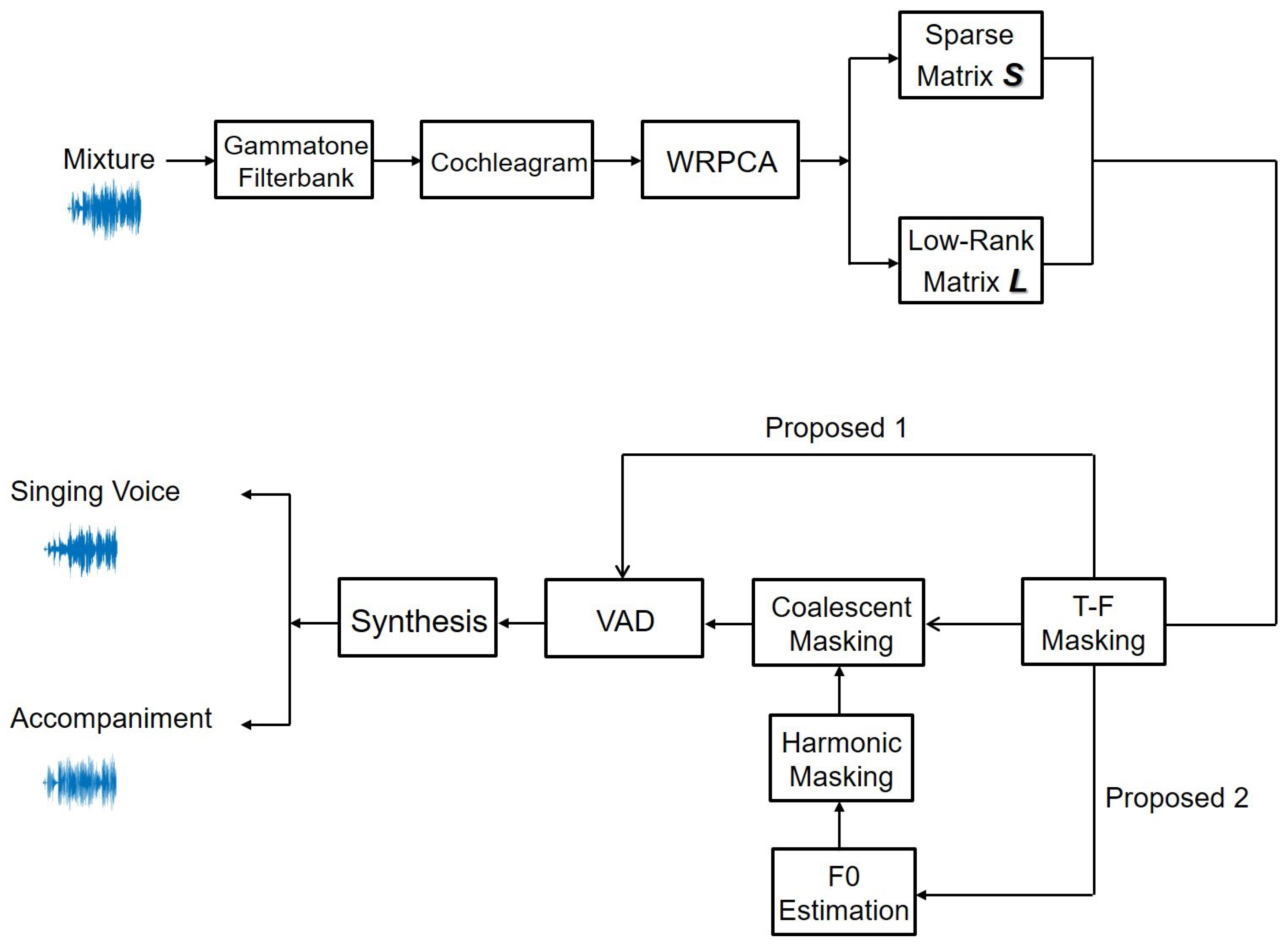
3. Proposed Method
3.1. Overview of WRPCA
| Algorithm 1 WRPCA for SVS |
| Input: Mixture music , weight |
| 1: Initialize: |
| 2: While not convergence do: |
| 3: repeat |
| 4: arg |
| 5: arg |
| 6: |
| 7: |
| 8: |
| 9: end while. |
| Output: |
3.2. Weighted Values
3.3. Gammatone Filterbank
3.4. T-F Masking
3.5. F0 Estimation
3.6. Harmonic Masking
3.7. Coalescent Masking
3.8. Vocal Activity Detection
4. Experimental Evaluation
4.1. Datasets
4.2. Settings
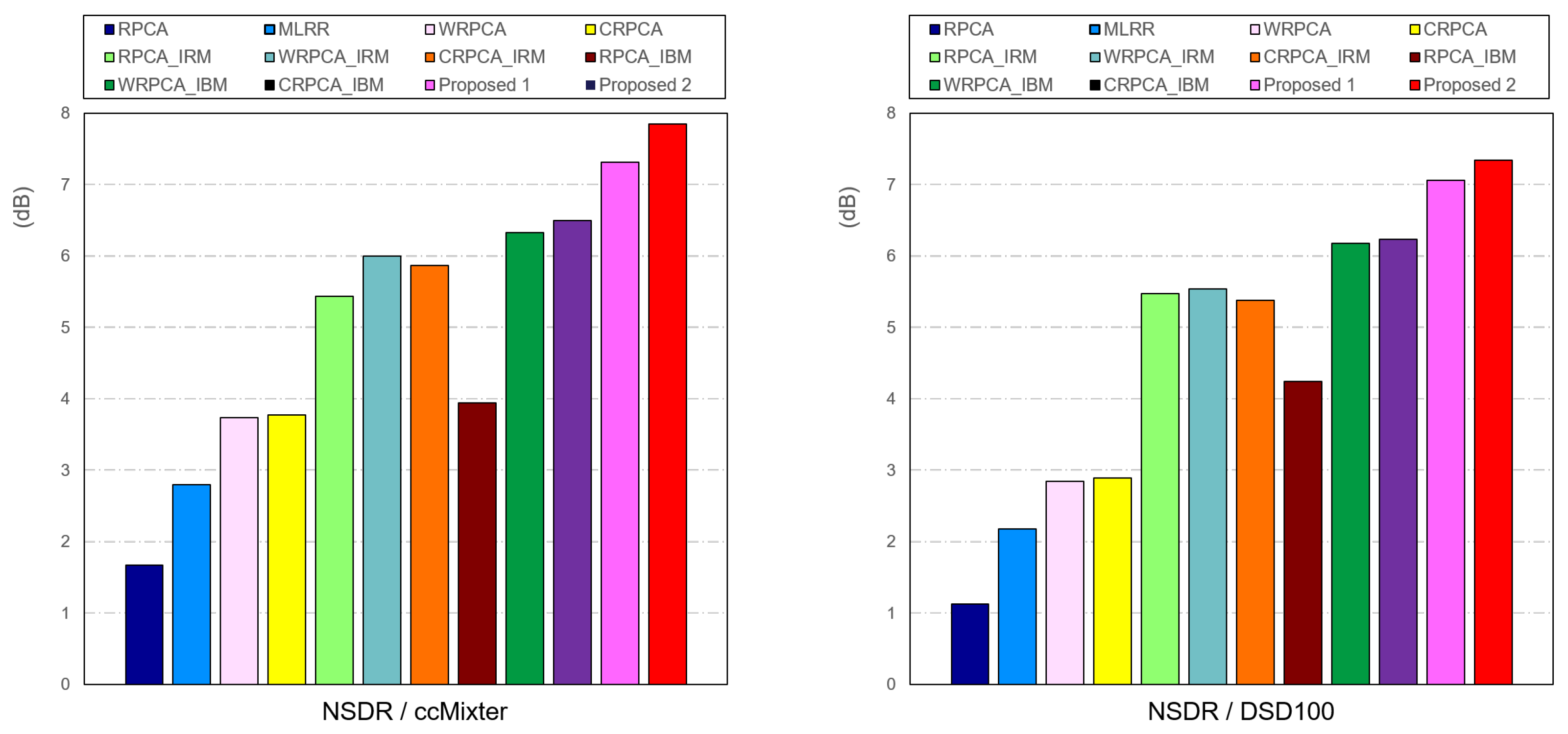
4.3. Experiment Results
- Proposed 1: WRPCA with T-F masking
- Proposed 2: WRPCA with coalescent masking.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| SVS | singing voice separation |
| RPCA | robust principal component analysis |
| MLRR | multiple low-rank representation |
| WRPCA | weighted robust principal component analysis |
| VAD | voice activity detection |
| IBM | ideal binary mask |
| IRM | ideal ratio mask |
| ALM | augmented lagrange multiplier |
| APG | accelerated proximal gradient |
| SVD | singular value decomposition |
| T-F | time-frequency |
| CNN | convolutional neural network |
| NMF | nonnegative matrix factorization |
| SNMF | sparse nonnegative matrix factorization |
| SDR | source-to-distortion ratio |
| SAR | source-to-artifact ratio |
| NSDR | normalized SDR |
References
- Schulze-Forster, K.; Doire, C.S.; Richard, G.; Badeau, R. Phoneme level lyrics alignment and text-informed singing voice separation. IEEE/ACM Trans. Audio Speech Lang. Process. 2021, 29, 2382–2395. [Google Scholar] [CrossRef]
- Gupta, C.; Li, H.; Goto, M. Deep Learning Approaches in Topics of Singing Information Processing. IEEE/ACM Trans. Audio Speech Lang. Process. 2022, 30, 2422–2451. [Google Scholar] [CrossRef]
- Yu, S.; Li, C.; Deng, F.; Wang, X. Rethinking Singing Voice Separation With Spectral-Temporal Transformer. In Proceedings of the Asia-Pacific Signal and Information Processing Association Annual Summit and Conference (APSIPA ASC), Tokyo, Japan, 14–17 December 2021; pp. 884–889. [Google Scholar]
- Basak, S.; Agarwal, S.; Ganapathy, S.; Takahashi, N. End-to-end Lyrics Recognition with Voice to Singing Style Transfer. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Toronto, ON, Canada, 6–12 June 2021; pp. 266–270. [Google Scholar]
- Zhang, X.; Qian, J.; Yu, Y.; Sun, Y.; Li, W. Singer identification using deep timbre feature learning with knn-net. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Toronto, ON, Canada, 6–12 June 2021; pp. 3380–3384. [Google Scholar]
- Hu, S.; Liang, B.; Chen, Z.; Lu, X.; Zhao, E.; Lui, S. Large-scale singer recognition using deep metric learning: An experimental study. In Proceedings of the 2021 International Joint Conference on Neural Networks (IJCNN), Shenzhen, China, 18–22 July 2021; pp. 1–6. [Google Scholar]
- da Silva, A.C.M.; Silva, D.F.; Marcacini, R.M. Multimodal representation learning over heterogeneous networks for tag-based music retrieval. Expert Syst. Appl. 2022, 207, 117969. [Google Scholar] [CrossRef]
- Wang, Y.; Song, W.; Tao, W.; Liotta, A.; Yang, D.; Li, X.; Gao, S.; Sun, Y.; Ge, W.; Zhang, W.; et al. A systematic review on affective computing: Emotion models, databases, and recent advances. Inf. Fusion 2022, 83–84, 19–52. [Google Scholar] [CrossRef]
- Stoller, D.; Dur, S.; Ewert, S. End-to-end lyrics alignment for polyphonic music using an audio-to-character recognition model. In Proceedings of the ICASSP 2019–2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brighton, UK, 12–17 May 2019; pp. 181–185. [Google Scholar]
- Gupta, C.; Yılmaz, E.; Li, H. Automatic lyrics alignment and transcription in polyphonic music: Does background music help? In Proceedings of the ICASSP 2020—2020 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Barcelona, Spain, 4–8 May 2020; pp. 496–500. [Google Scholar]
- Huang, J.; Benetos, E.; Ewert, S. Improving Lyrics Alignment Through Joint Pitch Detection. In Proceedings of the ICASSP 2022—2022 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Singapore, 22–27 May 2022; pp. 451–455. [Google Scholar]
- Gupta, C.; Sharma, B.; Li, H.; Wang, Y. Lyrics-to-audio alignment using singing-adapted acoustic models and non-vocal suppression. Music Inf. Retr. Eval. Exch. Audio-Lyrics Alignment Chall. 2022. Available online: https://www.music-ir.org/mirex/abstracts/2018/GSLW3.pdf (accessed on 2 January 2023).
- Srinivasa Murthy, Y.V.; Koolagudi, S.G.; Jeshventh Raja, T.K. Singer identification for Indian singers using convolutional neural networks. Int. J. Speech Technol. 2021, 24, 781–796. [Google Scholar] [CrossRef]
- Tuncer, T.; Dogan, S.; Akbal, E.; Cicekli, A.; Rajendra Acharya, U. Development of accurate automated language identification model using polymer pattern and tent maximum absolute pooling techniques. Neural Comput. Appl. 2022, 34, 4875–4888. [Google Scholar] [CrossRef]
- Chen, T.P.; Su, L. Attend to chords: Improving harmonic analysis of symbolic music using transformer-based models. Trans. Int. Soc. Music. Inf. Retr. 2021, 4, 1–13. [Google Scholar] [CrossRef]
- Chen, T.P.; Su, L. Harmony Transformer: Incorporating chord segmentation into harmony recognition. Neural Netw. 2019, 12, 15. [Google Scholar]
- Byambatsogt, G.; Choimaa, L.; Koutaki, G. Data generation from robotic performer for chord recognition. IEEE Trans. Electron. Inf. Syst. 2021, 141, 205–213. [Google Scholar] [CrossRef]
- Mirbeygi, M.; Mahabadi, A.; Ranjbar, A. Speech and music separation approaches—A survey. Multimed. Tools Appl. 2022, 81, 21155–21197. [Google Scholar] [CrossRef]
- Ju, Y.; Rao, W.; Yan, X.; Fu, Y.; Lv, S.; Cheng, L.; Wang, Y.; Xie, L.; Shang, S. TEA-PSE: Tencent-ethereal-audio-lab personalized speech enhancement system for ICASSP 2022 DNS CHALLENGE. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Singapore, 22–27 May 2022; pp. 9291–9295. [Google Scholar]
- Mitsufuji, Y.; Fabbro, G.; Uhlich, S.; Stöter, F.R.; Défossez, A.; Kim, M.; Choi, W.; Yu, C.Y.; Cheuk, K.W. Music demixing challenge 2021. Front. Signal Process. 2022, 1, 18. [Google Scholar] [CrossRef]
- Ji, X.; Han, J.; Jiang, X.; Hu, X.; Guo, L.; Han, J.; Shao, L.; Liu, T. Analysis of music/speech via integration of audio content and functional brain response. Inf. Sci. 2015, 297, 271–282. [Google Scholar] [CrossRef]
- Chen, K.; Yu, S.; Wang, C.I.; Li, W.; Berg-Kirkpatrick, T.; Dubnov, S. Tonet: Tone-octave network for singing melody extraction from polyphonic music. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Singapore, 22–27 May 2022; pp. 621–625. [Google Scholar]
- Petermann, D.; Wichern, G.; Wang, Z.Q.; Le Roux, J. The cocktail fork problem: Three-stem audio separation for real-world soundtracks. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Singapore, 22–27 May 2022; pp. 526–530. [Google Scholar]
- Yu, Y.; Peng, C.; Tang, Q.; Wang, X. Monaural Music Source Separation Using Deep Convolutional Neural Network Embedded with Feature Extraction Module. In Proceedings of the 2022 Asia Conference on Algorithms, Computing and Machine Learning (CACML), Shanghai, China, 17–19 March 2022; pp. 546–551. [Google Scholar]
- Hu, Y.; Chen, Y.; Yang, W.; He, L.; Huang, H. Hierarchic Temporal Convolutional Network With Cross-Domain Encoder for Music Source Separation. IEEE Signal Process. Lett. 2022, 29, 1517–1521. [Google Scholar] [CrossRef]
- Guizzo, E.; Weyde, T.; Tarroni, G. Anti-transfer learning for task invariance in convolutional neural networks for speech processing. Neural Netw. 2021, 142, 238–251. [Google Scholar] [CrossRef]
- Ni, X.; Ren, J. FC-U 2-Net: A Novel Deep Neural Network for Singing Voice Separation. IEEE/ACM Trans. Audio Speech Lang. Process. 2022, 30, 489–494. [Google Scholar] [CrossRef]
- Xu, Y.; Wang, W.; Cui, H.; Xu, M.; Li, M. Paralinguistic singing attribute recognition using supervised machine learning for describing the classical tenor solo singing voice in vocal pedagogy. EURASIP J. Audio Speech Music Process. 2022, 2022, 1–16. [Google Scholar] [CrossRef]
- Zhou, Y.; Lu, X. HiFi-SVC: Fast High Fidelity Cross-Domain Singing Voice Conversion. In Proceedings of the ICASSP 2022—2022 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Singapore, 22–27 May 2022; pp. 6667–6671. [Google Scholar]
- Kum, S.; Lee, J.; Kim, K.L.; Kim, T.; Nam, J. Pseudo-Label Transfer from Frame-Level to Note-Level in a Teacher-Student Framework for Singing Transcription from Polyphonic Music. In Proceedings of the ICASSP 2022—2022 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Singapore, 22–27 May 2022; pp. 796–800. [Google Scholar]
- Wang, Y.; Stoller, D.; Bittner, R.M.; Bello, J.P. Few-Shot Musical Source Separation. In Proceedings of the ICASSP 2022—2022 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Singapore, 22–27 May 2022; pp. 121–125. [Google Scholar]
- Zhang, X.; Wang, J.; Cheng, N.; Xiao, J. Mdcnn-sid: Multi-scale dilated convolution network for singer identification. In Proceedings of the 2022 International Joint Conference on Neural Networks (IJCNN), Padova, Italy, 18–23 July 2022; pp. 1–7. [Google Scholar]
- Wang, D.; Chen, J. Supervised speech separation based on deep learning: An overview. IEEE/ACM Trans. Audio Speech Lang. Process. 2018, 26, 1702–1726. [Google Scholar] [CrossRef]
- Huang, P.S.; Chen, S.D.; Smaragdis, P.; Hasegawa-Johnson, M. Singing-voice separation from monaural recordings using robust principal component analysis. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Kyoto, Japan, 25–30 March 2012; pp. 57–60. [Google Scholar]
- Yang, Y.-H. On sparse and low-rank matrix decomposition for singing voice separation. In Proceedings of the 20th ACM International Conference on Multimedia, Nara, Japan, 29 October–2 November 2012; pp. 757–760. [Google Scholar]
- Yang, Y.-H. Low-Rank Representation of Both Singing Voice and Music Accompaniment Via Learned Dictionaries. In Proceedings of the ISMIR, Curitiba, Brazil, 4–8 November 2013; pp. 427–432. [Google Scholar]
- Li, F.; Akagi, M. Unsupervised singing voice separation based on robust principal component analysis exploiting rank-1 constraint. In Proceedings of the 2018 26th European Signal Processing Conference (EUSIPCO), Rome, Italy, 3–7 September 2018; pp. 1920–1924. [Google Scholar]
- Yuan, S.; Wang, Z.; Isik, U.; Giri, R.; Valin, J.M.; Goodwin, M.M.; Krishnaswamy, A. Improved singing voice separation with chromagram-based pitch-aware remixing. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Singapore, 22–27 May 2022; pp. 111–115. [Google Scholar]
- Gao, B.; Woo, W.L.; Ling, B.W.K. Machine learning source separation using maximum a posteriori nonnegative matrix factorization. IEEE Trans. Cybern. 2013, 44, 1169–1179. [Google Scholar]
- Gao, B.; Woo, W.L.; Tian, G.Y.; Zhang, H. Unsupervised diagnostic and monitoring of defects using waveguide imaging with adaptive sparse representation. IEEE Trans. Ind. Inform. 2015, 12, 405–416. [Google Scholar] [CrossRef]
- Li, F.; Akagi, M. Weighted robust principal component analysis with gammatone auditory filterbank for singing voice separation. In Proceedings of the Neural Information Processing: 24th International Conference, ICONIP 2017, Guangzhou, China, 14–18 November 2017; Springer: Cham, Switzerland, 2017; pp. 849–858. [Google Scholar]
- Li, Y.P.; Wang, D.L. On the optimality of ideal binary time-frequency masks. Speech Commun. 2009, 51, 230–239. [Google Scholar] [CrossRef]
- Healy, E.W.; Vasko, J.L.; Wang, D. The optimal threshold for removing noise from speech is similar across normal and impaired hearing—A time-frequency masking study. J. Acoust. Soc. Am. 2019, 145, EL581–EL586. [Google Scholar] [CrossRef]
- Luo, Y.; Mesgarani, N. Conv-tasnet: Surpassing ideal time–frequency magnitude masking for speech separation. IEEE/ACM Trans. Audio Speech Lang. Process. 2019, 27, 1256–1266. [Google Scholar] [CrossRef]
- Fujihara, H.; Goto, M.; Ogata, J.; Okuno, H.G. Lyric Synchronizer: Automatic synchronization system between musical audio signals and lyrics. IEEE J. Sel. Top. Signal Process. 2011, 5, 1252–1261. [Google Scholar] [CrossRef]
- Lehner, B.; Widmer, G.; Bock, S. A low-latency, real-time-capable singing voice detection method with LSTM recurrent neural networks. In Proceedings of the 2015 23rd European signal processing conference (EUSIPCO), Nice, France, 31 August–4 September 2015; pp. 21–25. [Google Scholar]
- Ramona, M.; Richard, G.; David, B. Vocal detection in music with support vector machines. In Proceedings of the 2008 IEEE International Conference on Acoustics, Speech and Signal Processing, Las Vegas, NV, USA, 31 March–4 April 2008; pp. 1885–1888. [Google Scholar]
- Candès, E.J.; Li, X.; Ma, Y.; Wright, J. Robust principal component analysis? J. ACM (JACM) 2011, 58, 1–37. [Google Scholar] [CrossRef]
- Lin, Z.; Chen, M.; Ma, Y. The augmented lagrange multiplier method for exact recovery of corrupted low-rank matrices. arXiv 2010, arXiv:1009.5055. [Google Scholar]
- Gu, S.H.; Xie, Q.; Meng, D.Y.; Zuo, W.M.; Feng, X.C.; Zhang, L. Weighted nuclear norm minimization and its applications to low level vision. Int. J. Comput. Vis. 2017, 121, 183–208. [Google Scholar] [CrossRef]
- Candes, E.J.; Wakin, M.B.; Boyd, S.P. Enhancing sparsity by reweighted l1 minimization. J. Fourier Anal. Appl. 2008, 14, 877–905. [Google Scholar] [CrossRef]
- Johannesma, P.L.M. The pre-response stimulus ensemble of neurons in the cochlear nucleus. In Symposium on Hearing Theory; IPO: Bristol, UK, 1972. [Google Scholar]
- Abdulla, W.H. Auditory based feature vectors for speech recognition systems. Adv. Commun. Softw. Technol. 2002, 231–236. [Google Scholar]
- Zhang, Y.; Abdulla, W.H. Gammatone auditory filterbank and independent component analysis for speaker identification. In Proceedings of the Ninth International Conference on Spoken Language Processing, Pittsburgh, PA, USA, 17–21 September 2006; pp. 2098–2101. [Google Scholar]
- Li, F.; Akagi, M. Blind monaural singing voice separation using rank-1 constraint robust principal component analysis and vocal activity detection. Neurocomputing 2019, 350, 44–52. [Google Scholar] [CrossRef]
- Salamon, J.; Gomez, E. Melody extraction from polyphonic music signals using pitch contour characteristics. IEEE Trans. Audio Speech Lang. Process. 2012, 20, 1759–1770. [Google Scholar] [CrossRef]
- Wang, D.L.; Brown, G.J. Computational Auditory Scene Analysis: Principles, Algorithms, and Applications; Wiley-IEEE Press: Hoboken, NJ, USA, 2006. [Google Scholar]
- Liutkus, A.; Fitzgerald, D.; Rafii, Z. Scalable audio separation with light kernel additive modelling. In Proceedings of the 2015 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), South Brisbane, QLD, Australia, 19–24 April 2015; pp. 76–80. [Google Scholar]
- Liutkus, A.; Stoter, F.R.; Rafii, Z.; Kitamura, D.; Rivet, B.; Ito, N.; Ono, N.; Fontecave, J. The 2016 signal separation evaluation campaign. In Proceedings of the Latent Variable Analysis and Signal Separation: 13th International Conference, LVA/ICA 2017, Grenoble, France, 21–23 February 2017; pp. 323–332. [Google Scholar]
- Stöter, F.R.; Liutkus, A.; Ito, N. The 2018 signal separation evaluation campaign. In Proceedings of the Latent Variable Analysis and Signal Separation: 14th International Conference, LVA/ICA 2018, Guildford, UK, 2–5 July 2018; Springer: Berlin/Heidelberg, Germany, 2018; pp. 293–305. [Google Scholar]
- Vincent, E.; Gribonval, R.; Févotte, C. Performance measurement in blind audio source separation. IEEE Trans. Audio Speech Lang. Process. 2006, 14, 1462–1469. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, F.; Hu, Y.; Wang, L. Unsupervised Single-Channel Singing Voice Separation with Weighted Robust Principal Component Analysis Based on Gammatone Auditory Filterbank and Vocal Activity Detection. Sensors 2023, 23, 3015. https://doi.org/10.3390/s23063015
Li F, Hu Y, Wang L. Unsupervised Single-Channel Singing Voice Separation with Weighted Robust Principal Component Analysis Based on Gammatone Auditory Filterbank and Vocal Activity Detection. Sensors. 2023; 23(6):3015. https://doi.org/10.3390/s23063015
Chicago/Turabian StyleLi, Feng, Yujun Hu, and Lingling Wang. 2023. "Unsupervised Single-Channel Singing Voice Separation with Weighted Robust Principal Component Analysis Based on Gammatone Auditory Filterbank and Vocal Activity Detection" Sensors 23, no. 6: 3015. https://doi.org/10.3390/s23063015
APA StyleLi, F., Hu, Y., & Wang, L. (2023). Unsupervised Single-Channel Singing Voice Separation with Weighted Robust Principal Component Analysis Based on Gammatone Auditory Filterbank and Vocal Activity Detection. Sensors, 23(6), 3015. https://doi.org/10.3390/s23063015




