Identification and Classification of Small Sample Desert Grassland Vegetation Communities Based on Dynamic Graph Convolution and UAV Hyperspectral Imagery
Abstract
1. Introduction
- To provide a new high-efficiency and high-precision monitoring method for grassland degradation monitoring. The limitations of manual survey and satellite remote sensing are addressed.
- Propose a spatial neighborhood-based dynamic graph convolution classification algorithm. The classification accuracy of the model is greatly improved under small samples, which is better than other related deep learning classification methods.
- A method for constructing graph structures in the spatial neighborhood is proposed. The method effectively alleviates the large memory consumption and time cost of graph convolutional networks in hyperspectral images.
2. Materials and Methods
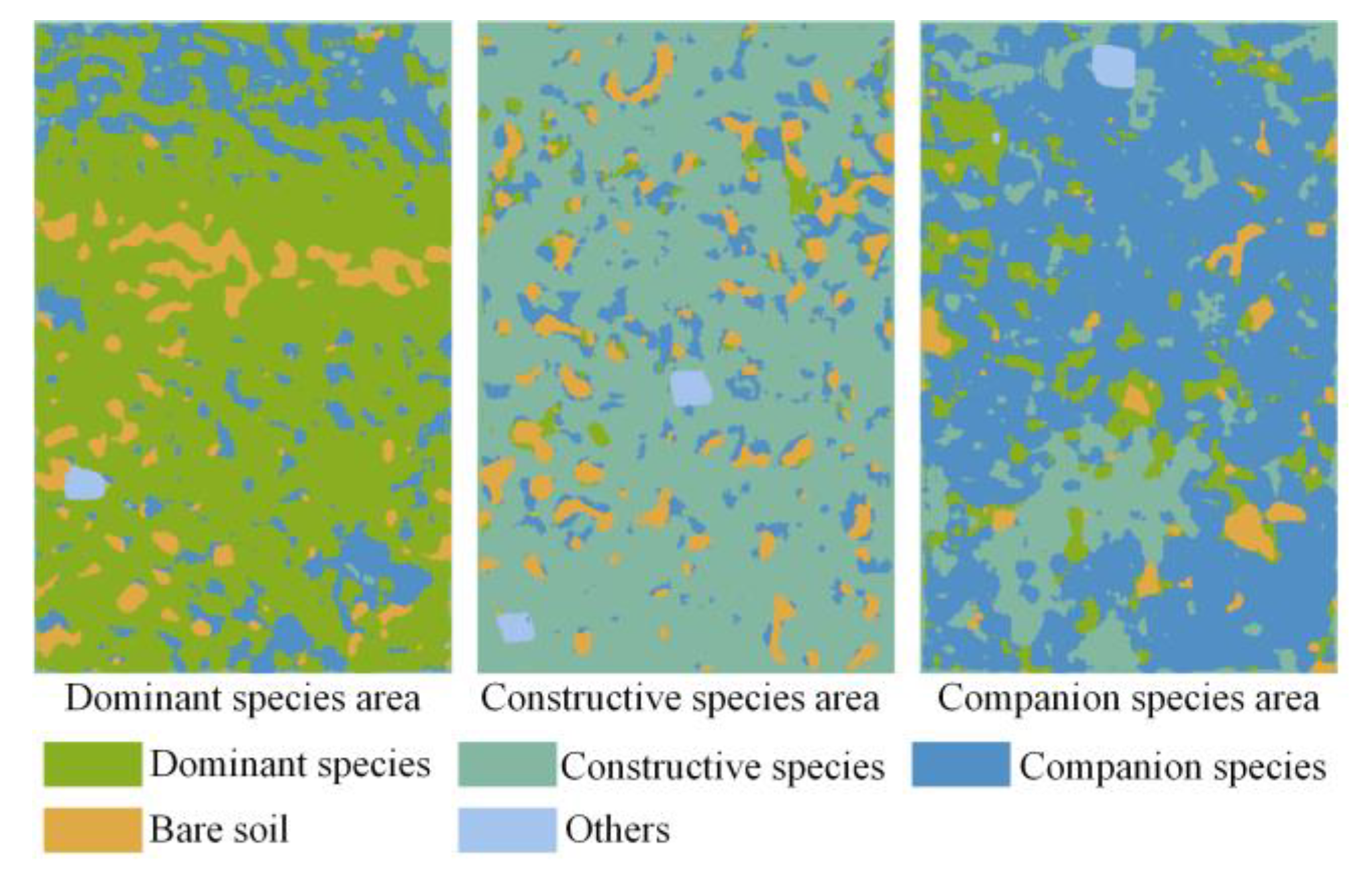
2.1. Overview of the Study Area
2.2. Experiment Equipment
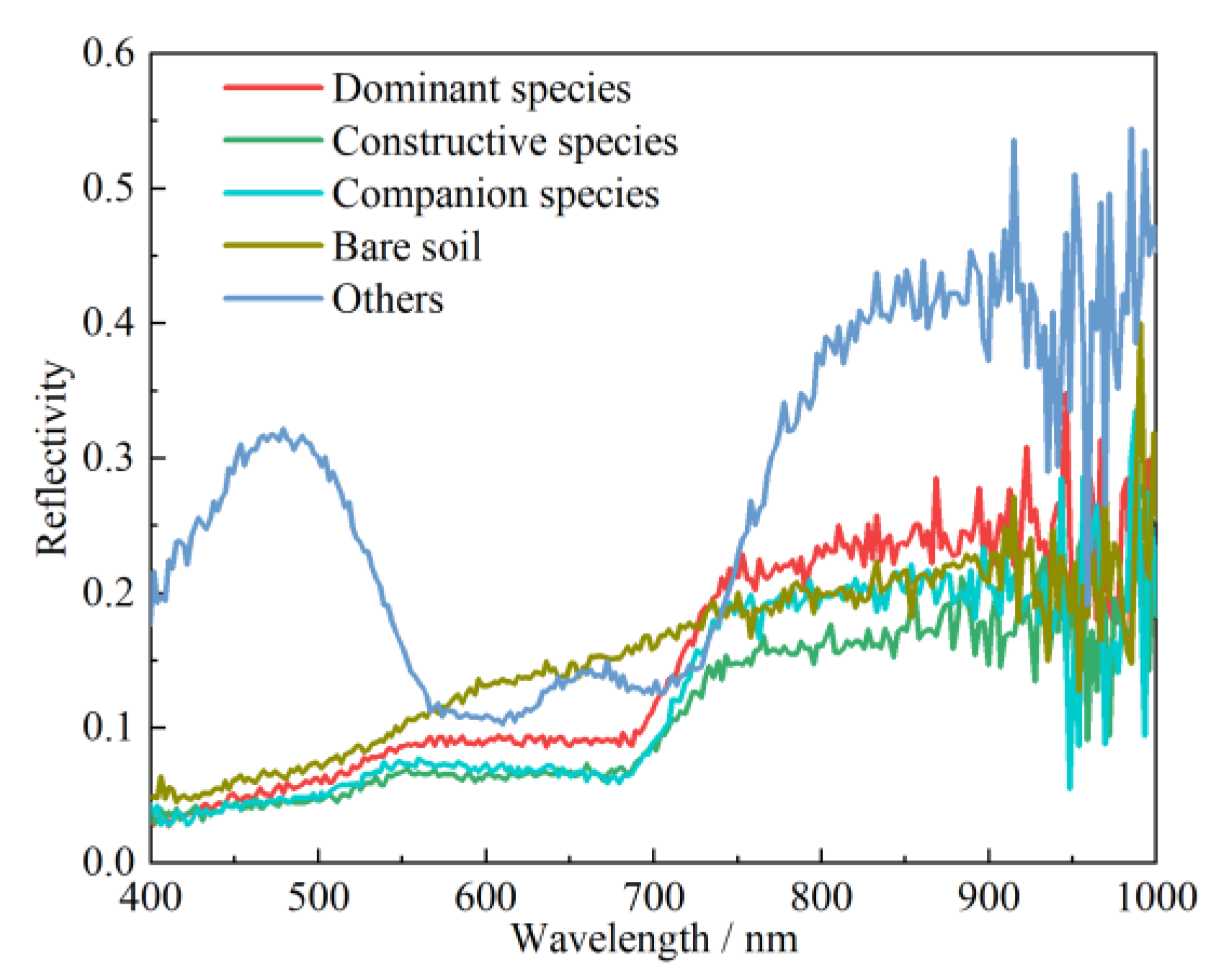
2.3. Data Collection
2.4. Data Processing
3. Principle of the Algorithm
3.1. Construction of Spatial Neighborhood Graph
3.2. Edge Convolution Block
3.3. Spatial Neighborhood Dynamic Graph Convolution
4. Experimental Results and Analysis
4.1. Analysis of Experimental Parameters
4.1.1. Analysis of the Numbers of Neighboring Nodes k
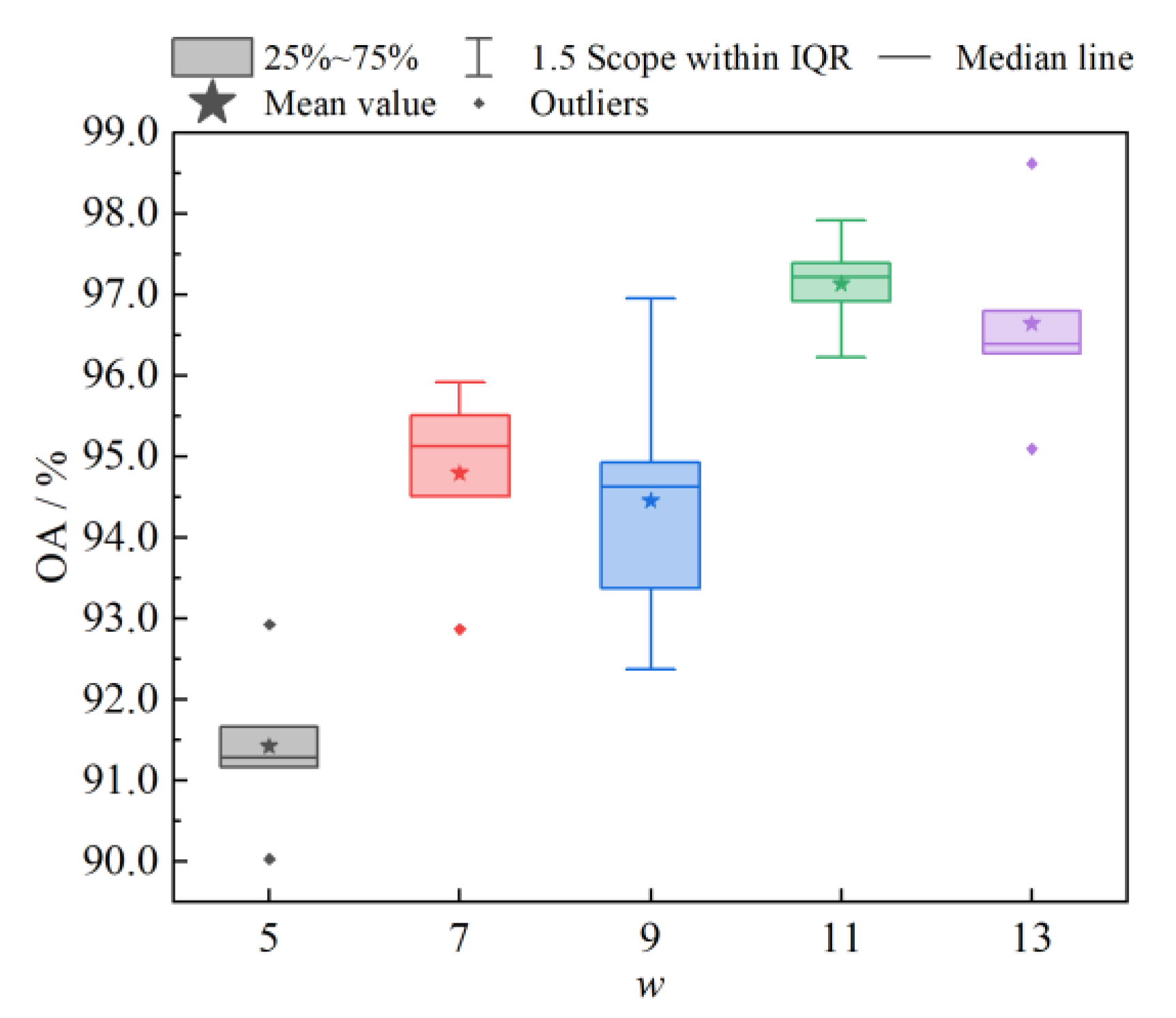
4.1.2. Analysis of the Sliding Windows w
4.2. Model Classification Performances Compare Experiments
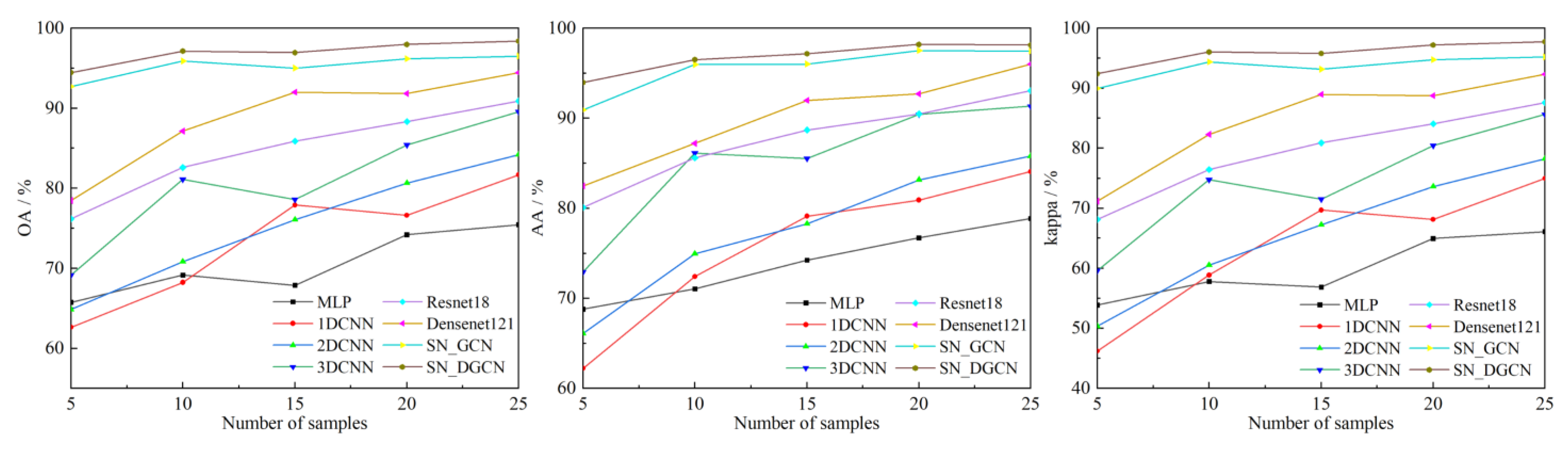
4.3. Model Comparison Experiment with Different Training Samples
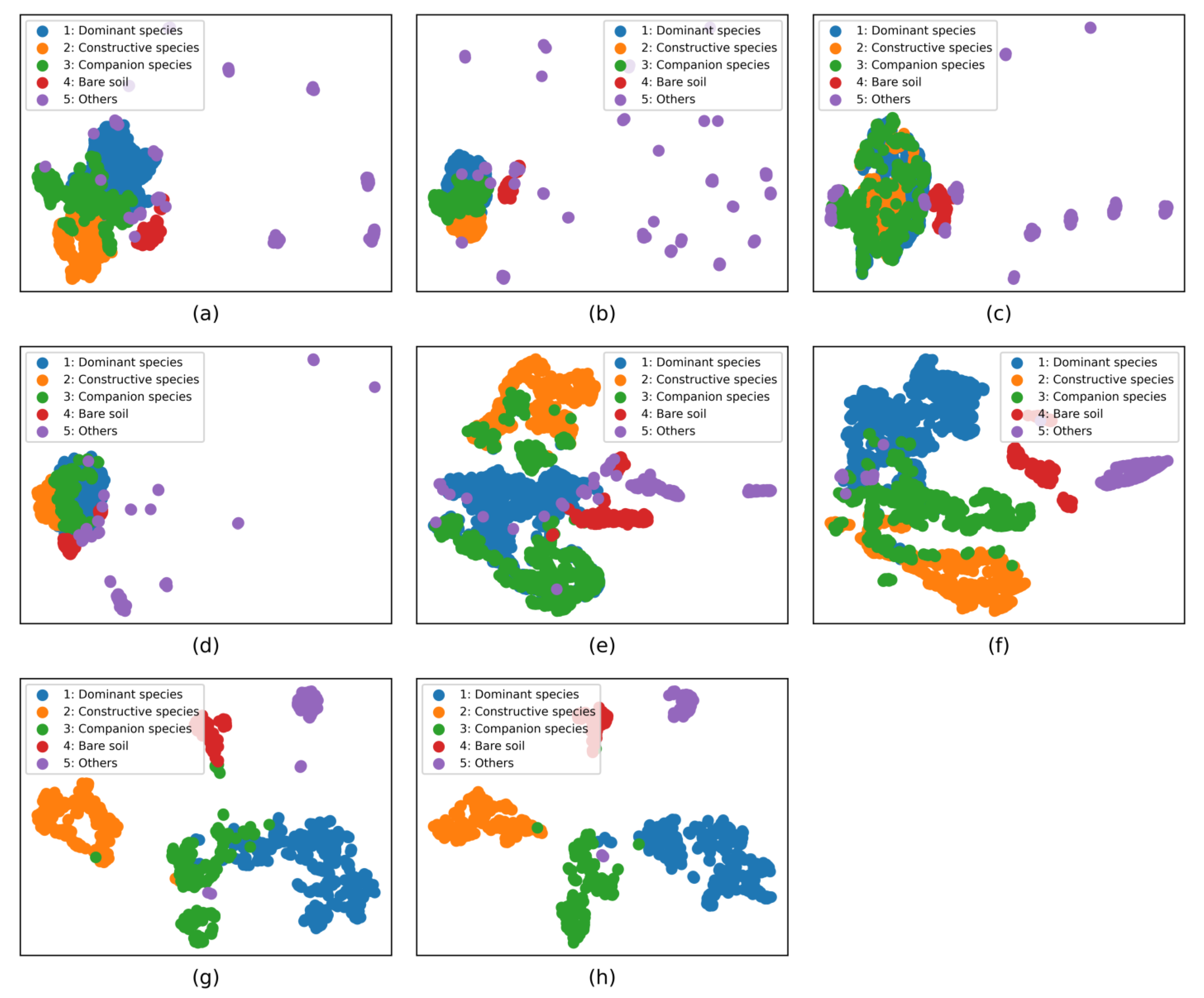
4.4. Feature Visualization Analysis
4.5. Discussion
4.6. Visualization of Experimental Sample Area Classification
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, X.; Yang, X.; Wang, L.; Chen, L.; Song, N.; Gu, J.; Xue, Y. A six-year grazing exclusion changed plant species diversity of a stipa breviflora desert steppe community, northern china. PeerJ 2018, 6, e4359. [Google Scholar] [PubMed]
- Guo, B.; Wei, C.; Yu, Y.; Liu, Y.; Li, J.; Meng, C.; Cai, Y. The dominant influencing factors of desertification changes in the source region of yellow river: Climate change or human activity? Sci. Total Environ. 2022, 813, 152512. [Google Scholar] [PubMed]
- Dong, S.; Shang, Z.; Gao, J.; Boone, R.B. Enhancing sustainability of grassland ecosystems through ecological restoration and grazing management in an era of climate change on qinghai-tibetan plateau. Agric. Ecosyst. Environ. 2020, 287, 106684. [Google Scholar]
- Li, F.R.; Kang, L.F.; Zhang, H.; Zhao, L.Y.; Shirato, Y.; Taniyama, I. Changes in intensity of wind erosion at different stages of degradation development in grasslands of inner mongolia, China. J. Arid. Environ. 2005, 62, 567–585. [Google Scholar]
- Lyu, X.; Li, X.; Dang, D.; Dou, H.; Xuan, X.; Liu, S.; Li, M.; Gong, J. A new method for grassland degradation monitoring by vegetation species composition using hyperspectral remote sensing. Ecol. Indic. 2020, 114, 106310. [Google Scholar]
- Lussem, U.; Bolten, A.; Menne, J.; Gnyp, M.L.; Schellberg, J.; Bareth, G. Estimating biomass in temperate grassland with high resolution canopy surface models from uav-based rgb images and vegetation indices. J. Appl. Remote Sens. 2019, 13, 34525. [Google Scholar]
- Théau, J.; Lauzier-Hudon, É.; Aubé, L.; Devillers, N. Estimation of forage biomass and vegetation cover in grasslands using uav imagery. PLoS ONE 2021, 16, e245784. [Google Scholar]
- Zhang, H.; Sun, Y.; Chang, L.; Qin, Y.; Chen, J.; Qin, Y.; Du, J.; Yi, S.; Wang, Y. Estimation of grassland canopy height and aboveground biomass at the quadrat scale using unmanned aerial vehicle. Remote Sens. 2018, 10, 851. [Google Scholar]
- Li, S.; Song, W.; Fang, L.; Chen, Y.; Ghamisi, P.; Benediktsson, J.A. Deep learning for hyperspectral image classification: An overview. IEEE Trans. Geosci. Remote Sens. 2019, 57, 6690–6709. [Google Scholar]
- Nguyen, C.; Sagan, V.; Maimaitiyiming, M.; Maimaitijiang, M.; Bhadra, S.; Kwasniewski, M.T. Early detection of plant viral disease using hyperspectral imaging and deep learning. Sensors 2021, 21, 742. [Google Scholar]
- Li, R.; Zhang, B.; Wang, B. Remote sensing image scene classification based on multilayer feature context encoding network. J. Infrared Millim. Waves 2021, 40, 530–538. [Google Scholar]
- Peiyuan, J.; Miao, Z.; Wenbo, Y.; Fei, S.; Yi, S. Convolutional neural network based classification for hyperspectral data. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 5075–5078. [Google Scholar]
- Hu, J.; Li, X.; Coleman, K.; Schroeder, A.; Ma, N.; Irwin, D.J.; Lee, E.B.; Shinohara, R.T.; Li, M. Spagcn: Integrating gene expression, spatial location and histology to identify spatial domains and spatially variable genes by graph convolutional network. Nat. Methods 2021, 18, 1342–1351. [Google Scholar]
- Shang, J.; Jiang, J.; Sun, Y. Bacteriophage classification for assembled contigs using graph convolutional network. Bioinformatics 2021, 37, i25–i33. [Google Scholar] [PubMed]
- Lim, S.; Lu, Y.; Cho, C.Y.; Sung, I.; Kim, J.; Kim, Y.; Park, S.; Kim, S. A review on compound-protein interaction prediction methods: Data, format, representation and model. Comput. Struct. Biotec. 2021, 19, 1541–1556. [Google Scholar]
- Xibing, Z.; Bing, L.; Xuchul, Y.; Penggiang, Z.; Kuiliang, G.; Enze, Z. Graph convolutional network method for small sample classification of hyperspectral images. Acta Geod. Et Cartogr. Sin. 2021, 50, 1358–1369. [Google Scholar]
- Zhang, T.; Du, J.; Zhang, H.; Pi, W.; Gao, X.; Zhu, X. Research on recognition method of desert steppe rat hole based on unmanned aerial vehicle hyperspectral. J. Optoelectron. Laser 2022, 33, 120–126. [Google Scholar]
- Lv, G.; Wang, Z.; Guo, N.; Xu, X.; Liu, P.; Wang, C. Status of stipa breviflora as the constructive species will be lost under climate change in the temperate desert steppe in the future. Ecol. Indic. 2021, 126, 107715. [Google Scholar]
- Avolio, M.L.; Forrestel, E.J.; Chang, C.C.; La Pierre, K.J.; Burghardt, K.T.; Smith, M.D. Demystifying dominant species. New Phytol. 2019, 223, 1106–1126. [Google Scholar]
- Wang, Y.; Sun, Y.; Liu, Z.; Sarma, S.; Bronstein, M.; Solomon, J. Dynamic graph cnn for learning on point clouds. ACM Trans. Graph. 2019, 38, 1–12. [Google Scholar]
- Parsaie, A. Predictive modeling the side weir discharge coefficient using neural network. Model. Earth Syst. Environ. 2016, 2, 1–11. [Google Scholar]
- Hu, W.; Huang, Y.; Wei, L.; Zhang, F.; Li, H.; Wu, T. Deep convolutional neural networks for hyperspectral image classification. J. Sens. 2015, 2015, 1–12. [Google Scholar]
- Yue, J.; Zhao, W.; Mao, S.; Liu, H. Spectral-spatial classification of hyperspectral images using deep convolutional neural networks. Remote Sens. Lett. 2015, 6, 468–477. [Google Scholar] [CrossRef]
- Pi, W.; Du, J.; Bi, Y.; Gao, X.; Zhu, X. 3d-cnn based uav hyperspectral imagery for grassland degradation indicator ground object classification research. Ecol. Inform. 2021, 62, 101278. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Gao, H.; Zhuang, L.; Laurens, V.D.M.; Kilian, Q.W. Densely connected convolutional networks. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 2261–2269. [Google Scholar]
- Van Der Maaten, L. Accelerating t-sne using tree-based algorithms. J. Mach. Learn. Res. 2014, 15, 3221–3245. [Google Scholar]
- Pi, W.; Du, J.; Liu, H.; Zhu, X. Desertification glassland classification and three-dimensional convolution neural network model for identifying desert grassland landforms with unmanned aerial vehicle hyperspectral remote sensing images. J. Appl. Spectrosc. 2020, 87, 309–318. [Google Scholar]
- Zhu, X.; Bi, Y.; Du, J.; Gao, X.; Zhang, T.; Pi, W.; Zhang, Y.; Wang, Y.; Zhang, H. Research on deep learning method recognition and a classification model of grassland grass species based on unmanned aerial vehicle hyperspectral remote sensing. Grassl. Sci. 2023, 69, 3–11. [Google Scholar]
- Zhang, T.; Bi, Y.; Du, J.; Zhu, X.; Gao, X. Classification of desert grassland species based on a local-global feature enhancement network and uav hyperspectral remote sensing. Ecol. Inform. 2022, 72, 101852. [Google Scholar]
- Zhang, T.; Bi, Y.; Hao, F.; Du, J.; Zhu, X.; Gao, X. Transformer attention network and unmanned aerial vehicle hyperspectral remote sensing for grassland rodent pest monitoring research. J. Appl. Remote Sens. 2022, 16, 044525. [Google Scholar]





| No. | Class | Training | Test |
|---|---|---|---|
| 1 | Dominant species | 10 | 1355 |
| 2 | Constructive species | 10 | 801 |
| 3 | Companion species | 10 | 745 |
| 4 | Bare soil | 10 | 274 |
| 5 | Others | 10 | 234 |
| Total | 50 | 3409 | |
| No. | MLP | 1DCNN | 2DCNN | 3DCNN | Resnet18 | Densenet121 | SN_GCN | SN_DGCN |
|---|---|---|---|---|---|---|---|---|
| 1 | 70.76 ± 0.09 | 70.76 ± 0.10 | 69.98 ± 0.08 | 72.96 ± 0.06 | 75.69 ± 0.04 | 90.20 ± 0.04 | 96.25 ± 0.02 | 98.23 ± 0.01 |
| 2 | 77.95 ± 0.10 | 71.61 ± 0.12 | 71.89 ± 0.06 | 95.31 ± 0.02 | 96.18 ± 0.03 | 90.94 ± 0.06 | 98.18 ± 0.01 | 98.15 ± 0.01 |
| 3 | 49.18 ± 0.06 | 46.98 ± 0.10 | 59.95 ± 0.07 | 70.71 ± 0.03 | 74.66 ± 0.11 | 75.60 ± 0.05 | 92.16 ± 0.01 | 94.82 ± 0.01 |
| 4 | 100.00 ± 0.00 | 99.49 ± 0.01 | 99.27 ± 0.01 | 97.81 ± 0.03 | 97.81 ± 0.02 | 94.60 ± 0.08 | 100.00 ± 0.00 | 100.00 ± 0.00 |
| 5 | 57.26 ± 0.07 | 73.25 ± 0.07 | 73.67 ± 0.09 | 93.76 ± 0.03 | 83.59 ± 0.06 | 84.62 ± 0.08 | 93.16 ± 0.07 | 91.37 ± 0.06 |
| OA | 69.16 ± 0.02 | 68.24 ± 0.03 | 70.84 ± 0.03 | 81.14 ± 0.03 | 82.60 ± 0.02 | 87.15 ± 0.02 | 95.90 ± 0.01 | 97.13 ± 0.01 |
| AA | 71.03 ± 0.02 | 72.42 ± 0.01 | 74.95 ± 0.02 | 86.11 ± 0.02 | 85.59 ± 0.02 | 87.19 ± 0.03 | 95.95 ± 0.01 | 96.50 ± 0.01 |
| Kappa | 57.77 ± 0.02 | 58.88 ± 0.04 | 60.51 ± 0.04 | 74.77 ± 0.04 | 76.46 ± 0.03 | 82.29 ± 0.03 | 94.37 ± 0.01 | 96.05 ± 0.01 |
| No. | DGC-3D-CNN | DIS-O | LGFEN | TAN | SN_DGCN |
|---|---|---|---|---|---|
| 1 | 73.22 ± 0.09 | 81.16 ± 0.07 | 93.83 ± 0.04 | 96.37 ± 0.02 | 98.23 ± 0.01 |
| 2 | 90.43 ± 0.04 | 82.82 ± 0.05 | 98.30 ± 0.02 | 98.60 ± 0.01 | 98.15 ± 0.01 |
| 3 | 56.05 ± 0.09 | 62.25 ± 0.09 | 88.08 ± 0.06 | 90.33 ± 0.05 | 94.82 ± 0.01 |
| 4 | 94.38 ± 0.08 | 100.00 ± 0.09 | 89.41 ± 0.09 | 97.59 ± 0.05 | 100.00 ± 0.00 |
| 5 | 82.91 ± 0.09 | 75.30 ± 0.05 | 83.76 ± 0.07 | 86.41 ± 0.10 | 91.37 ± 0.06 |
| OA | 75.88 ± 0.04 | 78.53 ± 0.02 | 92.57 ± 0.03 | 94.99 ± 0.01 | 97.13 ± 0.01 |
| AA | 79.40 ± 0.03 | 80.31 ± 0.01 | 90.68 ± 0.03 | 93.86 ± 0.02 | 96.50 ± 0.01 |
| Kappa | 67.41 ± 0.05 | 70.73 ± 0.03 | 89.79 ± 0.04 | 93.09 ± 0.01 | 96.05 ± 0.01 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, T.; Bi, Y.; Zhu, X.; Gao, X. Identification and Classification of Small Sample Desert Grassland Vegetation Communities Based on Dynamic Graph Convolution and UAV Hyperspectral Imagery. Sensors 2023, 23, 2856. https://doi.org/10.3390/s23052856
Zhang T, Bi Y, Zhu X, Gao X. Identification and Classification of Small Sample Desert Grassland Vegetation Communities Based on Dynamic Graph Convolution and UAV Hyperspectral Imagery. Sensors. 2023; 23(5):2856. https://doi.org/10.3390/s23052856
Chicago/Turabian StyleZhang, Tao, Yuge Bi, Xiangbing Zhu, and Xinchao Gao. 2023. "Identification and Classification of Small Sample Desert Grassland Vegetation Communities Based on Dynamic Graph Convolution and UAV Hyperspectral Imagery" Sensors 23, no. 5: 2856. https://doi.org/10.3390/s23052856
APA StyleZhang, T., Bi, Y., Zhu, X., & Gao, X. (2023). Identification and Classification of Small Sample Desert Grassland Vegetation Communities Based on Dynamic Graph Convolution and UAV Hyperspectral Imagery. Sensors, 23(5), 2856. https://doi.org/10.3390/s23052856







