A Novel Method for Detecting Fe2+ at a Micromolar Concentration Based on Multiple Self-Mixing Interference Using a Fiber Laser
Abstract
1. Introduction
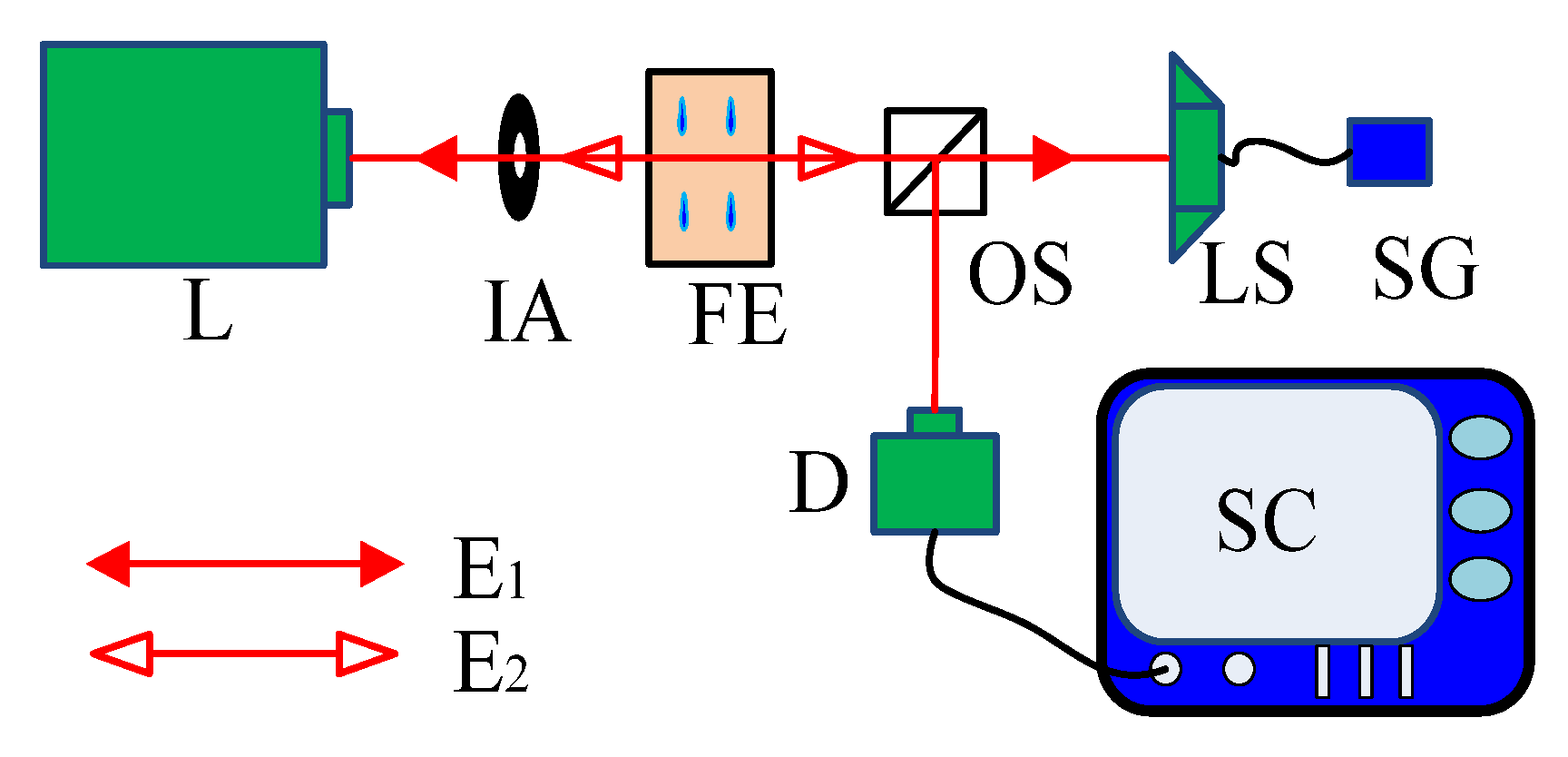
2. Materials and Methods
r1(t2)2r3f2·exp[−j·4π(L + l)/λ) + gL]·E0 + r1r2(t2)2(r3)2f4·exp[−j·4π(L + 2l)/λ + gL]·E0.
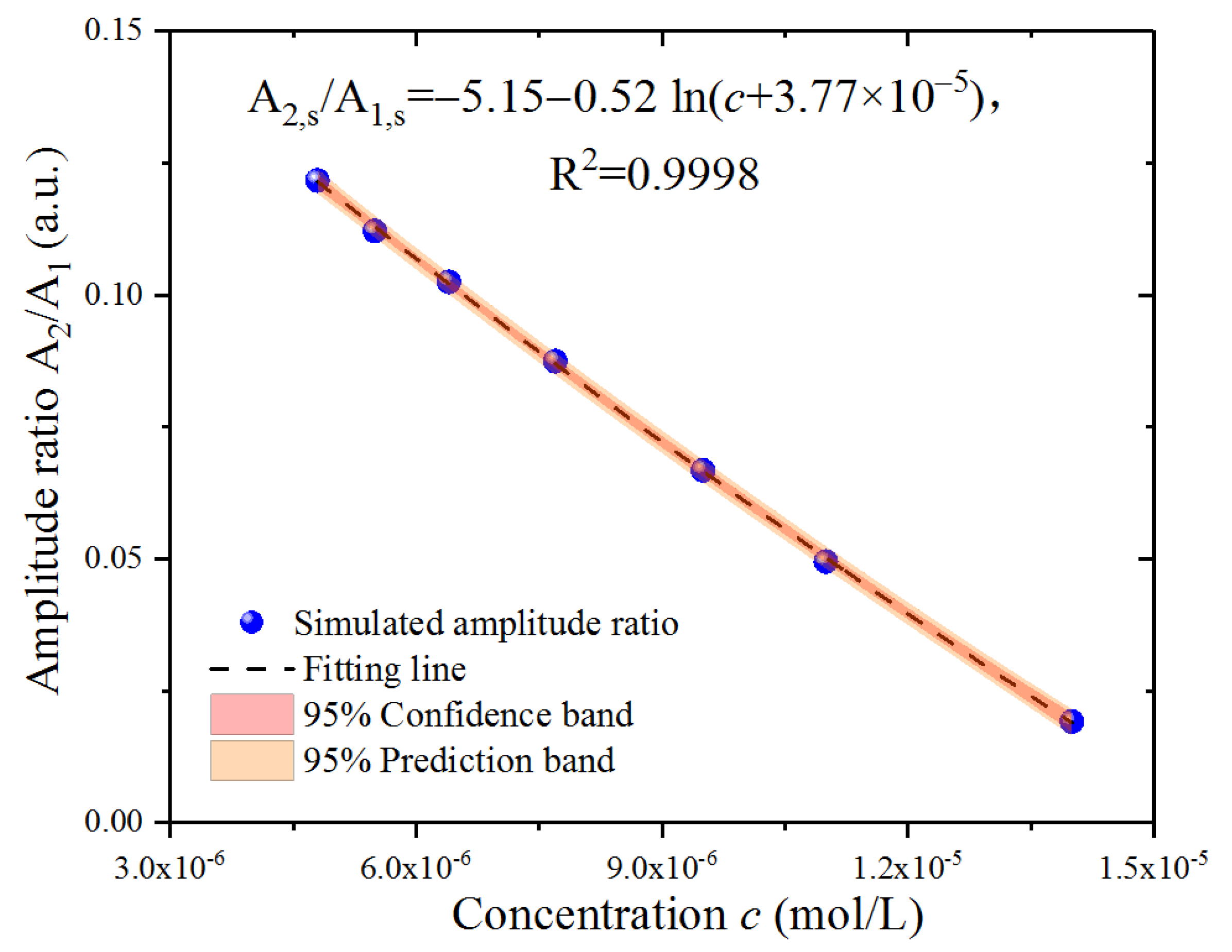
3. Results
3.1. Simulated Results
3.2. Experimental Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Donati, S. Laser interferometry by induced modulation of cavity field. J. Appl. Phys. 1978, 49, 495. [Google Scholar] [CrossRef]
- Taimre, T.; Nikolic, M.; Bertling, K.; Lim, Y.L.; Bosch, T.; Rakic, A.D. Laser feedback interferometry: Atutorial on the self-mixing effect for coherent sensing. Adv. Opt. Photonics 2015, 7, 570–631. [Google Scholar] [CrossRef]
- Donati, S.; Norgia, M. Overview of self-mixing interferometer applications to mechanical engineering. Opt. Eng. 2018, 57, 051506. [Google Scholar] [CrossRef]
- Siddiqui, A.A.; Zabit, U.; Bernal, O.D. Fringe detection and displacement sensing for variable optical feedback-based self-mixing interferometry by using deep neural networks. Sensors 2022, 22, 9831. [Google Scholar] [CrossRef]
- Li, R.F.; Hu, Z.J.; Li, H.T.; Zhao, Y.K.; Liu, K.Y.; Tu, Y.R.; Du, Z.T.; Yu, Q.; Yu, B.; Lu, L. All-fiber laser-self-mixing interferometer with adjustable injection intensity for remote sensing of 40 km. J. Lightwave Technol. 2022, 40, 4863–4870. [Google Scholar] [CrossRef]
- Tu, Y.R.; Zhao, Y.Y.; Zhu, D.S.; Li, R.F.; Liu, K.Y.; Xu, L.; Zhang, L.; Cao, Z.G.; Yu, B.L.; Lu, L. Optical feedback interferometry with 40 km transmission distance based on a distributed feedback fiber laser. Opt. Lett. 2021, 46, 3805–3808. [Google Scholar] [CrossRef] [PubMed]
- Zhu, D.S.; Zhao, Y.Y.; Tu, Y.R.; Li, H.T.; Xu, L.; Yu, B.L.; Lu, L. All-fiber laser feedback interferometer using a DBR fiber laser for effective sub-picometre displacement measurement. Opt. Lett. 2021, 46, 114–117. [Google Scholar] [CrossRef]
- Tan, Y.D.; Zhu, K.Y.; Zhang, S.L. New method for lens thickness measurement by the frequency-shifted confocal feedback. Opt. Commun. 2016, 380, 91–94. [Google Scholar] [CrossRef]
- Zhao, Y.Y.; Zhu, D.S.; Chen, Y.Z.; Tu, Y.R.; Bi, T.Z.; Zhao, Y.K.; Yu, B.L.; Lu, L. All-fiber self-mixing laser Doppler velocimetry with much less than 0.1 pW optical feedback based on adjustable gain. Opt. Lett. 2020, 45, 3565–3568. [Google Scholar] [CrossRef] [PubMed]
- Lu, L.P.; Hu, L.; Li, Z.; Qiu, L.R.; Huang, W.C.; Wang, X.L. High precision self-mixing interferometer based on reflective phase modulation method. IEEE Access 2020, 8, 204153. [Google Scholar] [CrossRef]
- Hao, H.; Lin, H.; Chen, J.B.; Xia, W.; Guo, D.M.; Wang, M. Enhanced laser self-mixing interferometry based on tunable fabry-perot filter. Opt. Laser Technol. 2021, 135, 106666. [Google Scholar] [CrossRef]
- Wu, Y.; Tan, Y.D.; Zeng, Z.L.; Zhang, S.L. Note: High-performance HeNe laser feedback interferometer with birefringence feedback cavity scanned by piezoelectric transducer. Rev. Sci. Instrum. 2013, 84, 056103. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.B.; Wang, X.M.; Wu, Y.B.; Yang, Y.T.; Qiu, M.Y.; Wang, M.; Li, Y.Z. Ultralow Doppler frequency extraction for the self-mixing dual-frequency laser velocimetry. Appl. Opt. 2022, 61, 4687–4692. [Google Scholar] [CrossRef] [PubMed]
- Wu, S.; Wang, D.H.; Xiang, R.; Zhou, J.F.; Ma, Y.C.; Gui, H.Q.; Liu, J.G.; Wang, H.Q.; Lu, L.; Yu, B.L. All-fiber configuration laser self-mixing doppler velocimeter based on distributed feedback fiber laser. Sensors 2016, 16, 1179. [Google Scholar] [CrossRef] [PubMed]
- Magnani, A.; Norgia, M. Spectral analysis for velocity measurement through self-mixing interferometry. IEEE J. Quantum Electron. 2013, 49, 765–769. [Google Scholar] [CrossRef]
- Kliese, R.; Rakic, A.D. Spectral broadening caused by dynamic speckle in self-mixing velocimetry sensors. Opt. Express 2012, 20, 18757–18771. [Google Scholar] [CrossRef]
- Donati, S.; Rossi, D.; Norgia, M. Single channel self-mixing interferometer measures simultaneously displacement and tilt and yaw angles of a reflective target. IEEE J. Quantum Electron. 2015, 51, 1400108. [Google Scholar] [CrossRef]
- Norgia, M.; Donati, S. A displacement-measuring instrument utilizing self-mixing interferometry. IEEE Trans. Instrum. Meas. 2003, 52, 1765–1770. [Google Scholar] [CrossRef]
- Guo, D.; Wang, M.; Hao, H. Displacement measurement using a laser feedback grating interferometer. Appl. Opt. 2015, 54, 9320–9325. [Google Scholar] [CrossRef]
- Jha, A.; Azcona, F.J.; Royo, S. Frequency-modulated optical feedback interferometry for nanometric scale vibrometry. IEEE Photonics Technol. Lett. 2016, 28, 1217–1220. [Google Scholar] [CrossRef]
- Donati, S.; Norgia, M.; Giuliani, G. Self-mixing differential vibrometer based on electronic channel subtraction. Appl. Opt. 2006, 45, 7264–7268. [Google Scholar] [CrossRef] [PubMed]
- Giuliani, G.; Pietra, S.B.; Donati, S. Self-mixing laser diode vibrometer. Meas. Sci. Technol. 2003, 14, 24–32. [Google Scholar] [CrossRef]
- Norgia, M.; Giuliani, G.; Donati, S. Absolute distance measurement with improved accuracy using laser diode self-mixing interferometry in a closed loop. IEEE Trans. Instrum. Meas. 2007, 56, 1894–1900. [Google Scholar] [CrossRef]
- Norgia, M.; Magnani, A.; Pesatorim, A. High resolution self-mixing laser rangefinder. Rev. Sci. Instrum. 2012, 83, 045113. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.K.; Wang, C.C.; Zhao, Y.Y.; Zhu, D.S.; Lu, L. An all-fiber self-mixing range finder with tunable fiber ring cavity laser source. J. Lightwave Technol. 2020, 8, 204153–204159. [Google Scholar] [CrossRef]
- Cavedo, F.; Esmaili, P.; Norgia, M. Self-Mixing Laser Distance-Sensor Enhanced by Multiple Modulation Waveforms. Sensors 2022, 22, 8456. [Google Scholar] [CrossRef] [PubMed]
- Norgia, M.; Pesatori, A.; Donati, S. Compact laser diode instrument for flow measurement. IEEE Trans. Instrum. Meas. 2016, 65, 1478–1483. [Google Scholar] [CrossRef]
- Wang, H.; Shen, J. Power spectral density of self-mixing signals from a flowing Brownian motion system. Appl. Phys. B 2012, 106, 127–134. [Google Scholar] [CrossRef]
- Nikolic, M.; Lim, Y.L.; Bertling, K.; Taimre, T.; Rakic, A.D. Multiple signal classification for self-mixing flowmetry. Appl. Opt. 2015, 54, 2193–2198. [Google Scholar] [CrossRef]
- Norgia, M.; Pesatori, A.; Rovati, L. Self-mixing laser Doppler spectra of extracorporeal blood flow: A theoretical and experimental study. IEEE Sens. J. 2012, 12, 552–557. [Google Scholar] [CrossRef]
- Zhao, Y.K.; Xiang, R.; Huang, Z.T.; Chen, J.S.; Zhai, L.H.; Wang, X.; Ma, Y.C.; Yu, B.L.; Lu, L. Research on the multi-longitudinal mode laser self-mixing static angle-measurement system using a right-angle prism. Measurement 2020, 162, 107906. [Google Scholar] [CrossRef]
- Zhao, Y.K.; Guo, Y.; Wang, C.C.; Yang, B.; Ma, Y.C.; Lu, L. Design and experimental study of the biorthogonal linkage laser self-mixing angle sensor. Opt. Commun. 2020, 475, 126248. [Google Scholar] [CrossRef]
- Giuliani, G.; Donati, S.; Passerini, M.; Bosch, T. Angle measurement by injection detection in a laser diode. Opt. Eng. 2021, 40, 95–99. [Google Scholar] [CrossRef]
- Zhao, Y.K.; Fan, X.W.; Wang, C.C.; Lu, L. An improved intersection feedback micro-radian angle-measurement system based on the Laser self-mixing interferometry. Opt. Lasers Eng. 2022, 126, 105866. [Google Scholar] [CrossRef]
- Donadello, S.; Finazzi, V.; Demir, A.G.; Previtali, B. Time-resolved quantification of plasma accumulation induced by multi-pulse laser ablation using self-mixing interferometry. J. Phys. D Appl. Phys. 2020, 53, 495201. [Google Scholar] [CrossRef]
- Chen, C.; Zhang, Y.; Wang, X.; Wang, X.; Huang, W. Refractive index measurement with high precision by a laser diode self-mixing interferometer. IEEE Photon. J. 2015, 7, 2600506. [Google Scholar] [CrossRef]
- Jiang, C.L.; Wen, X.; Li, C.W. Multiple self-mixing interference based on phase modulation and demodulation for vibration measurement. App. Optics 2017, 56, 1006–1011. [Google Scholar] [CrossRef]
- Shi, L.S.; Guo, D.M.; Cui, Y.F.; Hao, H.; Xia, W.; Wang, W.P.; Ni, X.Q.; Wang, M. Design of a multiple self-mixing interferometer for a fiber ring laser. Opt. Lett. 2018, 43, 4124–4127. [Google Scholar] [CrossRef]
- Hang, Y.T.; Wang, R.; Wei, Z.; Wang, X.L.; Xu, H.Z.; Sun, H.F.; Huang, W.C. Broad range and high precision self-mixing interferometer based on spectral analysis with multiple reflections. IEEE Sens. J. 2019, 19, 926–932. [Google Scholar]
- Sun, H.F.; Zhang, Y.T.; Chen, H.Q.; Xiong, Y.B.; Huang, W.C.; Wang, X.L.; Xu, H.Z. Large-range nanoscale self-mixing interferometer based on multiple reflections and even-power fast algorithm. Opt. Commun. 2019, 443, 160–165. [Google Scholar] [CrossRef]
- Wang, X.L.; Lv, L.P.; Huang, W.C. Laser self-mixing interferometer based on multiple reflections and phase-modulation technique. Photonics 2022, 9, 430. [Google Scholar] [CrossRef]
- Isborn, C.M.; Zuehlsdorff, T.J. Modeling absorption spectra of molecules in solution. Int. J. Quantum. Chem. 2019, 119, e25719. [Google Scholar]
- Brannon, P.J. Laser feedback: Its effect on laser frequency. Appl. Opt. 1976, 15, 1119–1120. [Google Scholar] [CrossRef] [PubMed]
- Goldberg, L.; Taylor, H.F.; Dandridge, A.; Weller, J.F.; Miles, R.O. Spectral characteristics of semiconductor lasers with optical feedback. IEEE J. Quantum Electron. 1982, 18, 555–564. [Google Scholar] [CrossRef]
- Wang, W.M.; Grattan, K.T.V.; Palmer, A.W.; Boyle, W.J. Self-mixing interference inside a single-mode diode laser for optical sensing applications. J. Lightwave Technol. 1994, 12, 1577–1588. [Google Scholar] [CrossRef]
- Sun, W.; Duan, C.C. External cavity length dependence of multiple self-mixing interference sensing applications based on finite apertures of laser front faces. Opt. Commun. 2019, 440, 229–233. [Google Scholar] [CrossRef]
- Ding, H.; Hu, P.; Liu, Z.H.; Sun, P.; Liu, Y.F.; Luo, Z.H.; Chao, K.F.; Jiang, H.C.; Jiang, J. Effect of Ca2+-Si4+ on Y3Al5O12:Ce ceramic phosphors for white laser-diodes lighting. Appl. Phys. Lett. 2021, 118, 211902. [Google Scholar] [CrossRef]
- Peng, Y.; Liu, J.X.; Mou, Y.; Chen, M.X.; Luo, X.B. Heat dissipation enhancement of phosphor-converted white laser diodes by thermally self-managing phosphor-in-glass. IEEE Trans. Electron. Devices 2020, 67, 4288–4292. [Google Scholar] [CrossRef]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, W.; Yang, Z.; Feng, G.; Chen, Z.; Chang, Q.; Hai, L.; Guo, Z. A Novel Method for Detecting Fe2+ at a Micromolar Concentration Based on Multiple Self-Mixing Interference Using a Fiber Laser. Sensors 2023, 23, 2838. https://doi.org/10.3390/s23052838
Sun W, Yang Z, Feng G, Chen Z, Chang Q, Hai L, Guo Z. A Novel Method for Detecting Fe2+ at a Micromolar Concentration Based on Multiple Self-Mixing Interference Using a Fiber Laser. Sensors. 2023; 23(5):2838. https://doi.org/10.3390/s23052838
Chicago/Turabian StyleSun, Wu, Zhuo Yang, Guo Feng, Zhou Chen, Qiaoyun Chang, Lan Hai, and Zeqing Guo. 2023. "A Novel Method for Detecting Fe2+ at a Micromolar Concentration Based on Multiple Self-Mixing Interference Using a Fiber Laser" Sensors 23, no. 5: 2838. https://doi.org/10.3390/s23052838
APA StyleSun, W., Yang, Z., Feng, G., Chen, Z., Chang, Q., Hai, L., & Guo, Z. (2023). A Novel Method for Detecting Fe2+ at a Micromolar Concentration Based on Multiple Self-Mixing Interference Using a Fiber Laser. Sensors, 23(5), 2838. https://doi.org/10.3390/s23052838





