Hexagonal-Grid-Layout Image Segmentation Using Shock Filters: Computational Complexity Case Study for Microarray Image Analysis Related to Machine Learning Approaches
Abstract
1. Introduction
1.1. Main Findings
- The image-processing workflow represents a general solution for both rectangular and hexagonal grid alignment, which has been successfully applied to both medical images and images of material structures.
- The shock-filter-based grid alignment also delivers segmentation information, and guided by an autocorrelation procedure, it estimates the locations of missing objects within the hexagonal grid layout.
- The computational complexity required to determine the grid layout is minimized, taking into account that the PDEs are targeting the one-dimensional luminance function profiles,
- The segmentation accuracy was evaluated by computing the means and standard deviations of distances between the annotated and detected centers and showed improved results compared with state-of-the-art research.
1.2. Shock-Filter Fundamentals
2. Shock-Filter-Based Approach for Microarray Image Segmentation
2.1. Materials and Methods
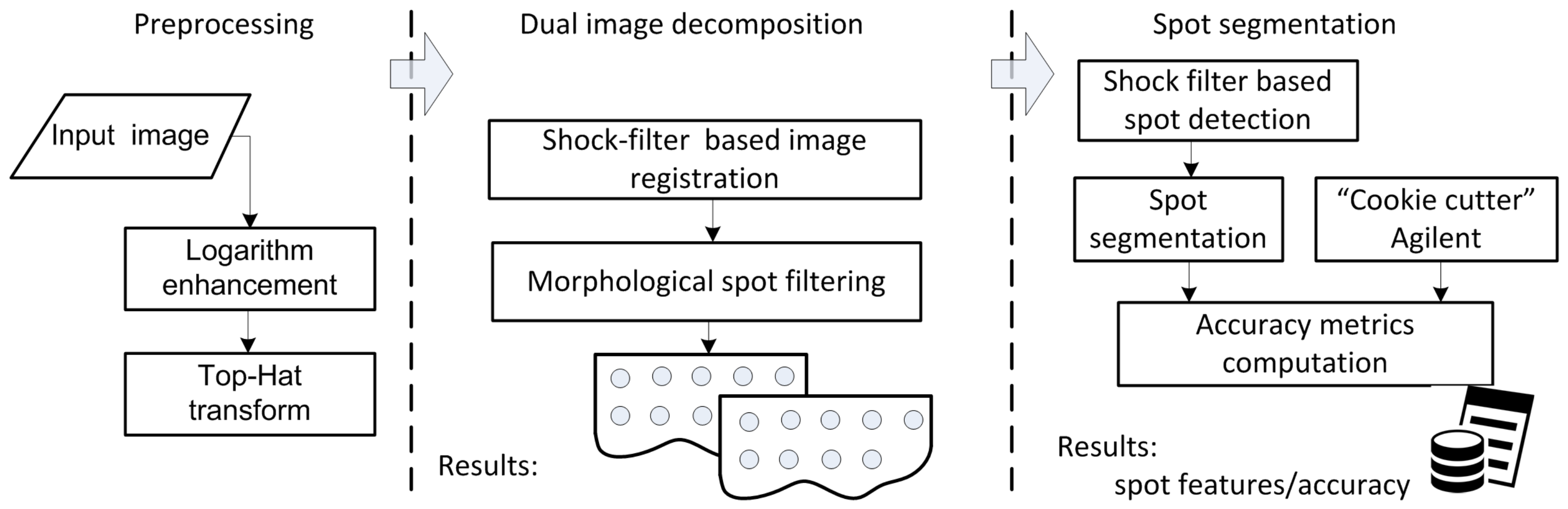
2.2. Preprocessing
2.3. Grid-Line Detection for Image Registration
2.4. Spot Segmentation
3. Results and Discussions
3.1. Microarray Image Registration and Segmentation Accuracy
3.2. Shock Filters as a General Approach for Hexagonal-Grid-Layout Registration
3.3. Computational Complexity Analysis for the Hexagonal-Grid-Layout Image Segmentation
- (i)
- The morphological opening procedure and the autocorrelation spot size estimation cost are given by the upper bound function , with s representing one computational step, and representing the size of the structural element used for morphological filtering.
- (ii)
- The computational complexity of the shock-filter-based procedure for grid alignment is based on the number of microarray spots found on each line and in each column of spots, denoted by and , respectively. Let d be the average of the microarray spot diameter and be the average width for a line or a column of spots. We computed for each spot line and spot column, the horizontal and vertical image profiles, respectively, with the total complexity of . Shock filters were applied to each of the determined profiles having a complexity of , where represents p iterations performed on the number of profiles (i.e., one profile for each line of spots), and each profile was of size M. This led to the estimation of the computational cost given by , with . Consequently, the order of growth for the total computational cost was approximated to , and it represents the total computational complexity of the proposed method.
| Reference | Method | Cost Arguments | Order of Growth |
|---|---|---|---|
| [1,33] | Voronoi diagrams | S | |
| [52] | Growing concentric hexagons | ||
| [43,71] | Support vector machines | ||
| [72] | Evolutionary algorithms | ||
| [67,68] | Deep neural Networks | - | - |
| present | Shock filters driven by morphology |
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Galinsky, V.L. Automatic registration of microarray images. II. Hexagonal grid. Bioinformatics 2003, 19, 1832–1836. [Google Scholar] [CrossRef]
- Chen, Y.; Hu, Z.; Zhao, D.; Zhou, K.; Huang, Z.; Zhao, W.; Yang, X.; Gao, C.; Cao, Y.; Hsu, Y.; et al. Self-assembled hexagonal superparamagnetic cone structures for fabrication of cell cluster arrays. ACS Appl. Mater. Interfaces 2021, 13, 10667–10673. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Gu, M.; Liu, X.; Zhang, J.; Liu, B.; Huang, S.; Ni, C. Simulated performances of pixelated CsI (Tl) scintillation screens with different micro-column shapes and array structures in X-ray imaging. Sci. Rep. 2018, 8, 16819. [Google Scholar] [CrossRef]
- Ahmed, R.; Yetisen, A.K.; Butt, H. High numerical aperture hexagonal stacked ring-based bidirectional flexible polymer microlens array. ACS Nano 2017, 11, 3155–3165. [Google Scholar] [CrossRef]
- Wu, H.; Pan, J.; Li, Z.; Wen, Z.; Qin, J. Automated Skin Lesion Segmentation via an Adaptive Dual Attention Module. IEEE Trans. Med. Imaging 2021, 40, 357–370. [Google Scholar] [CrossRef] [PubMed]
- Budai, A.; Suhai, F.I.; Csorba, K.; Toth, A.; Szabo, L.; Vago, H.; Merkely, B. Fully automatic segmentation of right and left ventricle on short-axis cardiac MRI images. Comput. Med. Imaging Graph. 2020, 85, 101786. [Google Scholar] [CrossRef] [PubMed]
- Yu, F.; Liu, M.; Chen, W.; Wen, H.; Wang, Y.; Zeng, T. Automatic Repair of 3-D Neuron Reconstruction Based on Topological Feature Points and an MOST-Based Repairer. IEEE Trans. Instrum. Meas. 2021, 70, 5004913. [Google Scholar] [CrossRef]
- Zhou, Y.; Chen, H.; Li, Y.; Liu, Q.; Xu, X.; Wang, S.; Yap, P.T.; Shen, D. Multi-task learning for segmentation and classification of tumors in 3D automated breast ultrasound images. Med. Image Anal. 2021, 70, 101918. [Google Scholar] [CrossRef]
- Guo, Z.; Zhang, H.; Chen, Z.; van der Plas, E.; Gutmann, L.; Thedens, D.; Nopoulos, P.; Sonka, M. Fully automated 3D segmentation of MR-imaged calf muscle compartments: Neighborhood relationship enhanced fully convolutional network. Comput. Med. Imaging Graph. 2021, 87, 101835. [Google Scholar] [CrossRef]
- Qin, F.; Lin, S.; Li, Y.; Bly, R.A.; Moe, K.S.; Hannaford, B. Towards Better Surgical Instrument Segmentation in Endoscopic Vision: Multi-Angle Feature Aggregation and Contour Supervision. IEEE Robot. Autom. Lett. 2020, 5, 6639–6646. [Google Scholar] [CrossRef]
- Ren, H.; Hu, T. A Local Neighborhood Robust Fuzzy Clustering Image Segmentation Algorithm Based on an Adaptive Feature Selection Gaussian Mixture Model. Sensors 2020, 20, 2391. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Sun, Y.; Liu, H.; Hou, Z.; Zhao, F.; Zhang, C. Improved clustering algorithms for image segmentation based on non-local information and back projection. Inf. Sci. 2021, 550, 129–144. [Google Scholar] [CrossRef]
- Bai, X.; Zhang, Y.; Liu, H.; Wang, Y. Intuitionistic Center-Free FCM Clustering for MR Brain Image Segmentation. IEEE J. Biomed. Health Inform. 2019, 23, 2039–2051. [Google Scholar] [CrossRef] [PubMed]
- Jiao, X.; Chen, Y.; Dong, R. An unsupervised image segmentation method combining graph clustering and high-level feature representation. Neurocomputing 2020, 409, 83–92. [Google Scholar] [CrossRef]
- Daniels, C.J.; Ferdia, A.G. Unsupervised Segmentation of 5D Hyperpolarized Carbon-13 MRI Data Using a Fuzzy Markov Random Field Model. IEEE Trans. Med. Imaging 2018, 37, 840–850. [Google Scholar] [CrossRef]
- Relan, D.; Relan, R. Unsupervised sorting of retinal vessels using locally consistent Gaussian mixtures. Comput. Methods Programs Biomed. 2021, 199, 105894. [Google Scholar] [CrossRef]
- Xing, F.; Xie, Y.; Su, H.; Liu, F.; Yang, L. Deep Learning in Microscopy Image Analysis: A Survey. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 4550–4568. [Google Scholar] [CrossRef]
- Lazic, I.; Agullo, F.; Ausso, S.; Alves, B.; Barelle, C.; Berral, J.L.; Bizopoulos, P.; Bunduc, O.; Chouvarda, I.; Dominguez, D.; et al. The Holistic Perspective of the INCISIVE Project; Artificial Intelligence in Screening Mammography. Appl. Sci. 2022, 12, 8755. [Google Scholar] [CrossRef]
- Hagerty, J.R.; Stanley, R.J.; Almubarak, H.A.; Lama, N.; Kasmi, R.; Guo, P.; Drugge, R.J.; Rabinovitz, H.S.; Oliviero, M.; Stoecker, W.V. Deep Learning and Handcrafted Method Fusion: Higher Diagnostic Accuracy for Melanoma Dermoscopy Images. IEEE J. Biomed. Health Inform. 2019, 23, 1385–1391. [Google Scholar] [CrossRef]
- Sari, C.T.; Gunduz-Demir, C. Unsupervised Feature Extraction via Deep Learning for Histopathological Classification of Colon Tissue Images. IEEE Trans. Med. Imaging 2019, 38, 1139–1149. [Google Scholar] [CrossRef]
- Singh, M.; Pujar, G.V.; Kumar, S.A.; Bhagyalalitha, M.; Akshatha, H.S.; Abuhaija, B.; Alsoud, A.R.; Abualigah, L.; Beeraka, N.M.; Gandomi, A.H. Evolution of Machine Learning in Tuberculosis Diagnosis: A Review of Deep Learning-Based Medical Applications. Electronics 2022, 11, 2634. [Google Scholar] [CrossRef]
- Jeon, B.; Jang, Y.; Shim, H.; Chang, H.J. Identification of coronary arteries in CT images by Bayesian analysis of geometric relations among anatomical landmarks. Pattern Recognit. 2019, 96, 106958. [Google Scholar] [CrossRef]
- Uslu, F.; Bharath, A.A. A recursive Bayesian approach to describe retinal vasculature geometry. Pattern Recognit. 2019, 87, 157–169. [Google Scholar] [CrossRef]
- Obayya, M.; Haj Hassine, S.B.; Alazwari, S.; Nour, M.K.; Mohamed, A.; Motwakel, A.; Yaseen, I.; Sarwar Zamani, A.; Abdelmageed, A.A.; Mohammed, G.P. Aquila Optimizer with Bayesian Neural Network for Breast Cancer Detection on Ultrasound Images. Appl. Sci. 2022, 12, 8679. [Google Scholar] [CrossRef]
- Pathan, S.; Kumar, P.; Pai, R.; Bhandary, S.V. Automated detection of optic disc contours in fundus images using decision tree classifier. Biocybern. Biomed. Eng. 2020, 40, 52–64. [Google Scholar] [CrossRef]
- Liu, F.; Lin, G.; Qiao, R.; Shen, C. Structured learning of tree potentials in CRF for image segmentation. IEEE Trans. Neural Netw. Learn. Syst. 2017, 29, 2631–2637. [Google Scholar] [CrossRef] [PubMed]
- Peptenatu, D.; Andronache, I.; Ahammer, H.; Taylor, R.; Liritzis, I.; Radulovic, M.; Ciobanu, B.; Burcea, M.; Perc, M.; Pham, T.D.; et al. Kolmogorov compression complexity may differentiate different schools of Orthodox iconography. Sci. Rep. 2022, 12, 10743. [Google Scholar] [CrossRef]
- Dolz, J.; Gopinath, K.; Yuan, J.; Lombaert, H.; Desrosiers, C.; Ben Ayed, I. HyperDense-Net: A Hyper-Densely Connected CNN for Multi-Modal Image Segmentation. IEEE Trans. Med. Imaging 2019, 38, 1116–1126. [Google Scholar] [CrossRef]
- Dai, Y.; Jin, T.; Song, Y.; Sun, S.; Wu, C. Convolutional Neural Network with Spatial-Variant Convolution Kernel. Remote Sens. 2020, 12, 2811. [Google Scholar] [CrossRef]
- Ma, J.; Yang, X. Automatic dental root CBCT image segmentation based on CNN and level set method. In Proceedings of the Medical Imaging 2019: Image Processing, San Diego, CA, USA, 19–21 February 2019; Angelini, E.D., Landman, B.A., Eds.; International Society for Optics and Photonics, SPIE: Bellingham, WA, USA, 2019; Volume 10949, p. 109492N. [Google Scholar] [CrossRef]
- Joseph, S.M.; Sathidevi, P.S. An Automated cDNA Microarray Image Analysis for the determination of Gene Expression Ratios. IEEE ACM Trans. Comput. Biol. Bioinform. 2021, 20, 136–150. [Google Scholar] [CrossRef]
- Almugren, N.; Alshamlan, H. A Survey on Hybrid Feature Selection Methods in Microarray Gene Expression Data for Cancer Classification. IEEE Access 2019, 7, 78533–78548. [Google Scholar] [CrossRef]
- Giannakeas, N.; Kalatzis, F.; Tsipouras, M.G.; Fotiadis, D.I. Spot addressing for microarray images structured in hexagonal grids. Comput. Methods Programs Biomed. 2012, 106, 1–13. [Google Scholar] [CrossRef]
- Osher, S.; Rudin, L.I. Feature-Oriented Image Enhancement Using Shock Filters. SIAM J. Numer. Anal. 1990, 27, 919–940. [Google Scholar] [CrossRef]
- van den Boomgaard, R.; Smeulders, A. The morphological structure of images: The differential equations of morphological scale-space. IEEE Trans. Pattern Anal. Mach. Intell. 1994, 16, 1101–1113. [Google Scholar] [CrossRef]
- Kramer, H.P.; Bruckner, J.B. Iterations of a non-linear transformation for enhancement of digital images. Pattern Recognit. 1975, 7, 53–58. [Google Scholar] [CrossRef]
- Alvarez, L.; Mazorra, L. Signal and Image Restoration Using Shock Filters and Anisotropic Diffusion. SIAM J. Numer. Anal. 1994, 31, 590–605. [Google Scholar] [CrossRef]
- Vacavant, A. Smoothed Shock Filtering: Algorithm and Applications. J. Imaging 2021, 7, 56. [Google Scholar] [CrossRef] [PubMed]
- Campbell, A.M.; Hatfield, W.T.; Heyer, L.J. Make microarray data with known ratios. CBE Life Sci. Educ. 2007, 6, 196–197. [Google Scholar] [CrossRef]
- Xiao, J.; Lucas, A.; D’Andrade, P.; Visitacion, M.; Tangvoranuntakul, P.; Fulmer-Smentek, S. Performance of the Agilent Microarray Platform for One-Color Analysis of Gene Expression; Agilent Technologies, Inc.: Santa Clara, CA, USA, 2006; pp. 1–15. [Google Scholar]
- Dobroiu, S.; van Delft, F.; Aveyard-Hanson, J.; Shetty, P.; Nicolau, D. Fluorescence Interference Contrast-enabled structures improve the microarrays performance. Biosens. Bioelectron. 2019, 123, 251–259. [Google Scholar] [CrossRef]
- Bariamis, D.; Maroulis, D.; Iakovidis, D.K. Unsupervised SVM-based gridding for DNA microarray images. Comput. Med. Imaging Graph. 2010, 34, 418–425. [Google Scholar] [CrossRef]
- Rueda, L.; Rezaeian, I. A fully automatic gridding method for cDNA microarray images. BMC Bioinform. 2011, 12, 113. [Google Scholar] [CrossRef] [PubMed]
- Rueda, L.; Vidyadharan, V. A hill-climbing approach for automatic gridding of cDNA microarray images. IEEE ACM Trans. Comput. Biol. Bioinform. 2006, 3, 72–83. [Google Scholar] [CrossRef] [PubMed]
- Bozinov, D.; Rahnenführer, J. Unsupervised technique for robust target separation and analysis of DNA microarray spots through adaptive pixel clustering. Bioinformatics 2002, 18, 747–756. [Google Scholar] [CrossRef] [PubMed]
- Giannakeas, N.; Fotiadis, D.I. An automated method for gridding and clustering-based segmentation of cDNA microarray images. Comput. Med. Imaging Graph. 2009, 33, 40–49. [Google Scholar] [CrossRef]
- Ho, J.; Hwang, W.L. Automatic Microarray Spot Segmentation Using a Snake-Fisher Model. IEEE Trans. Med. Imaging 2008, 27, 847–857. [Google Scholar] [CrossRef]
- Ni, S.; Wang, P.; Paun, M.; Dai, W.; Paun, A. Spotted cDNA microarray image segmentation using ACWE. Rom. J. Inf. Sci. Technol. 2009, 12, 249–263. [Google Scholar]
- Zacharia, E.; Maroulis, D. 3-D Spot Modeling for Automatic Segmentation of cDNA Microarray Images. IEEE Trans. Nanobiosci. 2010, 9, 181–192. [Google Scholar] [CrossRef]
- Zahoor, J.; Zafar, K. Classification of Microarray Gene Expression Data Using an Infiltration Tactics Optimization (ITO) Algorithm. Genes 2020, 11, 819. [Google Scholar] [CrossRef]
- Katzer, M.; Kummert, F.; Sagerer, G. Methods for automatic microarray image segmentation. IEEE Trans. Nanobiosci. 2003, 2, 202–214. [Google Scholar] [CrossRef]
- Giannakeas, N.; Kalatzis, F.; Tsipouras, M.G.; Fotiadis, D.I. A generalized methodology for the gridding of microarray images with rectangular or hexagonal grid. Signal Image Video Process. 2016, 10, 719–728. [Google Scholar] [CrossRef]
- Tcheslavski, G.V. Morphological Image Processing: Gray-Scale Morphology; Springer: London, UK, 2010. [Google Scholar]
- Brändle, N.; Bischof, H.; Lapp, H. Robust DNA microarray image analysis. Mach. Vis. Appl. 2003, 15, 11–28. [Google Scholar] [CrossRef]
- Belean, B.; Gutt, R.; Costea, C.; Balacescu, O. Microarray Image Analysis: From Image Processing Methods to Gene Expression Levels Estimation. IEEE Access 2020, 8, 159196–159205. [Google Scholar] [CrossRef]
- Agilent Technologies. Feature Extraction Reference Guide; Agilent Technologies, Inc.: Santa Clara, CA, USA, 2012. [Google Scholar]
- Handran, S.; Zhai, J.Y. Biological Relevance of GenePix, Results; Molecular Devices—Application Notes: San Jose, CA, USA, 2003. [Google Scholar]
- Athanasiadis, E.; Cavouras, D.; Kostopoulos, S.; Glotsos, D.; Kalatzis, I.; Nikiforidis, G. A wavelet-based Markov random field segmentation model in segmenting microarray experiments. Comput. Methods Programs Biomed. 2011, 104, 307–315. [Google Scholar] [CrossRef] [PubMed]
- Athanasiadis, E.I.; Cavouras, D.A.; Spyridonos, P.P.; Glotsos, D.T.; Kalatzis, I.K.; Nikiforidis, G.C. Complementary DNA Microarray Image Processing Based on the Fuzzy Gaussian Mixture Model. IEEE Trans. Inf. Technol. Biomed. 2009, 13, 419–425. [Google Scholar] [CrossRef] [PubMed]
- Zacharia, E.; Maroulis, D. An Original Genetic Approach to the Fully Automatic Gridding of Microarray Images. IEEE Trans. Med. Imaging 2008, 27, 805–813. [Google Scholar] [CrossRef]
- Jung, H.Y.; Cho, H.G. An automatic block and spot indexing with k-nearest neighbors graph for microarray image analysis. Bioinformatics 2002, 18, S141–S151. [Google Scholar] [CrossRef]
- Zhao, J.; Yu, X.; Yang, X.; Xiang, Q.; Duan, H.; Yu, Y. Polarization independent subtractive color printing based on ultrathin hexagonal nanodisk-nanohole hybrid structure arrays. Opt. Express 2017, 25, 23137–23145. [Google Scholar] [CrossRef]
- Singh, C.; Bhatia, N.; Kaur, A. Hough transform based fast skew detection and accurate skew correction methods. Pattern Recognit. 2008, 41, 3528–3546. [Google Scholar] [CrossRef]
- Bao, W.; Yang, C.; Wen, S.; Zeng, M.; Guo, J.; Zhong, J.; Xu, X. A Novel Adaptive Deskewing Algorithm for Document Images. Sensors 2022, 22, 7944. [Google Scholar] [CrossRef]
- Tai, Y.L.; Huang, S.J.; Chen, C.C.; Lu, H.H.S. Computational Complexity Reduction of Neural Networks of Brain Tumor Image Segmentation by Introducing Fermi–Dirac Correction Functions. Entropy 2021, 23, 223. [Google Scholar] [CrossRef]
- Gadosey, P.K.; Li, Y.; Agyekum, E.A.; Zhang, T.; Liu, Z.; Yamak, P.T.; Essaf, F. SD-UNet: Stripping down U-Net for Segmentation of Biomedical Images on Platforms with Low Computational Budgets. Diagnostics 2020, 10, 110. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Zineddin, B.; Liang, J.; Zeng, N.; Li, Y.; Du, M.; Cao, J.; Liu, X. A novel neural network approach to cDNA microarray image segmentation. Comput. Methods Programs Biomed. 2013, 111, 189–198. [Google Scholar] [CrossRef] [PubMed]
- Rojas-Thomas, J.C.; Mora, M.; Santos, M. Neural networks ensemble for automatic DNA microarray spot classification. Neural Comput. Appl. 2019, 31, 2311–2327. [Google Scholar] [CrossRef]
- Barequet, G.; Eppstein, D.; Goodrich, M.; Mamano, N. Stable-matching Voronoi diagrams: Combinatorial complexity and algorithms. J. Comput. Geom. 2020, 11, 26–59. [Google Scholar]
- Zhang, K.; Lan, L.; Wang, Z.; Moerchen, F. Scaling up kernel SVM on limited resources: A low-rank linearization approach. In Proceedings of the Artificial Intelligence and Statistics, PMLR, La Palma, Spain, 21–23 April 2012; pp. 1425–1434. [Google Scholar]
- Bariamis, D.; Iakovidis, D.K.; Maroulis, D. M3G: Maximum margin microarray gridding. BMC Bioinform. 2010, 11, 49. [Google Scholar] [CrossRef]
- Morris, D. Blind Microarray Gridding: A New Framework. IEEE Trans. Syst. Man Cybern. Part C Appl. Rev. 2008, 38, 33–41. [Google Scholar] [CrossRef]
- Oliveto, P.S.; He, J.; Yao, X. Time complexity of evolutionary algorithms for combinatorial optimization: A decade of results. Int. J. Autom. Comput. 2007, 4, 281–293. [Google Scholar] [CrossRef]



| Exp. ID | ||||||
|---|---|---|---|---|---|---|
| FE18398 | 0.988 | 0.075 | 0.420 | 0.412 | ||
| FE18399 | 0.993 | 0.029 | 0.395 | 0.406 | ||
| FE18400 | 0.982 | 0.093 | 536 | 524 | 0.414 | 0.385 |
| FE18401 | 0.994 | 0.046 | 0.392 | 0.397 |
| Reference/ | Method Description | Image, Grid Type | Image Size / | Spot | Metric | Value |
|---|---|---|---|---|---|---|
| Dataset | Number of Spots | Diam. | ||||
| SMD | Gridding based on support vector | Real, Rectangular grid | 1980 × 1917 | 10 | Mean | 2.52 |
| [42,60] | machines and genetic algorithms | 9196 | Std | 2.59 | ||
| Acc | 96.4 | |||||
| Nycter | K-nearest neighbor | Synthetic, | 3188 × 9552 | 14 | Mean | 1.77 |
| [61] | Rectangular grid | 576,756 | Std | 1.16 | ||
| Acc | 98.9 | |||||
| CNV370 | Voronoi diagrams | Real, Rectangular grid | 2800 × 2800 | 6 | Mean | 1.88 |
| [52] | 9216 | Std | 0.82 | |||
| Acc | 99.8 | |||||
| Nycter | Gridding based on support vector | Real, Rectangular grid | 2800 × 2800 | 14 | Mean | 1.91 |
| machines and genetic algorithms | 9216 | Std | 1.03 | |||
| Acc | 99.3 | |||||
| SMD | Voronoi diagrams | Real, Synthetic with | various sizes | 14 | Mean | 1.94 |
| Nycter | rectangular and | Std | 2.32 | |||
| [52] | hexagonal grids | Acc | 97.5 | |||
| FEdata | Shock filter driven by mathematical | Real, Hexagonal | 1650 × 4320 | 14 | Mean | 1.52 |
| (present) | morphology | 9196 | Std | 0.68 | ||
| Acc | 100 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baloi, A.; Costea, C.; Gutt, R.; Balacescu, O.; Turcu, F.; Belean, B. Hexagonal-Grid-Layout Image Segmentation Using Shock Filters: Computational Complexity Case Study for Microarray Image Analysis Related to Machine Learning Approaches. Sensors 2023, 23, 2582. https://doi.org/10.3390/s23052582
Baloi A, Costea C, Gutt R, Balacescu O, Turcu F, Belean B. Hexagonal-Grid-Layout Image Segmentation Using Shock Filters: Computational Complexity Case Study for Microarray Image Analysis Related to Machine Learning Approaches. Sensors. 2023; 23(5):2582. https://doi.org/10.3390/s23052582
Chicago/Turabian StyleBaloi, Aurel, Carmen Costea, Robert Gutt, Ovidiu Balacescu, Flaviu Turcu, and Bogdan Belean. 2023. "Hexagonal-Grid-Layout Image Segmentation Using Shock Filters: Computational Complexity Case Study for Microarray Image Analysis Related to Machine Learning Approaches" Sensors 23, no. 5: 2582. https://doi.org/10.3390/s23052582
APA StyleBaloi, A., Costea, C., Gutt, R., Balacescu, O., Turcu, F., & Belean, B. (2023). Hexagonal-Grid-Layout Image Segmentation Using Shock Filters: Computational Complexity Case Study for Microarray Image Analysis Related to Machine Learning Approaches. Sensors, 23(5), 2582. https://doi.org/10.3390/s23052582








