Centroid Optimization of DNN Classification in DOA Estimation for UAV
Abstract
1. Introduction
2. Theory
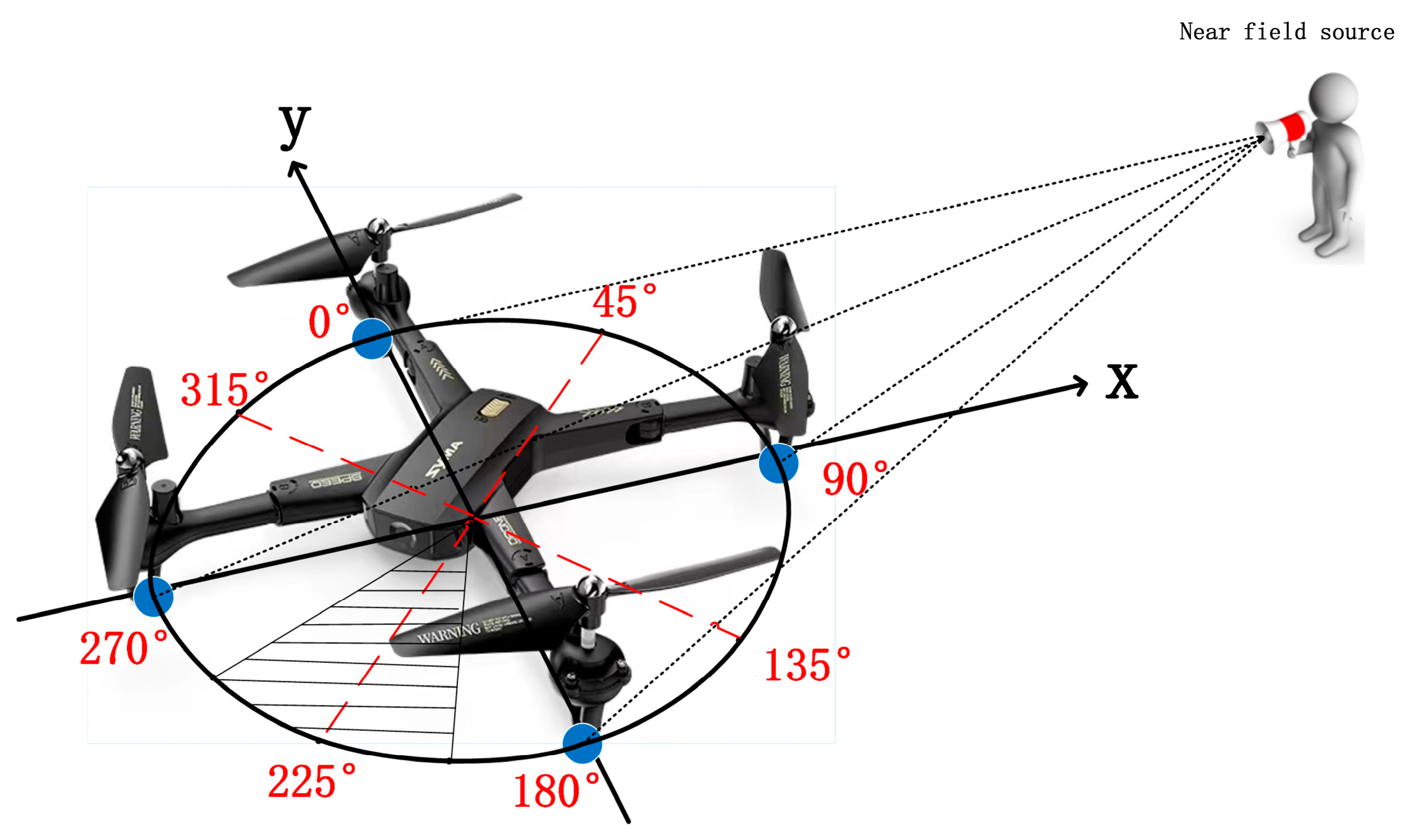
2.1. Signal Model
2.2. DNN Classification (DNNC) and Centroid Optimization of DNN Classification (CO-DNNC)
3. Experiments
3.1. Datasets
3.2. Performance Metrics
3.3. Experiment Validation
4. Discussion
4.1. Impact of Number of Classes and SNR
4.2. Impact of Tolerance
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Andrea, R.D. Guest editorial can drones deliver? IEEE Trans. Autom. Sci. Eng. 2014, 11, 647–648. [Google Scholar] [CrossRef]
- Lopez-Fuentes, L.; van de Weijer, J.; Gonzalez-Hidalgo, M.; Skinnemoen, H.; Bagdanov, A.D. Review on computer vision techniques in emergency situations. Multimed. Tools Appl. 2018, 77, 17069–17107. [Google Scholar] [CrossRef]
- Basiri, M.; Schill, F.; Lima, P.U.; Floreano, D. Robust acoustic source localization of emergency signals from micro air vehicles. In Proceedings of the 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems, Algarve, Portugal, 7 October 2012. [Google Scholar]
- Zhang, R.; Shim, B.; Wu, W. Direction-of-arrival estimation for large antenna arrays with hybrid analog and digital architectures. IEEE Trans. Signal Process. 2021, 70, 72–88. [Google Scholar] [CrossRef]
- Schmidt, R. Multiple emitter location and signal parameter estimation. IEEE Trans. Antennas Propag. 1986, 34, 276–280. [Google Scholar] [CrossRef]
- Roy, R.; Kailath, T. ESPRIT-estimation of signal parameters via rotational invariance techniques. IEEE Trans. Acoust. Speech Signal Process. 1989, 37, 984–995. [Google Scholar] [CrossRef]
- Ping, Z. DOA estimation method based on neural network. In Proceedings of the 2015 10th International Conference on P2P, Parallel, Grid, Cloud and Internet Computing (3PGCIC), Krakow, Poland, 4 November 2015. [Google Scholar]
- Ge, S.; Li, K.; Rum, S. Deep learning approach in DOA estimation: A systematic literature review. Mob. Inf. Syst. 2021, 2021, 1–14. [Google Scholar] [CrossRef]
- Zhang, X.; Yu, J.; Feng, G.; Xu, D. Blind direction of arrival estimation of coherent sources using multi-invariance property. Prog. Electromagn. Res. 2008, 88, 181–195. [Google Scholar] [CrossRef]
- Wang, H.; Kaveh, M. Coherent signal-subspace processing for the detection and estimation of angles of arrival of multiple wide-band sources. IEEE Trans. Acoust. Speech Signal Process. 1985, 33, 823–831. [Google Scholar] [CrossRef]
- Goodman, J.; Salmond, D.; Davis, C.; Acosta, C. Ambiguity resolution in direction of arrival estimation using mixed integer optimiztion and deep learning. In Proceedings of the IEEE National Aerospace and Electronics Conference, Dayton, Ohio, 15 July 2019. [Google Scholar]
- Yu, L.; Li, Z.; Chu, N.; Mohammad-Djafari, A.; Guo, Q.; Wang, R. Achieving the sparse acoustical holography via the sparse bayesian learning. Appl. Acoust. 2022, 191, 1–14. [Google Scholar] [CrossRef]
- Küçük, A.; Panahi, I.M.S. Convolutional recurrent neural network based direction of arrival estimation method using two microphones for hearing studies. In Proceedings of the IEEE 30th International Workshop on Machine Learning for Signal Processing (MLSP), Virtual Conference, 19 April 2020. [Google Scholar]
- Xiang, H.; Chen, B.; Yang, T.; Liu, D. Improved de-multipath neural network models with self-paced feature-to-feature learning for DOA estimation in multipath environment. IEEE Trans. Veh. Technol. 2020, 69, 5068–5078. [Google Scholar] [CrossRef]
- Liu, Y.; Tong, F.; Zhong, S.; Hong, Q.; Li, L. Reverberation aware deep learning for environment tolerant microphone array DOA estimation. Appl. Acoust. 2021, 184, 1–8. [Google Scholar] [CrossRef]
- Li, P.; Tian, Y. DOA estimation of underwater acoustic signals based on deep learning. In Proceedings of the 2021 2nd International Seminar on Artificial Intelligence. Networking and Information Technology (AINIT), Shanghai, China, 17 October 2021. [Google Scholar]
- Huang, M.; Zheng, B.; Cai, T.; Li, X.; Liu, J.; Qian, C.; Chen, H. Machine–learning-enabled metasurface for direction of arrival estimation. Nanophotonics 2022, 11, 2001–2010. [Google Scholar] [CrossRef]
- Qayyum, A.; Hassan, K.; Anika, A.; Shadiq, F.; Rahman, M.; Islam, T.; Imran, S.A.; Hossain, S.; Haque, M.A. DOANet: A deep dilated convolutional neural network approach for search and rescue with drone-embedded sound source localization. EURASIP J. Audio Speech Music Process. 2020, 2020, 1–18. [Google Scholar] [CrossRef]
- Yamano, R.; Kikuma, N.; Sakakibara, K. Effect of redundancy of element placement on DOA estimation with circular array. In Proceedings of the 2016 International Symposium on Antennas and Propagation (ISAP), Guilin, China, 18 October 2016. [Google Scholar]
- Ji, X.; Wang, L.; Sun, W.; Wang, H. A k-weighted centroid algorithm based on proximity beacon node optimization. In Proceedings of the 2017 13th International Conference on Natural Computation, Fuzzy Systems and Knowledge Discovery (ICNC-FSKD), Guilin, China, 29 July 2017. [Google Scholar]
- IEEE Signal Processing Cup 2019. Available online: http://dregon.inria.fr/datasets/signal-processing-cup-2019/ (accessed on 22 October 2020).
- Strauss, M.; Mordel, P.; Miguet, V.; Deleforge, A. DREGON: Dataset and methods for UAV-embedded sound source localization. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1 October 2018. [Google Scholar]
- Xiang, H.; Chen, B.; Yang, M.; Xu, S. Angle separation learning for coherent DOA estimation with deep sparse prior. IEEE Commun. Lett. 2021, 25, 465–469. [Google Scholar] [CrossRef]
- Cheng, L.; Sun, X.; Yao, D.; Li, J.; Yan, Y. Estimation reliability function assisted sound source localization with enhanced steering vector phase difference. IEEE/ACM Trans. Audio Speech Lang. Process. 2021, 29, 421–435. [Google Scholar] [CrossRef]



| Predicted Azimuth of DOA | True Azimuth of DOA | |||||||
|---|---|---|---|---|---|---|---|---|
| 0° | 45° | 90° | 135° | 180° | 225° | 270° | 315° | |
| 0° | 78.5 | 9.625 | 0.25 | 0 | 0 | 0 | 0.5 | 11.125 |
| 45° | 11.25 | 79.375 | 8.625 | 0 | 0 | 0 | 0.125 | 0.125 |
| 90° | 0.125 | 10.75 | 78.5 | 10.5 | 0 | 0 | 0.125 | 0 |
| 135° | 0 | 0.125 | 10.375 | 78.625 | 10.625 | 0.25 | 0 | 0 |
| 180° | 0 | 0 | 0.625 | 11.875 | 77.0 | 10.375 | 0.125 | 0 |
| 225° | 0 | 0 | 0 | 0.25 | 12.25 | 76.125 | 10.875 | 0.5 |
| 270° | 0.5 | 0.125 | 0 | 0 | 0.375 | 11.125 | 75.75 | 12.125 |
| 315° | 12.125 | 0.25 | 0 | 0 | 0 | 0.25 | 8.75 | 78.625 |
| Performance Metrics | SNR | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| −20 dB | −10 dB | 0 dB | 10 dB | 20 dB | |||||||
| Accuracy (%) | 36.4 | 54.2 | 76.2 | 89.2 | 95.6 | ||||||
| RMSE (°) of DNNC | RMSE (°) of CO-DNNC | 95.1 | 50.9 | 70.3 | 44.6 | 42.3 | 28.9 | 30.1 | 19.5 | 26.9 | 19.9 |
| Accuracy (%) | 18.5 | 33.0 | 58.7 | 77.8 | 88.8 | ||||||
| RMSE (°) of DNNC | RMSE (°) of CO-DNNC | 91.0 | 30.6 | 65.8 | 34.8 | 36.0 | 27.6 | 20.1 | 15.1 | 15.2 | 10.2 |
| Accuracy (%) | 13.0 | 23.6 | 47.6 | 71.4 | 87.3 | ||||||
| RMSE (°) of DNNC | RMSE (°) of CO-DNNC | 87.8 | 25.4 | 64.2 | 36.2 | 34.4 | 28.2 | 16.7 | 13.8 | 10.6 | 7.2 |
| Accuracy (%) | 8.4 | 15.9 | 35.9 | 62.4 | 81.8 | ||||||
| RMSE (°) of DNNC | RMSE (°) of CO-DNNC | 93.9 | 24.6 | 67.6 | 38 | 35.6 | 30.2 | 16.2 | 14.7 | 9.0 | 6.6 |
| Number of Classes | SNR | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| −20 dB | −10 dB | 0 dB | 10 dB | 20 dB | |||||||
| 4 | 45° | 36.4 | 56.3 | 54.2 | 71.9 | 76.2 | 88.7 | 89.2 | 97.9 | 95.6 | 99.6 |
| 22.5° | 18.3 | 29.0 | 29.3 | 42.5 | 41.8 | 66.2 | 47.4 | 77.0 | 48.4 | 66.3 | |
| 10° | 7.8 | 12.3 | 12.8 | 20.3 | 18.7 | 36.2 | 22.6 | 35.5 | 20.6 | 26.5 | |
| 8 | 22.5° | 18.5 | 51.4 | 31.9 | 59.0 | 58.8 | 68.1 | 77.8 | 88.0 | 88.8 | 96.5 |
| 11.25° | 9.4 | 27.0 | 16.2 | 30.8 | 31.6 | 42.8 | 43.7 | 66.0 | 48.7 | 78.1 | |
| 10° | 8.4 | 24.4 | 14.6 | 27.2 | 28.4 | 38.7 | 38.9 | 62.3 | 42.4 | 70.8 | |
| 12 | 15° | 13.0 | 44.0 | 21.6 | 55.8 | 47.6 | 53.1 | 71.4 | 81.3 | 87.3 | 94.9 |
| 7.5° | 6.3 | 23.0 | 11.1 | 28.6 | 25.6 | 30.1 | 40.0 | 61.1 | 47.8 | 80.8 | |
| 10° | 8.5 | 30.2 | 14.8 | 38.3 | 33.6 | 38.9 | 51.6 | 69.9 | 62.4 | 88.3 | |
| 18 | 10° | 8.4 | 31.7 | 15.1 | 49.9 | 24.7 | 57.5 | 62.4 | 69.0 | 81.7 | 90.3 |
| 5° | 4.2 | 16.2 | 7.7 | 26.2 | 12.5 | 29.3 | 34.5 | 47.8 | 44.4 | 74.7 | |
| 10° | 8.4 | 31.7 | 15.1 | 49.9 | 24.7 | 57.5 | 62.4 | 69.0 | 81.7 | 90.3 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, L.; Zhang, Z.; Yang, X.; Xu, L.; Chen, S.; Zhang, Y.; Zhang, J. Centroid Optimization of DNN Classification in DOA Estimation for UAV. Sensors 2023, 23, 2513. https://doi.org/10.3390/s23052513
Wu L, Zhang Z, Yang X, Xu L, Chen S, Zhang Y, Zhang J. Centroid Optimization of DNN Classification in DOA Estimation for UAV. Sensors. 2023; 23(5):2513. https://doi.org/10.3390/s23052513
Chicago/Turabian StyleWu, Long, Zidan Zhang, Xu Yang, Lu Xu, Shuyu Chen, Yong Zhang, and Jianlong Zhang. 2023. "Centroid Optimization of DNN Classification in DOA Estimation for UAV" Sensors 23, no. 5: 2513. https://doi.org/10.3390/s23052513
APA StyleWu, L., Zhang, Z., Yang, X., Xu, L., Chen, S., Zhang, Y., & Zhang, J. (2023). Centroid Optimization of DNN Classification in DOA Estimation for UAV. Sensors, 23(5), 2513. https://doi.org/10.3390/s23052513






