Discrete Geodesic Distribution-Based Graph Kernel for 3D Point Clouds
Abstract
1. Introduction
Related Works
2. Methodology
2.1. Simplicial Complexes
- For and is face of , ;
- When , is empty or is simultaneously a face of and .
2.2. Kernel Function
3. Results
3.1. Data Set
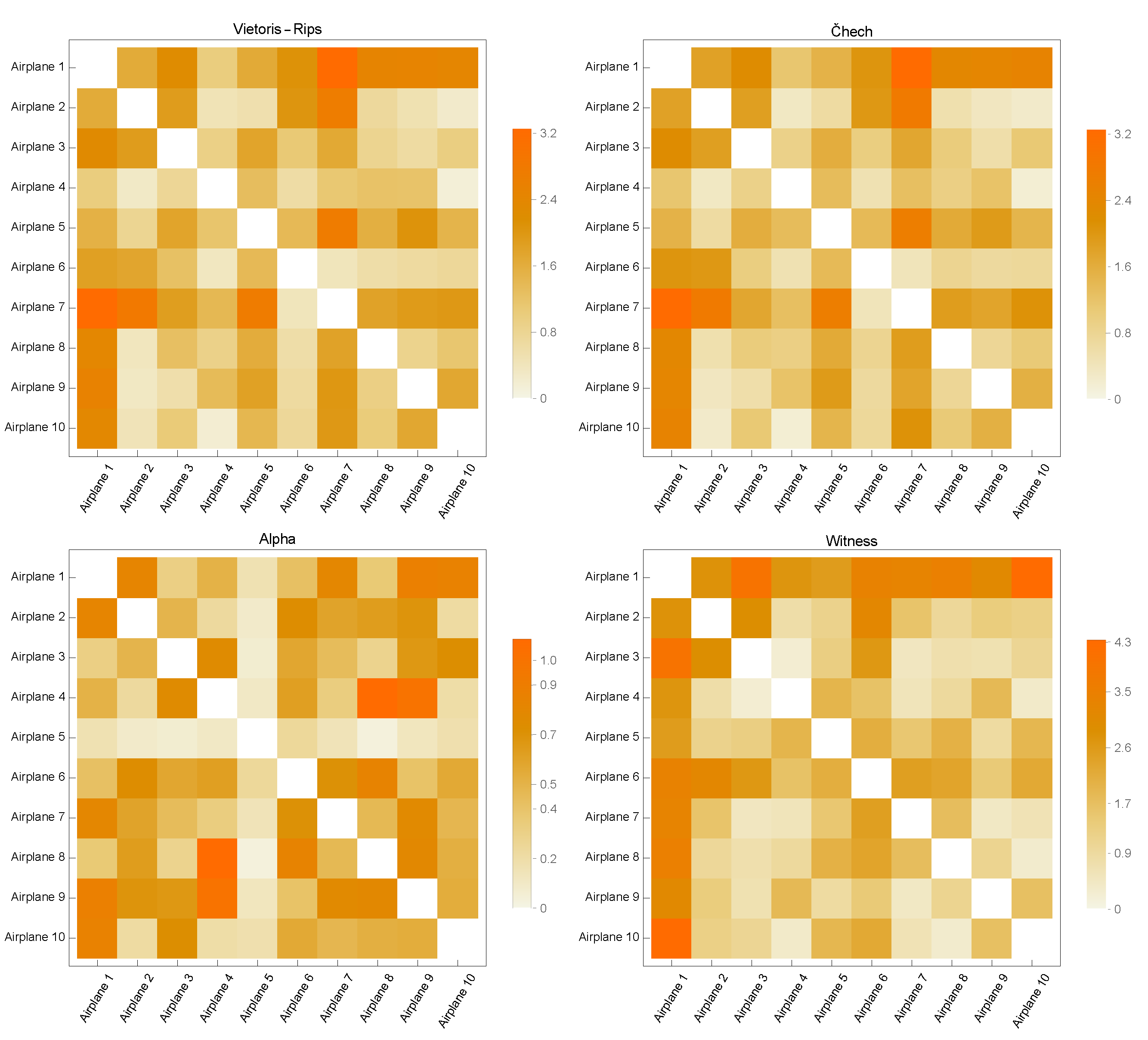
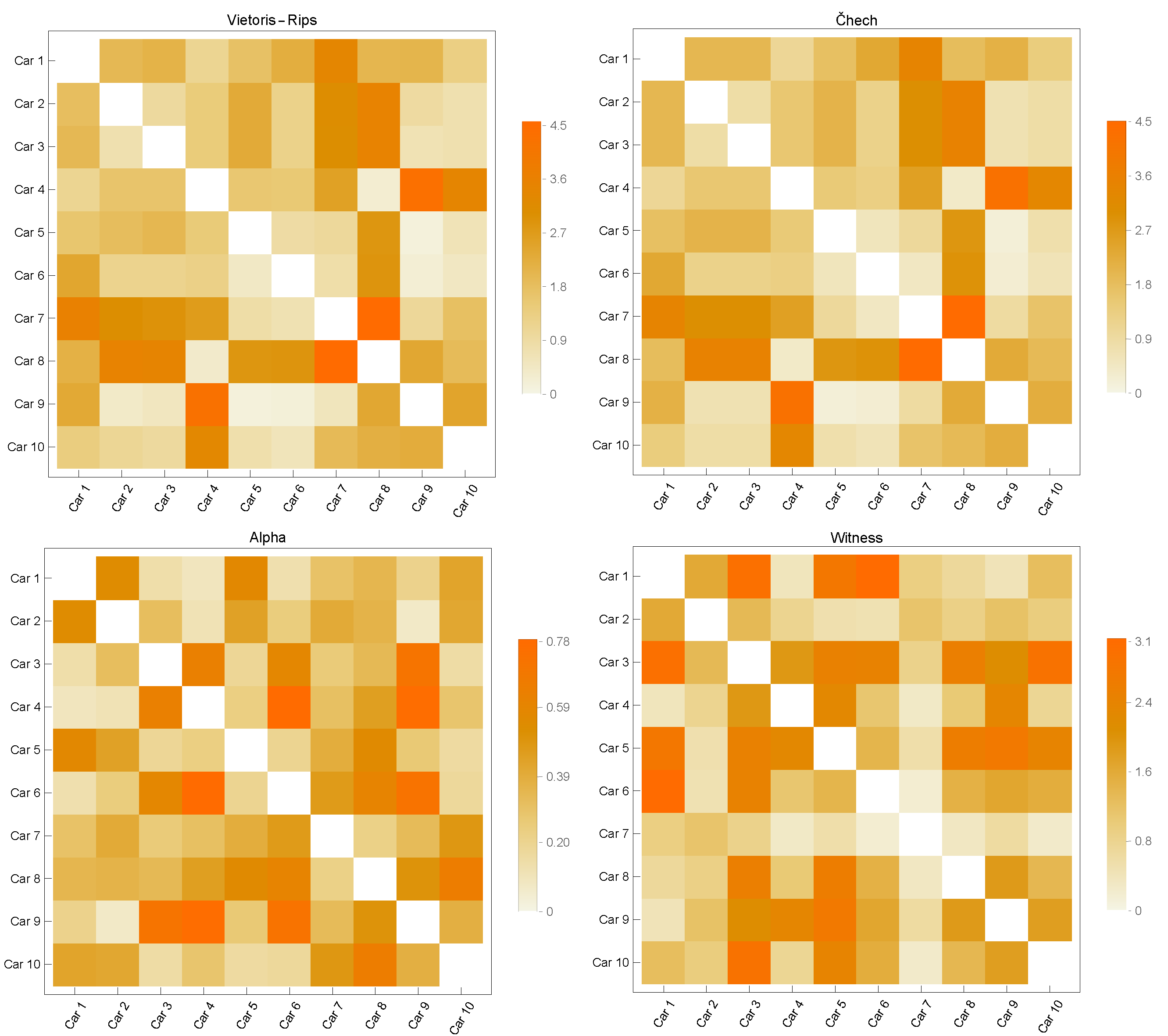
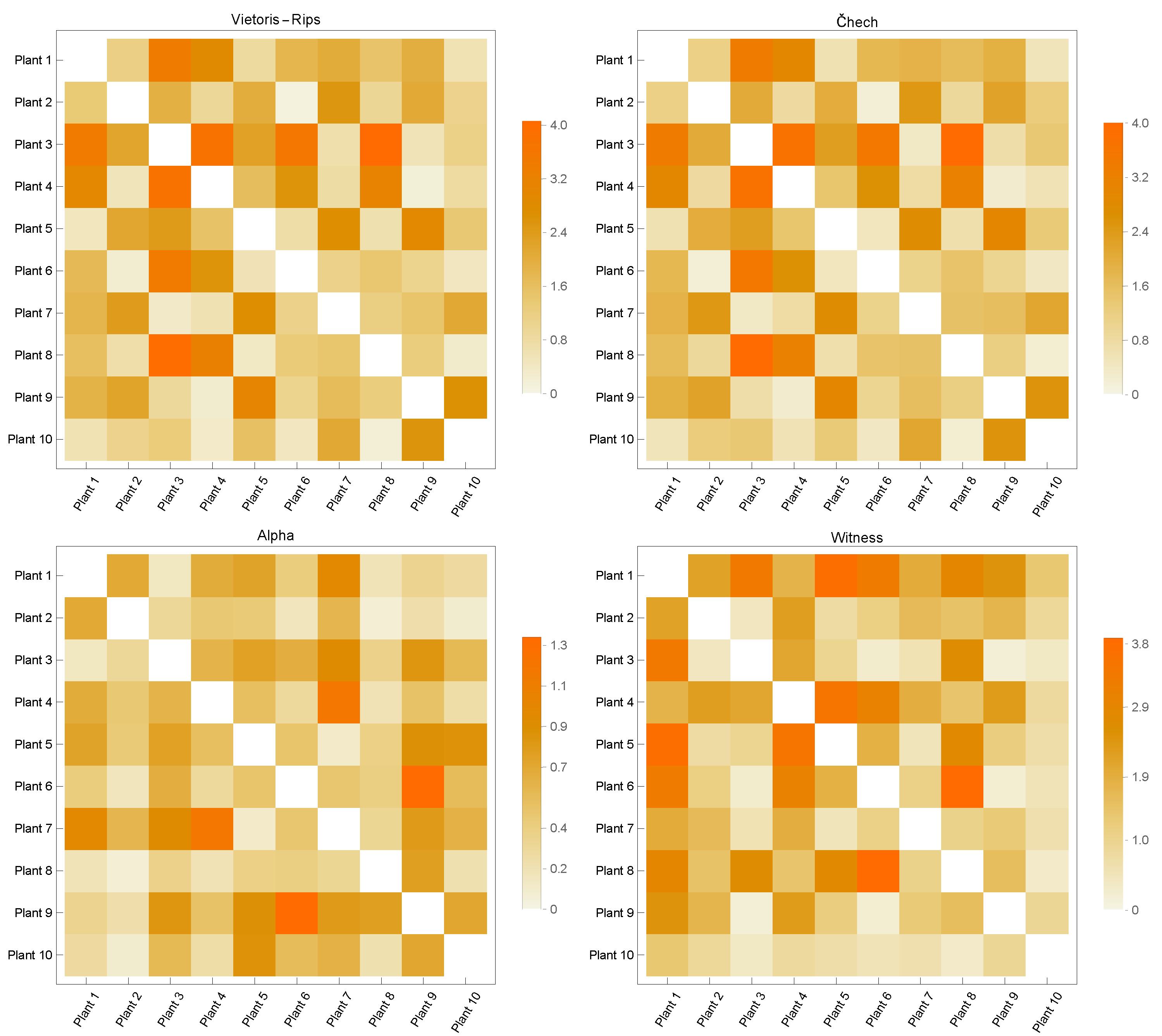
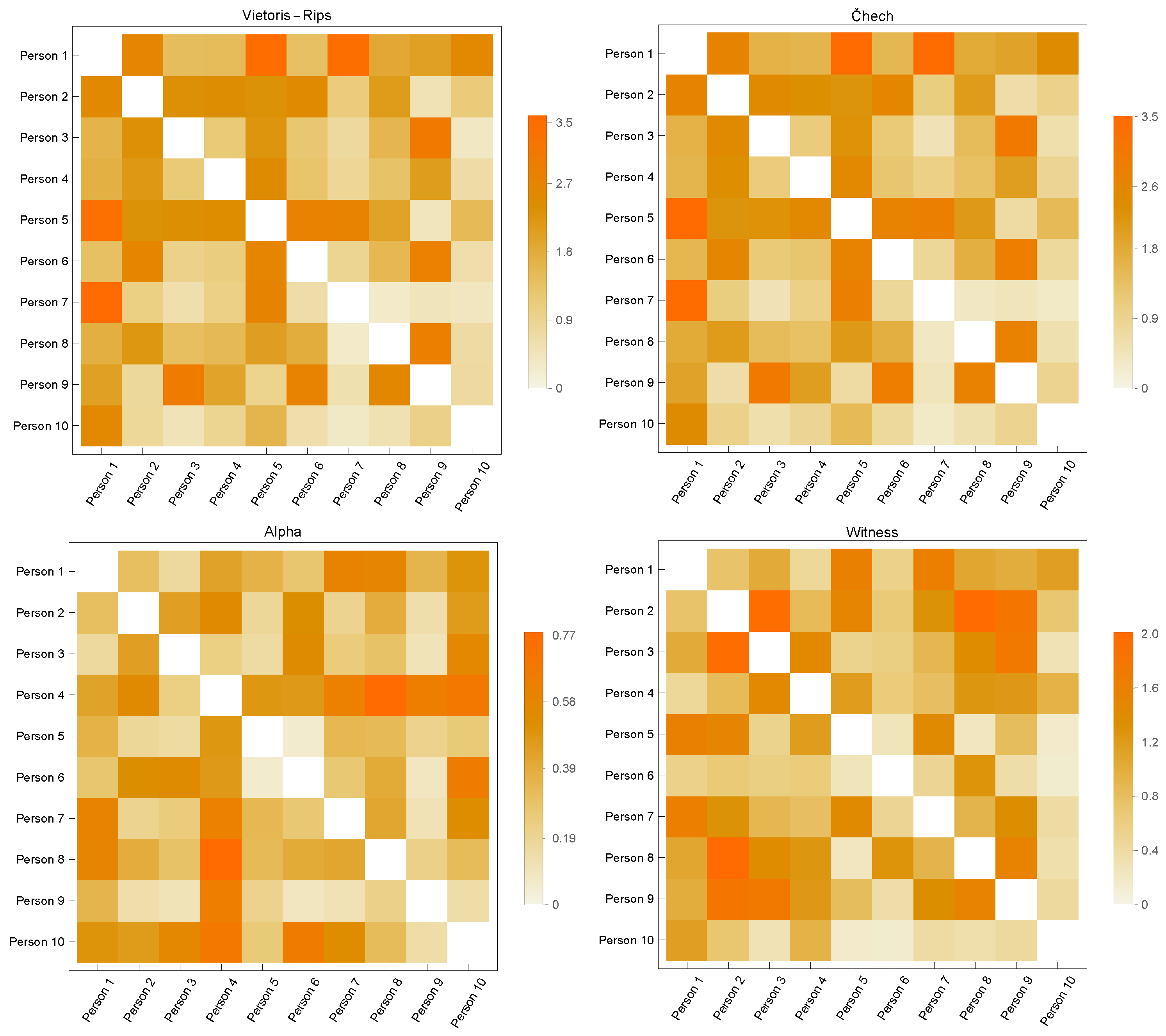
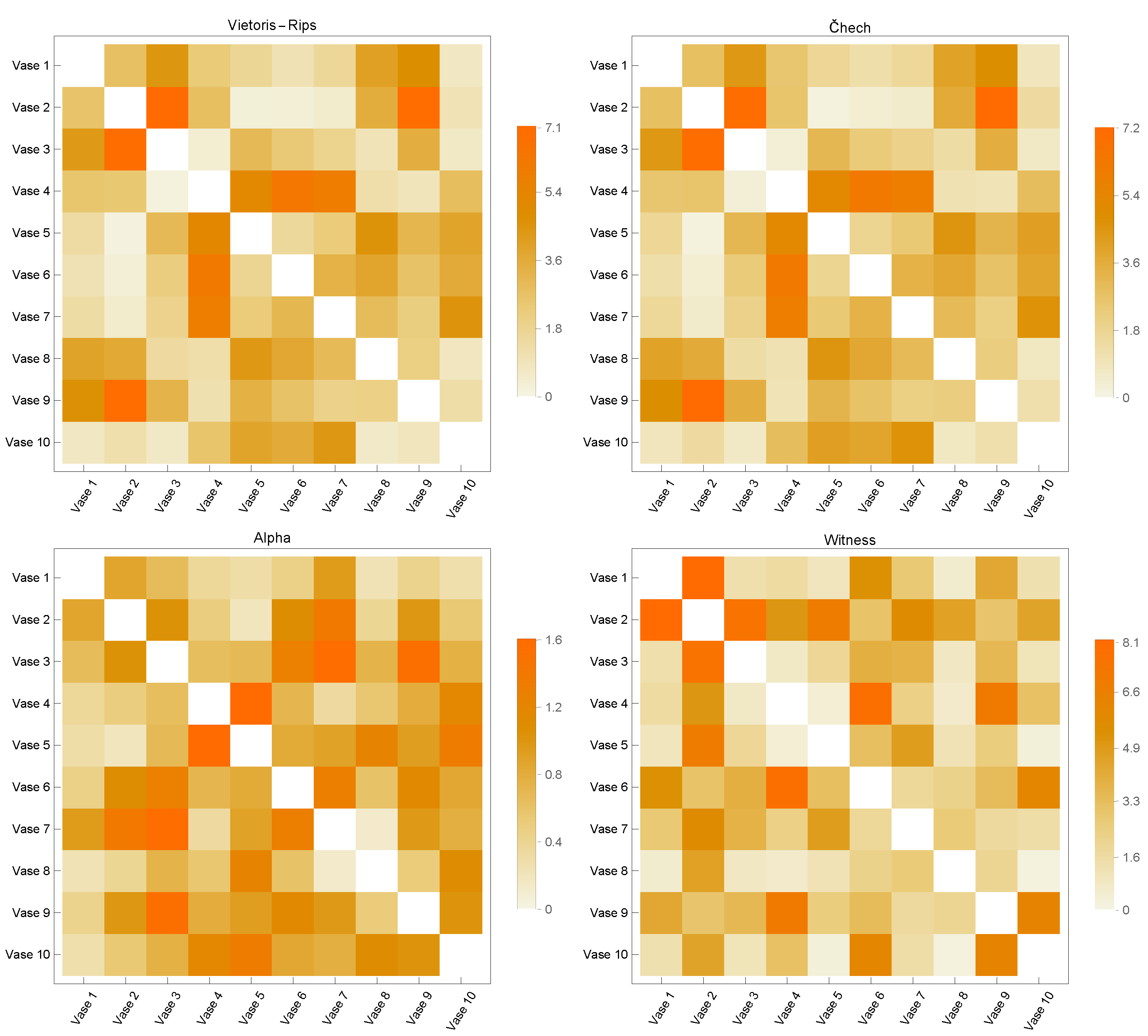
3.2. Point Cloud Comparison
3.3. Classification
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
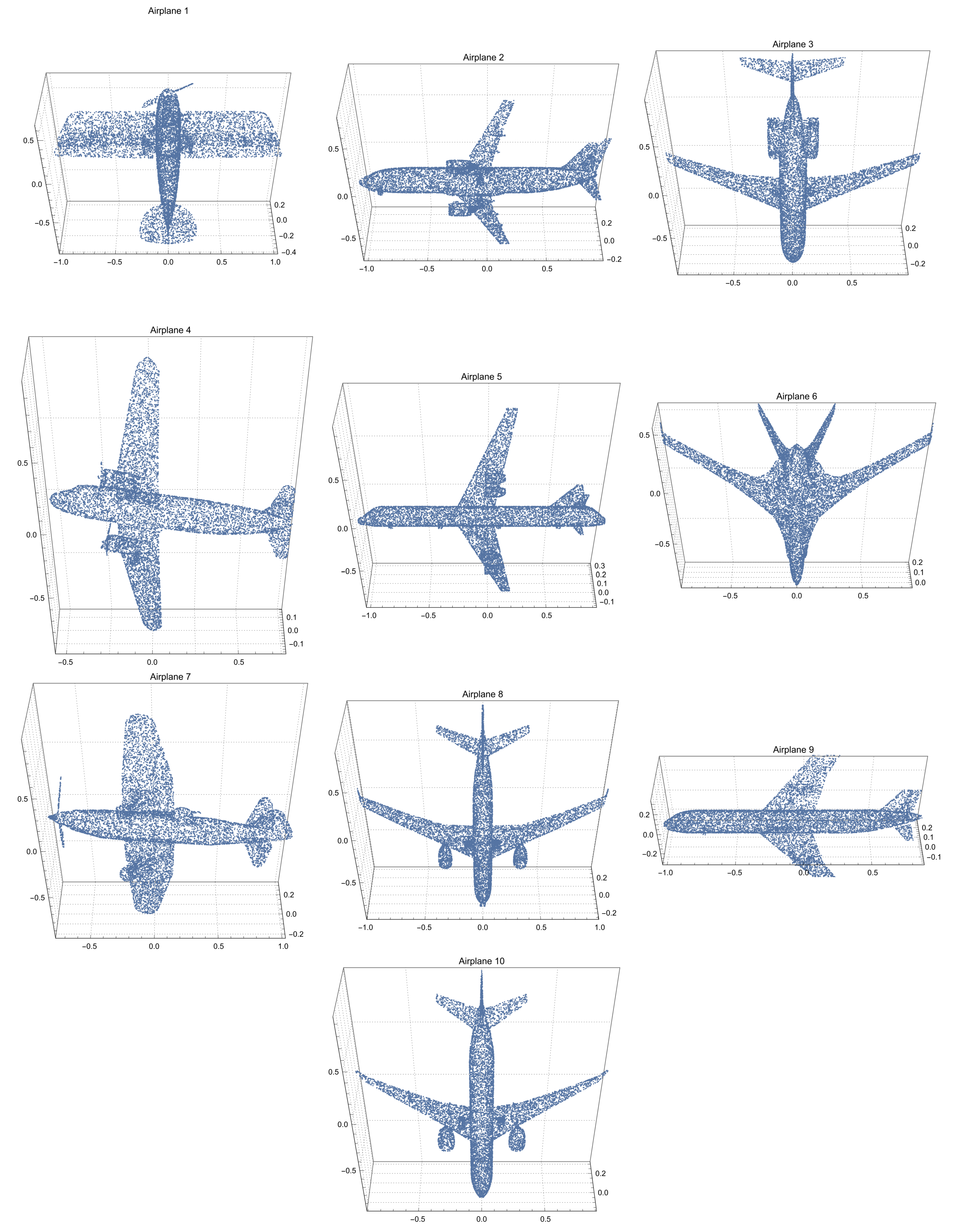

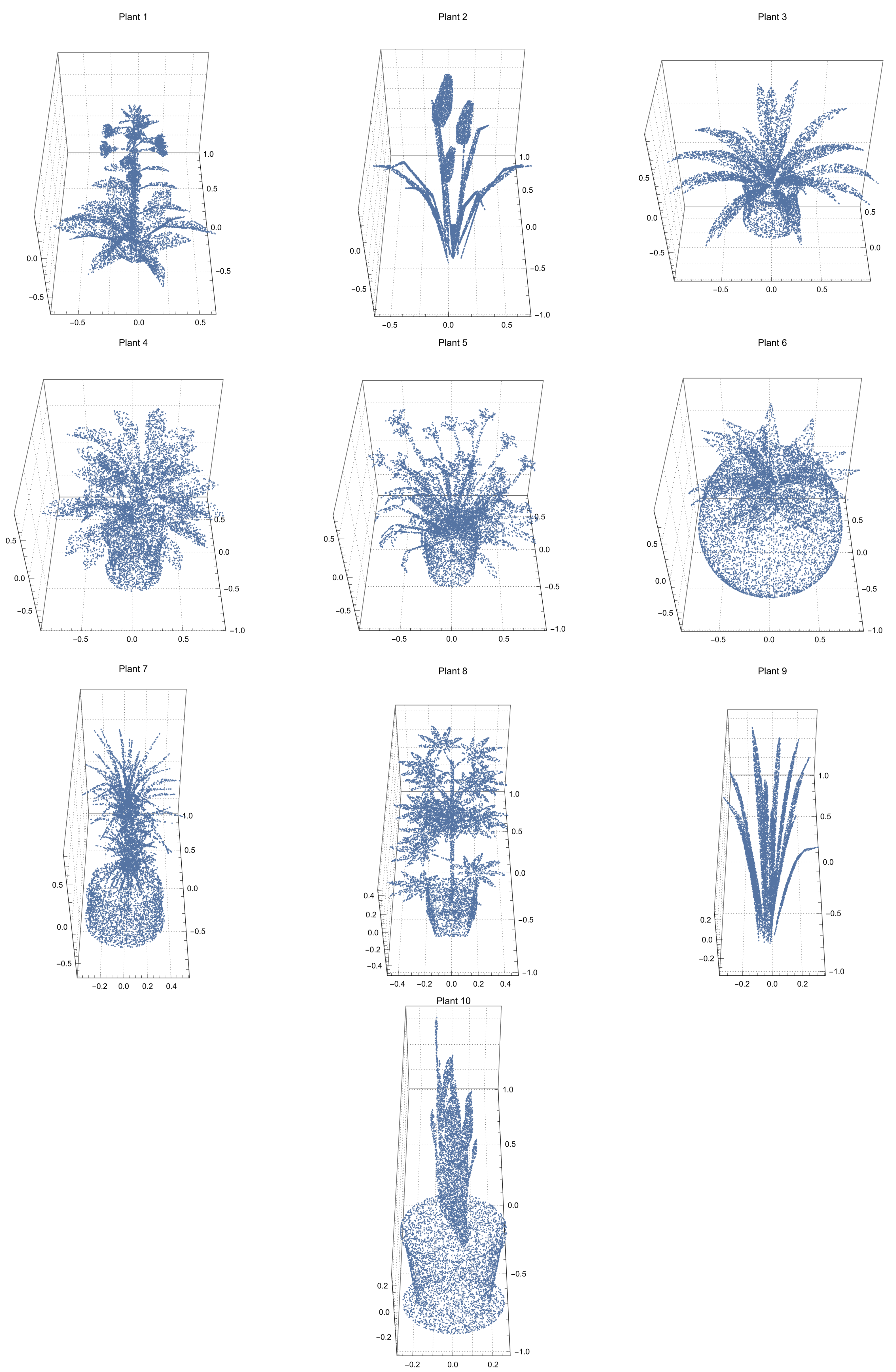

References
- Chougule, V.; Mulay, A.; Ahuja, B. Three dimensional point cloud generations from CT scan images for bio-cad modeling. In Proceedings of the International Conference on Additive Manufacturing Technologies—AM2013, Bengaluru, India, 7–8 October 2013; Volume 7, p. 8. [Google Scholar]
- Fu, Y.; Lei, Y.; Wang, T.; Patel, P.; Jani, A.B.; Mao, H.; Curran, W.J.; Liu, T.; Yang, X. Biomechanically constrained non-rigid MR-TRUS prostate registration using deep learning based 3D point cloud matching. Med Image Anal. 2021, 67, 101845. [Google Scholar] [CrossRef]
- Gidea, M.; Katz, Y. Topological data analysis of financial time series: Landscapes of crashes. Phys. A Stat. Mech. Its Appl. 2018, 491, 820–834. [Google Scholar] [CrossRef]
- Ismail, M.S.; Hussain, S.I.; Noorani, M.S.M. Detecting early warning signals of major financial crashes in bitcoin using persistent homology. IEEE Access 2020, 8, 202042–202057. [Google Scholar] [CrossRef]
- Liu, J.; Guo, P.; Sun, X. An Automatic 3D Point Cloud Registration Method Based on Biological Vision. Appl. Sci. 2021, 11, 4538. [Google Scholar] [CrossRef]
- Barra, V.; Biasotti, S. 3D shape retrieval and classification using multiple kernel learning on extended Reeb graphs. Vis. Comput. 2014, 30, 1247–1259. [Google Scholar] [CrossRef]
- Chen, L.M. Digital and Discrete Geometry: Theory and Algorithms; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Song, M. A personalized active method for 3D shape classification. Vis. Comput. 2021, 37, 497–514. [Google Scholar] [CrossRef]
- Wang, F.; Lv, J.; Ying, G.; Chen, S.; Zhang, C. Facial expression recognition from image based on hybrid features understanding. J. Vis. Commun. Image Represent. 2019, 59, 84–88. [Google Scholar] [CrossRef]
- Boulch, A.; Puy, G.; Marlet, R. FKAConv: Feature-kernel alignment for point cloud convolution. In Proceedings of the Asian Conference on Computer Vision, Kyoto, Japan, 30 November–4 December 2020. [Google Scholar]
- Gou, J.; Yi, Z.; Zhang, D.; Zhan, Y.; Shen, X.; Du, L. Sparsity and geometry preserving graph embedding for dimensionality reduction. IEEE Access 2018, 6, 75748–75766. [Google Scholar] [CrossRef]
- Meltzer, P.; Mallea, M.D.G.; Bentley, P.J. PiNet: Attention Pooling for Graph Classification. arXiv 2020, arXiv:2008.04575. [Google Scholar]
- Wang, T.; Liu, H.; Li, Y.; Jin, Y.; Hou, X.; Ling, H. Learning combinatorial solver for graph matching. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 7568–7577. [Google Scholar]
- Wu, J.; Pan, S.; Zhu, X.; Zhang, C.; Philip, S.Y. Multiple structure-view learning for graph classification. IEEE Trans. Neural Netw. Learn. Syst. 2017, 29, 3236–3251. [Google Scholar] [CrossRef]
- Mitchell, J.S.; Mount, D.M.; Papadimitriou, C.H. The discrete geodesic problem. SIAM J. Comput. 1987, 16, 647–668. [Google Scholar] [CrossRef]
- Polthier, K.; Schmies, M. Straightest geodesics on polyhedral surfaces. In ACM SIGGRAPH 2006 Courses; Association for Computing Machinery: New York, NY, USA, 2006; pp. 30–38. [Google Scholar]
- Atici, M.; Vince, A. Geodesics in graphs, an extremal set problem, and perfect hash families. Graphs Comb. 2002, 18, 403–413. [Google Scholar] [CrossRef]
- Bernstein, M.; De Silva, V.; Langford, J.C.; Tenenbaum, J.B. Graph Approximations to Geodesics on Embedded Manifolds; Technical Report; Citeseer: University Park, PA, USA, 2000. [Google Scholar]
- Alexa, M.; Behr, J.; Cohen-Or, D.; Fleishman, S.; Levin, D.; Silva, C.T. Point set surfaces. In Proceedings of the Visualization, 2001—VIS’01, San Diego, CA, USA, 21–26 October 2001; pp. 21–29. [Google Scholar]
- Amenta, N.; Kil, Y.J. Defining point-set surfaces. ACM Trans. Graph. (TOG) 2004, 23, 264–270. [Google Scholar] [CrossRef]
- Levin, D. Mesh-independent surface interpolation. In Geometric Modeling for Scientific Visualization; Springer: Berlin/Heidelberg, Germany, 2004; pp. 37–49. [Google Scholar]
- Adamson, A.; Alexa, M. Approximating and intersecting surfaces from points. In Proceedings of the 2003 Eurographics/ACM SIGGRAPH Symposium on Geometry Processing, Aachen, Germany, 23–25 June 2003; pp. 230–239. [Google Scholar]
- Amenta, N.; Choi, S.; Kolluri, R.K. The power crust, unions of balls, and the medial axis transform. Comput. Geom. 2001, 19, 127–153. [Google Scholar] [CrossRef]
- Dey, T.K.; Goswami, S. Provable surface reconstruction from noisy samples. Comput. Geom. 2006, 35, 124–141. [Google Scholar] [CrossRef]
- Attene, M.; Patanè, G. Hierarchical structure recovery of point-sampled surfaces. Comput. Graph. Forum 2010, 29, 1905–1920. [Google Scholar] [CrossRef]
- Chen, X. Hierarchical rigid registration of femur surface model based on anatomical features. Mol. Cell. Biomech. 2020, 17, 139. [Google Scholar] [CrossRef]
- Nakarmi, U.; Wang, Y.; Lyu, J.; Liang, D.; Ying, L. A kernel-based low-rank (KLR) model for low-dimensional manifold recovery in highly accelerated dynamic MRI. IEEE Trans. Med. Imaging 2017, 36, 2297–2307. [Google Scholar] [CrossRef]
- Zhang, S.; Cui, S.; Ding, Z. Hypergraph spectral analysis and processing in 3D point cloud. IEEE Trans. Image Process. 2020, 30, 1193–1206. [Google Scholar] [CrossRef]
- Connor, M.; Kumar, P. Fast construction of k-nearest neighbor graphs for point clouds. IEEE Trans. Vis. Comput. Graph. 2010, 16, 599–608. [Google Scholar] [CrossRef] [PubMed]
- Natali, M.; Biasotti, S.; Patanè, G.; Falcidieno, B. Graph-based representations of point clouds. Graph. Model. 2011, 73, 151–164. [Google Scholar] [CrossRef]
- Klein, J.; Zachmann, G. Point cloud surfaces using geometric proximity graphs. Comput. Graph. 2004, 28, 839–850. [Google Scholar] [CrossRef]
- Fan, H.; Wang, Y.; Gong, J. Layout graph model for semantic façade reconstruction using laser point clouds. Geo-Spat. Inf. Sci. 2021, 24, 403–421. [Google Scholar] [CrossRef]
- Wang, Y.; Ma, Y.; Zhu, A.x.; Zhao, H.; Liao, L. Accurate facade feature extraction method for buildings from three-dimensional point cloud data considering structural information. ISPRS J. Photogramm. Remote Sens. 2018, 139, 146–153. [Google Scholar] [CrossRef]
- Wang, Y.; Li, H.; Liao, L. DEM Construction Method for Slopes Using Three-Dimensional Point Cloud Data Based on Moving Least Square Theory. J. Surv. Eng. 2020, 146, 04020013. [Google Scholar] [CrossRef]
- Wu, B.; Yang, L.; Wu, Q.; Zhao, Y.; Pan, Z.; Xiao, T.; Zhang, J.; Wu, J.; Yu, B. A Stepwise Minimum Spanning Tree Matching Method for Registering Vehicle-Borne and Backpack LiDAR Point Clouds. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–13. [Google Scholar] [CrossRef]
- Guo, Q.; Wang, Y.; Yang, S.; Xiang, Z. A method of blasted rock image segmentation based on improved watershed algorithm. Sci. Rep. 2022, 12, 7143. [Google Scholar] [CrossRef]
- Wang, Y.; Tu, W.; Li, H. Fragmentation calculation method for blast muck piles in open-pit copper mines based on three-dimensional laser point cloud data. Int. J. Appl. Earth Obs. Geoinf. 2021, 100, 102338. [Google Scholar] [CrossRef]
- Wang, Y.; Zhou, T.; Li, H.; Tu, W.; Xi, J.; Liao, L. Laser point cloud registration method based on iterative closest point improved by Gaussian mixture model considering corner features. Int. J. Remote Sens. 2022, 43, 932–960. [Google Scholar] [CrossRef]
- Alaba, S.Y.; Ball, J.E. A survey on deep-learning-based lidar 3d object detection for autonomous driving. Sensors 2022, 22, 9577. [Google Scholar] [CrossRef] [PubMed]
- Song, F.; Shao, Y.; Gao, W.; Wang, H.; Li, T. Layer-wise geometry aggregation framework for lossless lidar point cloud compression. IEEE Trans. Circuits Syst. Video Technol. 2021, 31, 4603–4616. [Google Scholar] [CrossRef]
- Wang, S.; Jiao, J.; Cai, P.; Wang, L. R-pcc: A baseline for range image-based point cloud compression. In Proceedings of the 2022 International Conference on Robotics and Automation (ICRA), Philadelphia, PA, USA, 23–27 May 2022; pp. 10055–10061. [Google Scholar]
- Xiong, J.; Gao, H.; Wang, M.; Li, H.; Ngan, K.N.; Lin, W. Efficient geometry surface coding in V-PCC. IEEE Trans. Multimed. 2022; early access. [Google Scholar] [CrossRef]
- Zhao, L.; Ma, K.K.; Liu, Z.; Yin, Q.; Chen, J. Real-time scene-aware LiDAR point cloud compression using semantic prior representation. IEEE Trans. Circuits Syst. Video Technol. 2022, 32, 5623–5637. [Google Scholar] [CrossRef]
- Sun, X.; Wang, S.; Wang, M.; Cheng, S.S.; Liu, M. An advanced LiDAR point cloud sequence coding scheme for autonomous driving. In Proceedings of the 28th ACM International Conference on Multimedia, Seattle, WA, USA, 12–16 October 2020; pp. 2793–2801. [Google Scholar]
- Sun, X.; Wang, M.; Du, J.; Sun, Y.; Cheng, S.S.; Xie, W. A Task-Driven Scene-Aware LiDAR Point Cloud Coding Framework for Autonomous Vehicles. IEEE Trans. Ind. Inform. 2022; early access. [Google Scholar] [CrossRef]
- Filippone, M.; Camastra, F.; Masulli, F.; Rovetta, S. A survey of kernel and spectral methods for clustering. Pattern Recognit. 2008, 41, 176–190. [Google Scholar] [CrossRef]
- Kriege, N.M.; Johansson, F.D.; Morris, C. A survey on graph kernels. Appl. Netw. Sci. 2020, 5, 1–42. [Google Scholar] [CrossRef]
- Nikolentzos, G.; Siglidis, G.; Vazirgiannis, M. Graph Kernels: A Survey. J. Artif. Intell. Res. 2021, 72, 943–1027. [Google Scholar] [CrossRef]
- Gaidon, A.; Harchaoui, Z.; Schmid, C. A time series kernel for action recognition. In Proceedings of the BMVC 2011-British Machine Vision Conference, Dundee, UK, 29 August–2 September 2011; pp. 63.1–63.11. [Google Scholar]
- Bach, F.R. Graph kernels between point clouds. In Proceedings of the 25th International Conference on Machine Learning, Helsinki, Finland, 5–9 July 2008; pp. 25–32. [Google Scholar]
- Wang, L.; Sahbi, H. Directed acyclic graph kernels for action recognition. In Proceedings of the IEEE International Conference on Computer Vision, Sydney, Australia, 1–8 December 2013; pp. 3168–3175. [Google Scholar]
- Harchaoui, Z.; Bach, F. Image classification with segmentation graph kernels. In Proceedings of the 2007 IEEE Conference on Computer Vision and Pattern Recognition, Minneapolis, MN, USA, 17–22 June 2007; pp. 1–8. [Google Scholar]
- Borgwardt, K.M.; Kriegel, H.P. Shortest-path kernels on graphs. In Proceedings of the Fifth IEEE International Conference on Data Mining (ICDM’05), Houston, TX, USA, 27–30 November 2005; p. 8. [Google Scholar]
- Aziz, F.; Wilson, R.C.; Hancock, E.R. Backtrackless walks on a graph. IEEE Trans. Neural Netw. Learn. Syst. 2013, 24, 977–989. [Google Scholar] [CrossRef]
- Johansson, F.; Jethava, V.; Dubhashi, D.; Bhattacharyya, C. Global graph kernels using geometric embeddings. In Proceedings of the International Conference on Machine Learning, Beijing, China, 22–24 June 2014; pp. 694–702. [Google Scholar]
- Shervashidze, N.; Schweitzer, P.; Van Leeuwen, E.J.; Mehlhorn, K.; Borgwardt, K.M. Weisfeiler-lehman graph kernels. J. Mach. Learn. Res. 2011, 12, 2539–2561. [Google Scholar]
- Bai, L.; Rossi, L.; Zhang, Z.; Hancock, E. An aligned subtree kernel for weighted graphs. In Proceedings of the International Conference on Machine Learning, Lille, France, 7–9 July 2015; pp. 30–39. [Google Scholar]
- Fröhlich, H.; Wegner, J.K.; Sieker, F.; Zell, A. Optimal assignment kernels for attributed molecular graphs. In Proceedings of the 22nd International Conference on Machine Learning, Bonn, Germany, 7–11 August 2005; pp. 225–232. [Google Scholar]
- Hatcher, A. Algebraic Topology; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Dey, T.K. Curve and Surface Reconstruction: Algorithms with Mathematical Analysis; Cambridge University Press: Cambridge, UK, 2006; Volume 23. [Google Scholar]
- Shewchuk, J.R. Lecture Notes on Delaunay Mesh Generation. 1999. Available online: https://people.eecs.berkeley.edu/~jrs/meshpapers/delnotes.pdf (accessed on 10 January 2023).
- Edelsbrunner, H.; Mücke, E.P. Three-dimensional alpha shapes. ACM Trans. Graph. (TOG) 1994, 13, 43–72. [Google Scholar] [CrossRef]
- De Floriani, L.; Hui, A. Data Structures for Simplicial Complexes: An Analysis Furthermore, A Comparison. In Proceedings of the Symposium on Geometry Processing, Vienna, Austria, 4–6 July 2005; pp. 119–128. [Google Scholar]
- Edelsbrunner, H.; Harer, J. Persistent homology-a survey. AMS Contemp. Math. 2008, 453, 257–282. [Google Scholar]
- Kahle, M. Topology of random simplicial complexes: A survey. AMS Contemprory Math. 2014, 620, 201–222. [Google Scholar]
- Zomorodian, A. Fast construction of the Vietoris-Rips complex. Comput. Graph. 2010, 34, 263–271. [Google Scholar] [CrossRef]
- Boissonnat, J.D.; Guibas, L.J.; Oudot, S.Y. Manifold reconstruction in arbitrary dimensions using witness complexes. Discret. Comput. Geom. 2009, 42, 37–70. [Google Scholar] [CrossRef]
- Burnham, K.P.; Anderson, D.R. Kullback–Leibler information as a basis for strong inference in ecological studies. Wildl. Res. 2001, 28, 111–119. [Google Scholar] [CrossRef]
- Pérez-Cruz, F. Kullback–Leibler divergence estimation of continuous distributions. In Proceedings of the 2008 IEEE International Symposium on Information Theory, Toronto, ON, Canada, 6–11 July 2008; pp. 1666–1670. [Google Scholar]
- Yu, S.; Mehta, P.G. The Kullback–Leibler rate pseudo-metric for comparing dynamical systems. IEEE Trans. Autom. Control 2010, 55, 1585–1598. [Google Scholar]
- Potamias, M.; Bonchi, F.; Castillo, C.; Gionis, A. Fast shortest path distance estimation in large networks. In Proceedings of the 18th ACM Conference on Information and Knowledge Management, Hong Kong, China, 2–6 November 2009; pp. 867–876. [Google Scholar]
- Panaretos, V.M.; Zemel, Y. Statistical Aspects of Wasserstein Distances. Annu. Rev. Stat. Its Appl. 2019, 6, 405–431. [Google Scholar] [CrossRef]
- Wu, Z.; Song, S.; Khosla, A.; Yu, F.; Zhang, L.; Tang, X.; Xiao, J. 3d shapenets: A deep representation for volumetric shapes. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1912–1920. [Google Scholar]
- Kriege, N.M.; Giscard, P.L.; Wilson, R. On valid optimal assignment kernels and applications to graph classification. Adv. Neural Inf. Process. Syst. 2016, 29, 1623–1631. [Google Scholar]
- Kudo, T.; Maeda, E.; Matsumoto, Y. An application of boosting to graph classification. Adv. Neural Inf. Process. Syst. 2004, 17, 1–8. [Google Scholar]
- Ma, T.; Shao, W.; Hao, Y.; Cao, J. Graph classification based on graph set reconstruction and graph kernel feature reduction. Neurocomputing 2018, 296, 33–45. [Google Scholar] [CrossRef]
- Wu, J.; He, J.; Xu, J. Net: Degree-specific graph neural networks for node and graph classification. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 4–8 August 2019; pp. 406–415. [Google Scholar]
- Yao, H.R.; Chang, D.C.; Frieder, O.; Huang, W.; Lee, T.S. Graph Kernel prediction of drug prescription. In Proceedings of the 2019 IEEE EMBS International Conference on Biomedical & Health Informatics (BHI), Chicago, IL, USA, 19–22 May 2019; pp. 1–4. [Google Scholar]
- Parés, F.; Gasulla, D.G.; Vilalta, A.; Moreno, J.; Ayguadé, E.; Labarta, J.; Cortés, U.; Suzumura, T. Fluid communities: A competitive, scalable and diverse community detection algorithm. In Proceedings of the International conference on Complex Networks and Their Applications, Lyon, France, 29 November–1 December 2017; pp. 229–240. [Google Scholar]
- Hua, B.S.; Tran, M.K.; Yeung, S.K. Pointwise convolutional neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 984–993. [Google Scholar]
- Zaheer, M.; Kottur, S.; Ravanbakhsh, S.; Poczos, B.; Salakhutdinov, R.R.; Smola, A.J. Deep sets. Adv. Neural Inf. Process. Syst. 2017, 30, 3391–3401. [Google Scholar]
- Simonovsky, M.; Komodakis, N. Dynamic edge-conditioned filters in convolutional neural networks on graphs. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 3693–3702. [Google Scholar]
- Qi, C.R.; Su, H.; Mo, K.; Guibas, L.J. Pointnet: Deep learning on point sets for 3d classification and segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 652–660. [Google Scholar]
- Xie, S.; Liu, S.; Chen, Z.; Tu, Z. Attentional shapecontextnet for point cloud recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 4606–4615. [Google Scholar]
- Groh, F.; Wieschollek, P.; Lensch, H. Flex-convolution (million-scale point-cloud learning beyond grid-worlds). arXiv 2018, arXiv:1803.07289. [Google Scholar]
- Klokov, R.; Lempitsky, V. Escape from cells: Deep kd-networks for the recognition of 3d point cloud models. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 863–872. [Google Scholar]
- Qi, C.R.; Yi, L.; Su, H.; Guibas, L.J. Pointnet++: Deep hierarchical feature learning on point sets in a metric space. Adv. Neural Inf. Process. Syst. 2017, 30, 1–14. [Google Scholar]
- Shen, Y.; Feng, C.; Yang, Y.; Tian, D. Mining point cloud local structures by kernel correlation and graph pooling. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 4548–4557. [Google Scholar]
- Wang, Y.; Sun, Y.; Liu, Z.; Sarma, S.E.; Bronstein, M.M.; Solomon, J.M. Dynamic graph cnn for learning on point clouds. Acm Trans. Graph. (TOG) 2019, 38, 1–12. [Google Scholar] [CrossRef]
- Atzmon, M.; Maron, H.; Lipman, Y. Point convolutional neural networks by extension operators. arXiv 2018, arXiv:1803.10091. [Google Scholar] [CrossRef]
- Liu, Y.; Fan, B.; Xiang, S.; Pan, C. Relation-shape convolutional neural network for point cloud analysis. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 8895–8904. [Google Scholar]



| K | Dimension | Time Complexity | Guarantee |
|---|---|---|---|
| Approx. Geometry | |||
| Nerve Theorem | |||
| Approx. | |||
| Approx. Geometry |
| Method | Input | No. Points | Accuracy |
|---|---|---|---|
| [80] | xyz | 1024 | % 86.1 |
| [81] | xyz | 1024 | % 87.1 |
| [82] | xyz | 1024 | % 87.4 |
| [83] | xyz | 1024 | % 89.2 |
| [84] | xyz | 1024 | % 90.0 |
| [85] | xyz | 1024 | % 90.2 |
| [86] | xyz | 1024 | % 90.6 |
| [87] | xyz | 1024 | % 90.7 |
| [88] | xyz | 1024 | % 91.0 |
| [89] | xyz | 1024 | % 92.2 |
| [90] | xyz | 1024 | % 92.3 |
| [91] | xyz | 1024 | % 93.6 |
| Ours | xyz | 1024 | % 93.7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Balcı, M.A.; Akgüller, Ö.; Batrancea, L.M.; Gaban, L. Discrete Geodesic Distribution-Based Graph Kernel for 3D Point Clouds. Sensors 2023, 23, 2398. https://doi.org/10.3390/s23052398
Balcı MA, Akgüller Ö, Batrancea LM, Gaban L. Discrete Geodesic Distribution-Based Graph Kernel for 3D Point Clouds. Sensors. 2023; 23(5):2398. https://doi.org/10.3390/s23052398
Chicago/Turabian StyleBalcı, Mehmet Ali, Ömer Akgüller, Larissa M. Batrancea, and Lucian Gaban. 2023. "Discrete Geodesic Distribution-Based Graph Kernel for 3D Point Clouds" Sensors 23, no. 5: 2398. https://doi.org/10.3390/s23052398
APA StyleBalcı, M. A., Akgüller, Ö., Batrancea, L. M., & Gaban, L. (2023). Discrete Geodesic Distribution-Based Graph Kernel for 3D Point Clouds. Sensors, 23(5), 2398. https://doi.org/10.3390/s23052398







