Unsupervised Hyperspectral Band Selection via Multimodal Evolutionary Algorithm and Subspace Decomposition
Abstract
:1. Introduction
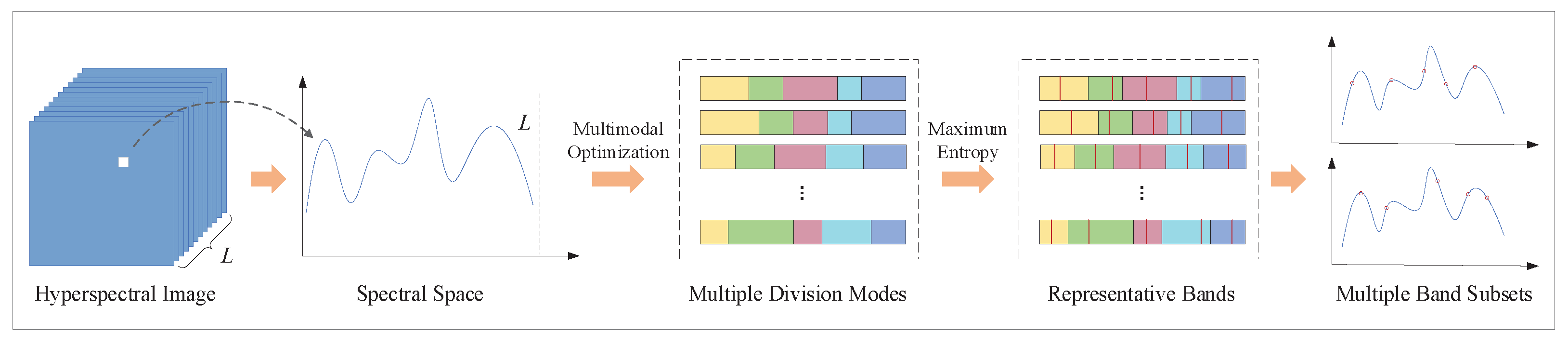
- To increase the diversity of obtained solutions, the multimodal evolutionary algorithm is first applied to hyperspectral band selection. It converges the candidate solutions towards different directions. Therefore, it can seek out multiple optimal (global or local) band subsets, in which each of them can express the original HSI information well.
- In consideration of the ordered property of spectral bands, a boundary encoding strategy and modified evaluation criterion for subspace decomposition is proposed. Different from seeking the spectral bands directly, the target of boundary encoding strategy is to find the optimal division modes of band space. Additionally, a modified evaluation criterion, endeavoring to increase the difference between neighbor subspaces rather than all clusters, is employed to evaluate the divided subspaces. Therefore, the selected bands from each subspace are scattered and lower correlative.
- Although a single band subset can express original hyperspectral information, the generalization ability might be poor. In order to alleviate this problem, an integrated utilization strategy is employed to utilize the acquired diverse band subsets.
2. Related Work
2.1. Greedy-Based Methods
2.2. Ranking-Based Methods
2.3. Clustering-Based Methods
2.4. EA-Based Methods
3. Unsupervised Band Selection Based on Multimodal Evolutionary Algorithm and Subspace Decomposition (MEA-SD)
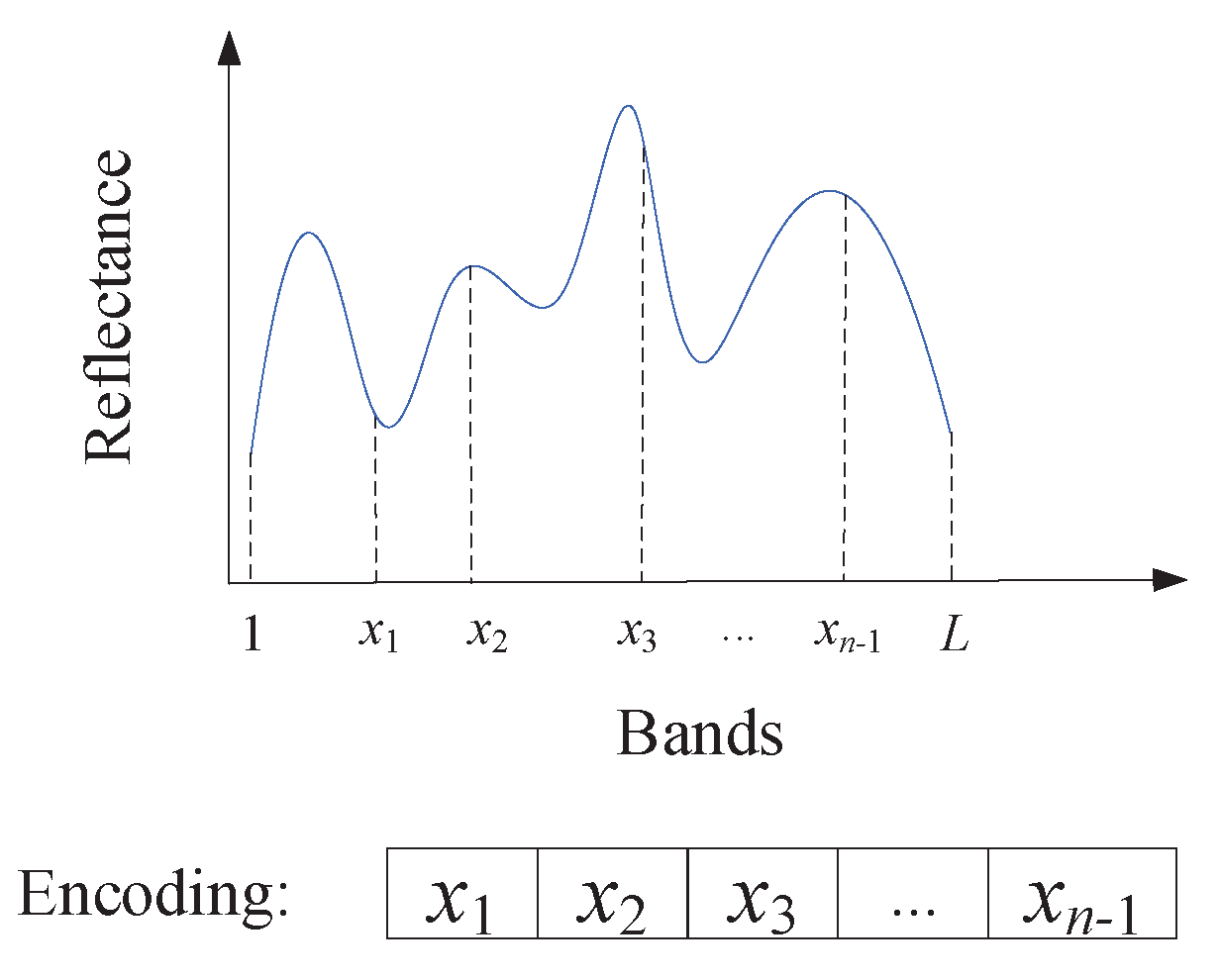
3.1. Boundary Encoding Strategy
3.2. Fitness Evaluation Criterion
3.3. Multimodal Optimization Framework
| Algorithm 1 Procedure of FERDE. |
|
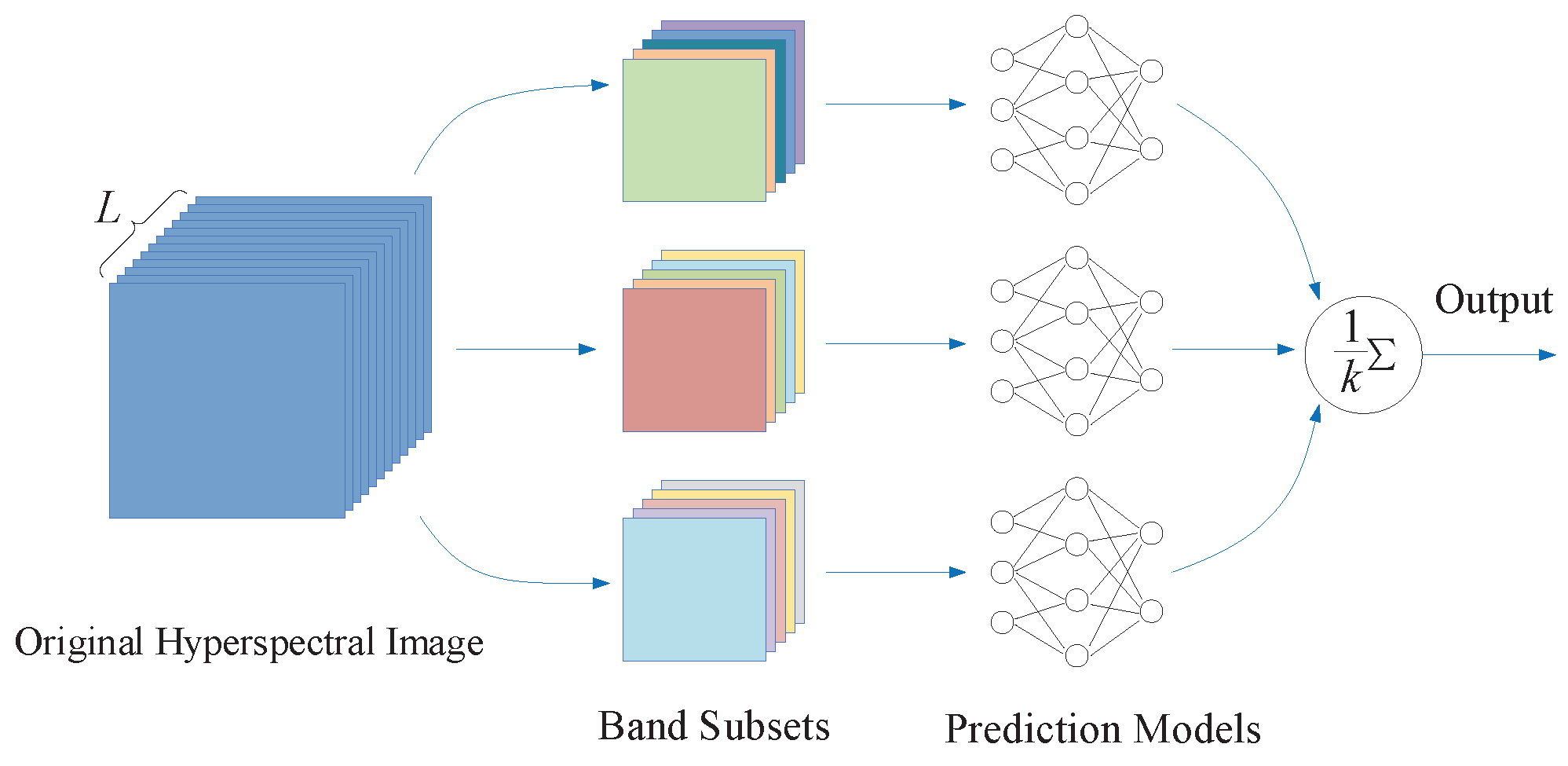
3.4. Integrated Utilization Strategy
- Calculate information entropy of all bands according to Equation (7).
- Sort the obtained solution set P according the fitness values, and select the top k different individuals, denote as X.
- For each individual in X, the corresponding band subset is composed of the bands with the maximum entropy in each subspace.
- According to k band subsets, operate corresponding pattern recognition tasks (classification or regression), respectively.
- Implement integration operation and output the final prediction results.
3.5. Computational Complexity
4. Experiments on Remote Sensing Datasets
4.1. Description of Remote Sensing Datasets
4.2. Experimental Setup
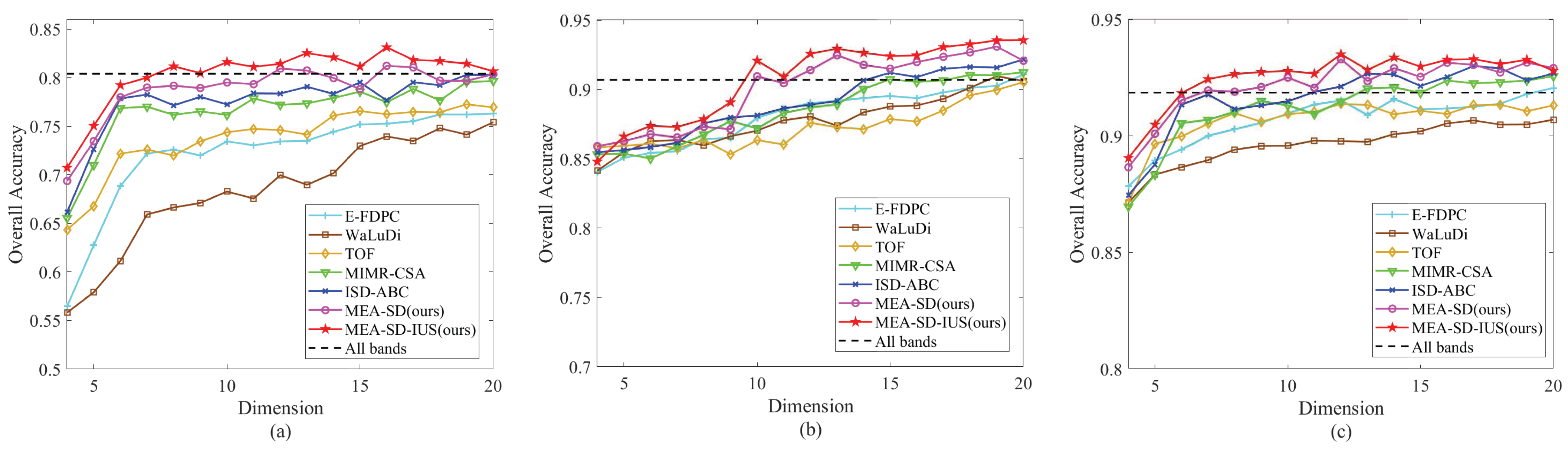
4.3. Experimental Results
4.3.1. Parameter Analysis
4.3.2. Comparison of Experimental Results
4.3.3. Comparison of Execution Time
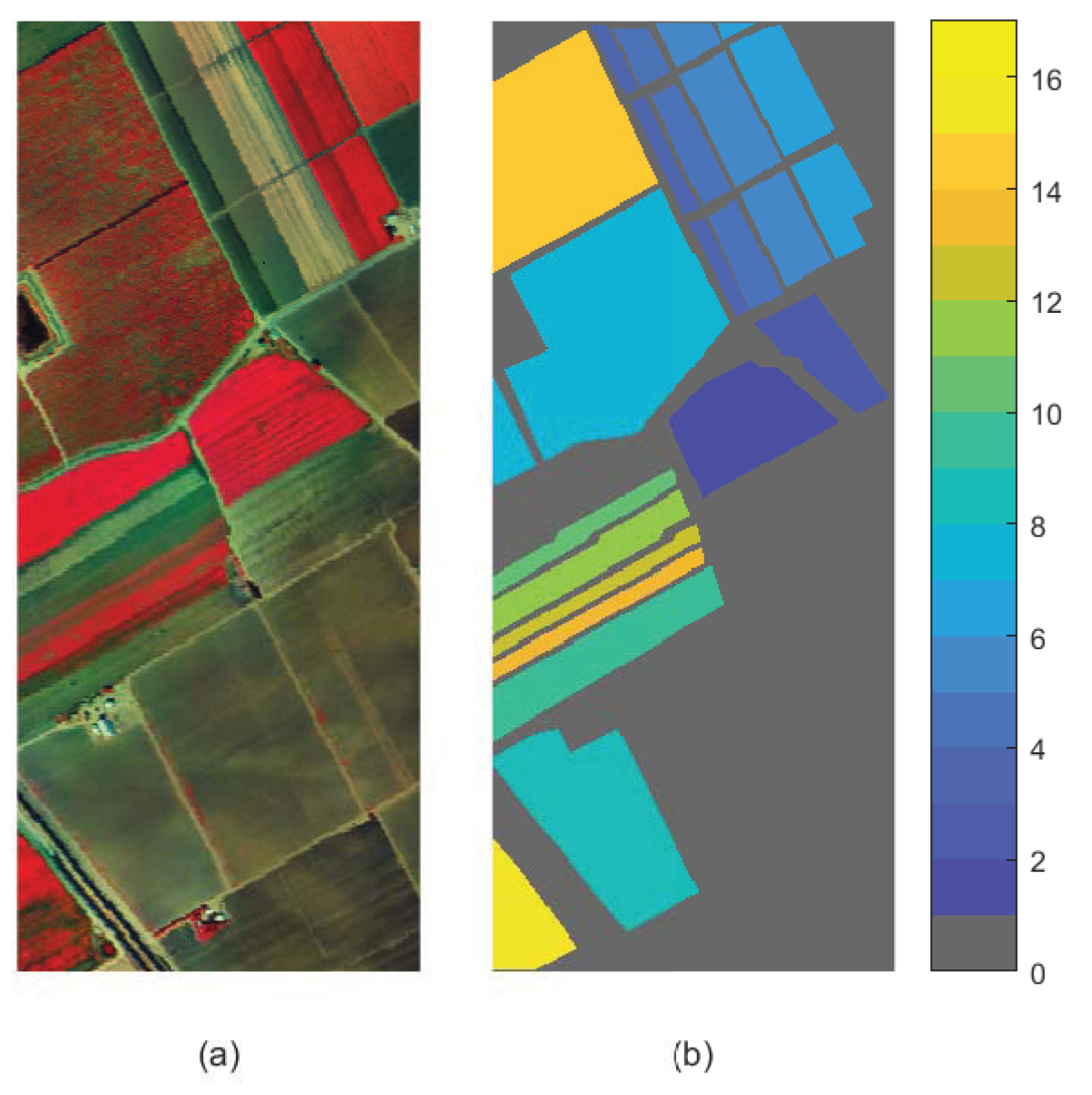
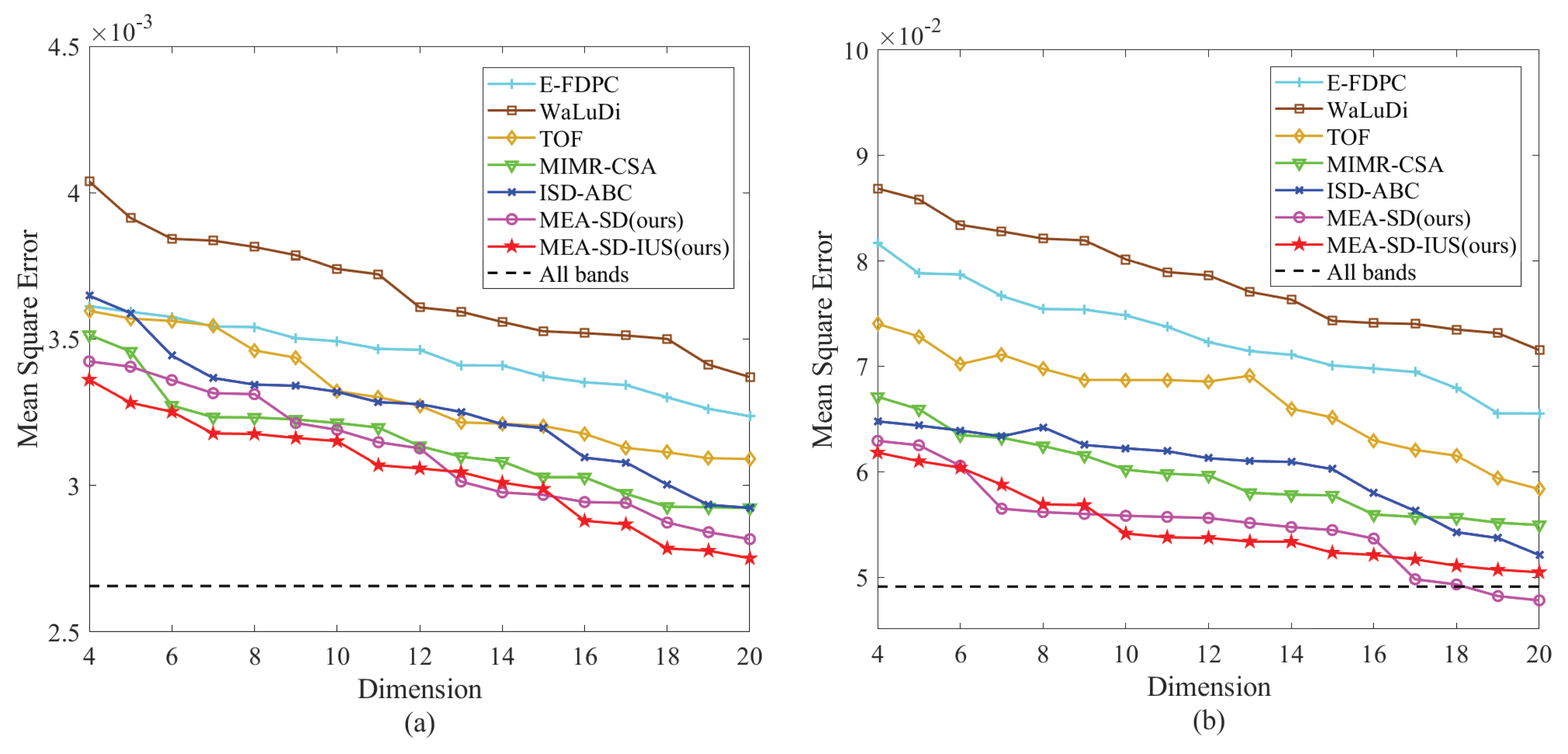
5. Experiments on Mulberry Fruit Dataset
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bitar, A.W.; Cheong, L.F.; Ovarlez, J.P. Sparse and low-rank matrix decomposition for automatic target detection in hyperspectral imagery. IEEE Trans. Geosci. Remote Sens. 2019, 57, 5239–5251. [Google Scholar] [CrossRef]
- Cao, X.; Lu, H.; Ren, M.; Jiao, L. Non-overlapping classification of hyperspectral imagery with superpixel segmentation. Appl. Soft Comput. 2019, 83, 105630. [Google Scholar] [CrossRef]
- Zhao, J.; Tian, S.; Geiß, C.; Wang, L.; Zhong, Y.; Taubenböck, H. Spectral-spatial classification integrating band selection for hyperspectral imagery with severe noise bands. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 1597–1609. [Google Scholar] [CrossRef]
- Feng, D.; Xu, W.; He, Z.; Zhao, W.; Yang, M. Advances in plant nutrition diagnosis based on remote sensing and computer application. Neural Comput. Appl. 2020, 32, 16833–16842. [Google Scholar] [CrossRef]
- Huang, L.; Zhou, Y.; Meng, L.; Wu, D.; He, Y. Comparison of different CCD detectors and chemometrics for predicting total anthocyanin content and antioxidant activity of mulberry fruit using visible and near infrared hyperspectral imaging technique. Food Chem. 2017, 224, 1–10. [Google Scholar] [CrossRef]
- Khan, M.H.; Saleem, Z.; Ahmad, M.; Sohaib, A.; Ayaz, H.; Mazzara, M.; Raza, R.A. Hyperspectral imaging-based unsupervised adulterated red chili content transformation for classification: Identification of red chili adulterants. Neural Comput. Appl. 2021, 33, 14507–14521. [Google Scholar] [CrossRef]
- Lv, M.; Li, W.; Chen, T.; Zhou, J.; Tao, R. Discriminant tensor-based manifold embedding for medical hyperspectral imagery. IEEE J. Biomed. Health Inform. 2021, 25, 3517–3528. [Google Scholar] [CrossRef]
- Nageswaran, K.; Nagarajan, K.; Bandiya, R. A novel algorithm for hyperspectral image denoising in medical application. J. Med. Syst. 2019, 43, 1–12. [Google Scholar] [CrossRef]
- Wang, Q.; Sun, L.; Wang, Y.; Zhou, M.; Hu, M.; Chen, J.; Wen, Y.; Li, Q. Identification of melanoma from hyperspectral pathology image using 3D convolutional networks. IEEE Trans. Med. Imaging 2020, 40, 218–227. [Google Scholar] [CrossRef]
- Abend, K.; Harley, T.; Chandrasekaran, B.; Hughes, G. Comments on the mean accuracy of statistical pattern recognizers. IEEE Trans. Inf. Theory 1969, 15, 420–423. [Google Scholar] [CrossRef]
- Sun, W.; Du, Q. Hyperspectral band selection: A review. IEEE Geosci. Remote Sens. Mag. 2019, 7, 118–139. [Google Scholar] [CrossRef]
- Kang, X.; Li, S.; Benediktsson, J.A. Feature extraction of hyperspectral images with image fusion and recursive filtering. IEEE Trans. Geosci. Remote Sens. 2013, 52, 3742–3752. [Google Scholar] [CrossRef]
- Zhong, C.; Zhang, J.; Zhang, Y. Multiscale feature extraction based on convolutional sparse decomposition for hyperspectral image classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 4960–4972. [Google Scholar] [CrossRef]
- Liu, B.; Yu, X.; Zhang, P.; Yu, A.; Fu, Q.; Wei, X. Supervised deep feature extraction for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2017, 56, 1909–1921. [Google Scholar] [CrossRef]
- Zhang, M.; Gong, M.; Chan, Y. Hyperspectral band selection based on multi-objective optimization with high information and low redundancy. Appl. Soft Comput. 2018, 70, 604–621. [Google Scholar] [CrossRef]
- Zhang, Y.; He, C.; Song, X.; Sun, X. A multi-strategy integrated multi-objective artificial bee colony for unsupervised band selection of hyperspectral images. Swarm Evol. Comput. 2021, 60, 100806. [Google Scholar]
- Wang, M.; Liu, W.; Chen, M.; Huang, X.; Han, W. A band selection approach based on a modified gray wolf optimizer and weight updating of bands for hyperspectral image. Appl. Soft Comput. 2021, 112, 107805. [Google Scholar] [CrossRef]
- Das, A.; Patra, S. A rough-GA based optimal feature selection in attribute profiles for classification of hyperspectral imagery. Soft Comput. 2020, 24, 12569–12585. [Google Scholar] [CrossRef]
- Shukla, U.P.; Nanda, S.J. A binary social spider optimization algorithm for unsupervised band selection in compressed hyperspectral images. Expert Syst. Appl. 2018, 97, 336–356. [Google Scholar] [CrossRef]
- Cao, X.; Wei, C.; Ge, Y.; Feng, J.; Zhao, J.; Jiao, L. Semi-supervised hyperspectral band selection based on dynamic classifier selection. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 1289–1298. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, K.; Dong, Y.; Wu, K.; Hu, X. Semisupervised classification based on SLIC segmentation for hyperspectral image. IEEE Geosci. Remote Sens. Lett. 2019, 17, 1440–1444. [Google Scholar] [CrossRef]
- Sellami, A.; Farah, M.; Farah, I.R.; Solaiman, B. Hyperspectral imagery classification based on semi-supervised 3-D deep neural network and adaptive band selection. Expert Syst. Appl. 2019, 129, 246–259. [Google Scholar] [CrossRef]
- Barman, B.; Patra, S. Variable precision rough set based unsupervised band selection technique for hyperspectral image classification. Knowl.-Based Syst. 2020, 193, 105414. [Google Scholar] [CrossRef]
- Zhao, H.; Bruzzone, L.; Guan, R.; Zhou, F.; Yang, C. Spectral-Spatial Genetic Algorithm-Based Unsupervised Band Selection for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2021, 59, 9616–9632. [Google Scholar] [CrossRef]
- Tschannerl, J.; Ren, J.; Yuen, P.; Sun, G.; Zhao, H.; Yang, Z.; Wang, Z.; Marshall, S. MIMR-DGSA: Unsupervised hyperspectral band selection based on information theory and a modified discrete gravitational search algorithm. Inf. Fusion 2019, 51, 189–200. [Google Scholar] [CrossRef]
- Wang, J.; Wang, H.; Ma, Z.; Wang, L.; Wang, Q.; Li, X. Unsupervised Hyperspectral Band Selection Based on Hypergraph Spectral Clustering. IEEE Geosci. Remote Sens. Lett. 2021, 19, 5509905. [Google Scholar] [CrossRef]
- Yuan, Y.; Zheng, X.; Lu, X. Discovering diverse subset for unsupervised hyperspectral band selection. IEEE Trans. Image Process. 2016, 26, 51–64. [Google Scholar] [CrossRef]
- Wang, Q.; Li, Q.; Li, X. Hyperspectral band selection via adaptive subspace partition strategy. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 4940–4950. [Google Scholar] [CrossRef]
- Hu, X.M.; Zhang, S.R.; Li, M.; Deng, J.D. Multimodal particle swarm optimization for feature selection. Appl. Soft Comput. 2021, 113, 107887. [Google Scholar] [CrossRef]
- Geng, X.; Sun, K.; Ji, L.; Zhao, Y. A fast volume-gradient-based band selection method for hyperspectral image. IEEE Trans. Geosci. Remote Sens. 2014, 52, 7111–7119. [Google Scholar] [CrossRef]
- Ji, L.; Zhu, L.; Wang, L.; Xi, Y.; Yu, K.; Geng, X. FastVGBS: A fast version of the volume-gradient-based band selection method for hyperspectral imagery. IEEE Geosci. Remote Sens. Lett. 2020, 18, 514–517. [Google Scholar] [CrossRef]
- Jia, S.; Tang, G.; Zhu, J.; Li, Q. A novel ranking-based clustering approach for hyperspectral band selection. IEEE Trans. Geosci. Remote Sens. 2015, 54, 88–102. [Google Scholar] [CrossRef]
- Su, P.; Tarkoma, S.; Pellikka, P.K. Band ranking via extended coefficient of variation for hyperspectral band selection. Remote Sens. 2020, 12, 3319. [Google Scholar] [CrossRef]
- MartÍnez-UsÓMartinez-Uso, A.; Pla, F.; Sotoca, J.M.; García-Sevilla, P. Clustering-based hyperspectral band selection using information measures. IEEE Trans. Geosci. Remote Sens. 2007, 45, 4158–4171. [Google Scholar] [CrossRef]
- Wang, Q.; Li, Q.; Li, X. A fast neighborhood grouping method for hyperspectral band selection. IEEE Trans. Geosci. Remote Sens. 2020, 59, 5028–5039. [Google Scholar] [CrossRef]
- Wang, Q.; Zhang, F.; Li, X. Optimal clustering framework for hyperspectral band selection. IEEE Trans. Geosci. Remote Sens. 2018, 56, 5910–5922. [Google Scholar] [CrossRef]
- Feng, J.; Jiao, L.; Liu, F.; Sun, T.; Zhang, X. Unsupervised feature selection based on maximum information and minimum redundancy for hyperspectral images. Pattern Recognit. 2016, 51, 295–309. [Google Scholar] [CrossRef]
- Xie, F.; Li, F.; Lei, C.; Yang, J.; Zhang, Y. Unsupervised band selection based on artificial bee colony algorithm for hyperspectral image classification. Appl. Soft Comput. 2019, 75, 428–440. [Google Scholar] [CrossRef]
- Wei, W.; Zhang, L.; Tian, C.; Plaza, A.; Zhang, Y. Structured sparse coding-based hyperspectral imagery denoising with intracluster filtering. IEEE Trans. Geosci. Remote Sens. 2017, 55, 6860–6876. [Google Scholar] [CrossRef]
- Stella, X.Y.; Shi, J. Multiclass spectral clustering. In Proceedings of the Ninth IEEE International Conference on Computer Vision, Nice, France, 13–16 October 2003; Volume 2, p. 313. [Google Scholar]
- Shi, J.; Malik, J. Normalized cuts and image segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 888–905. [Google Scholar]
- Zelnik-Manor, L.; Perona, P. Self-tuning spectral clustering. In Advances in Neural Information Processing Systems 17; The MIT Press: Cambridge, MA, USA, 2004. [Google Scholar]
- Liang, J.J.; Qu, B.Y.; Mao, X.; Niu, B.; Wang, D. Differential evolution based on fitness Euclidean-distance ratio for multimodal optimization. Neurocomputing 2014, 137, 252–260. [Google Scholar] [CrossRef]

| Dataset | Size | Samples | Classes | Bands |
|---|---|---|---|---|
| Indian Pines | 145 × 145 | 10,249 | 16 | 200 |
| Pavia University | 610 × 340 | 42,776 | 9 | 103 |
| Salinas | 512 × 217 | 54,129 | 16 | 204 |
| Dataset | k | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 |
|---|---|---|---|---|---|---|---|---|---|---|
| Indian Pines | 1 | 69.36 | 77.99 | 79.18 | 79.51 | 80.94 | 79.97 | 81.22 | 80.70 | 81.36 |
| 3 | 70.72 | 79.23 | 81.17 | 81.60 | 81.43 | 82.09 | 83.31 | 82.72 | 82.66 | |
| 5 | 71.37 | 79.89 | 81.51 | 81.91 | 83.20 | 83.01 | 83.56 | 82.98 | 82.79 | |
| Pavia University | 1 | 85.91 | 86.78 | 87.31 | 91.55 | 91.41 | 91.78 | 91.98 | 92.69 | 92.08 |
| 3 | 84.79 | 87.38 | 87.85 | 92.09 | 92.59 | 92.65 | 92.47 | 93.28 | 93.32 | |
| 5 | 84.92 | 87.27 | 88.70 | 92.54 | 92.85 | 93.18 | 92.92 | 93.33 | 93.56 | |
| Salinas | 1 | 88.66 | 91.54 | 91.91 | 92.51 | 93.30 | 92.92 | 93.15 | 92.74 | 92.92 |
| 3 | 89.06 | 91.84 | 92.67 | 92.80 | 93.51 | 93.37 | 93.28 | 93.09 | 92.81 | |
| 5 | 89.30 | 91.59 | 92.91 | 92.90 | 93.30 | 93.62 | 93.59 | 93.51 | 93.47 |
| Dataset | Selected Bands |
|---|---|
| 18, 29, 42, 117, 131, 160 | |
| Indian Pines | 18, 29, 42, 75, 117, 131 |
| 29, 42, 54, 89, 117, 160 | |
| 21, 36, 47, 63, 78, 91 | |
| Pavia University | 11, 21, 40, 63, 78, 91 |
| 21, 36, 49, 63, 77, 91 | |
| 15, 34, 45, 57, 120, 164 | |
| Salinas | 34, 45, 57, 79, 120, 164 |
| 15, 34, 45, 93, 120, 164 |
| Dataset | Selected Bands |
|---|---|
| 5, 8, 17, 21, 38, 42, 60, 69, 71, 117, 131, 134, 160, 166, 174, 191 | |
| Indian Pines | 17, 29, 42, 69, 71, 75, 97, 99, 117, 130, 136, 159, 160, 176, 183, 191 |
| 18, 21, 28, 29, 42, 54, 70, 89, 117, 130, 132, 154, 160, 166, 182, 190 | |
| 2, 4, 13, 18, 21, 24, 39, 45, 48, 57, 63, 64, 74, 83, 91, 96 | |
| Pavia University | 2, 15, 18, 21, 23, 34, 40, 49, 55, 59, 63, 67, 71, 78, 83, 91 |
| 4, 13, 21, 31, 36, 38, 41, 47, 57, 58, 63, 65, 76, 87, 91, 103 | |
| 8, 15, 21, 45, 52, 72, 88, 93, 94, 120, 125, 135, 158, 164, 187, 191 | |
| Salinas | 24, 28, 34, 45, 52, 64, 72, 78, 125, 135, 138, 158, 164, 172, 179, 187 |
| 1, 9, 15, 27, 34, 45, 60, 71, 72, 117, 120, 125, 131, 158, 164, 180 |
| Classes | E-FDPC | WaLuDi | TOF | MIMR-CSA | ISD-ABC | MEA-SD (ours) | MEA-SD-IUS (ours) |
|---|---|---|---|---|---|---|---|
| 1. Alfalfa | 78.05 ± 7.54 | 14.63 ± 17.10 | 65.85 ± 3.93 | 84.37 ± 9.5 | 56.10 ± 2.09 | 85.37 ± 3.55 | 80.49 ± 2.72 |
| 2. Corn-notill | 61.13 ± 4.26 | 63.35 ± 2.05 | 66.21 ± 1.16 | 65.86 ± 3.0 | 62.88 ± 1.28 | 74.01 ± 2.01 | 73.46 ± 1.76 |
| 3. Corn-mintill | 64.79 ± 3.87 | 57.56 ± 3.83 | 64.66 ± 0.69 | 62.45 ± 2.8 | 63.59 ± 1.24 | 63.99 ± 0.90 | 68.61 ± 0.87 |
| 4. Corn | 48.83 ± 6.45 | 23.94 ± 3.25 | 63.38 ± 0.80 | 73.24 ± 4.1 | 72.77 ± 2.38 | 76.06 ± 1.82 | 77.00 ± 1.13 |
| 5. Grass-pasture | 87.59 ± 1.71 | 83.91 ± 1.63 | 88.51 ± 0.16 | 86.51 ± 1.5 | 90.80 ± 0.61 | 92.13 ± 0.24 | 90.80 ± 0.17 |
| 6. Grass-trees | 87.20 ± 0.66 | 88.45 ± 1.94 | 87.85 ± 0.17 | 89.30 ± 0.8 | 88.58 ± 0.52 | 91.02 ± 0.48 | 92.54 ± 0.35 |
| 7. Grass-pasture-mowed | 76.14 ± 1.81 | 48.90 ± 1.81 | 72.49 ± 2.05 | 84.60 ± 2.7 | 76.05 ± 3.91 | 88.41 ± 1.33 | 88.99 ± 0.76 |
| 8. Hay-windrowed | 91.86 ± 0.72 | 97.67 ± 0.92 | 91.40 ± 0.08 | 94.98 ± 0.7 | 92.79 ± 0.49 | 95.12 ± 0.74 | 95.58 ± 0.58 |
| 9. Oats | 51.14 ± 6.23 | 38.89 ± 15.09 | 48.60 ± 3.26 | 62.67 ± 8.3 | 38.89 ± 4.22 | 65.35 ± 3.59 | 74.40 ± 2.23 |
| 10. Soybean-notill | 74.29 ± 2.40 | 73.24 ± 3.17 | 72.11 ± 1.46 | 76.91 ± 3.2 | 74.40 ± 1.18 | 78.39 ± 0.90 | 79.43 ± 0.53 |
| 11. Soybean-mintill | 75.02 ± 0.74 | 72.19 ± 2.08 | 75.18 ± 0.42 | 78.05 ± 1.2 | 81.63 ± 0.57 | 82.26 ± 0.81 | 82.81 ± 0.71 |
| 12. Soybean-clean | 56.93 ± 2.59 | 42.23 ± 4.28 | 57.68 ± 1.71 | 74.29 ± 2.9 | 79.21 ± 1.80 | 76.03 ± 1.56 | 73.78 ± 1.44 |
| 13. Wheat | 96.22 ± 0.70 | 88.11 ± 2.76 | 95.68 ± 0.08 | 92.97 ± 0.2 | 97.84 ± 0.43 | 94.59 ± 0.18 | 94.62 ± 0.13 |
| 14. Woods | 85.61 ± 0.92 | 87.69 ± 1.10 | 90.68 ± 0.67 | 92.54 ± 0.9 | 93.94 ± 0.67 | 95.00 ± 0.81 | 96.05 ± 0.47 |
| 15. Buildings-grass-trees | 44.67 ± 2.28 | 23.34 ± 2.87 | 36.60 ± 1.79 | 36.31 ± 3.3 | 47.84 ± 2.88 | 44.96 ± 4.33 | 41.79 ± 3.67 |
| 16. Stone-steel-towers | 85.71 ± 3.45 | 75.24 ± 5.57 | 80.29 ± 0.41 | 81.48 ± 1.6 | 85.95 ± 1.13 | 89.29 ± 1.84 | 90.48 ± 1.21 |
| OA | 73.44 ± 0.48 | 69.96 ± 0.71 | 74.61 ± 0.35 | 77.21 ± 0.69 | 78.37 ± 0.67 | 80.94 ± 0.72 | 81.43 ± 0.54 |
| AA | 72.82 ± 2.90 | 61.21 ± 4.34 | 72.32 ± 1.18 | 77.03 ± 2.92 | 75.20 ± 1.59 | 80.75 ± 1.57 | 81.30 ± 1.17 |
| Classes | E-FDPC | WaLuDi | TOF | MIMR-CSA | ISD-ABC | MEA-SD (ours) | MEA-SD-IUS (ours) |
|---|---|---|---|---|---|---|---|
| 1. Asphalt | 89.53 ± 0.28 | 89.65 ± 0.30 | 91.15 ± 0.14 | 90.80 ± 0.20 | 89.18 ± 0.21 | 92.85 ± 0.23 | 92.85 ± 0.23 |
| 2. Meadows | 95.25 ± 0.15 | 95.85 ± 0.18 | 96.18 ± 0.20 | 95.31 ± 0.14 | 95.98 ± 0.22 | 96.11 ± 0.17 | 97.38 ± 0.12 |
| 3. Gravel | 66.79 ± 1.39 | 63.68 ± 2.36 | 65.43 ± 1.16 | 68.13 ± 1.68 | 69.75 ± 0.89 | 74.11 ± 0.73 | 74.38 ± 0.40 |
| 4. Trees | 89.51 ± 0.86 | 87.93 ± 1.51 | 87.35 ± 0.33 | 88.87 ± 1.85 | 89.65 ± 0.36 | 90.65 ± 0.80 | 91.88 ± 0.27 |
| 5. Painted metal sheets | 99.42 ± 0.25 | 99.39 ± 0.45 | 99.34 ± 0.30 | 99.47 ± 0.33 | 98.59 ± 0.17 | 99.60 ± 0.12 | 99.51 ± 0.13 |
| 6. Bare soil | 73.67 ± 1.48 | 65.36 ± 3.52 | 59.36 ± 1.74 | 67.69 ± 2.2 | 70.70 ± 0.39 | 80.20 ± 0.36 | 82.48 ± 0.35 |
| 7. Bitumen | 75.52 ± 0.18 | 74.02 ± 0.69 | 75.86 ± 0.11 | 80.86 ± 0.10 | 71.17 ± 0.25 | 81.95 ± 0.41 | 83.54 ± 0.30 |
| 8. Self-blocking bricks | 88.77 ± 0.29 | 88.53 ± 0.31 | 86.63 ± 0.21 | 87.96 ± 0.55 | 88.16 ± 0.11 | 89.20 ± 0.24 | 91.52 ± 0.21 |
| 9. Shadows | 96.53 ± 0.20 | 99.65 ± 0.18 | 97.65 ± 0.16 | 99.53 ± 0.23 | 98.77 ± 0.18 | 99.55 ± 0.25 | 99.65 ± 0.15 |
| OA | 89.01 ± 0.16 | 88.05 ± 0.34 | 87.60 ± 0.16 | 88.71 ± 0.30 | 88.91 ± 0.23 | 91.41 ± 0.17 | 92.59 ± 0.16 |
| AA | 85.40 ± 0.56 | 83.82 ± 1.06 | 83.13 ± 0.48 | 85.71 ± 0.81 | 84.98 ± 0.31 | 88.95 ± 0.37 | 89.97 ± 0.24 |
| Classes | E-FDPC | WaLuDi | TOF | MIMR-CSA | ISD-ABC | MEA-SD (ours) | MEA-SD-IUS (ours) |
|---|---|---|---|---|---|---|---|
| 1. Brocoli_greenweeds_1 | 98.67 ± 0.22 | 98.06 ± 0.14 | 97.43 ± 0.07 | 98.45 ± 0.24 | 98.56 ± 0.18 | 98.78 ± 0.15 | 99.45 ± 0.08 |
| 2. Brocoli_greenweeds_2 | 99.73 ± 0.19 | 99.46 ± 0.12 | 99.78 ± 0.06 | 99.69 ± 0.22 | 99.91 ± 0.07 | 99.97 ± 0.02 | 99.94 ± 0.02 |
| 3. Fallow | 98.71 ± 0.14 | 98.59 ± 0.17 | 97.98 ± 0.13 | 97.47 ± 0.08 | 98.99 ± 0.24 | 98.59 ± 0.25 | 99.33 ± 0.09 |
| 4. Fallow_rough_plow | 99.44 ± 0.34 | 99.68 ± 0.23 | 99.68 ± 0.19 | 99.60 ± 0.11 | 99.52 ± 0.35 | 99.52 ± 0.19 | 99.44 ± 0.16 |
| 5. Fallow_smooth | 98.76 ± 0.18 | 97.76 ± 0.25 | 98.76 ± 0.10 | 97.97 ± 0.32 | 98.55 ± 0.22 | 98.55 ± 0.18 | 98.71 ± 0.09 |
| 6. Stubble | 99.75 ± 0.12 | 99.64 ± 0.08 | 99.78 ± 0.05 | 99.80 ± 0.11 | 99.83 ± 0.13 | 99.83 ± 0.09 | 99.83 ± 0.12 |
| 7. Celery | 99.38 ± 0.27 | 99.47 ± 0.14 | 99.47 ± 0.09 | 99.25 ± 0.22 | 99.50 ± 0.13 | 99.63 ± 0.19 | 99.60 ± 0.16 |
| 8. Grapes_untrained | 84.86 ± 0.20 | 80.39 ± 0.18 | 84.52 ± 0.12 | 85.28 ± 0.14 | 86.18 ± 0.09 | 88.40 ± 0.15 | 88.91 ± 0.14 |
| 9. Soil_vinyard_develop | 98.68 ± 0.13 | 98.98 ± 0.06 | 98.92 ± 0.14 | 99.80 ± 0.07 | 99.73 ± 0.20 | 99.91 ± 0.05 | 99.93 ± 0.05 |
| 10. Corn_senesced_green | 95.59 ± 0.31 | 90.20 ± 0.11 | 93.12 ± 0.08 | 94.64 ± 0.21 | 95.02 ± 0.18 | 95.83 ± 0.12 | 96.00 ± 0.13 |
| 11. Lettuce_romaine_4wk | 95.42 ± 0.25 | 93.76 ± 0.23 | 95.53 ± 0.15 | 95.84 ± 0.39 | 92.92 ± 0.27 | 98.96 ± 0.14 | 99.06 ± 0.11 |
| 12. Lettuce_romaine_5wk | 99.83 ± 0.06 | 99.88 ± 0.09 | 99.83 ± 0.05 | 99.83 ± 0.07 | 98.87 ± 0.19 | 99.84 ± 0.05 | 99.88 ± 0.03 |
| 13. Lettuce_romaine_6wk | 98.67 ± 0.17 | 98.42 ± 0.13 | 98.91 ± 0.20 | 98.55 ± 0.21 | 99.03 ± 0.16 | 99.52 ± 0.25 | 99.39 ± 0.23 |
| 14. Lettuce_romaine_7wk | 94.70 ± 0.21 | 92.63 ± 0.26 | 95.95 ± 0.12 | 94.81 ± 0.09 | 93.67 ± 0.23 | 97.40 ± 0.27 | 96.68 ± 0.20 |
| 15. Vinyard_untrained | 67.59 ± 0.19 | 65.37 ± 0.15 | 67.97 ± 0.08 | 66.54 ± 0.14 | 69.59 ± 0.17 | 72.53 ± 0.20 | 72.86 ± 0.16 |
| 16. Vinyard_vertical | 97.79 ± 0.26 | 96.25 ± 0.18 | 98.59 ± 0.10 | 98.71 ± 0.21 | 99.08 ± 0.16 | 99.04 ± 0.22 | 99.14 ± 0.19 |
| OA | 91.53 ± 0.16 | 89.79 ± 0.21 | 91.38 ± 0.08 | 91.49 ± 0.23 | 92.13 ± 0.15 | 93.30 ± 0.19 | 93.51 ± 0.13 |
| AA | 95.07 ± 0.20 | 93.78 ± 0.16 | 94.99 ± 0.11 | 94.96 ± 0.18 | 95.21 ± 0.19 | 96.38 ± 0.16 | 96.49 ± 0.12 |
| Data Set | E-FDPC | WaLuDi | TOF | MIMR-CSA | ISD-ABC | MEA-SD (ours) |
|---|---|---|---|---|---|---|
| Indian Pines | 0.202 | 2.238 | 0.694 | 4.084 | 3.253 | 3.392 |
| Pavia University | 0.217 | 1.449 | 0.712 | 2.750 | 1.898 | 1.791 |
| Salinas | 0.635 | 2.730 | 2.127 | 4.553 | 5.823 | 3.542 |
| The Number of Bands | Selected Bands |
|---|---|
| 15, 30, 86, 110, 114, 128, 164, 173, 235, 243, 255, 269 | |
| 12 | 15, 30, 40, 77, 133, 164, 170, 223, 235, 242, 249, 272 |
| 13, 15, 30, 53, 63, 68, 86, 128, 147, 164, 241, 273 | |
| 13, 15, 30, 77, 83, 89, 108, 127, 128, 135, 142, 164, 194, 203, 235, 239, 255, 266 | |
| 18 | 2, 30, 72, 110, 127, 128, 135, 144, 148, 170, 194, 198, 235, 241, 251, 258, 267, 279 |
| 2, 15, 30, 63, 76, 93, 110, 128, 142, 146, 164, 172, 229, 235, 245, 250, 270, 277 |
| Anthocyanin | Flavonoid | |||
|---|---|---|---|---|
| MSE () | MSE () | |||
| E-FDPC | 3.46 ± 0.18 | 0.85 | 7.23 ± 0.82 | 0.86 |
| WaLuDi | 3.61 ± 0.41 | 0.85 | 7.86 ± 1.10 | 0.84 |
| TOF | 3.27 ± 0.17 | 0.86 | 6.86 ± 0.36 | 0.86 |
| MIMR-CSA | 3.14 ± 0.09 | 0.87 | 5.96 ± 0.68 | 0.88 |
| ISD-ABC | 3.28 ± 0.13 | 0.86 | 6.13 ± 0.79 | 0.88 |
| MEA-SD | 3.13 ± 0.08 | 0.87 | 5.56 ± 0.57 | 0.89 |
| MEA-SD-IUS | 3.06 ± 0.05 | 0.87 | 5.37 ± 0.44 | 0.89 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, Y.; Hu, H.; Xu, H.; Mao, X. Unsupervised Hyperspectral Band Selection via Multimodal Evolutionary Algorithm and Subspace Decomposition. Sensors 2023, 23, 2129. https://doi.org/10.3390/s23042129
Wei Y, Hu H, Xu H, Mao X. Unsupervised Hyperspectral Band Selection via Multimodal Evolutionary Algorithm and Subspace Decomposition. Sensors. 2023; 23(4):2129. https://doi.org/10.3390/s23042129
Chicago/Turabian StyleWei, Yunpeng, Huiqiang Hu, Huaxing Xu, and Xiaobo Mao. 2023. "Unsupervised Hyperspectral Band Selection via Multimodal Evolutionary Algorithm and Subspace Decomposition" Sensors 23, no. 4: 2129. https://doi.org/10.3390/s23042129
APA StyleWei, Y., Hu, H., Xu, H., & Mao, X. (2023). Unsupervised Hyperspectral Band Selection via Multimodal Evolutionary Algorithm and Subspace Decomposition. Sensors, 23(4), 2129. https://doi.org/10.3390/s23042129





