Achieving Reliability in Cloud Computing by a Novel Hybrid Approach
Abstract
:1. Introduction
2. Literature Review
3. Problem Statement
Mathematical Equation for Reliability
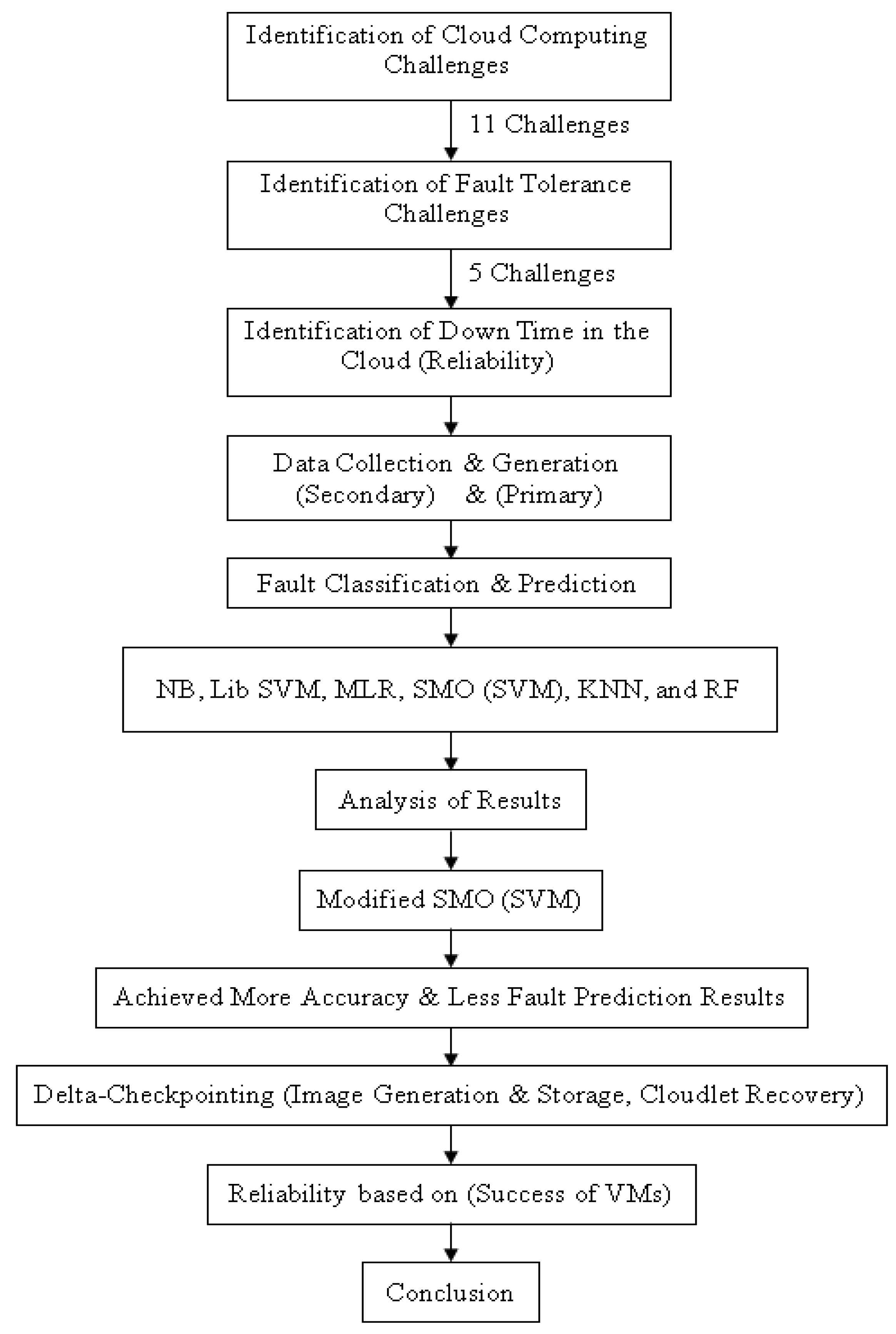
4. Research Methodology
4.1. Research Design
4.1.1. Data Collected and Generated
4.1.2. Machine Learning Algorithms
4.1.3. Fault-Tolerance Approach
4.1.4. Reliability
4.2. Implementation View of Research Framework
4.3. Acquired Secondary Data
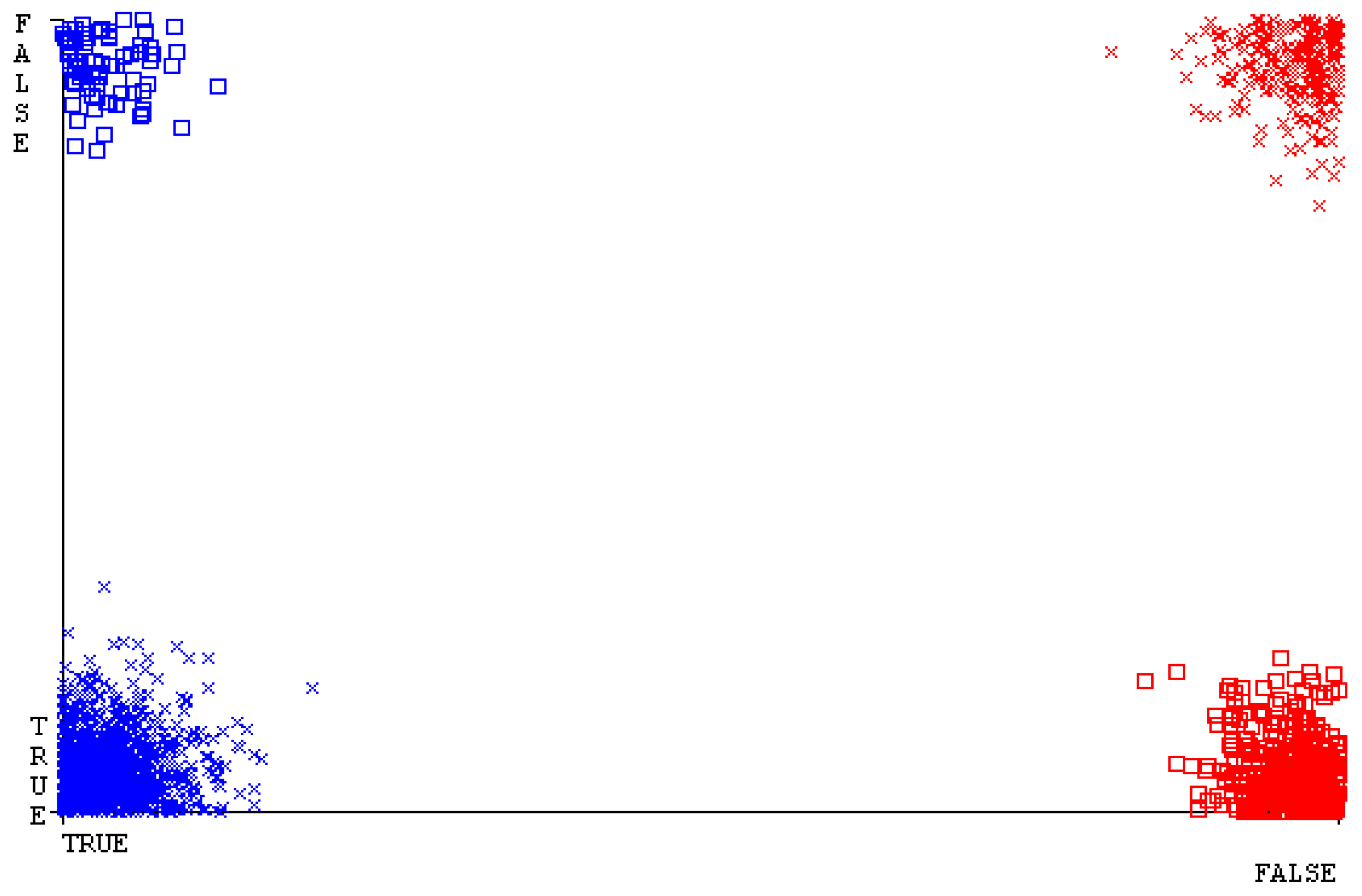
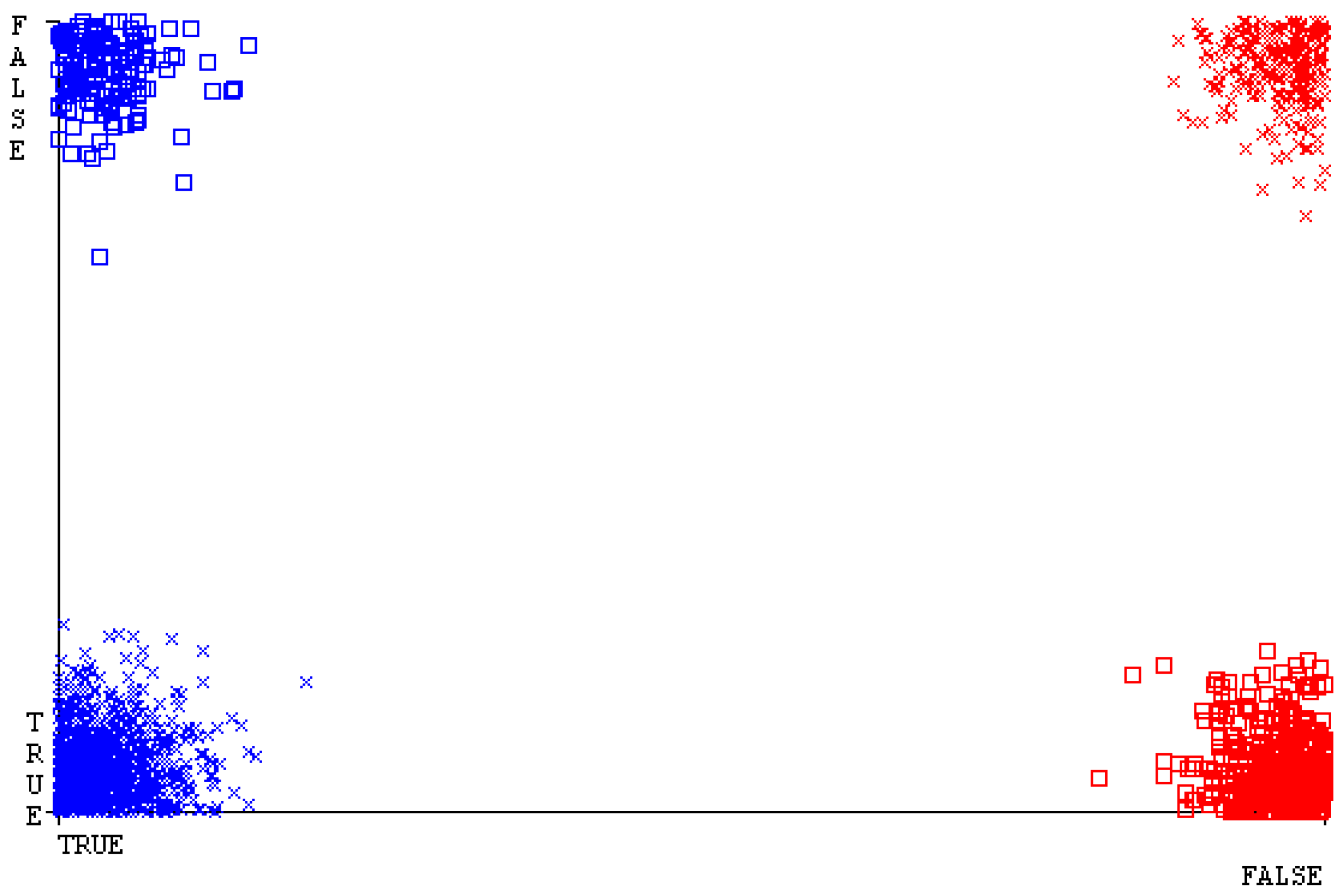
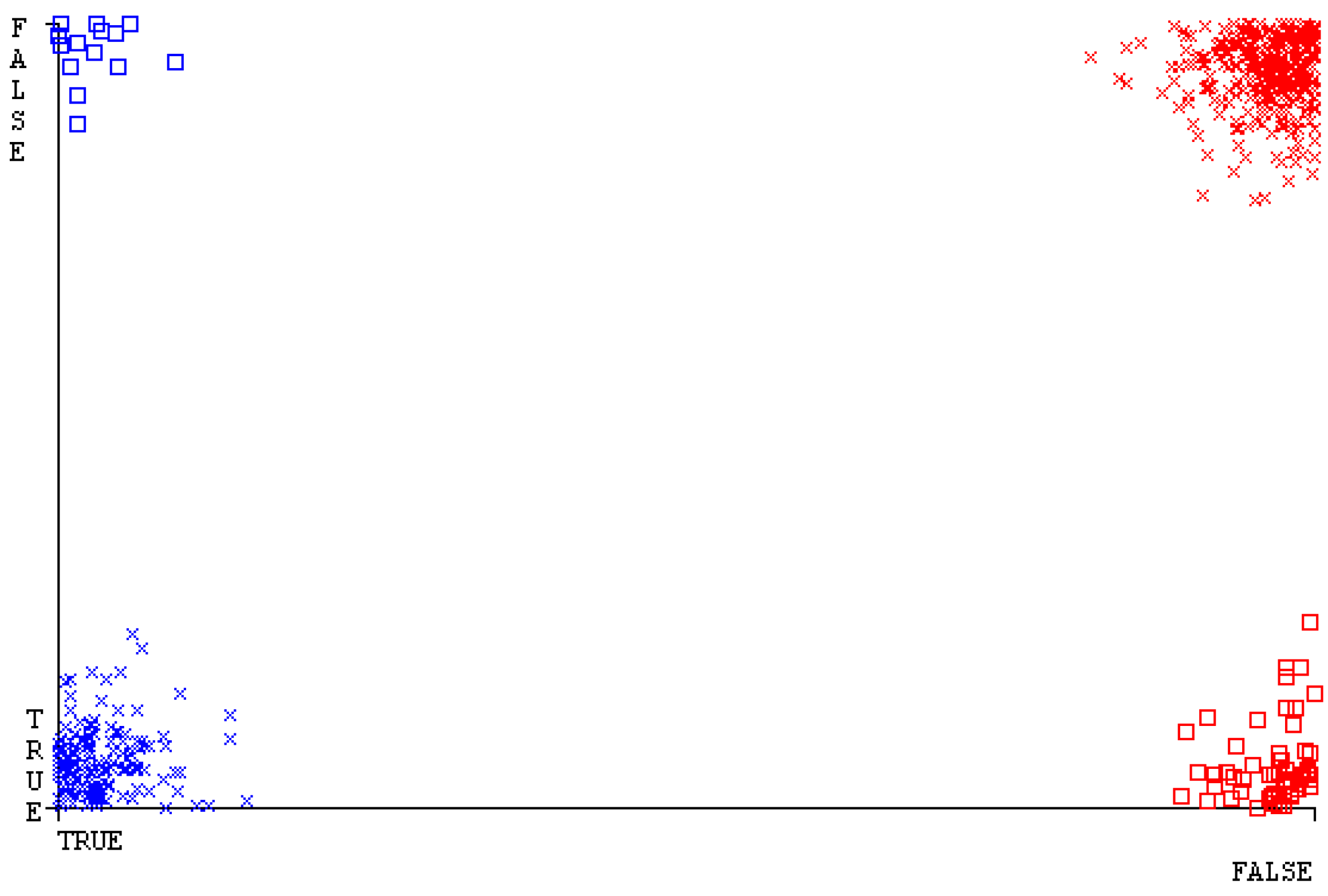
4.3.1. Exploratory Data Analysis on Secondary Dataset
4.3.2. Data Pre-Processing on Secondary Dataset
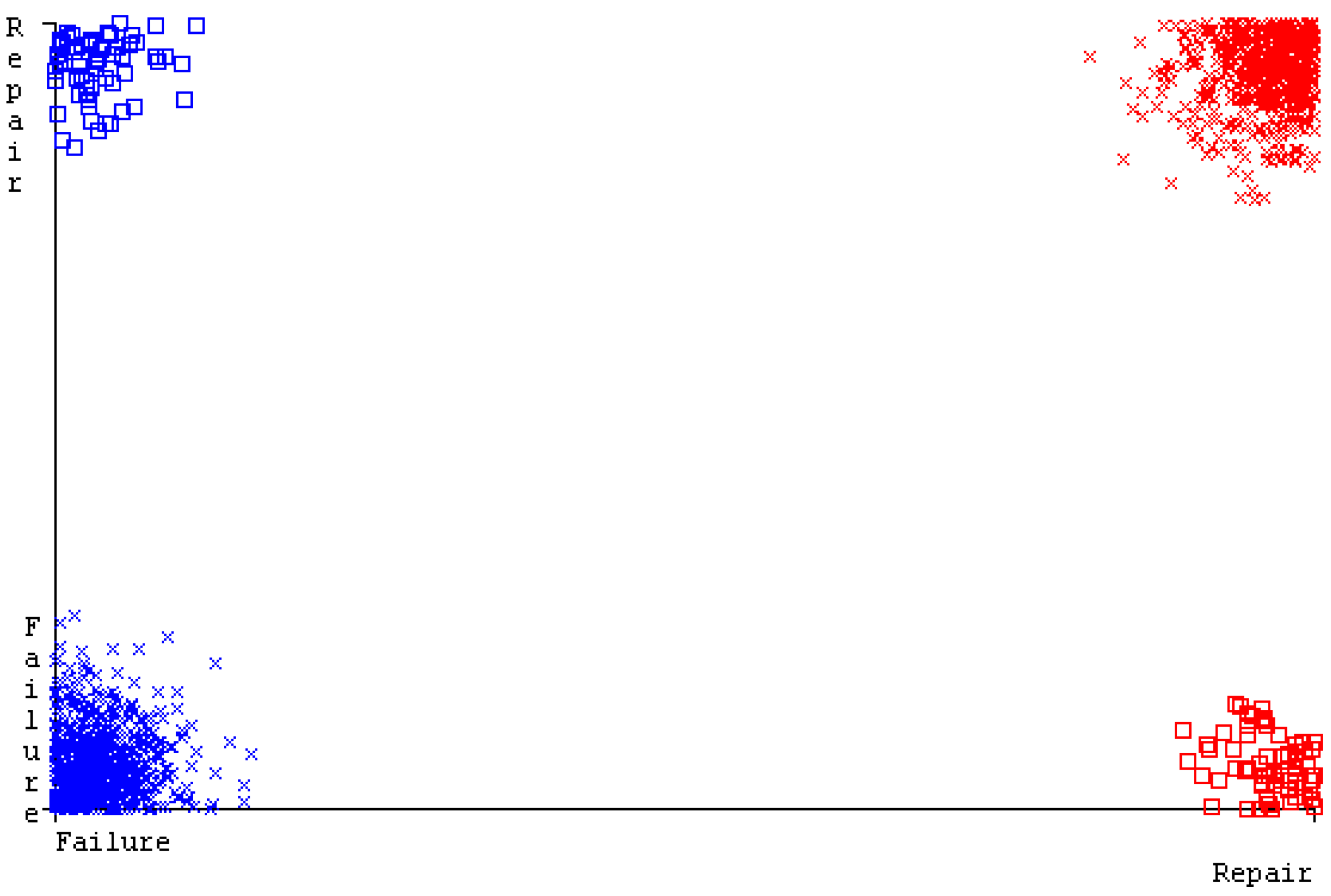
4.4. Generated Primary Data
4.5. Data Analysis Techniques
4.5.1. Naïve Bayes
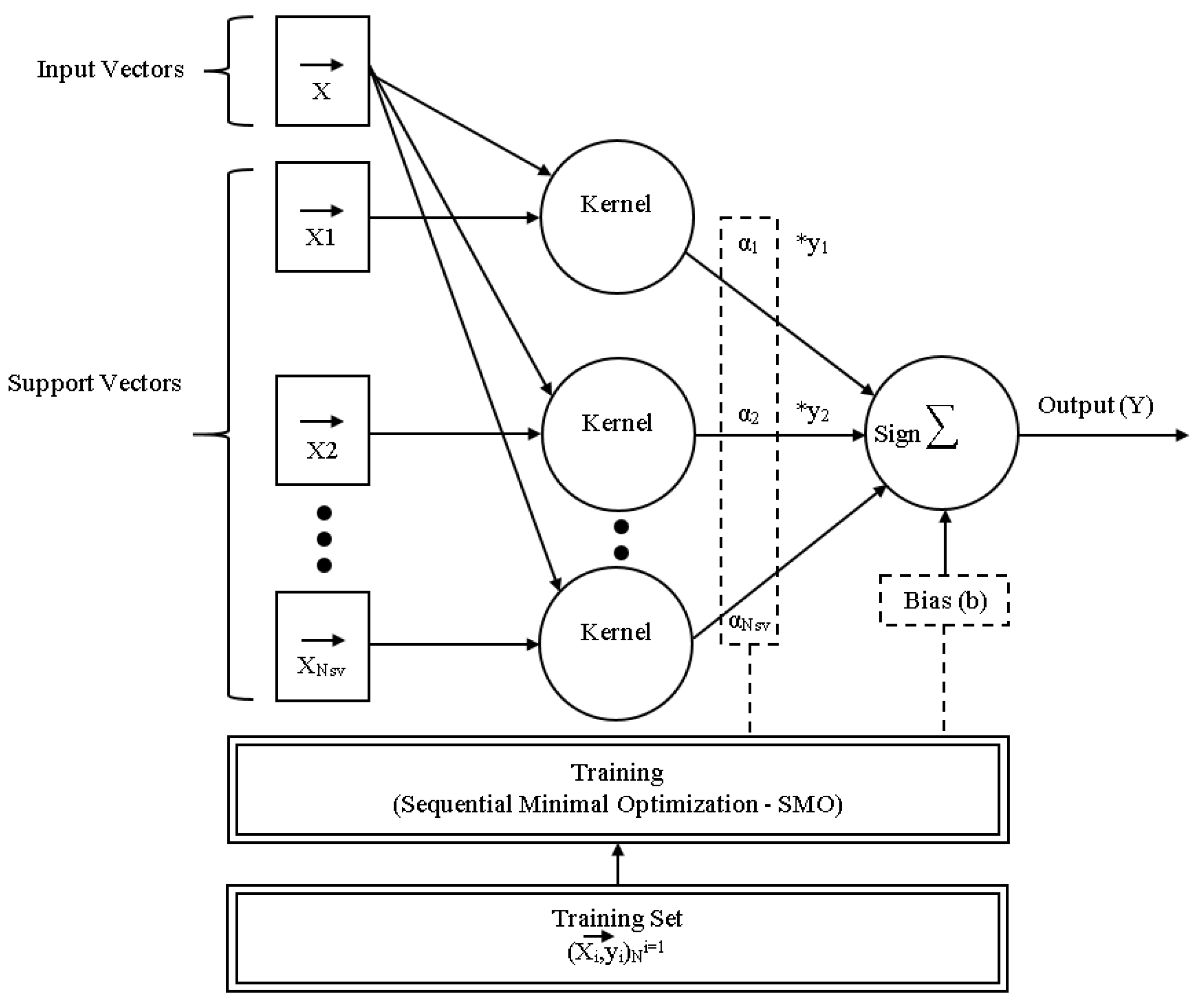
4.5.2. Library Support Vector Machine
4.5.3. Multinomial Logistic Regression
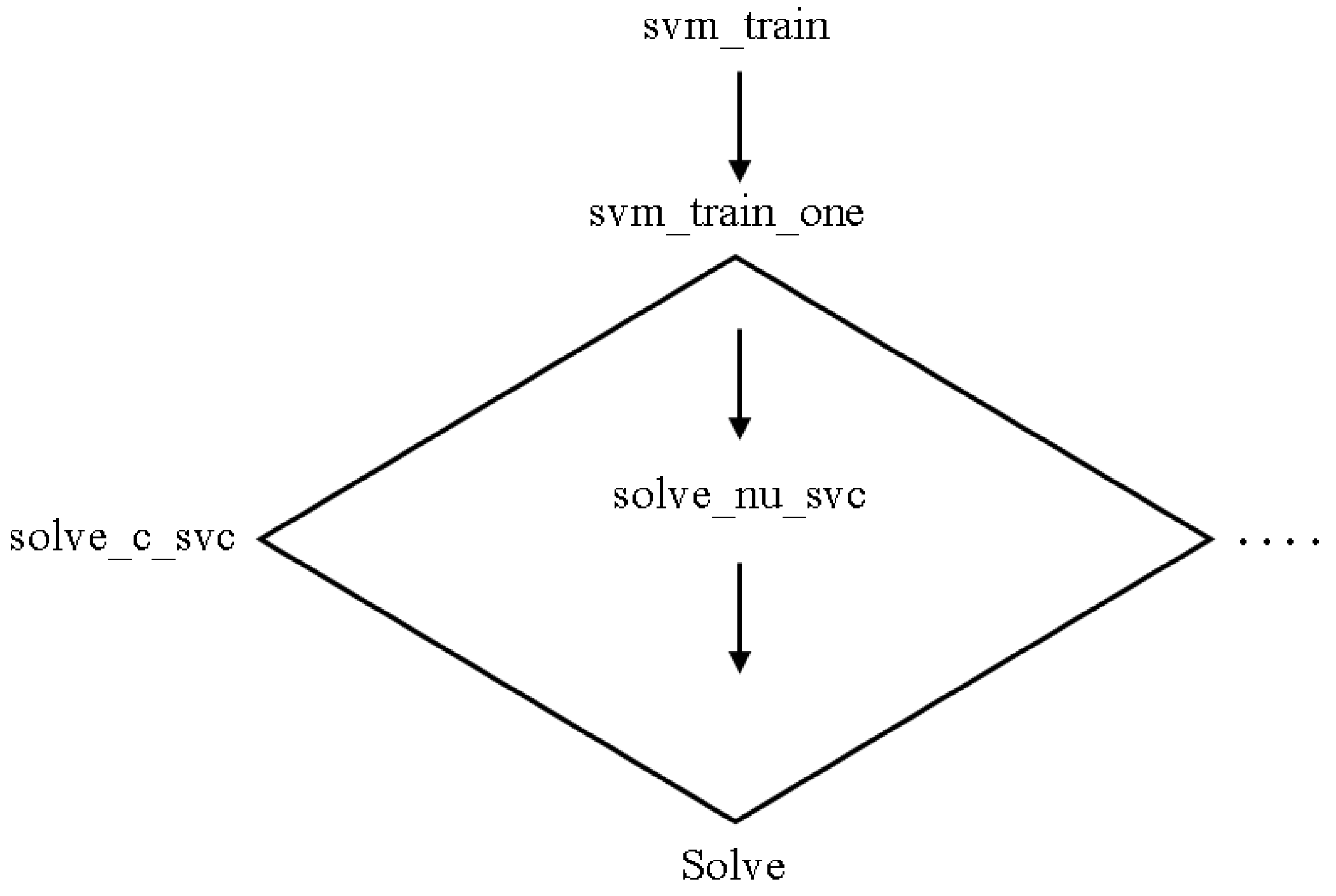
4.5.4. Sequential Minimal Optimization
4.5.5. K-Nearest Neighbor
- Determine the parameter K defining the number of nearest neighbors [35];
- Calculate the distance between the query and all training examples [35];
- Using the kth minimum, sort the distance and find the closest neighbors [35];
- Gather the closest neighbors category [35];
- Use the majority in the category of nearest neighbors as the instance’s prediction value [35].
- Fine and Medium KNN: The fine and medium KNN algorithms use the Euclidean distance function to calculate the nearest neighbors, as shown in Equations (10) and (11).
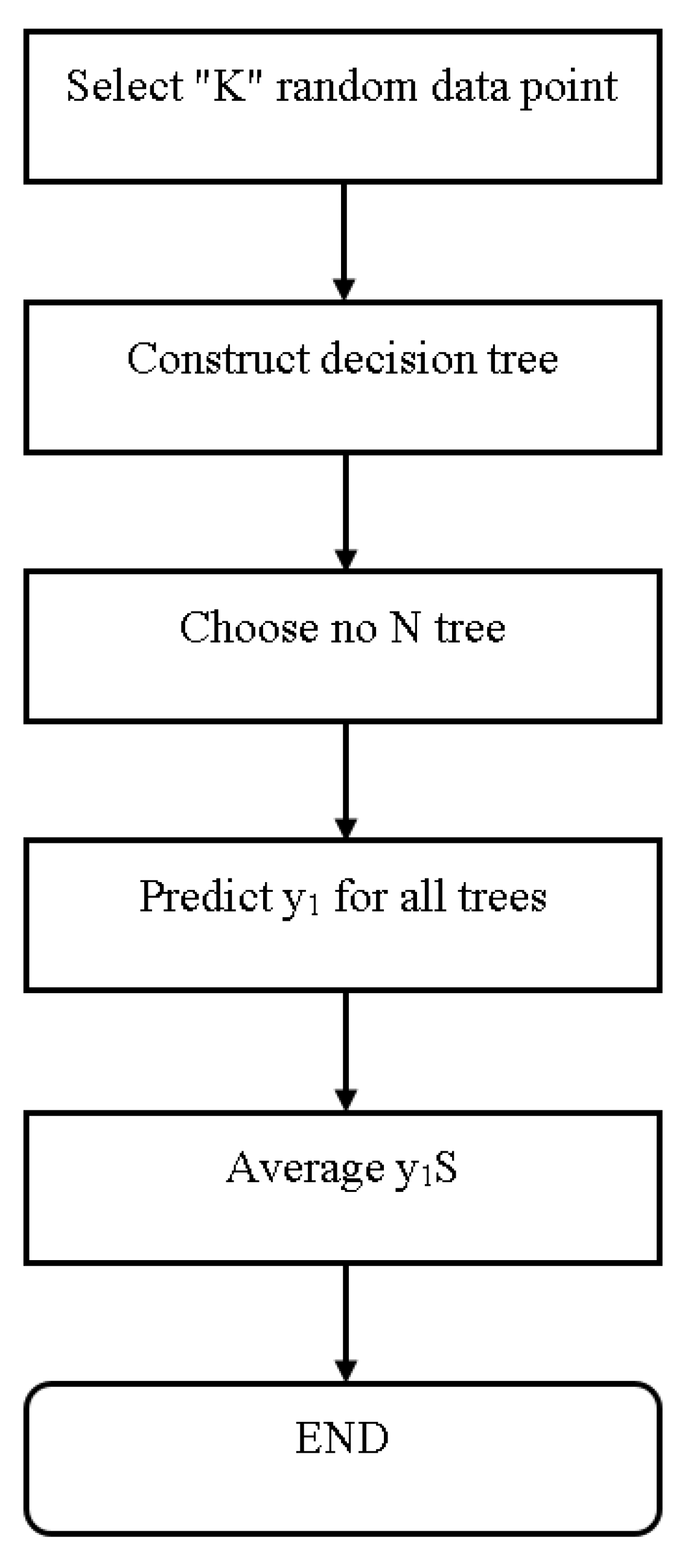
4.5.6. Random Forest
4.6. Parameters Configuration of ML Classifiers
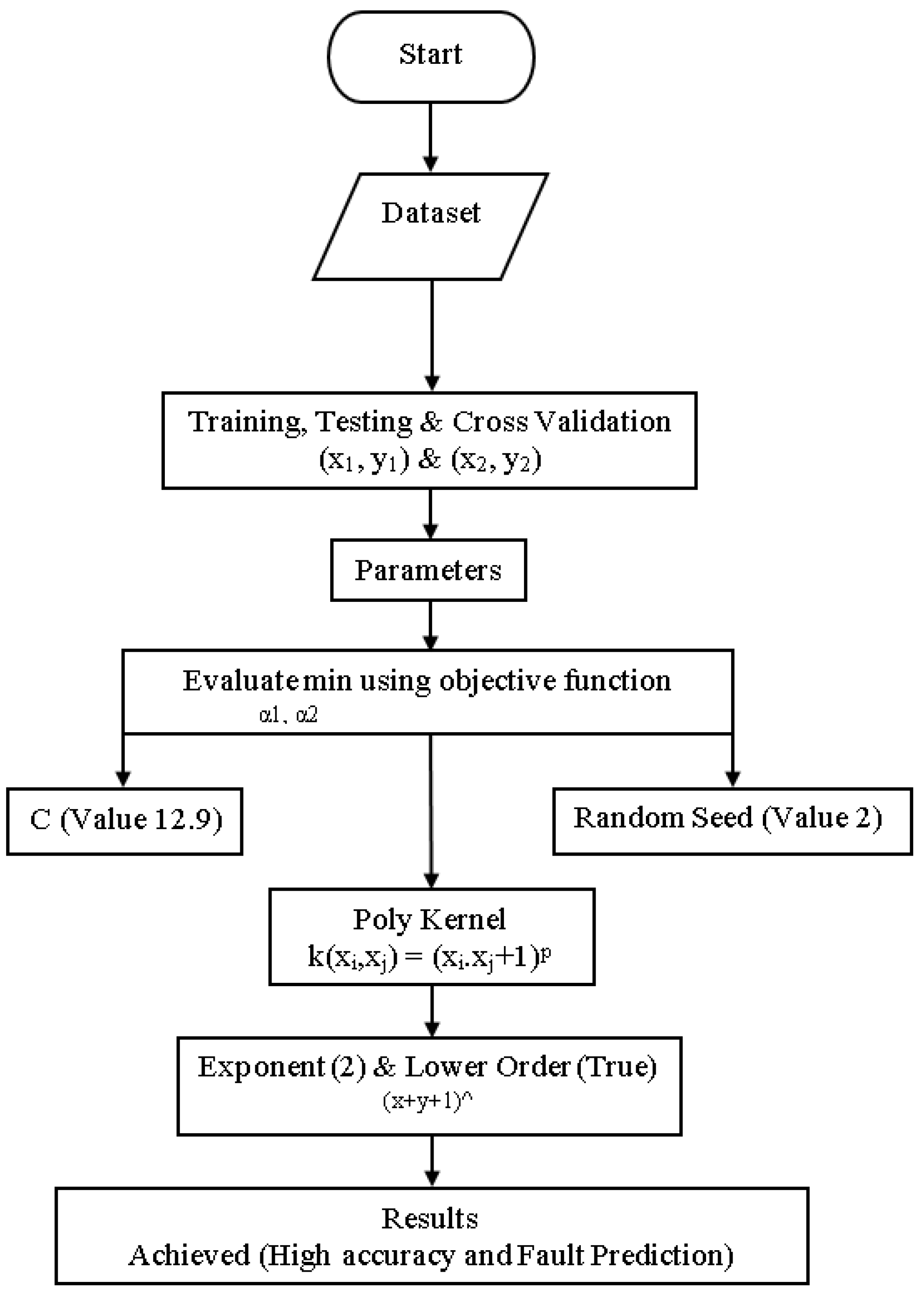
4.7. Modified Sequential Minimal Optimization
4.8. Delta Checkpointing
Description of D-CP Algorithm
4.9. Reliability
5. Results and Findings
- The RMSE is a commonly used measure of the difference between predicted and observed values by a model or estimator [39];
- MAE is a distinct measure of two continuous variables [39];
- The relative absolute error normalizes the total absolute error by dividing it by the total absolute error of the simple predictor [40];
- The relative squared error normalizes the total squared error by dividing it by the simple predictor’s total squared error [40].
5.1. Simulation Setup of ML Classifiers to Achieve High Accuracy and Less Fault Prediction
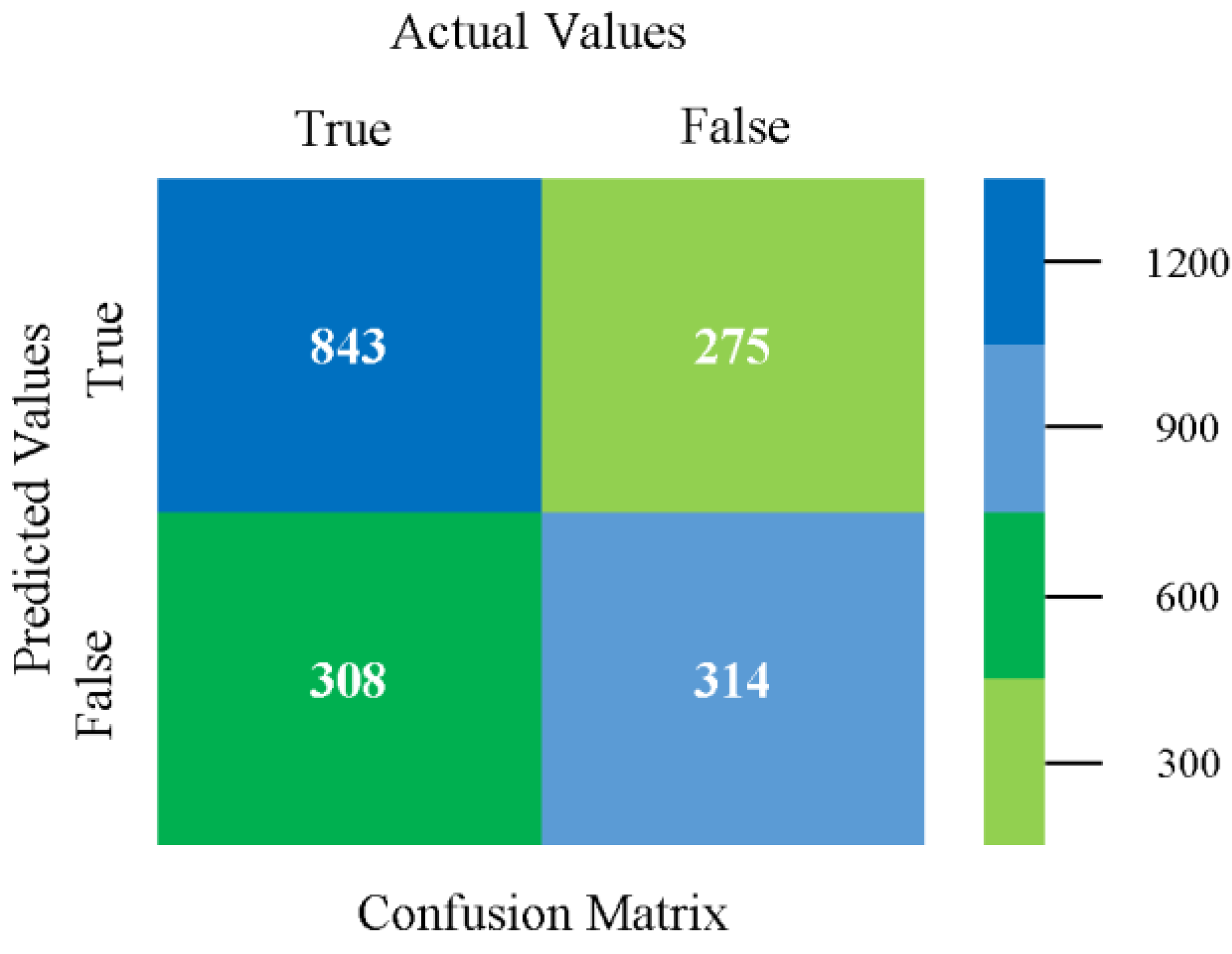
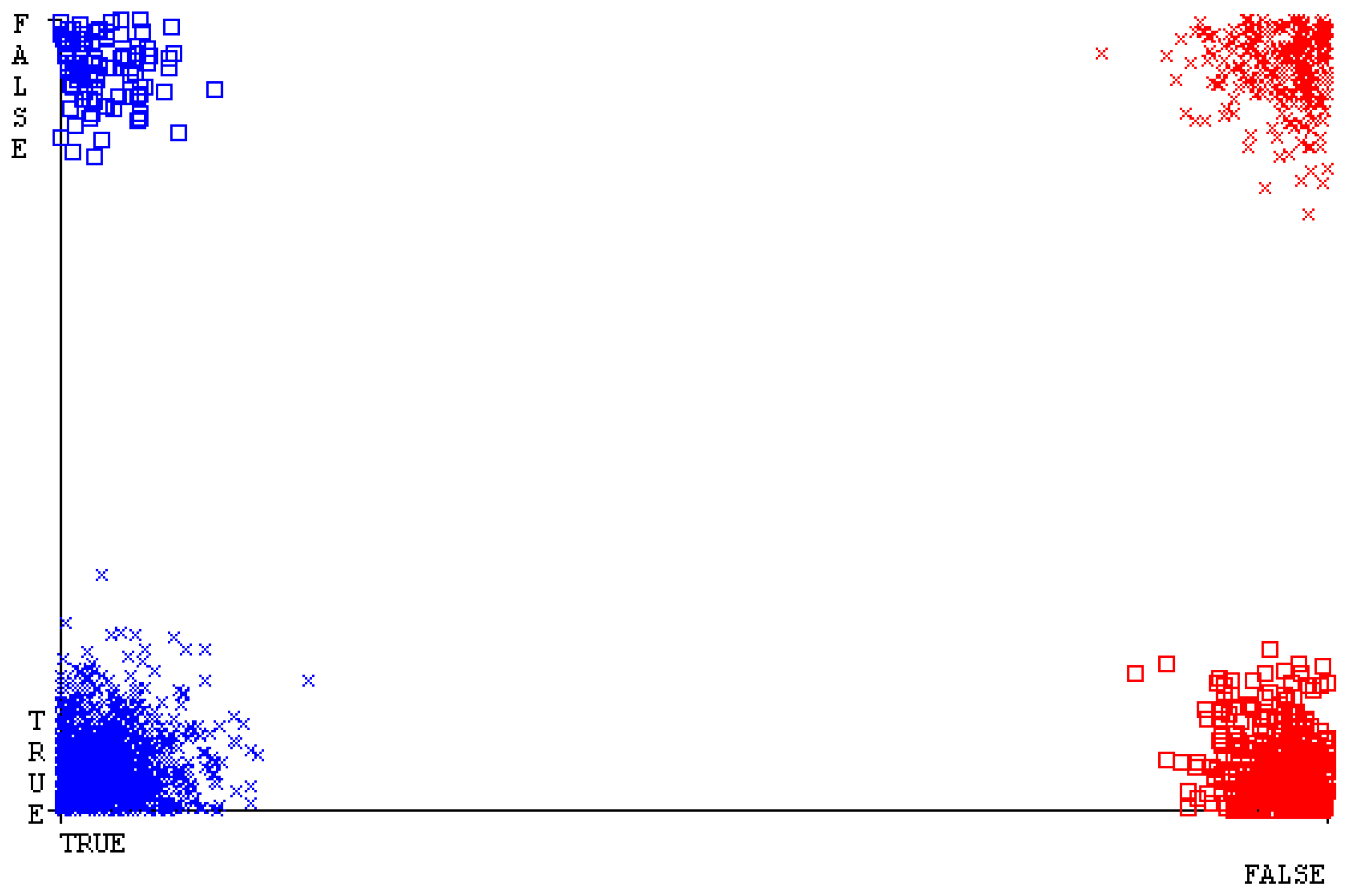
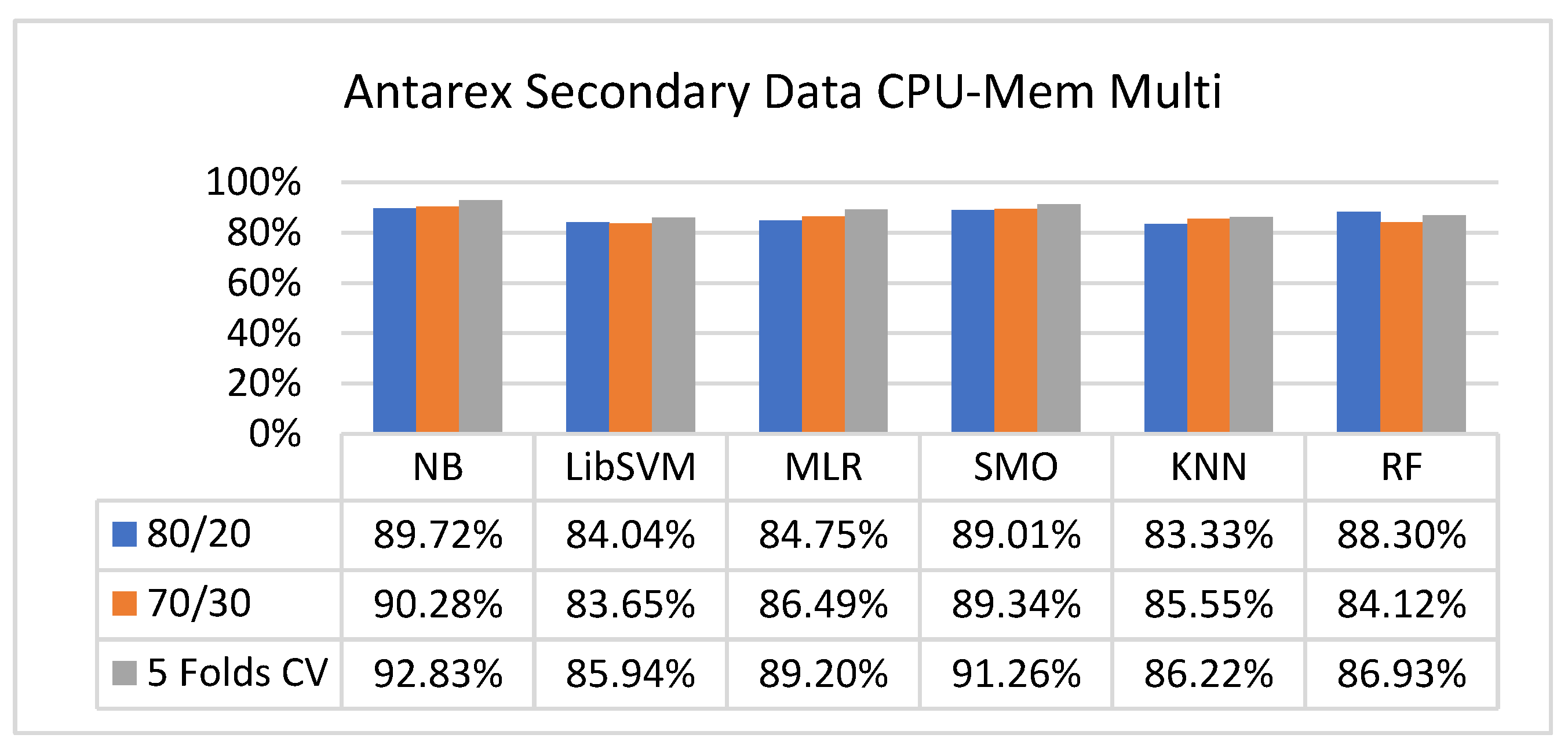
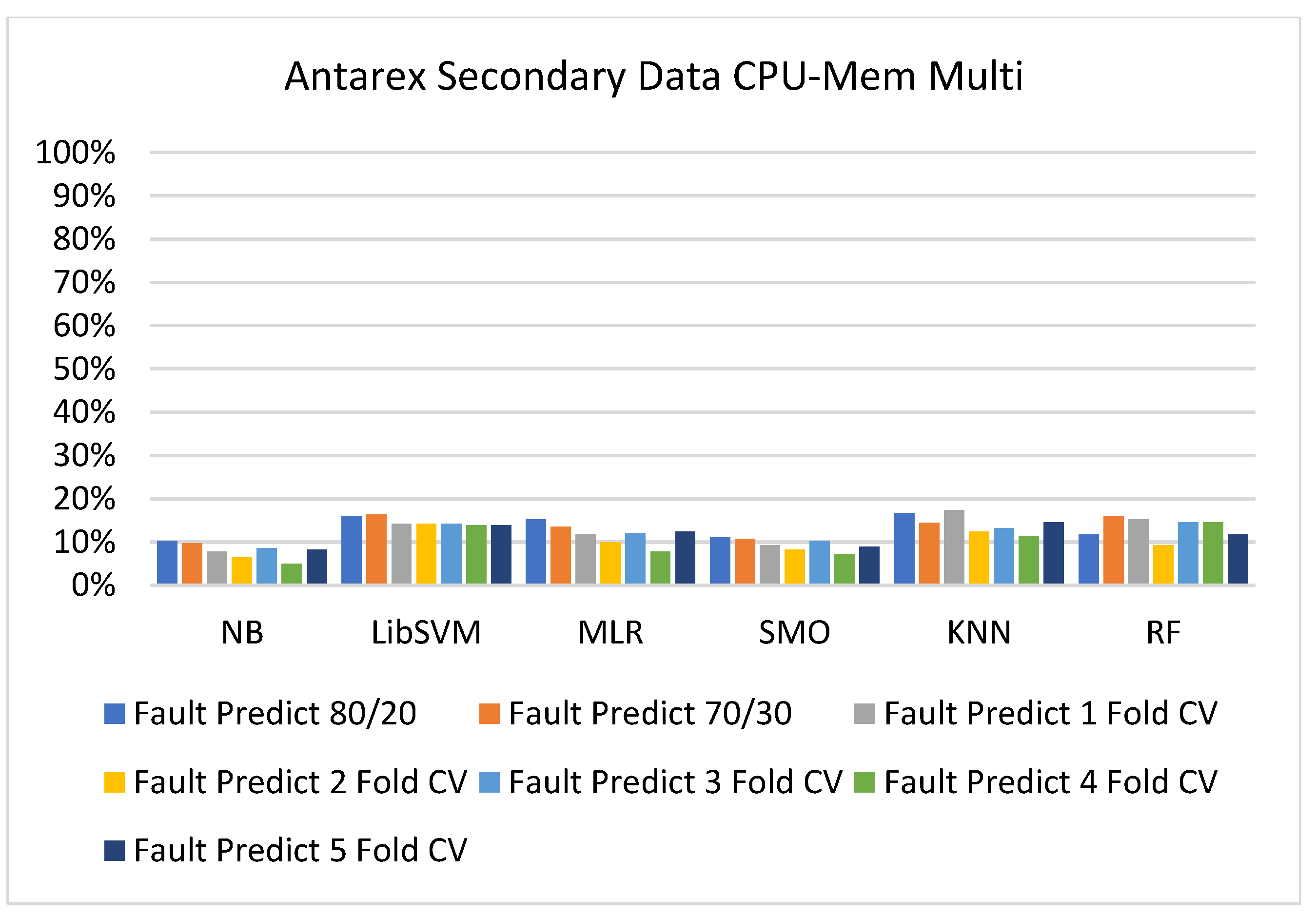
5.2. Comparison of Classification Models on Secondary Dataset
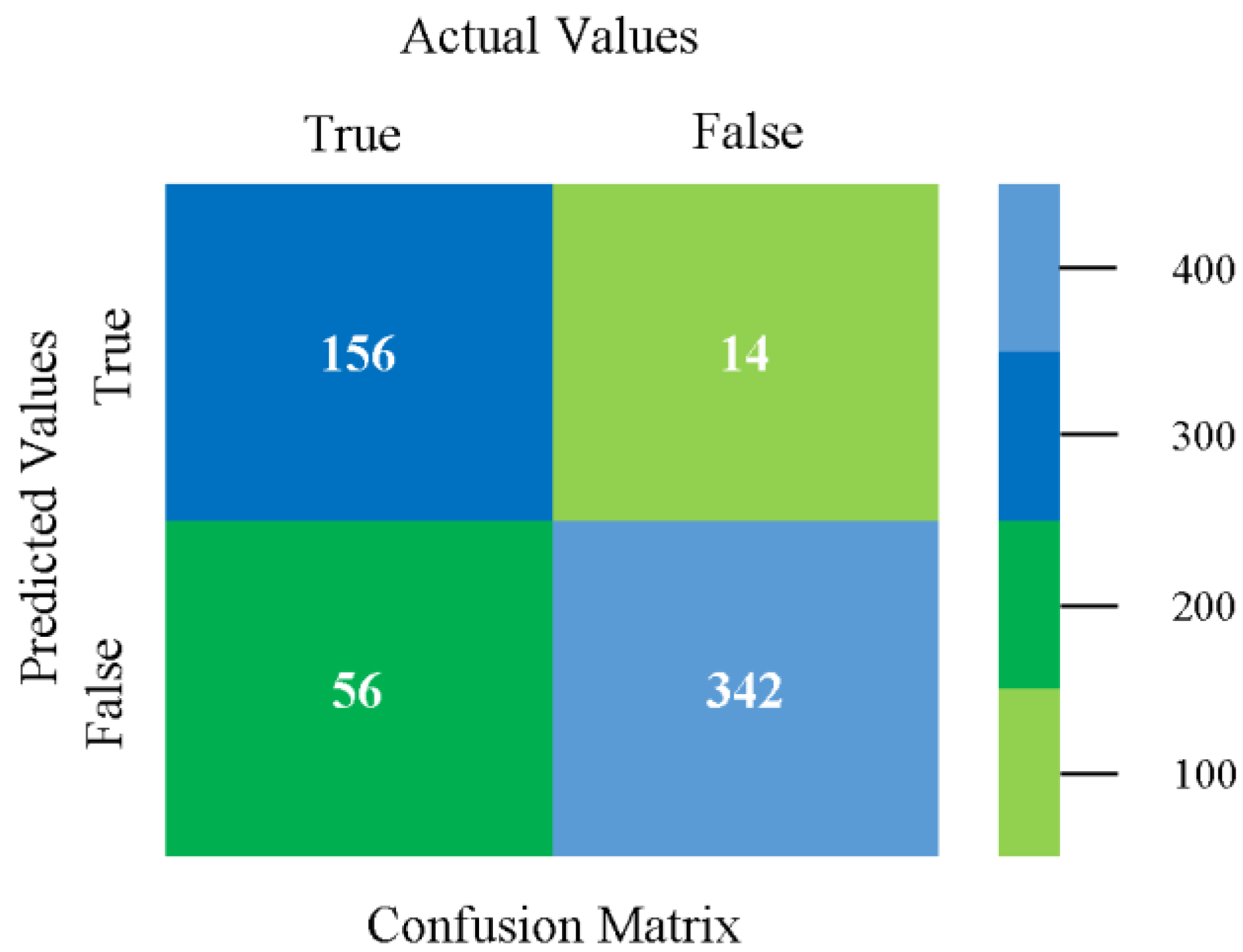
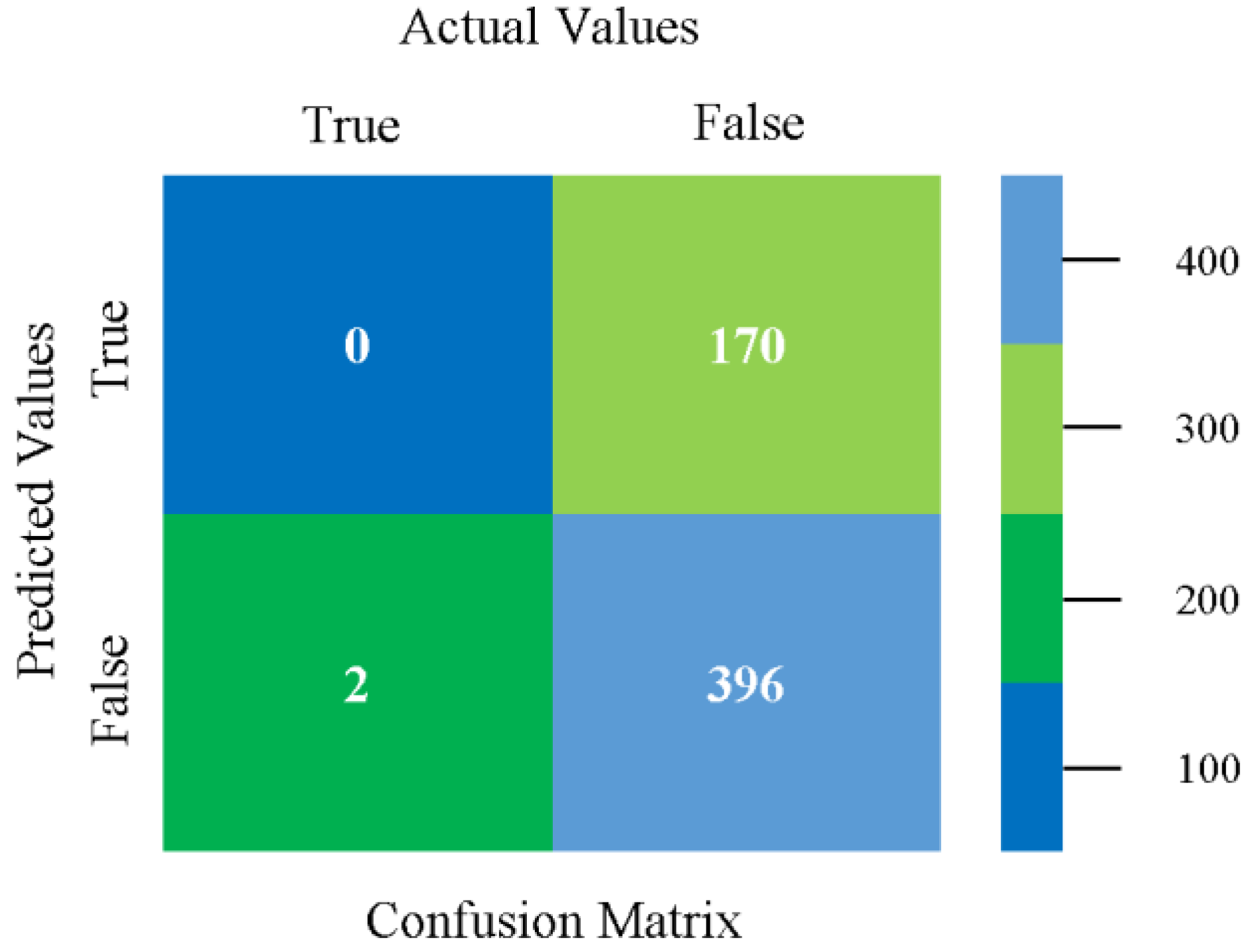
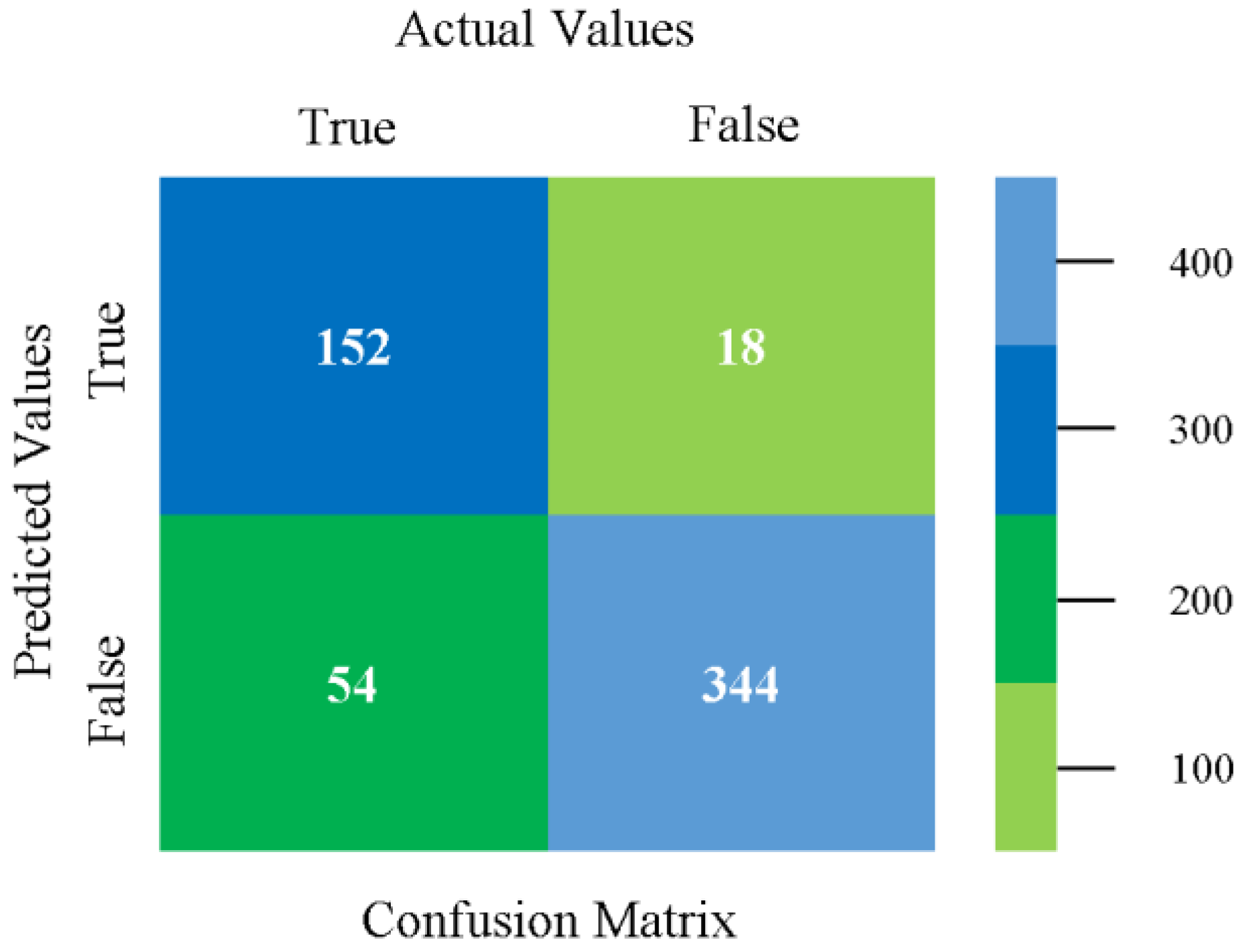
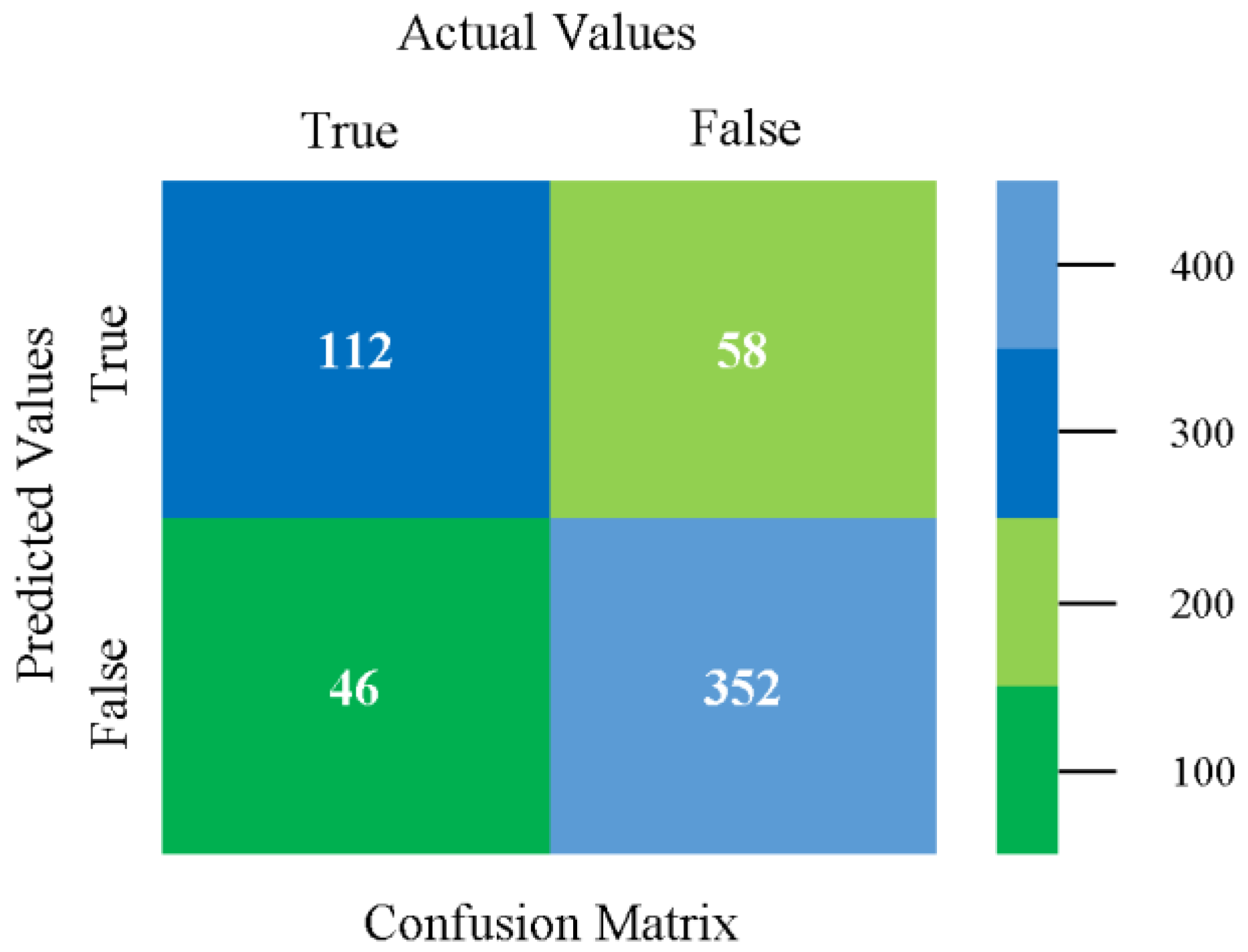
5.2.1. Secondary Dataset CPU-Mem Mono Block-I
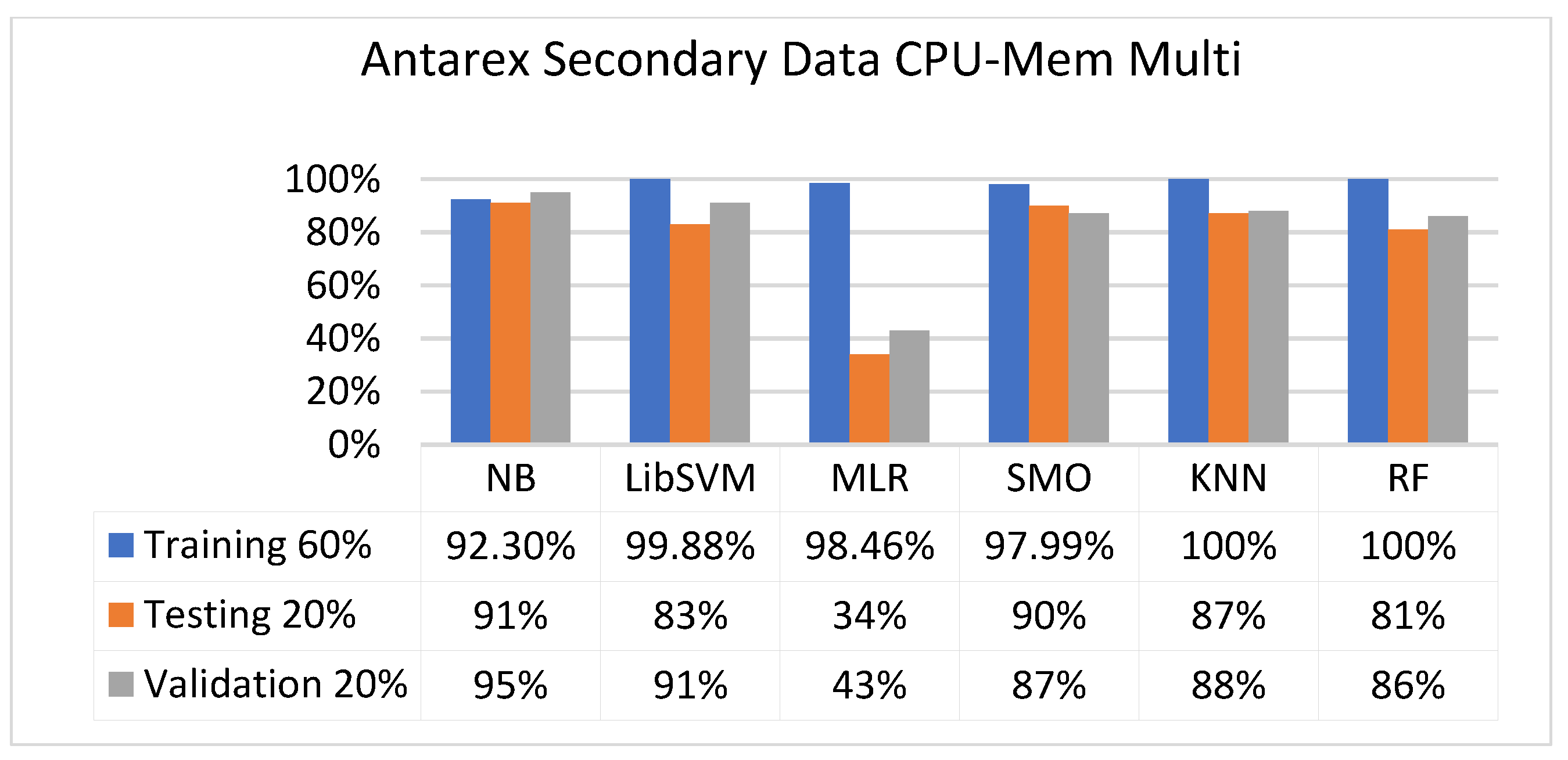
5.2.2. Secondary Dataset CPU-Mem Multi Block-II
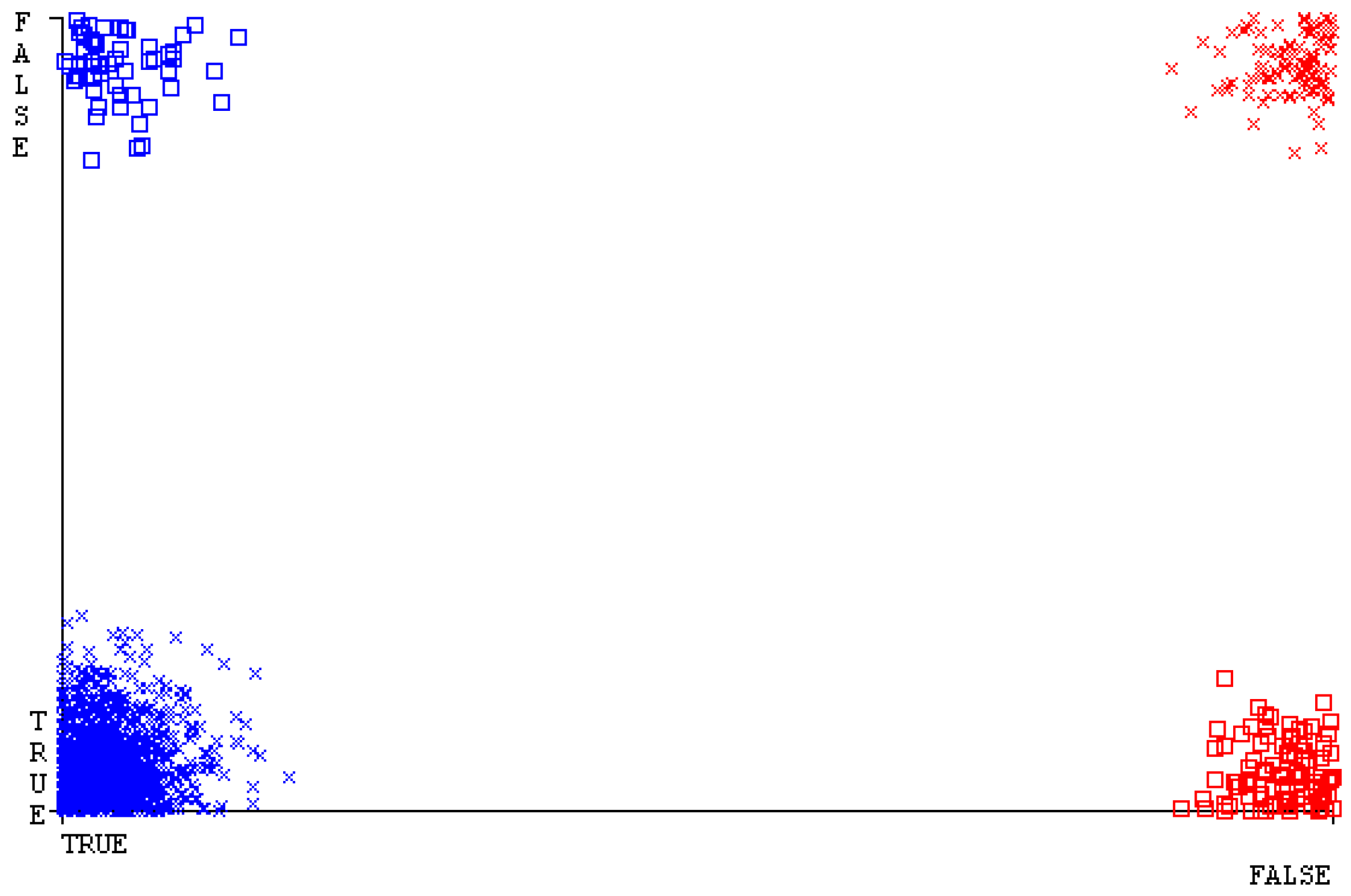
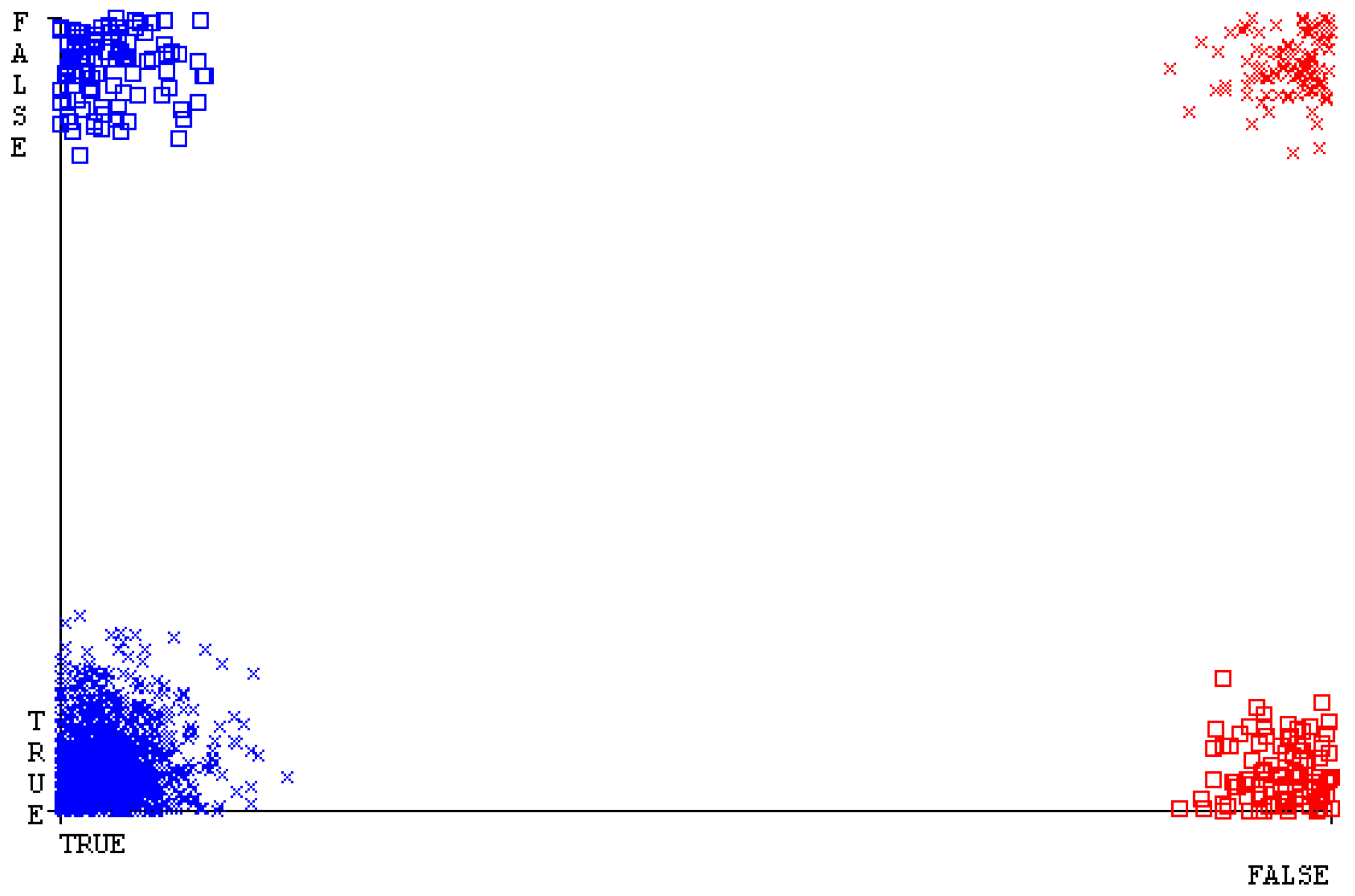
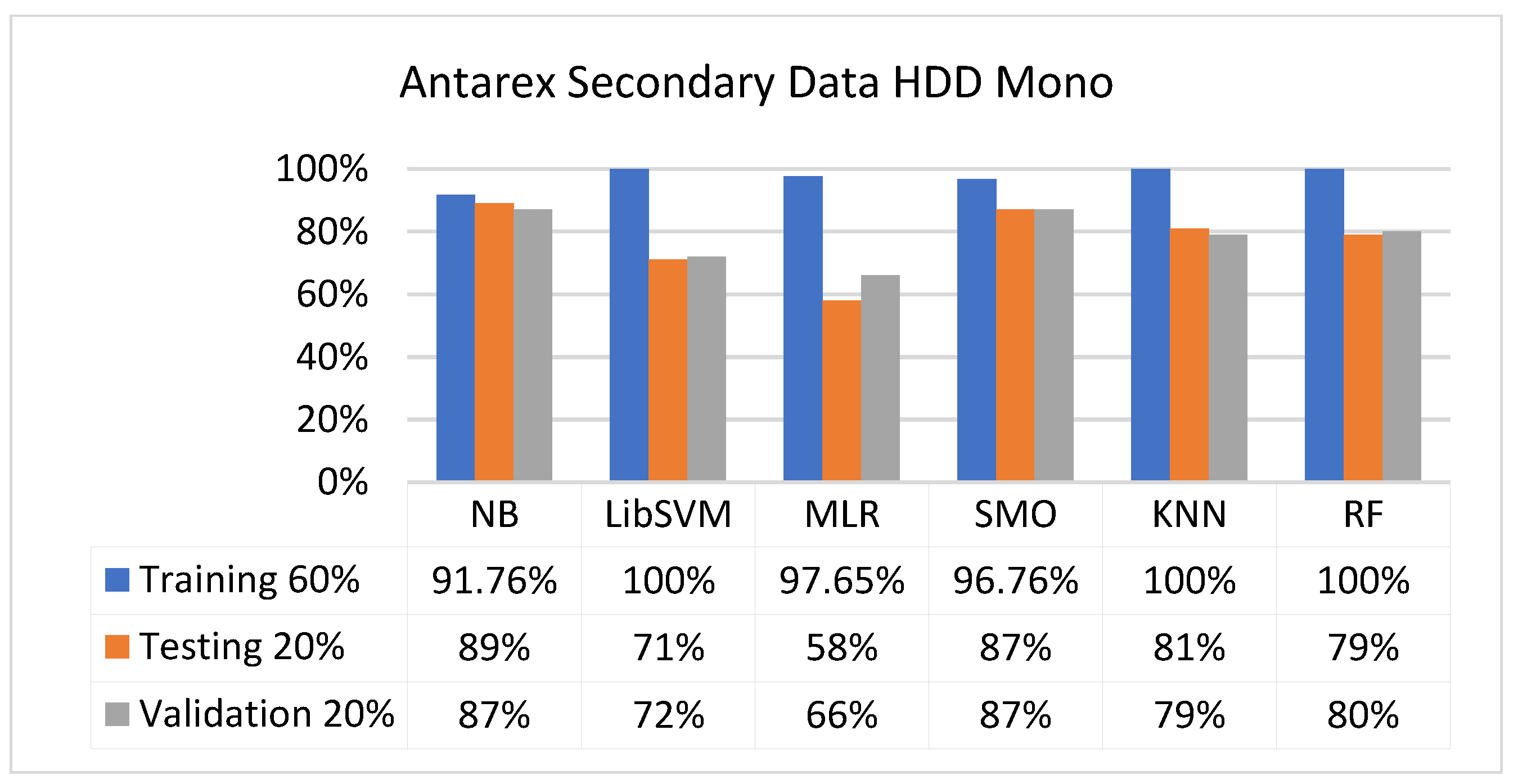
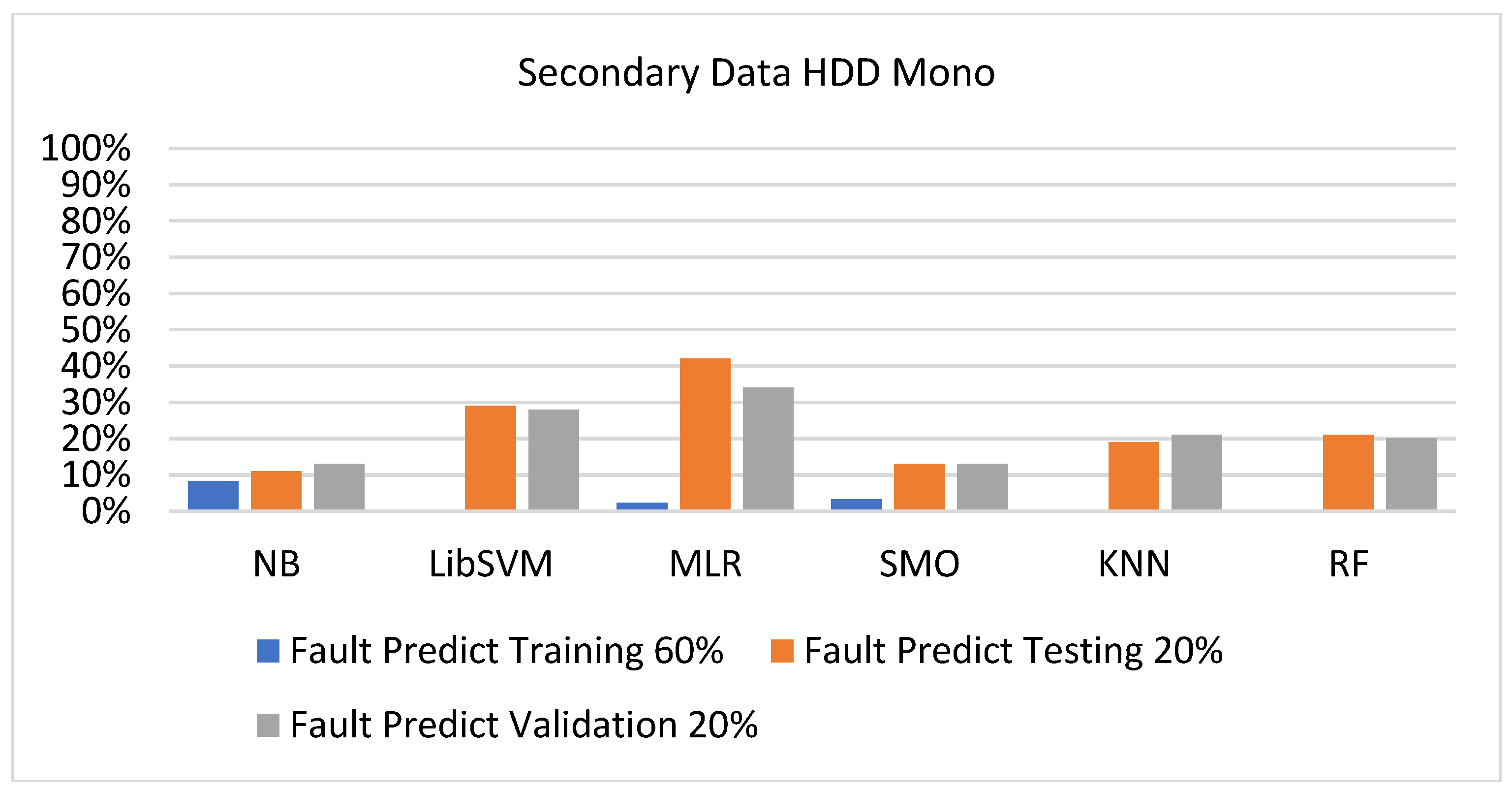
5.2.3. Secondary Dataset HDD Mono Block-III
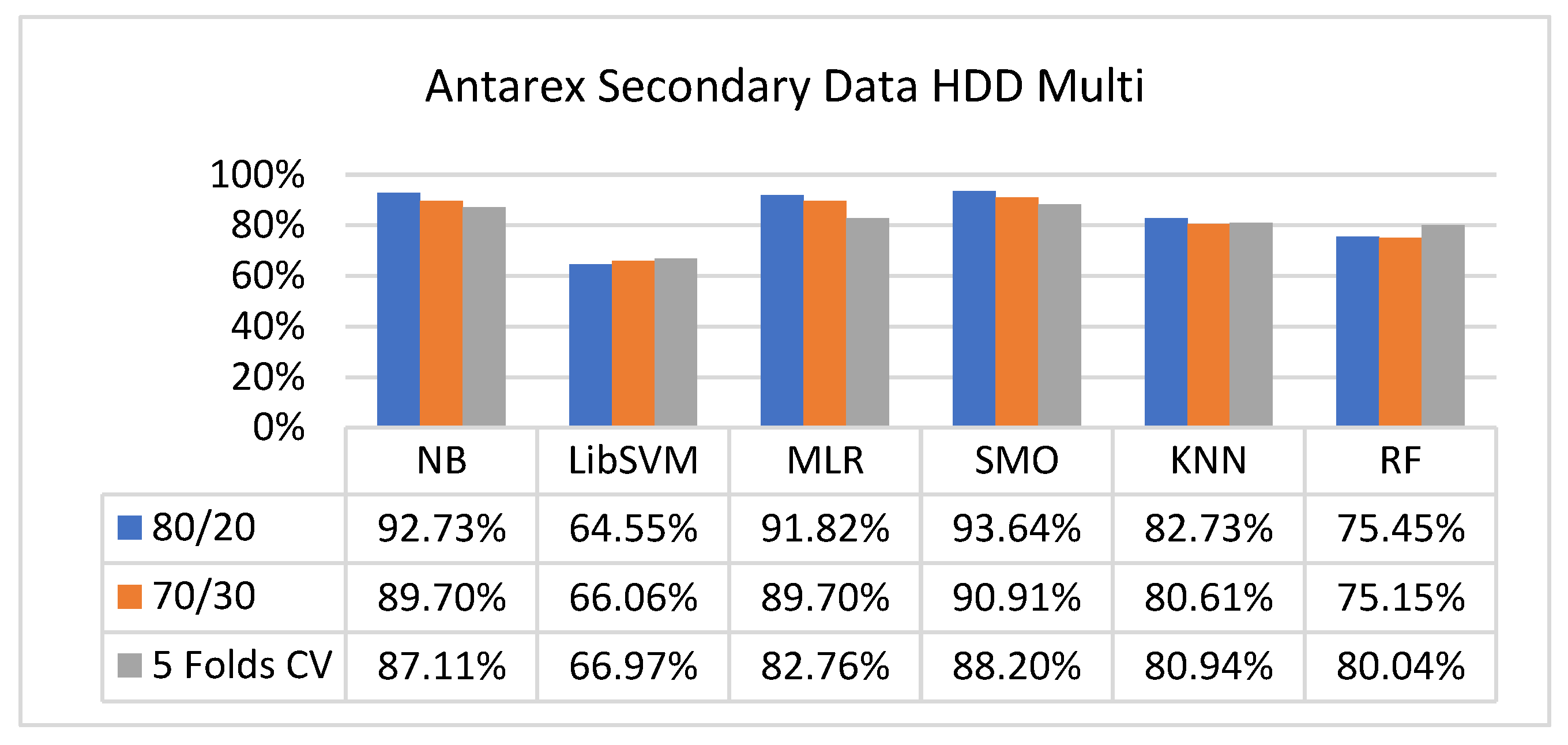
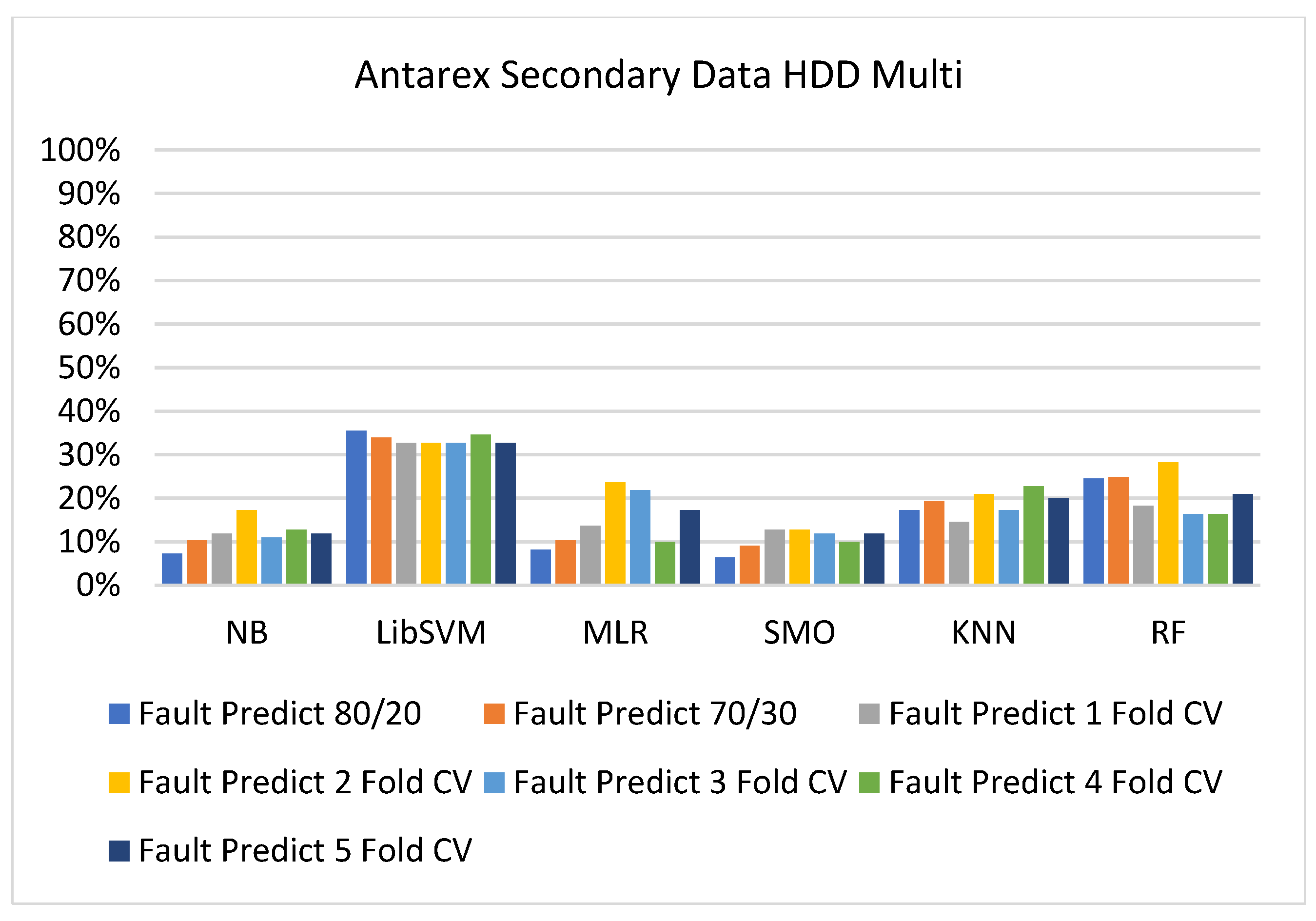
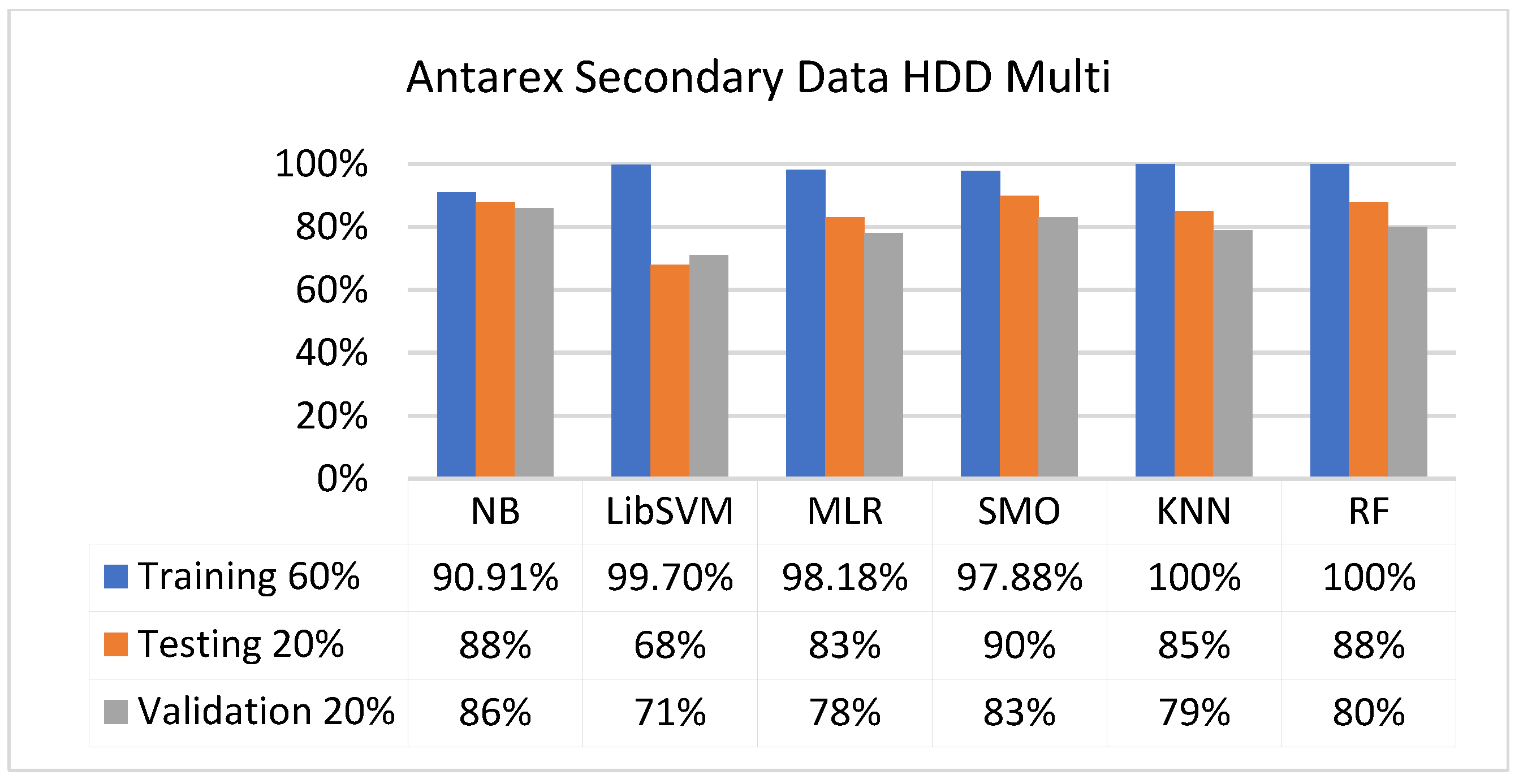
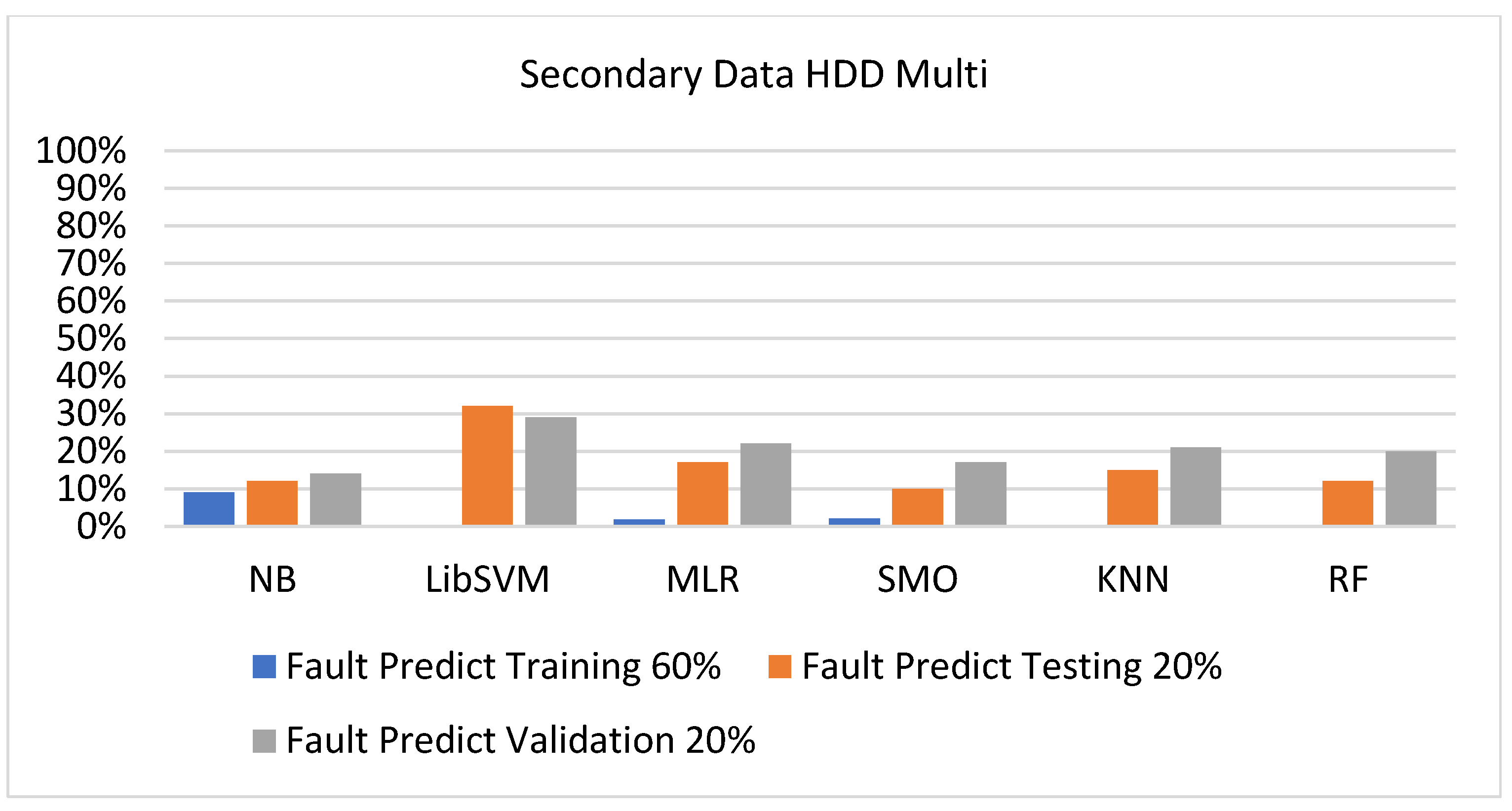
5.2.4. Secondary Dataset HDD Multi Block-IV
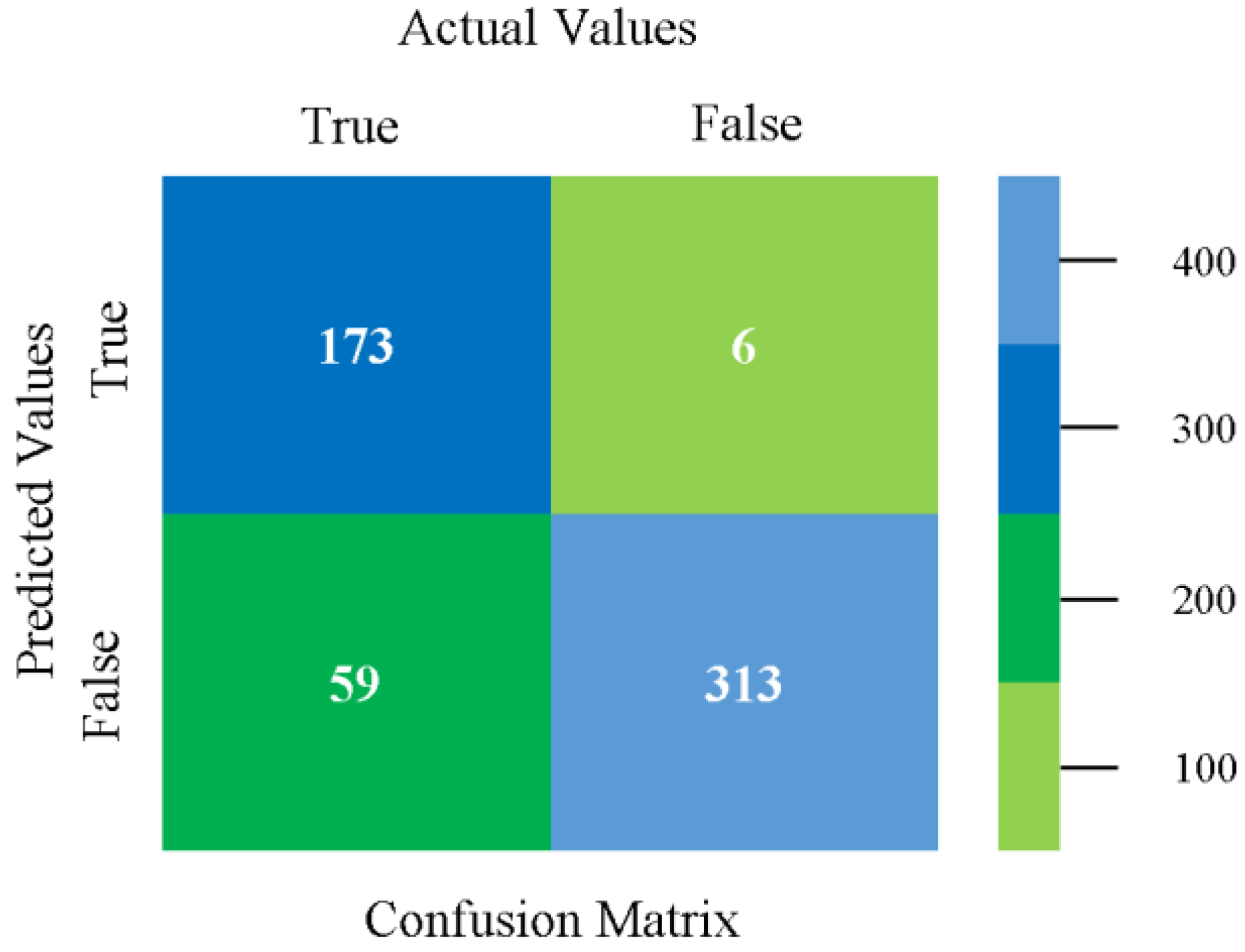
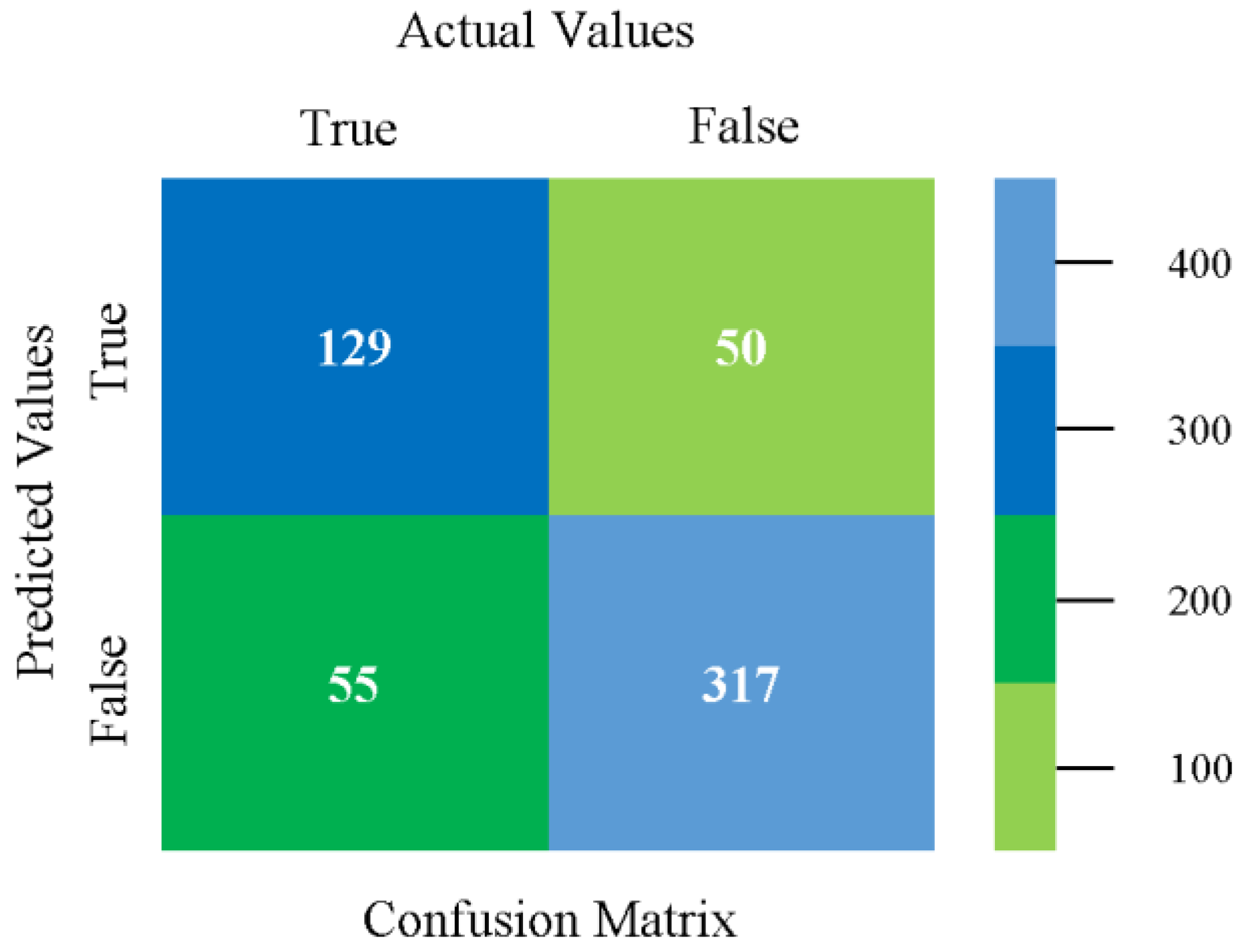
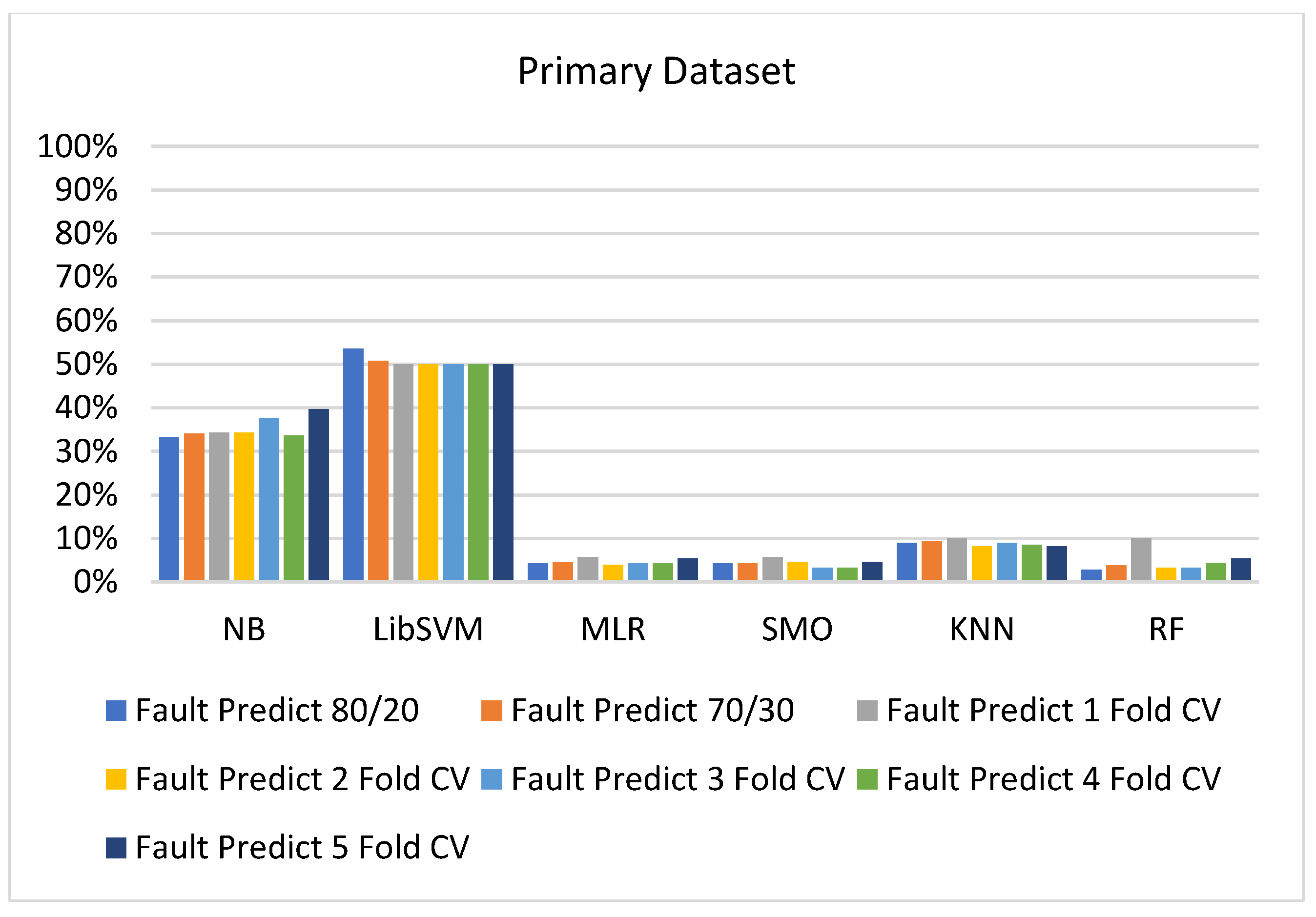
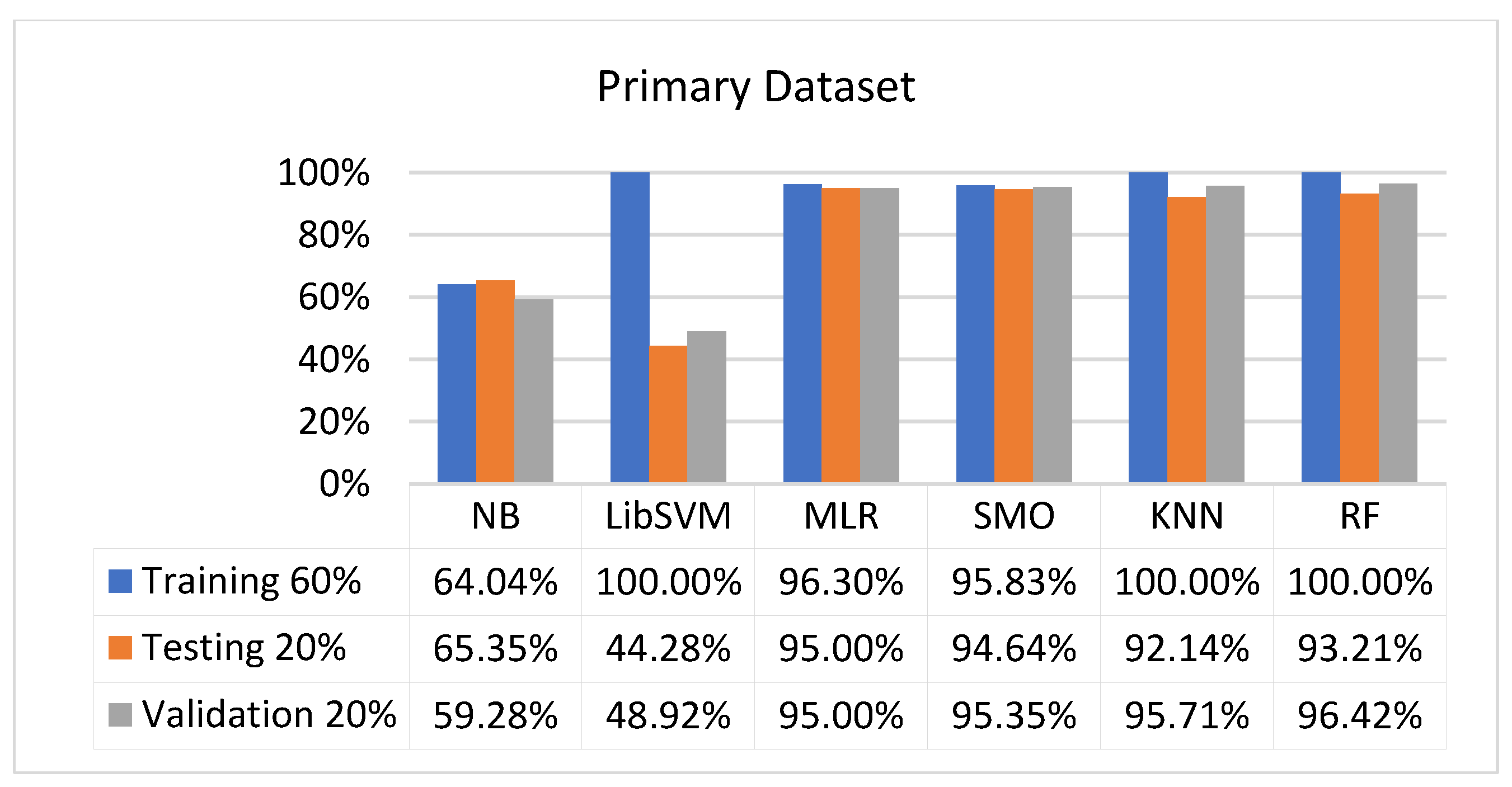
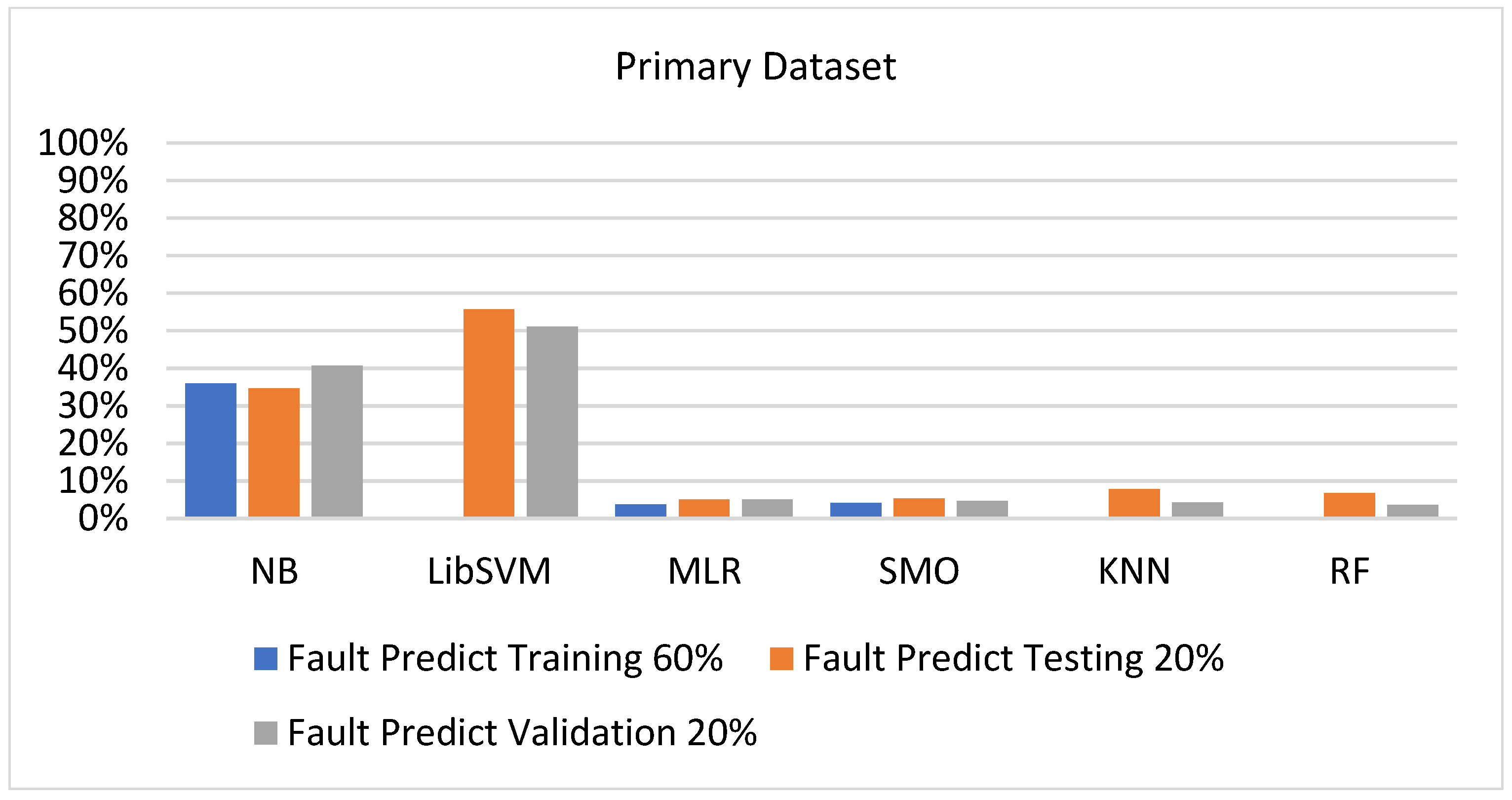
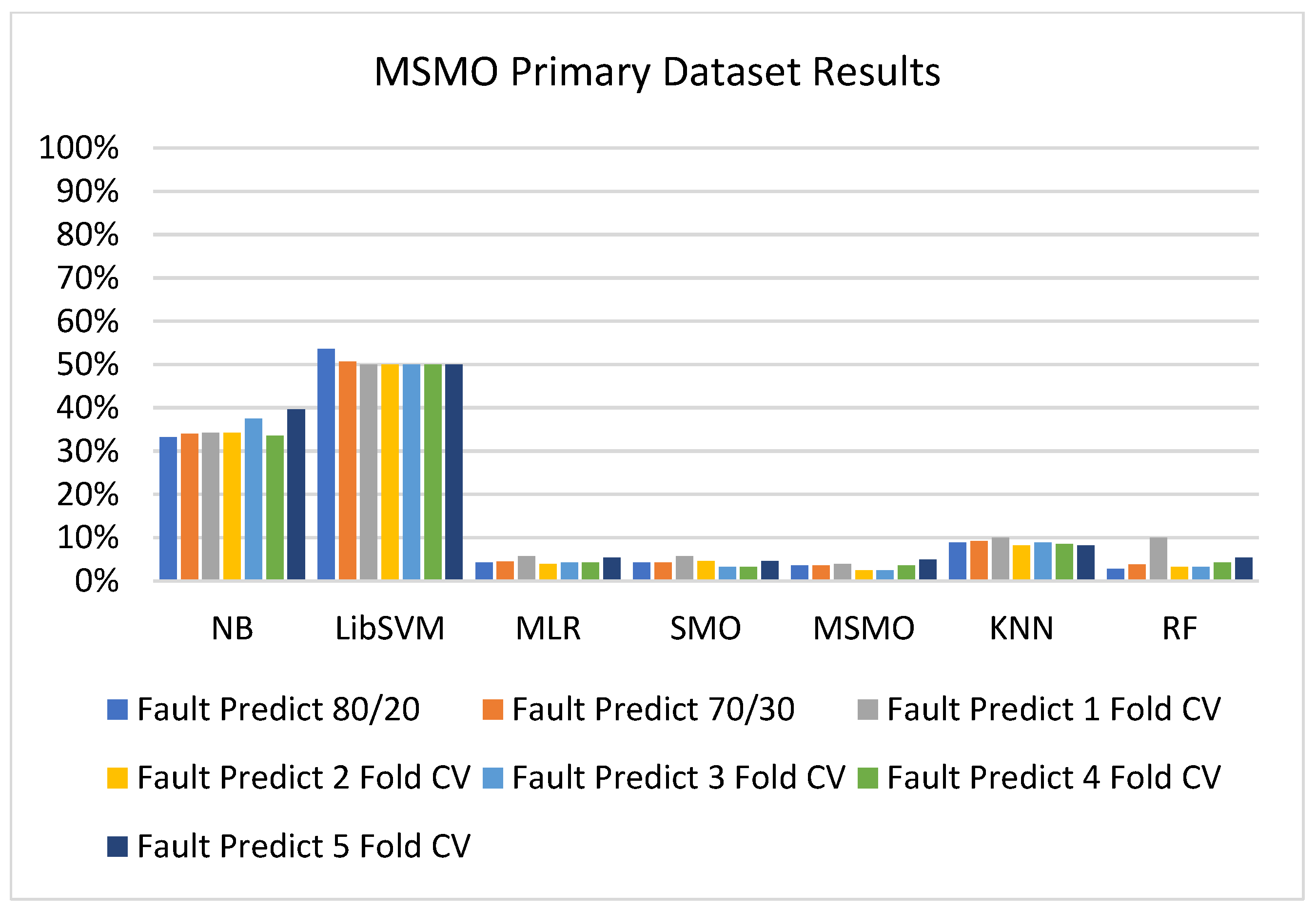
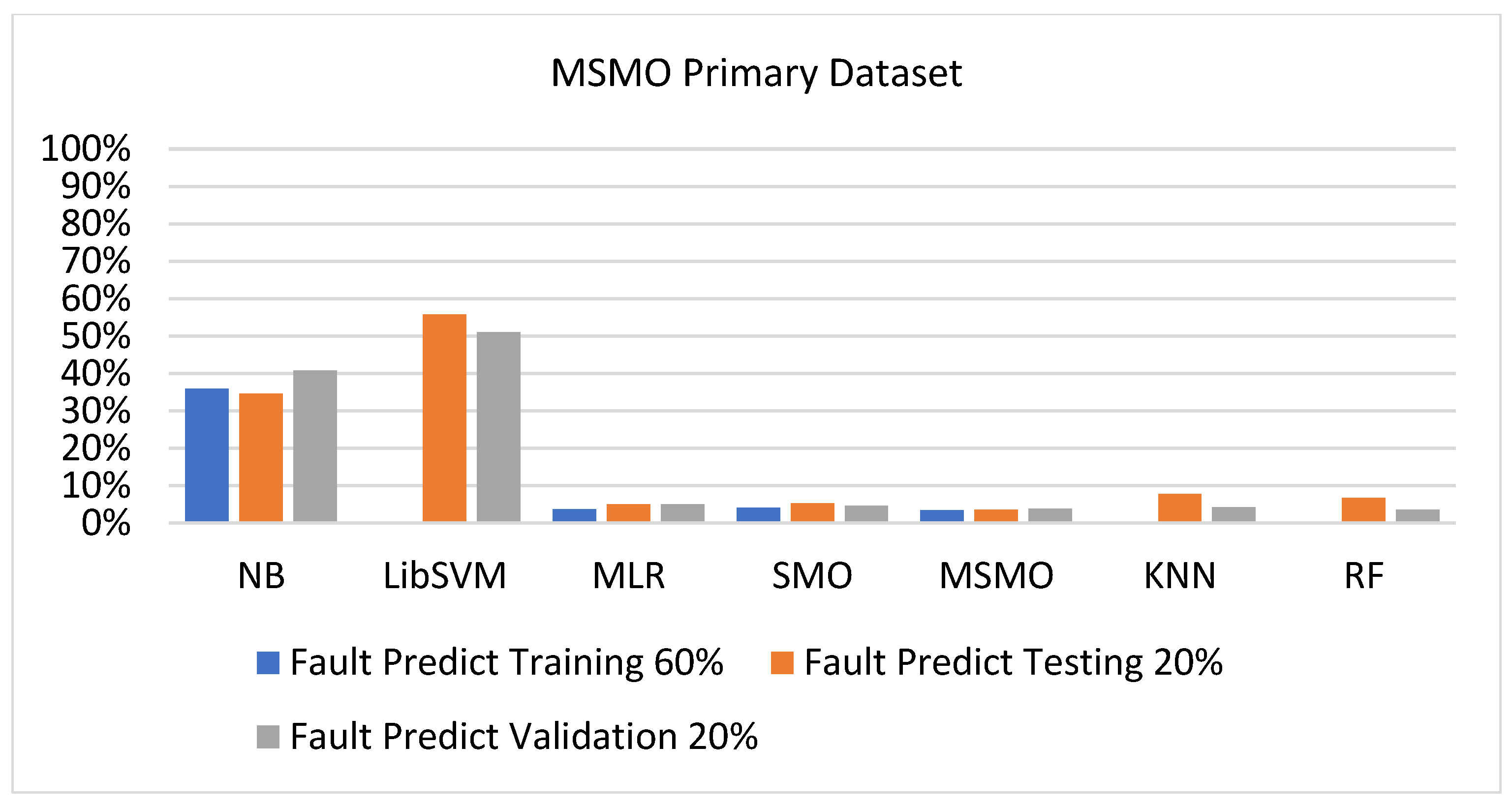
5.3. Comparison of Classification Models on Primary Dataset
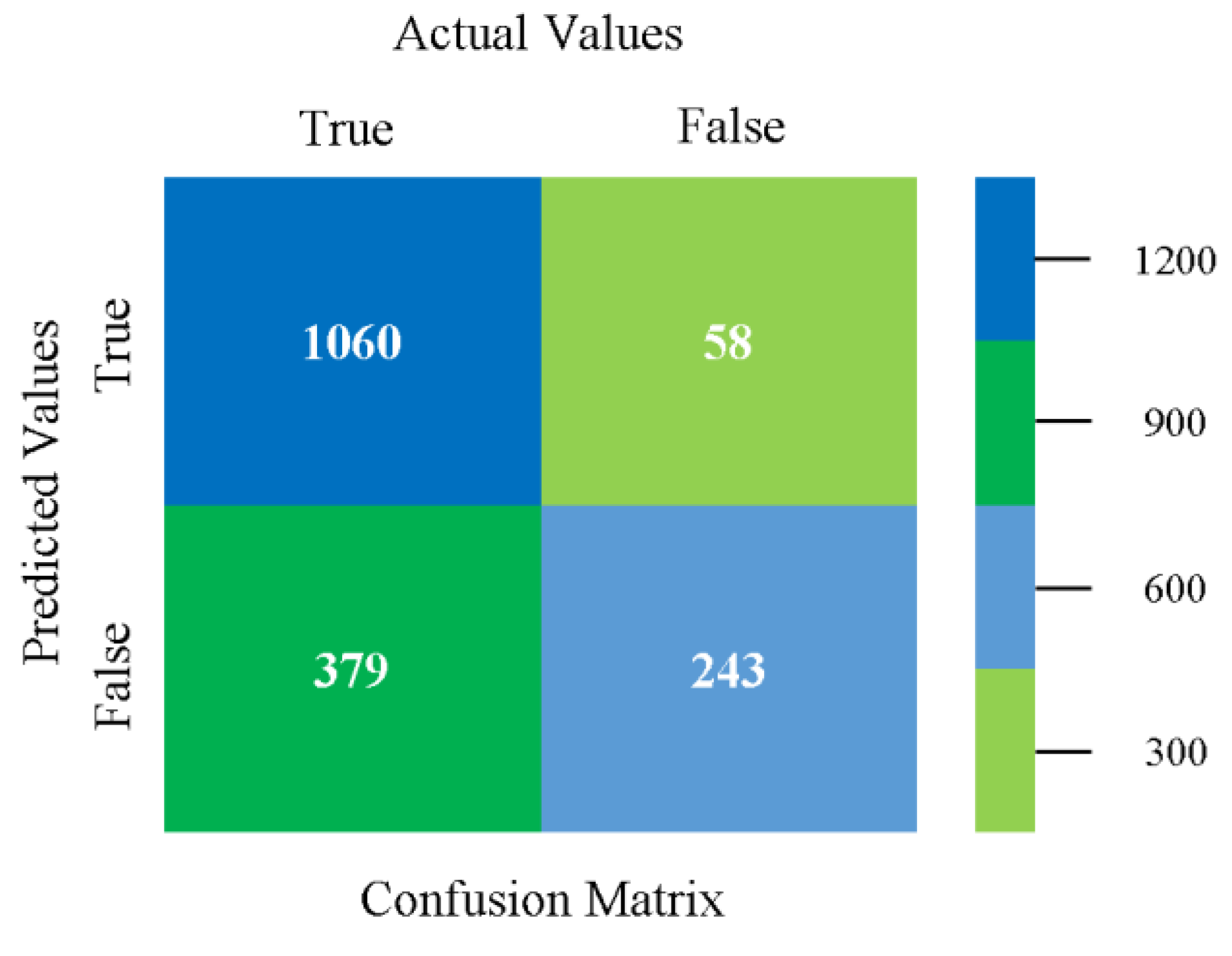
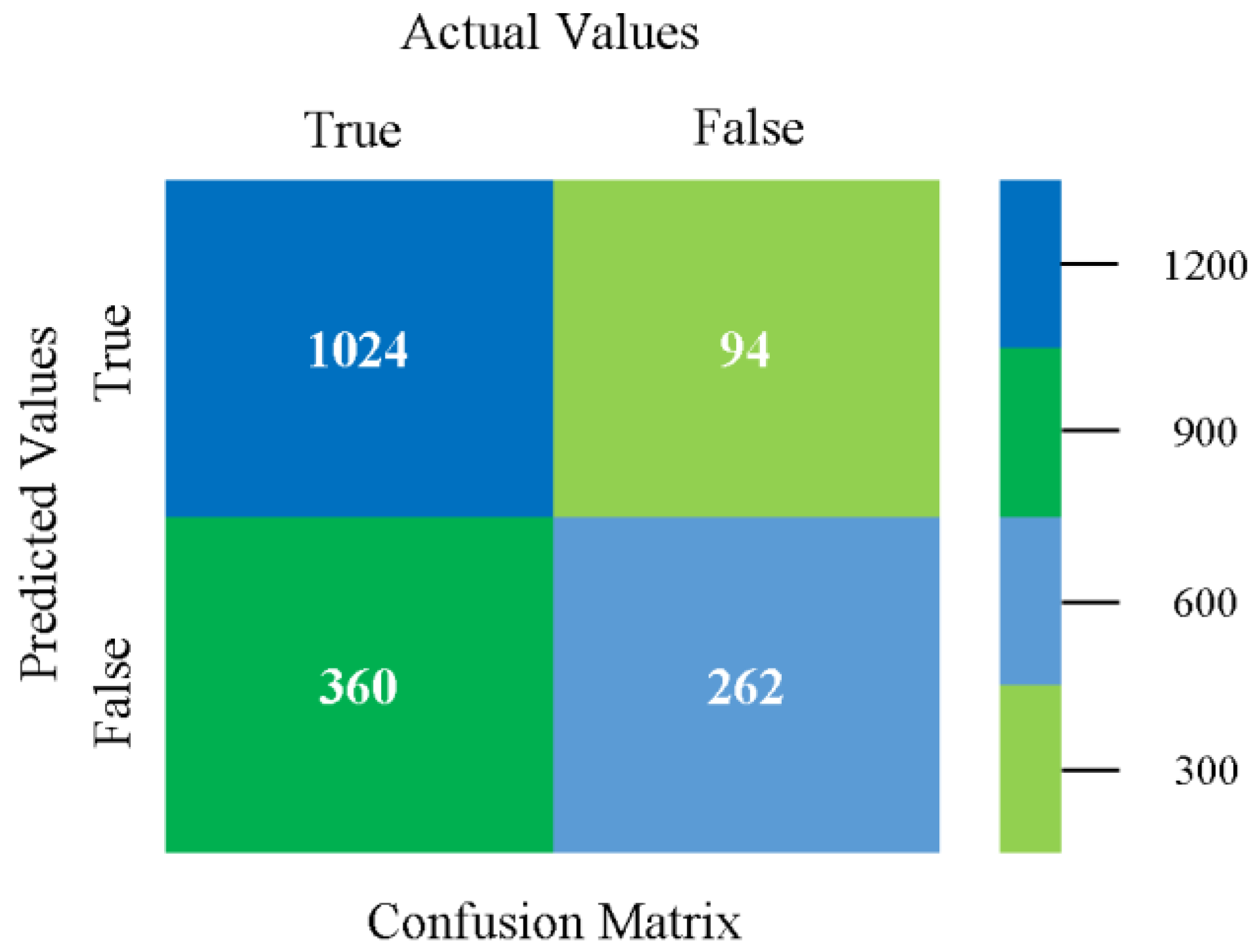
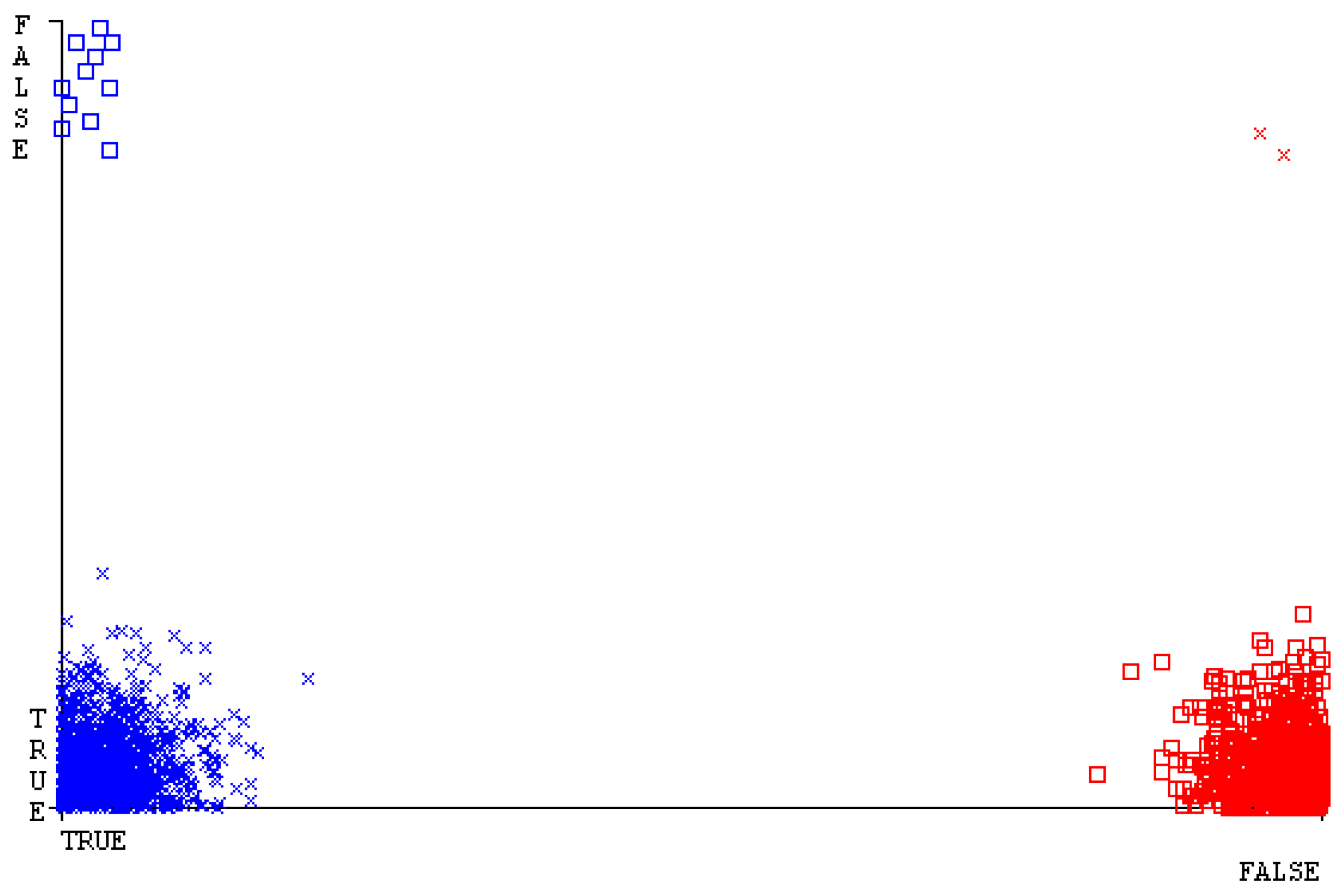
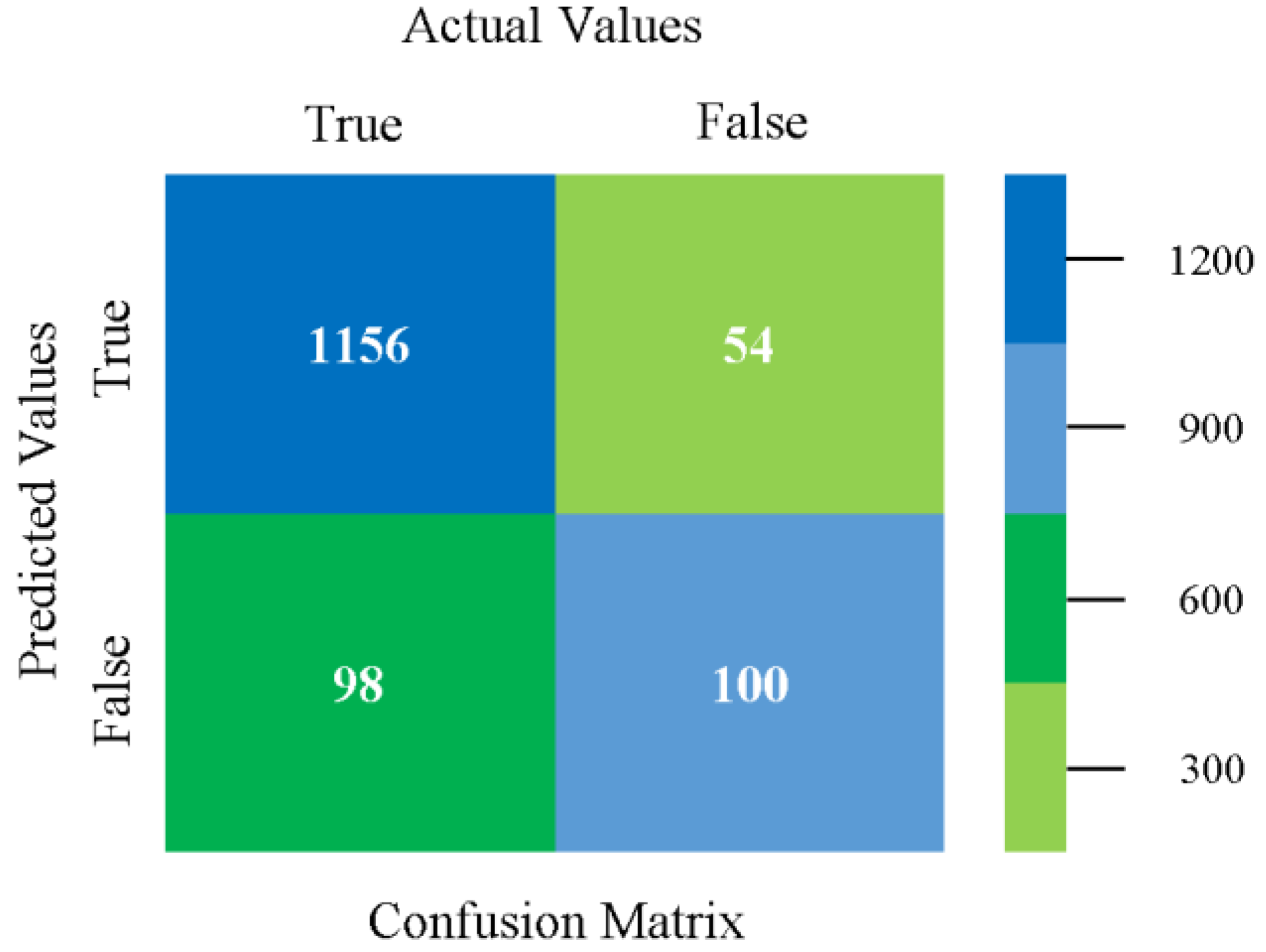
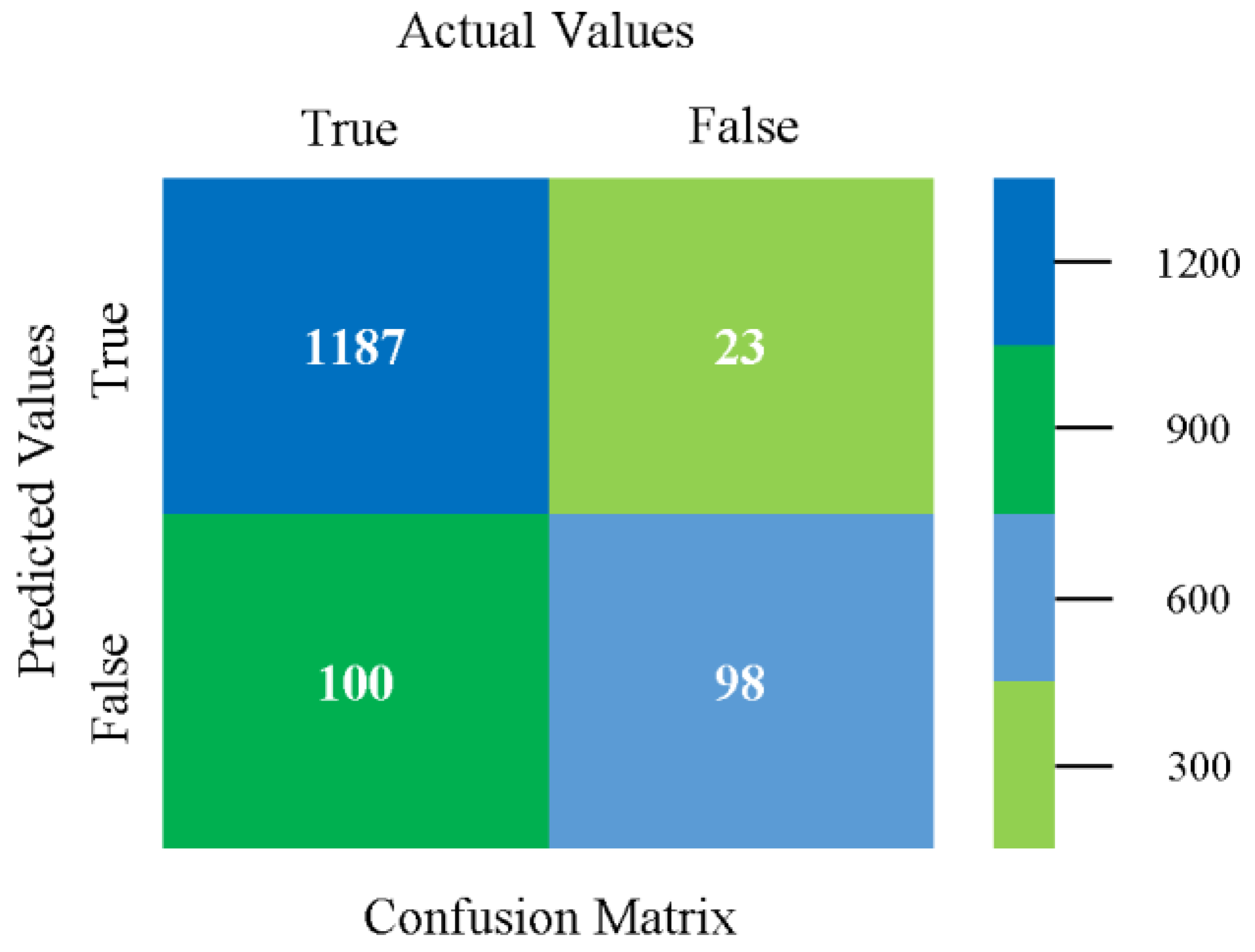
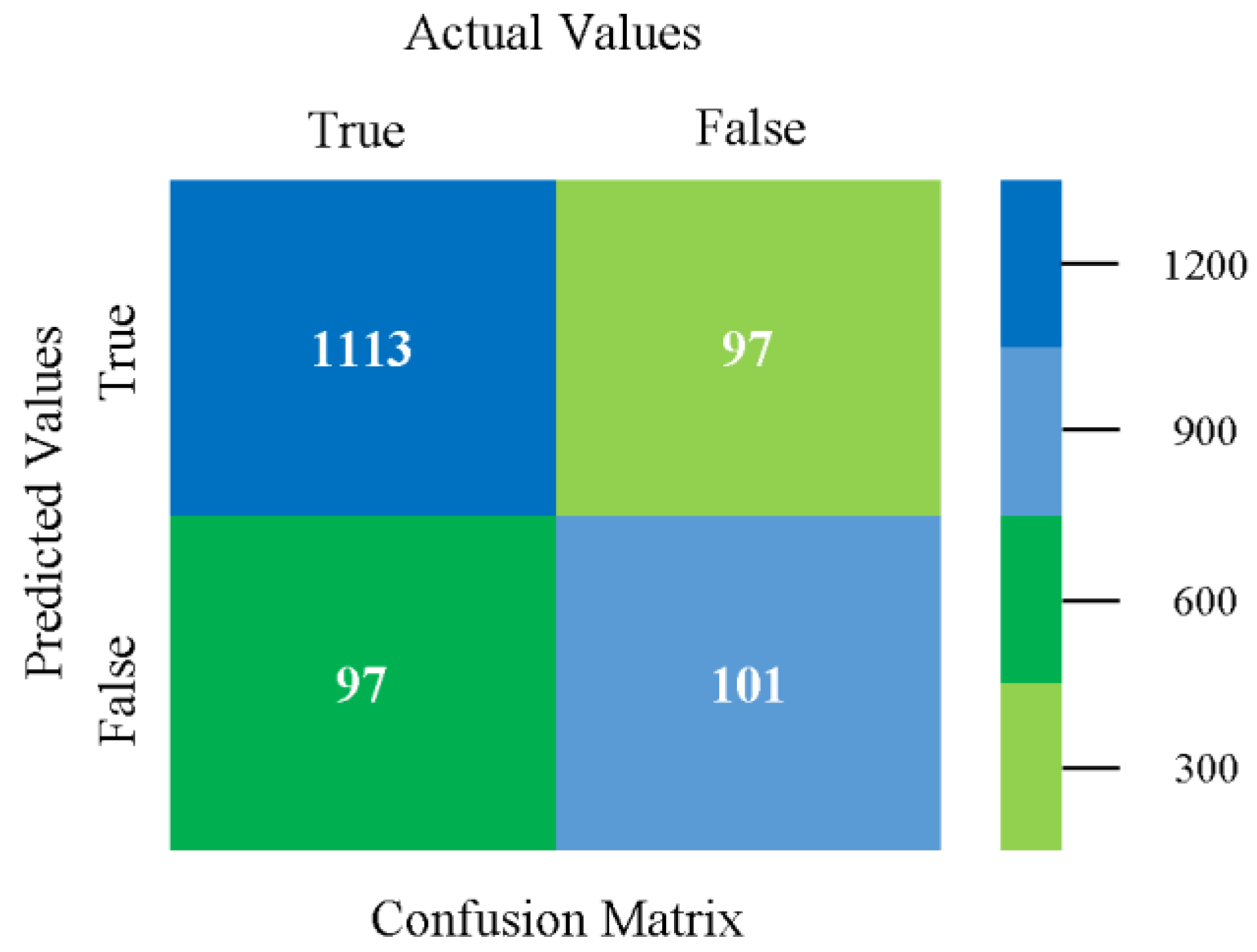
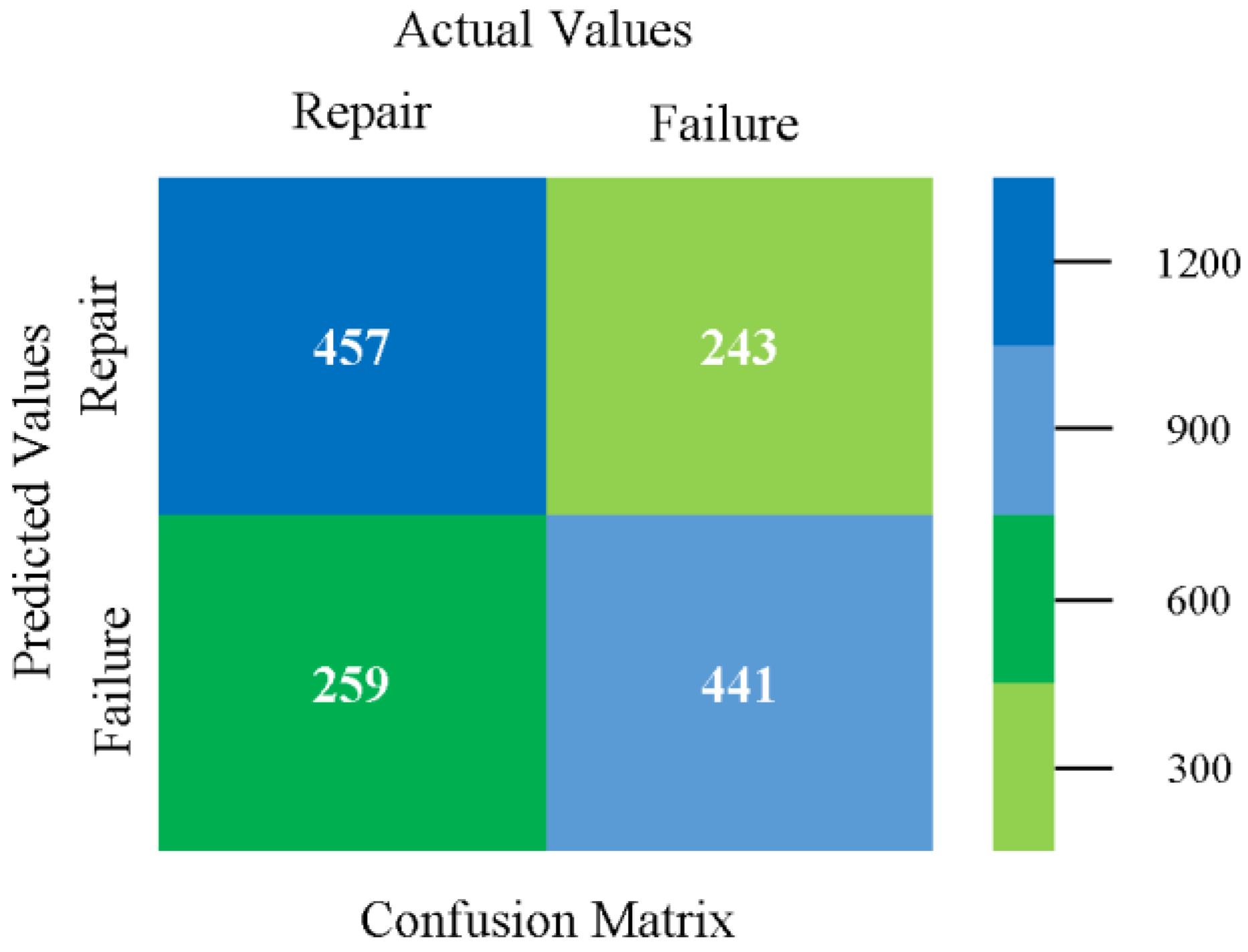
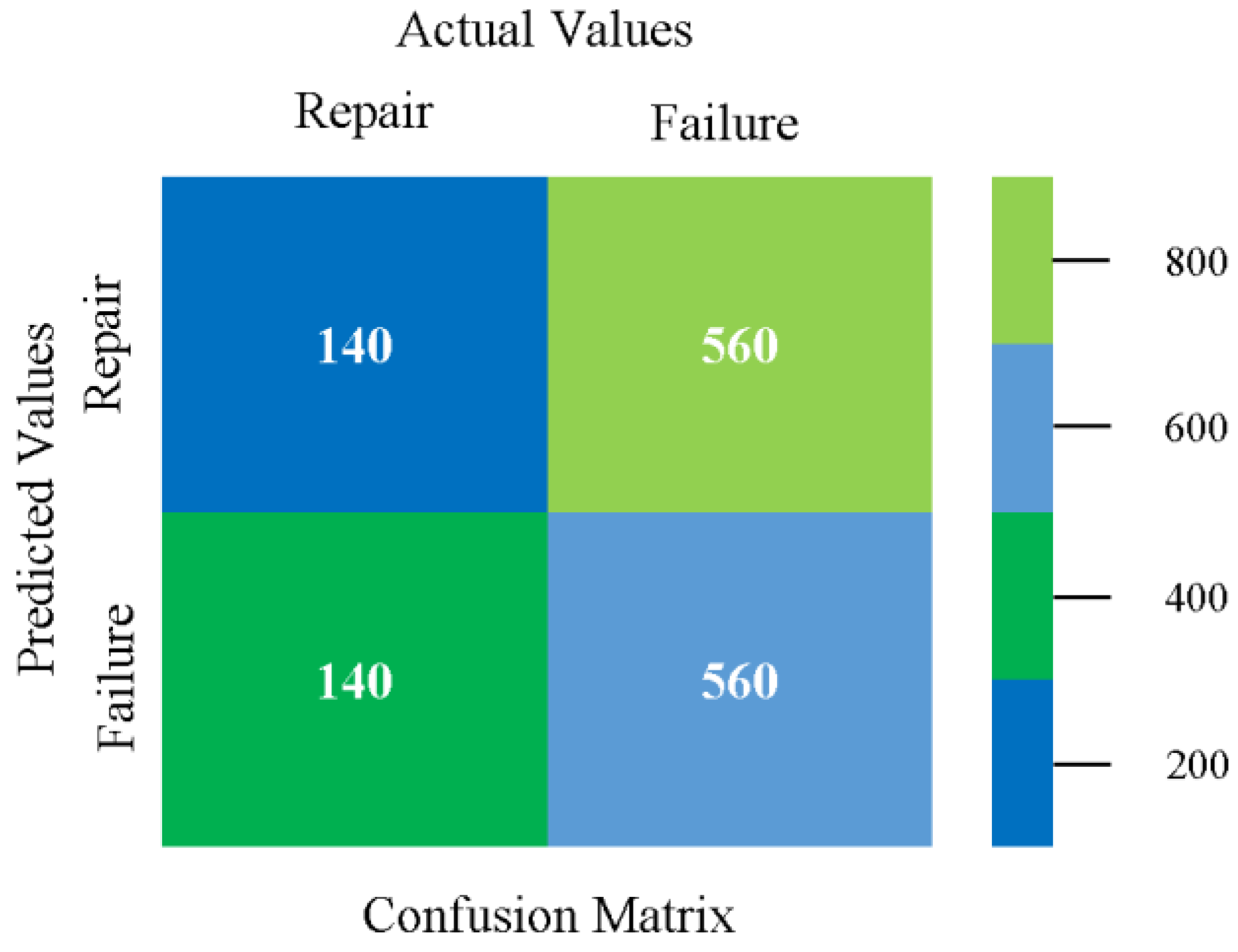
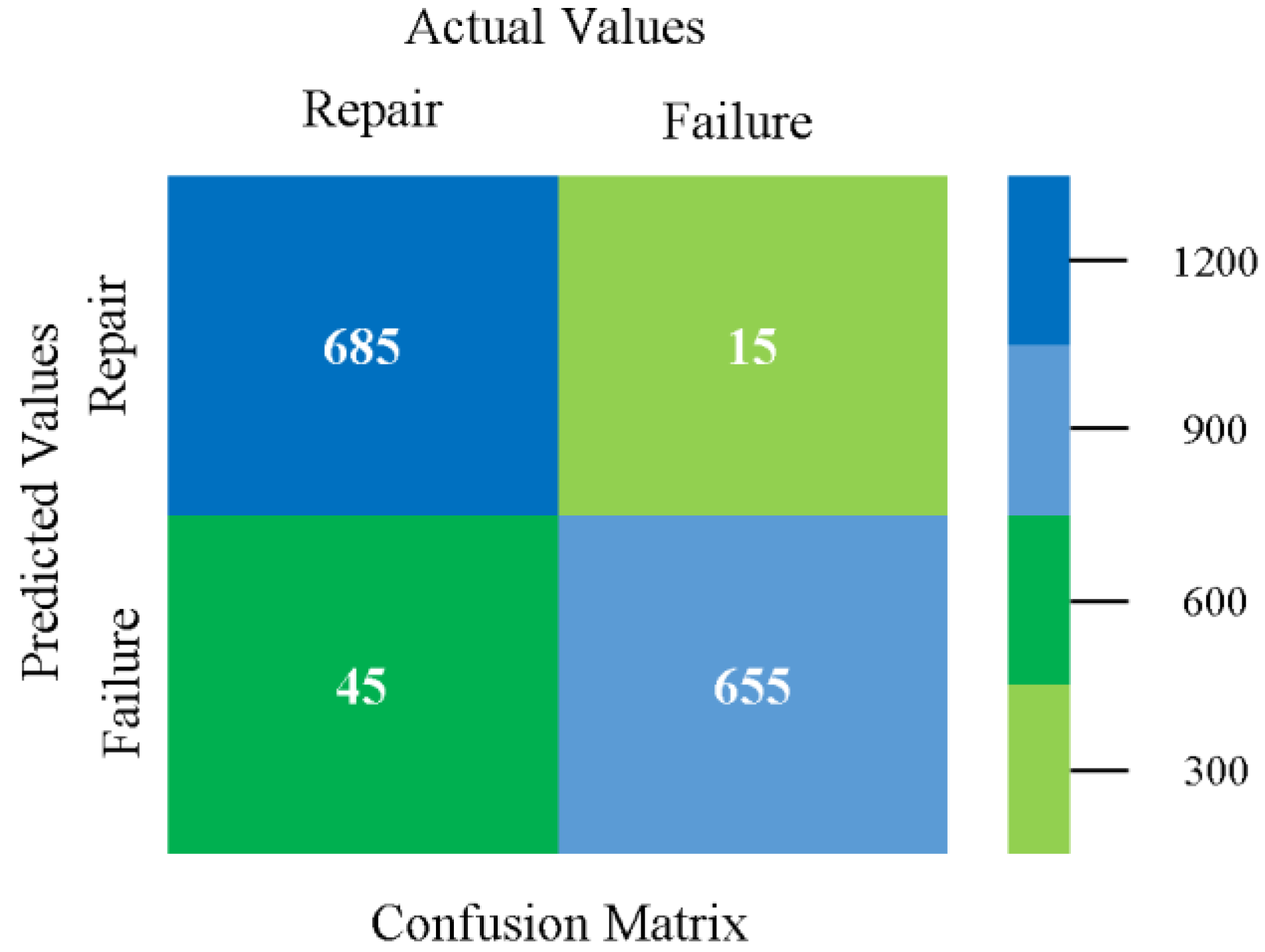
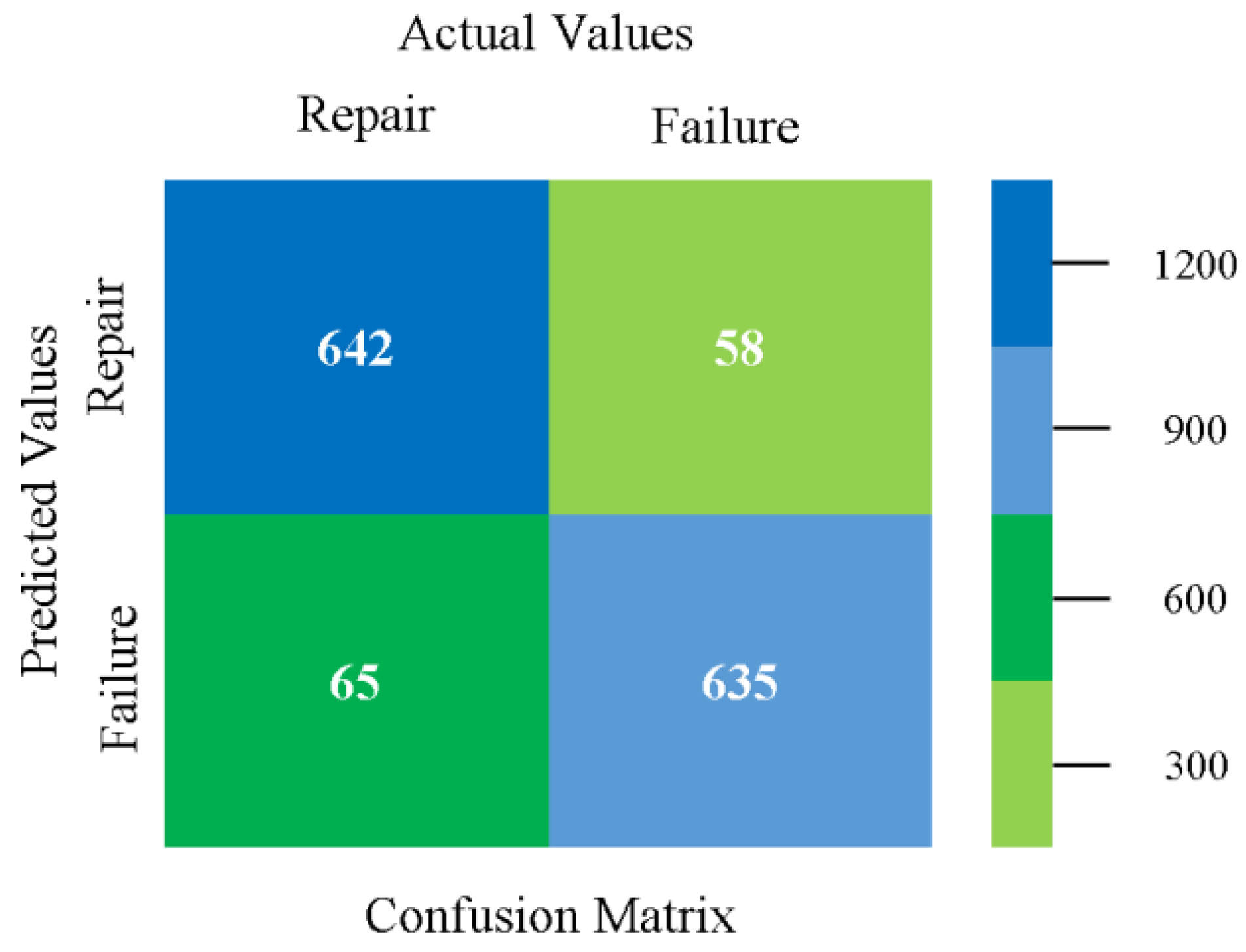
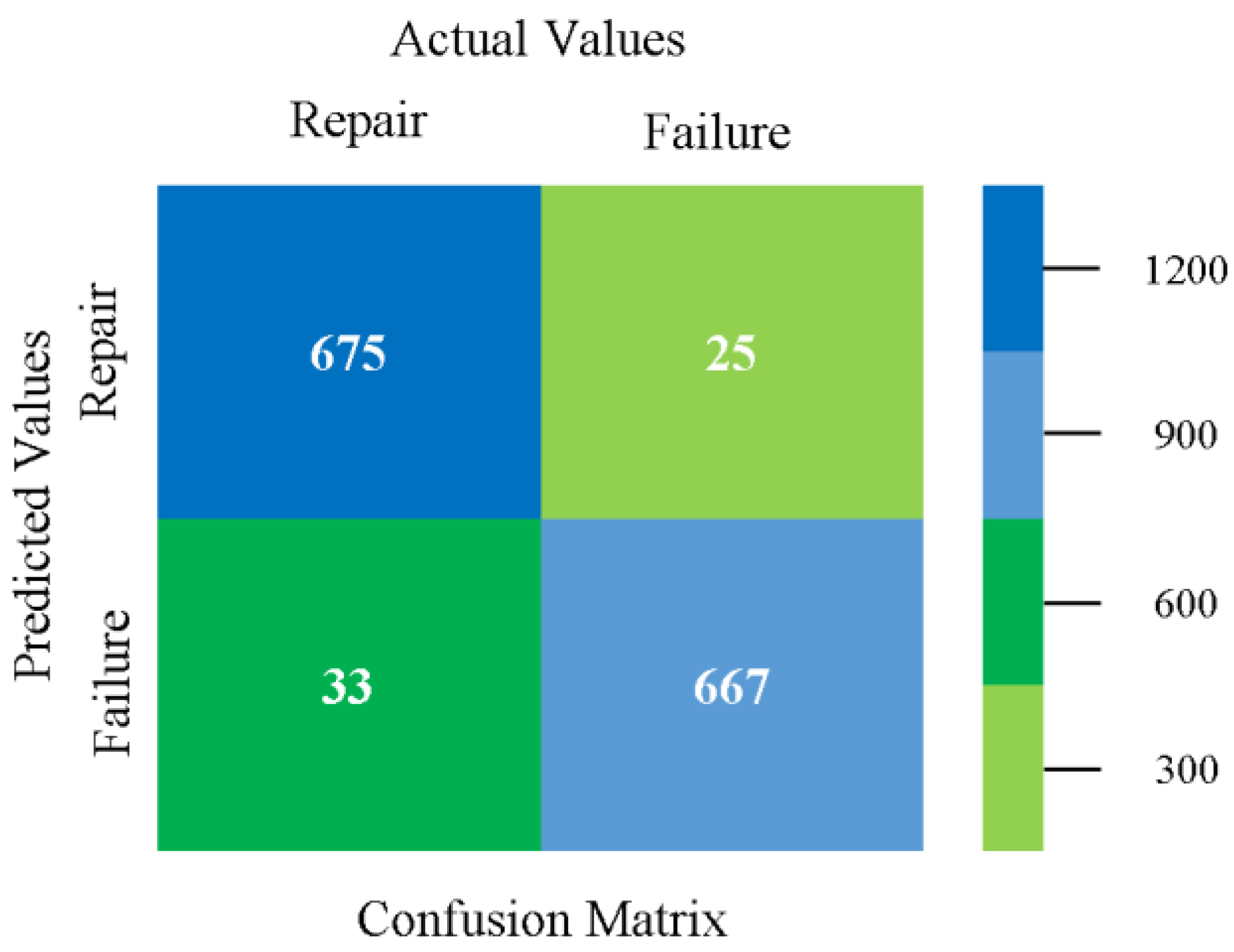
5.4. Modified Sequential Minimal Optimization Results
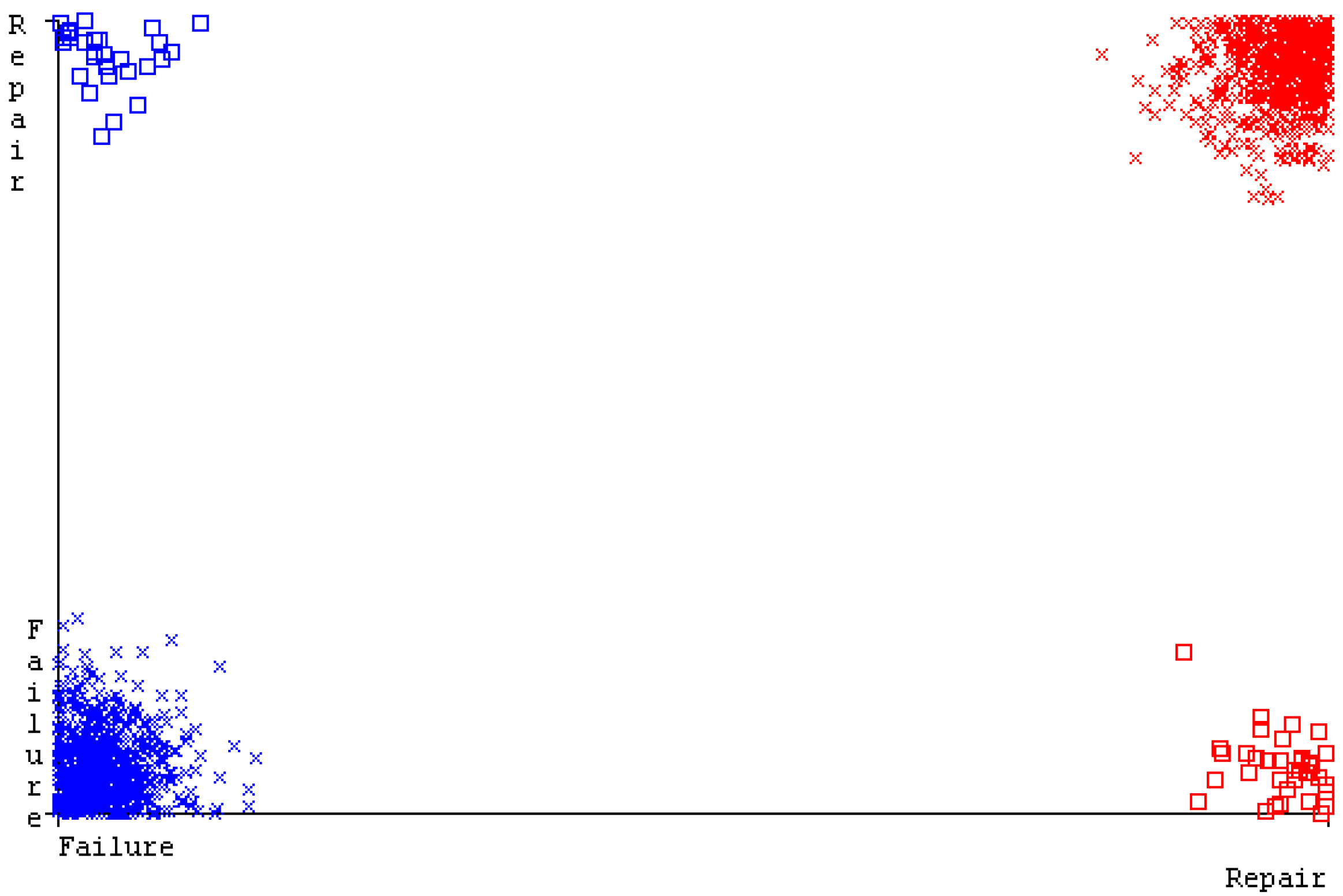
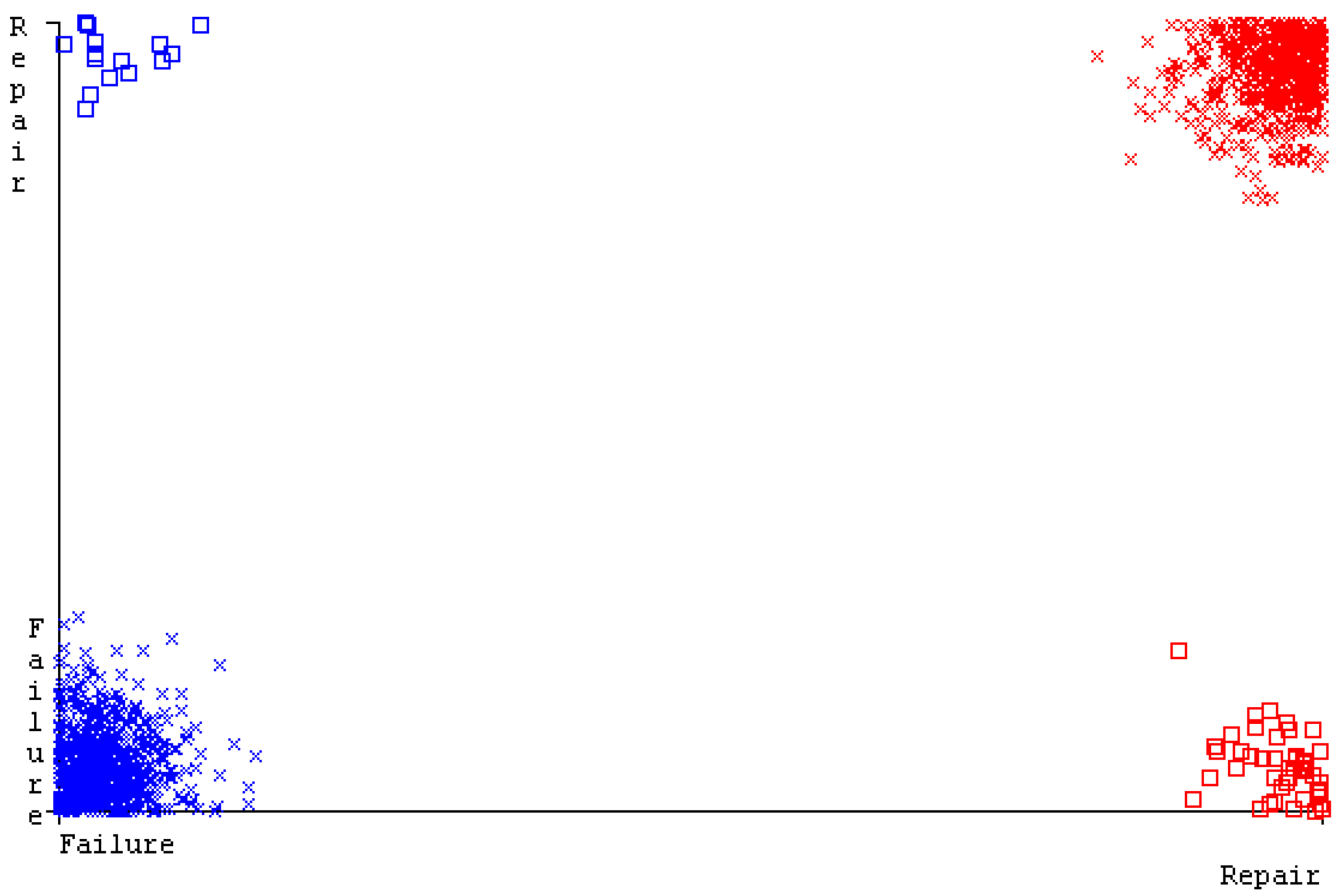
5.5. Simulation Setup of D-CP to Achieve Reliability
5.6. Delta-Checkpointing Results
6. Discussion
7. Conclusions
7.1. Research Contribution
- The challenges of CC and challenges of FT that may compromise the success of reliability in the CC environment were identified from the literature review;
- The reliability of VMs in terms of node failure could have a negative impact on users;
- The MSMO classifier and D-CP FT approach was used to achieve high accuracy, less fault prediction, and successful execution of VMs, which all have a positive impact on users in the CC environment.
7.2. Limitations
- Antarex secondary data collection is possible, but more computational resources are required because this is an HPC fault dataset; however, we can download this dataset through the ZONODO website;
- The Weibull distribution was not provided to generate a fault dataset for primary data generation;
- An effort was made to achieve the primary dataset using the Weibull distribution;
- Achievement of high accuracy and less fault prediction compared to the proposed MSMO classifier results was not available in the computing environment to prove the reliability of the results.
7.3. Future Directions
- Using the Weibull distribution approach, a graphical user interface can be created to generate the primary dataset in cloud simulation 3.0.3;
- Tuning parameters can be automatically adjusted using code, but keep in mind that to find the best tuning parameter value, the code must not become stuck;
- Random forest can be implemented to achieve high accuracy and low fault prediction, but more work on the algorithm’s complexity is required. Comparative analysis can also be performed with this proposed work;
- Deep learning algorithms can also be used to achieve high accuracy while predicting fewer faults. The sample size should be increased. The larger the sample size, the more accurate and reliable the results. When the dataset is large, DL techniques outperform ML techniques;
- Reinforcement learning can be used to implement or improve the FT capability of a system. Such ideas are easily adaptable to cloud environments;
- To achieve reliability, the D-CP approach can be combined with deep learning and reinforcement learning.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sunyaev, A. Internet Computing: Principles of Distributed Systems and Emerging Internet-Based Technologies; Springer International Publishing: Cham, Switzerland, 2020; ISBN 978-3-030-34956-1. [Google Scholar]
- Kumar, S.; Rana, D.S.; Dimri, S.C. Fault Tolerance and Load Balancing Algorithm in Cloud Computing: A Survey. Int. J. Adv. Res. Comput. Commun. Eng. 2015, 4, 92–96. [Google Scholar]
- Shahid, M.A.; Islam, N.; Alam, M.M.; Mazliham, M.S.; Musa, S. Towards Resilient Method: An Exhaustive Survey of Fault Tolerance Methods in the Cloud Computing Environment. Comput. Sci. Rev. 2021, 40, 100398. [Google Scholar] [CrossRef]
- Arabnejad, H.; Pahl, C.; Estrada, G.; Samir, A.; Fowley, F. A Fuzzy Load Balancer for Adaptive Fault Tolerance Management in Cloud Platforms. In Service-Oriented and Cloud Computing; De Paoli, F., Schulte, S., Broch Johnsen, E., Eds.; Lecture Notes in Computer Science; Springer International Publishing: Cham, Switzerland, 2017; Volume 10465, pp. 109–124. ISBN 978-3-319-67261-8. [Google Scholar]
- Mukwevho, M.A.; Celik, T. Toward a Smart Cloud: A Review of Fault-Tolerance Methods in Cloud Systems. IEEE Trans. Serv. Comput. 2021, 14, 589–605. [Google Scholar] [CrossRef]
- Jain, P. A dynamic process for fault tolerance techniques in cloud computing (dpft). J. Gujrat Res. Soc. 2019, 21, 10. [Google Scholar]
- Khaldi, M.; Rebbah, M.; Meftah, B.; Smail, O. Fault Tolerance for a Scientific Workflow System in a Cloud Computing Environment. Int. J. Comput. Appl. 2020, 42, 705–714. [Google Scholar] [CrossRef]
- Mesbahi, M.R.; Rahmani, A.M.; Hosseinzadeh, M. Reliability and High Availability in Cloud Computing Environments: A Reference Roadmap. Hum. Cent. Comput. Inf. Sci. 2018, 8, 20. [Google Scholar] [CrossRef]
- Zhou, A.; Wang, S.; Cheng, B.; Zheng, Z.; Yang, F.; Chang, R.N.; Lyu, M.R.; Buyya, R. Cloud Service Reliability Enhancement via Virtual Machine Placement Optimization. IEEE Trans. Serv. Comput. 2017, 10, 902–913. [Google Scholar] [CrossRef]
- Netti, A.; Kiziltan, Z.; Babaoglu, O.; Sirbu, A.; Bartolini, A.; Borghesi, A. Antarex HPC Fault Dataset. 2018. Available online: https://zenodo.org/record/1453949#.Y-Ij8HVByM8 (accessed on 7 November 2022).
- Weibull Distribution—An Overview|ScienceDirect Topics. Available online: https://www.sciencedirect.com/topics/physics-and-astronomy/weibull-distribution (accessed on 27 November 2022).
- Shahid, M.A.; Islam, N.; Alam, M.M.; Su’ud, M.M.; Musa, S. A Comprehensive Study of Load Balancing Approaches in the Cloud Computing Environment and a Novel Fault Tolerance Approach. IEEE Access 2020, 8, 130500–130526. [Google Scholar] [CrossRef]
- Gupta, V.; Kaur, B.P.; Jangra, S. An Efficient Method for Fault Tolerance in Cloud Environment Using Encryption and Classification. Soft Comput. 2019, 23, 13591–13602. [Google Scholar] [CrossRef]
- Rakesh, M.G.; Baunthiyal, A.; Jain, A.K. Preemptive Fault Tolerance in DDS Based Distributed System Using Application Migration. IJRASET 2020, 8, 963–970. [Google Scholar] [CrossRef]
- Efficient Fault Tolerance on Cloud Environments. Available online: https://www.researchgate.net/publication/326102831_Efficient_Fault_Tolerance_on_Cloud_Environments (accessed on 27 November 2022).
- Edemo, M.K. Developing Fault Tolerance Architecture for Real-Time Systems of Cloud Computing; Addis Ababa Science and Technology University: Addis Ababa, Ethiopia, 2019; p. 94. [Google Scholar]
- Kamiri, J.; Mariga, G. Research Methods in Machine Learning: A Content Analysis. Int. J. Comput. Inf. Technol. 2021, 10, 15. [Google Scholar] [CrossRef]
- Sarker, I.H. Machine Learning: Algorithms, Real-World Applications and Research Directions. SN Comput. Sci. 2021, 2, 160. [Google Scholar] [CrossRef]
- Butt, U.A.; Mehmood, M.; Shah, S.B.H.; Amin, R.; Shaukat, M.W.; Raza, S.M.; Suh, D.Y.; Piran, M.J. A Review of Machine Learning Algorithms for Cloud Computing Security. Electronics 2020, 9, 1379. [Google Scholar] [CrossRef]
- Sun, S.; Cao, Z.; Zhu, H.; Zhao, J. A Survey of Optimization Methods from a Machine Learning Perspective. IEEE Trans. Cybern. 2020, 50, 3668–3681. [Google Scholar] [CrossRef] [PubMed]
- Kochhar, D.; Kumar, A.; Hilda, J. An approach for fault tolerance in cloud computing using machine learning technique. Int. J. Pure Appl. Math. 2017, 117, 345–351. [Google Scholar]
- Chang, C.-C.; Lin, C.-J. LIBSVM: A Library for Support Vector Machines. ACM Trans. Intell. Syst. Technol. 2011, 2, 1–27. [Google Scholar] [CrossRef]
- Mohamad, N.A.; Ali, Z.; Noor, N.M.; Baharum, A. Multinomial Logistic Regression Modelling of Stress Level among Secondary School Teachers in Kubang Pasu District, Kedah. AIP Conf. Proc. 2016, 1750, 060018. [Google Scholar]
- Li, C.R.; Guo, J. An Improved Algorithm for Parallelizing Sequential Minimal Optimization. In Proceedings of the 2015 International Conference on Industrial Technology and Management Science, Tianjin, China, 27–28 March 2015; Atlantis Press: Beijing, China, 2015. [Google Scholar]
- Sen, P.C.; Hajra, M.; Ghosh, M. Supervised Classification Algorithms in Machine Learning: A Survey and Review. In Emerging Technology in Modelling and Graphics; Mandal, J.K., Bhattacharya, D., Eds.; Advances in Intelligent Systems and Computing; Springer Singapore: Singapore, 2020; Volume 937, pp. 99–111. ISBN 9789811374029. [Google Scholar]
- Attallah, S.M.A.; Fayek, M.B.; Nassar, S.M.; Hemayed, E.E. Proactive Load Balancing Fault Tolerance Algorithm in Cloud Computing. Concurr. Comput. Pract. Exp. 2021, 33, e6172. [Google Scholar] [CrossRef]
- Suguna, S.; Devi, K. VMFT: Virtual Machine Fault Tolerance in Cloud Computing. Int. J. Innov. Sci. Res. 2016, 22, 256. [Google Scholar]
- Netti, A.; Kiziltan, Z.; Babaoglu, O.; Sîrbu, A.; Bartolini, A.; Borghesi, A. A Machine Learning Approach to Online Fault Classification in HPC Systems. Future Gener. Comput. Syst. 2020, 110, 1009–1022. [Google Scholar] [CrossRef]
- John, G.H.; Langley, P. Estimating Continuous Distributions in Bayesian Classifiers. arXiv 2013, arXiv:1302.4964. [Google Scholar]
- Ramadhan, W.P.; Astri Novianty, S.T.M.T.; Casi Setianingsih, S.T.M.T. Sentiment Analysis Using Multinomial Logistic Regression. In Proceedings of the 2017 International Conference on Control, Electronics, Renewable Energy and Communications (ICCREC), Yogyakarta, Indonesia, 26–28 September 2017; pp. 46–49. [Google Scholar]
- How Multinomial Logistic Regression Model Works in Machine Learning. Available online: https://dataaspirant.com/multinomial-logistic-regression-model-works-machine-learning/ (accessed on 27 November 2022).
- Platt, J.C. Sequential Minimal Optimization: A Fast Algorithm for Training Support Vector Machines. p. 21. Available online: https://web.iitd.ac.in/~sumeet/tr-98-14.pdf (accessed on 27 November 2022).
- Noronha, D.H.; Torquato, M.F.; Fernandes, M.A.C. A Parallel Implementation of Sequential Minimal Optimization on FPGA. Microprocess. Microsyst. 2019, 69, 138–151. [Google Scholar] [CrossRef]
- Moldagulova, A.; Sulaiman, R.B. Using KNN Algorithm for Classification of Textual Documents. In Proceedings of the 2017 8th International Conference on Information Technology (ICIT), Amman, Jordan, 17–18 May 2017; pp. 665–671. [Google Scholar]
- Mynavathi, R.; Bhuvaneswari, V.; Karthikeyan, T.; Kavina, C. K Nearest Neighbor Classifier over Secured Perturbed Data. In Proceedings of the 2016 World Conference on Futuristic Trends in Research and Innovation for Social Welfare (Startup Conclave), Coimbatore, India, 29 February–1 March 2016; pp. 1–4. [Google Scholar]
- Shah, K.; Patel, H.; Sanghvi, D.; Shah, M. A Comparative Analysis of Logistic Regression, Random Forest and KNN Models for the Text Classification. Augment. Hum. Res. 2020, 5, 12. [Google Scholar] [CrossRef]
- Amoon, M. Adaptive Framework for Reliable Cloud Computing Environment. IEEE Access 2016, 4, 9469–9478. [Google Scholar] [CrossRef]
- Charity, T.J.; Hua, G.C. Resource Reliability Using Fault Tolerance in Cloud Computing. In Proceedings of the 2016 2nd International Conference on Next Generation Computing Technologies (NGCT), Dehradun, India, 14–16 October 2016; pp. 65–71. [Google Scholar]
- Hodson, T.O. Root-Mean-Square Error (RMSE) or Mean Absolute Error (MAE): When to Use Them or Not. Geosci. Model Dev. 2022, 15, 5481–5487. [Google Scholar] [CrossRef]
- Relative Absolute Error. Available online: https://www.gepsoft.com/GeneXproTools/AnalysesAndComputations/MeasuresOfFit/RelativeAbsoluteError.htm (accessed on 22 December 2022).
- Merlini, D.; Rossini, M. Text Categorization with WEKA: A Survey. Mach. Learn. Appl. 2021, 4, 100033. [Google Scholar] [CrossRef]
- Bilal, A.; Hasany, S.M.N.; Pitafi, A.H. Effective Modelling of Sinkhole Detection Algorithm for Edge-Based Internet of Things (IoT) Sensing Devices. IET Commun. 2022, 16, 845–855. [Google Scholar] [CrossRef]



























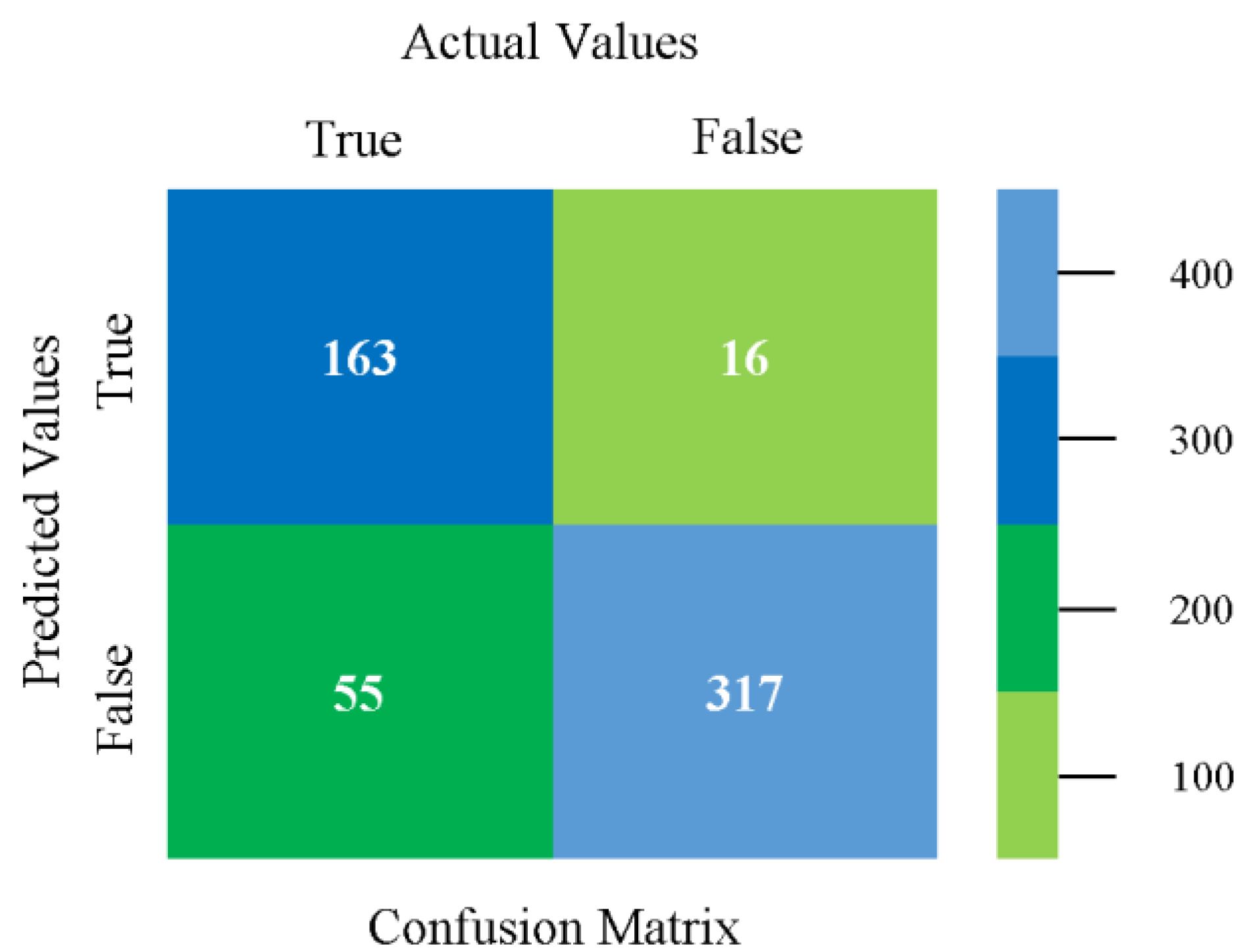
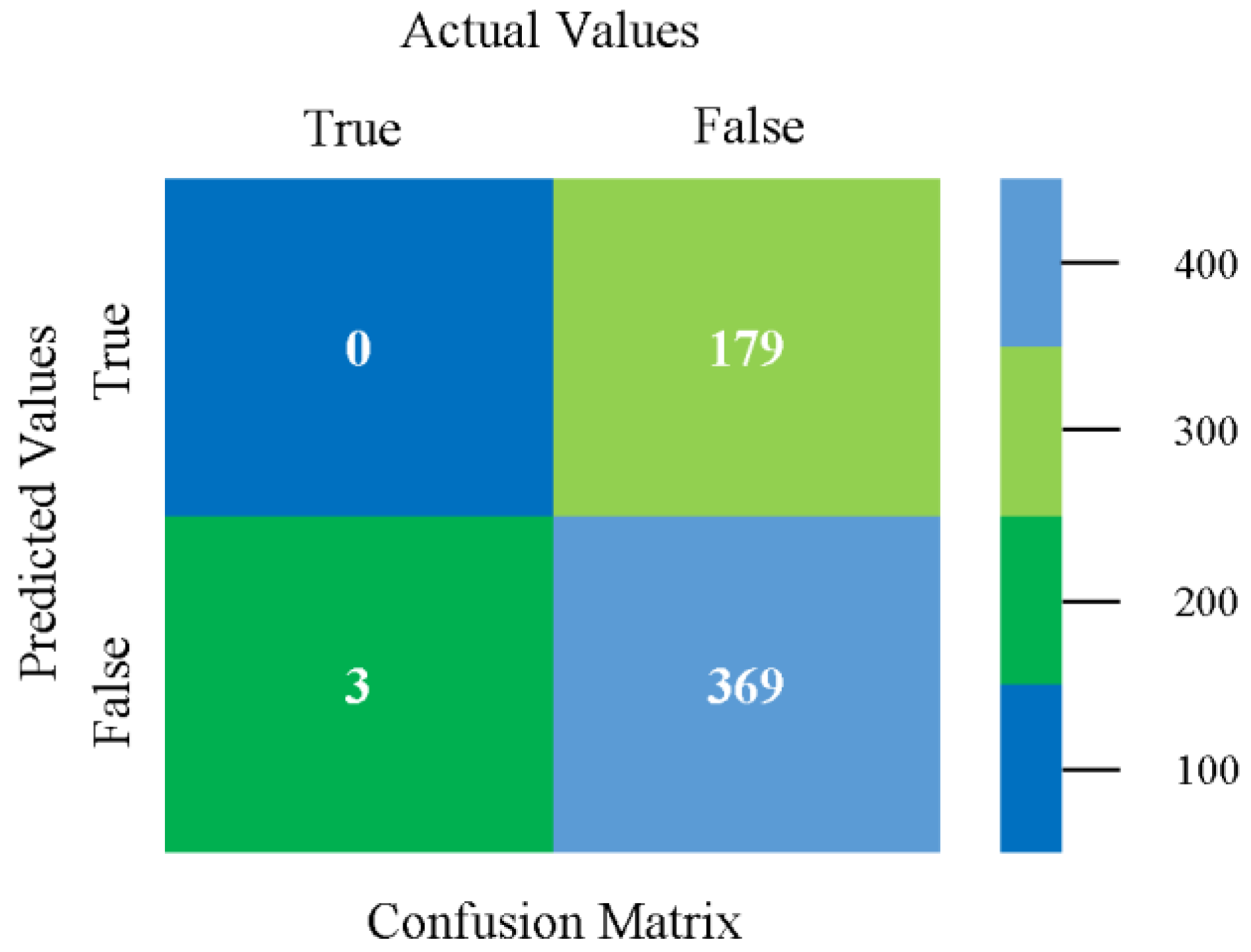
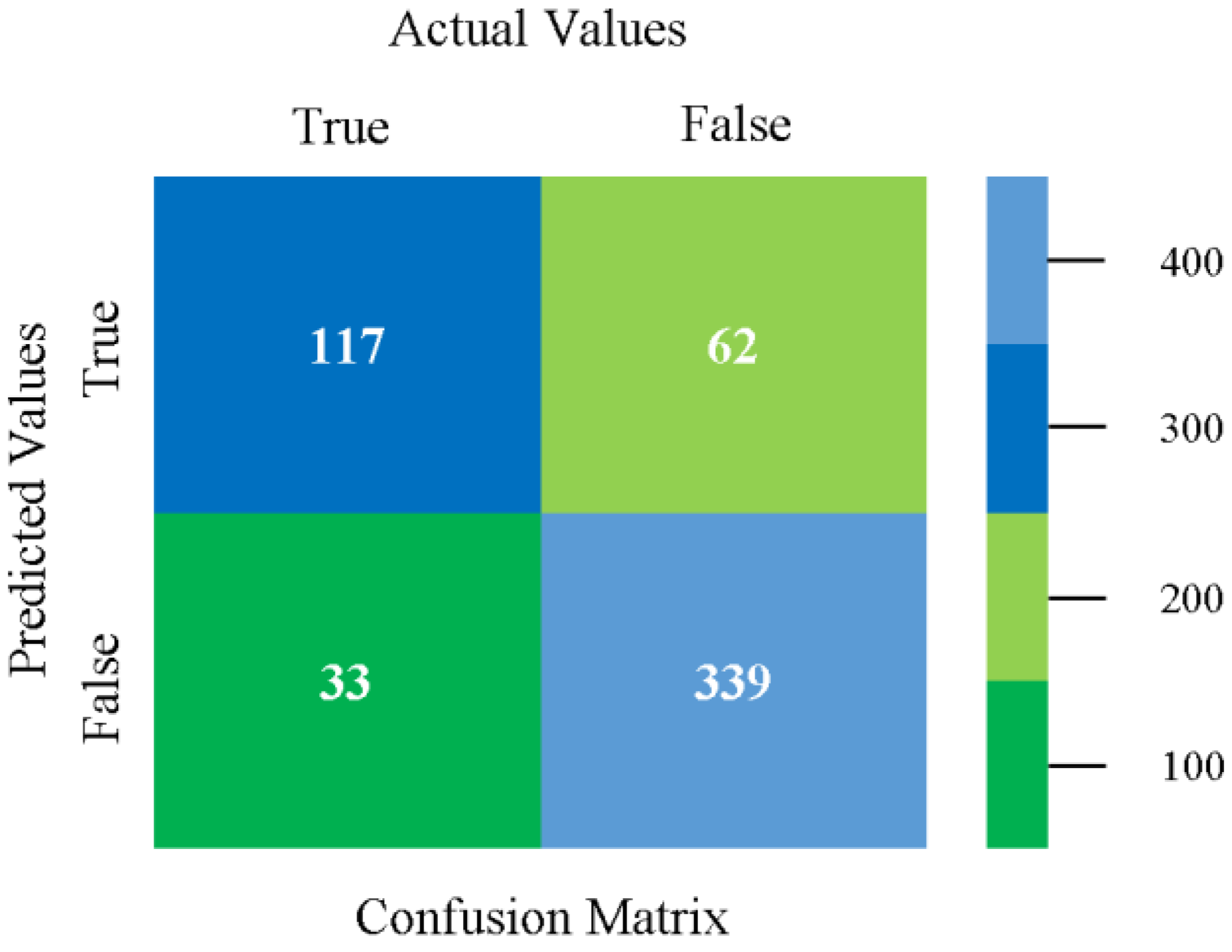
















| Ref | Author Name | Year | Benefits | Drawbacks |
|---|---|---|---|---|
| [12] | Muhammad Asim Shahid et al. | 2020 | They identify the need for FT efficiency metrics in algorithms in this article, which is one of the main concerns in cloud environments. | They do not provide quality of service in terms of reliability. |
| [13] | Vipul Gupta et al. | 2019 | In this article, they show that the accuracy value of the fault tolerance is 79%, which is better than in the existing method. | They do not provide classification techniques for selecting fault-tolerance nodes based on virtual machine success/failure. |
| [14] | Rakesh et al. | 2020 | In this article, reactive FT mechanisms were found to likely result in failure. | In this article, they do not implement machine learning algorithms for better fault prediction, so they are not providing high accuracy and less fault prediction. |
| [15] | Sam Goundar and Akashdeep Bhardwaj | 2018 | This article discusses fault-tolerance systems for cloud computing environments and examines whether or not they are effective in a cloud environment. | They do not address accuracy and fault prediction to achieve reliability. |
| [16] | Mihiretu Kebede Edemo | 2019 | The author created a fault-tolerance architecture that can effectively use versions in real-time cloud computing systems. | The limitation is that the architecture cannot tolerate faults if an equal number of versions fail in each subpart at the same time, especially if the number of failed versions exceeds the number of error-free versions in all subparts. |
| [17] | Jackson Kamiri and Geoffrey Mariga | 2021 | The primary goal of this paper was to investigate current machine learning research methods, emerging themes, and the implications of those themes in machine learning research. | They do not offer content analysis for machine learning applications such as supervised learning, text analytics, classification, and prediction. |
| [18] | Iqbal H. Sarker | 2021 | The author provides a comprehensive overview of machine learning algorithms, which can be used to improve an application’s intelligence and capabilities. | There is a lack of analysis on machine learning algorithms. |
| [19] | Umer Ahmed Butt et al. | 2020 | They present an analysis of CC security threats, issues, and solutions that used one or more ML algorithms in this review paper. | There is a lack of a proposed solution to achieve reliability based on VM failure. |
| [20] | Shiliang Sun et al. | 2019 | In this article, they use of ML algorithms to improve accuracy. | There is a lack of challenges and open problems in ML optimization methods. |
| [21] | Deepak Kochhar et al. | 2017 | The proactive fault-tolerance technique is used in this article, and they propose using the NB classifier to classify the nodes. | There is a lack of use of other classification algorithms to improve accuracy and achieve less fault prediction. |
| [22] | Chih-Chung Chang and Chih-Jen Lin | 2022 | In this article, they present the implementation of LibSVM and discuss all issues. | There is a lack of ensuring good system reliability. |
| [23] | Nor Amira Mohamad et al. | 2016 | This study used MLR model to determine fault prediction. | There is a lack of use of other classification algorithms to determine fault prediction. |
| [24] | C.R. LI and J. GUO | 2015 | The authors of this paper proposed an improved version of SVM that can avoid falling into endless loops. | The article was unable to determine the optimal parameter in an n-way that can speed up training. |
| [25] | Pratap Chandra Sen et al. | 2020 | This paper attempts to compare various types of classification algorithms and provides a thorough review of all supervised learning classifications. | There is a lack of a proposed solution to achieve reliability based on VM failure. |
| [26] | Salma M.A. Attallah et al. | 2020 | The main goal of the proposed model is to track changes in CPU utilization and make a decision when a high value of CPU utilization is identified. | There is a lack of a proposed solution to achieve reliability based on VM failure. |
| [27] | S. Suguna and K. Devi | 2015 | The authors proposed a virtual machine fault-tolerance technique in this article to achieve reliability. | In this article, the authors only achieved one virtual machine result that was successful, and the remaining were failures. |
| Dataset Directories | Attributes | Attributes Names + Types | Instances | |||
|---|---|---|---|---|---|---|
| CPU-Mem Mono | 8 |
| Nume |
| Nomi | 4005 |
| CPU- Mem Multi | 8 |
| Nomi |
| Nume | 4380 |
| HDD Mono | 8 |
| Nume |
| Nume | 3244 |
| HDD Multi | 8 |
| Nomi |
| Nomi | 2493 |
| User | Port NO | Host NO | Network Host | Distribution |
|---|---|---|---|---|
| 1 | 16 | 192 | Mips, Ram, Storage, and Bandwidth | Weibull (this includes both rising and decreasing failure rate functions). |
| Attributes | Attributes Names | Attributes Type | Instances | |
|---|---|---|---|---|
| 7 |
|
| Numeric and Nominal | 1400 |
|
| |||
|
| |||
| ||||
| Classifiers | Configuration Parameters | Values |
|---|---|---|
| NB | Batch size | 100 |
| Debug | False | |
| Display model in old format | False | |
| Do not check capabilities | False | |
| Num decimal places | 2 | |
| Use kernel estimator | False | |
| Use supervised discretization | False | |
| LIBSVM | SVM type | C-SVC (Classification) |
| Degree | 3 | |
| EPS | 0.001 | |
| Gamma | 0.0 | |
| Kernel type | radial basic function | |
| Normalize | False | |
| Seed | 1 | |
| MLR | Batch size | 100 |
| Do not check capabilities | False | |
| Num decimal places | 4 | |
| Ridge | 1.0 × 10−8 | |
| SMO | C complexity parameter | 1.0 |
| Epsilon | 1.0 × 10−12 | |
| Filter type | normalize training data | |
| Kernel | Polykernel −10 1.0−C 25,007 | |
| Num folds | 1 | |
| Random seed | 1 | |
| Tolerance parameter | 0.001 | |
| KNN | KNN | 1 |
| Batch size | 100 | |
| Cross validate | False | |
| Nearest neighbor search algorithm | linear NN search | |
| RF | Batch size | 100 |
| Max depth | 0 | |
| Num decimal places | 2 | |
| Num features | 0 | |
| Num iterations | 100 | |
| Seed | 1 |
| System | |
|---|---|
| Processor | Intel (R) Core (TM) i7 2620M CPU 2.7 GHz |
| RAM | 8.00 GB |
| Windows | 8.1 Platform |
| IDE | WEKA (3.8.6) |
| Weka Interface | Explorer |
| Java Version | 17.0.2 |
| System | |
|---|---|
| Processor | Intel (R) Core (TM) i7 2620M CPU 2.7 GHz |
| RAM | 8.00 GB |
| Windows | 8.1 Platform |
| IDE-1 | Eclipse IDE for Java Developer Release 2021-09 (4.21.0) |
| IDE-2 | Cloud simulation 3.0.3 |
| Parameters | Values |
|---|---|
| Number of cloud users | 1 |
| Number of data centers | 1 |
| Number of VMs | 11 |
| VM frequency | 1000 MIPS |
| VM memory (RAM) | 4 GB |
| VM bandwidth | 10 Gbps |
| VM storage | 1000 GB |
| Cloudlet ID | Status | DC ID | VM ID | Time | Start Time | Finish Time |
|---|---|---|---|---|---|---|
| 69 | SUCCESS | 1029 | 282 | 36,534 | 0 | 36,534 |
| 98 | SUCCESS | 1029 | 1385 | 36,640 | 0 | 36,640 |
| 74 | SUCCESS | 1029 | 780 | 37,189 | 0 | 37,189 |
| 40 | SUCCESS | 1029 | 1121 | 37,575 | 0 | 37,575 |
| 105 | SUCCESS | 1029 | 774 | 37,855 | 0 | 37,855 |
| 0 | SUCCESS | 1029 | 2992 | 38,030 | 0 | 38,030 |
| 44 | SUCCESS | 1029 | 375 | 38,225 | 0 | 38,225 |
| 87 | SUCCESS | 1029 | 3771 | 38,226 | 0 | 38,226 |
| 77 | SUCCESS | 1029 | 457 | 38,302 | 0 | 38,302 |
| 142 | SUCCESS | 1029 | 2064 | 38,535 | 0 | 38,535 |
| 128 | SUCCESS | 1029 | 3227 | 38,758 | 0 | 38,758 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shahid, M.A.; Alam, M.M.; Su’ud, M.M. Achieving Reliability in Cloud Computing by a Novel Hybrid Approach. Sensors 2023, 23, 1965. https://doi.org/10.3390/s23041965
Shahid MA, Alam MM, Su’ud MM. Achieving Reliability in Cloud Computing by a Novel Hybrid Approach. Sensors. 2023; 23(4):1965. https://doi.org/10.3390/s23041965
Chicago/Turabian StyleShahid, Muhammad Asim, Muhammad Mansoor Alam, and Mazliham Mohd Su’ud. 2023. "Achieving Reliability in Cloud Computing by a Novel Hybrid Approach" Sensors 23, no. 4: 1965. https://doi.org/10.3390/s23041965
APA StyleShahid, M. A., Alam, M. M., & Su’ud, M. M. (2023). Achieving Reliability in Cloud Computing by a Novel Hybrid Approach. Sensors, 23(4), 1965. https://doi.org/10.3390/s23041965






