In this section, experimental strain and displacement results will be presented, derived from core instrumentation, and compared to surface instrumentation.
3.1. LVDTs and DFOS
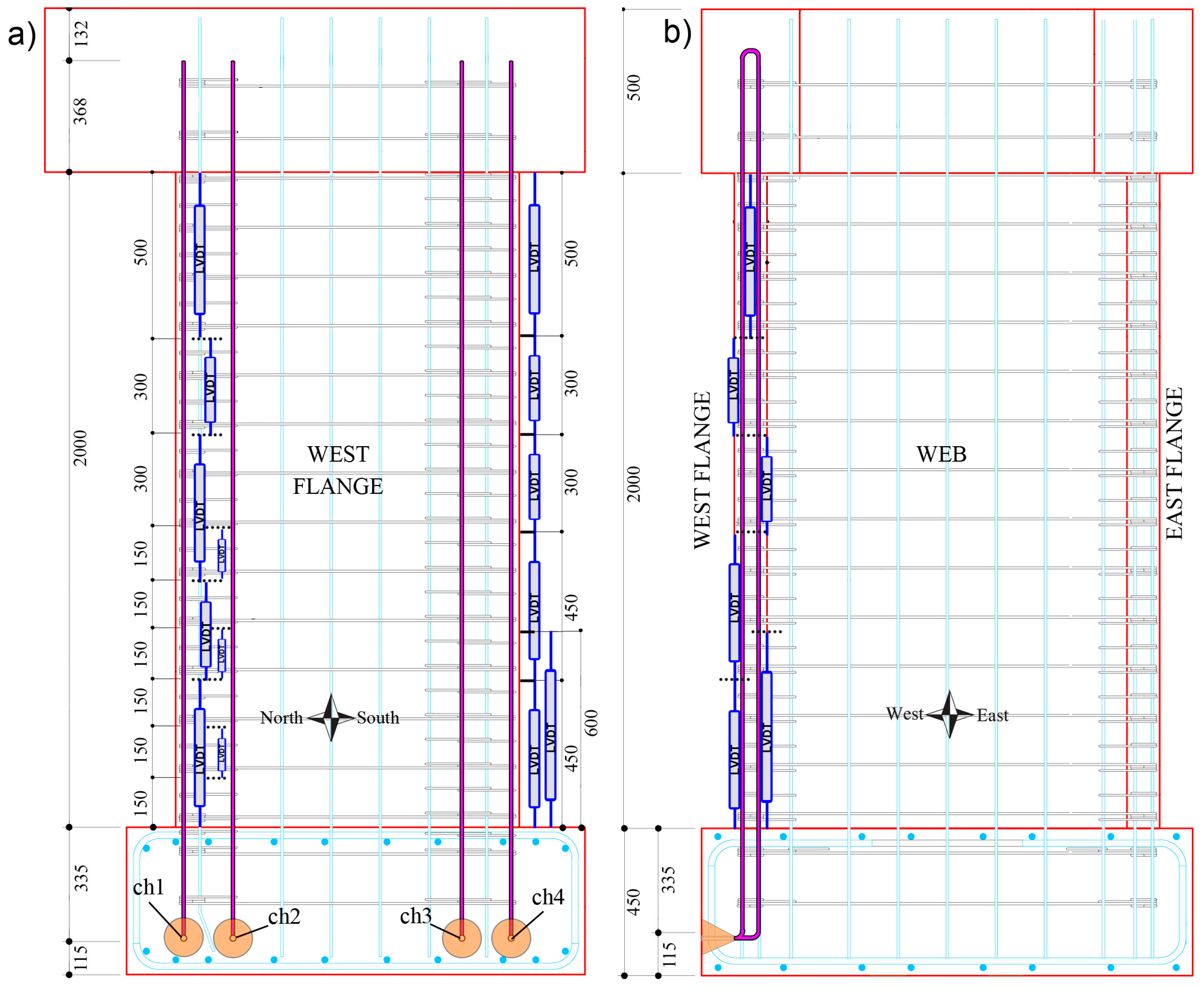
This section compares the average strains calculated from the two arrays of LVDTs, located on the west flange towards the north (i.e., flange-web intersection) and south (boundary end), with the channels 1 (“ch1”) and 4 (“ch4”) of the DFOS system (
Figure 3), respectively.
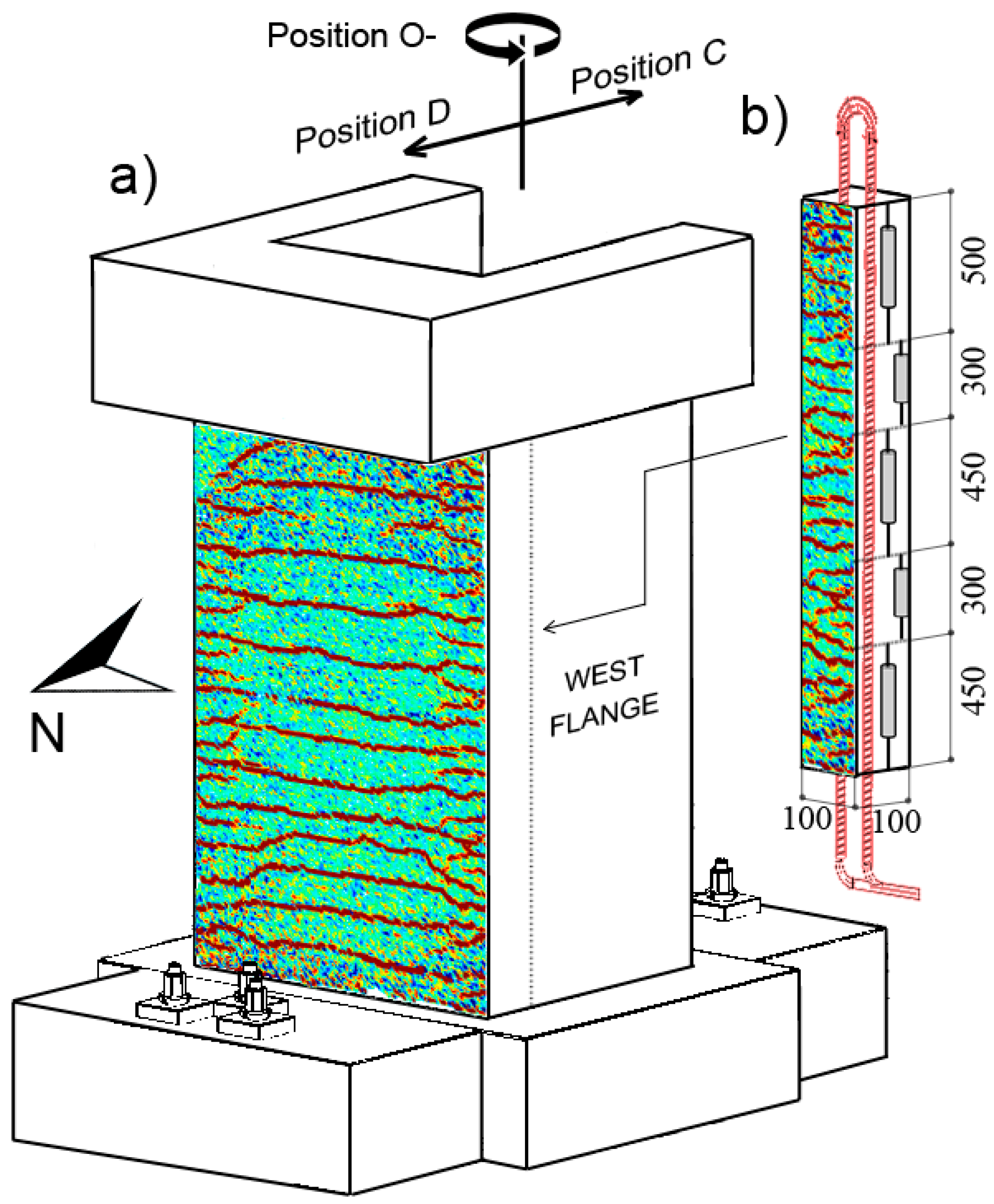
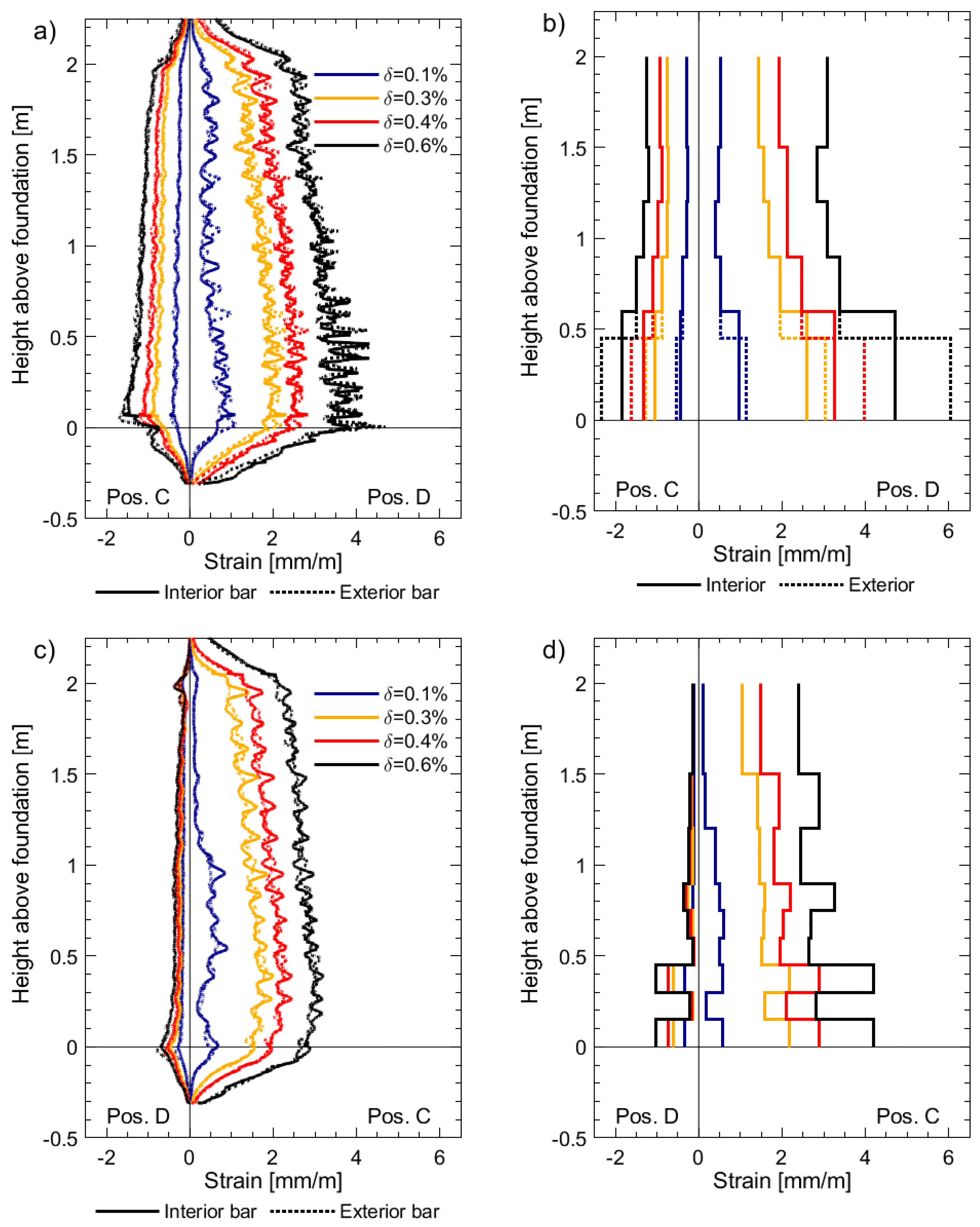
Figure 7 presents the strain profiles derived from DFOS and LVDTs for specimen UW1, which was subjected to in-plane bending about its minor axis (positions C and D,
Figure 2a) at different imposed drifts. Both of the LVDTs at the base of the boundary end, i.e., the exterior and interior LVDTs pictured in
Figure 6, with base lengths of 450 mm and 600 mm, respectively, were used to derive the base strains in
Figure 7b. As expected, the base strain for the 450 mm LVDT is larger than for the 600 mm LVDT, since the contribution of the strain penetration in the foundation is unsurprisingly more significant than the wall deformation between the heights of 450 mm and 600 mm. As is well known in the structural and seismic design and analysis of RC structures, strain penetration effects can contribute to a significant amount of the overall lateral displacement capacity [
41]. Additionally, it can be observed that the LVDT tensile strains at the base are, in general, greater than those measured on average by the DFOS. For example, in
Figure 7b, when the wall is pushed towards position D and the west flange boundary end is in tension, the base strain determined from the exterior bottom LVDT (450 mm base length) is approximately 6 mm/m for a drift (
δ) of 0.6%, whereas ch4 of the DFOS measures an average strain of 3.6 mm/m (
Figure 7a) over the same base length of 450 mm. It is interesting to note that the DFOS on the exterior rebar outputs a strain at the foundation wall interface crack of 4.6 mm/m, attaining a local minimum of 3.3 mm/m at mid-crack spacing above (i.e., at a height of approximately 40 mm); such variation will increase for walls UW2 and UW3, as it will be shown. In reality, recalling that the DFOS results correspond to a moving average over a length of approximately 10 mm, the peak strain of 4.6 mm/m hides, in fact, a larger local strain of 6.1 mm/m. The discrepancy between base LVDT measurements and DFOS can again be explained due to the effects of strain penetration, which are not considered in the LVDT-derived strain outputs. Had strain penetration effects been considered, they would increase the required effective base length for strain computations. In fact, without the strains from the DFOS, which clearly capture the strain penetration into the foundation, it is very difficult to determine the contribution to the LVDT strain output coming from deformations inside the foundation. Other investigations have proposed methods aiming at approximately removing deformation contributions in RC members from outside the gauged region [
42]. Please also refer to
Section 3.3. LVDT chains, such as those used here at the extreme compression and tension fiber regions of the wall, are used in most wall tests to determine average curvatures along the wall height [
43]. However, without consideration of strain penetration effects, it is inevitable that base curvatures are overestimated using these LVDT average strains. Previous researchers have recommended that the base length of the lowest instrument in the LVDT chain be sufficiently small, such that it only extends over the base crack between the wall and foundation [
43]. However, even when using a sufficiently small base length, the resulting strains and curvatures from the LVDTs will not be accurately represented without defining a meaningful base length that includes the strain penetration [
44]. The average strains determined by the LVDTs higher up the wall from the base appear to provide more reasonable estimates in comparison to the DFOS strain profiles in
Figure 7.
The measured strain profiles for the interior and exterior longitudinal rebars (along the thickness) are almost identical, which was expected with the type of loading subjected to unit UW1. In addition to the gradual change of strain along the wall height, local strain peaks can be observed from the DFOS in
Figure 7a,c, which correspond to the location of flexural cracks. Using the tensile strain profile from channel 4 of the DFOS for
δ = 0.6% (
Figure 7a, position D), the average spacing of these strain peaks (crack spacing) was calculated to be 68 mm, which is approximately the spacing of the stirrups (≈ 75 mm), corroborating previous observations in beams [
13].
In comparison to the DFOS strain profiles, the resulting LVDT strain profiles appear to be very dependent on where the surface sensors are placed. A good example is shown in
Figure 7d, where two peaks in tensile strain can be observed at a height of approximately 0.85 m and 1.35 m from the foundation. In comparison to the gradual and smooth DFOS strains in
Figure 7c, these peaks of tensile strain calculated from the LVDTs are likely caused by asymmetric inclusion of concrete surface cracks in the gauged areas.
Figure 8 presents the strain profiles derived from DFOS and LVDTs for specimen UW2, which was subjected to a reverse-cyclic rotation about its vertical axis (positions O+ and O−,
Figure 2a). Unfortunately, one of the LVDTs on the face of the west flange-web intersection, from a height between 900 mm and 1200 mm, malfunctioned, and hence there is a loss of information in
Figure 8d. Many of the same comparisons observed for UW1 in the previous paragraphs can be made here with respect to the results in
Figure 8 for UW2. However, unlike the loading imposed to UW1, the rotation applied to UW2 resulted in a strain gradient across the flange thickness, and hence a difference in the DFOS strain profiles was measured for the interior and exterior rebars, particularly for the west flange boundary end in
Figure 8a. This difference in strain, which is due to the combination of circulatory and warping torsion [
45] of the flange, is not captured with the array of LVDTs, although there is clearly some difference in tensile strains calculated by the two base LVDTs in
Figure 8b. Thus, the LVDT surface instrumentation, in comparison to the DFOS, is unable to capture the detailed information about the behavior of the wall with regards to strain gradients across the thickness of the wall.
Figure 8a,c also clearly show the existence of a steep moment gradient along the flange height, which can only be very insufficiently captured by the LVDTs. It is hence not surprising that the peak strain measured by channel 4 of the DFOS at the foundation wall interface, which takes a value of 6.5 mm/m, is larger than the average strain of 5.4 mm/m given by the bottom LVDT, unlike what happened for UW1. The strains measured by the DFOS attached to the interior bar in the boundary end of UW2 capture the compression at the head of the wall and tensile strains at the base when loaded to position O+ (
Figure 8a). Such distribution is not captured by the LVDT array in the boundary end (
Figure 8b), and instead, the average strains at the top of the wall, over a base length of 500 mm, are close to zero. As explained in the data paper [
19], it is postulated that the application of the axial load to the walls, which was distributed evenly to three vertical actuators, is responsible for the partial warping restraint, corresponding to this observed behavior. It is worth mentioning that while it was possible to place two LVDTs at the base of the boundary end, two layers of LVDTs could not be achieved along the full height of the west flange boundary end because of the small thickness of 100 mm.
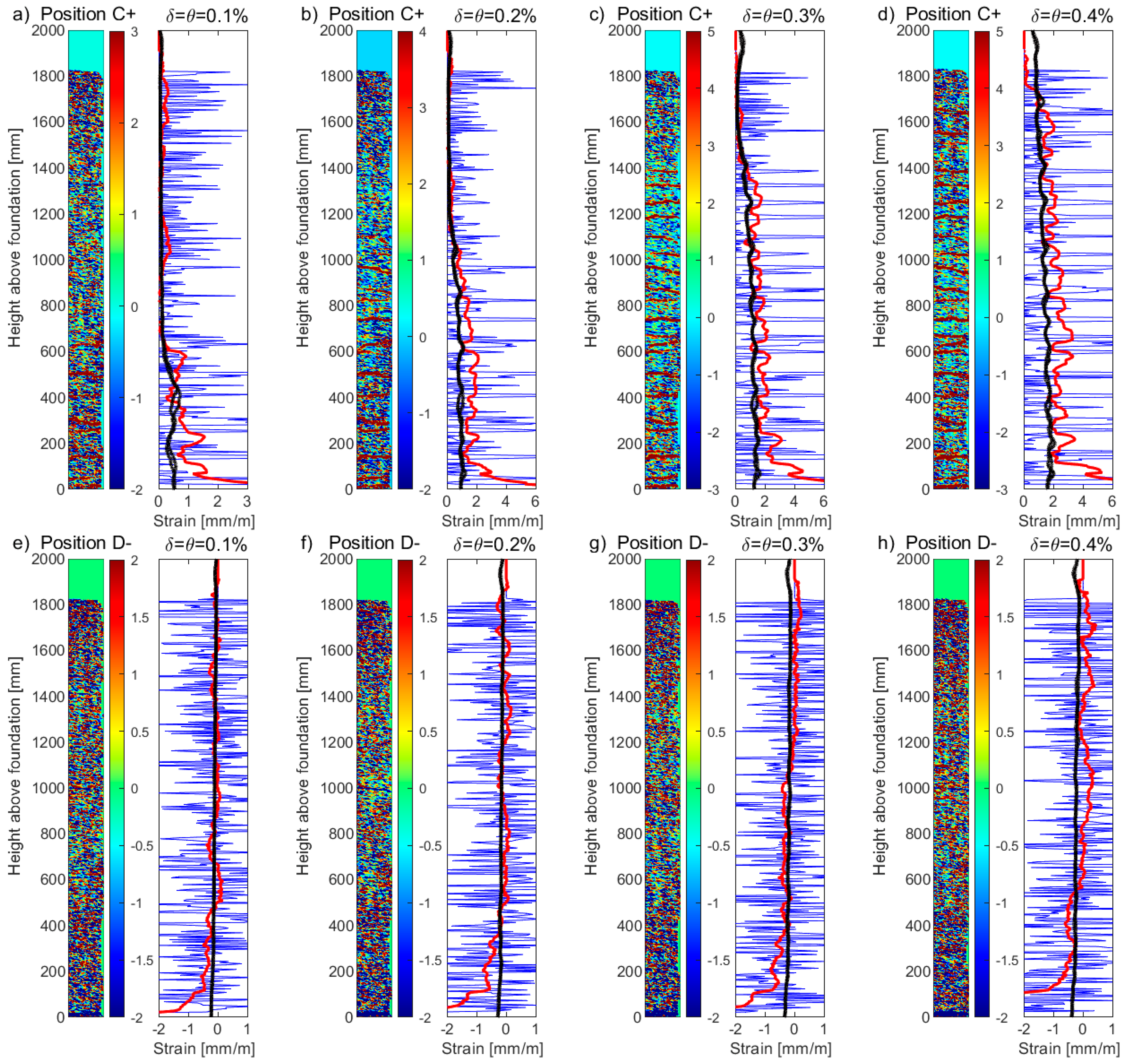
Figure 9 presents the strain profiles derived from the DFOS and LVDTs for specimen UW3, which was simultaneously subjected to both an in-plane translation and twist (positions D- and C+,
Figure 2a). Some of the observations for the comparisons made between the LVDTs and DFOS strains for UW1 and UW2 are consistent with the strain profiles in
Figure 9. for UW3. For this wall unit, a drift (δ) and simultaneous rotation (θ) of 0.8% and 8 mrad, respectively, result in DFOS tensile strains in the boundary end rebars greater than yield (>2.9 mm/m) at position D− (
Figure 9a). For the exterior bar, in particular, a peak tensile strain of 12.6 mm/m was attained in the first crack above the foundation wall interface. This peak strain value contrasts with local minima of 4.4 mm/m and 3.9 mm/m at mid-crack spacing below and above, respectively (i.e., at a depth of −50 mm and height of 156 mm from the foundation level). It is likely that the very large reported values of measured tensile strains by the DFOS do not exactly correspond to actual strains inside the steel rebars. In fact, at the abovementioned level of loading, some information loss in the regions close to the localized strain peaks may occur. As suggested by Brault and Hoult [
18], inaccuracy in the strain readings from the DFOS once plasticity occurs is likely to be caused by one or a combination of factors: (i) After deterioration of the bond between the concrete and the steel reinforcing, pinching of the fiber occurs, which affects the light transmitting through the fiber optic core; (ii) Significant crack openings with the potential to shear the surface of the fiber; and (iii) Large strain gradients, which result in measuring difficulties for the interrogator (i.e., analyzer) [
46]. For the results herein, it is unlikely that the first two factors accounted for the inaccurate readings. As the loading imposed is reverse-cyclic, the wall returns to its centered position (i.e., position O), where the strains decrease, and the strain information returns as the optical fiber is still intact. However, a net positive strain is measured by the DFOS within these regions of the localized plasticity from previous load stages. These localized peaks in tensile strain from the DFOS continue to the next load stage, at position C+, when the flange end is in compression (
Figure 9a). It is possible that the rebar in these localized areas has, on the previous load cycle, yielded in tension, deformed inelastically, and attains permanent damage that results in residual tension for the next load cycle. However, it is also possible that the reverse-cyclic tension-compression yielding of the rebar across these localized cracks has caused the fiber-optic cable to buckle, something that has been postulated to occur in previous experiments using DFOS in RC beam-column joints [
13]. Another explanation for this net-tension reading by the DFOS is due to thermal effects from plastic deformation of the rebars at these localized areas, which has not been accounted for in these experiments.
3.2. DIC and DFOS
In this section, the DFOS core strain measurements will be compared to the DIC surface measurements. Specifically, the DFOS strains from channel 1 (“ch1”,
Figure 3a) will be compared to the surface strain field of a boundary column, as
Figure 5 depicts.
High-to-medium resolution strain fields from DIC typically need to be smeared using a moving average to result in values that are more representative of the rebar and concrete strains of large-scale structural elements and more compatible with most of the existing stress-strain models. For example, a base length equivalent to the wall thickness (
tw) was previously used as a basis to average the high-resolution (20mm grid spacing) DIC data from the test of two RC walls [
47]. Similarly, the DIC data from two tested planar RC walls used a base length of 100 mm (0.5
tw) to average the strain distribution across the faces of the units [
48]. However, the resulting strains from the aforementioned research investigations were not validated against other instrumentation, such as LVDTs. In another study focusing on RC beams [
3], a procedure was used to average DIC surface strains to calculate crack widths in comparison to the estimates from the DFOS strains, which involved applying a threshold strain limit to remove noise, fitting a Gaussian distribution, and taking a mean. However, this resulted in “corrected” DIC strain profiles with distinctive peaks that were larger than the “smoothed” strain profile obtained from the DFOS, as the focus of the study was on providing accurate crack width calculations and not on strain profiles. This is explained by Ruocci et al. [
49], where the crack is locally detected by the DIC as a displacement discontinuity leading to a peak in the strain fields. The local strain peaks from DIC were also visually interpreted in an experimental study on a beam-column joint, resulting in the authors to conclude that the DFOS provided more reliable strain measurements [
13]. In fact, the majority of literature reporting on RC wall tests and using DIC focus on crack detection [
50,
51] or measuring crack width and spacing [
49], rather than accurate strain profile measurements. As such, and as suggested in the introduction, there appears to be a lack of guidance as to what sort of averaging method or procedure should be used on high-resolution DIC strain data to provide more accurate strain measurements in the testing of large-scale RC structures.
For the above reasons, in the initial part of this section, the authors use DIC and DFOS results from one wall specimen to recommend a base length value.
Figure 10 presents the longitudinal DIC strain values of UW1’s boundary column of the flange-web intersection in tension and compression (position C and position D, respectively, for a drift δ of 0.6%). The average of the longitudinal strains determined across the 100 mm width of the boundary column (
Figure 5b) was computed, whereas different base lengths (
Bl) were used to take a moving average vertically: (i) No moving average (“uncorrected”); (ii)
Bl = 50 mm; (iii)
Bl = 100 mm; and (iv)
Bl = 200 mm. The latter of these values represents an upper limit, equivalent to 2.0 × the thickness of the wall (2.0
tw). The 50 mm and 100 mm were chosen based on 0.5 × and 1.0 × the thickness
tw. For reference, the DFOS strains (average of the two rebars, black solid line) and calculated strains from the LVDT array (black dashed line) are superimposed in these figures. As mentioned previously in
Section 3.1, the loading applied to UW1 resulted in closely resembling DFOS strain profiles between the two layers of rebars, which justified taking the average to result in a single profile here. The “uncorrected” DIC strains, with no applied moving average, show peaks of large tensile strains (
Figure 10b), which correspond to the local strains captured across small, open flexural cracks at the surface of the concrete. The average of the spacing between the tensile peaks (or crack spacing) is 64.7 mm, which is close to the designed spacing of the transverse confinement (= 75 mm). While many factors ultimately determine the crack spacing of a RC member in tension [
9], the spacing of the transverse reinforcement is a primary factor. Interestingly, the average spacing distance between the “uncorrected” DIC compression strain peaks (
Figure 10a) is 31.9 mm, approximately half of the spacing distance between the tensile peaks. In this case, it is likely that compression strain peaks from the DIC coincide with the location of cracks closing, as well as the concrete in between the cracks, whereas the reinforcing bar in compression exhibits a smooth strain profile (as indicated with the DFOS strains). If it is assumed that the reference strains from the DFOS and LVDTs are more reliable indicators of the strain profile, the DIC tensile strains with
Bl = 200 mm appear to provide better estimates representative of the compression and tensile strain profiles. There is a clear difference of DFOS measured strains and the DIC calculated strains at the base of the wall in both compression and tension (
Figure 10a and
Figure 10b, respectively). Firstly, when the boundary column under consideration is in tension (Position C,
Figure 10b), the tension at the base is not adequately captured by the DIC technique due to strain penetration not being considered [
47]. The uncorrected DIC strains at the very base of this column have been ignored for the purposes of deriving the corrected DIC strain profiles due to the unrealistically high concreated strain values, which, in some cases, will result in a poor estimate of the base tensile strain. Secondly, when the boundary column is in compression (Position D,
Figure 10a), it is expected, under the current flexural loading, that compressive strains in the concrete surface, captured by DIC, would be greater than the compression in the steel bars, captured by the DFOS, which are embedded at some 25 mm from the surface of the boundary column. For large drift levels towards Position D, the neutral axis is located somewhere in the web of the wall (see
Figure 1a for the wall segment definitions). Therefore, the web surface of the wall captured by the DIC, or in this case, the surface of boundary column under consideration, represents the extreme compression fiber region (for loading towards position D), which is expected to experience greater compression strains than the rebars closer to the neutral axis.
Figure 11a–d and
Figure 11e–h present the DIC tensile and compression strain profiles, respectively, from the surface of the boundary column for unit UW1, subjected to in-plane bending, for four different levels of drift (
δ): 0.2%, 0.4%, 0.6%, and 0.8%. Drift levels greater than this were found to cause some information loss in channel 1 of the DFOS. A heatmap is presented to the left side of each plot, representing the uncorrected, raw DIC strain data (in units of mm/m) for the entire 100 × 2000 mm
2 surface of the boundary column (illustrated in
Figure 5b). The right side of each figure plots the uncorrected DIC strains (blue thin lines), where the average of the longitudinal DIC strains across the 100 mm width of the boundary column have been computed for each vertical increment. Superimposed in these plots are the corrected (vertical moving average with
Bl = 200 mm) DIC strains (red thick lines) and the strain profiles measured from the DFOS bonded to the two
Φ12 mm rebars (black solid lines). Note again that for the loading applied to UW1 (i.e., in-plane loading to position C and D,
Figure 2a), the resulting DFOS strain profiles of these two rebars were essentially the same. Overall, the corrected DIC strains provide more representative estimates for these drift levels, assuming that the reference strains from the DFOS are more reliable indicators of the strain profile. Due to the fact that the DIC technique captures the tensile strains across the cracks of the concrete surface, slightly larger tensile strain oscillations can be observed in comparison to the smoother DFOS strains occurring in the section core. This smoothness is due to the bond stress transfer that occurs between the steel rebar and the surrounding cover concrete (recall that the fiber-optic cables are placed on the outside of the steel rebar, to the east and to the west for the exterior and interior bar, respectively—see
Figure 4a,b), of which only the surface manifestation of this phenomenon is captured by the DIC. Several other factors could have contributed to the limited discrepancies of strain profiles observed between the surface and core measurements, with the most obvious being the difference in the location of the surface plane (i.e., the web of the wall,
Figure 5) captured by the DIC and the location of the embedded rebars with DFOS in the boundary column, some 25 mm from the web surface. Furthermore, local bending of steel reinforcement has been shown to produce variations in the magnitude of the resulting strain measurements [
52], where, for this study, the fiber-optical cables are located on the outside of the rebar. Other factors include the strain “transfer effect”, which could result in the strains determined by the sensors being different from the strains of the host structure (i.e., the steel rebar) [
15,
53,
54]. While the authors took a number of precautions to reduce these strain transfer effects [
55] (e.g., see
Section 2.2.1, consideration of adhesive type, engraving a small groove, fiber bonded directly to the reinforcement [
3], etc.), these effects cannot be completely ruled out.
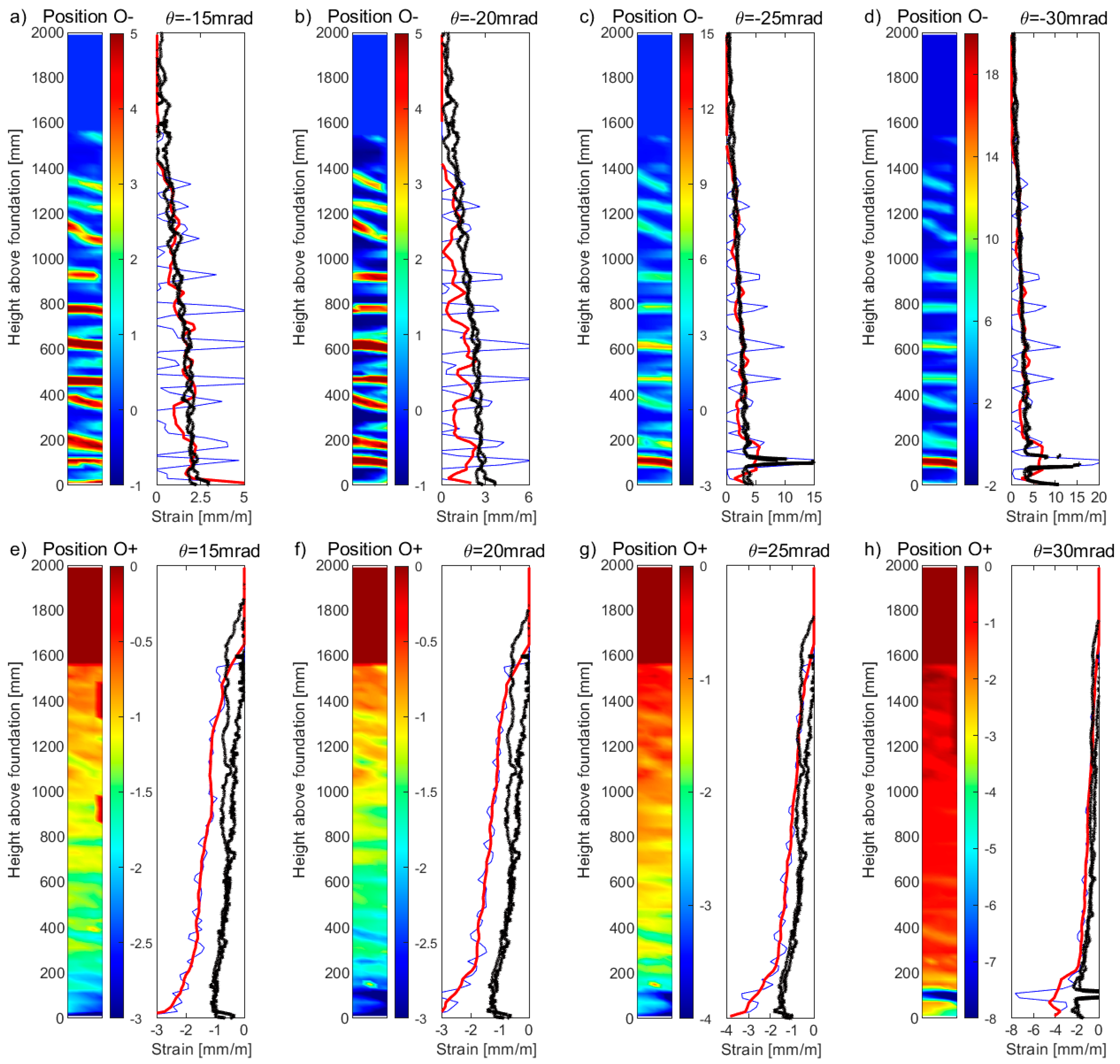
For the boundary column of unit UW2, which was subjected to a reverse-cyclic torsional rotation,
Figure 12a–d and
Figure 12e–h present the DIC tensile and compression strain profiles, respectively, for four different rotation (
θ) levels: 15 mrad, 20 mrad, 25 mrad, and 30 mrad. This type of loading caused slight differences in the DFOS strain profiles of the two longitudinal rebars, represented by the black thick lines. While the rather gradual gradient of the strain profiles measured from channel 1 of the DFOS system for UW2 meant that strains greater than yield could be achieved, rotation levels greater than 30 mrad started to cause some information loss in this channel. The latter can be observed at the base of the boundary column in
Figure 12c,d, where loss of DFOS data occurs for strains greater than 10–15 mm/m, corresponding to the limits given in the technical dataset for the LUNA system used (see
Section 2.2.1). Note that the DFOS in both layers of the rebars measured the localized strain increase at the same location. Interestingly, the uncorrected (raw) DIC strain peak towards the base in
Figure 12c and
Figure 12d compare reasonably well to the strain peak measured with the DFOS, corresponding to where the information loss occurs. These strain levels also cause a noticeable net-tension strain measurement in the DFOS at the next load stage in compression, presented in
Figure 12h with the black thick lines. Note that the DFOS in both layers of the rebars measured this localized net-tension in strain measurement. A list of possible explanations for this was included in
Section 3.1, with a possibility of this reflecting a real, localized phenomenon. However, the maximum DIC compression strains appear to concentrate at approximately 100 mm from the base in
Figure 12h, which is the same location of the maximum tensile strains in the previous load stage in
Figure 12d. Thus, it is also possible, and maybe more likely, that this level of rotation (θ = −30 mrad) has caused the DFOS to be pinched or buckle, resulting in a false reading of strain at this location. This explanation appears to be consistent with the reasons given in Zhang et al. [
13], where the phenomenon was observed for DFOS bonded to rebar embedded in a RC beam-column joint that was reverse-cyclically tested. Overall, the corrected DIC data in
Figure 12a–d (red thick lines) appear to reasonably represent the strain profiles for all levels of rotation considered in comparison to the tensile strain profiles measured by the DFOS. These results also show that the recommended correction, using a simple moving average with a base length
Bl of 200 mm, can be applied to DIC data of high, medium, and low resolution, with the latter of these represented by the DIC data attained for unit UW2. For example, while a clear smearing effect of the uncorrected DIC data could be observed in
Figure 11 for UW1, the effects are less prominent in
Figure 12 for UW2, particularly for the compression strain profiles in
Figure 12e–h. Thus, it appears that the recommended correction method for DIC strains has its greatest effect when the resulting vertical grid spacing is much less than the base length
Bl recommended here of 200 mm. However, the corrected DIC compression strain profiles in
Figure 12e–h appear to overestimate the compression strain profiles of the rebars measured by the DFOS. Similar to the DIC and DFOS results for UW1 in
Figure 11e–h, the large compression strains could be expected, given that the DIC is measuring the compression strains of the concrete surface, representing the extreme compression fiber region; instead, the DFOS are attached to the longitudinal rebar embedded at some cover distance away from the surface.
The DIC data attained from the web of UW3 had the highest resolutions of all three wall units with a resulting vertical grid spacing of 5 mm (
Figure 2a). This is compared to a vertical grid spacing of 10 mm and 20 mm for UW1 and UW2, respectively. Wall unit UW3 was subjected to both a reverse-cyclic torsional rotation and a translational push-pull, simultaneously (i.e., position C+ and D− in
Figure 2a). The uncorrected and corrected DIC tensile and compressive strains for the web boundary column of UW3 are presented in
Figure 13a–d and
Figure 13e–h, respectively, for four different drift-rotation (
δ-
θ) levels:
δ = 0.1% and
θ = 1 mrad,
δ = 0.2% and
θ = 2 mrad,
δ = 0.3% and
θ = 3 mrad, and
δ = 0.4% and
θ = 4 mrad. The high-resolution, uncorrected DIC data in
Figure 13 (blue thin lines) results in high-frequency peaks of tensile and compressive strain, which make it difficult to interpret without processing the data using, for example, a moving average (red thick lines). In comparison to the DFOS strain profiles in
Figure 13 (black dashed lines), the corrected DIC strain profiles compare reasonably well. Larger DIC tensile strains can be observed at the base of the boundary column (i.e.,
Figure 13d), which is a consequence of this surface instrumentation method not being able to measure the strain penetration into the foundation, similar to the observations for the LVDTs in
Section 3.1. There is also some small, but noticeable, positive (tensile) surface strains in
Figure 13h from above mid-height, calculated from the corrected (red thick line) DIC data, which is not measured by the DFOS (black thick lines). It is worth noting that this type of strain gradient was similarly illustrated in the data paper [
19] and measured by the DFOS for UW2 (i.e., pure rotation), particularly for the rebars of channel 4 in the west flange boundary end.
3.3. Micrometers and DFOS
In this section, the vertical displacement as measured from three of the sixteen Mitutoyo micrometers, specifically M5, M2, and M1 in
Figure 1a, are compared to the displacement from the DFOS, specifically channels (“ch”) 2, 3, and 4 in
Figure 3a. The vertical displacement (Δ
v) from the DFOS is calculated by integrating the measured strain over the length (
L) of the undeformed bar (and optical fiber) defined below, according to Equation (1).
where
ε is the vertical strain measured from the DFOS.
The length
L considered here for calculating Δ
v is approximately 0.34 m, which is the anchorage length of the rebar into the foundation. However, for each rebar and wall unit, the specific depth into the foundation is more accurately determined from pre-established gauge locations of the DFOS along the rebar. For simplicity, this displacement is called “anchorage slip”. Calculating the anchorage slip (Δ
v, Equation (1)) using this depth of approximately 0.34 m provides a lower bound estimate, as the micrometer surface sensors were attached to the wall at approximately 60 mm above the foundation. Furthermore, as the surface sensors (micrometers) were placed on the inside of the wall (
Figure 14), only the DFOS bonded to the interior rebar is used for comparison purposes here.
Figure 14 plots the resulting Δ
v for UW1 as calculated with the DFOS strains (black solid line) and as measured from the micrometers (grey solid line), where the difference between the two is also indicated in the figure (red dashed line). Load stage (LS) numbers 5 and 18 were not recorded by the DFOS system due to instrumentation errors, and hence, the data is not present in
Figure 14 for these two LS. It is worth noting that for UW1, the measurement point of the three micrometers was found to be below the bottom-most flexural wall crack; this crack should be distinguished from the base crack at the foundation wall region. Overall, the anchorage slip calculated from the DFOS from all three channels and for the LS range considered here reasonably matches the measurements from the three micrometers, albeit there are some small differences for some load stages. As wall unit UW1 was loaded in-plane parallel to the flanges, strain gradients across the thickness of the two wall flanges (see
Figure 1a for segment definition) are expected to be unimportant (at least until out-of-plane deformations are developed during the last load stages), and are mainly attributable to inevitable small construction and loading asymmetries. In fact, the DFOS strain profiles from the two rebars across the thickness show negligible variations. Thus, the small differences in Δ
v that are observed in
Figure 14 between each pair of instruments are instead likely to be due to the slip of the rebar from the concrete, where the micrometers are only able to measure a fraction of the vertical deformation at the surface.
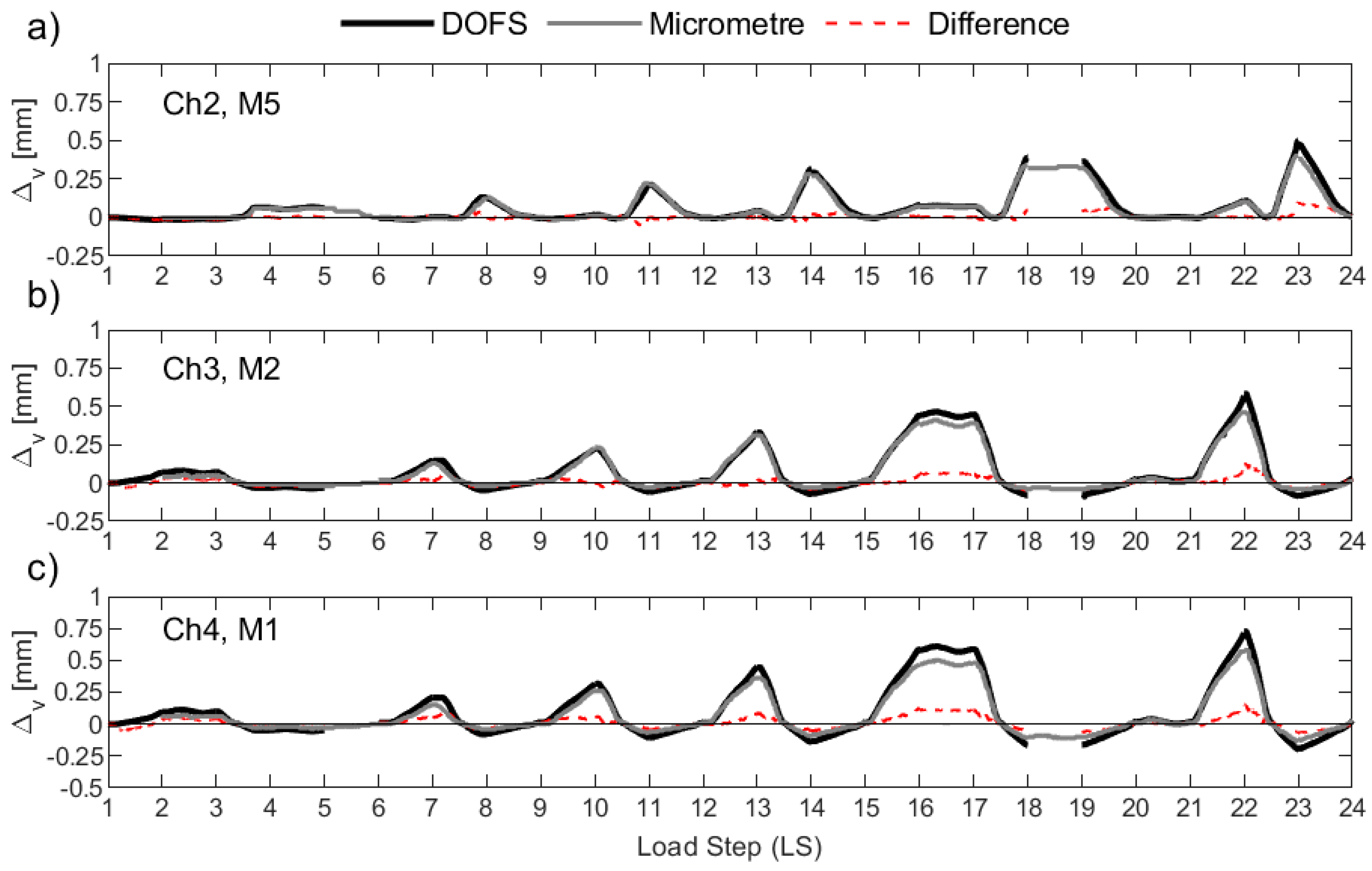
Wall unit UW2 was loaded in reverse-cyclic rotation, and, due to a combination of warping and circulatory torsion, a strain gradient was observed through the thickness of the flanges with the DFOS strain profiles. It was therefore interesting to compare the anchorage slip as measured by the micrometers and calculated with the DFOS strains. The results are shown in
Figure 15, and they are largely consistent with those observed for UW1, subjected to in-plane flexure. However, channel 4 (i.e., “Ch4” in
Figure 15c) of the DFOS, located at the outermost region of the flange boundary end, provides reasonable estimates in tension (i.e., positive Δ
v values), but lower estimates in compression compared to the micrometer measurements. This observation could be a product of the lower bond depth used to calculated the DFOS Δ
v as well as the strain gradient across the thickness of the wall, where larger tensile and compressive strains are expected towards the inside of the wall. In fact, as shown in
Figure 6b, the offset distance from the attachment of the metal plate to the wall and the application of the tip of the micrometer will amplify the anchorage slip, as measured by the micrometer, due to the strain gradient across the thickness of the wall. Channel 3 of the DFOS (
Figure 15b), which was bonded to rebars also located within the boundary end of the west flange, was found to produce higher values of the anchorage slip throughout the LS range in comparison to the measurements for M2, but only in tension. In compression, micrometer M2 measured larger values of displacement compared to the computed Δ
v from Ch3. Regarding the west flange-web intersection (see
Figure 1a), channel 2 of the DFOS is shown to compare reasonably well with micrometer M5 in
Figure 15a. Within this latter comparison, it is noted that there are at least two LS levels that produce some discrepancies between the different sensors: at LS 12–13 and LS 21–22, when the wall is rotated to position O+ (
Figure 2a),
Figure 15a shows micrometer M5 measuring a positive (tensile) Δ
v, whereas the value calculated from Ch2 of the DFOS is insignificant and close to zero. A possible explanation is that, at this wall position (O+), the warping of the wall is likely to cause a distribution of longitudinal strains across the wall flange at the base, but with a diagonal neutral axis (across the thickness) close to the position of this rebar and micrometer (Ch2 and M5 in
Figure 15a). On further investigation, it was found that, at these two LS levels, Ch2 of the DFOS indicate that a large portion of the development length of the interior rebar into the foundation was in tension, contrasting the exterior rebar, which measured compression strains throughout its profile. This further suggests a complicated strain gradient through the thickness, and into the foundation, due to the loading imposed with the neutral axis, at these LS levels, within the vicinity of these two rebars. In fact, the two following LS levels that rotate the wall to position O- (i.e., LS 14–15 and LS22–23) also show the micrometer return to a measured Δ
v of close to zero before increasing in positive (tension) anchorage slip again, further substantiating the diagonal neutral axis theory.
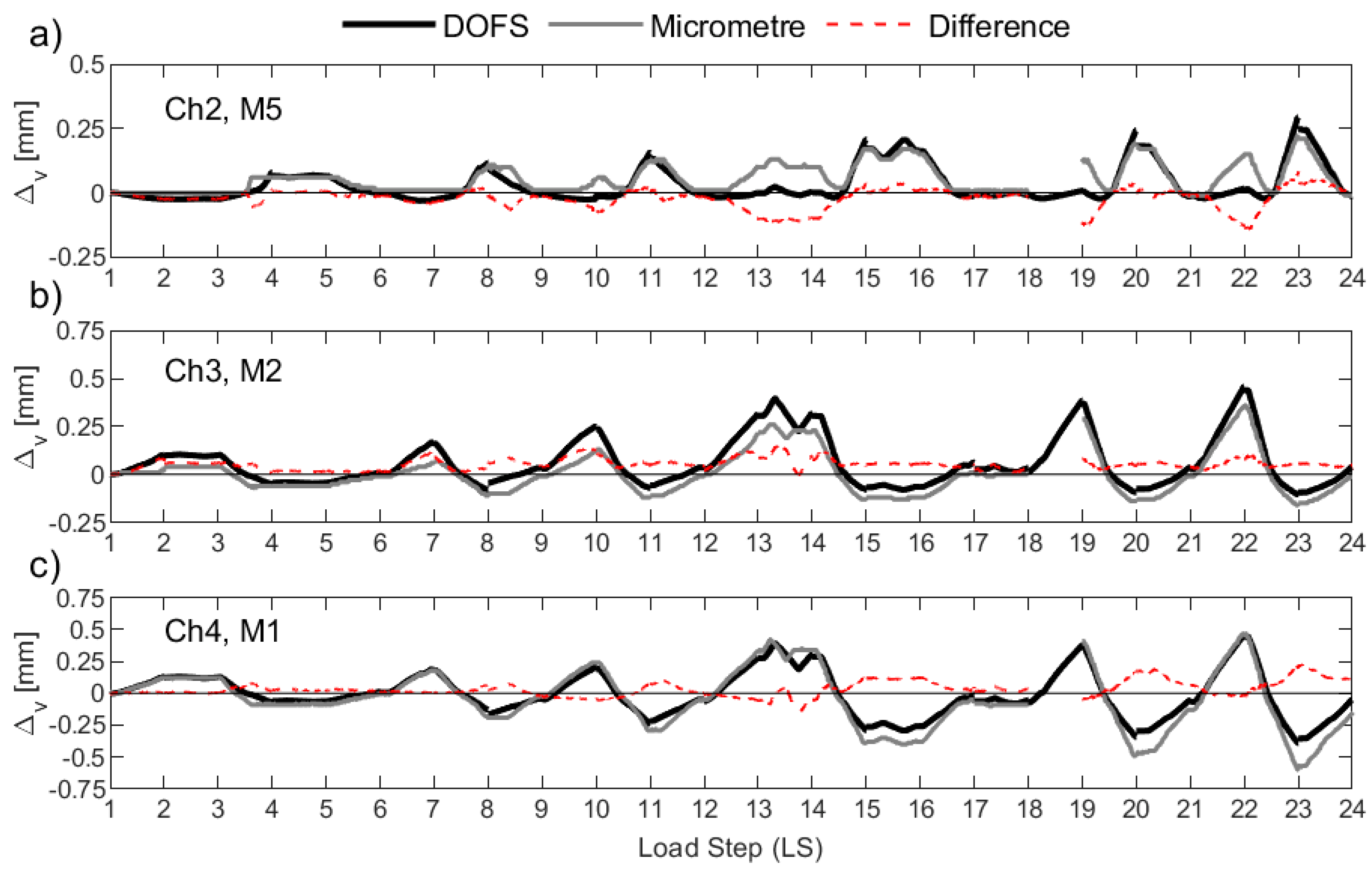
Test unit UW3 was subjected to a combination of reverse-cyclic torsional rotation and translation simultaneously, corresponding to positions D− and C+ (
Figure 2a). The corresponding Δ
v measurements from the micrometers of UW3 are presented in
Figure 16, which can be compared to the calculated anchorage slip using the DFOS strains. The comparisons between the core and surface sensors look reasonable up to load stage 13. At the end of LS 13 (Position D-), an increase in the measured Δ
v by M1 and M2 (
Figure 16c and
Figure 16b, respectively) can be observed, with respect to that computed from the DFOS. For each LS that follows corresponding to a wall push to Position D− (i.e., LS 16-17, 19-20, and 22-23 in
Figure 16), a significant increase in the measured anchorage slip can be observed from the micrometers M1 and M2 in comparison to the computed Δ
v from channels 3 and 4 of the DFOS. One explanation for this increase of the anchorage slip measured by the two micrometers (M1 and M2) for when the west flange boundary end is in tension (position D−) is that a flexural crack has formed and runs through the application points of the two micrometers along the inside of the flange. Photos from the experiment support this (
Figure 6b), where it is possible that the concrete surface crack affects the attachment of the micrometer to the wall, causing some small uplift. As discussed in the previous paragraph for UW2, another possible explanation for these discrepancies is the obvious increase in vertical deformation as measured by the micrometer if a strain gradient across the thickness is present, which was likely, due to the imposed rotation to the wall. For example, comparing the measured strain profiles for the interior and exterior rebars from Ch4 of the DFOS for wall unit UW3 confirms that a strain gradient was present (e.g.,
Figure 9a). The offset distance of the micrometer from the wall surface would inherently amplify the actual anchorage slip in the presence of strain gradients through the wall thickness. Furthermore, potential slip between the tip of the micrometer and the glass plate (see
Figure 6b), which was glued to the metal plate for attachment to the wall, would only have exacerbated this behavior. On closer inspection, the glass plates were not used to support the tip of these micrometers for testing unit UW1 (i.e., compare
Figure 6a with
Figure 6b). While there were less discrepancies between the comparisons of the micrometer measurements and the calculated DFOS anchorage slip, the loading imposed to UW1 meant that there was negligible strain gradient through the thickness, which also made comparisons of these instruments more favorable. Another observation in
Figure 16a is the larger Δ
v as measured by micrometer M5 in comparison to the DFOS at position D- (i.e., LS 10, LS 13, LS 16, etc.). One possible explanation for this was provided in the previous paragraph regarding the same observation with unit UW2 (i.e., the twisting applied causes the neutral axis to be skewed diagonally across the thickness of the wall). One last curious observation is the increasing residual vertical deformation by M5 after LS 18 (
Figure 16a), which results in a larger measured anchorage slip by the micrometer in comparison to that calculated by the DFOS. The DFOS strains corresponding to the interior rebar in this region confirm that, at the beginning of LS 18, the rebars were performing pre-yield (max strain of 2.364 mm/m). Thus, the residual deformation is unlikely to be a result of inelastic behavior from the reinforcing steel. Instead, it is again possible that flexural cracks have formed close to the fixation of the micrometer on the surface of the wall. If these cracks cannot close all the way, it is possible that the micrometer does not return to an anchorage slip measurement (Δ
v) of zero on return to centering the wall (at position O).