Implementation of the Digital QS-SVM-Based Beamformer on an FPGA Platform
Abstract
1. Introduction
- Recent FPGA technology has programmable logic and the capability of algorithm parallelization for further enhancing power consumption, flexibility, and accuracy.
- Recent advances in the FPGA architectures include a higher storage density, a drastic reduction in power consumption and cost, a large number of gates, and a high-performance processor.
- Recent FPGA software and high-level optimizations have to be accompanied by architectural changes in the FPGA board in order to satisfy drastic computations of SVM-based applications. Advances in FPGA technology have rigorously presented high-level software tools to be easily adjusted to the FPGA hardware.
- For the first time, the QS-SVM-based beamformer has been implemented using the hybrid antenna array with bowtie elements on an FPGA board.
- For the first time, this work presents an implementation of the proposed digital beamformer in both the real environment and hardware board.
- The implementation of the QS-SVM optimization method for the DoA estimation on an FPGA board has been rigorously demonstrated for the first time.
- We have achieved a superior performance of the digital QS-SVM-based beamformer in terms of beamforming, nullsteering, and beamsteering.
- A performance evaluation of the QS-SVM-based beamformer has been fulfilled in terms of throughput, latency, and performance efficiency.
2. Literature Review and Related Work
3. Proposed Methodology and Techniques for the Spatial Signal Processing
3.1. Hybrid Antenna Array
3.2. Methodology and Theoretical Framework
4. Methods of Modeling and Producing Data
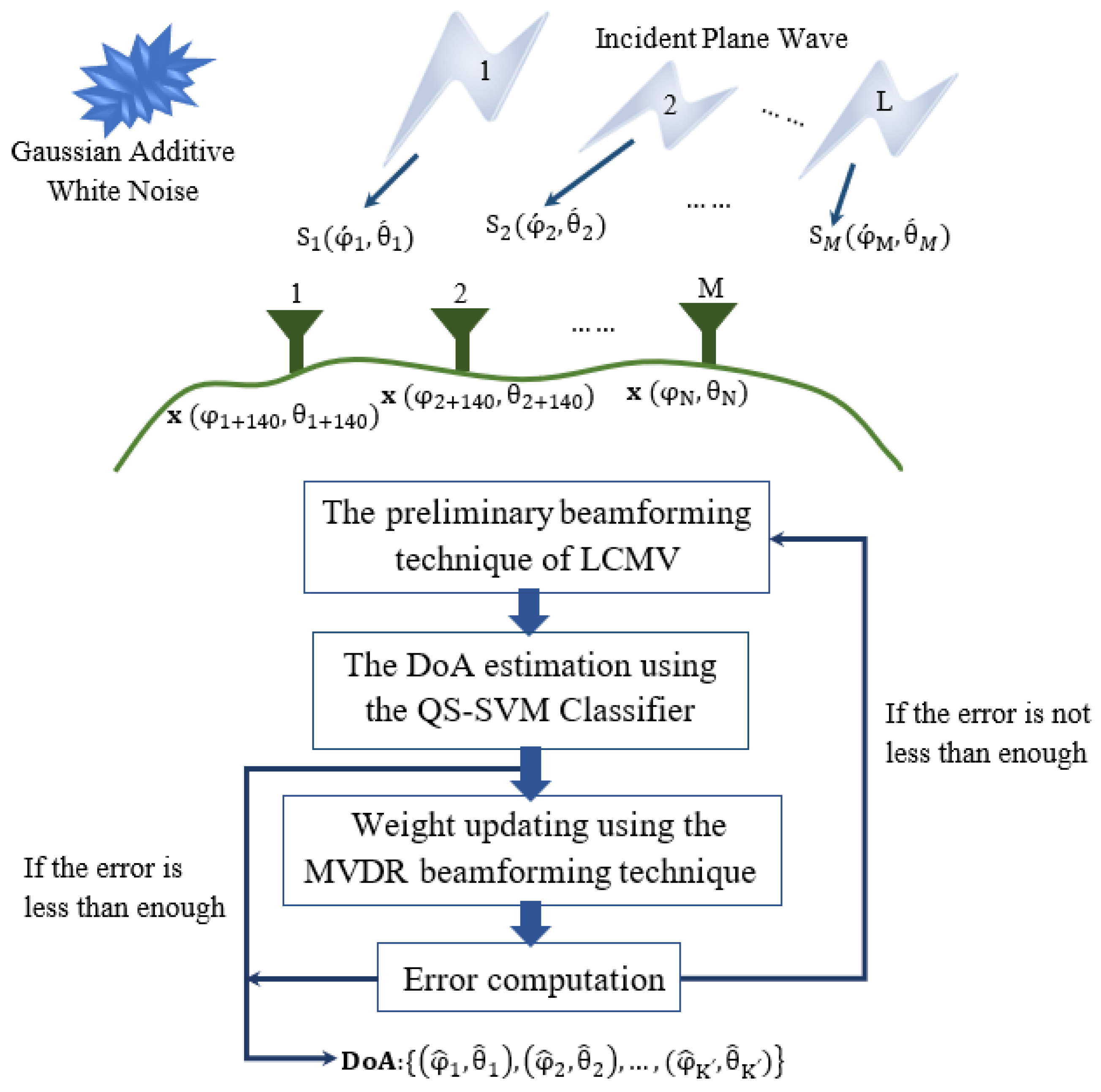
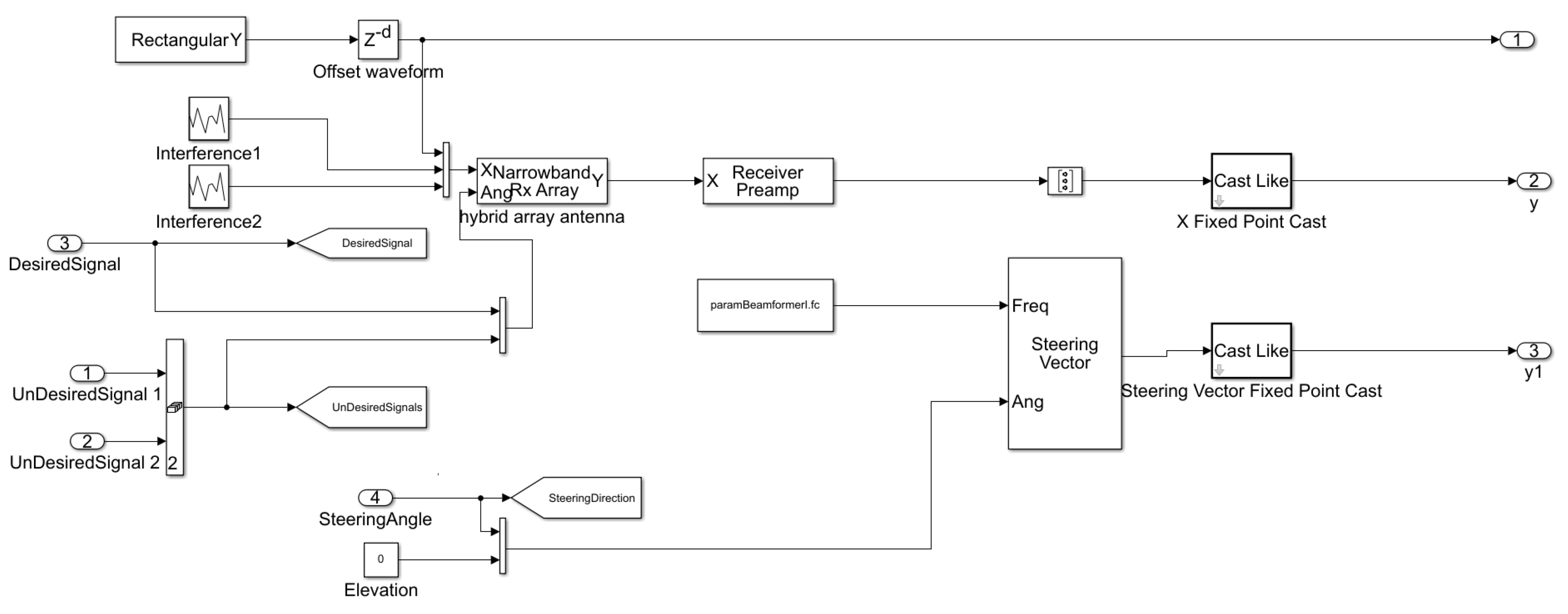
4.1. The Proposed Beamforming Technique
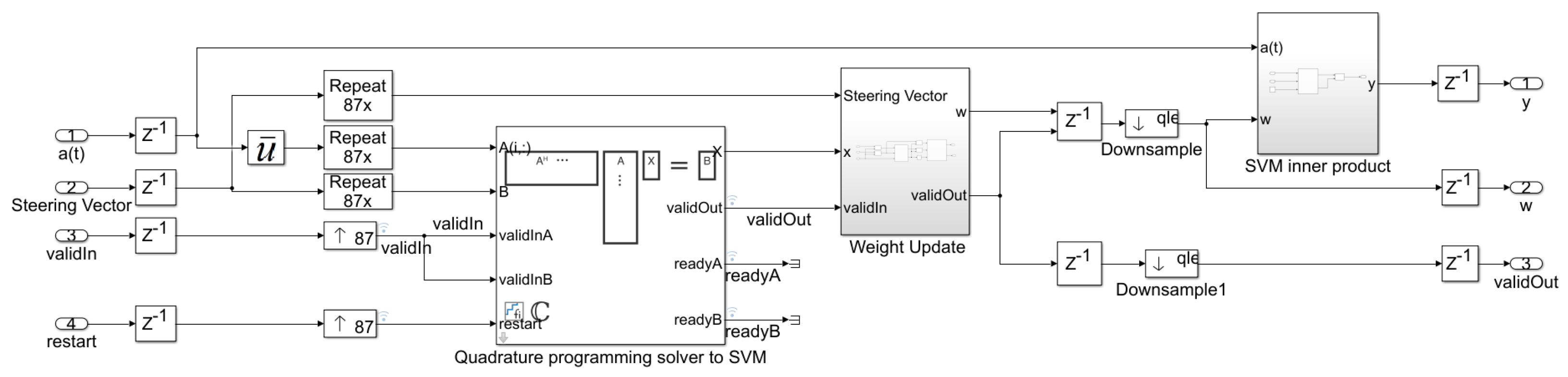
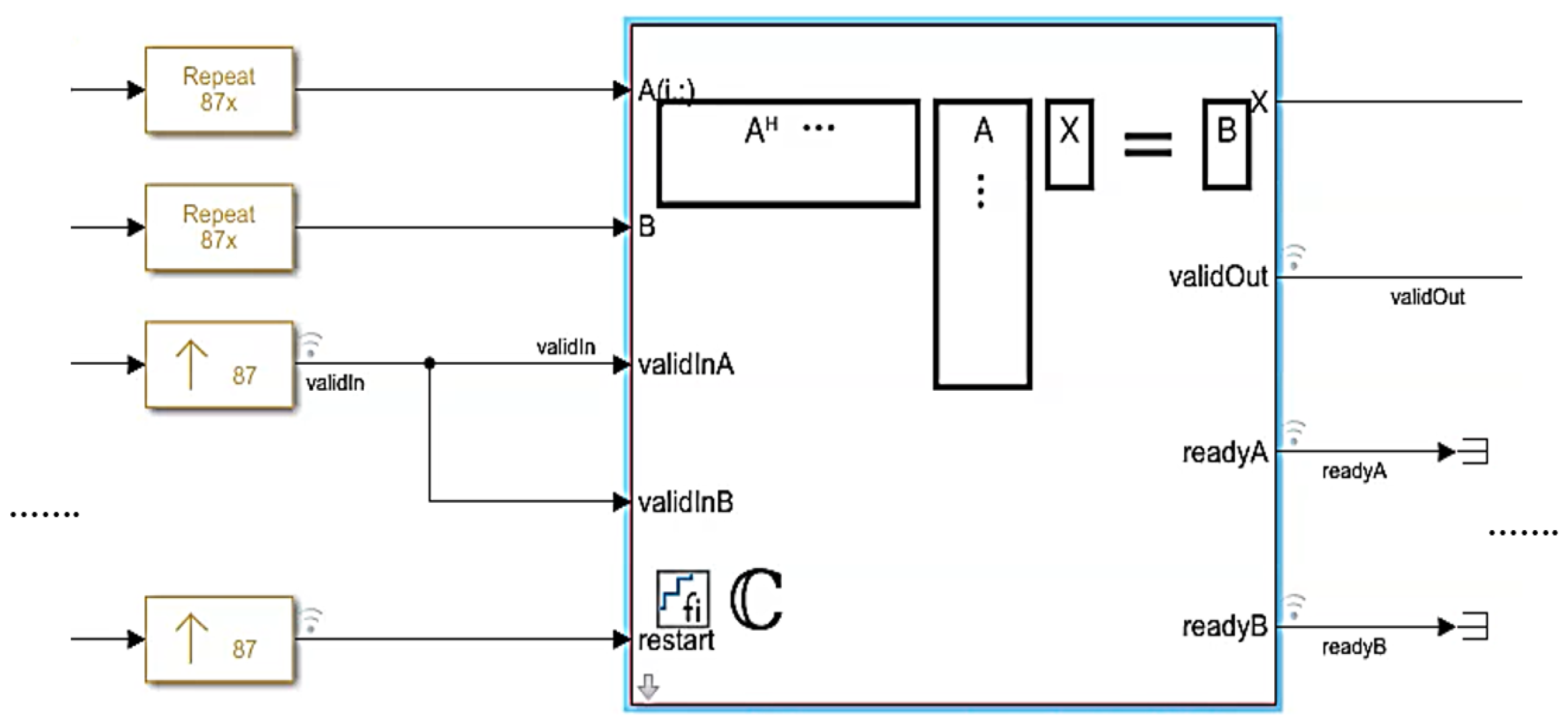
4.2. The QS-SVM Technique for the DoA Estimation
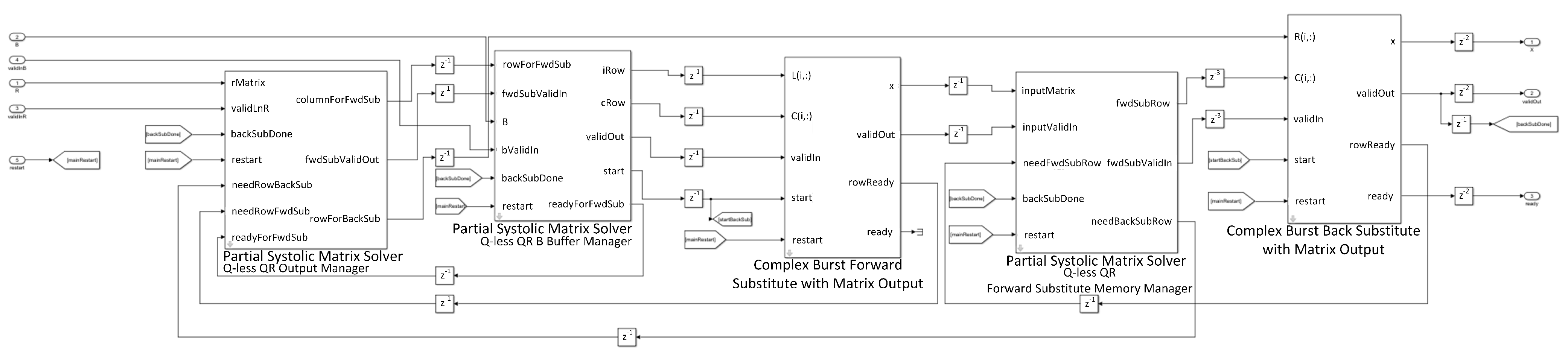
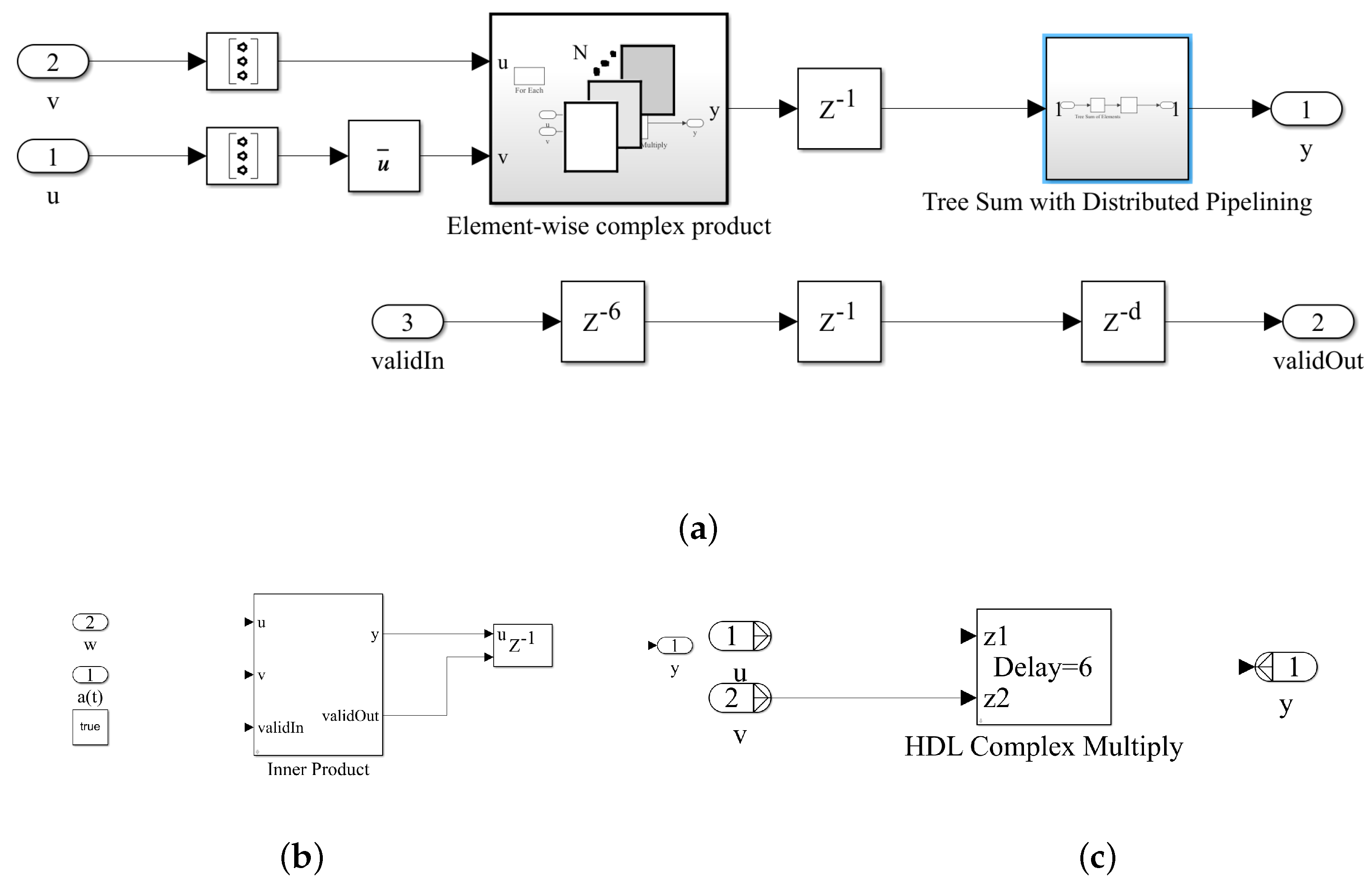
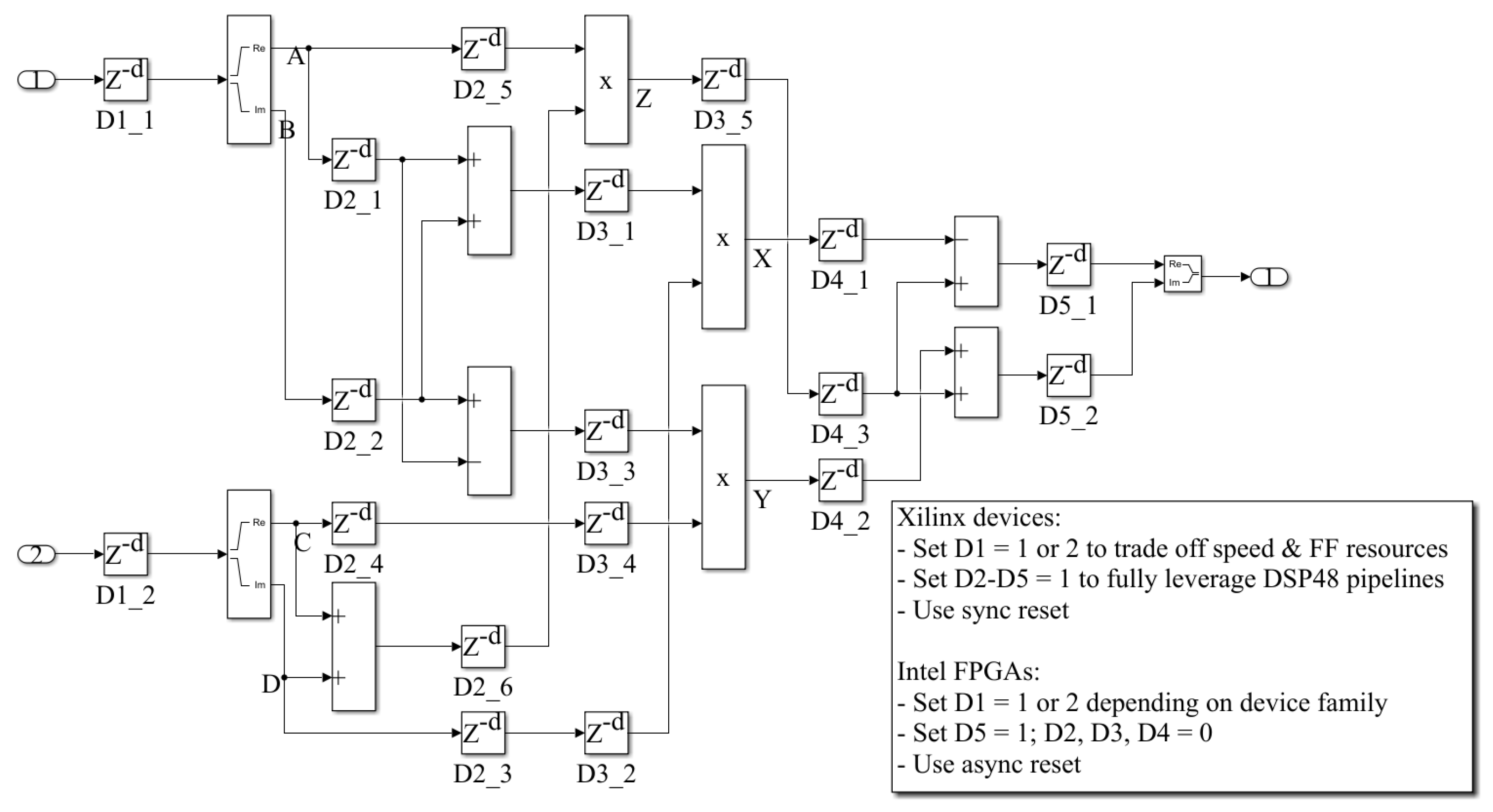
5. Implementation Setup of the QS-SVM-Based Beamformer on the FPGA Board
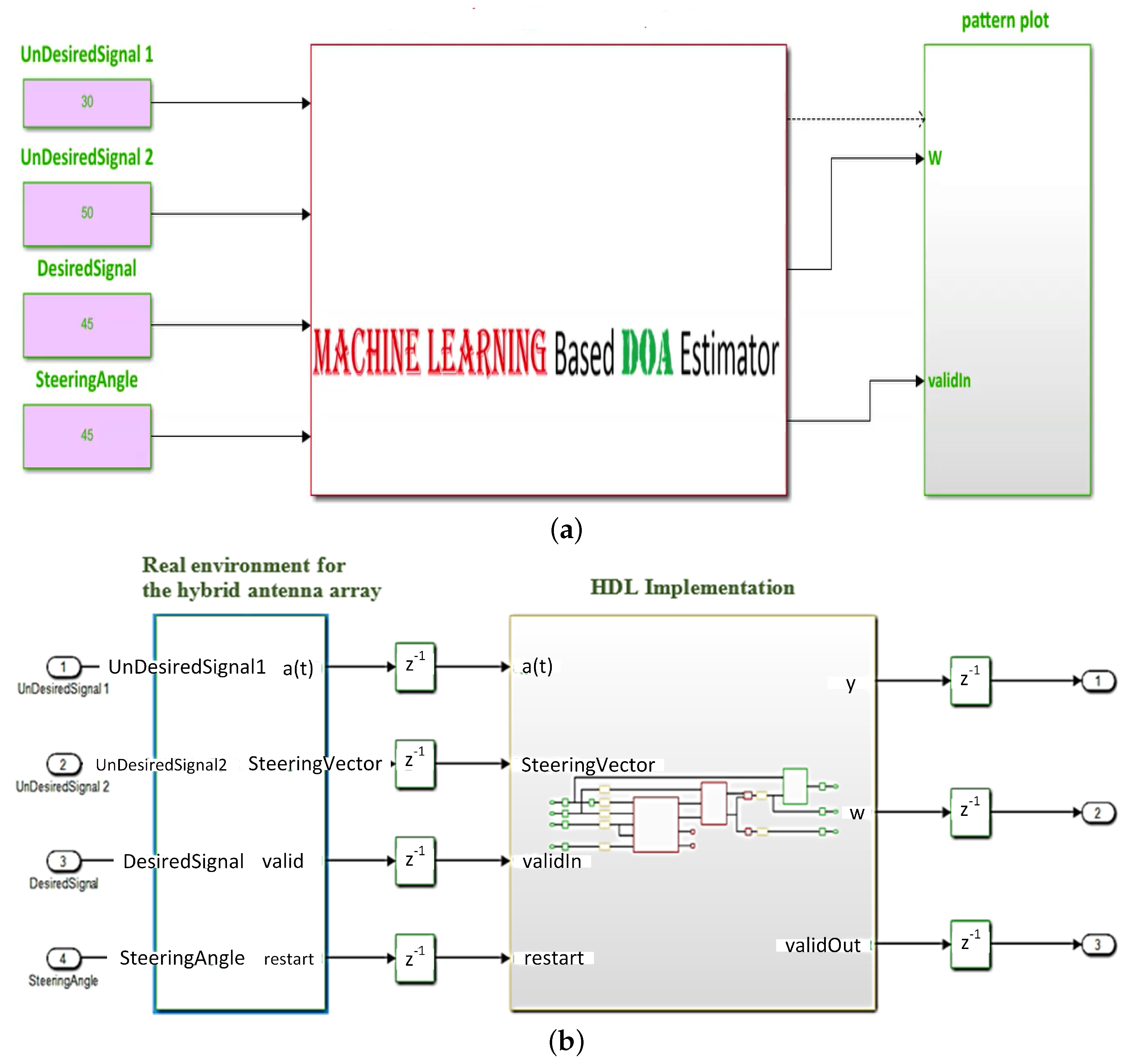
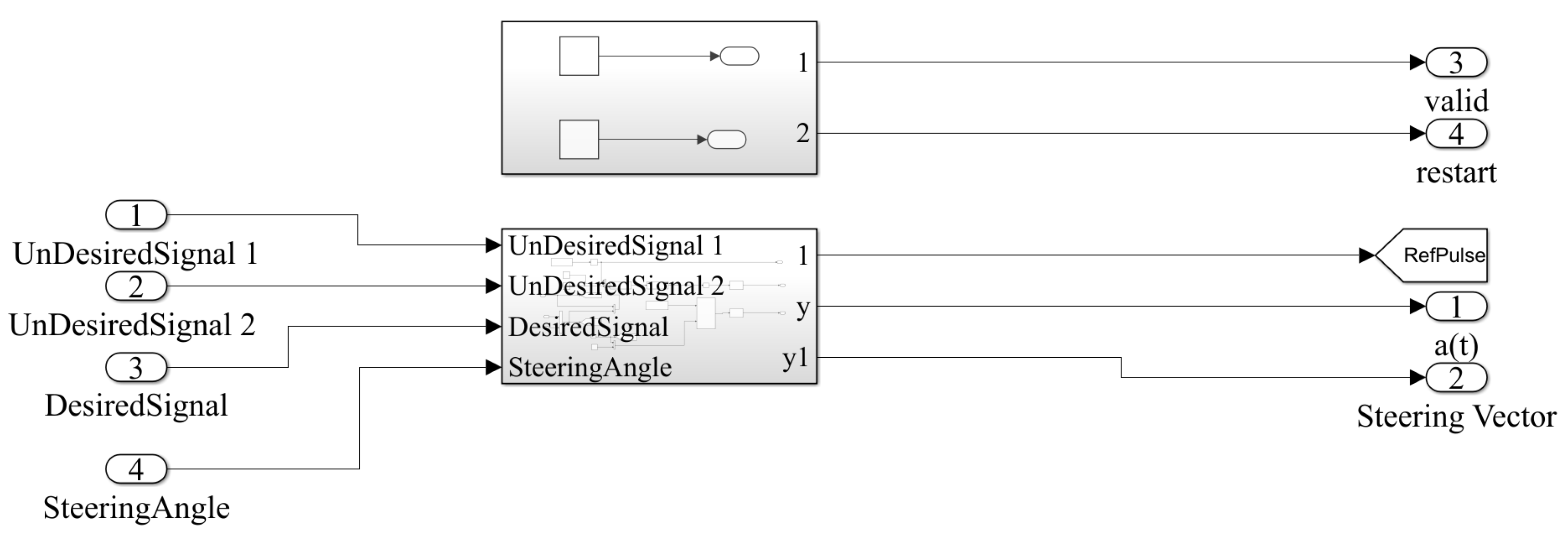
5.1. Real Environment and Software Implementation
5.2. Hardware Environment and FPGA Implementation
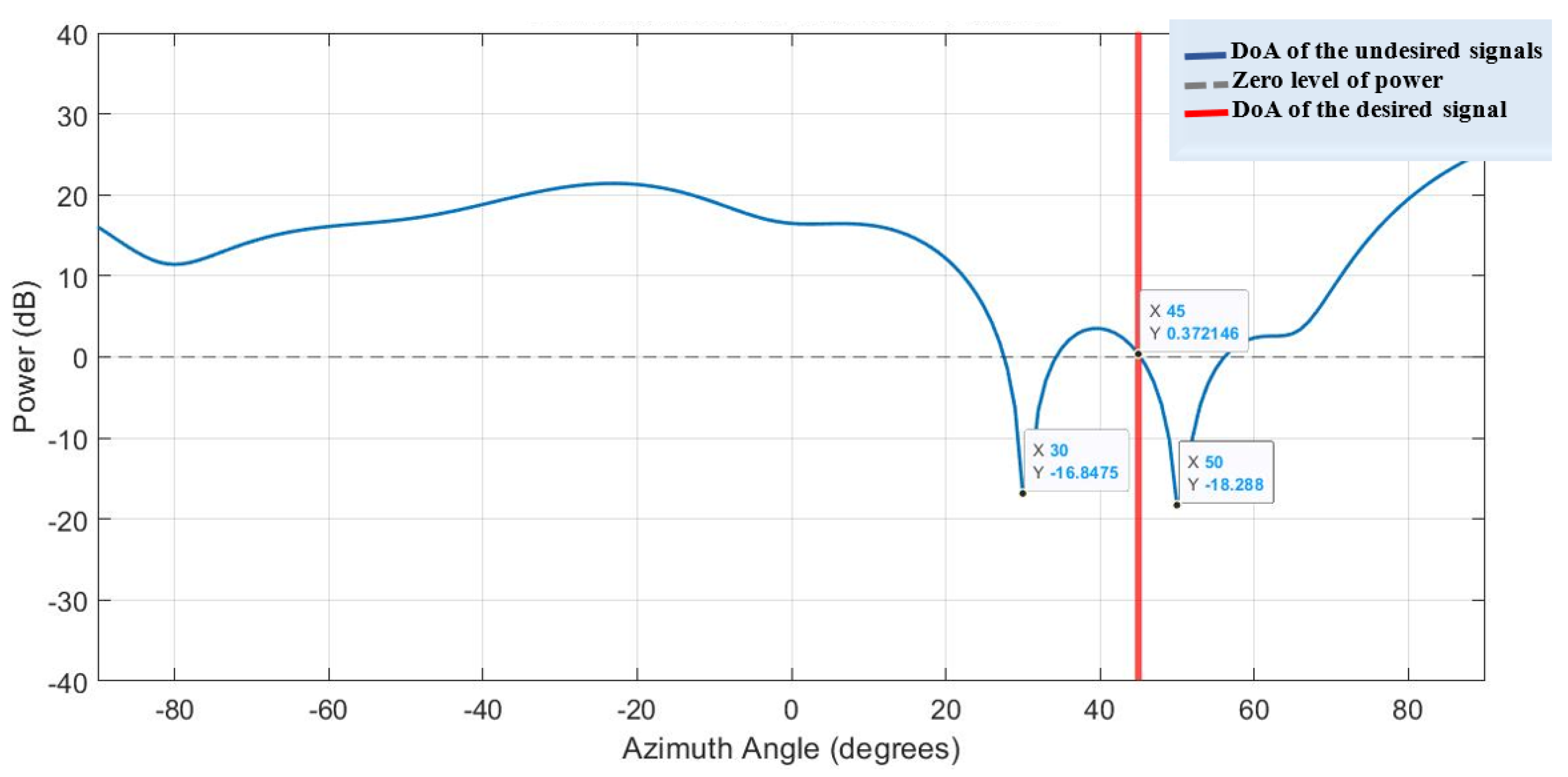
6. Results of the QS-SVM-Based Beamformer on the FPGA Board
- Null steering for undesired signals by replacing nulls of the radiation pattern of the proposed hybrid antenna array in the detected directions of undesired signals. Hence, we can weaken significantly or eliminate undesired signals.
- Keeping the desired signal unchanged by exerting power with the 0dB level in the detected direction of the desired signal. We should neither strengthen nor weaken the desired signal, due to the following two reasons: (1) since the desired signals may include noise, jamming, interference, and other unwanted signals, any amplification in the desired signal results in magnifying noise and other unwanted signals, and (2) any reduction in the desired signal is not of practical interest.
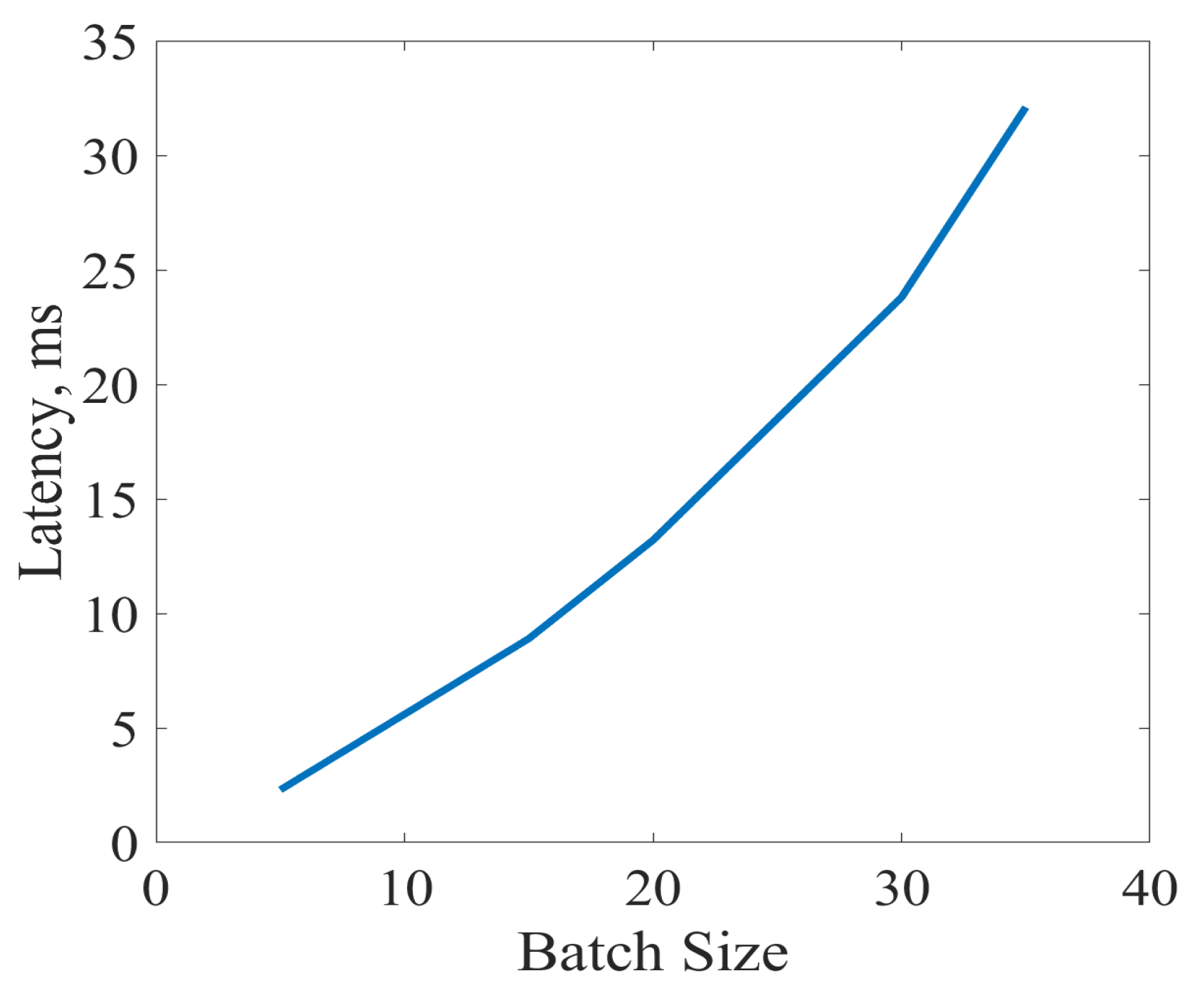
7. Performance Evaluation of the FPGA-Based Beamformer
7.1. Throughput Evaluation
7.2. Latency Evaluation
7.3. Performance Efficiency
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Abbreviations
| MDPI | Multidisciplinary Digital Publishing Institute |
| DOAJ | Directory of Open Access Journals |
| TLA | Three Letter Acronym |
| LD | Linear Dichroism |
References
- Ioushua, S.S.; Eldar, Y.C. A Family of Hybrid Analog–Digital Beamforming Methods for Massive MIMO Systems. IEEE Trans. Signal Process. 2019, 67, 3243–3257. [Google Scholar] [CrossRef]
- Fulton, C.; Salazar, J.L.; Zhang, Y.; Zhang, G.; Kelly, R.; Meier, J.; McCord, M.; Schmidt, D.; Byrd, A.D.; Bhowmik, L.M.; et al. Cylindrical polarimetric phased array radar: Beamforming and calibration for weather applications. IEEE Trans. Geosci. Remote. Sens. 2017, 55, 2827–2841. [Google Scholar] [CrossRef]
- Nallabolu, P.; Li, C. RF Compressed Sensing Radar Based on Digital Beamforming for Localization and IoT Applications. In Proceedings of the 2019 International Applied Computational Electromagnetics Society Symposium (ACES), Nanjing, China, 8–11 August 2019; pp. 1–2. [Google Scholar]
- Hsu, C.W.; Su, S.J.; Chen, Y.W.; Zhou, Q.; Alfadhli, Y.; Chang, G.K. Real-time Demonstration of 5G MMW Beamforming and Tracking Using Integrated Visible Light Positioning System. In Proceedings of the 2021 Optical Fiber Communications Conference and Exhibition (OFC), Washington, DC, USA, 6–11 June 2021; pp. 1–3. [Google Scholar]
- Boser, B.E.; Guyon, I.M.; Vapnik, V.N. A Training Algorithm for Optimal Margin Classifiers. In Proceedings of the Proceedings of the Fifth Annual Workshop on Computational Learning Theory; COLT ’92; Association for Computing Machinery: New York, NY, USA, 1992; pp. 144–152. [Google Scholar] [CrossRef]
- Luo, J.; Hong, T.; Fang, S.C. Benchmarking robustness of load forecasting models under data integrity attacks. Int. J. Forecast. 2018, 34, 89–104. [Google Scholar] [CrossRef]
- Komeylian, S.; Paolini, C. Implementation of a Three-class Classification LS-SVM Model for the Hybrid Antenna Array with Bowtie Elements in the Adaptive Beamforming Application. arXiv 2022, arXiv:2210.00317. [Google Scholar]
- Hussain, A.A.; Tayem, N.; Butt, M.O.; Soliman, A.H.; Alhamed, A.; Alshebeili, S. FPGA Hardware Implementation of DOA Estimation Algorithm Employing LU Decomposition. IEEE Access 2018, 6, 17666–17680. [Google Scholar] [CrossRef]
- Abusultan, M.; Harkness, S.; LaMeres, B.J.; Huang, Y. FPGA implementation of a Bartlett direction of arrival algorithm for a 5.8ghz circular antenna array. In Proceedings of the 2010 IEEE Aerospace Conference, Big Sky, MT, USA, 6–13 March 2010; pp. 1–10. [Google Scholar] [CrossRef]
- Dick, C.; Harris, F.; Pajic, M.; Vuletic, D. Real-Time QRD-Based Beamforming on an FPGA Platform. In Proceedings of the 2006 Fortieth Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 29 October–1 November 2006; pp. 1200–1204. [Google Scholar] [CrossRef]
- Lopes, F.F.; Silva, S.N.; Fernandes, M.A.C. FPGA Implementation of the Adaptive Digital Beamforming for Massive Array. In Proceedings of the 2021 IEEE 93rd Vehicular Technology Conference (VTC2021-Spring), Virtual, 25–28 April 2021; pp. 1–5. [Google Scholar] [CrossRef]
- Lu, M.; Wang, C.; Jin, S.; Zhu, R.; Zhang, J.; Li, H. Research on Beamspace Adaptive Digital Beamforming Algorithm and FPGA Implementation. In Proceedings of the 2022 7th International Conference on Intelligent Computing and Signal Processing (ICSP), Virtual, 15–17 April 2022; pp. 52–56. [Google Scholar] [CrossRef]
- Xin, X.; Qinghong, Y.; Zhaolin, S.; Qingjiang, L.; Yinan, W.; Wenli, L. The Realization of Digital Beamforming Based on FPGA and DSP. In Proceedings of the 2010 International Conference on Intelligent System Design and Engineering Application, Changsha, China, 13–14 October 2010; Volume 2, pp. 713–716. [Google Scholar] [CrossRef]
- Ullah, K.; Venkatakrishnan, S.B.; Volakis, J.L. Millimeter-Wave Digital Beamforming Receiver Using RFSoC FPGA for MIMO Communications. In Proceedings of the 2022 IEEE 22nd Annual Wireless and Microwave Technology Conference (WAMICON), Clearwater Beach, FL, USA, 27–28 April 2022; pp. 1–4. [Google Scholar] [CrossRef]
- Hussain, M. Theory and analysis of adaptive cylindrical array antenna for ultrawideband wireless communications. IEEE Trans. Wirel. Commun. 2005, 4, 3075–3083. [Google Scholar] [CrossRef]
- Noordin, N.H.; Zuniga, V.; El-Rayis, A.O.; Haridas, N.; Erdogan, A.T.; Arslan, T. Uniform circular arrays for phased array antenna. In Proceedings of the 2011 Loughborough Antennas & Propagation Conference, Loughborough, UK, 14–15 November 2011; pp. 1–4. [Google Scholar] [CrossRef]
- Tataria, H.; Smith, P.J.; Greenstein, L.J.; Dmochowski, P.A.; Matthaiou, M. Impact of Line-of-Sight and Unequal Spatial Correlation on Uplink MU-MIMO Systems. IEEE Wirel. Commun. Lett. 2017, 6, 634–637. [Google Scholar] [CrossRef]
- Tan, W.; Assimonis, S.D.; Matthaiou, M.; Han, Y.; Li, X.; Jin, S. Analysis of Different Planar Antenna Arrays for mmWave Massive MIMO Systems. In Proceedings of the 2017 IEEE 85th Vehicular Technology Conference (VTC Spring), Sydney, Australia, 4–7 June 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Komeylian, S. Optimization Modeling of the Hybrid Antenna Array for the DoA Estimation. Int. J. Electron. Commun. Eng. 2021, 15, 72–77. [Google Scholar]
- Luo, J.; Yan, X.; Tian, Y. Unsupervised quadratic surface support vector machine with application to credit risk assessment. Eur. J. Oper. Res. 2020, 280, 1008–1017. [Google Scholar] [CrossRef]
- Darzi, S.; Kiong, T.; Islam, M.; Ismail, M.; Kibria, S.; Salem, B. Null Steering of Adaptive Beamforming Using Linear Constraint Minimum Variance Assisted by Particle Swarm Optimization, Dynamic Mutated Artificial Immune System, and Gravitational Search Algorithm. Sci. World J. 2014, 2014, 724639. [Google Scholar] [CrossRef] [PubMed]
- Vorobyov, S. Principles of minimum variance robust adaptive beamforming design. Signal Process. 2013, 93, 3264–3277. [Google Scholar] [CrossRef]
- Komeylian, S. Deep Neural Network Modeling of Different Antenna Arrays; Analysis, Evaluation, and Application. IEEE Can. J. Electr. Comput. Eng. 2021, 44, 261–274. [Google Scholar] [CrossRef]
- Hashemi Fath, A.; Madanifar, F.; Abbasi, M. Implementation of multilayer perceptron (MLP) and radial basis function (RBF) neural networks to predict solution gas-oil ratio of crude oil systems. Petroleum 2020, 6, 80–91. [Google Scholar] [CrossRef]
- Komeylian, S. Implementation and Evaluation of LS-SVM Optimization Methods for Estimating DoAs. In Proceedings of the 2020 IEEE Canadian Conference on Electrical and Computer Engineering (CCECE), London, ON, Canada, 30 August–2 September 2020; pp. 1–8. [Google Scholar] [CrossRef]
- Suykens, J.; Vandewalle, J. Least Squares Support Vector Machine Classifiers. Neural Process. Lett. 1999, 9, 293–300. [Google Scholar] [CrossRef]
- Yuan, Q.; Chen, Q.; Sawaya, K. Performance of adaptive array antenna with arbitrary geometry in the presence of mutual coupling. IEEE Trans. Antennas Propag. 2006, 54, 1991–1996. [Google Scholar] [CrossRef]
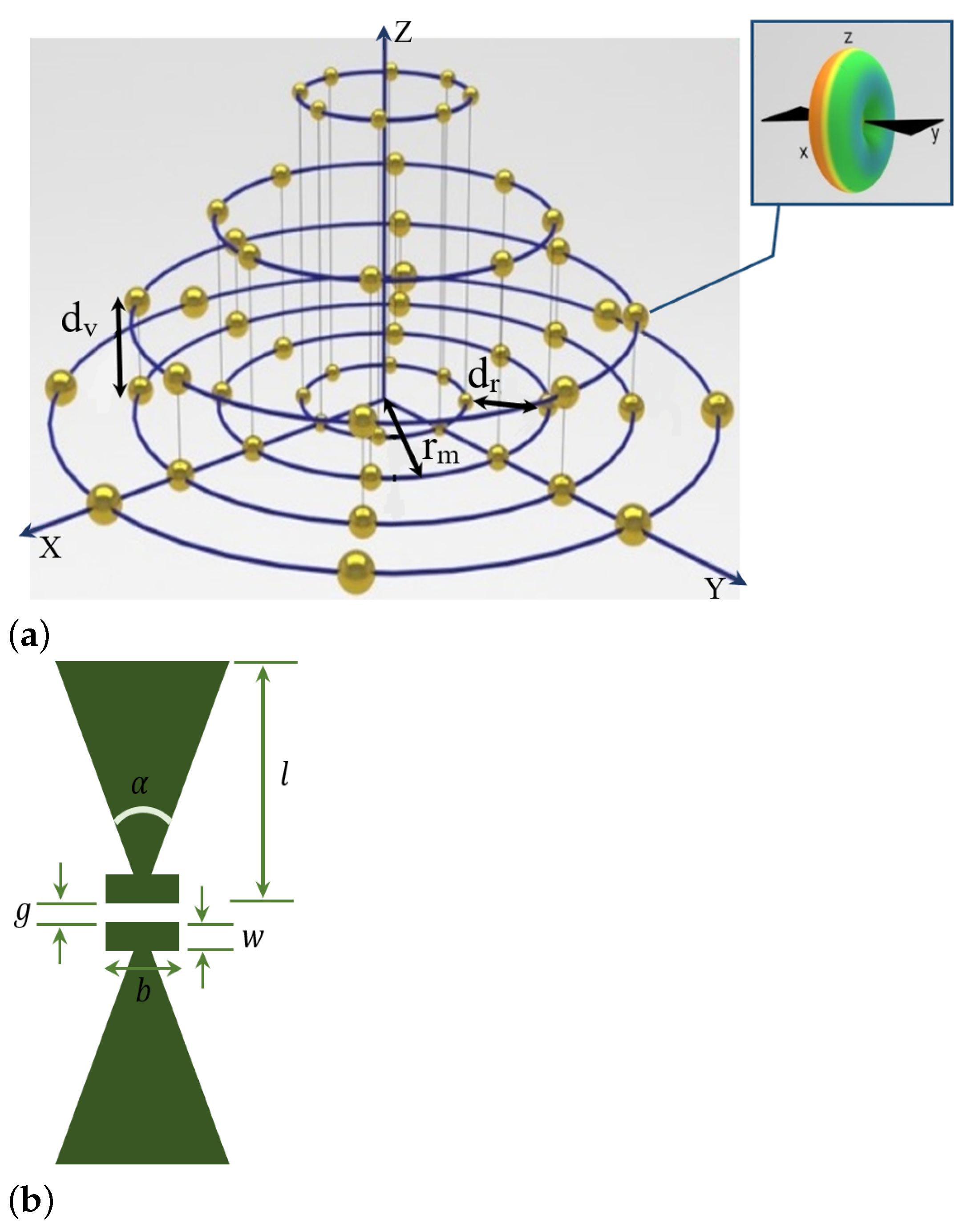

| Parameters | Definition | Value |
|---|---|---|
| Number of elements of any circular loop | ||
| Number of elements of any cylinder | ||
| Total number of cylinders in the proposed array | ||
| Number of circular loops in the cylinder | ||
| Vertical spacing between two consecutive circular loops | ||
| Horizontal spacing between two consecutive circular loops | ||
| Maximum scanning angles |
| Antenna array with bowtie elements | Antenna array with dipole elements | |
|
Performance efficiency of the proposed QS-SVM beamformer | 96% | 75% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Komeylian, S.; Paolini, C. Implementation of the Digital QS-SVM-Based Beamformer on an FPGA Platform. Sensors 2023, 23, 1742. https://doi.org/10.3390/s23031742
Komeylian S, Paolini C. Implementation of the Digital QS-SVM-Based Beamformer on an FPGA Platform. Sensors. 2023; 23(3):1742. https://doi.org/10.3390/s23031742
Chicago/Turabian StyleKomeylian, Somayeh, and Christopher Paolini. 2023. "Implementation of the Digital QS-SVM-Based Beamformer on an FPGA Platform" Sensors 23, no. 3: 1742. https://doi.org/10.3390/s23031742
APA StyleKomeylian, S., & Paolini, C. (2023). Implementation of the Digital QS-SVM-Based Beamformer on an FPGA Platform. Sensors, 23(3), 1742. https://doi.org/10.3390/s23031742







