Subwavelength Diffractive Optical Elements for Generation of Terahertz Coherent Beams with Pre-Given Polarization State
Abstract
1. Introduction
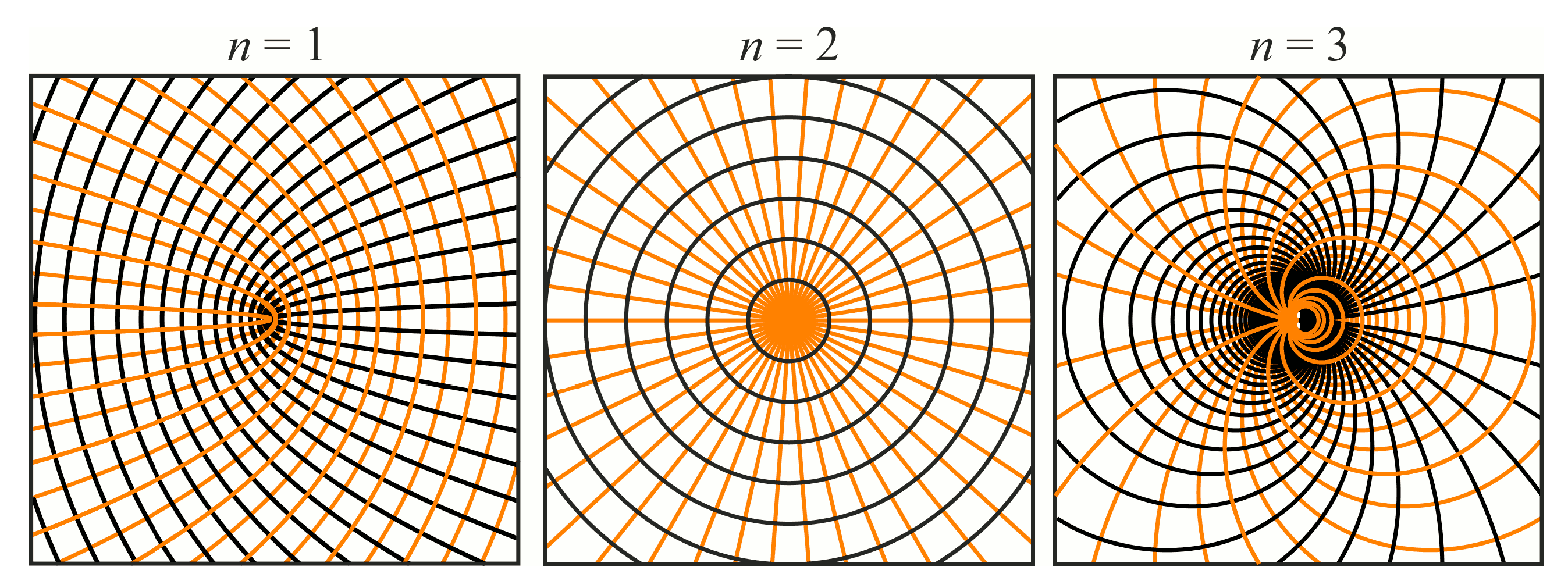
2. Theoretical Description of Subwavelength Diffractive Gratings Design
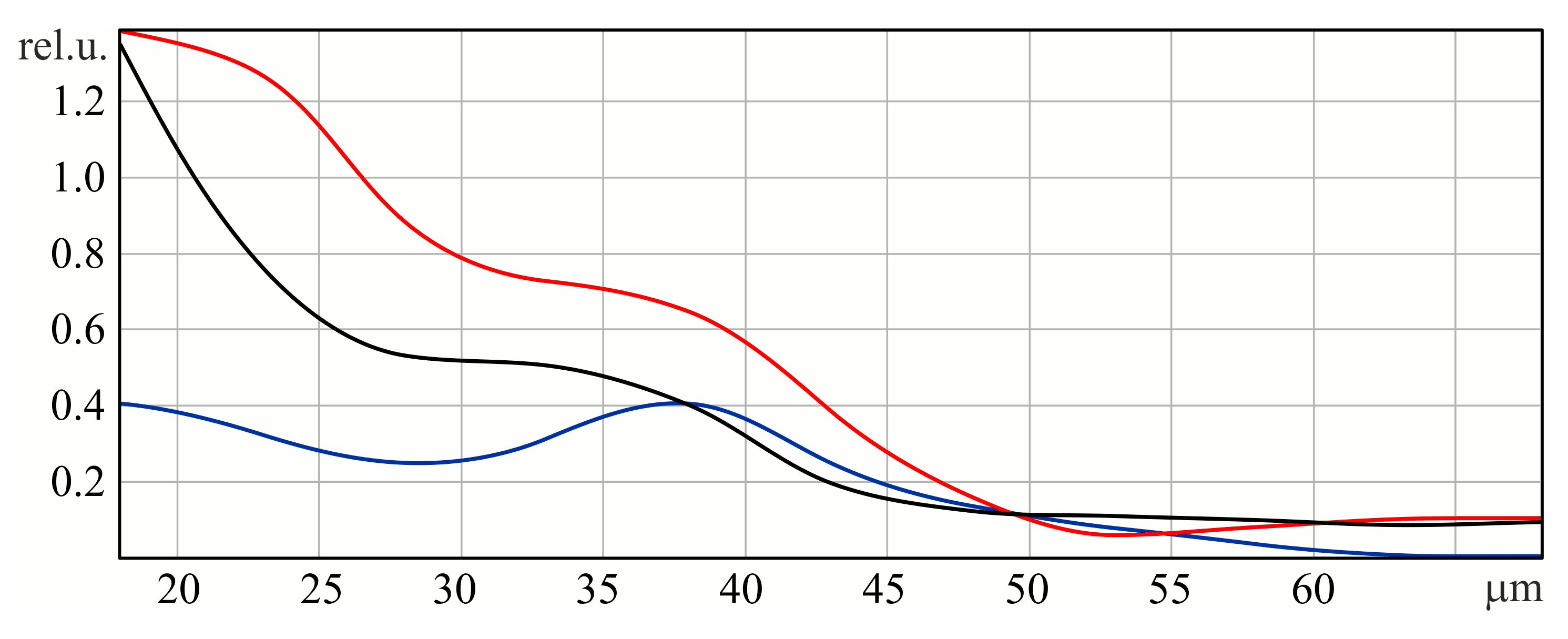
3. Design, Simulation, and Fabrication of Subwavelength Diffractive Optical Elements
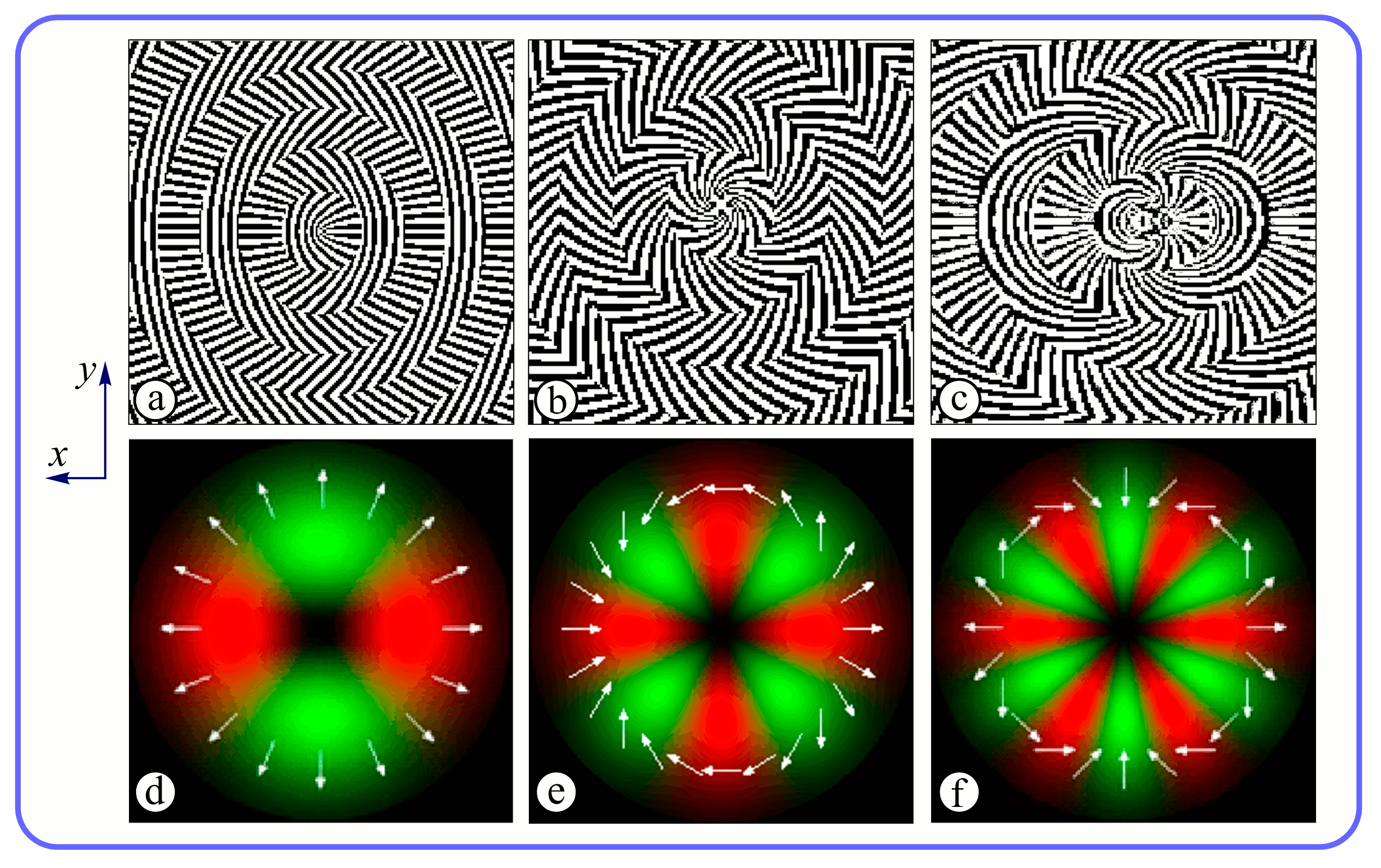
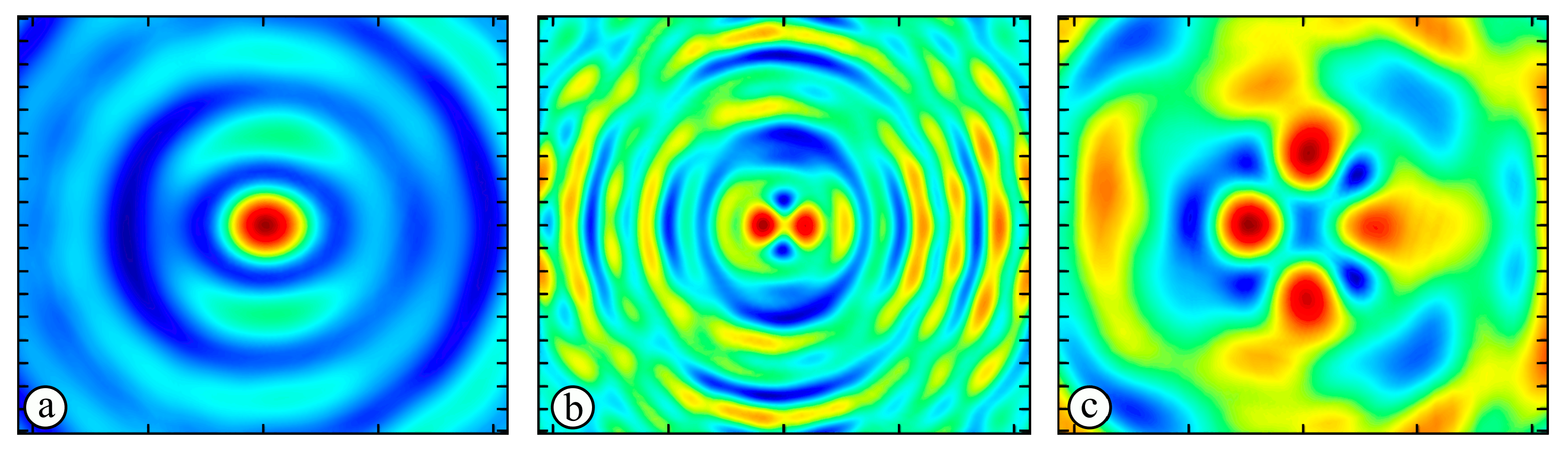
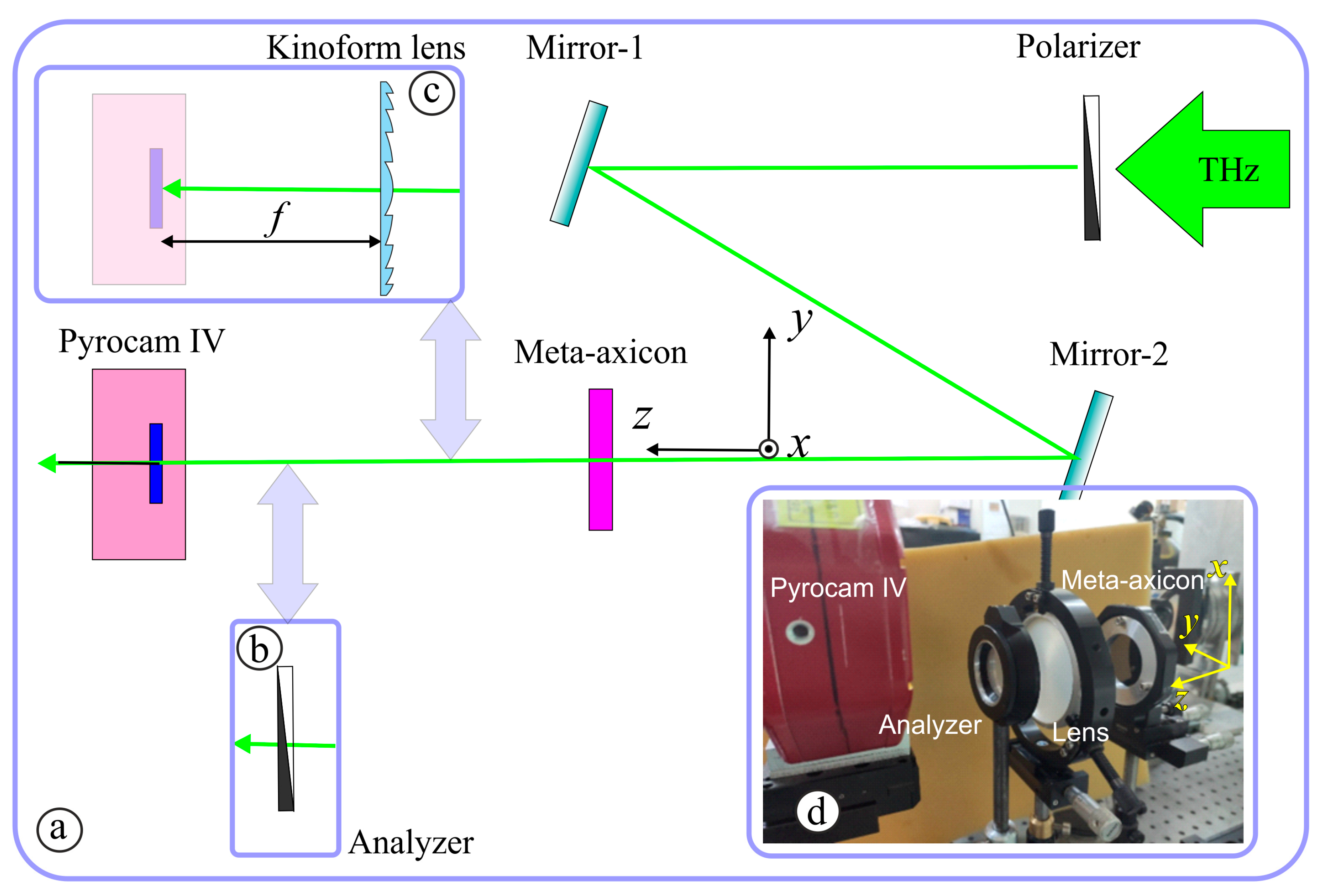
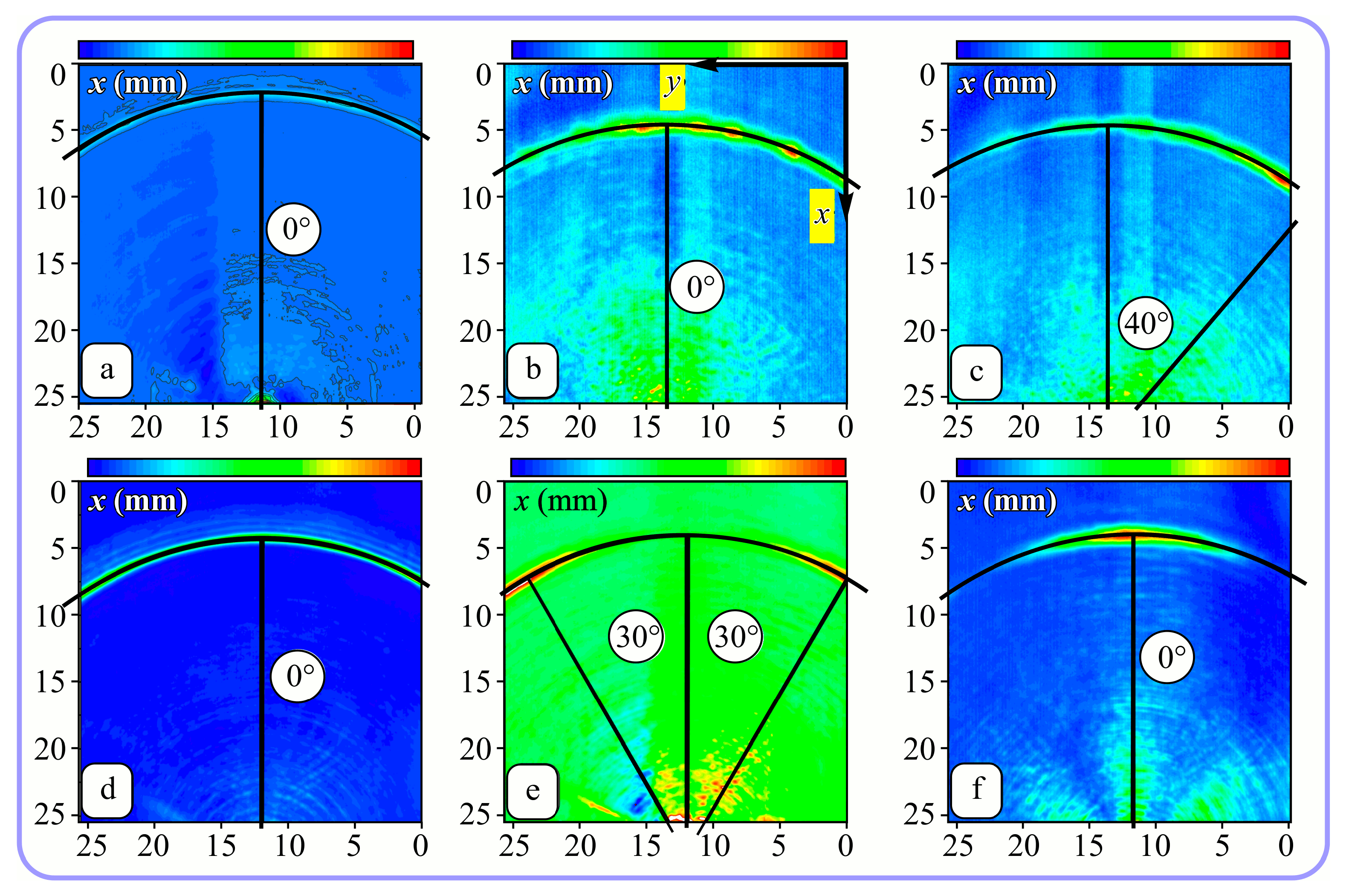
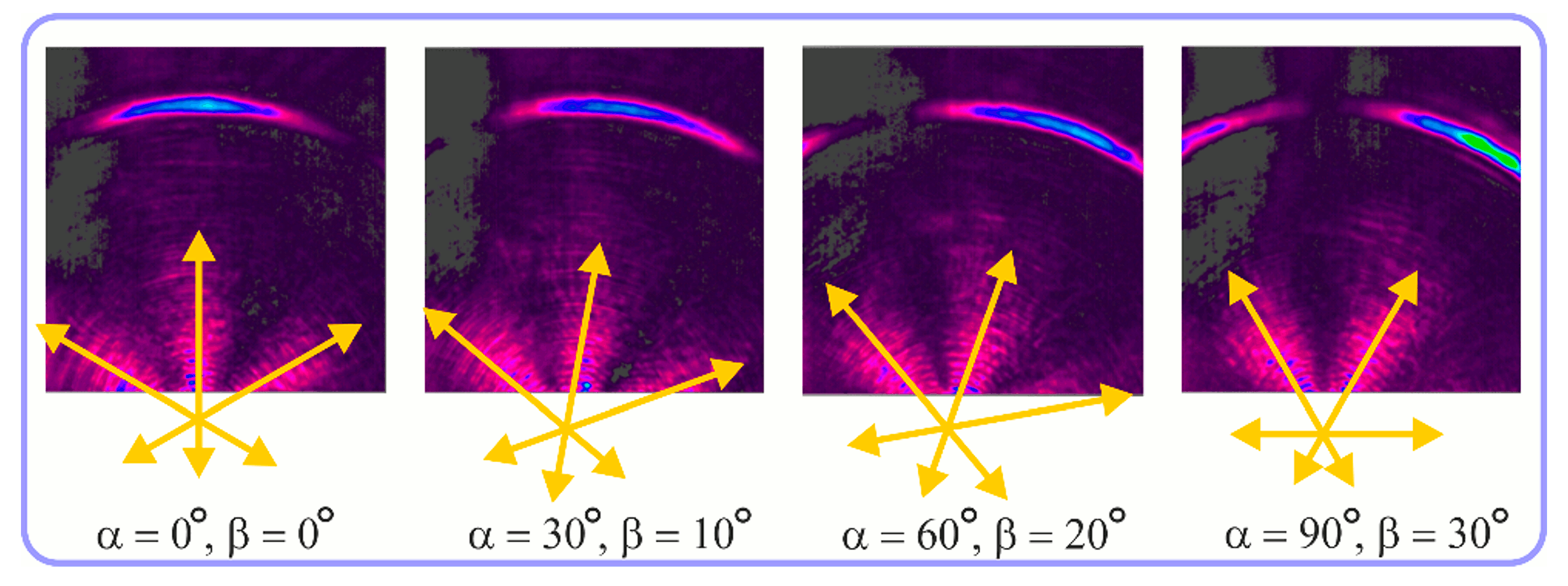
4. Experimental Investigation of Subwavelength Diffractive Optical Elements
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kogelnik, H.; Li, T. Laser Beams and Resonators. Appl. Opt. 1966, 5, 1550–1567. [Google Scholar] [CrossRef]
- Salvi, J.; Pagâ, J.; Batlle, J. Pattern codification strategies in structured light systems. Pattern Recognit. 2004, 37, 827–849. [Google Scholar] [CrossRef]
- Rubinsztein-Dunlop, H.; Forbes, A.; Berry, M.V.; Dennis, M.R.; Andrews, D.L.; Mansuripur, M.; Denz, C.; Alpmann, C.; Banzer, P.; Bauer, T.; et al. Roadmap on structured light. J. Opt. 2017, 19, 013001. [Google Scholar] [CrossRef]
- Forbes, A. Structured light from lasers. Laser Photonics Rev. 2019, 13, 1900140. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, L.; Chen, W.; Loiko, P.; Mateos, X.; Xu, X.; Liu, Y.; Shen, D.; Wang, Z.; Xu, X.; et al. Structured laser beams: Toward 2-μm femtosecond laser vortices. Photonics Res. 2021, 9, 357–363. [Google Scholar] [CrossRef]
- Forbes, A.; De Oliveira, M.; Dennis, M.R. Structured light. Nat. Photonics 2021, 15, 253–262. [Google Scholar] [CrossRef]
- Porfirev, A.P.; Kuchmizhak, A.A.; Gurbatov, S.O.; Juodkazis, S.; Khonina, S.N.; Kul’chin, Y.N. Phase singularities and optical vortices in photonics. Phys. Uspekhi 2022, 65, 789–811. [Google Scholar] [CrossRef]
- Dholakia, K.; Lee, W.M. Optical trapping takes shape: The use of structured light fields. Adv. At. Mol. Opt. Phys. 2008, 56, 261–337. [Google Scholar] [CrossRef]
- Woerdemann, M.; Alpmann, C.; Esseling, M.; Denz, C. Advanced optical trapping by complex beam shaping. Laser Photonics Rev. 2013, 7, 839–854. [Google Scholar] [CrossRef]
- Rodrigo, J.A.; Alieva, T. Freestyle 3D laser traps: Tools for studying light-driven particle dynamics and beyond. Optica 2015, 2, 812–815. [Google Scholar] [CrossRef]
- Yang, Y.; Ren, Y.X.; Chen, M.; Arita, Y.; Rosales-Guzmán, C. Optical trapping with structured light: A review. Adv. Photonics 2021, 3, 034001. [Google Scholar] [CrossRef]
- Corsettia, S.; Dholakia, K. Optical manipulation: Advances for biophotonics in the 21st century. J. Biomed. Opt. 2021, 26, 070602. [Google Scholar] [CrossRef]
- Huang, H.; Xie, G.; Yan, Y.; Ahmed, N.; Ren, Y.; Yue, Y.; Rogawski, D.; Willner, M.J.; Erkmen, B.I.; Birnbaum, K.M.; et al. 100 Tbit/s free-space data link enabled by three-dimensional multiplexing of orbital angular momentum, polarization, and wavelength. Opt. Lett. 2014, 39, 197–200. [Google Scholar] [CrossRef] [PubMed]
- Du, J.; Wang, J. High-dimensional structured light coding/decoding for freespace optical communications free of obstructions. Opt. Lett. 2015, 40, 4827–4830. [Google Scholar] [CrossRef] [PubMed]
- Lavery, M.P.; Peuntinger, C.; Günthner, K.; Banzer, P.; Elser, D.; Boyd, R.W.; Padgett, M.J.; Padgett, M.J.; Leuchs, G. Free-space propagation of high-dimensional structured optical fields in an urban environment. Sci. Adv. 2017, 3, e1700552. [Google Scholar] [CrossRef] [PubMed]
- Khonina, S.N.; Porfirev, A.P.; Karpeev, S.V. Recognition of polarization and phase states of light based on the interaction of non-uniformly polarized laser beams with singular phase structures. Opt. Express 2019, 27, 18484–18492. [Google Scholar] [CrossRef]
- Wang, J.; Yang, J.Y.; Fazal, I.; Ahmed, N.; Yan, Y.; Huang, H.; Ren, Y.; Yue, Y.; Dolinar, S.; Tur, M.; et al. Terabit free-space data transmission employing orbital angular momentum multiplexing. Nat. Photonics 2020, 6, 488–496. [Google Scholar] [CrossRef]
- Khonina, S.N.; Karpeev, S.V.; Butt, A.M. Spatial-Light-Modulator-Based Multichannel Data Transmission by Vortex Beams of Various Orders. Sensors 2021, 21, 2988. [Google Scholar] [CrossRef]
- Omatsu, T.; Chujo, K.; Miyamoto, K.; Okida, M.; Nakamura, K.; Aoki, N.; Morita, R. Metal microneedle fabrication using twisted light with spin. Opt. Express 2010, 18, 17967–17973. [Google Scholar] [CrossRef]
- Hnatovsky, C.; Shvedov, V.G.; Shostka, N.; Rode, A.V.; Krolikowski, W. Polarization-dependent ablation of silicon using tightly focused femtosecond laser vortex pulses. Opt. Lett. 2012, 37, 226–228. [Google Scholar] [CrossRef]
- Danilov, P.A.; Saraeva, I.N.; Kudryashov, S.I.; Porfirev, A.P.; Kuchmizhak, A.A.; Zhizhchenko, A.Y.; Rudenko, A.A.; Umanskaya, S.F.; Zayarny, D.A.; Ionin, A.A.; et al. Polarization-selective excitation of dye luminescence on a gold film by structured ultrashort laser pulses. JETP Lett. 2018, 107, 15–18. [Google Scholar] [CrossRef]
- Flamm, D.; Grossmann, D.G.; Sailer, M.; Kaiser, M.; Zimmermann, F.; Chen, K.; Jenne, M.; Kleiner, J.; Hellstern, J.; Tillkorn, C.; et al. Structured light for ultrafast laser micro- and nanoprocessing. Opt. Eng. 2021, 60, 025105. [Google Scholar] [CrossRef]
- Porfirev, A.P.; Khonina, S.N.; Ivliev, N.A.; Meshalkin, A.; Achimova, E.A.; Forbes, A. Writing and reading with the longitudinal component of light using carbazole-containing azopolymer thin films. Sci. Rep. 2022, 12, 3477. [Google Scholar] [CrossRef] [PubMed]
- Török, P.; Munro, P.R.T. The use of Gauss-Laguerre vector beams in STED microscopy. Opt. Express 2004, 12, 3605–3617. [Google Scholar] [CrossRef] [PubMed]
- Hao, X.; Kuang, C.; Wang, T.; Liu, X. Effects of polarization on the de-excitation dark focal spot in STED microscopy. J. Opt. 2010, 12, 115707. [Google Scholar] [CrossRef]
- Khonina, S.N.; Golub, I. How low can STED go? Comparison of different write-erase beam combinations for stimulated emission depletion microscopy. J. Opt. Soc. Am. 2012, 29, 2242–2246. [Google Scholar] [CrossRef]
- Wu, Y.; Shroff, H. Faster, sharper, and deeper: Structured illumination microscopy for biological imaging. Nat. Methods 2018, 15, 1011–1019. [Google Scholar] [CrossRef]
- Hasegawa, S.; Takahashi, H.; Ota, M.; Barada, D.; Ogura, Y.; Tanida, J.; Hayasaki, Y. Spatial phase shaping of ultrashort laser pulses to overcome the diffraction limit. OSA Contin. 2019, 2, 3240–3250. [Google Scholar] [CrossRef]
- Liu, M.; Lei, Y.; Yu, L.; Fang, X.; Ma, Y.; Liu, L.; Zheng, J.; Gao, P. Super-resolution optical microscopy using cylindrical vector beams. Nanophotonics 2022, 11, 3395–3420. [Google Scholar] [CrossRef]
- Weibin, C.; Zhan, Q. Realization of an evanescent Bessel beam via surface plasmon interference excited by a radially polarized beam. Opt. Lett. 2009, 34, 722–724. [Google Scholar] [CrossRef]
- Wang, D.; Wang, W.; Knudson, M.P.; Schatz, G.C.; Odom, T.W. Structural Engineering in Plasmon Nanolasers. Chem. Rev. 2018, 118, 2865–2881. [Google Scholar] [CrossRef] [PubMed]
- Rogel-Salazar, J.; Treviño, J.P.; Chávez-Cerda, S. Engineering structured light with optical vortices. J. Opt. Soc. Am. B 2014, 31, 46–50. [Google Scholar] [CrossRef]
- Barlev, O.; Golub, M.A. Multifunctional binary diffractive optical elements for structured light projectors. Opt. Express 2018, 26, 21092–21107. [Google Scholar] [CrossRef] [PubMed]
- Kazanskiy, N.L.; Khonina, S.N.; Karpeev, S.V.; Porfirev, A.P. Diffractive optical elements for multiplexing structured laser beams. Quantum Electron. 2020, 50, 629–635. [Google Scholar] [CrossRef]
- Davis, J.A.; McNamara, D.E.; Cottrell, D.M.; Sonehara, T. Two-dimensional polarization encoding with a phase-only liquid crystal spatial light modulator. Appl. Opt. 2000, 39, 1549–1554. [Google Scholar] [CrossRef]
- Moreno, I.; Davis, J.A.; Hernandez, T.M.; Cottrell, D.M.; Sand, D. Complete polarization control of light from a liquid crystal spatial light modulator. Opt. Express 2012, 20, 364–376. [Google Scholar] [CrossRef]
- Khonina, S.N.; Karpeev, S.V.; Paranin, V.D.; Morozov, A.A. Polarization conversion under focusing of vortex laser beams along the axis of anisotropic crystals. Phys. Lett. 2017, 381, 2444–2455. [Google Scholar] [CrossRef]
- He, Y.; Wang, P.; Wang, C.; Liu, J.; Ye, H.; Zhou, X.; Li, Y.; Chen, S.; Zhang, X.; Fan, D. All-optical signal processing in structured light multiplexing with dielectric meta-optics. ACS Photonics 2020, 7, 135–146. [Google Scholar] [CrossRef]
- Khonina, S.N.; Porfirev, A.P.; Kazanskiy, N.L. Variable transformation of singular cylindrical vector beams using anisotropic crystals. Sci. Rep. 2020, 10, 5590. [Google Scholar] [CrossRef]
- Wang, J.; Liang, Y. Generation and Detection of Structured Light: A Review. Front. Phys. 2021, 9, 688284. [Google Scholar] [CrossRef]
- Kulipanov, G.N.; Bagryanskaya, E.G.; Chesnokov, E.N.; Choporova, Y.Y.; Gerasimov, V.V.; Getmanov, Y.V.; Kiselev, S.L.; Knyazev, B.A.; Kubarev, V.V.; Peltek, S.E.; et al. Novosibirsk Free Electron Laser—Facility Description and Recent Experiments. IEEE Trans. Terahertz Sci. Technol. 2015, 5, 798–809. [Google Scholar] [CrossRef]
- Walsby, E.D.; Wang, S.; Xu, J.; Yuan, T.; Blaikie, R.; Durbin, S.M.; Zhang, X.C.; Cumming, D.R.S. Multilevel silicon diffractive optics for terahertz waves. J. Vac. Sci. Technol. 2002, 20, 2780–2783. [Google Scholar] [CrossRef]
- Furlan, W.D.; Ferrando, V.; Monsoriu, J.A.; Zagrajek, P.; Czerwinska, E.; Szustakowski, M. 3D printed diffractive terahertz lenses. Opt. Lett. 2016, 41, 1748–1751. [Google Scholar] [CrossRef]
- Castro-Camus, E.; Koch, M.; Hernandez-Serrano, A.I. Additive manufacture of photonic components for the terahertz band. J. Appl. Phys. 2020, 127, 210901. [Google Scholar] [CrossRef]
- Komorowski, P.; Czerwi’nska, P.; Kaluza, M.; Surma, M.; Zagrajek, P.; Sobczyk, A.; Ciurapi´nski, W.; Piramidowicz, R.; Siemion, A. Frequency Division Multiplexing of Terahertz Waves Realized by Diffractive Optical Elements. Appl. Sci. 2021, 11, 6246. [Google Scholar] [CrossRef]
- Siemion, A. The Magic of Optics—An Overview of Recent Advanced Terahertz Diffractive Optical Elements. Sensors 2021, 21, 100. [Google Scholar] [CrossRef] [PubMed]
- Rachon, M.; Liebert, K.; But, D.; Zagrajek, P.; Siemion, A.; Kolodziejczyk, A.; Sypek, M.; Suszek, J. Enhanced Sub-wavelength Focusing by Double-Sided Lens with Phase Correction in THz Range. J. Infrared Millim. Terahertz Waves 2020, 41, 685–696. [Google Scholar] [CrossRef]
- Agafonov, A.N.; Volodkin, B.O.; Kaveev, A.K.; Knyazev, B.A.; Kropotov, G.I.; Pavelyev, V.S.; Soifer, V.A.; Tukmakov, K.N.; Tsygankova, E.V.; Choporova, Y.Y. Silicon diffractive optical elements for high-power monochromatic terahertz radiation. Optoelectron. Instrum. Data Process. 2013, 49, 189–195. [Google Scholar] [CrossRef]
- Agafonov, A.N.; Volodkin, B.O.; Volotovsky, S.G.; Kaveev, A.K.; Knyazev, B.A.; Kropotov, G.I.; Tukmakov, K.N.; Pavelyev, V.S.; Tsygankova, E.V.; Tsypishka, D.I.; et al. Optical elements for focusing of terahertz laser radiation in a given two-dimensional domain. Opt. Mem. Neural Netw. Inf. Opt. 2014, 23, 185–190. [Google Scholar] [CrossRef]
- Liebert, K.; Rachon, M.; Siemion, A.; Suszek, J.; But, D.; Knap, W.; Sypek, M. THz beam shaper realizing fan-out patterns. J. Infrared Millim. Terahertz Waves 2017, 38, 1019–1030. [Google Scholar] [CrossRef]
- Mirzaei, B.; Silva, J.; Luo, Y.; Liu, X.; Wei, L.; Hayton, D.J.; Gao, J.; Groppi, C. Efficiency of multi-beam Fourier phase gratings at 1.4 THz. Opt. Express 2017, 25, 6581–6588. [Google Scholar] [CrossRef] [PubMed]
- Agafonov, A.N.; Choporova, Y.Y.; Kaveev, A.K.; Knyazev, B.A.; Kropotov, G.I.; Pavelyev, V.S.; Tukmakov, K.N.; Volodkin, B.O. Control of transverse mode spectrum of Novosibirsk free electron laser radiation. Appl. Opt. 2015, 54, 3635–3639. [Google Scholar] [CrossRef]
- Liu, C.; Wei, X.; Niu, L.; Wang, K.; Yang, Z.; Liu, J. Discrimination of orbital angular momentum modes of the terahertz vortex beam using a diffractive mode transformer. Opt. Express 2016, 24, 12534–12541. [Google Scholar] [CrossRef]
- Choporova, Y.Y.; Knyazev, B.A.; Kulipanov, G.N.; Pavelyev, V.S.; Scheglov, M.A.; Vinokurov, N.A.; Volodkin, B.O.; Zhabin, V.N. High-power Bessel beams with orbital angular momentum in the terahertz range. Phys. Rev. A 2017, 96, 023846. [Google Scholar] [CrossRef]
- Yang, T.; Liu, X.; Wang, C.; Liu, Z.; Sun, J.; Zhou, J. Polarization conversion in terahertz planar metamaterial composed of split-ring resonators. Opt. Commun. 2020, 472, 125897. [Google Scholar] [CrossRef]
- Deng, G.; Sun, H.; Lv, K.; Yang, J.; Yin, Z.; Chi, B. An efficient wideband crosspolarization converter manufactured by stacking metal/dielectric multilayers via 3D printing. J. Appl. Phys. 2020, 127, 093103. [Google Scholar] [CrossRef]
- Zou, M.; Su, M.; Yu, H. Ultra-broadband and wide-angle terahertz polarization converter based on symmetrical anchor-shaped metamaterial. Opt. Mater. 2020, 107, 110062. [Google Scholar] [CrossRef]
- Zi, J.; Xu, Q.; Wang, Q.; Tian, C.; Li, Y.; Zhang, X.; Han, J.; Zhang, W. Antireflection-assisted all-dielectric terahertz metamaterial polarization converter. Appl. Phys. Lett. 2018, 113, 101104. [Google Scholar] [CrossRef]
- Khonina, S.N.; Tukmakov, K.N.; Degtyarev, S.A.; Reshetnikov, A.S.; Pavelyev, V.S.; Knyazev, B.A.; Choporova, Y.Y. Design, fabrication and investigation of a subwavelength axicon for terahertz beam polarization transforming. Comput. Opt. 2019, 43, 756–764. [Google Scholar] [CrossRef]
- Pavelyev, V.S.; Degtyarev, S.A.; Tukmakov, K.N.; Reshetnikov, A.S.; Knyazev, B.A.; Choporova, Y.Y. Silicon subwavelength axicons for terahertz beam polarization transformation. J. Phys. Conf. Ser. 2021, 1745, 012022. [Google Scholar] [CrossRef]
- Degtyarev, S.A.; Savelyev, D.A.; Khonina, S.N.; Kazanskiy, N.L. Metasurfaces with continuous ridges for inverse energy flux generation. Opt. Express 2019, 27, 15129–15135. [Google Scholar] [CrossRef] [PubMed]
- Khonina, S.N.; Degtyarev, S.A.; Ustinov, A.V.; Porfirev, A.P. Metalenses for the generation of vector Lissajous beams with a complex Poynting vector density. Opt. Express 2021, 29, 18651–18662. [Google Scholar] [CrossRef] [PubMed]
- Bomzon, Z.E.; Biener, G.; Kleiner, V.; Hasman, E. Space-variant Pancharatnam–Berry phase optical elements with computer-generated subwavelength gratings. Opt. Lett. 2002, 40, 1141–1143. [Google Scholar] [CrossRef]
- Degtyarev, S.A.; Savelyev, D.A.; Karpeev, S.V. Diffractive optical elements for generating cylindrical beams of different orders. Comput. Opt. 2019, 43, 347–355. [Google Scholar] [CrossRef]
- Ayón, A.A.; Braff, R.; Lin, C.C.; Sawin, H.H.; Schmidt, M.A. Characterization of a time multiplexed inductively coupled plasma etcher. J. Electrochem. Soc. 1999, 146, 339–349. [Google Scholar] [CrossRef]
- Karpeev, S.V.; Paranin, V.D.; Khonina, S.N. Generation of a controlled double-ring-shaped radially polarized spiral laser beam using a combination of a binary axicon with an interference polarizer. J. Opt. 2017, 19, 055701. [Google Scholar] [CrossRef]
- Choporova, Y.; Knyazev, B.; Pavelyev, V. Holography with high-power CW coherent terahertz source: Optical components, imaging, and applications. Light Adv. Manuf. 2022, 3, 31. [Google Scholar] [CrossRef]




| Height of the Relief (μm) | E-Field Components | ||
|---|---|---|---|
| Full Amplitude | x-Component | y-Component | |
| 40 | 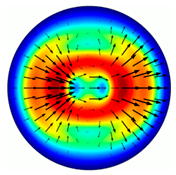 |  |  |
| 50 | 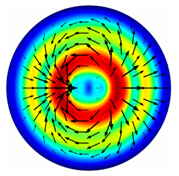 | 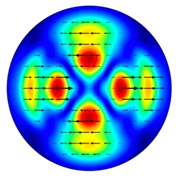 | 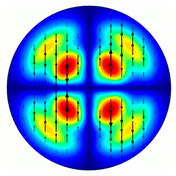 |
| 60 |  |  |  |
| Analyzer Rotation Angle (Deg) | Radial Polarization Order | ||
|---|---|---|---|
| n = 1 | n = 2 | n = 3 | |
| 0 | 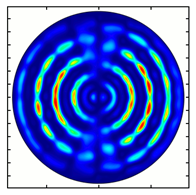 |  | 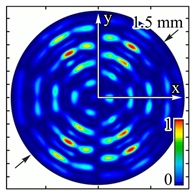 |
| 30 | 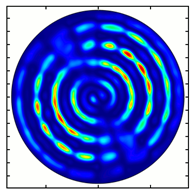 | 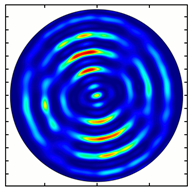 | 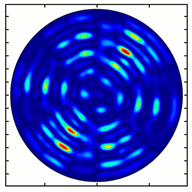 |
| 60 |  |  | 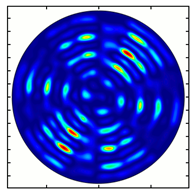 |
| 90 | 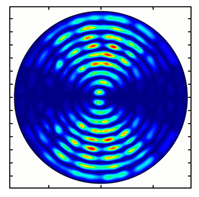 | 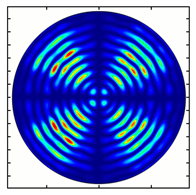 |  |
| 120 |  | 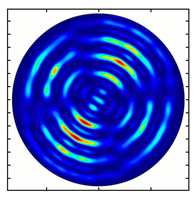 |  |
| 150 |  | 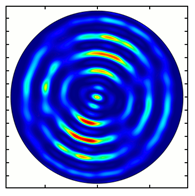 | 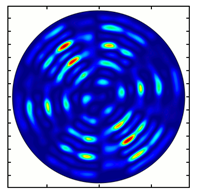 |
| 180 | 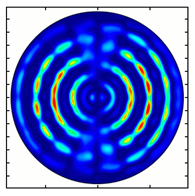 | 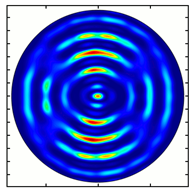 | 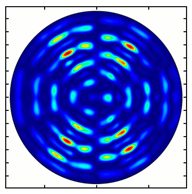 |
| 0 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | |
| 0 | 3 | 7 | 10 | 13 | 17 | 20 | 23 | 27 | 30 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pavelyev, V.; Khonina, S.; Degtyarev, S.; Tukmakov, K.; Reshetnikov, A.; Gerasimov, V.; Osintseva, N.; Knyazev, B. Subwavelength Diffractive Optical Elements for Generation of Terahertz Coherent Beams with Pre-Given Polarization State. Sensors 2023, 23, 1579. https://doi.org/10.3390/s23031579
Pavelyev V, Khonina S, Degtyarev S, Tukmakov K, Reshetnikov A, Gerasimov V, Osintseva N, Knyazev B. Subwavelength Diffractive Optical Elements for Generation of Terahertz Coherent Beams with Pre-Given Polarization State. Sensors. 2023; 23(3):1579. https://doi.org/10.3390/s23031579
Chicago/Turabian StylePavelyev, Vladimir, Svetlana Khonina, Sergey Degtyarev, Konstantin Tukmakov, Anton Reshetnikov, Vasily Gerasimov, Natalya Osintseva, and Boris Knyazev. 2023. "Subwavelength Diffractive Optical Elements for Generation of Terahertz Coherent Beams with Pre-Given Polarization State" Sensors 23, no. 3: 1579. https://doi.org/10.3390/s23031579
APA StylePavelyev, V., Khonina, S., Degtyarev, S., Tukmakov, K., Reshetnikov, A., Gerasimov, V., Osintseva, N., & Knyazev, B. (2023). Subwavelength Diffractive Optical Elements for Generation of Terahertz Coherent Beams with Pre-Given Polarization State. Sensors, 23(3), 1579. https://doi.org/10.3390/s23031579








