Abstract
The performance of TDOA positioning based on UWB is limited by the hyperbolic characteristics of TDOA, especially for tags away from the hyperbolic asymptote. Aiming at this problem, a new UWB indoor positioning system is proposed. Firstly, TOF ranging is adopted to build the positioning equations; then the weighted centroid algorithm of four base stations is presented to compute the initial rough position of the tag; and the residual weighting is introduced to optimize the initial tag position; then, the corresponding nonlinear positioning equations, which will be algebraically transformed to one distribution function, are solved, and the optimal tag coordinates can be obtained by the Newton iteration method. Simulation experiments have verified the positioning reliability of the proposed algorithm under different noise environments and for different tag positions.
1. Introduction
In the ultra-wideband (UWB) positioning system, the ranging accuracy and measuring range are the two key metrics, which can degrade with the noise level, tag location, base station (BS) quantity, and positioning methods, generally. In the LOS or NLOS scenario, the UWB positioning mode is commonly based on time of flight (TOF) [1,2] or time difference of arrival (TDOA) [3,4], which will construct nonlinear positioning equations if the measured distance between the tag and each BS is known; then the tag coordinates can be obtained by solving the positioning equations, such as the Fang algorithm [3], Chan algorithm [4], or Taylor [5,6,7] algorithm. In TDOA positioning, high-precision clock synchronization is required, and the positioning error will increase when the tag is away from the hyperbolic asymptote [8]. When adapting TOF ranging to construct a set of hyperbolic equations, the Chan–Taylor method is often used to solve the tag coordinates [9,10,11], which is time-consuming in computation; alternatively, the centroid algorithm is presented to obtain the initial tag positions, and the final tag coordinates can be optimized by the Taylor iterations to improve the positioning performance [12,13], especially in serious noise environments. However, in the Chan–Taylor iterations, the covariance matrix of TDOA measurements is employed, thus the final tag positioning will be affected by TDOA hyperbolic properties [14]. In addition, for the computed tag coordinates, the literature proposes a residual weighting algorithm (Rwgh) to improve the initial location results by utilizing the minimum residuals instead of the mean square error in the TDOA [15,16]; based on the above residual weighting idea, the higher power of residual as a weighting function is presented to improve the positioning accuracy [17], however, which brings higher complexity in computation. To overcome the impact of TDOA hyperbolic properties and improve location accuracy, the TOF-based UWB system is studied, especially under serious noise environments. In the proposed TOF algorithm, the weighted centroid algorithm is adapted to compute the rough tag position, and a new residual weighting algorithm is proposed to reflect the minimum residuals between the TOF ranging and the estimated distance between the rough tag coordinates and the four BS, aiming to mitigate the rough tag locating error. In addition, an efficient Newton iteration is presented to optimize the final tag positions, avoiding the locating error from the irreversibility of the Hesse matrix.
2. Algorithm Description
TOF ranging is realized by asymmetric double-sided two-way ranging (ADS-TWR) [18] shown in Figure 1. Firstly, the tag transmits a ranging request signal to the BS; and the BS feeds the ranging signal to the tag; then the tag sends a ranging request signal to the BS. The time T from the tag to the BS can be computed by Equation (1)
where Tround1 is the total time of transmitting the ranging signal from the tag to the BS and from the BS to the tag; Tround2 is the total time of the ranging signal transmitted from the BS to the tag and from the tag to the BS; Treply1 is the time delay from the BS reception of the tag ranging signal until the transmission of the reply; and Treply2 is the time delay from the tag reception of the BS ranging signal until the transmission of the reply. If c is the speed of light, then the distance from the tag to the BS is Equation (2)
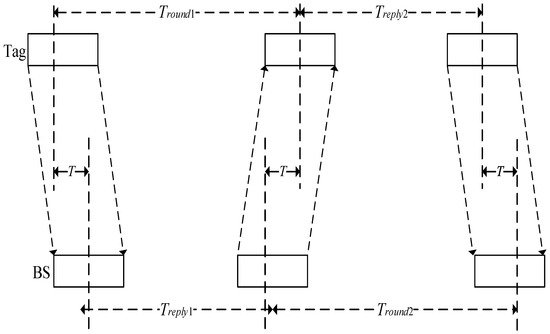
Figure 1.
ADS-TWR positioning schematic diagram.
Given Rn, the TOF positioning equations of the four BS can be represented as Equation (3)
where (x, y) is the abscissa and ordinate of the tag, and (x1, y1), (x2, y2), (x3, y3), and (x4, y4) are the abscissa and ordinate of the four BS respectively. R1, R2, R3, and R4 are the distances between the tag and the four BS stations, respectively. When solving the nonlinear positioning Equation (3), if each BS is taken as the center of the circle and the distance between each BS and the tag as the radius, four circles can be obtained that will have a common intersection, that is, the coordinate of the tag. However, in reality, there are multiple intersections or no intersections among the four positioning circles because of environmental noise or interference. As shown in Figure 2, where there is no intersection point between circles A, C, and D, which will result in no solution of Equation (3).
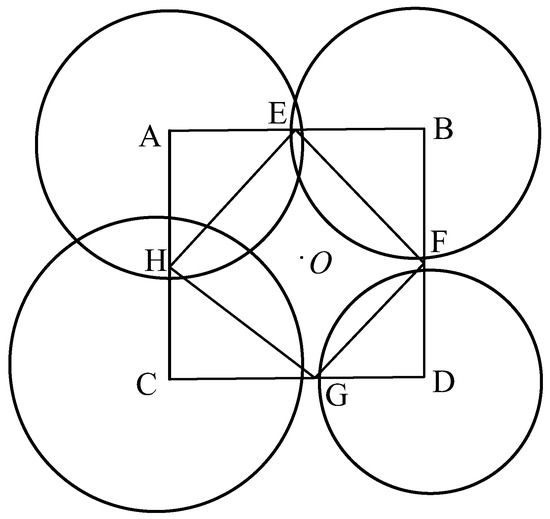
Figure 2.
Weighted centroid positioning.
Aiming at the above problem, in this study, one weighted centroid positioning algorithm is presented, firstly, the centers of the four circles are connected, as in Figure 2, selecting a point E on the AB side of the quadrilateral ABCD to satisfy Equation (4)
where R1 and R2 are the radii of circle A and circle B, respectively. Similarly, the coordinate positions of F, G, and H can be obtained. Thereby, the quadrilateral EFGH can be constructed, whose centroid is the tag coordinate O, denoted as (xo1, yo1) in Equation (5). Here point O is taken as the initial rough position of the tag.
where (xE, yE), (xF, yF), (xG, yG), and (xH, yH) are the abscissa and ordinate of E, F, G, and H, respectively.
Thereby, the standard residual between the TOF range Rn and the distance from each BS to the computed initial rough position is Equation (6)
The residual weighting is introduced to optimize the rough position of the tag as Equation (7)
where N represents the number of ranging times from the BS to the tag, thus solving N different initial rough position of the tag.
To improve positioning accuracy, (xo, yo) will be regarded as the initial value of the positioning equations, which can be optimized, generally by Gauss–Newton iteration [19] or iterative least squares [20]. However, the above optimization methods require Hesse matrix irreversibility, resulting in unsolvable problems [21]. To simplify the iteration process, the Newton iterative method is proposed in this paper. In the proposed Newton iterative method, the nonlinear positioning equations as Equation (3) are combined to obtain Equation (8)
Setting the variable z as Equation (9)
When z = 0, the solution of Equation (9) is the tag coordinate. Thus, solving nonlinear Equation (3) has been transformed into an optimization problem when z = 0. If we describe the partial derivative of x concerning z as Equation (10)
and the partial derivative of y concerning z as Equation (11)
Then the multivariate Newton iteration will be transformed into two univariate Newton iterations in the x direction and y direction, respectively.
If (xi, yi) is the rough estimated coordinate of the tag, the optimal tag position can be computed by the Newton iterative solution, which can be described as Equation (12)
where (xi, yi) and (xi+1, yi+1) are the coordinates of the tag position at the i-th iteration and the (i+1)-th iteration, respectively.
During each iteration, the target position is constantly updated as Equation (13)
where Δx and Δy are the difference between the abscissa and ordinate of the tag before and after the iteration, respectively.
Set the threshold ε, which satisfies Equation (14)
When Δx and Δy satisfy Equation (14), the iteration will stop, and the estimated final tag position can be obtained.
Compared with the Taylor algorithm and iterative least squares, the proposed Newton iterative algorithm does not need to use the Hesse matrix, avoiding the problem of the Hesse matrix irreversibility. Besides, the weighted centroid combined with the Newton iterative algorithm can provide the final tag position with higher positioning accuracy.
3. Simulation Experiment
Selecting four UWB BS under scatter plot analysis of tag positioning conditions, the coordinates are A(0, 0), B(100, 0), C(0, 100), and D(100, 100), respectively; and the tag coordinate is (x, y). When positioning, the tag receives and records signals from each BS, and the channel noise obeys N (0, δ2).
3.1. Parameter Optimization of the Proposed Residual Weighting
During the computing process of the standard residual as Equation (6), these singular values corresponding to the computed initial rough coordinates far away from the tag positions will be removed, and the optimal threshold is set to 0.0031 by experiment, that is Equation (15)
In Equation (7), N is one key optimized parameter. Generally, N is selected as the number of BS minus one [22], or [23], which is suitable in the Chan algorithm; when designing the optimize N, set N is equal to respectively, that is N = 7, 9 or 5, and the corresponding positioning Root Mean Square Error (RMSE) can be expressed as Equation (16)
where n is the number of experimental simulations.
Select N in (7, 9, 5), and the noise variance as 0.5, and 10 tag positions are randomly generated. The RMSE performance of the proposed position algorithm is shown in Figure 3. When N = 9, the RMSE of these 10 points is the smallest. This shows that when N = 9, the residual weighting effect is the best, and the optimal N is equal to .
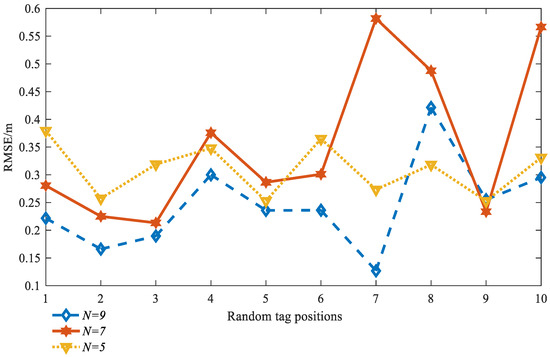
Figure 3.
The RMSE performance of the proposed position algorithm.
3.2. Contrast Experiments
To verify the feasibility of the proposed positioning algorithm, the simulation compares and analyzes the RMSE performance of the weighted centroid Taylor iterative positioning algorithm based on TOF (referred to as TOF-Taylor) [12] and the TDOA positioning algorithm based on TOF ranging (referred to as TOF-TDOA) [9].
3.2.1. The TOF-Taylor
TOF ranging constructs the positioning Equation (3), then the weighted centroid algorithm is introduced to compute the initial coarse coordinate O1(xo, yo) of the tag; then the Taylor algorithm is used to optimize O1 [12]. Assuming A (x1, y1) as the reference BS, Rn, n = 1, 2, 3, 4 is obtained by TOF ranging, and we can obtain the hyperbolic equations Equation (17)
where R1 is the distance between the tag and the reference BS A; and Rn, n = 2, 3, 4 are the distances between the tag and the other three BSs, respectively.
Expanding Equation (17) by a Taylor series at the rough coordinate O1 of the tag, ignoring the components above the second order gives Equation (18)
where , n = 2, 3, 4; and Δx1 and Δy1 are the errors between the true coordinates of the tag and the abscissa and ordinate coordinates of the solution coordinates, respectively.
Equation (18) can be described in matrix form as Equation (19)
where r is the error vector, and as Equations (20) and (21)
is the position deviation given by the WLS method as Equation (22)
Here, Q is the covariance matrix of the TDOA measurement.
The target positions will be continuously updated by solving Equation (18) recursively, until the updated Δx1 and Δy1 satisfy Equation (23)
Here, ε1 is the threshold of the positioning error. When the iteration is stopped, the final estimated tag position is recorded as (xo, yo).
3.2.2. The TOF-TDOA
In the TOF-TDOA [9], TOF ranging in round three is presented to obtain the distance from each BS to the tag, which is recorded as rn, and taking the BS A as the reference BS, the TDOA hyperbolic equations can be constructed as Equation (24)
Substituting Equation (24) into Equation (18), we can obtain Equation (25)
where , , , .
We can see that the nonlinear positioning Equation (18) has been transformed into the linear Equation (25), which can be rewritten in matrix form as Equation (26)
where , , .
Solving Equation (26) by the Chan algorithm [24], an initial rough tag position can be obtained as (xh, yh). In this process, twice WLS is adapted, and the output of the first WLS can be expressed as Equation (27)
where is the covariance matrix of the measurement.
The second WLS is Equation (28)
here , , e1 e2 e3 are the abscissa and ordinate of the tag and the estimation error of the ranging, respectively, and , , .
In L’, can be approximately replaced by H, that is the output initial rough tag position of the first WLS as Equation (27); thereby, after twice WLS, the initial rough tag position (xh, yh) can be solved as Equation (29)
Substituting Equation (29) into Equation (18), the final tag coordinate can be obtained by Taylor iteration, denoted as (xo, yo).
3.3. Experiment 1 Influence of Noise on Positioning Performance
To verify the performance of the proposed algorithm in a severe noise environment, the noise variance is set to 0.1, 0.25, 0.5, 0.75, and 1, respectively. The real coordinate of the tag is (60, 35), the experiment simulation is 1000 times, and the threshold ε and ε1 are set to 0.001. The positioning accuracy of the different positioning algorithms is shown in Figure 4.
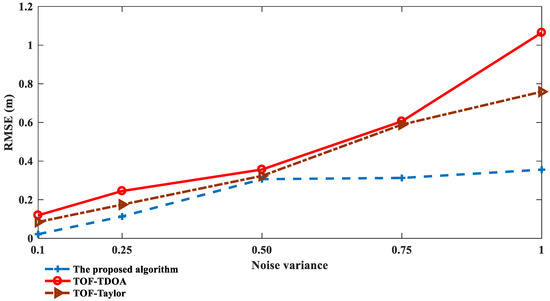
Figure 4.
Positioning performance under different noise levels.
As can be seen from Figure 4, the positioning error of the proposed algorithm shows a slow upward trend with the increase in the noise. When the noise variance is equal to 0.75, the positioning accuracy is improved by 46% and 48% compared with the TOF-Taylor and the TOF-TDOA, respectively; when the noise variance is equal to 1, the positioning accuracy is improved by 53% and 65%, respectively, and, at this condition, the TOF-Taylor and the TOF-TDOA are not applicable with an RMSE above 0.8. However, the proposed algorithm isn’t sensitive to noise, and, therefore, can be applied in a severe noise environment.
3.4. Experiment 2 Influence of Tag Position on Positioning Performance
To verify the performance of the proposed algorithm in special tag positions, we set the noise variance to 0.4 and five coordinates were randomly generated, {(40, 39), (80, 37), (89, 72), (9, 12), (58, 63)}, of which (40, 39), (58, 63) represent tags far from the hyperbolic asymptote and (80, 37), (89, 72), (9, 12) represent tags close to the BS. Comparison of the RMSE of the TOF-TDOA, TOF-Taylor, and the proposed algorithm, and the iterations of the proposed algorithm are shown in Figure 5 and Figure 6, respectively. The corresponding evaluation indexes are analyzed in Table 1.
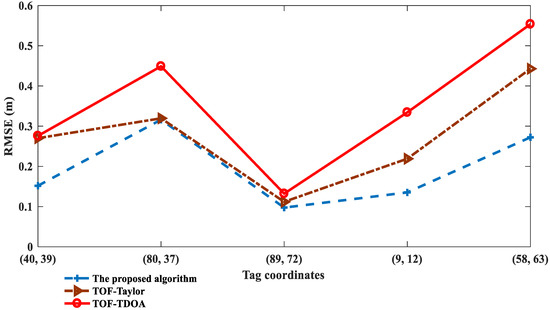
Figure 5.
RMSE of the proposed positioning algorithm under different tag coordinates.
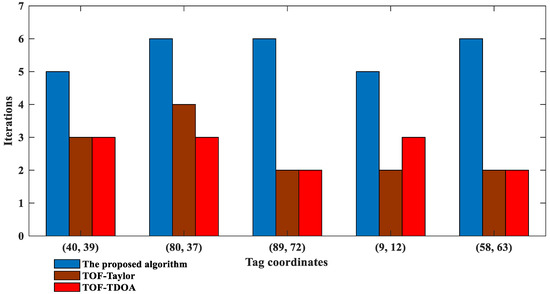
Figure 6.
Iterations of the proposed positioning algorithm under different tag coordinates.

Table 1.
Performance evaluation of the proposed positioning algorithm.
As can be seen from Figure 5, the positioning accuracy of the proposed algorithm is improved by 28% and 44% on average compared with the TOF-Taylor and the TOF-TDOA, respectively; in the given tag positions close to the BS or far from the hyperbolic asymptote, the RMSE of the proposed algorithm doesn’t exceed 0.3, however, the TOF-Taylor and the TOF-TDOA are not applicable with RMSE values above 0.5. In addition, the positioning accuracy of the proposed algorithm is further verified by standard deviation, mean error, and median error in Table 1. In comparison, from Figure 6, the proposed algorithm needs more iterations, but this is negligible because each iteration is about 0.005 s.
3.5. Experiment 3 Scatter Plot Analysis of Tag Positioning
The scatter plots of the three positioning algorithms are shown in Figure 7a,b, respectively. In experiments, the real tag coordinate is (70, 63), the noise variance is 0.8, and the number of experiments is 500.
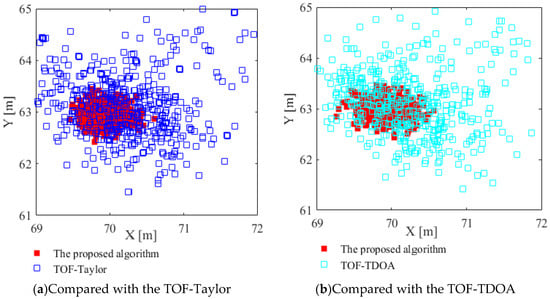
Figure 7.
Positioning scatter plots of the tag.
As can be seen from Figure 7, under a serious noise of variance 0.8, the positioning coordinates of the proposed algorithm show better concentration around the real tag coordinate; by comparison, the TOF-Taylor and the TOF-TDOA have a more divergent distribution of positioning coordinates, and several positioning coordinates have been seriously distorted, which can no longer satisfy the needs of indoor positioning
4. Conclusions
This paper describes a new UWB TOF combined residual weighting positioning method, which mainly involves the following approaches: (1) using TOF ADS-TWR ranging to construct a set of nonlinear positioning equations without the need for strict clock synchronization; (2) introducing the four-BS weighted centroid algorithm to obtain the initial rough coordinates of the tag, which solves the problem that the positioning equations cannot be solved due to the non-intersection of positioning circles caused by large noise environments or when the tags are located at the edge of the BS; (3) the residual weighting algorithm can optimize the rough coordinates, and the optimized rough tag position is substituted into Newton’s iterative formula as initial values; (4) when solving the nonlinear positioning equations, the method of algebraic transformation is used to construct the nonlinear positioning function, and its first-order differentiation will be imputed to the Newton iteration formula to optimize the final tag coordinates. The experiments show that the tag initial position estimation can simplify and optimize the final tag position solution process, and the estimation accuracy of the initial rough tag position helps to improve UWB positioning performance. In addition, the proposed UWB TOF indoor positioning combined residual weighting can also be applied in severe noise environments or for tags close to the BS.
Author Contributions
Conceptualization, J.Y. and C.Z.; methodology, J.Y.; software, J.Y.; validation, J.Y. and C.Z.; formal analysis, J.Y. and C.Z.; writing—original draft preparation, J.Y.; writing—review and editing, J.Y. and C.Z.; funding acquisition, C.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research is financially supported by National Science Foundation of China (61871176): Research of Abnormal Grain Conditions Detection using Radio Tomographic Imaging based on Channel State Information; Applied research plan of key scientific research projects in Henan colleges and Universities (22A510013): Research of Abnormal Grain Conditions Detection using Cone-beam CT based on Convolutional Neural Network; Open subject of Scientific research platform in Grain Information Processing Center (KFJJ2022011): Grain condition detection and classification-oriented semantic communication method in artificial intelligence of things; The Innovative Funds Plan of Henan University of Technology (2022ZKCJ13): Key technology research and demonstration application of air-ground integrated sensing and communication.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The experimental data used to support the findings of this study are available from the corresponding author upon request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Schmid, L.; Salido-Monzú, D.; Wieser, A. Accuracy assessment and learned error mitigation of UWB ToF ranging. In Proceedings of the International Conference on Indoor Positioning and Indoor Navigation (IPIN 2019), Pisa, Italy, 30 September–3 October 2019. [Google Scholar]
- Wang, X.; Huang, Z.; Zheng, F.; Tian, X. The Research of Indoor Three-Dimensional Positioning Algorithm Based on Ultra-Wideband Technology. In Proceedings of the 2020 39th Chinese Control Conference (CCC), Shenyang, China, 27–29 July 2020. [Google Scholar]
- Huang, Q.; Qu, L.; Wu, B.; Fang, G. UWB through-wall imaging based on compressive sensing. IEEE Trans. Geosci. Remote Sens. 2009, 48, 1408–1415. [Google Scholar] [CrossRef]
- Çetin, Ö.; Nazh, H.; Gürcan, R.; Öztürk, H.; Güneren, H.; Yelkovan, Y.; Çayir, M.; Çelebi, H.; Partal, H.P. An experimental study of high precision TOA based UWB positioning systems. In Proceedings of the 2012 IEEE International Conference on Ultra-Wideband, Syracuse, NY, USA, 17–20 September 2012. [Google Scholar]
- Mazraani, R.; Saez, M.; Govoni, L.; Knobloch, D. Experimental results of a combined TDOA/TOF technique for UWB based localization systems. In Proceedings of the 2017 IEEE International Conference on Communications Workshops (ICC Workshops), Paris, France, 21–25 May 2017. [Google Scholar]
- Bastida-Castillo, A.; Gómez-Carmona, C.D.; De La Cruz Sánchez, E.; Pino-Ortega, J. Comparing accuracy between global positioning systems and ultra-wideband-based position tracking systems used for tactical analyses in soccer. Eur. J. Sport Sci. 2019, 19, 1157–1165. [Google Scholar] [CrossRef] [PubMed]
- Yu, K.; Wen, K.; Li, Y.; Zhang, S.; Zhang, K. A novel NLOS mitigation algorithm for UWB localization in harsh indoor environments. IEEE Trans. Veh. Technol. 2018, 68, 686–699. [Google Scholar] [CrossRef]
- Wang, N.; Yuan, X.; Ma, L.; Tian, X. Research on Indoor Positioning Technology Based on UWB. In Proceedings of the 2020 Chinese Control And Decision Conference (CCDC), Hefei, China, 22–24 August 2020. [Google Scholar]
- Liu, C.; Bai, F.; Wu, C. A Joint Positioning Algorithm of TDOA and TOF Based on Ultra-wideband. In Proceedings of the 2021 2nd International Conference on Signal Processing and Computer Science (SPCS 2021), Qingdao, China, 20–22 August 2021. [Google Scholar]
- Wei, Z.; Chen, X.; Fang, L.; Zhao, N.; Guo, S.; Li, X. Joint positioning technique based on TOF and TDOA. In Proceedings of the 2018 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Houston, TX, USA, 14–17 May 2018. [Google Scholar]
- Bottigliero, S.; Milanesio, D.; Saccani, M.; Maggiora, R. A low-cost indoor real-time locating system based on TDOA estimation of UWB pulse sequences. IEEE Trans. Instrum. Meas. 2021, 70, 1–11. [Google Scholar] [CrossRef]
- Ren, J.; Huang, S.; Song, W.; Han, J. A Novel Indoor Positioning Algorithm for Wireless Sensor Network Based on Received Signal Strength Indicator Filtering and Improved Taylor Series Expansion. Traitement du Signal 2019, 36, 103–108. [Google Scholar] [CrossRef]
- Alsmadi, L.; Kong, X.; Sandrasegaran, K.; Fang, G. An improved indoor positioning accuracy using filtered RSSI and beacon weight. IEEE Sens. J. 2021, 21, 18205–18213. [Google Scholar] [CrossRef]
- Xu, H.; Hou, Q.; Li, G.; Xu, Z.; Lu, D.; Li, K. Research on the Algorithm of High-precision Ultra-Wide Band Indoor Positioning Based on CHAN-TAYLOR Cascaded Positioning Technology. In Proceedings of the International Conference on Frontiers of Electronics, Information and Computation Technologies, Changsha, China, 21–23 May 2021. [Google Scholar]
- Zhong, Y.; Wang, T.; Liu, Y.; Lou, X. Indoor UWB Location Based on Residual Weighted Chan Algorithm. In Proceedings of the 2018 7th International Conference on Digital Home (ICDH), Guilin, China, 30 November–1 December 2018. [Google Scholar]
- Wei, J.; Deng, Z.; Wang, H.; Zheng, X.; Fu, X.; Liu, Q. An Improved Chan/Newton Combined Position Estimate Algorithm. In Proceedings of the China Satellite Navigation Conference (CSNC 2020), Chengdu, China, 23–25 November 2020. [Google Scholar]
- Zhang, Y.; Shen, F.; Liu, Q.; Li, W. A UWB 3D Localization Algorithm Based on Residual Weighting. In Proceedings of the 2020 IEEE International Conference on Mechatronics and Automation (ICMA), Beijing, China, 13–16 October 2020. [Google Scholar]
- Gui, X.; Guo, S.; Chen, Q.; Han, L. A new calibration method of UWB antenna delay based on the ADS-TWR. In Proceedings of the 2018 37th Chinese Control Conference (CCC), Wuhan, China, 25–27 July 2018. [Google Scholar]
- Zare, H.; Hajarian, M. An efficient Gauss–Newton algorithm for solving regularized total least squares problems. Numer. Algorithms 2022, 89, 1049–1073. [Google Scholar] [CrossRef]
- Wan, L.; Ding, F.; Liu, X.; Chen, C. A new iterative least squares parameter estimation approach for equation-error autoregressive systems. Int. J. Control Autom. Syst. 2020, 18, 780–790. [Google Scholar] [CrossRef]
- Yang, L.; Cao, J.; Yang, W. TDOA location based on modified Newton method. In Proceedings of the 2016 IEEE 13th International Conference on Signal Processing (ICSP), Chengdu, China, 6–10 November 2016. [Google Scholar]
- Hua, J.; Yin, Y.; Lu, W.; Zhang, Y.; Li, F. NLOS identification and positioning algorithm based on localization residual in wireless sensor networks. Sensors 2018, 18, 2991. [Google Scholar] [CrossRef] [PubMed]
- He, C.; Yuan, Y.; Tan, B. Constrained L1-norm minimization method for range-based source localization under mixed sparse LOS/NLOS environments. Sensors 2021, 21, 1321. [Google Scholar] [CrossRef] [PubMed]
- Xu, J.; Ma, M.; Law, C.L. Position estimation using UWB TDOA measurements. In Proceedings of the 2006 IEEE International Conference on Ultra-Wideband, Waltham, MA, USA, 24–27 September 2006. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).