1. Introduction
The development of the internet and hardware resources in the last twenty years has facilitated access to a large amount of data. The data generated in recent years is expanding in variety and complexity, and the speed of collection is also increasing. Such exponential growth in the amount of data requires simple, fast, and accurate tools for processing. Artificial intelligence (AI) jumps in as a solution. Computer vision is one of the most attractive research areas today. Scientists in this field have achieved enormous progress in recent years, from the development of an algorithm for driving autonomous vehicles [
1], all the way to the detection of cancer using only information from images [
2].
In the past, data collection in astronomy was a manual and time-consuming job for humans, but with the advancement of technology and automation, today the amount of data collected by observing the sky is almost unimaginable. Looking back 20 years, efforts such as the Sloan Digital Sky Survey (SDSS) [
3], Pan-STARRS [
4], and the Large Synatopic Survey Telescope (LSST) [
5], have shifted from individualized data collection to studying larger parts of the sky and wider wavelength ranges of light, e.g., collecting data on more events, objects, and larger areas of the sky through larger areas and better light detectors. SDSS is one of the largest astronomical surveys today. Every night the SDSS telescope collects 200 GB of data, while there are telescopes that collect up to 90 terabytes of data every night (
Table 1) [
6]. Due to the enormous amount of data collected, astronomers struggle with more than 100 to 200 petabytes of data per year, which requires a large storage infrastructure. Therefore, it is crucial to process this large amount of collected data. Such an exponential increase in data provides an ideal opportunity to apply artificial intelligence and machine learning to help process all this data.
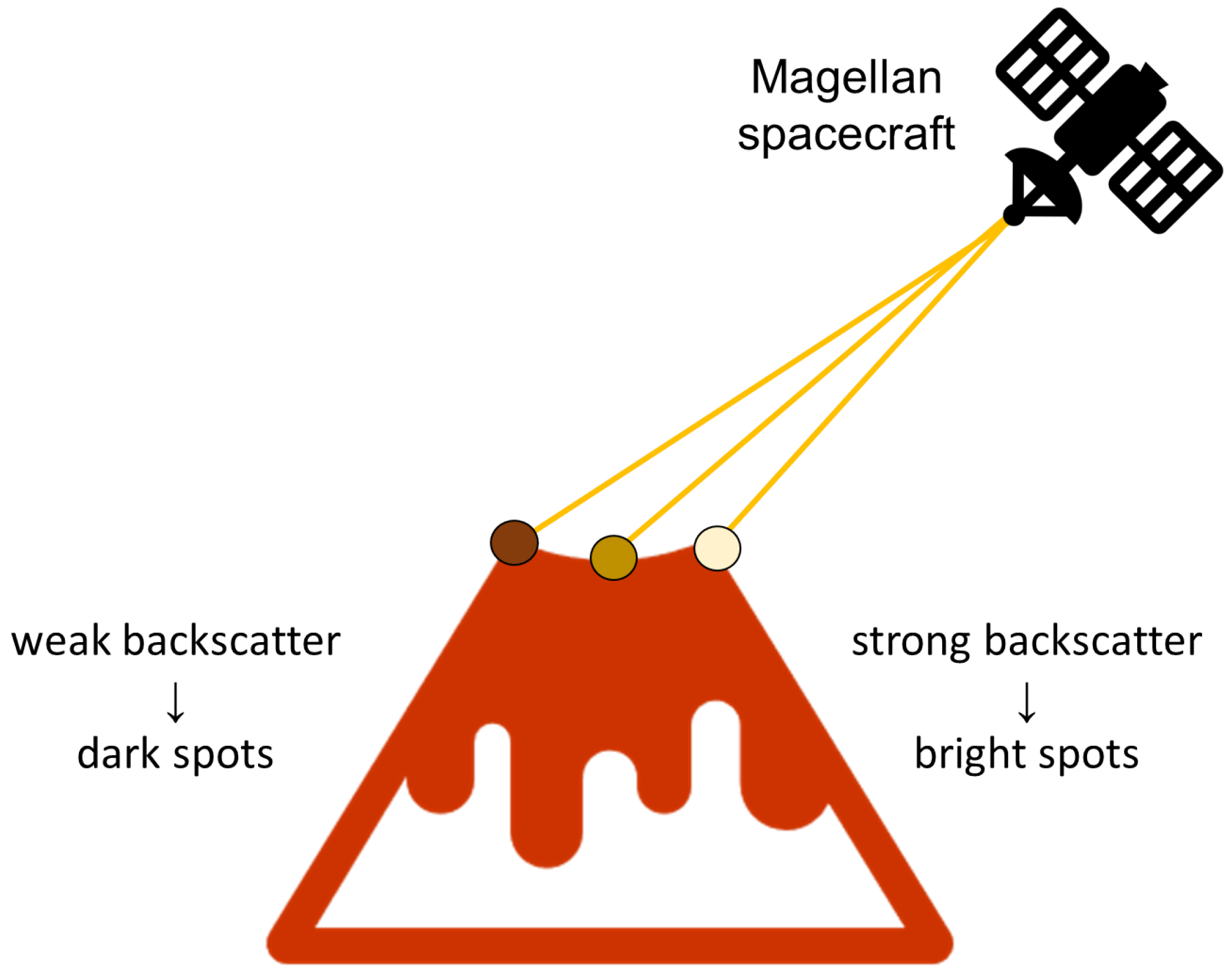
The application discussed in this paper focuses on data collected from the Magellan spacecraft, which was launched in 1989 and arrived in the orbit of Venus in 1990. During its four years in orbit around Earth’s sister planet, Magellan recorded 98% of the surface of Venus and collected the gravitational data of the planet itself in high resolution using synthetic aperture radar (SAR) [
7]. During Magellan’s active operation, about 30,000 images of the surface of Venus were collected, on which there are also numerous volcanoes, but the manual labeling of these images is time-consuming and so far, only 134 images have been processed by geological experts [
8]. It is believed that there are more than 1600 large volcanoes on the surface of Venus whose features are known so far, but their number may be over a hundred thousand or even over a million [
8,
9]. Understanding the global distribution of the volcanoes is critical to understanding the geologic evolution of the planet. Therefore, collecting relevant information, such as volcanoes size, location, and other relevant information, can provide the data that could answer questions about the geophysics of the planet Venus. The sheer volume of collected planetary data makes automated tools necessary if all of the collected data are to be analyzed. It was precisely for this reason that a tool was created using machine learning algorithms that would serve as an aid in labeling such a large amount of data.
Burl et al. proposed the JARtool System (JPL Adaptive Recognition Tool) [
8], which is a trainable visual recognition system developed for this specific problem. JARtool uses a matched filter derived from training examples, then via principal components analysis (PCA) provides a set of domain-specific features. On top of that, supervised machine learning techniques are applied to classify the data into two classes (volcano or non-volcano). For detecting possible volcanic locations, JARtool’s first component is the focus of attention (FOA) algorithm [
10], which outputs a discrete list of possible volcanic locations. Later mentioned, the investigation is concluded using a combination of classifiers in which each classifier is trained to detect a different volcano subclass. In their experiments, each label is counted as a volcano regardless of the assigned confidence (volcanoes are classified depending on their confidence score). Experiments were performed on two types of Magellan data products, Homogeneous and Heterogeneous images. Homogeneous images represent images that are relatively similar in appearance (homogeneous) and are mostly from the same area. Heteregoeneus images represent images chosen from random locations, and those images contained a significantly greater variety in appearance. The JARtool system performed relatively well on homogeneous image sets in the 50–64% range of detected volcanoes (one class, regardless of the classification), while performance on heterogeneous image sets was in the 35–40% range.
The scope of this problem is focused on detecting geological features over the SAR imagery, which can be noisy and thus challenging. Due to the nature of SAR images, they are affected by multiplicative noise, which is also known as speckle noise [
11]. This kind of noise is one of the main things that affect the overall performance of any classification methodology. Many studies have applied SAR imagery to machine learning-based algorithms, even including deep learning [
12]. The first attempts using deep learning methods in SAR imagery were for a variety of tasks, which includes terrain face classification [
13], object detection [
14], and even disaster detection [
15]. This problem requires both detection and classification of the desired object, which requires the usage of more known convolutional neural network (CNN) architectures such as Fast-RCNN [
16], You only look Once algorithm, etcetera. After some research, it is concluded that most of the object detection in SAR imagery is focused on detecting human-made objects. For example, there are deep learning methods used for detecting ships, airplanes, and other man-made features in SAR imagery.
In this paper, authors used the You Only Look Once (YOLO) version 5 algorithm [
17] as a base for an automatic tool for localizing and classifying Venusian volcanoes. YOLOv5 algorithm is currently one of the fastest and most precise algorithms for object detection and, today, it is used in almost every field. From the many studies concluded in the past years using YOLO on different problems, it demonstrates better results in more cases compared to other object detectors. For example, Mostafa et al. [
18] trained YOLOv5, YOLOX, and Faster R-CNN models for the detection of autonomous vehicles. YOLOv5, YOLOX, and Faster R-CNN achieved mean average precision (mAP) at 0.5 thresholds of 0.777, 0.849, and 0.688, respectively; therefore, YOLO outperforms Faster R-CNN. Wang et al. [
19] used the YOLOv5 algorithm in shape wake detection in SAR imagery and achieved an mAP score in the range of 80.1–84.8%, proving that YOLOv5 can successfully be used in complex conditions, such as different sea states and multiple targets. Xu et al. [
20] trained the YOLOv5 algorithm for ship detection in large-scene Sentinel-1 SAR images, effectivly scoring mAP of 0.7315. Yoshida and Ouchi also used YOLOv5 for ship detection cruising in the azimuth direction and achieved an mAP score of 0.85 [
21]. Reviewing the usage of YOLOv5 in SAR imagery proves that YOLOv5 can successfully be used to detect desired features in such complex imagery as SAR imagery. Furthermore, the mAP score in the range 0.7–0.85 seems to be a good score for detection in SAR imagery.
The goal of this paper is to examine a YOLOv5 algorithm as a backbone to an automation system for labeling small Venusian volcanoes over SAR imagery. Furthermore, this paper focuses on Magellan heterogeneous image sets, because it appears to be a larger problem when reviewing Burl et al. [
8] and trying to classify all four classes of volcanoes instead of just treating them as the same class. One of the problems with the Magellan dataset is that it contains a relatively small number of labeled images. Today deep learning models require a large number of images for successful training. Based on the idea of this investigation and the literature overview, the following questions were derived:
Is it possible to achieve good classification accuracy with the YOLOv5 algorithm on SAR imagery and such a small dataset?
Can classical training data augmentation techniques improve classification accuracy, or are some advanced methods are required?
The structure of this paper can be divided into the following sections: Materials and Methods, Results and Discussion, and Conclusions. In the Materials and Methods section, the dataset description is given as well as the used augmentation methods for training the YOLOv5 algorithm. In Results and Discussions, the results of conducted experiments are presented and discussed. The Conclusion section includes thoughts and conclusions that were obtained during the examination of the results of the experiment and provides answers to the hypotheses defined in the Introduction section.
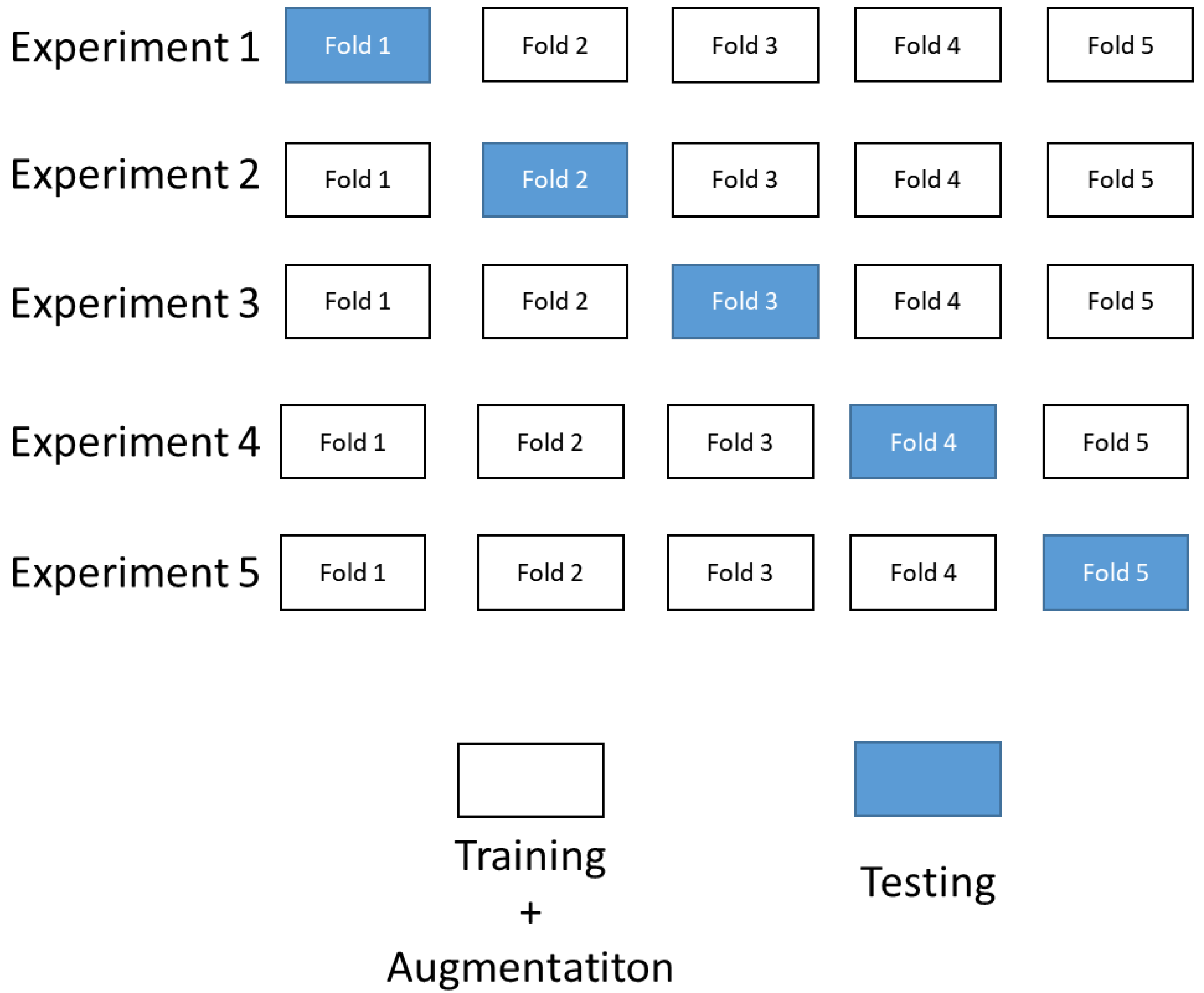
3. Results
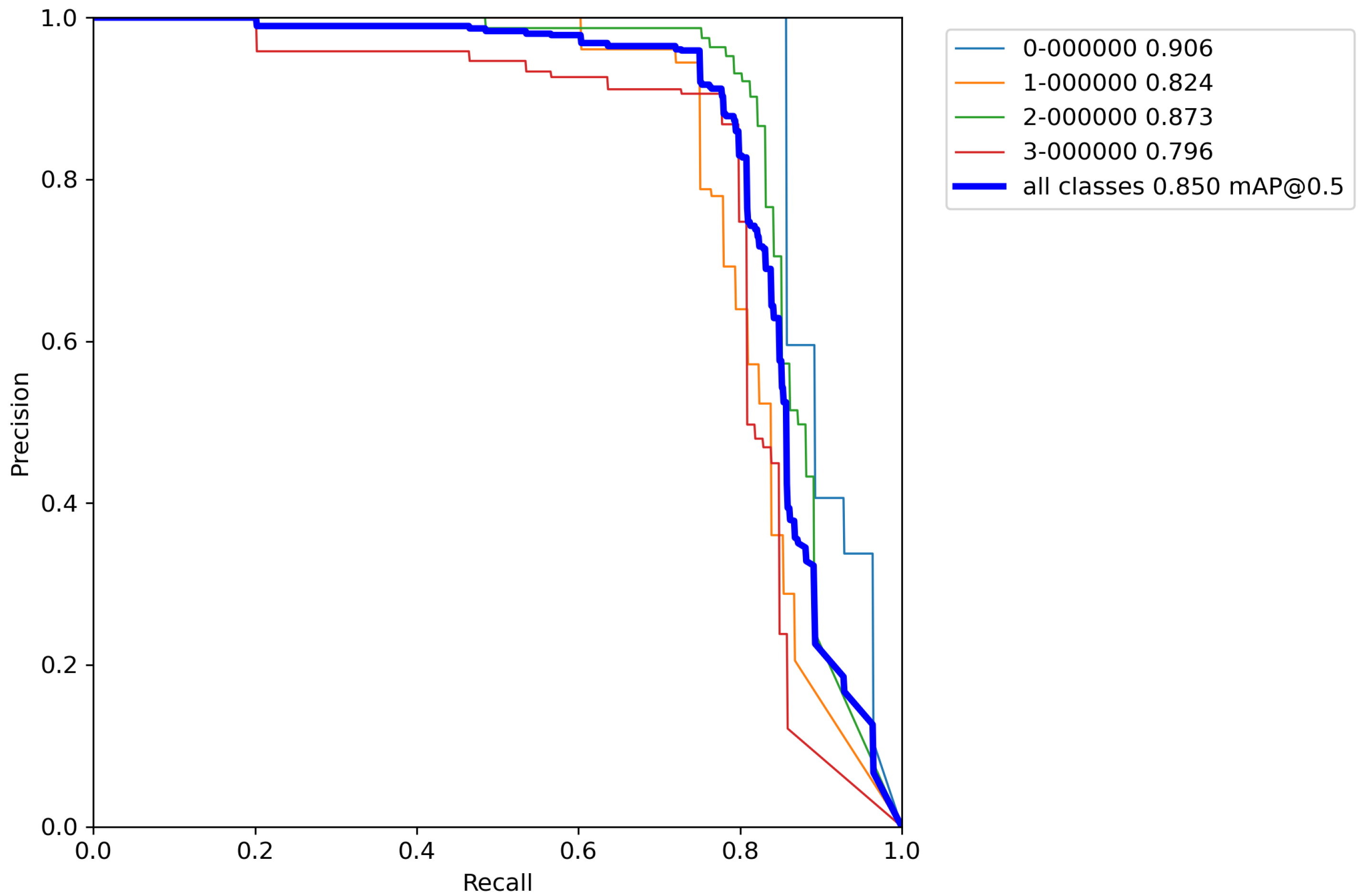
In this section, the results of the experiments using the YOLOv5 algorithm with cross-validation on the Magellan dataset are presented. Classification accuracy on a validation set is presented using previously described metrics such as mAP,
F1 score, Precision, and Recall. Furthermore,
Appendix A,
Appendix B and
Appendix C contains Precision–Recall (P-R) curves from all trained models using the cross-validation method.
Before starting training and evaluating the results of the model, it is necessary to determine the basic model based on which, by changing hyperparameters and data augmentation techniques, comparison and assessment of the accuracy of the investigated models will be made. The pretrained YOLOV5l6 model was used as the base model with the transfer learning method. YOLOv5l6 weights were pretrained on a COCO dataset [
37]. The reason for using transfer learning is that with randomly generated weight coefficients, due to the relatively small number of images, it would not be possible to obtain a sufficiently precise model, and this method has proven to be a good choice for relatively small datasets in the past. Hyperparameters of the YOLOv5l6 model are given in
Table 4.
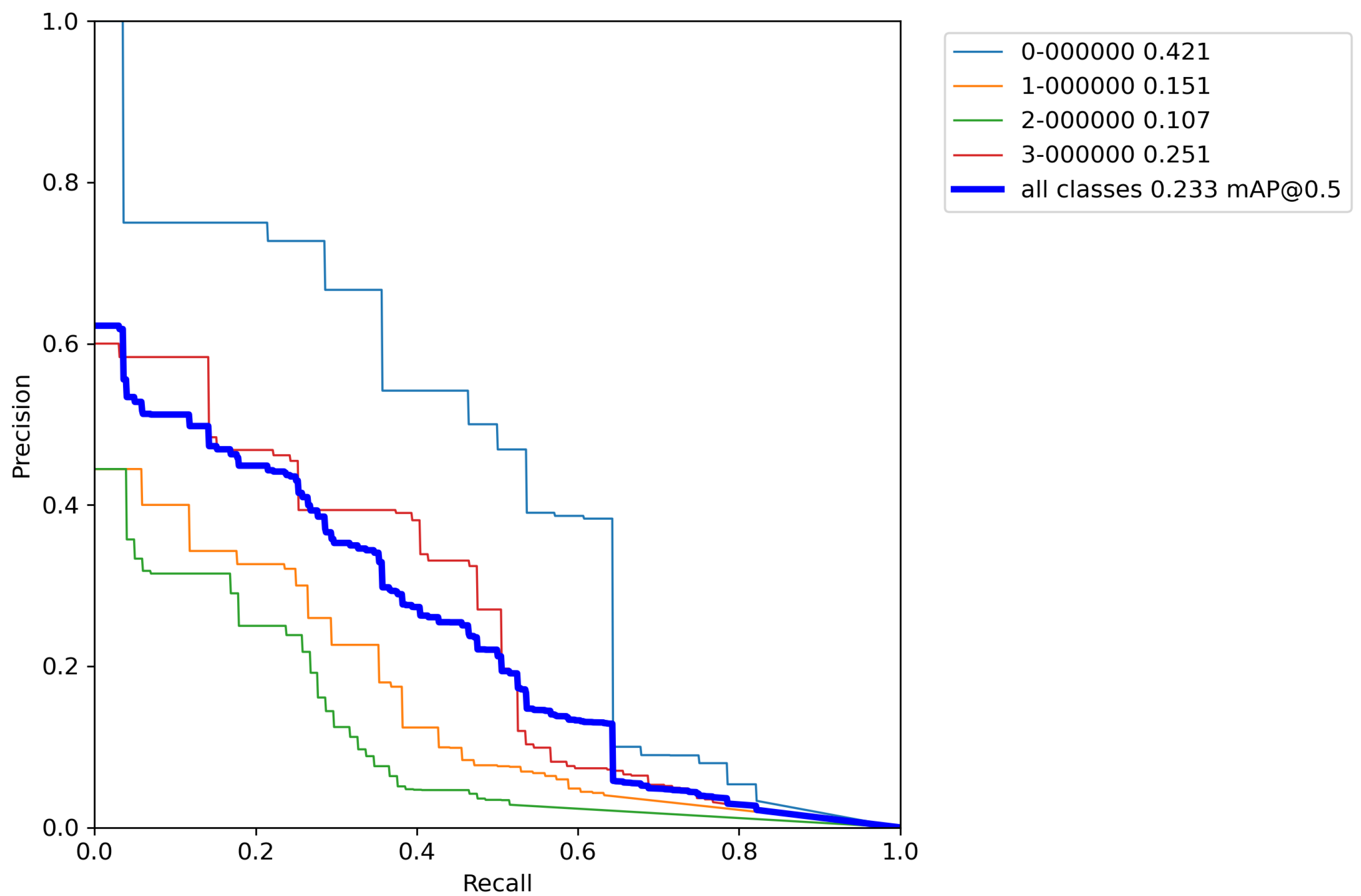
First, the base model with pretrained weights, and without performing any augmentation techniques on a training set was trained for reference. The results of cross-validation metrics for the base model can be seen in
Table 5 and
Appendix A.
After calculating the average value and standard deviation from all cross-validation experiments performed on a base model, the evaluation of a base model can be seen in
Table 6. Furthermore,
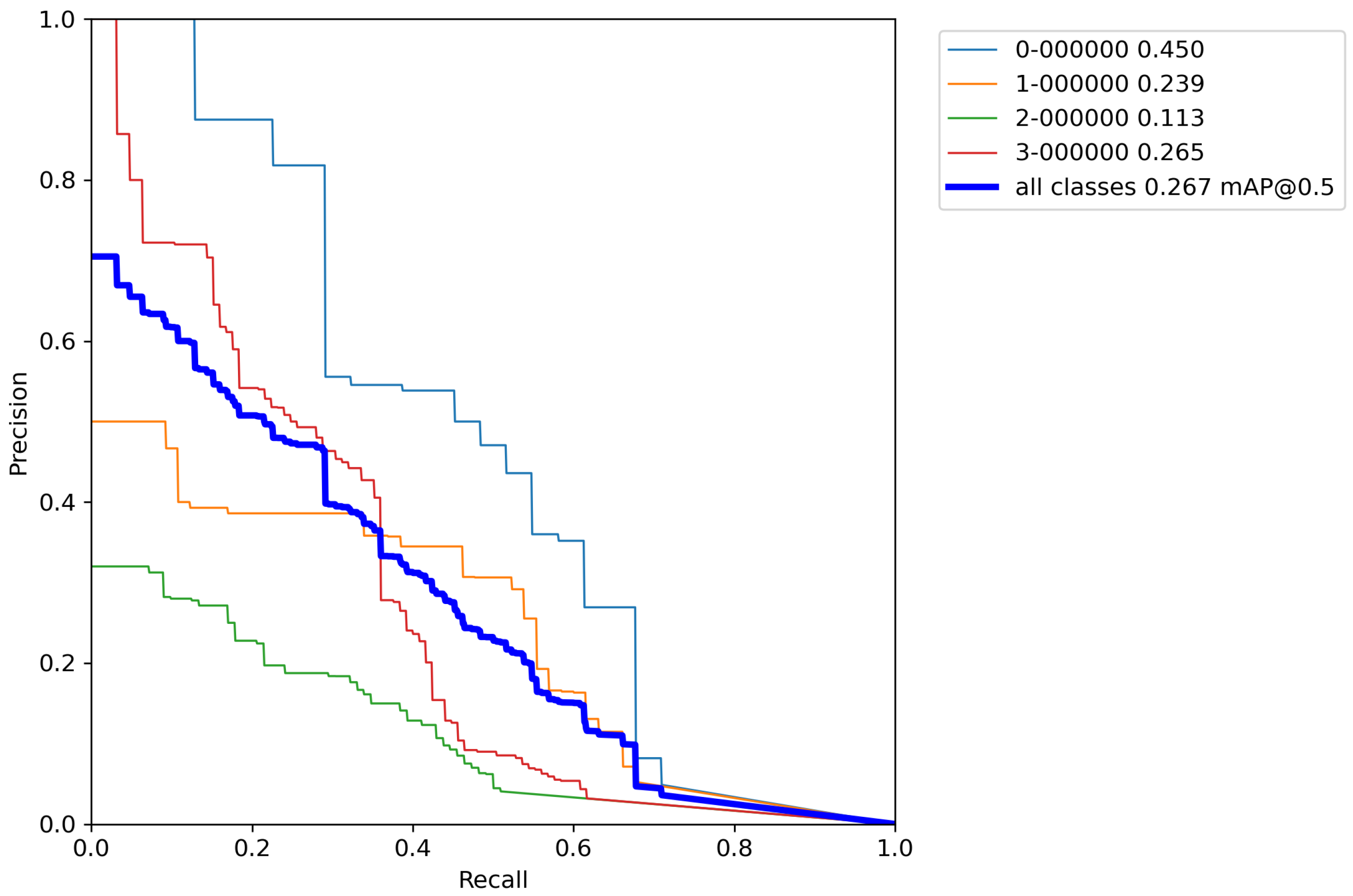
Figure A1,
Figure A2,
Figure A3,
Figure A4 and
Figure A5 contains
P–
R curves of the trained base model.
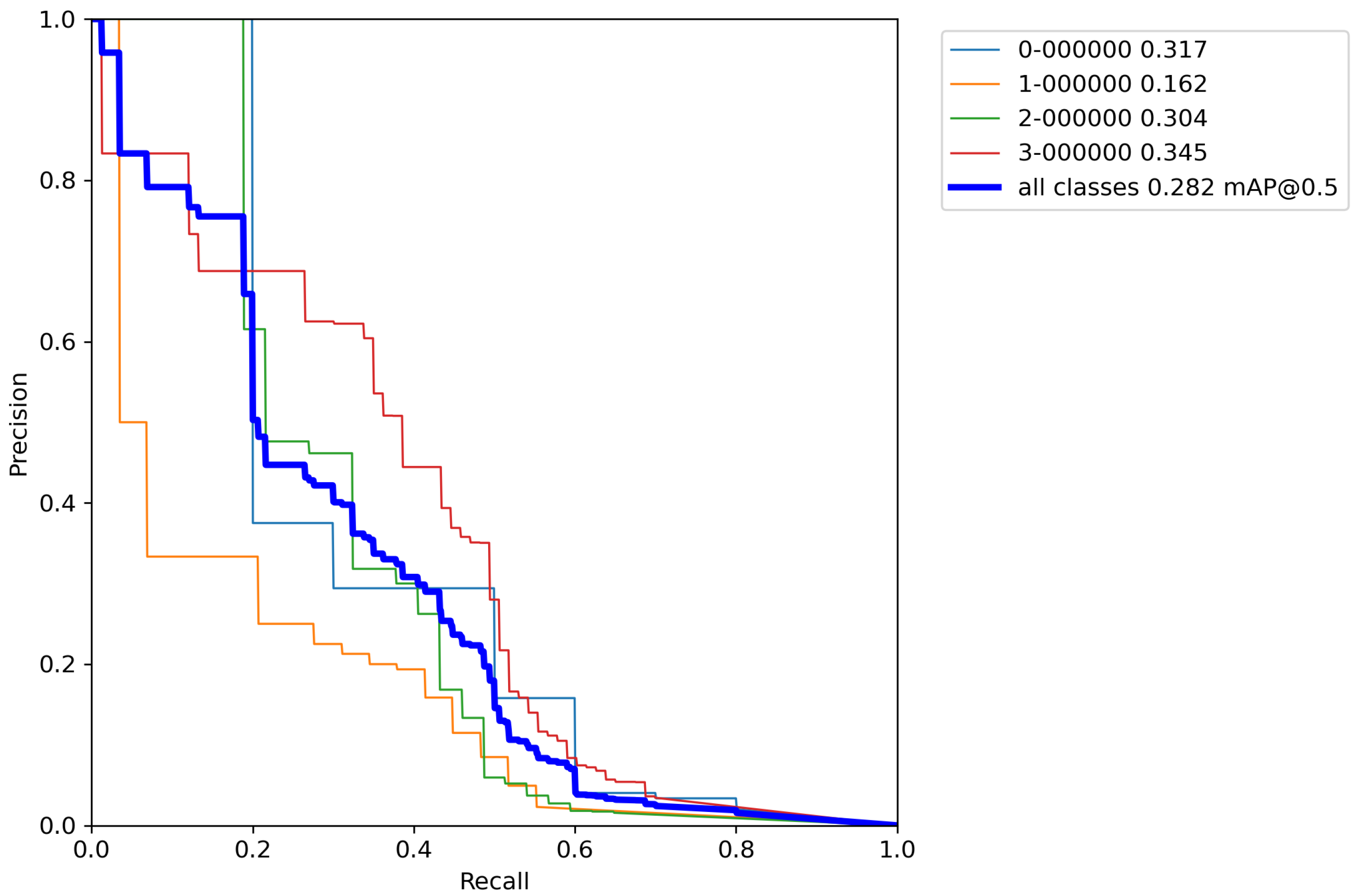
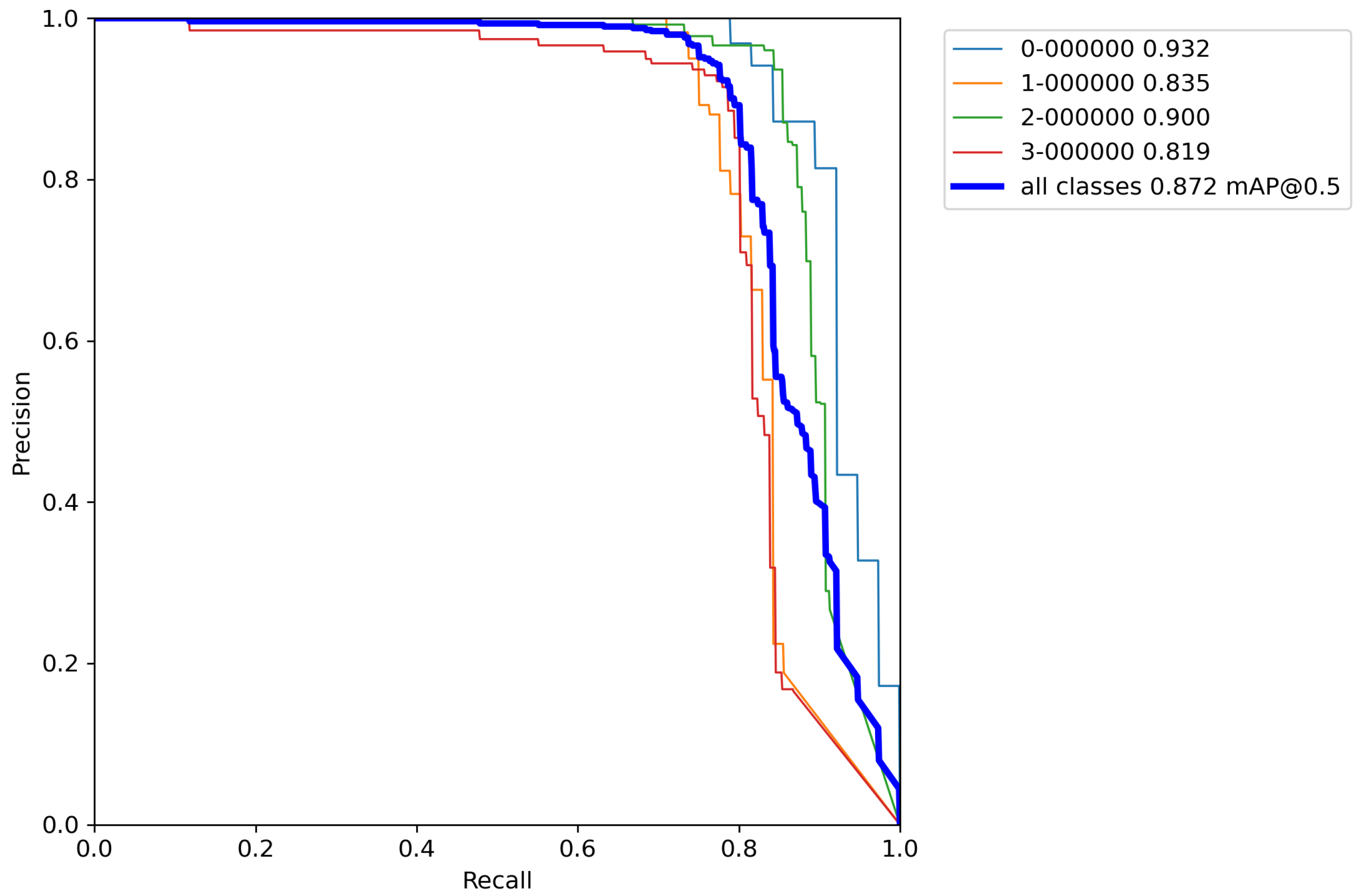
Next, the same cross-validation procedure was performed on a base model, but this time using classical augmentation techniques on a training set. Results of cross-validation metrics for the model can be seen in
Table 7.
After calculating the average value and standard deviation from all cross-validation experiments performed on a base model with classical augmentation techniques, the evaluation of a model can be seen in
Table 8. Furthermore,
Figure A6,
Figure A7,
Figure A8,
Figure A9 and
Figure A10 contains
P–
R curves of the model trained using classical augmentation techniques.
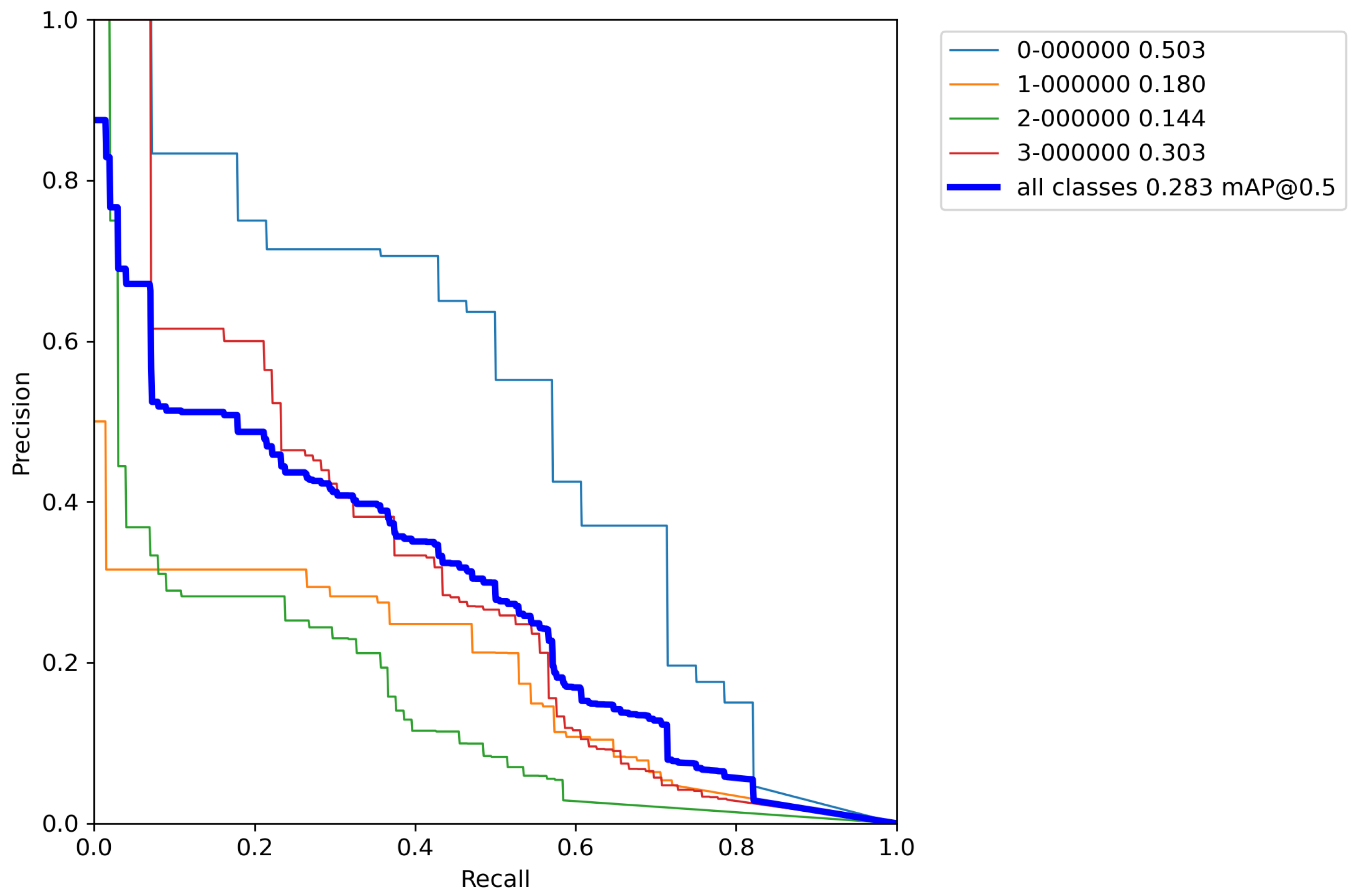
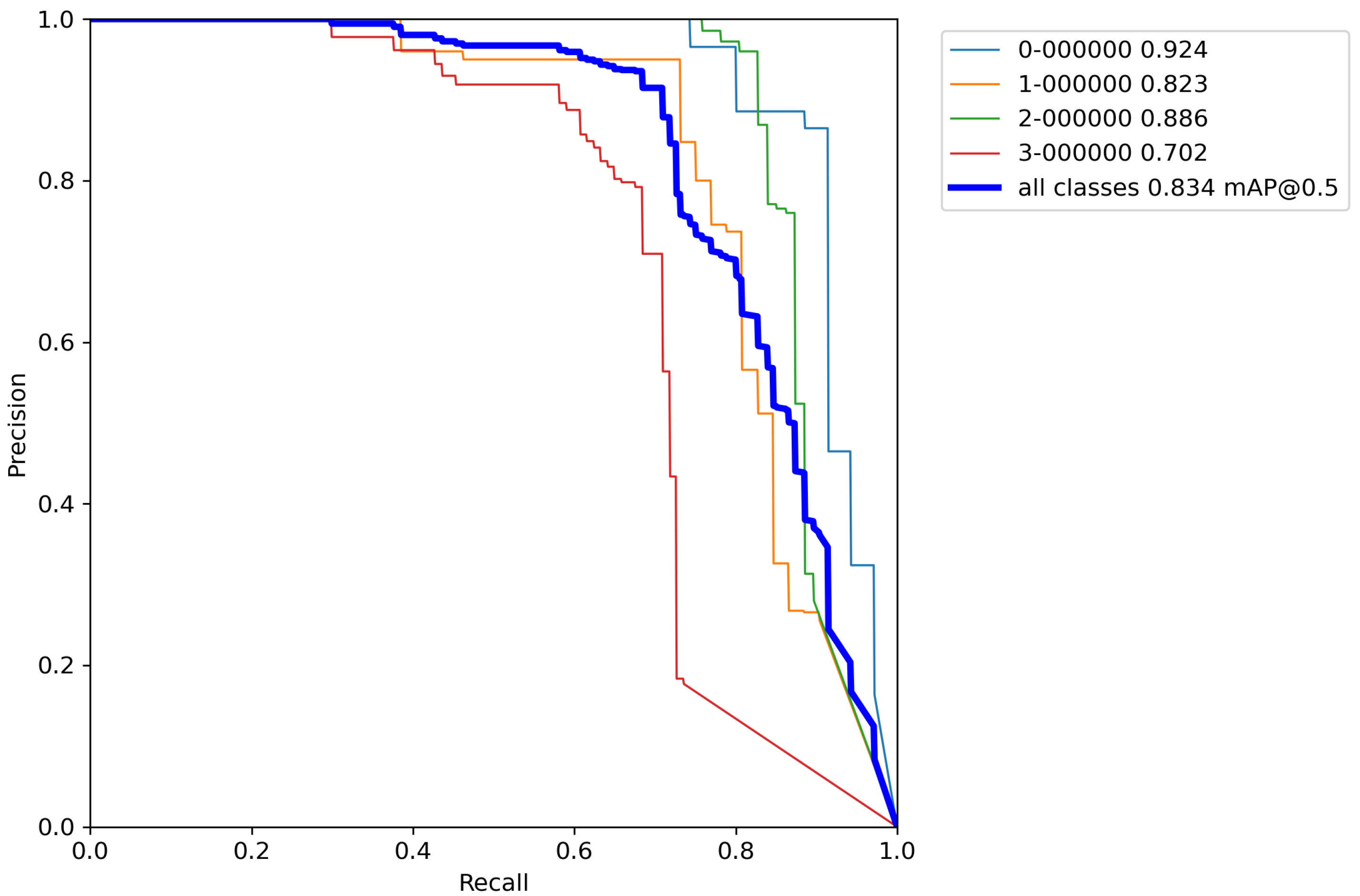
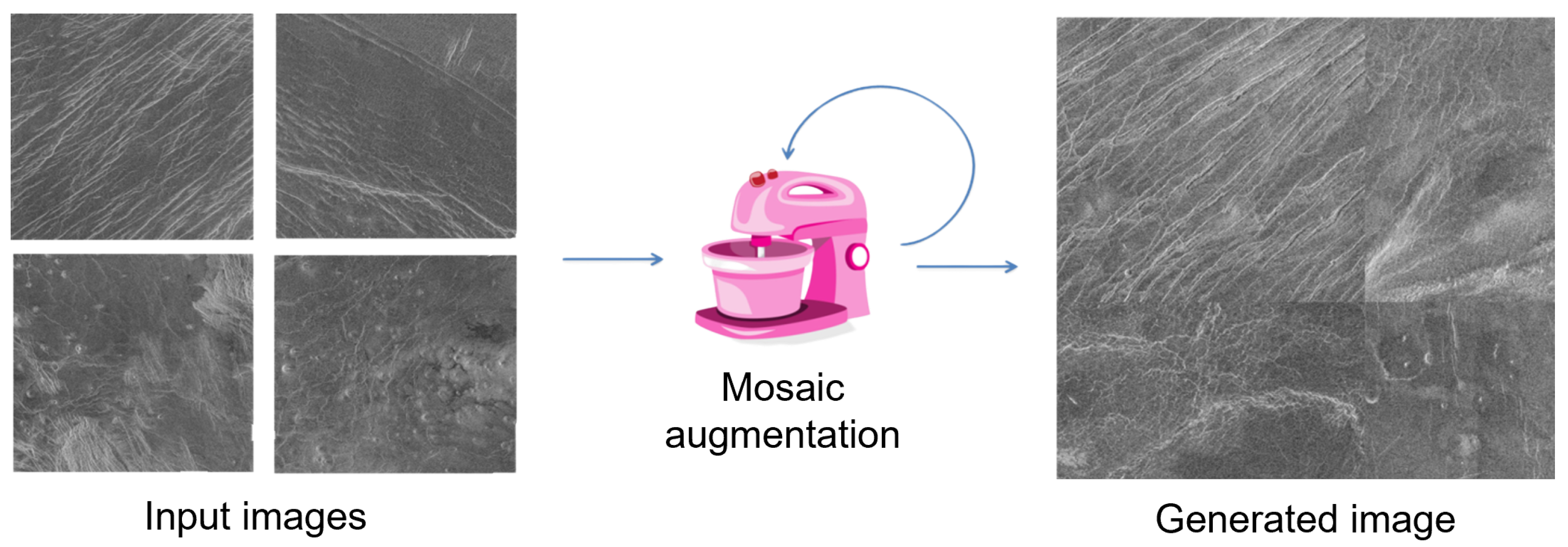
Finally, for the last cross-validation procedure, the proposed augmentation pipeline technique was used on a training set. The results of cross-validation metrics for the model can be seen in
Table 9.
After calculating the average value and standard deviation from all cross-validation experiments performed on a base model with classical augmentation techniques, the evaluation of a model can be seen in
Table 10. Moreover,
Figure A11,
Figure A12,
Figure A13,
Figure A14 and
Figure A15 contain
P–
R curves of the model trained using the proposed augmentation pipeline.
4. Discussion
From
Table 6 it can be seen that the base model after performing cross-validation scores the mean average accuracy value of mAP = 28.4%, which is low accuracy due to the extremely small number of images for training the model. This is why augmentation techniques were used on the training data set. Due to the relatively poor accuracy of the base model, classic augmentation methods were used and tested.
By using classical methods of augmentation over images in the training set and performing cross-validation,
Table 8 shows that there is an increase in the accuracy of the model by 2.5% versus the base model. Unfortunately, there is no drastic increase in precision and the obtained results are still unsatisfactory. The reason for this is still the relatively small number of images for training a model with such a large number of parameters. Although the number of images in the training set has been artificially increased by a factor of 8, it is still an insufficient number to successfully train the model. More than 1500 images per object and more than 10,000 total labeled objects per class are needed for successful model training [
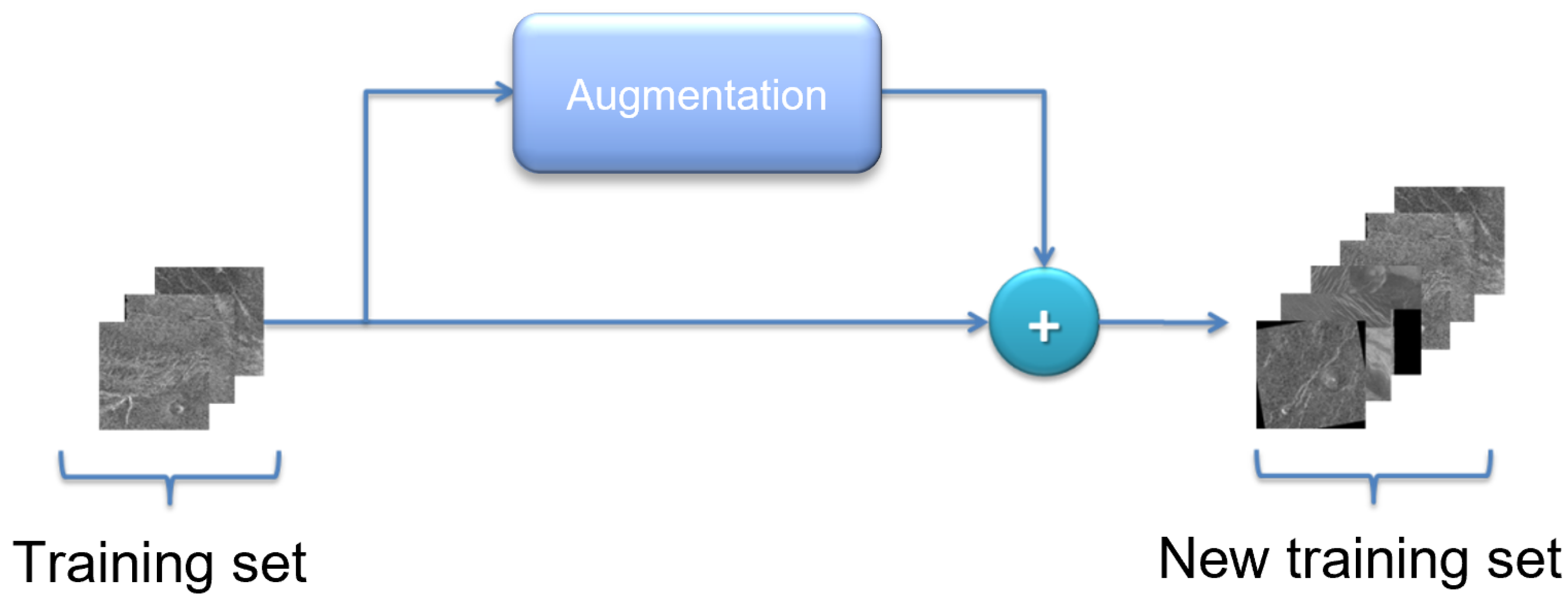
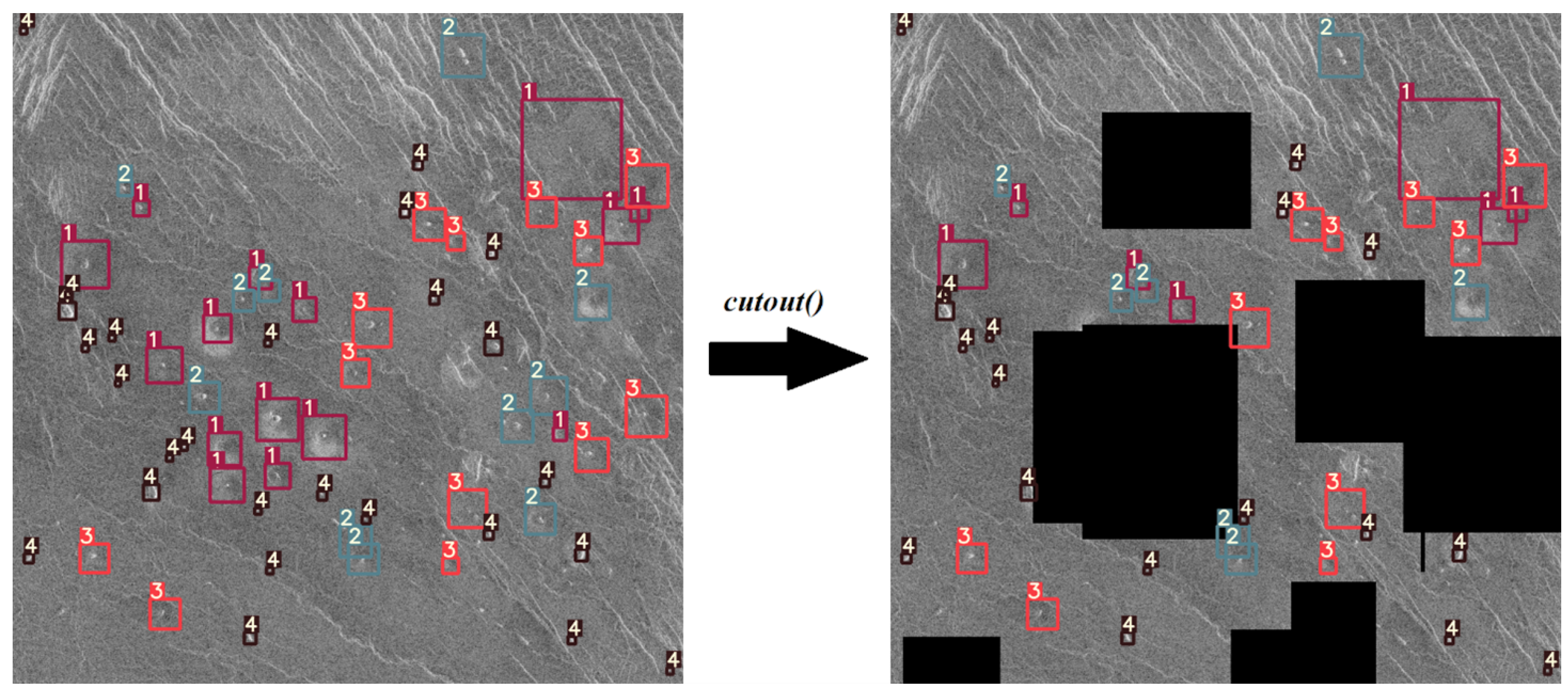
38]. Since in this case most of the images contain all the objects, for successful training it is enough to artificially increase the number of images to approximate that number. Unfortunately, using classic augmentation techniques, the number of images can be artificially increased only up to a certain limit (it can be increased by a factor of how many techniques are used). Another problem stems from the fact that the Magellan data set has an extremely small number of images (134 in total), and depending on the data set division, the model can be trained well. When dividing the data set, care had to be taken to take enough images for validation and testing to cover a large number of real-world cases, while also allowing a large enough number of images to train the model. For this reason, a more advanced data augmentation technique was used, such as implementing of the above-described augmentation pipeline.
By comparing the results from
Table 6,
Table 8, and
Table 10, it can be observed that the accuracy of the proposed model compared to the base model trained by the proposed increased by 55.1% versus the base model, and 52.6% versus the model trained with classical augmentation techniques, which is proof that this is a successful method for model training. Despite all that, the model gave satisfactory results for the detection and classification of volcanoes over SAR imagery on the surface of the planet Venus.
Testing the Developed Model
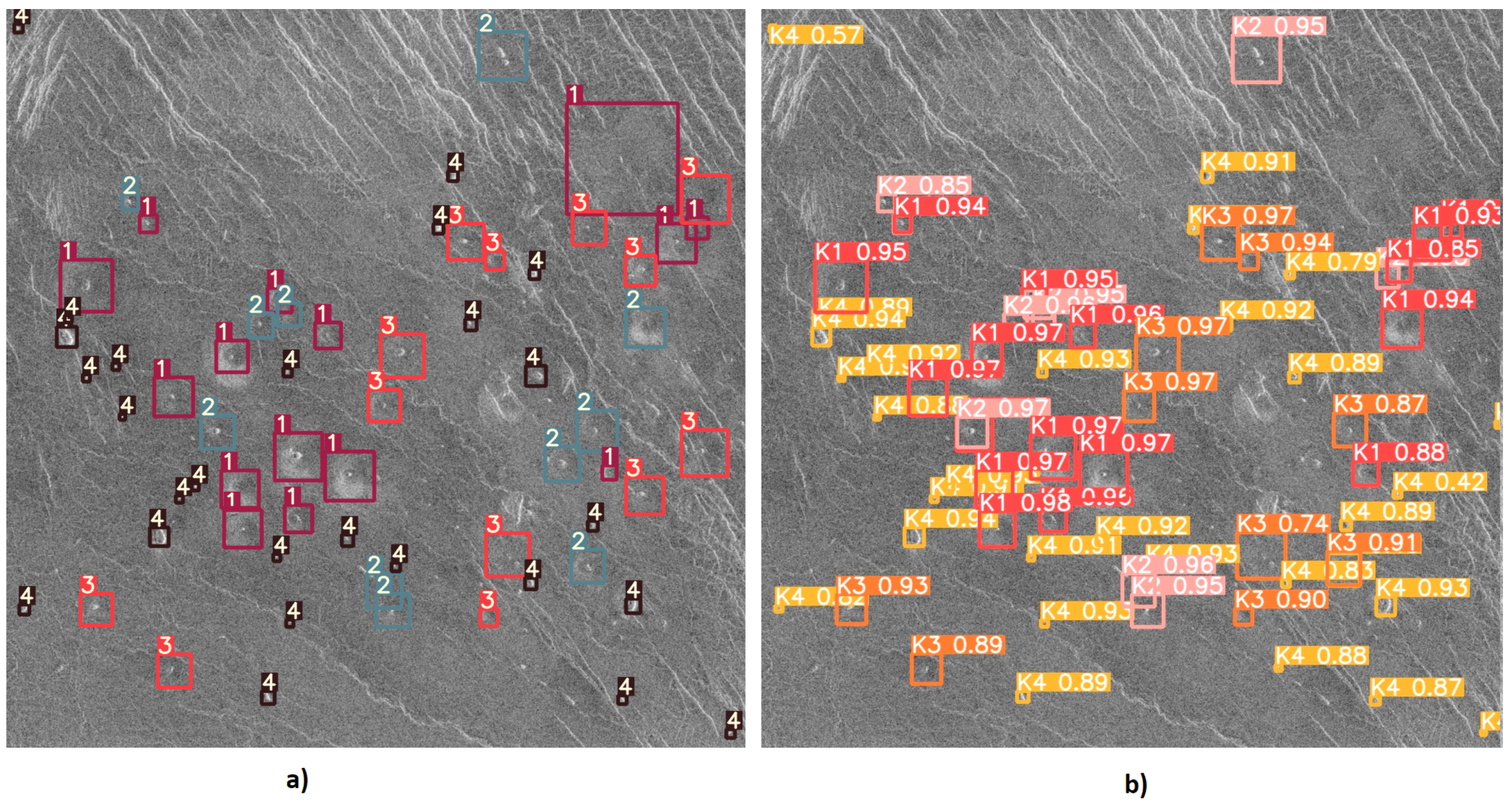
After training the YOLOv5l6 model using the methods described in the previous subsections, the weights that give the best results on testing were downloaded and tested. The detection results of the YOLOv5l6 model are shown in
Figure 17,
Figure 18 and
Figure 19. From
Figure 17, it can be noticed how the correct detection of the classification of most objects occurs correctly.
From
Figure 18 it can be noticed that the YOLO algorithm has a problem with the detection and classification of objects in places where there are many instances of various classes.
Figure 19 shows one of the cases where class K3 volcanoes were wrongly classified (as class K2) due to their similar characteristics between classes.
From
Figure 17,
Figure 18 and
Figure 19 it can be noticed that the model has successfully detected and classified the majority of volcanoes. Despite everything, the model gave satisfactory results of volcano detection and classification from satellite SAR imagery of the surface of Venus, and it can be concluded that a volcano detection system has been successfully developed and tested.