Adaptive Impact Mitigation Based on Predictive Control with Equivalent Mass Identification
Abstract
:1. Introduction
2. Considered Mechanical System and Its State–Space Model
2.1. Shock Absorber under Double-Impact Excitation
- Separate deceleration of the first object;
- Impact of the second object—the first is object under influence of the absorber reaction force and contact force between both decelerated objects;
- Deceleration of joint objects.

2.2. State–Space Model of the Considered System
3. Self-Adaptive Impact Mitigation Using Equivalent Parameter Predictive Control
3.1. Formulation of the Control Problem
- The sum of additional forces acting in the system is small in comparison to the pneumatic force;
- The change of the pneumatic force during a single control step is relatively small.
3.2. Derivation of Equivalent Parameter Predictive Control
- Automatic adaptation to unknown impacting object mass and its possible changes;
- Automatic adaptation to various initial velocities of the impacting object;
- Adaptation to additional external forces occurring during the process including the case of double-impact excitation;
- Robustness to process disturbances such as unknown friction forces inside the absorber.
- Numerical simulation of the system response for arbitrarily assumed change of valve opening via the arbitrary time-integration method—numerical dynamics prediction (NDP);
- Analytical simulation of the system response for selected time-histories of valve opening for which an analytical solution of the predictive model exists—analytical dynamics prediction (ADP).
4. Equivalent Parameter Predictive Control: Sub-Optimal Analytical Control Strategy
4.1. Determination of Analytical Functions Defining Change of Valve Opening
4.2. Analytical Solution of the Path-Tracking Problem
4.3. The Control Algorithm
- Identification step aimed at the measurement of actual system kinematics and values of pressures in absorber chambers, followed by identification of the equivalent mass parameter used to update the predictive model of the system;
- Prediction step including comparison of actual and optimal values of pneumatic force, and simulation of the system response with extreme valve opening in order to determine if optimal pneumatic force will be reached before the end of control step— if yes, the system starts control determination step; if not, it moves to process termination block;
- Control determination step in which constraints imposed on valve opening are transformed into constraints on vector ; optimization over vector is conducted in order to minimize path-tracking error at the actual prediction step, and termination condition is checked;
- The control execution step, which depends on the termination condition; if it is not met, the valve opening computed in the control determination step is applied at the actual control step and the system comes back to the identification step; otherwise, the full opening of the valve is applied, and the impact mitigation process is ended.

5. Numerical Verification of Equivalent Parameter Predictive Control
5.1. Single-Impact Scenario
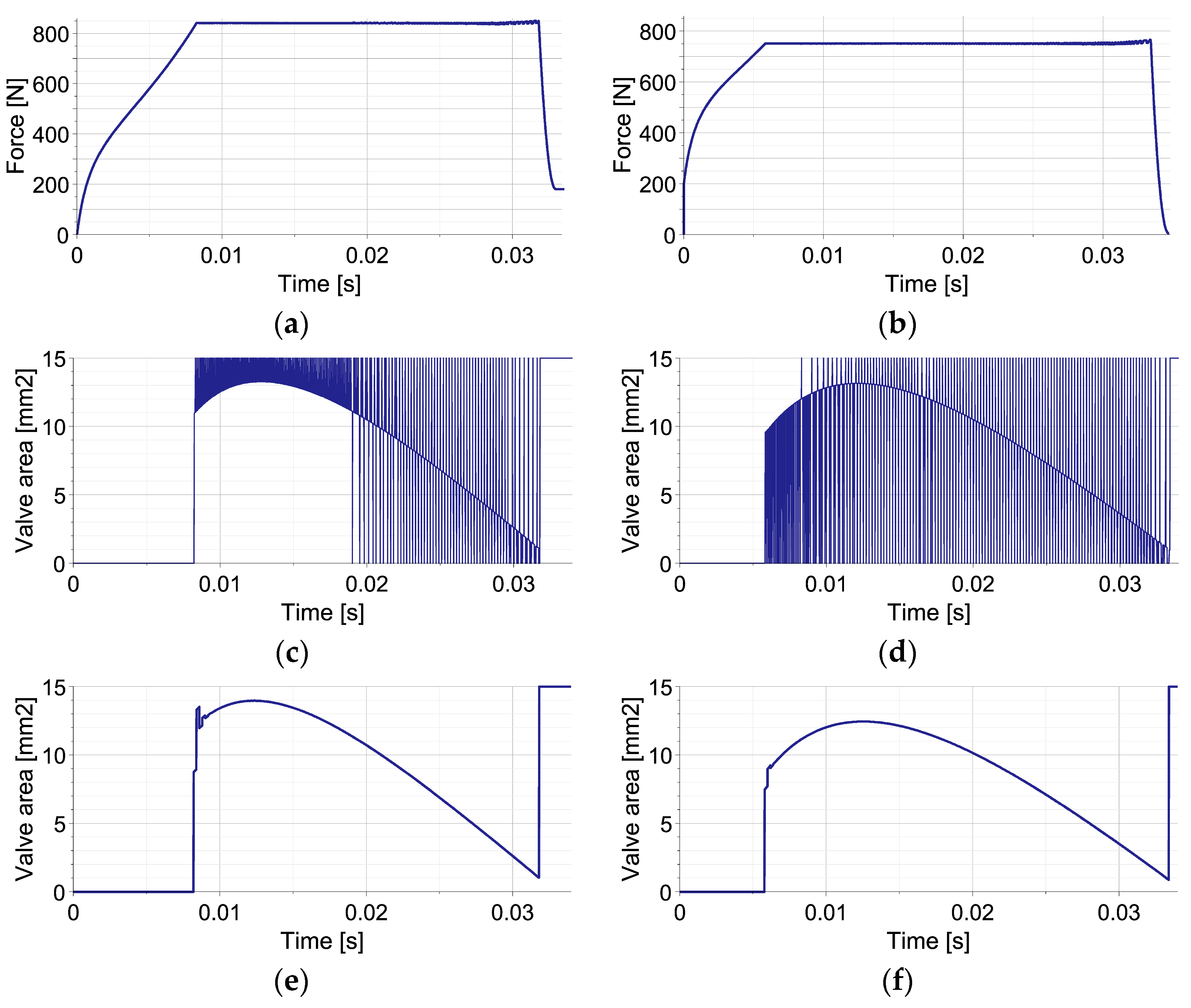
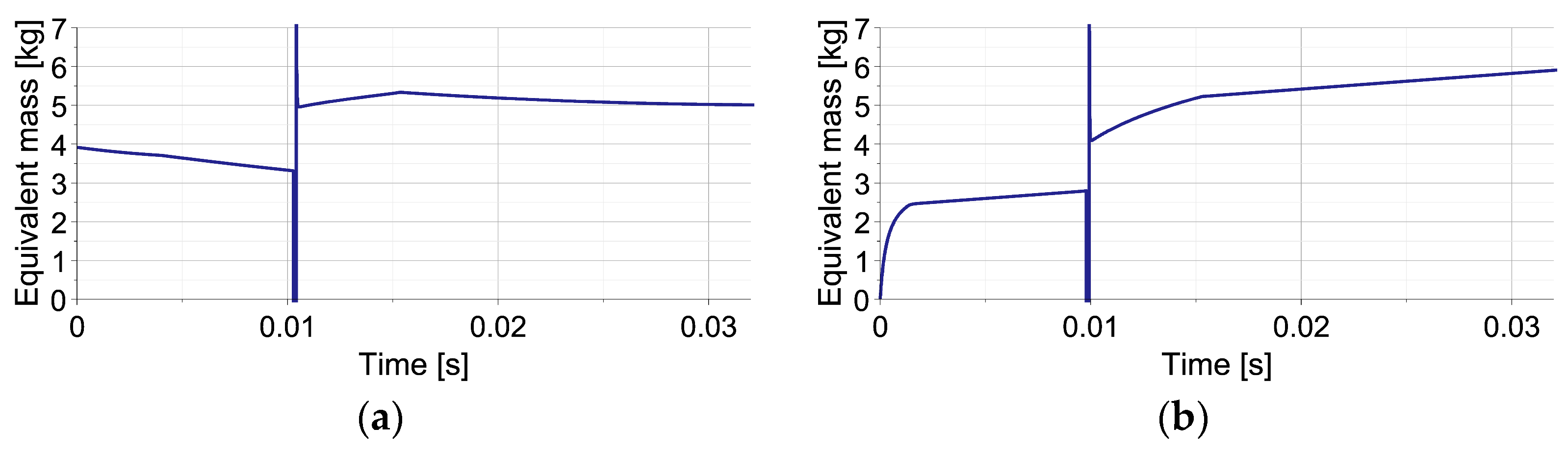
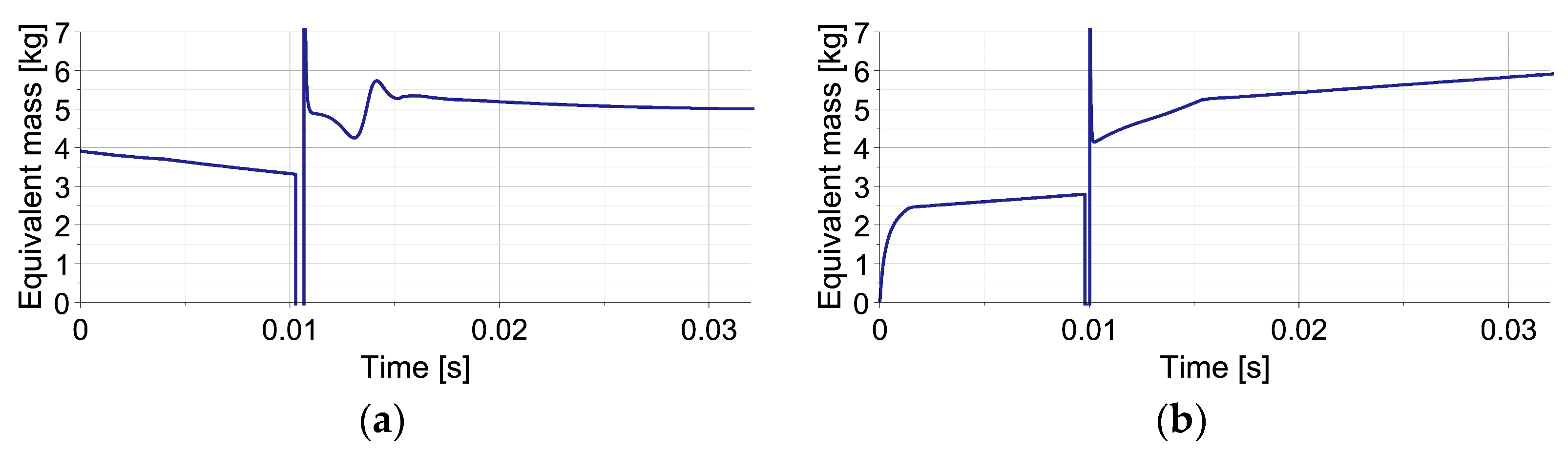
5.2. Double-Impact Scenario with Various Excitations
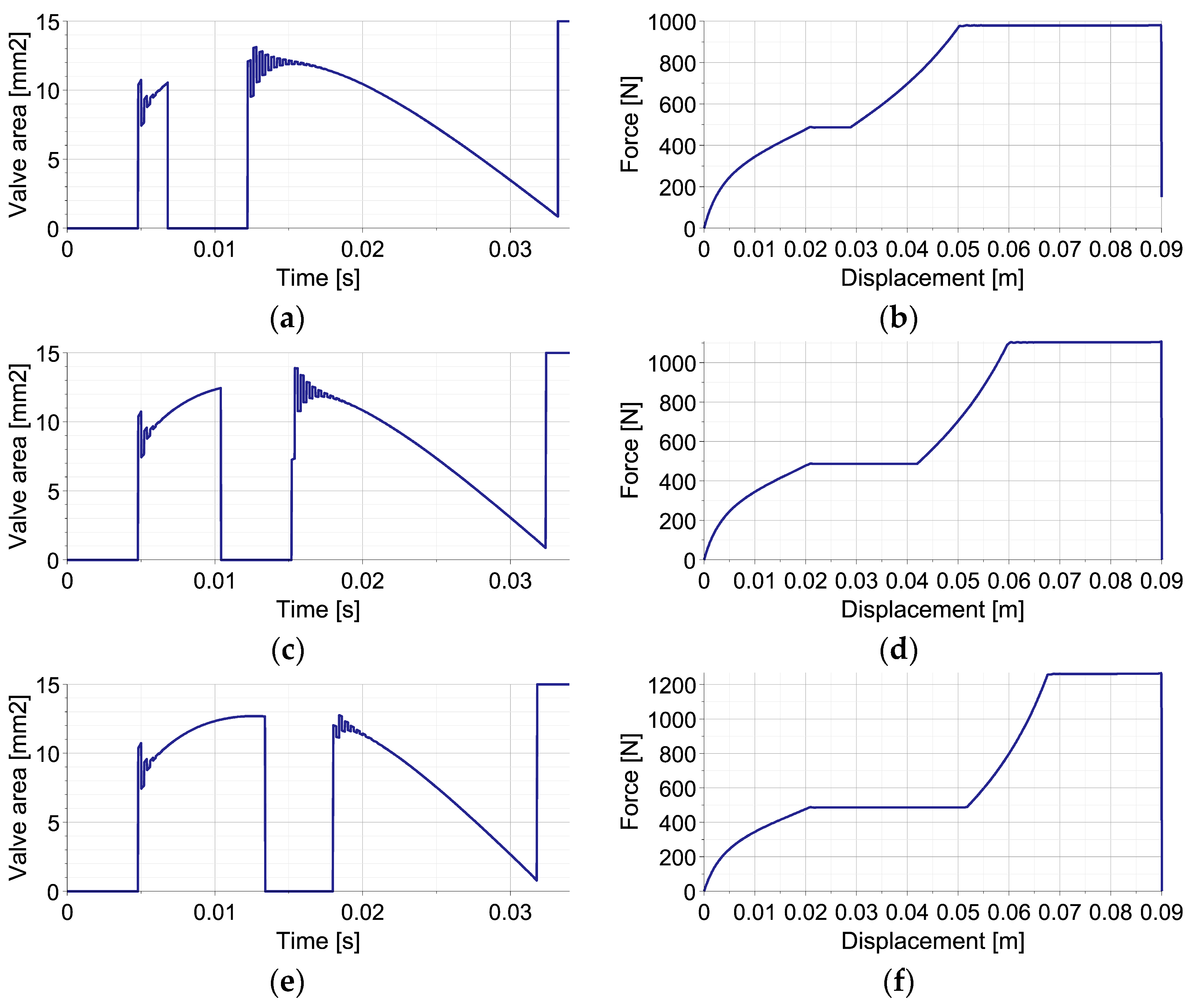
5.3. Double-Impact Scenario with Various Disturbances
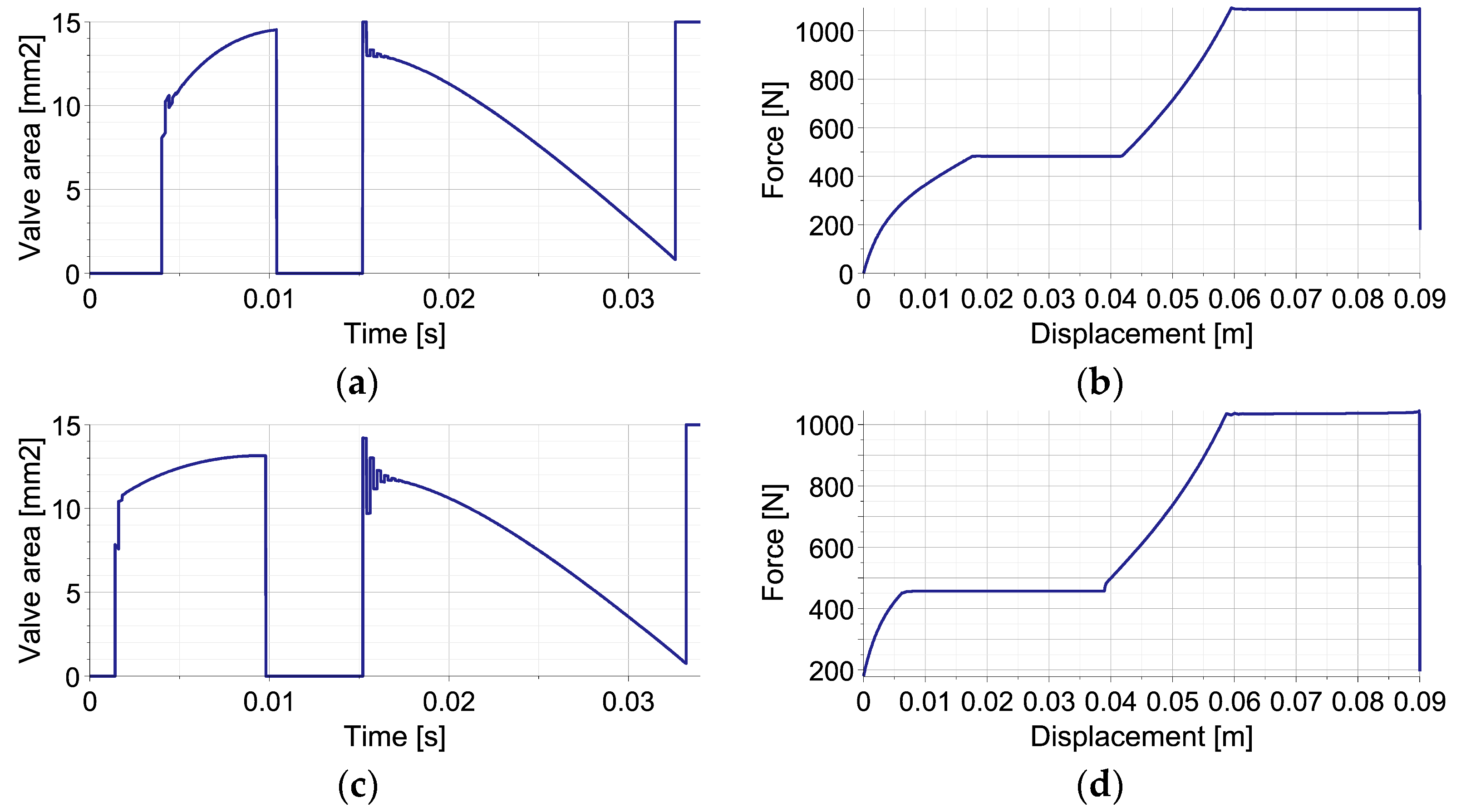
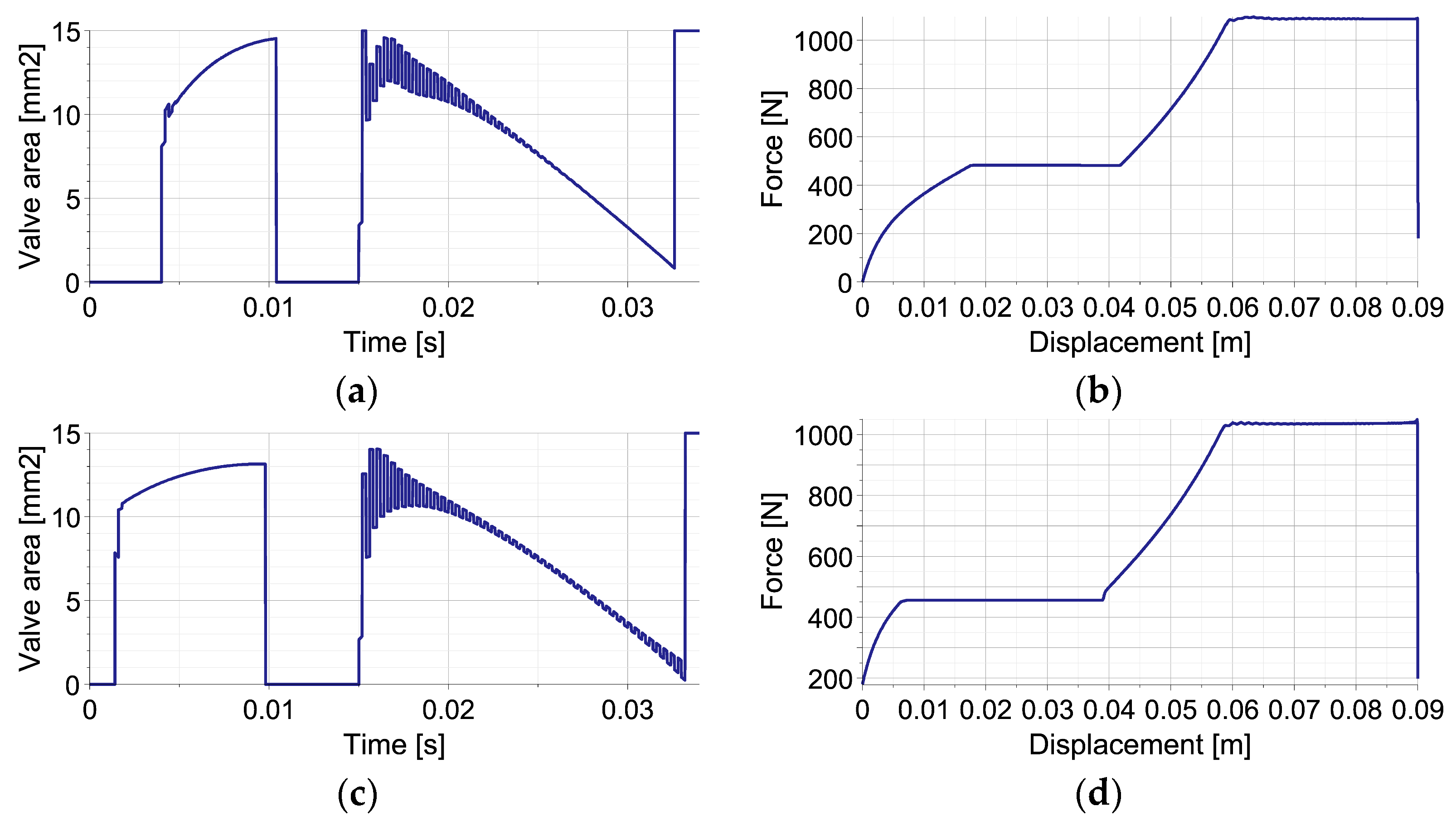
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| EPPC | Equivalent Parameter Predictive Control |
| AIA | Adaptive Impact Absorption |
| PID | Partial Integral–Differential |
| MPC | Model Predictive Control |
| HPC | Hybrid Prediction Control |
| IPC | Identification-based Predictive Control |
| FPGA | Field-programmable Gate Array |
Appendix A. Proof That Variational Formulation Given by Equation (33) Can Be Approximated by the Variational Formulation Given by Equation (34) under Specified Conditions
- i.
- When the additional force in the system tends towards zero: (trivial case);
- ii.
- When the coefficient defining the change of pneumatic force during a single control step tends towards one: , which indicates a situation when the change of pneumatic force during the considered control step is relatively small.
References
- Morato, M.M.; Nguyen, M.Q.; Sename, O.; Dugard, L. Design of a fast real-time LPV model predictive control system for semi-active suspension control of a full vehicle. J. Frankl. Inst. 2019, 356, 1196–1224. [Google Scholar] [CrossRef]
- Makowski, M.; Knap, L. Reduction of wheel force variations with magnetorheological devices. J. Vib. Control 2014, 20, 1552–1564. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, X.; Zhan, M.; Guo, K.; Zhao, F.; Liu, Z. Study on a novel hydraulic pumping regenerative suspension for vehicles. J. Frankl. Inst. 2015, 352, 485–499. [Google Scholar] [CrossRef]
- Krauze, P. Identification of Control-Related Signal Path for Semi-Active Vehicle Suspension with Magnetorheological Dampers. Sensors 2023, 23, 5770. [Google Scholar] [CrossRef] [PubMed]
- Richert, J.; Coutellier, D.; Götz, C.; Eberle, W. Advanced smart airbags: The solution for real-life safety? Int. J. Crashworthiness 2007, 12, 159–171. [Google Scholar] [CrossRef]
- Jawad, S.A.W. Intelligent hydraulic bumper for frontal collision mitigation. ASME Appl. Mech. Div. 1996, 218, 181–189. [Google Scholar]
- Woo, D.; Choi, S.-B.; Choi, Y.T.; Wereley, N.M. Frontal Crash Mitigation using MR Impact Damper for Controllable Bumper. J. Intell. Mater. Syst. Struct. 2007, 18, 1211–1215. [Google Scholar] [CrossRef]
- Noh, M.-H.; Lee, S.-Y. Parametric impact performances in a new type crash cushion barrier system using an energy absorption pipe. Int. J. Crashworthiness 2020, 25, 106–119. [Google Scholar] [CrossRef]
- Fiume, I.; Ghiringhelli, G.L. Combined fuzzy-deterministic semi-active control of a landing gear. Struct. Control Health Monit. 1995, 2, 31–57. [Google Scholar] [CrossRef]
- Ghiringhelli, G.L. Testing of semi-active landing gear control for a general aviation aircraft. AIAA J. Aircr. 2000, 37, 606–616. [Google Scholar] [CrossRef]
- Mikułowski, G.; Holnicki-Szulc, J. Adaptive landing gear concept-feedback control validation. Smart Mater. Struct. 2007, 16, 2146–2158. [Google Scholar] [CrossRef]
- Wang, M.; Chen, Z.; Wereley, N.M. Adaptive magnetorheological energy absorber control method for drop-induced shock mitigation. J. Intell. Mater. Syst. Struct. 2021, 32, 449–461. [Google Scholar] [CrossRef]
- Wang, H.; Rui, Q.; Hong, H.; Li, J. Airdrop Recovery Systems with Self-Inflating Airbag: Modeling and Analysis, 1st ed.; National Defense Industry Press: Beijing, China, 2017. [Google Scholar]
- Baruh, H.; Elsayed, E.A. Experimental design of a folded-structure energy-absorption system. Int. J. Mater. Prod. Technol. 2018, 56, 341–362. [Google Scholar] [CrossRef]
- Wołejsza, Z.; Holnicki-Szulc, J.; Graczykowski, C.; Hinc, K.; Faraj, R.; Kowalski, T.; Mikułowski, G.; Kaźmierczak, K.; Wiszowaty, R.; Pawłowski, P. Dynamics and control of adaptive airbags for UAV impact protection. In Proceedings of the ISMA 2018/USD 2018, International Conference on Noise and Vibration Engineering/International Conference on Uncertainty in Structural Dynamics, Leuven, Belgium, 17–19 September 2018; pp. 3661–3670. [Google Scholar]
- Maeda, T.; Otsuki, M.; Hashimoto, T. Protection against overturning of a lunar-planetary lander using a controlled landing gear. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2019, 233, 438–456. [Google Scholar] [CrossRef]
- Kim, Y.; Jung, H.; Koo, B.; Kim, J.; Kim, T.; Nam, Y. Detection of Pre-Impact Falls from Heights Using an Inertial Measurement Unit Sensor. Sensors 2020, 20, 5388. [Google Scholar] [CrossRef] [PubMed]
- Faraj, R.; Popławski, B.; Gabryel, D.; Kowalski, T.; Hinc, K. Adaptive airbag system for increased evacuation safety. Eng. Struct. 2022, 270, 114853. [Google Scholar] [CrossRef]
- Fanton, M.; Alizadeh, H.V.; Domel, A.; Devlin, M.; Kurt, M.; Mungal, G.M.; Camarilo, D.B.; Hawkes, E. Variable area, constant force shock absorption motivated by traumatic brain injury prevention. Smart Mater. Struct. 2020, 29, 085023. [Google Scholar] [CrossRef]
- Chen, Y.; Chiu, W.; Chen, Y. Effect of the Shock Absorber of the Shock Absorption Benefits for Upper Arm. In Mobile and Wireless Technology 2018. ICMWT 2018; Lecture Notes in Electrical Engineering; Kim, K., Kim, H., Eds.; Springer: Singapore, 2019; Volume 513. [Google Scholar]
- Jo, S.-H.; Woo, J.; Byun, G.-S.; Kwon, B.-S.; Jeong, J.-H. A Study on the Application of LSTM to Judge Bike Accidents for Inflating Wearable Airbags. Sensors 2021, 21, 6541. [Google Scholar] [CrossRef]
- Faraj, R.; Jankowski, Ł.; Graczykowski, C.; Holnicki-Szulc, J. Can the inerter be a successful shock-absorber? The case of a ball-screw inerter with a variable thread lead. J. Frankl. Inst. 2019, 356, 7855–7872. [Google Scholar] [CrossRef]
- Cetin, E.; Baykasoğlu, C. Energy absorption of thin-walled tubes enhanced by lattice structures. Int. J. Mech. Sci. 2019, 157–158, 471–484. [Google Scholar] [CrossRef]
- Li, S.; Guo, A.; Li, H.; Mao, C. An analysis of pounding mitigation and stress waves in highway bridges with shape memory alloy pseudo-rubber shock-absorbing devices. Struct. Control Health Monit. 2016, 23, 1237–1255. [Google Scholar] [CrossRef]
- Lu, Z.; Wang, Z.; Masri, S.F.; Lu, X. Particle impact dampers: Past, present, and future. Struct. Control Health Monit. 2018, 25, e2058. [Google Scholar] [CrossRef]
- Zalewski, R.; Chodkiewicz, P. Semi-active linear vacuum packed particles damper. J. Theor. Appl. Mech. 2016, 54, 311–316. [Google Scholar] [CrossRef]
- Bartkowski, P.; Zalewski, R. A concept of smart multiaxial impact damper made of vacuum packed particles. MATEC Web Conf. 2018, 157, 05001. [Google Scholar] [CrossRef]
- Wang, C.Y.; Li, Y.; Zhao, W.Z.; Zou, S.C.; Zhou, G.; Wang, Y.L. Structure design and multi-objective optimization of a novel crash box based on biomimetic structure. Int. J. Mech. Sci. 2018, 138–139, 489–501. [Google Scholar] [CrossRef]
- Rodríguez, A.; Pozo, F.; Bahar, A.; Acho, L.; Vidal, Y.; Rodellar, J. Force-derivative feedback semi-active control of base-isolated buildings using large-scale MR fluid dampers. Struct. Control Health Monit. 2012, 19, 120–145. [Google Scholar] [CrossRef]
- Powers, B.E.; Wereley, N.M.; Choi, Y.T. Analysis of impact loads in a magnetorheological energy absorber using a Bingham plastic model with refined minor loss factors accounting for turbulent transition. Meccanica 2016, 51, 3043–3054. [Google Scholar] [CrossRef]
- Aguirre, N.; Ikhouane, F.; Rodellar, J. Parametric identification of the Dahl model for large scale MR dampers. Struct. Control Health Monit. 2012, 19, 332–347. [Google Scholar] [CrossRef]
- Yang, Y.; Xu, Z.-D.; Guo, Y.-Q.; Sun, C.-L.; Zhang, J. Performance tests and microstructure-based sigmoid model for a three-coil magnetorheological damper. Struct Control Health Monit. 2021, 28, e2819. [Google Scholar] [CrossRef]
- Nguyen, Q.H.; Choi, S.B.; Park, Y.G. An analytical approach to optimally design of electrorheological fluid damper for vehicle suspension system. Meccanica 2012, 47, 1633–1647. [Google Scholar] [CrossRef]
- Mikułowski, G.; Wiszowaty, R. Pneumatic Adaptive Absorber: Mathematical Modelling with Experimental Verification. Math. Probl. Eng. 2016, 2016, 7074206. [Google Scholar] [CrossRef]
- Holnicki-Szulc, J.; Maćkiewicz, A.; Kołakowski, P. Design of Adaptive Structures for Improved Load Capacity. AIAA J. 1998, 36, 471–476. [Google Scholar] [CrossRef]
- Holnicki-Szulc, J.; Graczykowski, C.; Mikułowski, G.; Mróz, A.; Pawłowski, P.; Wiszowaty, R. Adaptive Impact Absorption-the Concept and Potential Applications. Int. J. Prot. Struct. 2015, 6, 357–377. [Google Scholar] [CrossRef]
- Ilchmann, A.; Sawodny, O.; Trenn, S. Pneumatic cylinders: Modelling and feedback force control. Int. J. Control 2016, 79, 650–661. [Google Scholar] [CrossRef]
- Ghiringhelli, G.L.; Gualdi, S. Evaluation of a landing gear semi-active control system for complete aircraft landing. Aerotec. Missili E Spaz. 2004, 83, 21–31. [Google Scholar]
- Wang, H.; Xing, J.T.; Price, W.G.; Li, W. An investigation of an active landing gear system to reduce aircraft vibrations caused by landing impacts and runway excitations. J. Sound Vib. 2008, 317, 50–66. [Google Scholar] [CrossRef]
- Hui, L.; Hongbin, G.; Dawei, C. Application of High-speed Solenoid Valve to the Semi-active Control of Landing Gear. Chin. J. Aeronaut. 2008, 21, 232–240. [Google Scholar] [CrossRef]
- Graczykowski, C.; Faraj, R. Development of control systems for fluid-based adaptive impact absorbers. Mech. Syst. Signal Process. 2019, 122, 622–641. [Google Scholar] [CrossRef]
- Faraj, R.; Graczykowski, C. Hybrid Prediction Control for self-adaptive fluid-based shock-absorbers. J. Sound Vib. 2019, 449, 427–446. [Google Scholar] [CrossRef]
- Faraj, R.; Mikułowski, G.; Wiszowaty, R. Study on the state-dependent path-tracking for smart pneumatic shock-absorber. Smart Mater. Struct. 2020, 29, 115008. [Google Scholar] [CrossRef]
- Graczykowski, C.; Faraj, R. Identification-based predictive control of semi-active shock-absorbers for adaptive dynamic excitation mitigation. Meccanica 2020, 55, 2571–2597. [Google Scholar] [CrossRef]
- Graczykowski, C.; Faraj, R. Extended Identification-Based Predictive Control for adaptive impact mitigation. Bull. Pol. Acad. Sci. Tech. Sci. 2023, 71, e145937. [Google Scholar] [CrossRef]
- Ishihara, K.; Morimoto, J. An optimal control strategy for hybrid actuator systems: Application to an artificial muscle with electric motor assist. Neural Netw. 2018, 99, 92–100. [Google Scholar] [CrossRef] [PubMed]
- Wu, Q.; Wang, X.; Chen, B.; Wu, H.; Shao, Z. Development and hybrid force/position control of a compliant rescue manipulator. Mechatronics 2017, 46, 143–153. [Google Scholar] [CrossRef]
- Noda, T.; Teramae, T.; Ugurlu, B.; Morimot, J. Development of an upper limb exoskeleton powered via pneumatic electric hybrid actuators with Bowden cable. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Chicago, IL, USA, 14–18 September 2014; pp. 3573–3578. [Google Scholar]
- Zahaf, A.; Bououden, S.; Chadli, M.; Chemachema, M. Robust fault tolerant optimal predictive control of hybrid actuators with time-varying delay for industrial robot arm. Asian J. Control 2022, 24, 1–15. [Google Scholar] [CrossRef]
- Bozza, A.; Cavone, G.; Dotoli, M. An Adaptive Model Predictive Control Approach for Position Tracking and Force Control of a Hydraulic Actuator. In Proceedings of the 2022 IEEE 18th International Conference on Automation Science and Engineering (CASE), Mexico City, Mexico, 20–24 August 2022. [Google Scholar]



| Unknown ) | Unknown Disturbance Force | Unknown Fluid Leakage | Actuator Time Delay | Actuator Fault | Comments | |
|---|---|---|---|---|---|---|
| Standard AIA approach [35] | No | No | No | No | No | Precomputed system path |
| Hybrid Prediction Control [42,43] | Yes | Yes | Yes | No | No | Updated system path, approx. solution |
| Identification-based Predictive Control [44,45] | No/Yes * | Yes | No/Yes * | No/Yes * | No | Updated system path, semi-optimal solution |
| Equivalent Parameter Predictive Control | Yes | Yes | No | No | No | Updated system path, multi-impact loads, numerically efficient semi-optimal solution |
| Robust Fault Tolerant Predictive Control [49] | - | Yes | No | Yes | Yes | Application for industrial arm robot |
| Adaptive Model Predictive Control [50] | - | Yes | No | Yes | No | Application for system with uncertainties |
| Suspended Mass (kg) | Initial Velocity of the Mass (m/s) | Initial Internal Pressure in Chambers (kPa) | Operational Gas | Piston Diameter (mm) |
|---|---|---|---|---|
| 5 | 5 | 300 | compressed air | 40 |
| Initial volume of top chamber (cm3) | Initial volume of bottom chamber (cm3) | Piston initial position (mm) | Entire absorber stroke (mm) | Initial temperature of the gas (K) |
| 7.54 | 118.12 | 6 | 94 | 293.15 |
| First Impacting Mass (kg) | Initial Velocity of the First Mass (m/s) | Second Impacting Mass (kg) | Initial Velocity of the Second Mass (m/s) |
|---|---|---|---|
| 4 | 4.5 | 2 | 5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Graczykowski, C.; Faraj, R. Adaptive Impact Mitigation Based on Predictive Control with Equivalent Mass Identification. Sensors 2023, 23, 9471. https://doi.org/10.3390/s23239471
Graczykowski C, Faraj R. Adaptive Impact Mitigation Based on Predictive Control with Equivalent Mass Identification. Sensors. 2023; 23(23):9471. https://doi.org/10.3390/s23239471
Chicago/Turabian StyleGraczykowski, Cezary, and Rami Faraj. 2023. "Adaptive Impact Mitigation Based on Predictive Control with Equivalent Mass Identification" Sensors 23, no. 23: 9471. https://doi.org/10.3390/s23239471
APA StyleGraczykowski, C., & Faraj, R. (2023). Adaptive Impact Mitigation Based on Predictive Control with Equivalent Mass Identification. Sensors, 23(23), 9471. https://doi.org/10.3390/s23239471






