Comprehensive Numerical Analysis of Temperature Sensitivity of Spherical Microresonators Based on Silica and Soft Glasses
Abstract
1. Introduction
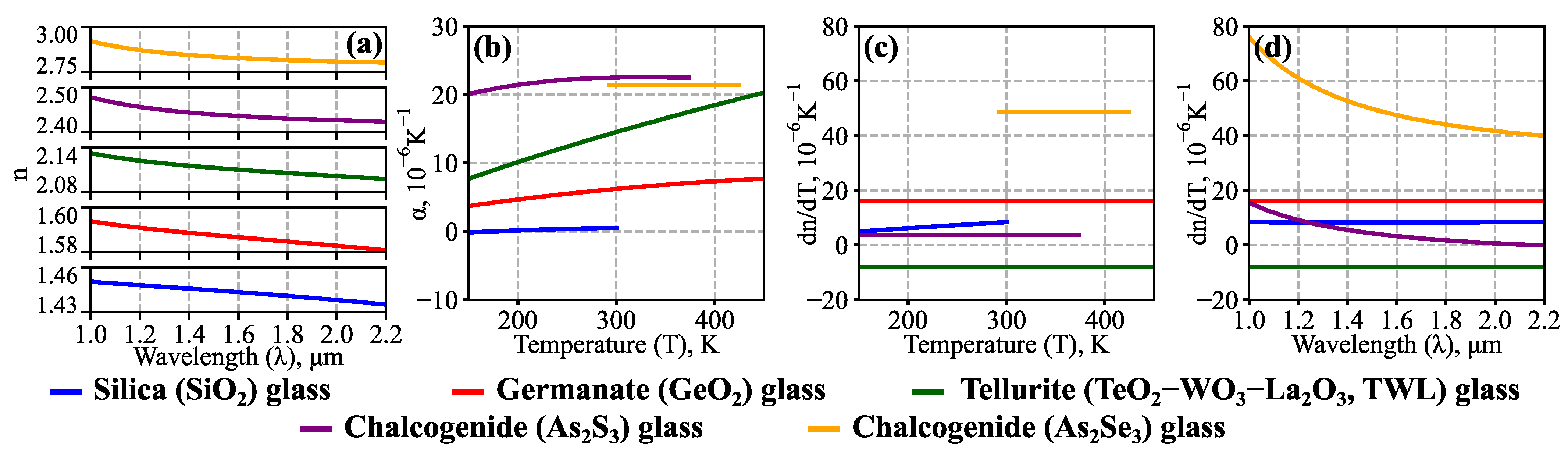
2. Materials and Methods
| Glass | n(λ) | Thermo-Optic Effect dn/dT | |||
|---|---|---|---|---|---|
| α, 10−6 K−1 | Available Data α(T) | 10−6 K−1 | |||
| SiO2 | [40] | 0.48 | α(T); 10 K ≤ T ≤ 300 K; [41] | 8.2 | ; 30 K ≤ T ≤ 300 K; [42] |
| GeO2 | [40] | 6.1 | α(T); 95 K ≤ T ≤ 720 K; [43] | 16 | = const; [44] |
| TeO2−WO3− La2O3 (TWL) | [36] | 14.2 | α(T); T ≤ 600 K; [45] | −8 | = const; [46] |
| As2S3 | [47] | 22.5 | α(T); 2 K ≤ T ≤ 373 K; [28,29] | 3.7 | (λ); [29] |
| As2Se3 | [48] | 21.4 | α = const; 293 K ≤ T ≤ 423 K; [30,31] | 48.6 | (λ); [31] |
3. Results
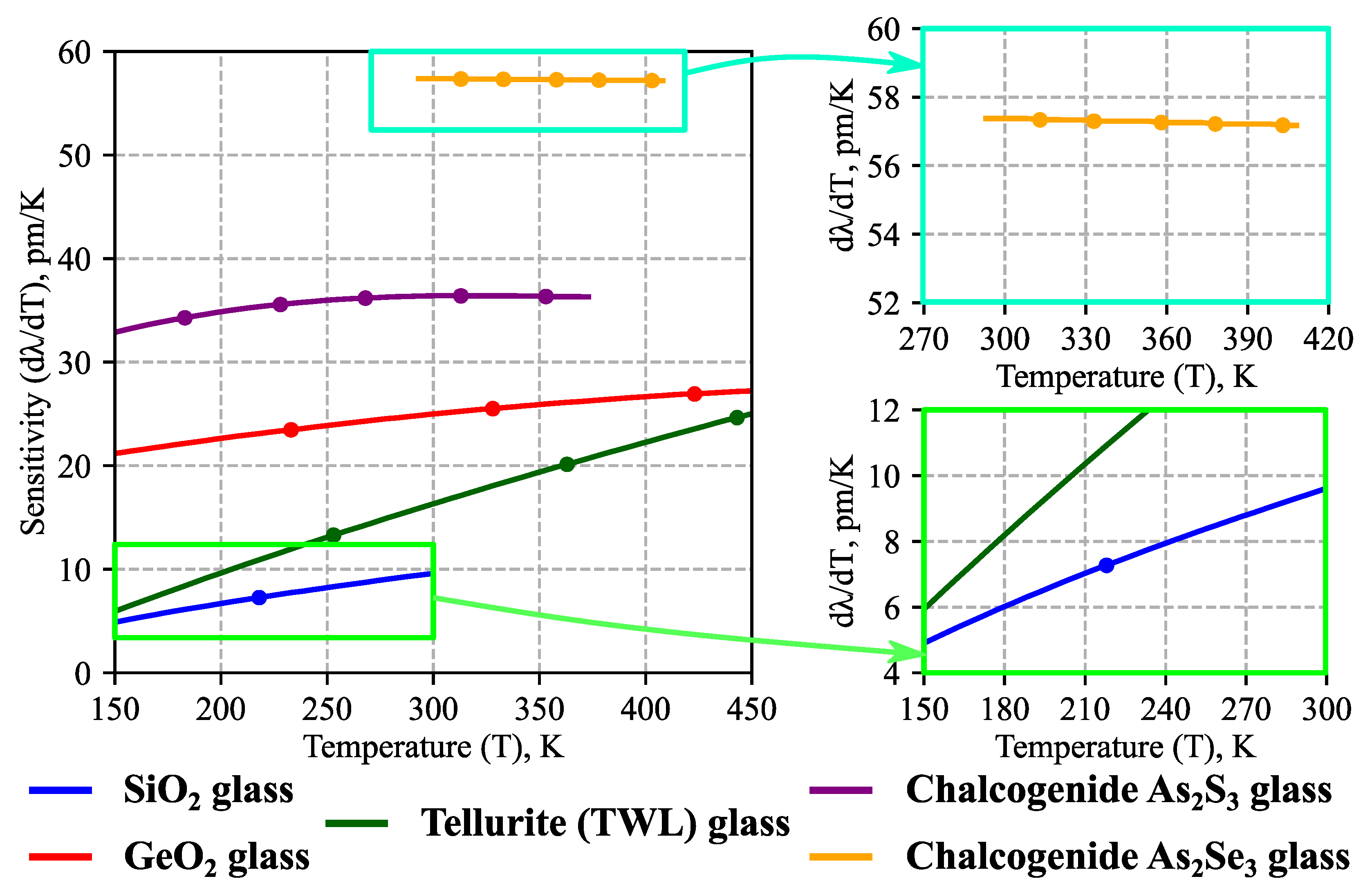
3.1. Temperature Sensitivity of Same-Sized Microspheres
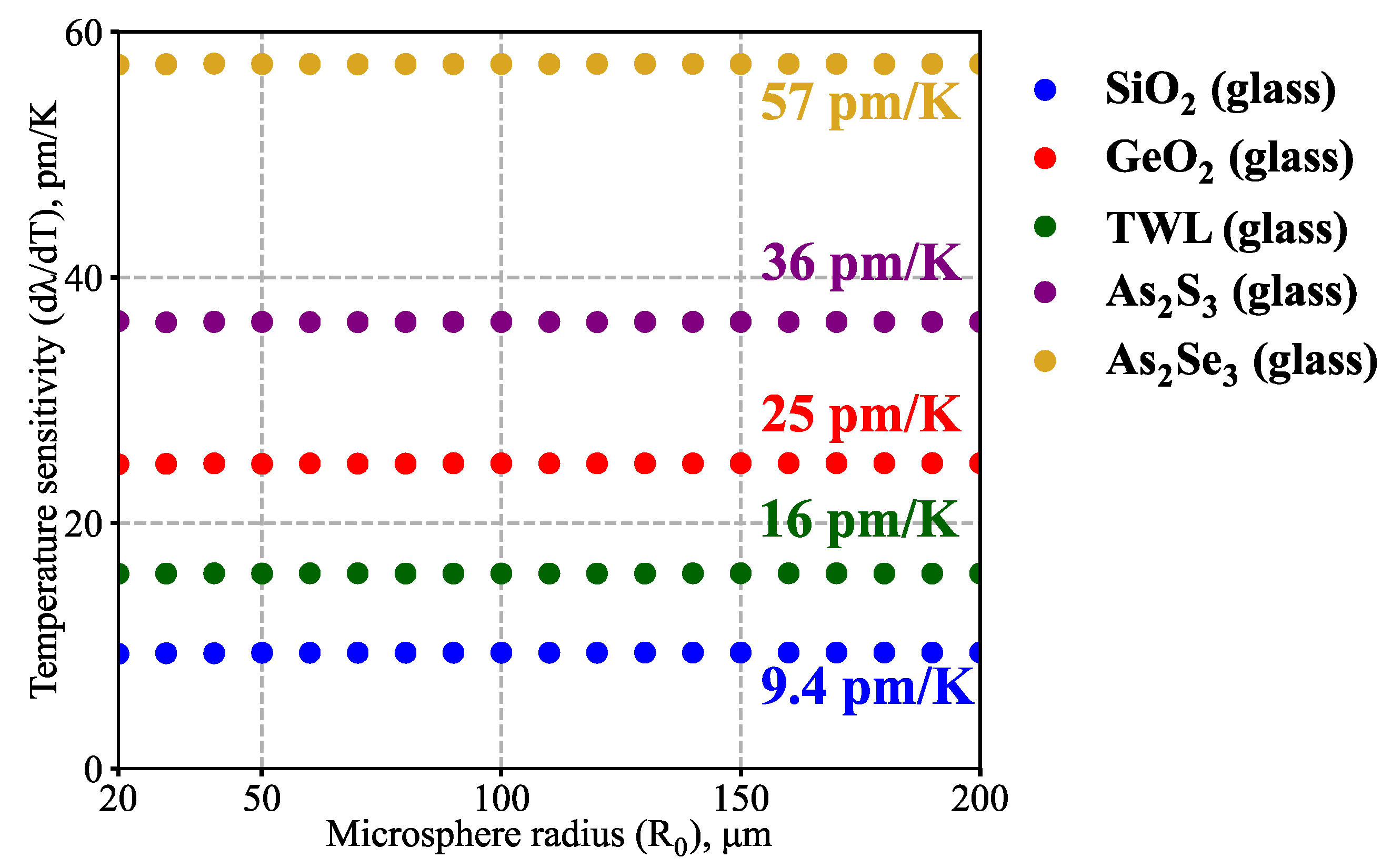
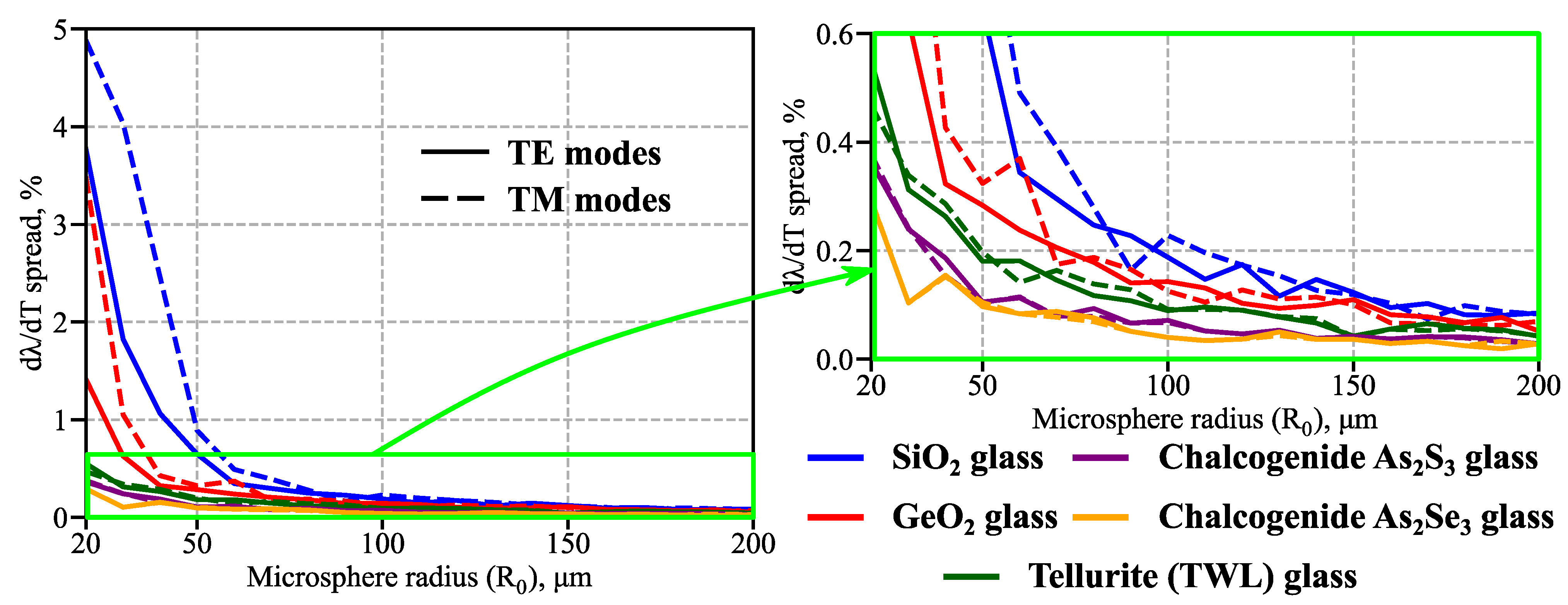
3.2. Temperature Sensitivity of Different-Sized Microspheres
3.3. Spectral Dependence of Temperature Sensitivity
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Childs, P.R.N.; Greenwood, J.R.; Long, C.A. Review of Temperature Measurement. Rev. Sci. Instrum. 2000, 71, 2959–2978. [Google Scholar] [CrossRef]
- Rai, V.K. Temperature Sensors and Optical Sensors. Appl. Phys. B 2007, 88, 297–303. [Google Scholar] [CrossRef]
- Yu, J.; Lewis, E.; Brambilla, G.; Wang, P. Temperature Sensing Performance of Microsphere Resonators. Sensors 2018, 18, 2515. [Google Scholar] [CrossRef] [PubMed]
- Pendão, C.; Silva, I. Optical Fiber Sensors and Sensing Networks: Overview of the Main Principles and Applications. Sensors 2022, 22, 7554. [Google Scholar] [CrossRef] [PubMed]
- Kuznetsov, A.G.; Kharenko, D.S.; Babin, S.A.; Tsydenzhapov, I.B.; Shelemba, I.S. Ultralong Fibre-Optic Distributed Raman Temperature Sensor. Quantum Electron. 2017, 47, 967–970. [Google Scholar] [CrossRef]
- Popov, S.M.; Butov, O.V.; Kolosovskii, A.O.; Voloshin, V.V.; Vorob’ev, I.L.; Isaev, V.A.; Ryakhovskii, D.V.; Vyatkin, M.Y.; Rybaltovskii, A.A.; Fotiadi, A.A.; et al. Optical Fibres with an Inscribed Fibre Bragg Grating Array for Sensor Systems and Random Lasers. Quantum Electron. 2021, 51, 1101–1106. [Google Scholar] [CrossRef]
- Righini, G.C.; Dumeige, Y.; Féron, P.; Ferrari, M.; Nunzi Conti, G.; Ristic, D.; Soria, S. Whispering Gallery Mode Microresonators: Fundamentals and Applications. Riv. del Nuovo Cim. 2011, 34, 435–488. [Google Scholar] [CrossRef]
- Reynolds, T.; Riesen, N.; Meldrum, A.; Fan, X.; Hall, J.M.M.; Monro, T.M.; François, A. Fluorescent and Lasing Whispering Gallery Mode Microresonators for Sensing Applications. Laser Photonics Rev. 2017, 11, 1600265. [Google Scholar] [CrossRef]
- Geints, Y.E.; Minin, O.V.; Minin, I.V. Proof-of-Concept of a Miniature Pressure Sensor Based on Coupled Optical WGMs Excited in a Dielectric Microsphere. Opt. Laser. Technol. 2022, 151, 108015. [Google Scholar] [CrossRef]
- Berkis, R.; Reinis, P.K.; Milgrave, L.; Draguns, K.; Salgals, T.; Brice, I.; Alnis, J.; Atvars, A. Wavelength Sensing Based on Whispering Gallery Mode Mapping. Fibers 2022, 10, 90. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, B.; Liu, J.; Song, Y.; Zhang, H. Recent Developments in Mid-Infrared Fiber Lasers: Status and Challenges. Opt. Laser Technol. 2020, 132, 106497. [Google Scholar] [CrossRef]
- Falconi, M.C.; Laneve, D.; Prudenzano, F. Advances in Mid-IR Fiber Lasers: Tellurite, Fluoride and Chalcogenide. Fibers 2017, 5, 23. [Google Scholar] [CrossRef]
- Falconi, M.C.; Loconsole, A.M.; Prudenzano, F. Modeling of Rare-Earth-Doped Glass Devices and Optical Parameter Indirect Evaluation. Opt. Mater. 2022, 132, 112835. [Google Scholar] [CrossRef]
- Shiryaev, V.S.; Sukhanov, M.V.; Velmuzhov, A.P.; Karaksina, E.V.; Kotereva, T.V.; Snopatin, G.E.; Denker, B.I.; Galagan, B.I.; Sverchkov, S.E.; Koltashev, V.V.; et al. Core-Clad Terbium Doped Chalcogenide Glass Fiber with Laser Action at 5.38 Μm. J. Non-Cryst. Solids 2021, 567, 120939. [Google Scholar] [CrossRef]
- Frolov, M.P.; Leonov, S.O.; Korostelin, Y.V.; Kozlovsky, V.I.; Skasyrsky, Y.K.; Sukhanov, M.V.; Velmuzhov, A.P.; Fjodorow, P.; Galagan, B.I.; Denker, B.I.; et al. Current Progress in Ce3+-Doped Selenide Glasses for Mid-Infrared Lasers. Opt. Mater. Express 2022, 12, 4619–4629. [Google Scholar] [CrossRef]
- Kamynin, V.A.; Filatova, S.A.; Denker, B.I.; Galagan, B.I.; Koltashev, V.V.; Medvedkov, O.I.; Sverchkov, S.E.; Tsvetkov, V.B. Tm3+-Doped Tellurite Fiber Weak Signal Amplifier at a Wavelength of 2.27 µm. Results Phys. 2021, 27, 104512. [Google Scholar] [CrossRef]
- Eggleton, B.J.; Luther-Davies, B.; Richardson, K. Chalcogenide Photonics. Nature Photon. 2011, 5, 141–148. [Google Scholar] [CrossRef]
- Bodrov, S.; Sergeev, Y.; Burova, E.; Korytin, A.; Murzanev, A.; Romashkin, A.; Stepanov, A. Cubic Nonlinearity of Tellurite and Chalcogenide Glasses: Terahertz-Field-Induced Second Harmonic Generation vs. Optical Kerr Effect. Appl. Sci. 2022, 12, 11608. [Google Scholar] [CrossRef]
- Kedenburg, S.; Strutynski, C.; Kibler, B.; Froidevaux, P.; Désévédavy, F.; Gadret, G.; Jules, J.-C.; Steinle, T.; Mörz, F.; Steinmann, A.; et al. High Repetition Rate Mid-Infrared Supercontinuum Generation from 1.3 to 5.3 µm in Robust Step-Index Tellurite Fibers. J. Opt. Soc. Am. B 2017, 34, 601–607. [Google Scholar] [CrossRef]
- Cai, D.; Xie, Y.; Guo, X.; Wang, P.; Tong, L. Chalcogenide Glass Microfibers for Mid-Infrared Optics. Photonics 2021, 8, 497. [Google Scholar] [CrossRef]
- Chang, P.; Luo, H.; Wu, Q.; Wang, Y.; Li, J. Tunable Mid-Infrared Raman Soliton Generation From 2.80 to 3.17 μm Based on Fluorotellurite Fiber. IEEE Photon. Technol. Lett. 2022, 34, 1183–1186. [Google Scholar] [CrossRef]
- Andrianov, A.V.; Anashkina, E.A. Tunable Raman Lasing in an As2S3 Chalcogenide Glass Microsphere. Opt. Express 2021, 29, 5580. [Google Scholar] [CrossRef]
- Suresh, S.; Thomas, S. Comprehensive Review of Advances in the Field of Chalcogenide Glass Microresonators. Int. J. Appl. Glass. Sci. 2022, 1–16. [Google Scholar] [CrossRef]
- Xia, D.; Huang, Y.; Zhang, B.; Zeng, P.; Zhao, J.; Yang, Z.; Sun, S.; Luo, L.; Hu, G.; Liu, D.; et al. Engineered Raman Lasing in Photonic Integrated Chalcogenide Microresonators. Laser Photonics Rev. 2022, 16, 2100443. [Google Scholar] [CrossRef]
- Ogusu, K.; Yamasaki, J.; Maeda, S.; Kitao, M.; Minakata, M. Linear and Nonlinear Optical Properties of Ag–As–Se Chalcogenide Glasses for All-Optical Switching. Opt. Lett. 2004, 29, 265–267. [Google Scholar] [CrossRef]
- Anashkina, E.A.; Sorokin, A.A.; Andrianov, A.V. Ultrashort Pulse Retrieval from Experimental Spectra Transformed in Chalcogenide and Silica Fibers. Fibers 2022, 10, 98. [Google Scholar] [CrossRef]
- Wu, Z.; Xu, Y.; Qi, D.; Nie, Q.; Zhang, X. Progress in Preparation and Applications of Te-As-Se Chalcogenide Glasses and Fibers. Infrared Phys. Technol. 2019, 102, 102981. [Google Scholar] [CrossRef]
- Morgan, G.J.; White, G.K.; Collins, J.G. Thermal expansion of amorphous As2S3 at low temperatures. Philos. Mag. B 1981, 43, 1039–1048. [Google Scholar] [CrossRef]
- SCHOTT IRG27 Glass Datasheet. Available online: https://www.schott.com/shop/advanced-optics/en/IRG-27/c/glass-IRG27 (accessed on 13 December 2022).
- Musgraves, J.D.; Wachtel, P.; Novak, S.; Wilkinson, J.; Richardson, K. Composition dependence of the viscosity and other physical properties in the arsenic selenide glass system. J. Appl. Phys. 2011, 110, 063503. [Google Scholar] [CrossRef]
- SCHOTT IRG26 Glass Datasheet. Available online: https://www.schott.com/shop/advanced-optics/en/IRG-26/c/glass-IRG26 (accessed on 13 December 2022).
- Anashkina, E.A.; Marisova, M.P.; Dorofeev, V.V.; Andrianov, A.V. Cascade Brillouin Lasing in a Tellurite-Glass Microsphere Resonator with Whispering Gallery Modes. Sensors 2022, 22, 2866. [Google Scholar] [CrossRef]
- Spolitis, S.; Murnieks, R.; Skladova, L.; Salgals, T.; Andrianov, A.V.; Marisova, M.P.; Leuchs, G.; Anashkina, E.A.; Bobrovs, V. IM/DD WDM-PON Communication System Based on Optical Frequency Comb Generated in Silica Whispering Gallery Mode Resonator. IEEE Access 2021, 9, 66335–66345. [Google Scholar] [CrossRef]
- Tebeneva, T.S.; Shitikov, A.E.; Benderov, O.V.; Lobanov, V.E.; Bilenko, I.A.; Rodin, A.V. Ultrahigh-Q WGM Microspheres from ZBLAN for the Mid-IR Band. Opt. Lett. 2022, 47, 6325–6328. [Google Scholar] [CrossRef] [PubMed]
- Andrianov, A.V.; Marisova, M.P.; Anashkina, E.A. Thermo-Optical Sensitivity of Whispering Gallery Modes in As2S3 Chalcogenide Glass Microresonators. Sensors 2022, 22, 4636. [Google Scholar] [CrossRef]
- Andrianov, A.V.; Marisova, M.P.; Dorofeev, V.V.; Anashkina, E.A. Thermal shift of whispering gallery modes in tellurite glass microspheres. Res. Phys. 2020, 17, 103128. [Google Scholar] [CrossRef]
- Yang, Z.; Wu, Y.; Zhang, X.; Zhang, W.; Xu, P.; Dai, S. Low Temperature Fabrication of Chalcogenide Microsphere Resonators for Thermal Sensing. IEEE Photon. Technol. Lett. 2017, 29, 66–69. [Google Scholar] [CrossRef]
- Oraevsky, A.N. Whispering-gallery waves. Quantum Electron. 2002, 32, 377–400. [Google Scholar] [CrossRef]
- Kher-Alden, J.; Maayani, S.; Martin, L.L.; Douvidzon, M.; Deych, L.; Carmon, T. Microspheres with atomic-scale tolerances generate hyperdegeneracy. Phys. Rev. X 2020, 10, 031049. [Google Scholar] [CrossRef]
- Fleming, J.W. Dispersion in GeO2-SiO2 glasses. Appl. Opt. 1984, 23, 4486–4493. [Google Scholar] [CrossRef]
- Barron, T.; White, G. Heat Capacity and Thermal Expansion at Low Temperatures, 1st ed.; Springer: New York, NY, USA, 1999; p. 307. [Google Scholar] [CrossRef]
- Leviton, D.B.; Frey, B.J. Temperature-dependent absolute refractive measurements of synthetic fused silica. In Proceedings of the SPIE Optomechanical Technologies for Astronomy, Orlando, FL, USA, 6 July 2006. [Google Scholar] [CrossRef]
- Napolitano, A.; Macedo, P.B. Spectrum of Relaxation Times in GeO2 Glass. J. Res. Natl. Bur. Stand. A Phys. Chem. 1968, 72A, 425–433. [Google Scholar] [CrossRef]
- Yin, Z.-Y.; Jessop, P.E.; Garside, B.K. Photoinduced grating filters in GeO2 thin-film waveguides. Appl. Opt. 1983, 22, 4088–4092. [Google Scholar] [CrossRef]
- Kut’in, A.M.; Dorofeev, V.V.; Moiseev, A.N.; Churbanov, M.F.; Plehovich, A.D.; Markin, A.V. Thermo-physical properties of 0.72TeO2–0.24WO3–0.04La2O3 glass. J. Non-Cryst. Solids 2013, 377, 16–20. [Google Scholar] [CrossRef]
- Pilla, V.; Chillcce, E.F.; Neves, A.A.R.; Munin, E.; Catunda, T.; Cesar, C.L.; Barbosa, L.C. Thermal-lens study of thermo-optical properties of tellurite glasses. J. Mater. Sci. 2007, 42, 2304–2308. [Google Scholar] [CrossRef]
- Rodney, W.S.; Malitson, I.H.; King, T.A. Refractive Index of Arsenic Trisulfide. J. Opt. Soc. Am. 1958, 48, 633–636. [Google Scholar] [CrossRef]
- Carlie, N.; Anheier, N.C.; Qiao, H.A.; Bernacki, B.; Phillips, M.C.; Petit, L.; Musgraves, J.D.; Richardson, K. Measurement of the refractive index dispersion of As2Se3 bulk glass and thin films prior to and after laser irradiation and annealing using prism coupling in the near- and mid-infrared spectral range. Rev. Sci. Instr. 2011, 82, 053103. [Google Scholar] [CrossRef]
- Schiller, S. Asymptotic expansion of morphological resonance frequencies in Mie scattering. Appl. Opt. 1993, 32, 2181–2185. [Google Scholar] [CrossRef]
- Ma, Q.; Rossmann, T.; Guo, Z. Whispering-Gallery Mode Silica Microsensors for Cryogenic to Room Temperature Measurement. Meas. Sci. Technol. 2010, 21, 025310. [Google Scholar] [CrossRef]
- Bhattacharya, S.; Veluthandath, A.V.; Murugan, G.S.; Bisht, P.B. Temperature Dependence of Whispering Gallery Modes of Quantum Dot-Doped Microbottle Resonators. J. Lumin. 2020, 221, 117050. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marisova, M.P.; Andrianov, A.V.; Anashkina, E.A. Comprehensive Numerical Analysis of Temperature Sensitivity of Spherical Microresonators Based on Silica and Soft Glasses. Sensors 2023, 23, 717. https://doi.org/10.3390/s23020717
Marisova MP, Andrianov AV, Anashkina EA. Comprehensive Numerical Analysis of Temperature Sensitivity of Spherical Microresonators Based on Silica and Soft Glasses. Sensors. 2023; 23(2):717. https://doi.org/10.3390/s23020717
Chicago/Turabian StyleMarisova, Maria P., Alexey V. Andrianov, and Elena A. Anashkina. 2023. "Comprehensive Numerical Analysis of Temperature Sensitivity of Spherical Microresonators Based on Silica and Soft Glasses" Sensors 23, no. 2: 717. https://doi.org/10.3390/s23020717
APA StyleMarisova, M. P., Andrianov, A. V., & Anashkina, E. A. (2023). Comprehensive Numerical Analysis of Temperature Sensitivity of Spherical Microresonators Based on Silica and Soft Glasses. Sensors, 23(2), 717. https://doi.org/10.3390/s23020717








