Modeling the Design Characteristics of Woven Textile Electrodes for long−Term ECG Monitoring
Abstract
1. Introduction
2. Materials and Methods
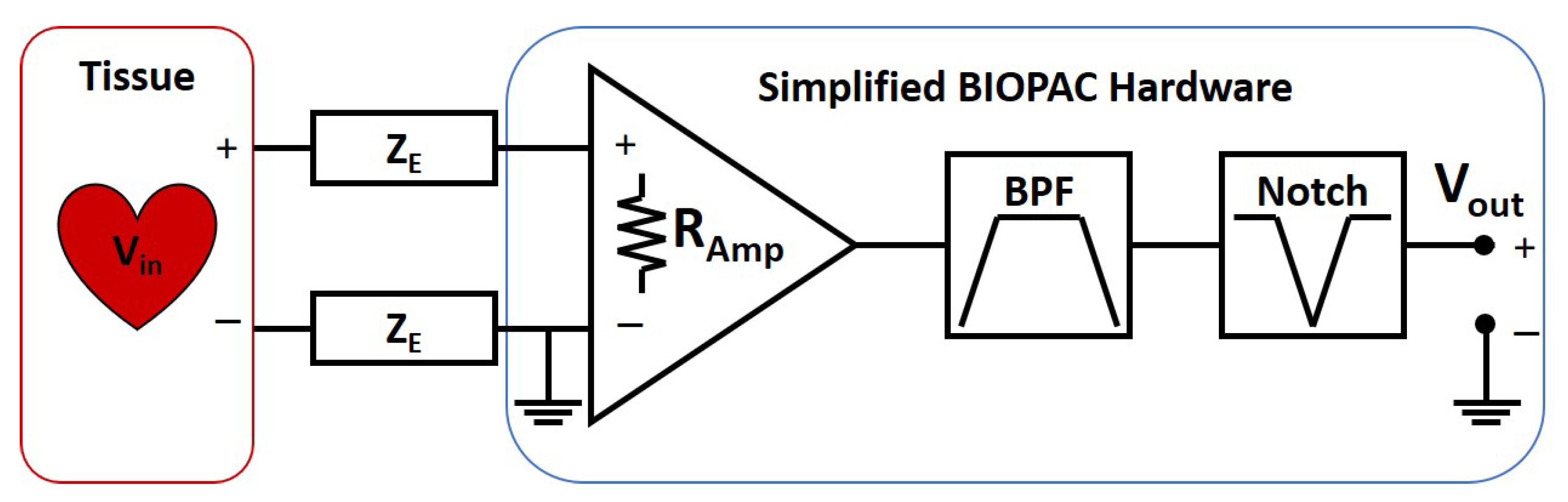
2.1. Procedure
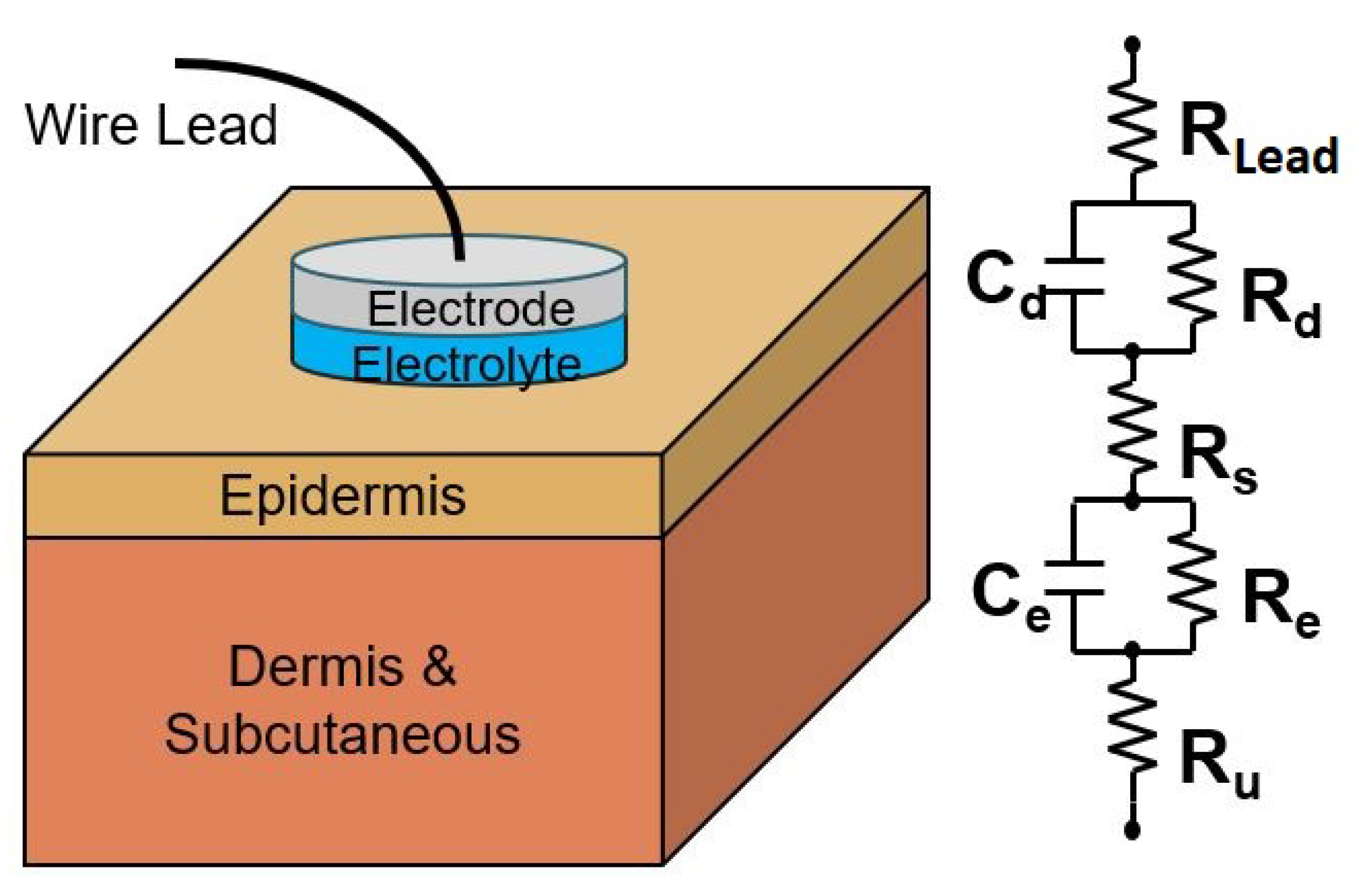
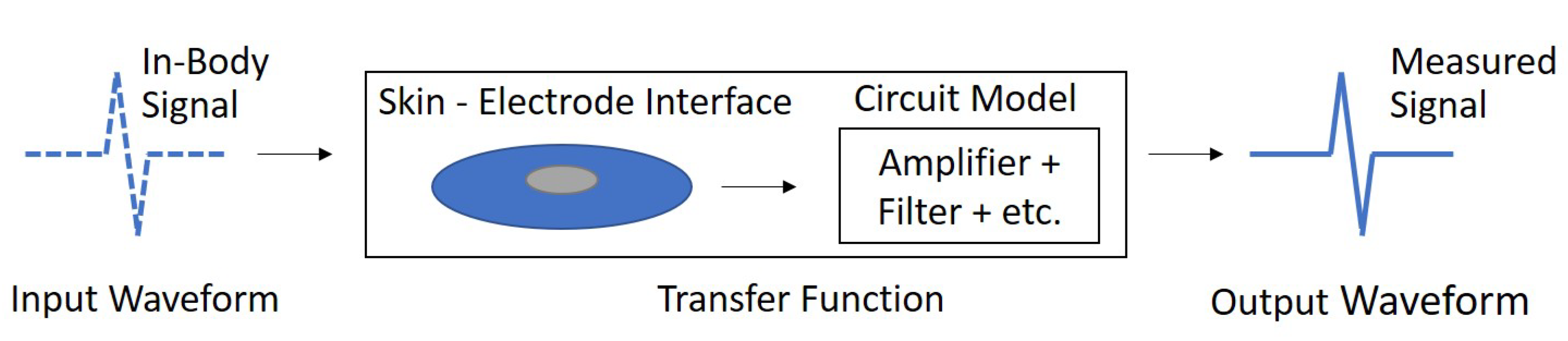
2.2. Models
2.3. Leave-One-Out Cross-Validation
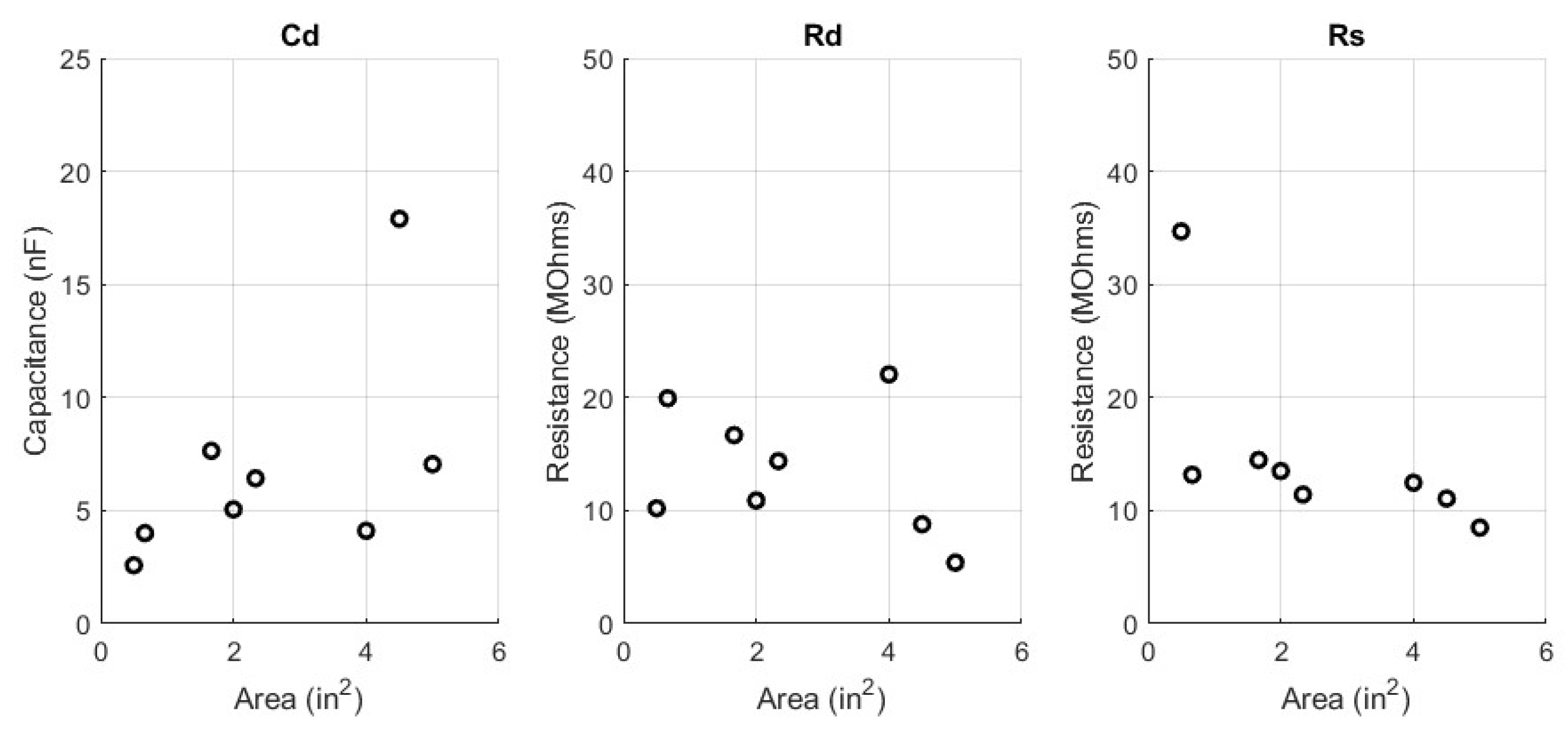
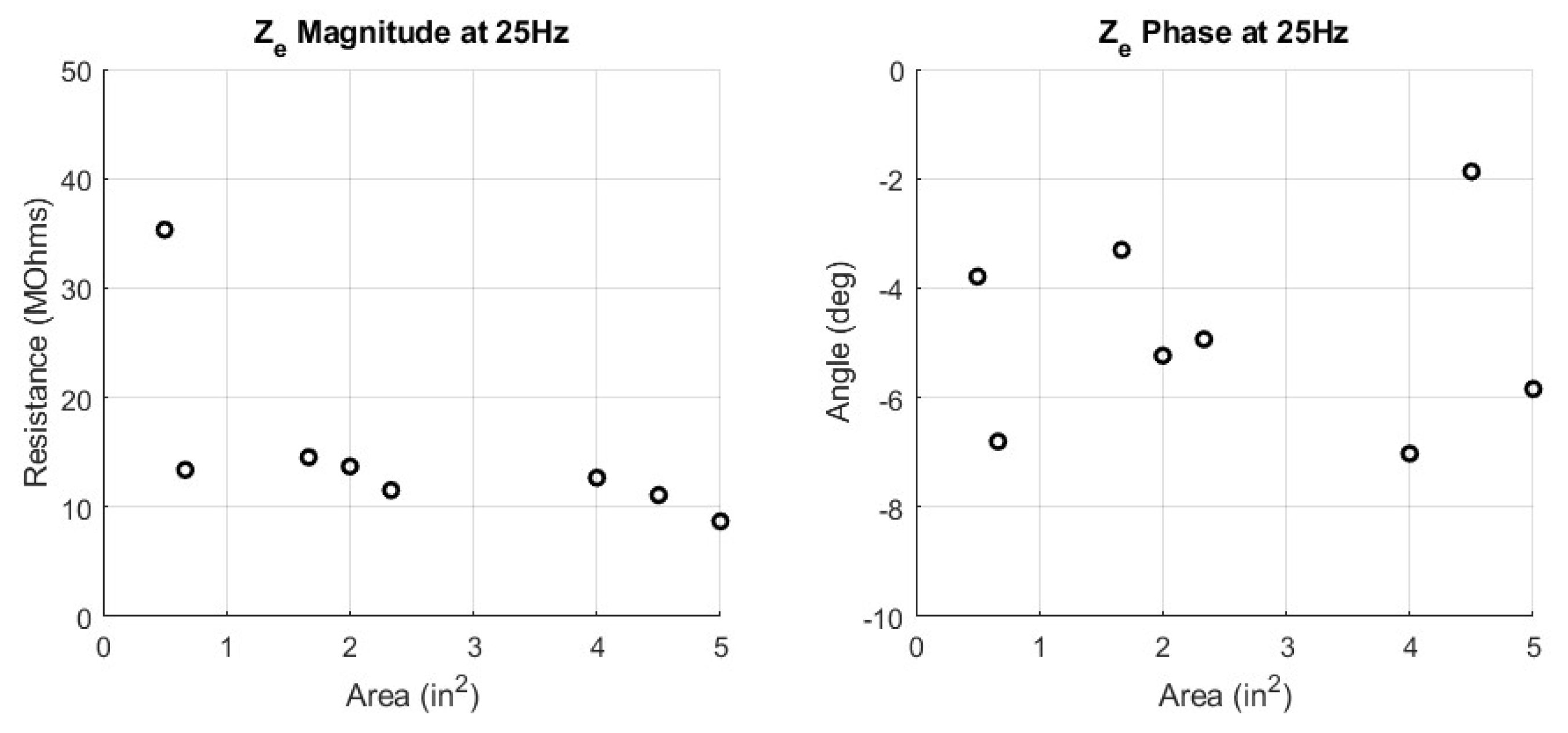
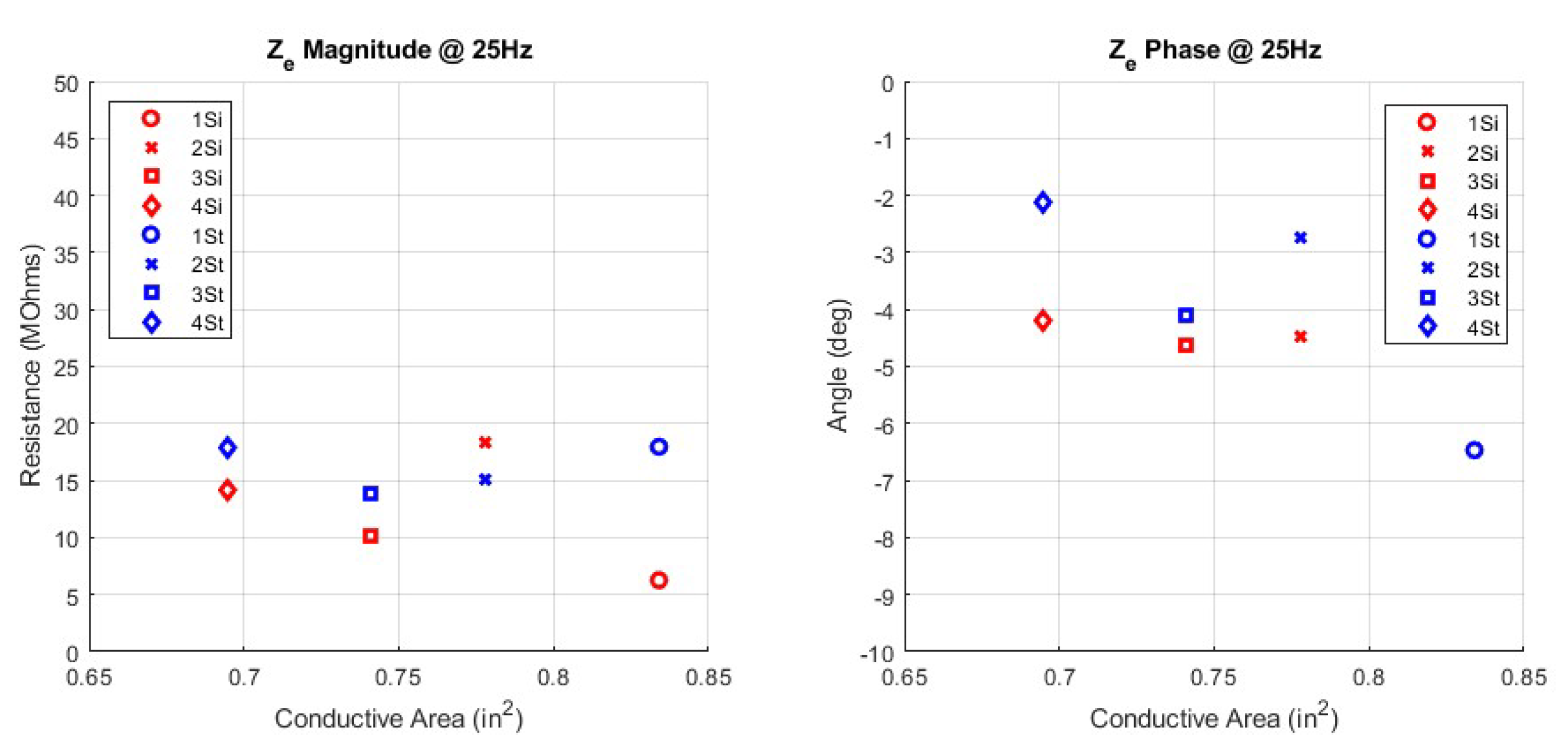
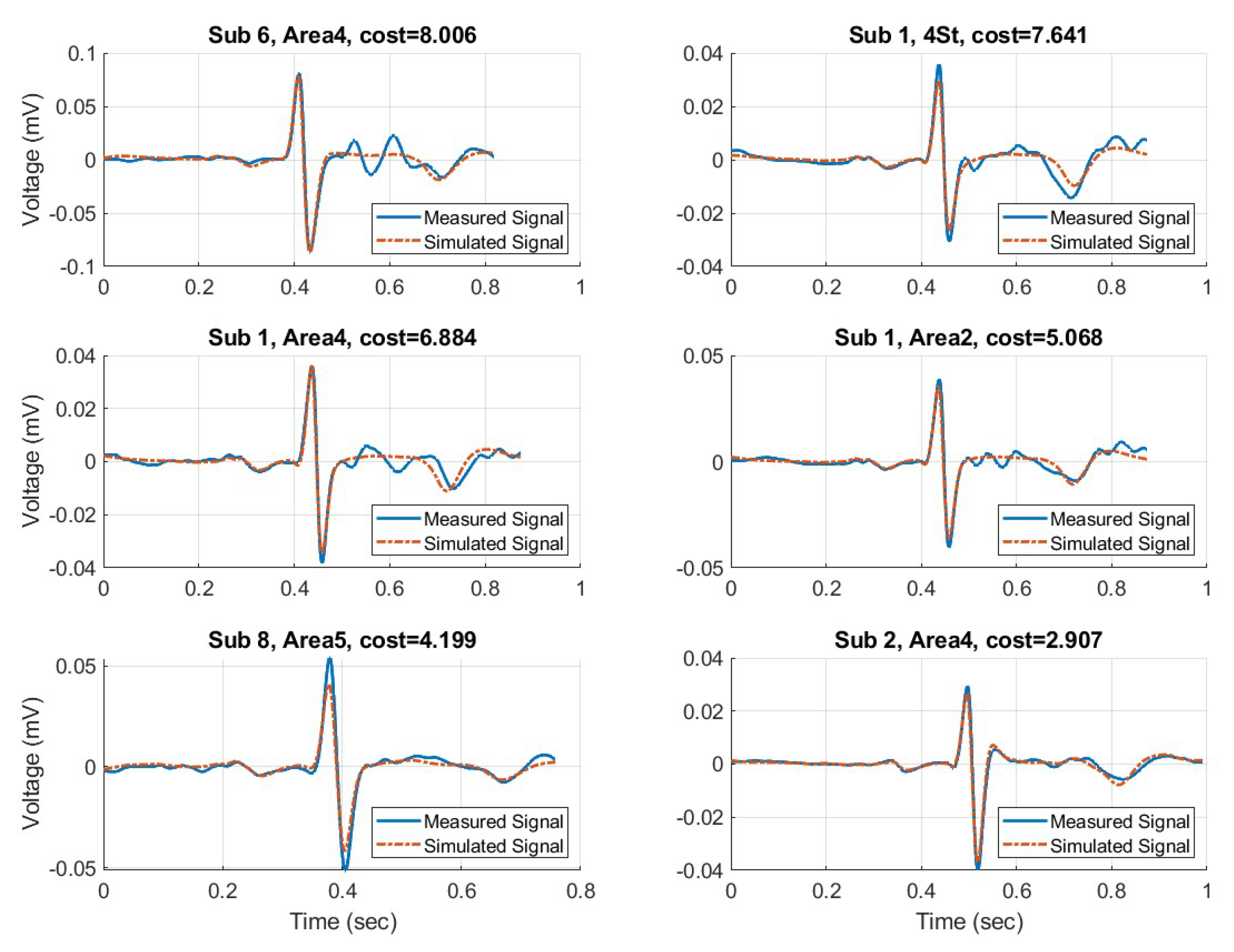
3. Results
4. Discussion
4.1. Area Type
4.2. Yarn Type
4.3. Pattern Type
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| BPF | Band Pass Filter |
| BSF | Band Stop Filter also known as Notch Filter |
| CDC | Center for Disease Control |
| CPE | Constant Phase Error |
| CVD | Cardiovascular disease |
| ECG | Electrocardiograph |
| FFT | Fast Fourier Transform |
| LOOCV | Leave-One-Out Cross-Validation |
| RC | Resistor Capacitor Pair |
| RMSE | Root Mean Squared Error |
| SNR | Signal to Noise Ratio |
| SSD | Sum of Squared Difference |
| TF | Transfer Function |
Appendix A
| Label | Cd (nF) | Rd (MOhm) | Rs (MOhm) | ∣Ze∣ (MOhm) | ∠Ze (deg) |
|---|---|---|---|---|---|
| Area1 | 2.6 | 10.20 | 34.69 | 35.33 | −3.77 |
| Area2 | 4.0 | 19.93 | 13.17 | 13.39 | −6.81 |
| Area3 | 7.6 | 16.67 | 14.48 | 14.55 | −3.32 |
| Area4 | 5.1 | 10.90 | 13.50 | 13.70 | −5.19 |
| Area5 | 6.4 | 14.38 | 11.42 | 11.53 | −4.96 |
| Area6 | 4.1 | 22.04 | 12.46 | 12.67 | −7.04 |
| Area7 | 17.9 | 8.80 | 11.06 | 11.09 | −1.87 |
| Area8 | 7.1 | 5.40 | 8.49 | 8.69 | −5.81 |
| 1Si | 9.0 | 6.15 | 6.14 | 6.26 | −6.47 |
| 2Si | 4.5 | 44.46 | 18.28 | 18.38 | −4.43 |
| 3Si | 7.7 | 5.98 | 10.03 | 10.18 | −4.61 |
| 4Si | 6.1 | 8.81 | 13.99 | 14.15 | −4.20 |
| 1St | 3.1 | 21.71 | 17.65 | 17.97 | −6.53 |
| 2St | 8.9 | 49.98 | 15.11 | 15.14 | −2.73 |
| 3St | 6.5 | 49.99 | 13.74 | 13.80 | −4.10 |
| 4St | 9.7 | 21.34 | 17.89 | 17.93 | −2.12 |
| Adh | 5800 | 0.0026 | 0.001 | 0.01 | −57.59 |
References
- De Giovanni, E. System-Level Design of Adaptive Wearable Sensors for Health and Wellness Monitoring; Technical report; EPFL: Lausanne, Switzerland, 2021. [Google Scholar]
- Kochanek, K.D.; Xu, J.Q.; Arias, E. Mortality in the United States, 2019; NCHS Data Brief, no 395; National Center for Health Statistics: Hyattsville, MD, USA, 2020; Available online: https://www.cdc.gov/nchs/products/databriefs/db395.htm (accessed on 24 December 2022).
- Xu, J.; Murphy, S.L.; Kochanek, K.D.; Arias, E. Deaths: Final Data for 2019. In National Vital Statistics Reports; no 8; National Center for Health Statistics: Hyattsville, MD, USA, 2021; Volume 70, Available online: https://www.cdc.gov/nchs/data/nvsr/nvsr70/nvsr70-08-508.pdf (accessed on 24 December 2022).
- Yokus, M.A.; Jur, J.S. Fabric-based wearable dry electrodes for body surface biopotential recording. IEEE Trans. Biomed. Eng. 2015, 63, 423–430. [Google Scholar] [CrossRef] [PubMed]
- Du, W.; Jose, W. Design of an ECG sensor circuitry for cardiovascular disease diagnosis. Int. J. f Biosens. Bioelectron. 2017, 2, 120–125. [Google Scholar]
- Cobarrubias, E. Design and Test Strategies for Biopotential Sensors in Smart Garments; North Carolina State University: Raleigh, NC, USA, 2020. [Google Scholar]
- Arquilla, K.; Webb, A.K.; Anderson, A.P. Woven electrocardiogram (ECG) electrodes for health monitoring in operational environments. In Proceedings of the 2020 42nd Annual International Conference of the IEEE Engineering in Medicine & Biology Society (EMBC), Montreal, QC, Canada, 20–24 July 2020; pp. 4498–4501. [Google Scholar]
- Arquilla, K. Monitoring Behavioral Health in Extreme Operational Environments. Ph.D. Thesis, University of Colorado at Boulder, Boulder, CO, USA, 2021. [Google Scholar]
- Webster, J.G. Medical Instrumentation: Application and Design; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Arquilla, K.; Anderson, A. Garment-integrated biosignal sensors for astronaut health during long-duration space missions. In Proceedings of the 2021 CHI Workshop on Human-Computer Interaction for Space Exploration (SpaceCHI), Virtual Conference, Yokohama, Japan, 8–13 May 2021; Volume 21. [Google Scholar]
- Arquilla, K.; Webb, A.K.; Anderson, A.P. Utility of the Full ECG Waveform for Stress Classification. Sensors 2022, 22, 7034. [Google Scholar] [CrossRef] [PubMed]
- Goyal, K.; Borkholder, D.A.; Day, S.W. Dependence of skin−electrode Contact Impedance on Material and Skin Hydration. Sensors 2022, 22, 8510. [Google Scholar] [CrossRef] [PubMed]
- Vojtech, L. Feasibility of rfid signal denoising using neural network. Adv. Electr. Electron. Eng. 2010, 8, 111–113. [Google Scholar]
- Heikenfeld, J.; Jajack, A.; Rogers, J.; Gutruf, P.; Tian, L.; Pan, T.; Li, R.; Khine, M.; Kim, J.; Wang, J. Wearable sensors: Modalities, challenges, and prospects. Lab Chip 2018, 18, 217–248. [Google Scholar] [CrossRef]
- Arquilla, K.; Webb, A.K.; Anderson, A.P. Textile electrocardiogram (ECG) electrodes for wearable health monitoring. Sensors 2020, 20, 1013. [Google Scholar] [CrossRef]
- Searle, A.; Kirkup, L. A direct comparison of wet, dry and insulating bioelectric recording electrodes. Physiol. Meas. 2000, 21, 271. [Google Scholar] [CrossRef]
- Yoo, J.; Yoo, H.J. Fabric circuit board-based dry electrode and its characteristics for long−term physiological signal recording. In Proceedings of the 2011 Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Boston, MA, USA, 30 August–3 September 2011; pp. 2497–2500. [Google Scholar]
- An, X.; Stylios, G.K. A hybrid textile electrode for electrocardiogram (ECG) measurement and motion tracking. Materials 2018, 11, 1887. [Google Scholar] [CrossRef]
- Arquilla, K.; Leary, S.; Webb, A.K.; Anderson, A.P. Wearable 3-lead electrocardiogram placement model for fleet sizing of medical devices. Aerosp. Med. Hum. Perform. 2020, 91, 868–875. [Google Scholar] [CrossRef]
- Yang, L.; Liu, Q.; Zhang, Z.; Gan, L.; Zhang, Y.; Wu, J. Materials for Dry Electrodes for the Electroencephalography: Advances, Challenges, Perspectives. Adv. Mater. Technol. 2022, 7, 2100612. [Google Scholar] [CrossRef]
- Arquilla, K.; Devendorf, L.; Webb, A.K.; Anderson, A.P. Detection of the complete ECG waveform with woven textile electrodes. Biosensors 2021, 11, 331. [Google Scholar] [CrossRef]
- Bystricky, T.; Moravcova, D.; Kaspar, P.; Soukup, R.; Hamacek, A. A comparison of embroidered and woven textile electrodes for continuous measurement of ECG. In Proceedings of the 2016 39th International Spring Seminar on Electronics Technology (ISSE), Pilsen, Czech Republic, 18–22 May 2016; pp. 7–11. [Google Scholar]
- Taji, B.; Shirmohammadi, S.; Groza, V.; Batkin, I. Impact of skin–electrode interface on electrocardiogram measurements using conductive textile electrodes. IEEE Trans. Instrum. Meas. 2013, 63, 1412–1422. [Google Scholar] [CrossRef]
- Assambo, C.; Baba, A.; Dozio, R.; Burke, M. Determination of the parameters of the skin−electrode impedance model for ECG measurement. In Proceedings of the 6th WSEAS International Conference on Electronics, Hardware, Wireless and Optical Communications, Corfu Island, Greece, 16–19 February 2007; pp. 90–95. [Google Scholar]
- MP Systems Hardware Guide; BIOPAC Systems, Inc.: Goleta, CA, USA, 2015. Available online: www.biopac.com (accessed on 1 February 2022).
- Geddes, L.; Valentinuzzi, M. Temporal changes in electrode impedance while recording the electrocardiogram with “dry” electrodes. Ann. Biomed. Eng. 1973, 1, 356–367. [Google Scholar] [CrossRef]
- Li, G.; Wang, S.; Duan, Y.Y. Towards gel-free electrodes: A systematic study of electrode-skin impedance. Sens. Actuators B Chem. 2017, 241, 1244–1255. [Google Scholar] [CrossRef]
- Gan, Y.; Rahajandraibe, W.; Vauche, R.; Ravelo, B.; Lorriere, N.; Bouchakour, R. A new method to reduce motion artifact in electrocardiogram based on an innovative skin−electrode impedance model. Biomed. Signal Process. Control 2022, 76, 103640. [Google Scholar] [CrossRef]
- Li, G.; Wang, S.; Duan, Y.Y. Towards conductive-gel-free electrodes: Understanding the wet electrode, semi-dry electrode and dry electrode-skin interface impedance using electrochemical impedance spectroscopy fitting. Sens. Actuators B Chem. 2018, 277, 250–260. [Google Scholar] [CrossRef]
- Schauss, G. Wearable Textile Electrocardiogram Sport Bra for Real Time Health Monitoring. Ph.D. Thesis, University of Colorado at Boulder, Boulder, CO, USA, 2022. [Google Scholar]
- Song, J.; Zhang, Y.; Yang, Y.; Liu, H.; Zhou, T.; Zhang, K.; Li, F.; Xu, Z.; Liu, Q.; Li, J. Electrochemical modeling and evaluation for textile electrodes to skin. Biomed. Eng. Online 2020, 19, 1–27. [Google Scholar] [CrossRef]
- Castrillón, R.; Pérez, J.J.; Andrade-Caicedo, H. Electrical performance of PEDOT: PSS-based textile electrodes for wearable ECG monitoring: A comparative study. Biomed. Eng. Online 2018, 17, 1–23. [Google Scholar] [CrossRef]
- Löfhede, J.; Seoane, F.; Thordstein, M. Textile electrodes for EEG recording—A pilot study. Sensors 2012, 12, 16907–16919. [Google Scholar] [CrossRef]
- Li, G.L.; Wu, J.T.; Xia, Y.H.; He, Q.G.; Jin, H.G. Review of semi-dry electrodes for EEG recording. J. Neural Eng. 2020, 17, 051004. [Google Scholar] [CrossRef] [PubMed]
- Li, G.; Wang, S.; Li, M.; Duan, Y.Y. Towards real-life EEG applications: Novel superporous hydrogel-based semi-dry EEG electrodes enabling automatically ‘charge–discharge’electrolyte. J. Neural Eng. 2021, 18, 046016. [Google Scholar] [CrossRef] [PubMed]
- Poh, M.Z.; Swenson, N.C.; Picard, R.W. A wearable sensor for unobtrusive, long−term assessment of electrodermal activity. IEEE Trans. Biomed. Eng. 2010, 57, 1243–1252. [Google Scholar] [PubMed]





| ID | Label | Surface Area (cm) | Yarn Type | Pattern |
|---|---|---|---|---|
| 1 | Area1 | 1.27 × 2.54 | Steel Spun | 1/15 Sateen |
| 2 | Area2 | 1.27 × 3.38 | Steel Spun | 1/15 Sateen |
| 3 | Area3 | 2.54 × 4.22 | Steel Spun | 1/15 Sateen |
| 4 | Area4 | 2.54 × 5.08 | Steel Spun | 1/15 Sateen |
| 5 | Area5 | 2.54 × 5.92 | Steel Spun | 1/15 Sateen |
| 6 | Area6 | 3.81 × 6.76 | Steel Spun | 1/15 Sateen |
| 7 | Area7 | 3.81 × 7.62 | Steel Spun | 1/15 Sateen |
| 8 | Area8 | 3.81 × 8.46 | Steel Spun | 1/15 Sateen |
| 9 | 1Si | 1.68 × 3.38 | Silver Nylon | 1/15 Sateen |
| 10 | 2Si | 1.68 × 3.38 | Silver Nylon | Broken Twill |
| 11 | 3Si | 1.68 × 3.38 | Silver Nylon | Twill |
| 12 | 4Si | 1.68 × 3.38 | Silver Nylon | Birds Eye |
| 13 | 1St | 1.68 × 3.38 | Steel Spun | 1/15 Sateen |
| 14 | 2St | 1.68 × 3.38 | Steel Spun | Broken Twill |
| 15 | 3St | 1.68 × 3.38 | Steel Spun | Twill |
| 16 | 4St | 1.68 × 3.38 | Steel Spun | Birds Eye |
| 17 | Adh | * 19.61 cm2 | * N/A | * N/A |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brehm, P.J.; Anderson, A.P. Modeling the Design Characteristics of Woven Textile Electrodes for long−Term ECG Monitoring. Sensors 2023, 23, 598. https://doi.org/10.3390/s23020598
Brehm PJ, Anderson AP. Modeling the Design Characteristics of Woven Textile Electrodes for long−Term ECG Monitoring. Sensors. 2023; 23(2):598. https://doi.org/10.3390/s23020598
Chicago/Turabian StyleBrehm, Peter J., and Allison P. Anderson. 2023. "Modeling the Design Characteristics of Woven Textile Electrodes for long−Term ECG Monitoring" Sensors 23, no. 2: 598. https://doi.org/10.3390/s23020598
APA StyleBrehm, P. J., & Anderson, A. P. (2023). Modeling the Design Characteristics of Woven Textile Electrodes for long−Term ECG Monitoring. Sensors, 23(2), 598. https://doi.org/10.3390/s23020598