Robust Localization for Underground Mining Vehicles: An Application in a Room and Pillar Mine
Abstract
:1. Introduction
- The combined use of 2D and 3D LIDARs and simultaneous localization and mapping (SLAM) algorithms to produce consistent 2D grid maps of underground tunnels that are only approximately 2D, which can be used in industrial applications, such as the one of LHD machines operating autonomously in the production tunnels of room and pillar mines.
- A heuristic method to produce incremental map updates with minimal human intervention, which is suited to be used in real mining applications where blasting is continuously used to expand the operation area of the mine, without interrupting the autonomous operation of the LHD vehicles.
- An industrial validation of the proposed 2D map building and localization systems, both in a real room and pillar mining environment, where the flat world assumption is partially broken, and using real mining equipment (an LHD) during autonomous operation, including muck pile loading, hauling, and dumping the loaded material.
2. Background and Literature Review
2.1. Mapping and Localization
2.2. Mapping and Localization in Room and Pillar Mines
3. Materials and Methods
3.1. Methodology
3.2. Three-Dimensional Map Building
3.3. Three-Dimensional-to-Two-Dimensional Conversion
3.4. To-Dimensional Localization
Localization While Loading
3.5. Incremental Map Update
| Algorithm 1: Map-merging algorithm |
 |
4. Experimental Results: LHD Autonomous Operation in a Room and Pillar Salt Mine
4.1. Vehicle and Sensors
4.2. Experimental Conditions
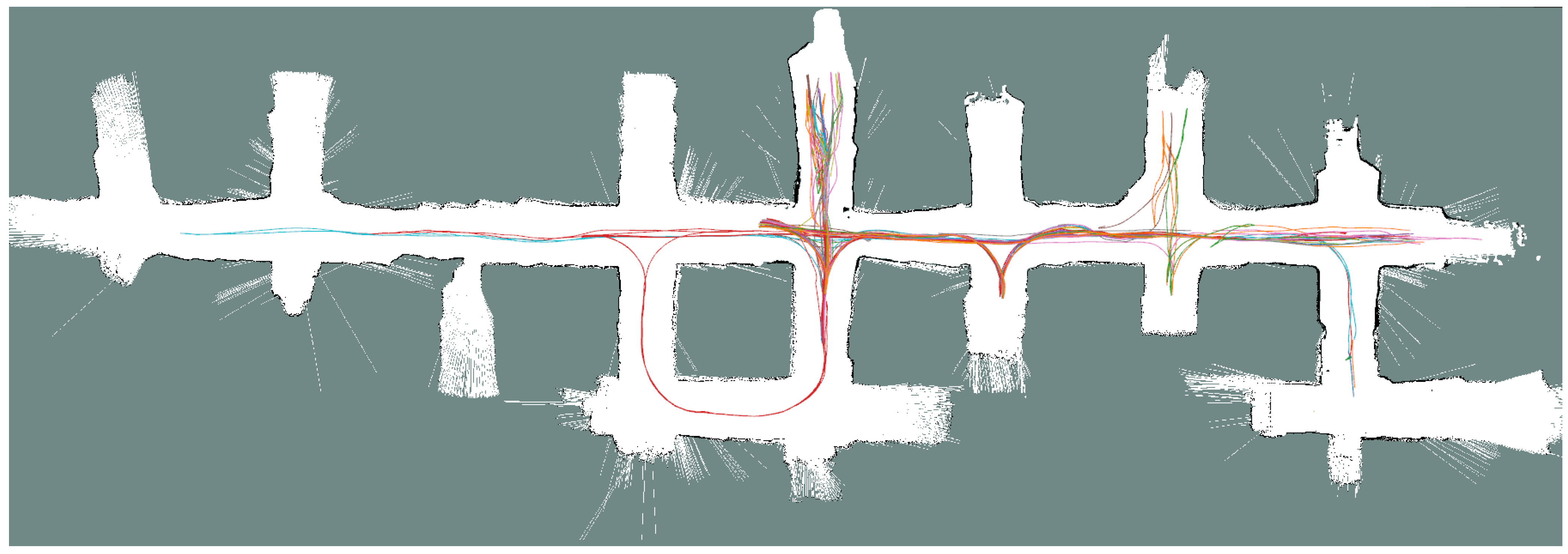
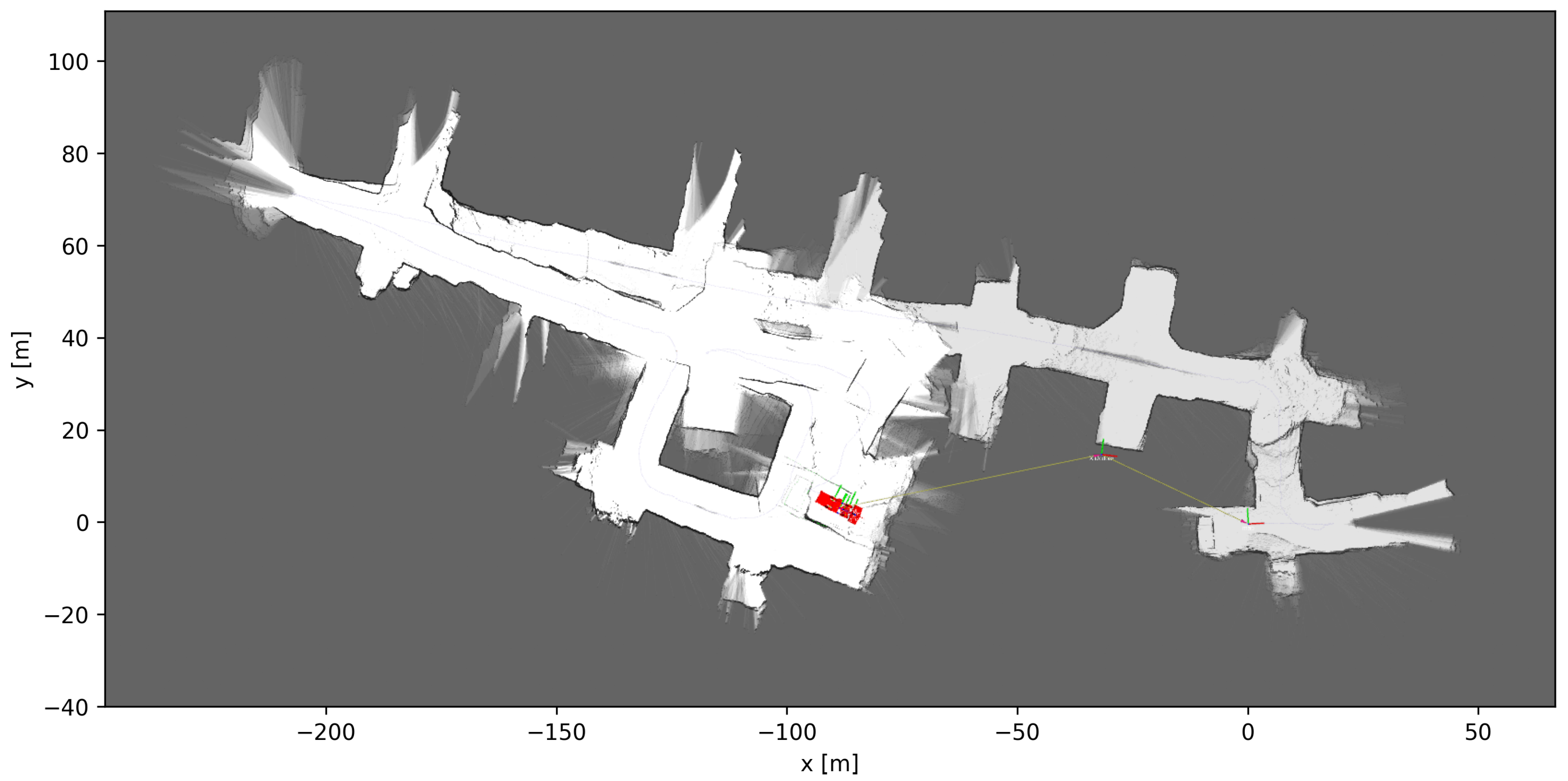
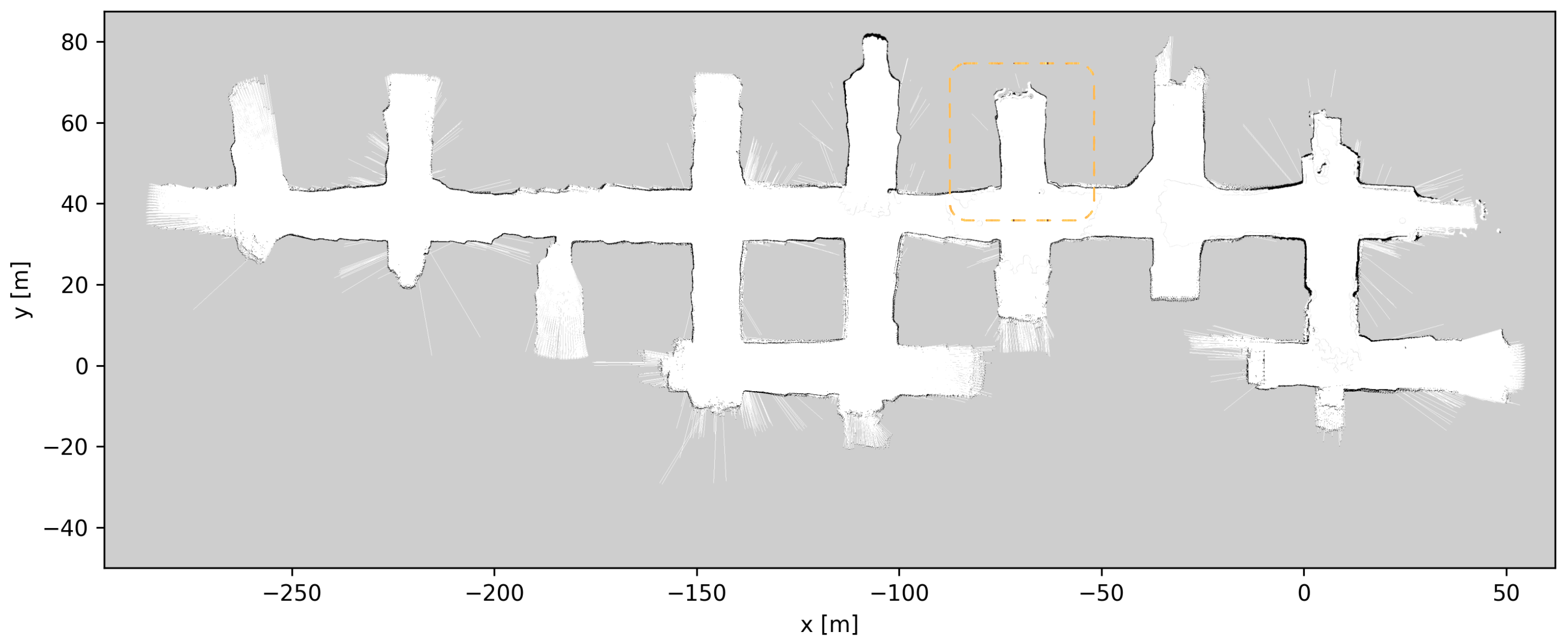
4.3. Mapping
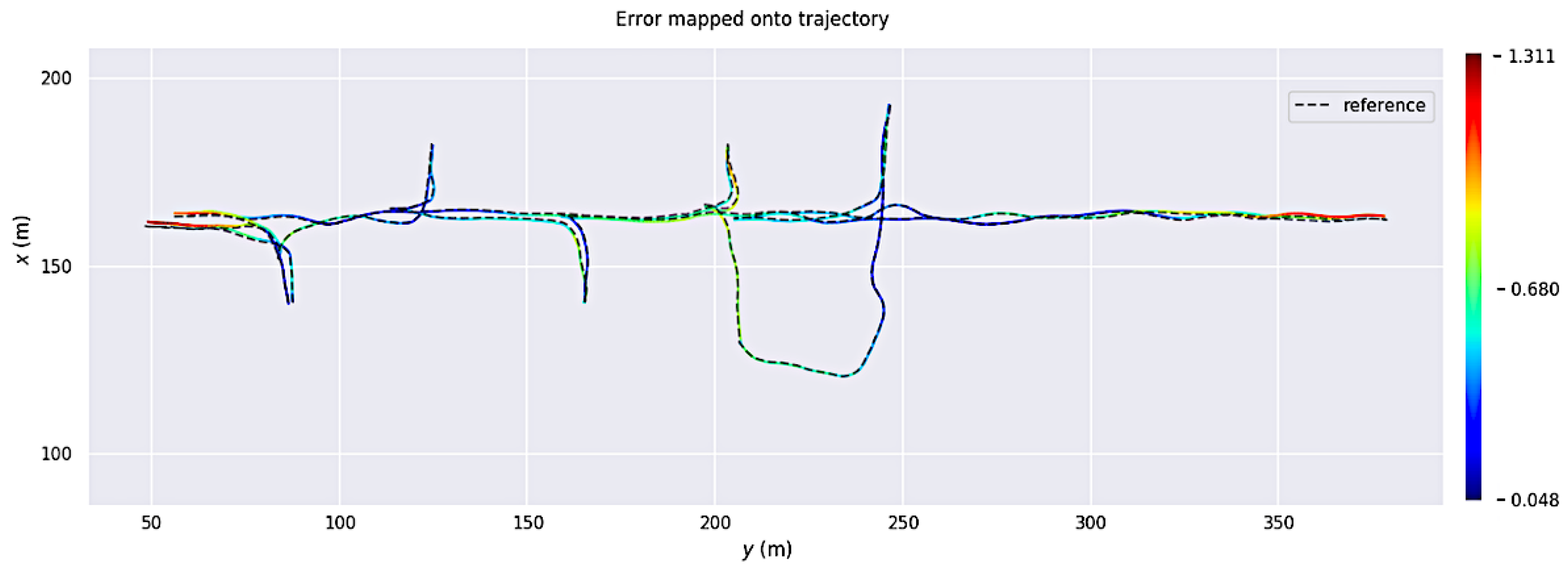
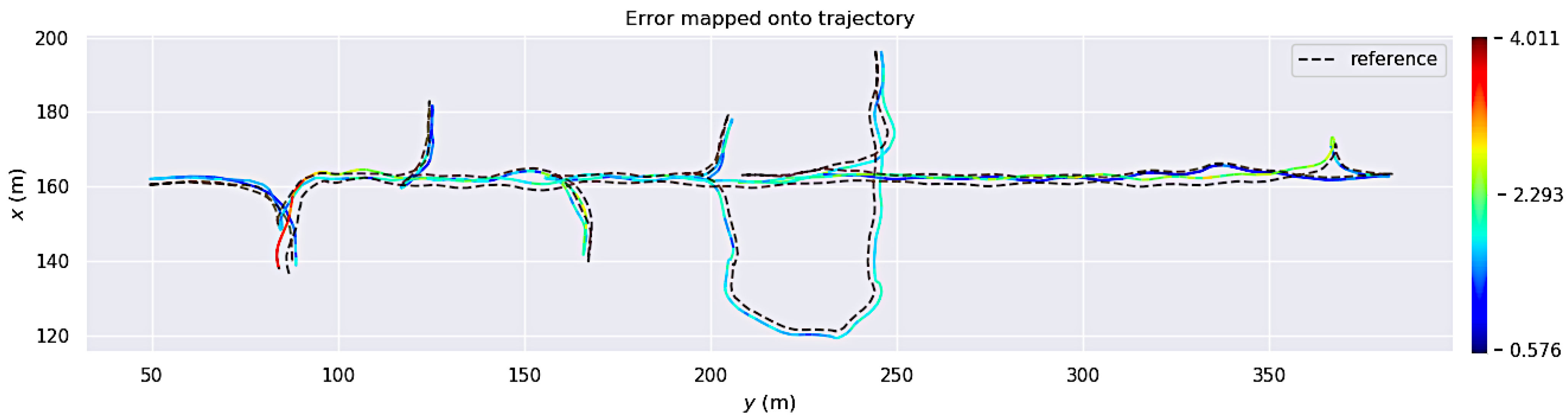
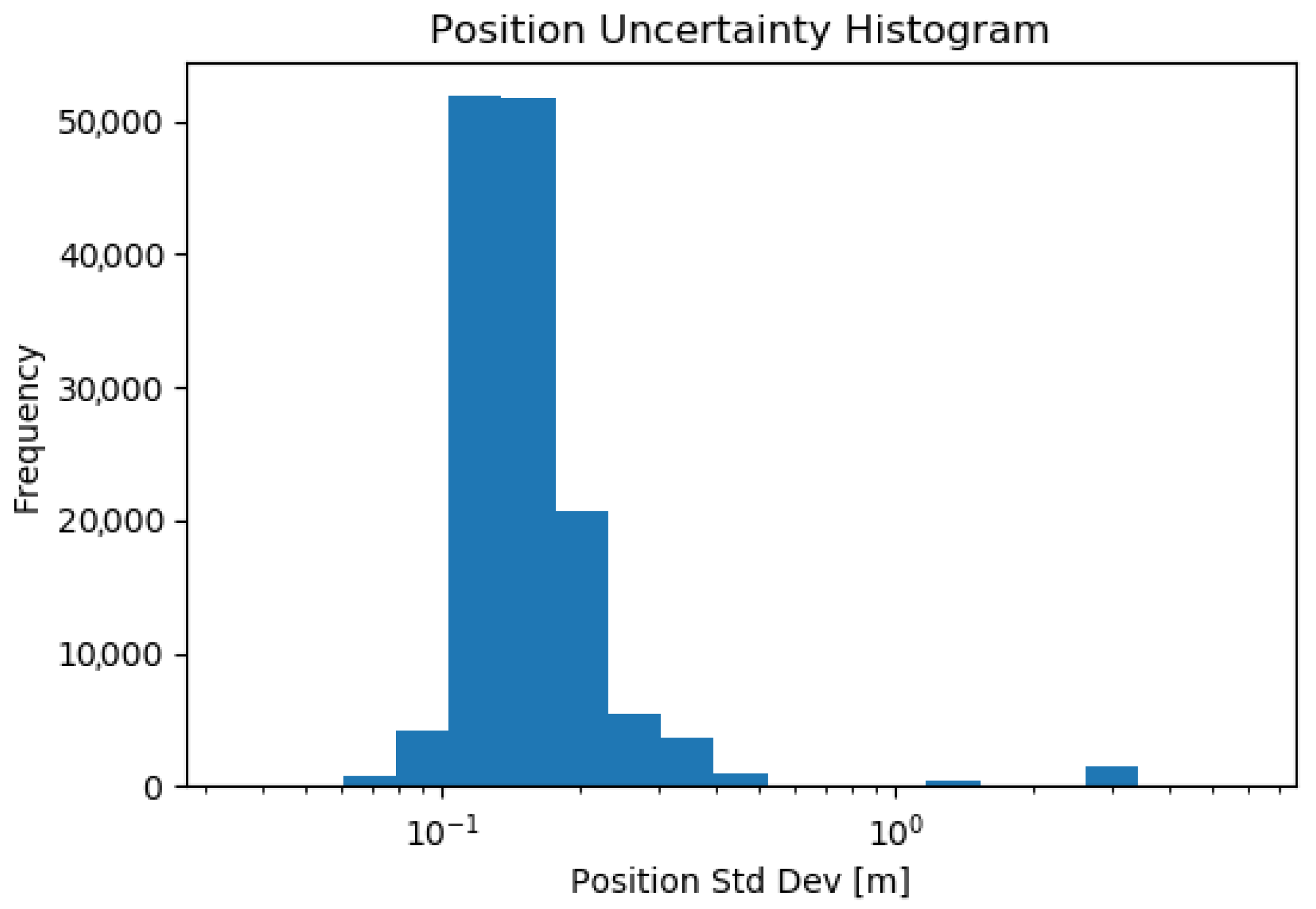
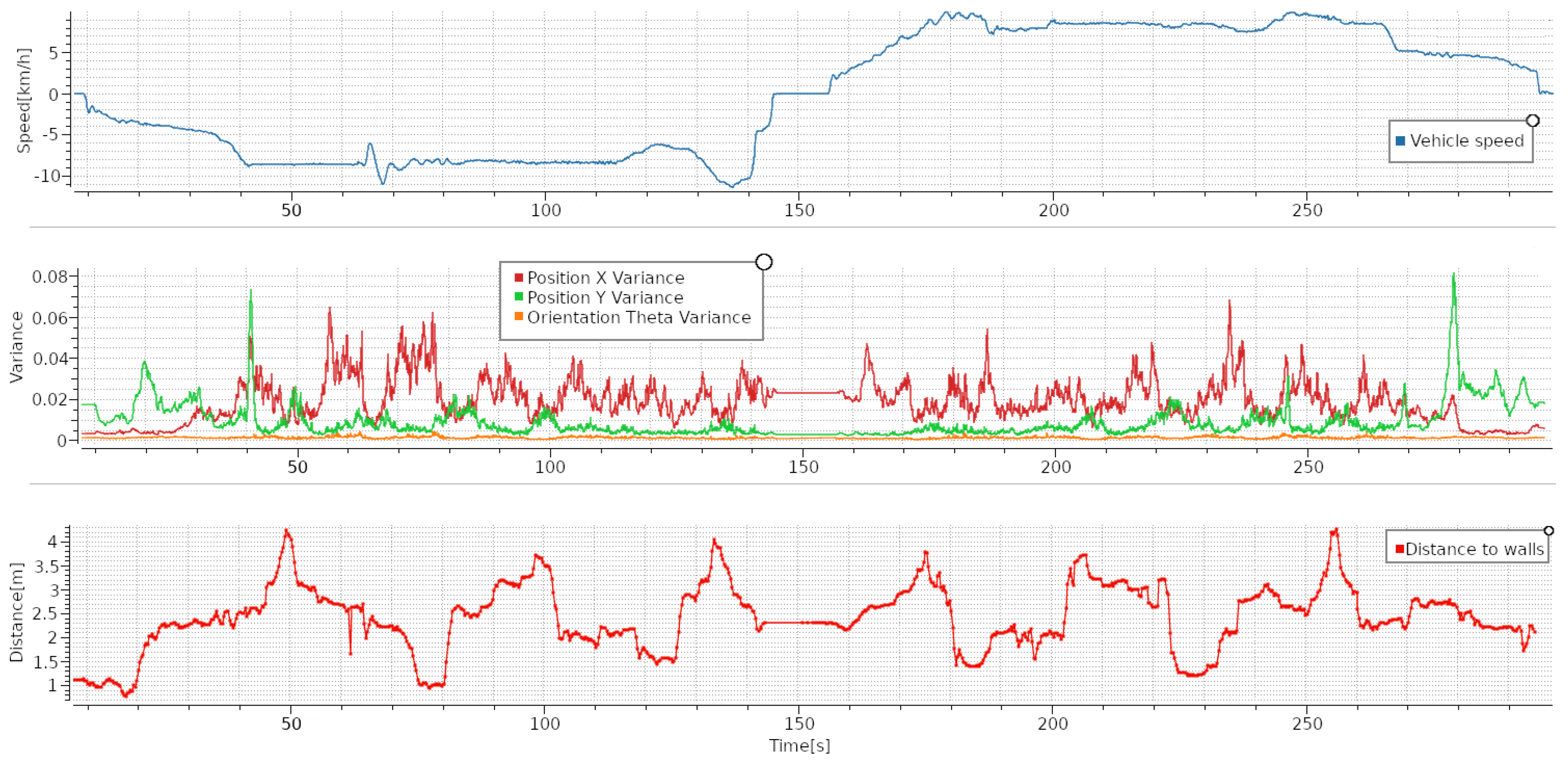
4.4. Self-Localization
4.5. Map Updates
5. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Salvador, C.; Mascaró, M.; Ruiz-del Solar, J. Automation of unit and auxiliary operations in block/panel caving: Challenges and opportunities. In Proceedings of the MassMin2020—The 8th International Conference on Mass Mining, Santiago, Chile, 9–11 December 2020. [Google Scholar]
- GHH. Loaders. Available online: https://ghhrocks.com/loaders/ (accessed on 13 April 2022).
- Kaupo Kikkas. Load Haul Dump Image. 2016. This File Is Licensed under the Creative Commons Attribution-Share Alike 4.0 International License. Available online: https://commons.wikimedia.org/wiki/File:VKG_Ojamaa_kaevandus.jpg (accessed on 29 August 2023).
- ΠAO «Γaйский ΓOK». Load Haul Dump Image. 2017. This File Is Licensed under the Creative Commons Attribution-Share Alike 4.0 International License. Available online: https://commons.wikimedia.org/wiki/File:Load_haul_dump_machine.jpg (accessed on 29 August 2023).
- Sandvik to Automate New LHD Fleet at Codelco’s El Teniente Copper Mine. 2021. Available online: https://im-mining.com/2021/02/16/sandvik-to-automate-new-lhd-fleet-at-codelcos-el-teniente-copper-mine/ (accessed on 29 August 2023).
- Larsson, J.; Appelgren, J.; Marshall, J. Next generation system for unmanned LHD operation in underground mines. In Proceedings of the Annual Meeting and Exhibition of the Society for Mining, Metallurgy & Exploration (SME), Phoenix, AZ, USA, 28 February–3 March 2010. [Google Scholar]
- Roberts, J.; Duff, E.; Corke, P.; Sikka, P.; Winstanley, G.; Cunningham, J. Autonomous control of underground mining vehicles using reactive navigation. In Proceedings of the 2000 ICRA. Millennium Conference. IEEE International Conference on Robotics and Automation. Symposia Proceedings (Cat. No.00CH37065), San Francisco, CA, USA, 24–28 April 2000; Volume 4, pp. 3790–3795. [Google Scholar] [CrossRef]
- Tampier, C.; Mascaró, M.; Ruiz-del Solar, J. Autonomous Loading System for Load-Haul-Dump (LHD) Machines Used in Underground Mining. Appl. Sci. 2021, 11, 8718. [Google Scholar] [CrossRef]
- Espinoza, J.P.; Mascaró, M.; Morales, N.; Solar, J.R.D. Improving productivity in block/panel caving through dynamic confinement of semi-autonomous load-haul-dump machines. Int. J. Min. Reclam. Environ. 2022, 36, 552–573. [Google Scholar] [CrossRef]
- Thrun, S.; Burgard, W.; Fox, D. Probabilistic Robotics; MIT Press: Cambridge, MA, USA, 2005; Volume 1. [Google Scholar]
- Williams, S. Efficient Solutions to Autonomous Mapping and Navigation Problems. Ph.D. Thesis, The University of Sydney, Camperdown, Australia, 2001. [Google Scholar]
- Montemerlo, M.; Thrun, S.; Koller, D.; Wegbreit, B. FastSLAM 2.0: An Improved Particle Filtering Algorithm for Simultaneous Localization and Mapping That Provably Converges. In Proceedings of the 18th International Joint Conference of Artificial Intelligence, IJCAI’03, Acapulco, Mexico, 9–15 August 2003; pp. 1151–1156. [Google Scholar]
- Kummerle, R.; Grisetti, G.; Strasdat, H.; Konolige, K.; Burgard, W. G2o: A general framework for graph optimization. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; IEEE: Shanghai, China, 2011; pp. 3607–3613. [Google Scholar] [CrossRef]
- Kaess, M.; Johannsson, H.; Roberts, R.; Ila, V.; Leonard, J.J.; Dellaert, F. iSAM2: Incremental smoothing and mapping using the Bayes tree. Int. J. Robot. Res. 2012, 31, 216–235. [Google Scholar] [CrossRef]
- Grisetti, G.; Stachniss, C.; Burgard, W. Improved Techniques for Grid Mapping with Rao-Blackwellized Particle Filters. IEEE Trans. Robot. 2007, 23, 34–46. [Google Scholar] [CrossRef]
- Hess, W.; Kohler, D.; Rapp, H.; Andor, D. Real-time loop closure in 2D LIDAR SLAM. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 1271–1278. [Google Scholar] [CrossRef]
- Geiger, A.; Lenz, P.; Stiller, C.; Urtasun, R. Vision meets Robotics: The KITTI Dataset. Int. J. Robot. Res. (IJRR) 2013, 32, 1231–1237. [Google Scholar] [CrossRef]
- Zhang, J.; Singh, S. LOAM: Lidar Odometry and Mapping in Real-time. In Proceedings of the Robotics: Science and Systems, Berkeley, CA, USA, 12–16 July 2014. [Google Scholar]
- Dellenbach, P.; Deschaud, J.E.; Jacquet, B.; Goulette, F. CT-ICP: Real-time Elastic LiDAR Odometry with Loop Closure. arXiv 2021, arXiv:cs.RO/2109.12979. [Google Scholar]
- Shan, T.; Englot, B. LeGO-LOAM: Lightweight and Ground-Optimized Lidar Odometry and Mapping on Variable Terrain. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 4758–4765. [Google Scholar] [CrossRef]
- Shan, T.; Englot, B.; Meyers, D.; Wang, W.; Ratti, C.; Rus, D. LIO-SAM: Tightly-coupled Lidar Inertial Odometry via Smoothing and Mapping. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 24–25 October 2020; pp. 5135–5142. [Google Scholar] [CrossRef]
- Orekhov, V.; Chung, T. The DARPA Subterranean Challenge: A Synopsis of the Circuits Stage. Field Robot. 2022, 2, 735–747. [Google Scholar] [CrossRef]
- Ebadi, K.; Chang, Y.; Palieri, M.; Stephens, A.; Hatteland, A.; Heiden, E.; Thakur, A.; Funabiki, N.; Morrell, B.; Wood, S.; et al. LAMP: Large-Scale Autonomous Mapping and Positioning for Exploration of Perceptually-Degraded Subterranean Environments. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; pp. 80–86. [Google Scholar] [CrossRef]
- Chang, Y.; Ebadi, K.; Denniston, C.; Ginting, M.; Rosinol, A.; Reinke, A.; Palieri, M.; Shi, J.; Chatterjee, A.; Morrell, B.; et al. LAMP 2.0: A Robust Multi-Robot SLAM System for Operation in Challenging Large-Scale Underground Environments. IEEE Robot. Autom. Lett. 2022, 7, 9175–9182. [Google Scholar] [CrossRef]
- Palieri, M.; Morrell, B.; Thakur, A.; Ebadi, K.; Nash, J.; Chatterjee, A.; Kanellakis, C.; Carlone, L.; Guaragnella, C.; Agha-mohammadi, A.A. LOCUS: A Multi-Sensor Lidar-Centric Solution for High-Precision Odometry and 3D Mapping in Real-Time. IEEE Robot. Autom. Lett. 2021, 6, 421–428. [Google Scholar] [CrossRef]
- Reinke, A.; Palieri, M.; Morrell, B.; Chang, Y.; Ebadi, K.; Carlone, L.; Agha-Mohammadi, A.A. LOCUS 2.0: Robust and Computationally Efficient Lidar Odometry for Real-Time 3D Mapping. IEEE Robot. Autom. Lett. 2022, 7, 9043–9050. [Google Scholar] [CrossRef]
- Koval, A.; Kanellakis, C.; Nikolakopoulos, G. Evaluation of Lidar-based 3D SLAM algorithms in SubT environment. IFAC-PapersOnLine 2022, 55, 126–131. [Google Scholar] [CrossRef]
- Nelson, E. B(erkeley) L(ocalization) A(nd) M(apping)! Available online: https://github.com/erik-nelson/blam (accessed on 21 September 2023).
- Nava, Y.; Jensfelt, P. Visual-LiDAR SLAM with Loop Closure. Masters Thesis, KTH Royal Institute of Technology, Stockholm, Sweden, 2018. [Google Scholar]
- Tong Qin, S.C. Advanced Implementation of Loam. Available online: https://github.com/HKUST-Aerial-Robotics/A-LOAM (accessed on 29 August 2023).
- Wang, H.; Wang, C.; Xie, L. Intensity Scan Context: Coding Intensity and Geometry Relations for Loop Closure Detection. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; pp. 2095–2101. [Google Scholar] [CrossRef]
- Ye, H.; Chen, Y.; Liu, M. Tightly Coupled 3D Lidar Inertial Odometry and Mapping. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 3144–3150. [Google Scholar] [CrossRef]
- Xu, W.; Zhang, F. FAST-LIO: A Fast, Robust LiDAR-Inertial Odometry Package by Tightly-Coupled Iterated Kalman Filter. IEEE Robot. Autom. Lett. 2021, 6, 3317–3324. [Google Scholar] [CrossRef]
- Wang, H.; Wang, C.; Chen, C.L.; Xie, L. F-LOAM: Fast LiDAR Odometry and Mapping. In Proceedings of the 2021 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Prague, Czech Republic, 27–30 September 2021; pp. 4390–4396. [Google Scholar] [CrossRef]
- Koide, K.; Miura, J.; Menegatti, E. A portable three-dimensional LIDAR-based system for long-term and wide-area people behavior measurement. Int. J. Adv. Robot. Syst. 2019, 16, 1729881419841532. [Google Scholar] [CrossRef]
- Surace, S.C.; Kutschireiter, A.; Pfister, J.P. How to Avoid the Curse of Dimensionality: Scalability of Particle Filters with and without Importance Weights. SIAM Rev. 2019, 61, 79–91. [Google Scholar] [CrossRef]
- Fox, D.; Burgard, W.; Dellaert, F.; Thrun, S. Monte Carlo Localization: Efficient Position Estimation for Mobile Robots. In Proceedings of the National Conference on Artificial Intelligence, Orlando, FL, USA, 18–22 July 1999. [Google Scholar]
- Biber, P.; Straßer, W. The Normal Distributions Transform: A New Approach to Laser Scan Matching. In Proceedings of the 2003 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS 2003) (Cat. No. 03CH37453), Las Vegas, NV, USA, 27–31 October 2003; Volume 3, pp. 2743–2748. [Google Scholar] [CrossRef]
- Caballero, F.; Merino, L. DLL: Direct LIDAR Localization. A map-based localization approach for aerial robots. In Proceedings of the 2021 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Prague, Czech Republic, 27–30 September 2021; pp. 5491–5498. [Google Scholar] [CrossRef]
- Mäkelä, H. Overview of LHD navigation without artificial beacons. Robot. Auton. Syst. 2001, 36, 21–35. [Google Scholar] [CrossRef]
- Mascaró, M.; Parra-Tsunekawa, I.; Tampier, C.; Ruiz-del Solar, J. Topological navigation and localization in tunnels—Application to autonomous load-haul-dump vehicles operating in underground mines. Appl. Sci. 2021, 11, 6547. [Google Scholar] [CrossRef]
- Dragt, B.J.; Craig, I.K.; Camisani-Calzolari, F.R. Navigation of Autonomous Underground Mine Vehicles. Available online: https://folk.ntnu.no/skoge/prost/proceedings/afcon03/Papers/068.pdf (accessed on 29 August 2023).
- Nielsen, K.; Hendeby, G. Multi-Hypothesis SLAM for Non-Static Environments with Reoccurring Landmarks. IEEE Trans. Intell. Veh. 2023, 8, 3191–3203. [Google Scholar] [CrossRef]
- Scheding, S.; Dissanayake, G.; Nebot, E.; Durrant-Whyte, H. An experiment in autonomous navigation of an underground mining vehicle. IEEE Trans. Robot. Autom. 1999, 15, 85–95. [Google Scholar] [CrossRef]
- Bakambu, J.; Polotski, V. Autonomous system for navigation and surveying in underground mines. J. Field Robot. 2007, 24, 829–847. [Google Scholar] [CrossRef]
- Stefaniak, P.; Jachnik, B.; Koperska, W.; Skoczylas, A. Localization of LHD Machines in Underground Conditions Using IMU Sensors and DTW Algorithm. Appl. Sci. 2021, 11, 6751. [Google Scholar] [CrossRef]
- Nielsen, K. Localization for Autonomous Vehicles in Underground Mines. Ph.D. Thesis, Linköping University Electronic Press, Linköping, Sweden, 2023. [Google Scholar] [CrossRef]
- Li, M.G.; Zhu, H.; You, S.Z.; Tang, C.Q. UWB-Based Localization System Aided with Inertial Sensor for Underground Coal Mine Applications. IEEE Sens. J. 2020, 20, 6652–6669. [Google Scholar] [CrossRef]
- Ren, Z.; Wang, L. Accurate Real-Time Localization Estimation in Underground Mine Environments Based on a Distance-Weight Map (DWM). Sensors 2022, 22, 1463. [Google Scholar] [CrossRef] [PubMed]
- Tabib, W.; Michael, N. Simultaneous Localization and Mapping of Subterranean Voids with Gaussian Mixture Models. In Field and Service Robotics; Ishigami, G., Yoshida, K., Eds.; Springer: Singapore, 2021; pp. 173–187. [Google Scholar]
- Li, Y.; Zhun, F.; Guijie, Z.; Wenji, L.; Chong, L.; Yupeng, W.; Honghui, X. A SLAM with simultaneous construction of 2D and 3D maps based on Rao-Blackwellized particle filters. In Proceedings of the 2018 Tenth International Conference on Advanced Computational Intelligence (ICACI), Xiamen, China, 29–31 March 2018; pp. 374–378. [Google Scholar] [CrossRef]
- Zhou, Y.; Li, B.; Wang, D.; Mu, J. 2D Grid map for navigation based on LCSD-SLAM. In Proceedings of the 2021 11th International Conference on Information Science and Technology (ICIST), Chengdu, China, 21–23 May 2021; pp. 499–504. [Google Scholar] [CrossRef]
- Sun, L.; Zhao, J.; He, X.; Ye, C. DLO: Direct LiDAR Odometry for 2.5D Outdoor Environment. In Proceedings of the 2018 IEEE Intelligent Vehicles Symposium (IV), Changshu, China, 26–30 June 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Zlot, R.; Bosse, M. Efficient Large-Scale 3D Mobile Mapping and Surface Reconstruction of an Underground Mine. In Field and Service Robotics; Yoshida, K., Tadokoro, S., Eds.; Springer Tracts in Advanced Robotics; Springer: Berlin/Heidelberg, Germany, 2012; Volume 92, pp. 479–493. [Google Scholar] [CrossRef]
- Grupp, M. evo: Python Package for the Evaluation of Odometry and SLAM. 2017. Available online: https://github.com/MichaelGrupp/evo (accessed on 29 August 2023).
- Evangelidis, G.D.; Psarakis, E.Z. Parametric Image Alignment Using Enhanced Correlation Coefficient Maximization. IEEE Trans. Pattern Anal. Mach. Intell. 2008, 30, 1858–1865. [Google Scholar] [CrossRef] [PubMed]
- Ouster. OS2 Long-Range Lidar Sensor for Autonomous Vehicles, Trucking and Drones. Available online: https://ouster.com/products/scanning-lidar/os2-sensor/ (accessed on 13 April 2022).
- SICK. LMS511-10100 PRO. Available online: https://www.sick.com/us/en/detection-and-ranging-solutions/2d-lidar-sensors/lms5xx/lms511-10100-pro/p/p215941/ (accessed on 13 April 2022).

















| 3D Sensor | 2D Sensor | |
|---|---|---|
| 3D map | LOAM, LeGo-LOAM | vertical + horizontal, 2D LIDAR |
| 2D map | Proposed solution | Cartographer, Gmapping |
| 3D Localization | 2D Localization | |
|---|---|---|
| 3D map | DLL, NDT-3D, AMCL3D | NDT-2D, AMCL |
| 2D map | not possible | AMCL, NDT-2D |
| System | Parameter | Value |
|---|---|---|
| AMCL | laser_min_range | 0.1 m |
| AMCL | laser_max_range | 35 m |
| AMCL | laser_max_beams | 360 |
| AMCL | laser_z_hit | 0.95 |
| AMCL | laser_z_short | 0.1 m |
| AMCL | laser_z_max | 0.05 m |
| AMCL | laser_z_rand | 0.1 m |
| AMCL | laser_sigma_hit | 0.1 m |
| AMCL | laser_lambda_short | 0.05 m |
| AMCL | odom_alpha1 | 0.08 |
| AMCL | odom_alpha2 | 0.05 |
| AMCL | odom_alpha3 | 0.05 |
| AMCL | loading_odom_alpha3 | 0.09 |
| AMCL | odom_alpha4 | 0.08 |
| AMCL | odom_alpha5 | 0.05 |
| AMCL | min_particles | 300 |
| AMCL | max_particles | 10,000 |
| AMCL | kld_err | 0.05 |
| AMCL | kld_z | 0.99 |
| Pullback | Pullback distance | 3 m |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Inostroza, F.; Parra-Tsunekawa, I.; Ruiz-del-Solar, J. Robust Localization for Underground Mining Vehicles: An Application in a Room and Pillar Mine. Sensors 2023, 23, 8059. https://doi.org/10.3390/s23198059
Inostroza F, Parra-Tsunekawa I, Ruiz-del-Solar J. Robust Localization for Underground Mining Vehicles: An Application in a Room and Pillar Mine. Sensors. 2023; 23(19):8059. https://doi.org/10.3390/s23198059
Chicago/Turabian StyleInostroza, Felipe, Isao Parra-Tsunekawa, and Javier Ruiz-del-Solar. 2023. "Robust Localization for Underground Mining Vehicles: An Application in a Room and Pillar Mine" Sensors 23, no. 19: 8059. https://doi.org/10.3390/s23198059
APA StyleInostroza, F., Parra-Tsunekawa, I., & Ruiz-del-Solar, J. (2023). Robust Localization for Underground Mining Vehicles: An Application in a Room and Pillar Mine. Sensors, 23(19), 8059. https://doi.org/10.3390/s23198059








