Nocturnal Blood Pressure Estimation from Sleep Plethysmography Using Machine Learning
Abstract
:1. Introduction
2. Materials and Methods
2.1. Participants
2.2. Laboratory Protocol
2.3. Data Acquisition
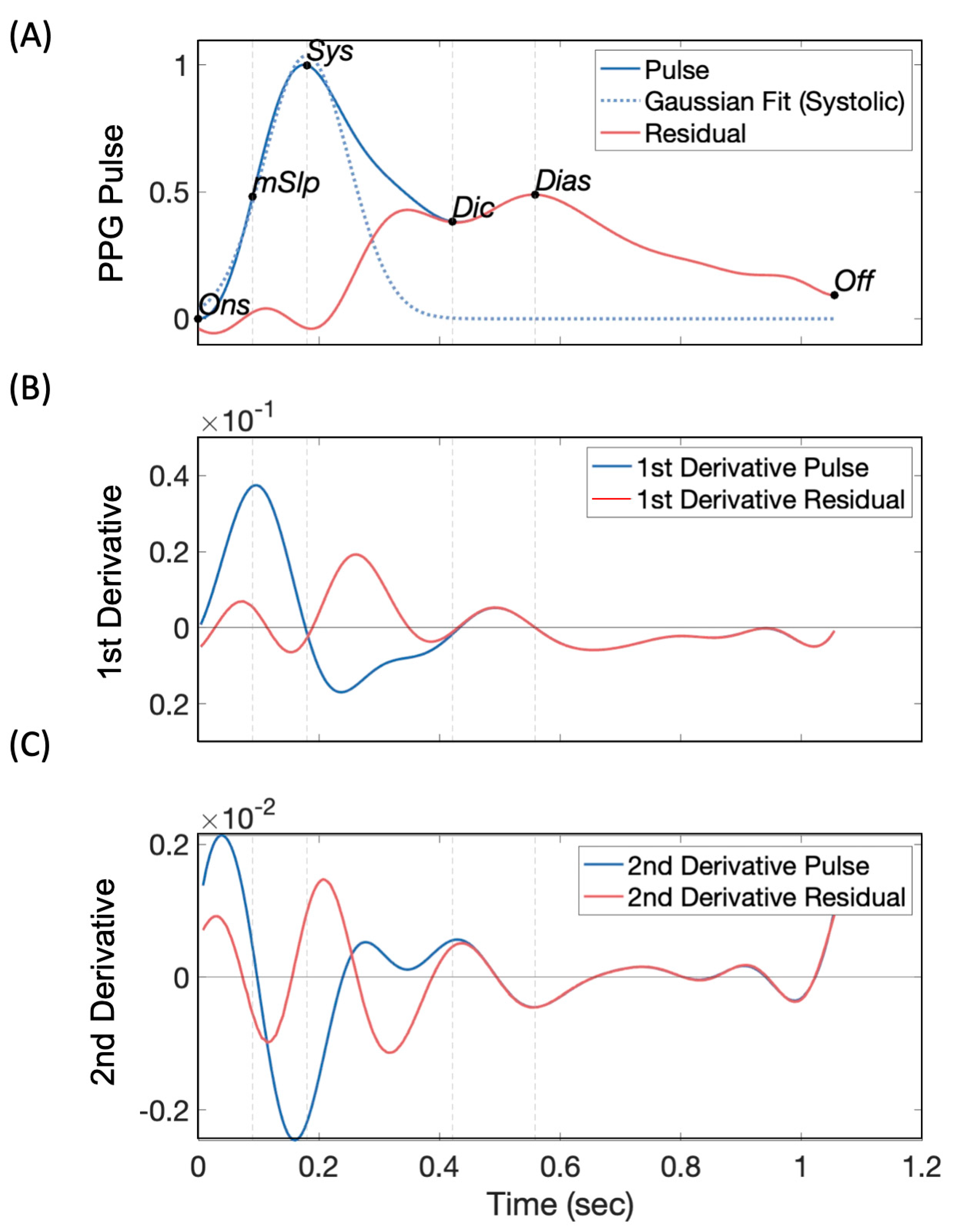
2.4. PPG Pulse Waveform Analysis and Feature Extraction
2.5. BP Prediction Model
2.6. Blood Pressure Prediction Performance Evaluation
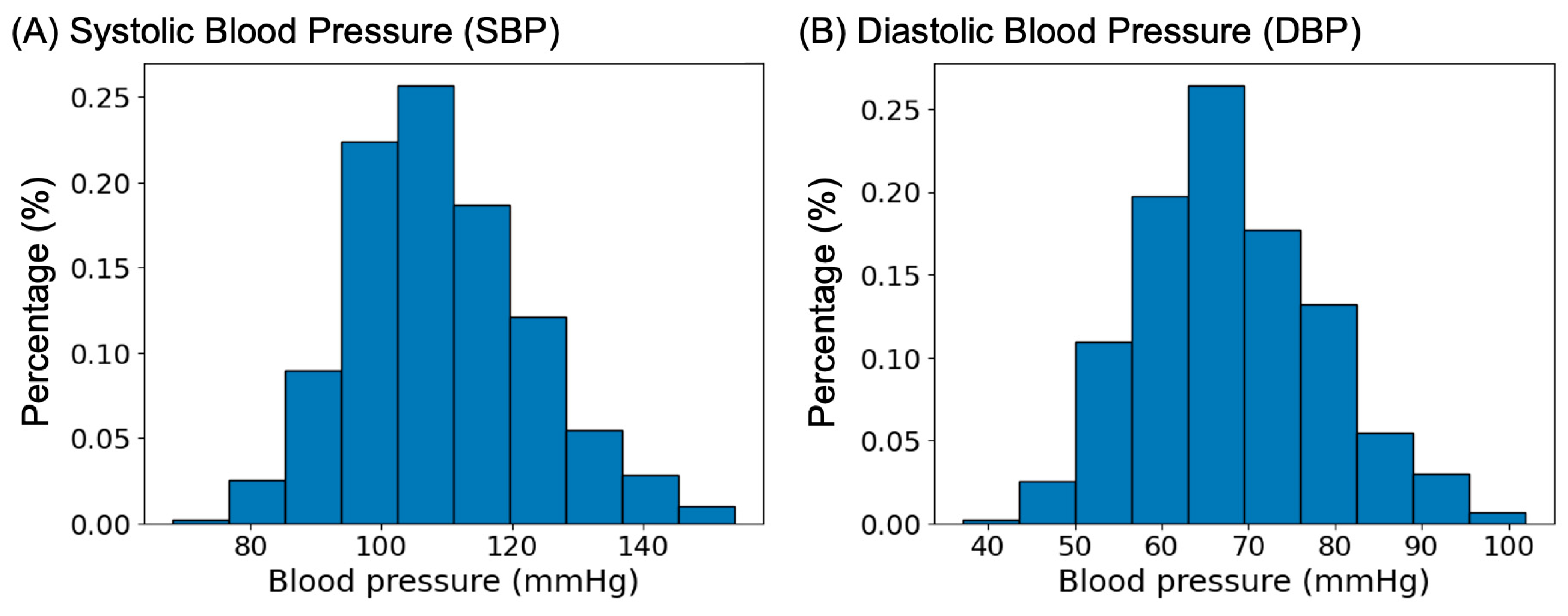
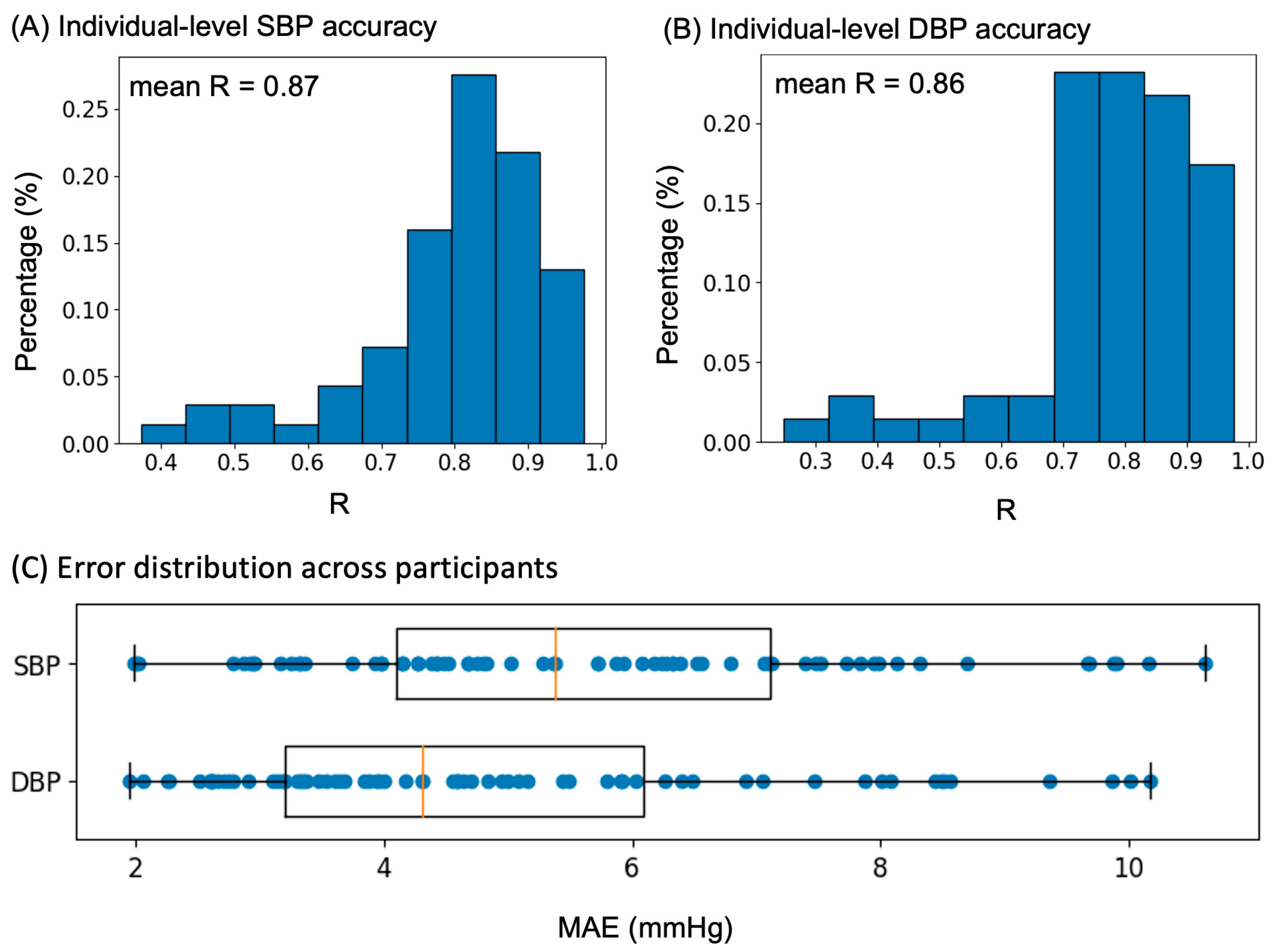
3. Results
4. Discussion
4.1. Nocturnal BP Prediction Using PPG Waveform
4.2. Pulse Waveform Modulation during Sleep
4.3. Clinical Importance of Nocturnal BP Measurement
4.4. Limitations
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- NCD Risk Factor Collaboration (NCD-RisC). Worldwide trends in blood pressure from 1975 to 2015: A pooled analysis of 1479 population-based measurement studies with 19·1 million participants. Lancet 2017, 389, 37–55. [Google Scholar] [CrossRef] [PubMed]
- Whelton, P.K.; Carey, R.M.; Aronow, W.S.; Casey, D.E., Jr.; Collins, K.J.; Himmelfarb, C.D.; DePalma, S.M.; Gidding, S.; Jamerson, K.A.; Jones, D.W.; et al. 2017 ACC/AHA/AAPA/ABC/ACPM/AGS/APhA/ASH/ASPC/NMA/PCNA Guideline for the Prevention, Detection, Evaluation, and Management of High Blood Pressure in Adults: Executive Summary: A Report of the American College of Cardiology/American Heart Association Task Force on Clinical Practice Guidelines. Hypertension 2018, 71, 1269–1324. [Google Scholar] [CrossRef] [PubMed]
- Williams, B.; Mancia, G.; Spiering, W.; Agabiti Rosei, E.; Azizi, M.; Burnier, M.; Clement, D.L.; Coca, A.; de Simone, G.; Dominiczak, A.; et al. 2018 ESC/ESH Guidelines for the management of arterial hypertension: The Task Force for the management of arterial hypertension of the European Society of Cardiology (ESC) and the European Society of Hypertension (ESH). Eur. Heart J. 2018, 39, 3021–3104. [Google Scholar] [CrossRef]
- Yang, W.-Y.; Melgarejo, J.D.; Thijs, L.; Zhang, Z.-Y.; Boggia, J.; Wei, F.-F.; Hansen, T.W.; Asayama, K.; Ohkubo, T.; Jeppesen, J.; et al. Association of Office and Ambulatory Blood Pressure With Mortality and Cardiovascular Outcomes. JAMA 2019, 322, 409–420. [Google Scholar] [CrossRef] [PubMed]
- Yano, Y.; Kario, K. Nocturnal blood pressure and cardiovascular disease: A review of recent advances. Hypertens. Res. 2012, 35, 695–701. [Google Scholar] [CrossRef] [PubMed]
- Dey, J.; Gaurav, A.; Tiwari, V.N. InstaBP: Cuff-less Blood Pressure Monitoring on Smartphone using Single PPG Sensor. In Proceedings of the 2018 40th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Honolulu, HI, USA, 18–21 July 2018; pp. 5002–5005. [Google Scholar]
- Chowdhury, M.H.; Shuzan, M.N.I.; Chowdhury, M.E.H.; Mahbub, Z.B.; Uddin, M.M.; Khandakar, A.; Reaz, M.B.I. Estimating Blood Pressure from the Photoplethysmogram Signal and Demographic Features Using Machine Learning Techniques. Sensors 2020, 20, 3127. [Google Scholar] [CrossRef]
- Liu, Q.; Zheng, Y.; Zhang, Y.; Poon, C.C.Y. Beats-to-Beats Estimation of Blood Pressure During Supine Cycling Exercise Using a Probabilistic Nonparametric Method. IEEE Access 2021, 9, 115655–115663. [Google Scholar] [CrossRef]
- Mukkamala, R.; Hahn, J.; Inan, O.T.; Mestha, L.K.; Kim, C.; Töreyin, H.; Kyal, S. Toward Ubiquitous Blood Pressure Monitoring via Pulse Transit Time: Theory and Practice. IEEE Trans. Biomed. Eng. 2015, 62, 1879–1901. [Google Scholar] [CrossRef]
- Monte-Moreno, E. Non-invasive estimate of blood glucose and blood pressure from a photoplethysmograph by means of machine learning techniques. Artif. Intell. Med. 2011, 53, 127–138. [Google Scholar] [CrossRef]
- El-Hajj, C.; Kyriacou, P.A. A review of machine learning techniques in photoplethysmography for the non-invasive cuff-less measurement of blood pressure. Biomed. Signal Process. Control 2020, 58, 101870. [Google Scholar] [CrossRef]
- Elgendi, M.; Fletcher, R.; Liang, Y.; Howard, N.; Lovell, N.H.; Abbott, D.; Lim, K.; Ward, R. The use of photoplethysmography for assessing hypertension. NPJ Digit. Med. 2019, 2, 60. [Google Scholar] [CrossRef]
- Charlton, P.H.; Paliakaitė, B.; Pilt, K.; Bachler, M.; Zanelli, S.; Kulin, D.; Allen, J.; Hallab, M.; Bianchini, E.; Mayer, C.C.; et al. Assessing hemodynamics from the photoplethysmogram to gain insights into vascular age: A review from VascAgeNet. Am. J. Physiol. Heart Circ. Physiol. 2022, 322, H493–H522. [Google Scholar] [CrossRef]
- Lin, W.-H.; Li, X.; Li, Y.; Li, G.; Chen, F. Investigating the physiological mechanisms of the photoplethysmogram features for blood pressure estimation. Physiol. Meas. 2020, 41, 044003. [Google Scholar] [CrossRef]
- Chowienczyk, P.J.; Kelly, R.P.; MacCallum, H.; Millasseau, S.C.; Andersson, T.L.G.; Gosling, R.G.; Ritter, J.M.; Änggård, E.E. Photoplethysmographic assessment of pulse wave reflection: Blunted response to endothelium-dependent beta2-adrenergic vasodilation in type II diabetes mellitus. J. Am. Coll. Cardiol. 1999, 34, 2007–2014. [Google Scholar] [CrossRef]
- Finnegan, E.; Davidson, S.; Harford, M.; Watkinson, P.; Tarassenko, L.; Villarroel, M. Features from the photoplethysmogram and the electrocardiogram for estimating changes in blood pressure. Sci. Rep. 2023, 13, 986. [Google Scholar] [CrossRef] [PubMed]
- Yilmaz, G.; Ong, J.L.; Ling, L.-H.; Chee, M.W.L. Insights Into Vascular Physiology From Sleep Photoplethysmography. Sleep 2023, zsad172. [Google Scholar] [CrossRef] [PubMed]
- Svedmyr, S.; Zou, D.; Sommermeyer, D.; Ficker, J.H.; Randerath, W.; Fietze, I.; Sanner, B.; Hedner, J.; Grote, L. Vascular stiffness determined from a nocturnal digital pulse wave signal: Association with sleep, sleep-disordered breathing, and hypertension. J. Hypertens. 2016, 34, 2427–2433. [Google Scholar] [CrossRef] [PubMed]
- Hirotsu, C.; Betta, M.; Bernardi, G.; Marques-Vidal, P.; Vollenweider, P.; Waeber, G.; Pichot, V.; Roche, F.; Siclari, F.; Haba-Rubio, J.; et al. Pulse wave amplitude drops during sleep: Clinical significance and characteristics in a general population sample. Sleep 2020, 43, zsz322. [Google Scholar] [CrossRef]
- El-Hajj, C.; Kyriacou, P. Deep learning models for cuffless blood pressure monitoring from PPG signals using attention mechanism. Biomed. Signal Process. Control 2021, 65, 102301. [Google Scholar] [CrossRef]
- Hsu, Y.-C.; Li, Y.-H.; Chang, C.-C.; Harfiya, L.N. Generalized Deep Neural Network Model for Cuffless Blood Pressure Estimation with Photoplethysmogram Signal Only. Sensors 2020, 20, 5668. [Google Scholar] [CrossRef]
- Khalid, S.G.; Liu, H.; Zia, T.; Zhang, J.; Chen, F.; Zheng, D. Cuffless Blood Pressure Estimation Using Single Channel Photoplethysmography: A Two-Step Method. IEEE Access 2020, 8, 58146–58154. [Google Scholar] [CrossRef]
- Radha, M.; de Groot, K.; Rajani, N.; Wong, C.C.P.; Kobold, N.; Vos, V.; Fonseca, P.; Mastellos, N.; Wark, P.A.; Velthoven, N.; et al. Estimating blood pressure trends and the nocturnal dip from photoplethysmography. Physiol. Meas. 2019, 40, 025006. [Google Scholar] [CrossRef]
- Zheng, Y.-L.; Yan, B.P.; Zhang, Y.-T.; Poon, C.C.Y. An Armband Wearable Device for Overnight and Cuff-Less Blood Pressure Measurement. IEEE Trans. Biomed. Eng. 2014, 61, 2179–2186. [Google Scholar] [CrossRef]
- Mukkamala, R.; Yavarimanesh, M.; Natarajan, K.; Hahn, J.-O.; Kyriakoulis, K.G.; Avolio, A.P.; Stergiou, G.S. Evaluation of the Accuracy of Cuffless Blood Pressure Measurement Devices: Challenges and Proposals. Hypertension 2021, 78, 1161–1167. [Google Scholar] [CrossRef]
- Kei Fong, M.W.; Ng, E.Y.K.; Er Zi Jian, K.; Hong, T.J. SVR ensemble-based continuous blood pressure prediction using multi-channel photoplethysmogram. Comput. Biol. Med. 2019, 113, 103392. [Google Scholar] [CrossRef]
- Su, P.; Ding, X.-R.; Zhang, Y.-T.; Liu, J.; Miao, F.; Zhao, N. Long-term blood pressure prediction with deep recurrent neural networks. In Proceedings of the 2018 IEEE EMBS International Conference on Biomedical & Health Informatics (BHI), Las Vegas, NV, USA, 4 March 2018; pp. 323–328. [Google Scholar] [CrossRef]
- Johns, M.W. A New Method for Measuring Daytime Sleepiness: The Epworth Sleepiness Scale. Sleep 1991, 14, 540–545. [Google Scholar] [CrossRef]
- de Greeff, A.; Shennan, A.H. Validation of the Spacelabs 90227 OnTrak device according to the European and British Hypertension Societies as well as the American protocols. Blood Press. Monit. 2020, 25, 110–114. [Google Scholar] [CrossRef] [PubMed]
- Vest, A.N.; Poian, G.D.; Li, Q.; Liu, C.; Nemati, S.; Shah, A.J.; Clifford, G.D. An Open Source Benchmarked Toolbox for Cardiovascular Waveform and Interval Analysis. Physiol. Meas. 2018, 39, 105004. [Google Scholar] [CrossRef]
- Elgendi, M. On the Analysis of Fingertip Photoplethysmogram Signals. Curr. Cardiol. Rev. 2012, 8, 14–25. [Google Scholar] [CrossRef] [PubMed]
- Couceiro, R.; Carvalho, P.; Paiva, R.P.; Henriques, J.; Antunes, M.; Quintal, I.; Muehlsteff, J. Multi-Gaussian fitting for the assessment of left ventricular ejection time from the Photoplethysmogram. In Proceedings of the 2012 Annual International Conference of the IEEE Engineering in Medicine and Biology Society, San Diego, CA, USA, 28 August–1 September 2012; pp. 3951–3954. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Lang. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Bakdash, J.Z.; Marusich, L.R. Repeated Measures Correlation. Front. Psychol. 2017, 8, 456. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Lee, S.-I. A Unified Approach to Interpreting Model Predictions. In Advances in Neural Information Processing Systems; Curran Associates, Inc.: New York, NY, USA, 2017; Volume 30, Available online: https://proceedings.neurips.cc/paper_files/paper/2017/hash/8a20a8621978632d76c43dfd28b67767-Abstract.html (accessed on 5 June 2023).
- Nadeau, C.; Bengio, Y. Inference for the Generalization Error. In Advances in Neural Information Processing Systems; Solla, S., Leen, T., Müller, K., Eds.; MIT Press: Cambridge, MA, USA, 1999; Volume 12, Available online: https://proceedings.neurips.cc/paper_files/paper/1999/file/7d12b66d3df6af8d429c1a357d8b9e1a-Paper.pdf (accessed on 15 September 2023).
- Bouckaert, R.R.; Frank, E. Evaluating the Replicability of Significance Tests for Comparing Learning Algorithms. In Advances in Knowledge Discovery and Data Mining; Dai, H., Srikant, R., Zhang, C., Eds.; Springer: Berlin/Heidelberg, Germany, 2004; pp. 3–12. [Google Scholar] [CrossRef]
- Millasseau, S.C.; Kelly, R.P.; Ritter, J.M.; Chowienczyk, P.J. Determination of age-related increases in large artery stiffness by digital pulse contour analysis. Clin. Sci. 2002, 103, 371–377. [Google Scholar] [CrossRef] [PubMed]
- Allen, J.; O’Sullivan, J.; Stansby, G.; Murray, A. Age-related changes in pulse risetime measured by multi-site photoplethysmography. Physiol. Meas. 2020, 41, 074001. [Google Scholar] [CrossRef] [PubMed]
- Martínez, G.; Howard, N.; Abbott, D.; Lim, K.; Ward, R.; Elgendi, M. Can Photoplethysmography Replace Arterial Blood Pressure in the Assessment of Blood Pressure? J. Clin. Med. 2018, 7, 316. [Google Scholar] [CrossRef]
- Delessert, A.; Espa, F.; Rossetti, A.; Lavigne, G.; Tafti, M.; Heinzer, R. Pulse Wave Amplitude Drops during Sleep are Reliable Surrogate Markers of Changes in Cortical Activity. Sleep 2010, 33, 1687–1692. [Google Scholar] [CrossRef] [PubMed]
- Colombo, R.; Marchi, A.; Borghi, B.; Fossali, T.; Rech, R.; Castelli, A.; Corona, A.; Guzzetti, S.; Raimondi, F. Pulse Photoplethysmographic Analysis Estimates the Sympathetic Activity Directed to Heart and Vessels. Anesthesiology 2015, 123, 336–345. [Google Scholar] [CrossRef] [PubMed]
- Bosi, M.; Milioli, G.; Riccardi, S.; Melpignano, A.; Vaudano, A.E.; Cortelli, P.; Poletti, V.; Parrino, L. Arousal responses to respiratory events during sleep: The role of pulse wave amplitude. J. Sleep Res. 2018, 27, 261–269. [Google Scholar] [CrossRef]
- Hermida, R.C.; Crespo, J.J.; Otero, A.; Domínguez-Sardiña, M.; Moyá, A.; Ríos, M.T.; Castiñeira, M.C.; Callejas, P.A.; Pousa, L.; Sineiro, E.; et al. Asleep blood pressure: Significant prognostic marker of vascular risk and therapeutic target for prevention. Eur. Heart J. 2018, 39, 4159–4171. [Google Scholar] [CrossRef]
- Sola, J.; Vybornova, A.; Fallet, S.; Polychronopoulou, E.; Wurzner-Ghajarzadeh, A.; Wuerzner, G. Validation of the optical Aktiia bracelet in different body positions for the persistent monitoring of blood pressure. Sci. Rep. 2021, 11, 20644. [Google Scholar] [CrossRef]
- Sayer, G.; Piper, G.; Vorovich, E.; Raikhelkar, J.; Kim, G.H.; Rodgers, D.; Shimbo, D.; Uriel, N. Continuous Monitoring of Blood Pressure Using a Wrist-Worn Cuffless Device. Am. J. Hypertens. 2022, 35, 407–413. [Google Scholar] [CrossRef]
- Kazuomi, K. Nocturnal Hypertension. Hypertension 2018, 71, 997–1009. [Google Scholar] [CrossRef]




| Study | Target BP | Reference Measure | PPG Location | Sample, Size, Age | Input Format | Method | Error (mmHg) | |
|---|---|---|---|---|---|---|---|---|
| SBP | DBP | |||||||
| [6] | Daytime | Point BP | Finger | Health N.R., N = 205, 39 ± 15 yo | PPG Features | Lasso | MAE: 6.9 | MAE: 5 |
| [26] | Daytime | Point BP | Forearm | Healthy, N = 40, 35 ± 15 yo | PPG Features | Ensemble SVR | MAE: 7.26 | MAE: 5.01 |
| [7] | Daytime | Point BP | Finger | Outpatients, N = 219, 57 ± 15 yo | PPG Features | GPR | MAE: 3.02 RMSE: 6.74 | MAE: 1.74 RMSE: 3.59 |
| [8] | Daytime | Finapress*, Point BP | Finger | Mixed, N = 62, 59 ± 10 yo | PPG Features + PTT | GPR | MAE: 4.8 | MAE: 3.4 |
| [27] | Daytime | Finapress*, Point BP | Finger | Healthy, N = 84, Age N.R. | PPG Features + PTT | Deep RNN | RMSE: 3.9 | RMSE: 2.6 |
| [23] | 24 h trend | ABPM | Wrist | Healthy, N = 106, 36.6 ± 11.7 yo | PPG Features | LSTM | RMSE: 8.2 | RMSE: 6.5 |
| This work | Night-time | ABPM | Finger | Healthy, N = 68, 29 (23–46) yo | PPG Features | Random forest | MAE: 5.7 RMSE: 6.5 | MAE: 4.5 RMSE: 4.6 |
| Sample Summary | N = 68 1 |
|---|---|
| Age | 29 (23, 46) |
| Gender | |
| Female | 32 (47%) |
| Male | 36 (53%) |
| BMI (kg/m2) | 22.8 (21.1, 24.3) |
| Office SBP (mmHg) | 110 (103, 121) |
| Office DBP (mmHg) | 71 (66, 77) |
| ABPM Summary | |
| Sleep SBP (mmHg) | 104 (99, 114) |
| Sleep DPB (mmHg) | 64 (60, 69) |
| BP readings per participant (n) | 15 (14, 16) |
| Sleep Summary | |
| Time in Bed (min) | 463 (420, 490) |
| Sleep Efficiency (%) | 88 (79, 92) |
| Window Length (s) | Systolic Blood Pressure | Diastolic Blood Pressure | ||||
|---|---|---|---|---|---|---|
| MAE (SD) | RMSE (SD) | R (SD) | MAE (SD) | RMSE (SD) | R (SD) | |
| 1 min | 6.38 | 6.51 | 0.866 | 4.92 | 5.14 | 0.864 |
| (−4.61) | (−1.87) | (−0.08) | (−3.63) | (−1.12) | (−0.06) | |
| 30 s | 6.09 | 6.53 | 0.868 | 4.81 | 4.92 | 0.869 |
| (−4.46) | (−1.87) | (−0.09) | (−3.52) | (−1.14) | (−0.08) | |
| 15 s | 5.9 | 6.48 | 0.869 | 4.64 | 4.67 | 0.871 |
| (−4.61) | (−1.76) | (−0.09) | (−3.54) | (−1.11) | (−0.08) | |
| 7 s | 5.72 | 6.47 | 0.87 | 4.52 | 4.62 | 0.868 |
| (−4.51) | (−1.88) | (−0.09) | (−3.6) | (−1.17) | (−0.08) | |
| 3 s | 6.63 | 6.72 | 0.865 | 6.78 | 6.92 | 0.857 |
| (−5.8) | (−1.91) | (−0.08) | (−4.5) | (−1.58) | (−0.08) | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yilmaz, G.; Lyu, X.; Ong, J.L.; Ling, L.H.; Penzel, T.; Yeo, B.T.T.; Chee, M.W.L. Nocturnal Blood Pressure Estimation from Sleep Plethysmography Using Machine Learning. Sensors 2023, 23, 7931. https://doi.org/10.3390/s23187931
Yilmaz G, Lyu X, Ong JL, Ling LH, Penzel T, Yeo BTT, Chee MWL. Nocturnal Blood Pressure Estimation from Sleep Plethysmography Using Machine Learning. Sensors. 2023; 23(18):7931. https://doi.org/10.3390/s23187931
Chicago/Turabian StyleYilmaz, Gizem, Xingyu Lyu, Ju Lynn Ong, Lieng Hsi Ling, Thomas Penzel, B. T. Thomas Yeo, and Michael W. L. Chee. 2023. "Nocturnal Blood Pressure Estimation from Sleep Plethysmography Using Machine Learning" Sensors 23, no. 18: 7931. https://doi.org/10.3390/s23187931
APA StyleYilmaz, G., Lyu, X., Ong, J. L., Ling, L. H., Penzel, T., Yeo, B. T. T., & Chee, M. W. L. (2023). Nocturnal Blood Pressure Estimation from Sleep Plethysmography Using Machine Learning. Sensors, 23(18), 7931. https://doi.org/10.3390/s23187931







