Image Reconstruction Using Supervised Learning in Wearable Electrical Impedance Tomography of the Thorax
Abstract
:1. Introduction
The Aim of the Work
2. Machine Learning Approach in CCEIT
2.1. Model of the Human Thorax
2.2. Measurement Simulation in Electrical Capacitively Coupled Electrical Impedance Tomography
2.3. Training Dataset
- The training set contained 9375 samples from each class and 44,000 samples with random ellipses, for a total of 194,000 samples. During training, this set was randomly split on the fly into learning and validation subsets with a ratio of 75:25.
- The test set contained 2500 samples from each class and 2500 samples with random ellipses, for a total of 42,500 samples.
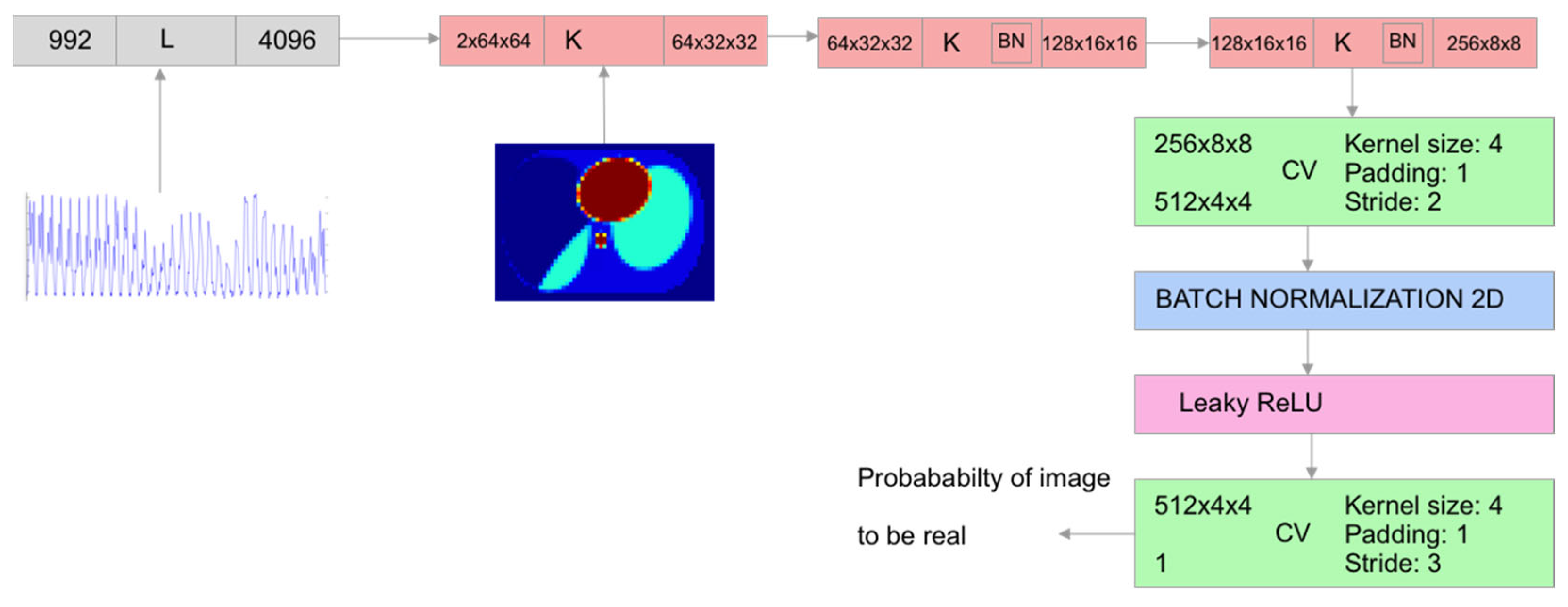
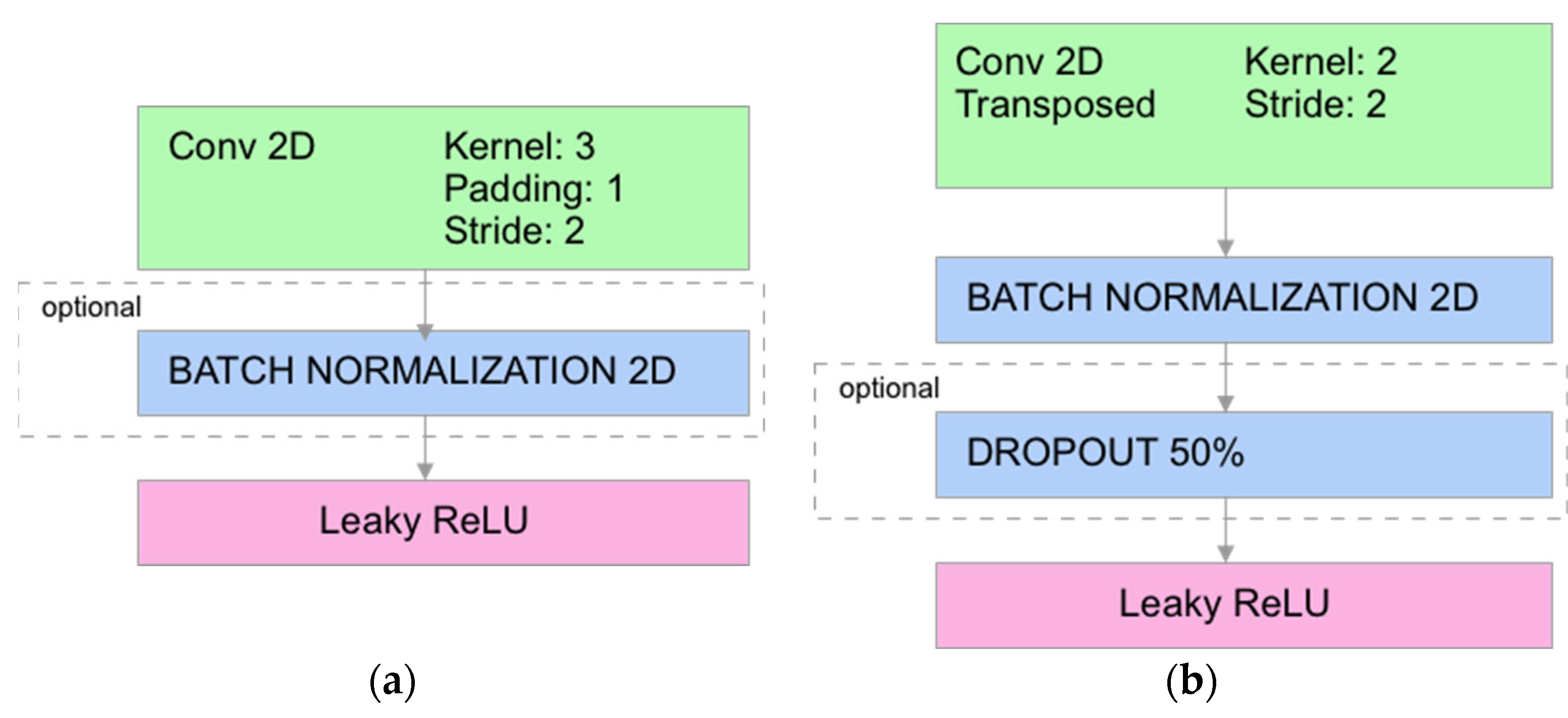
2.4. ANN Architecture Used
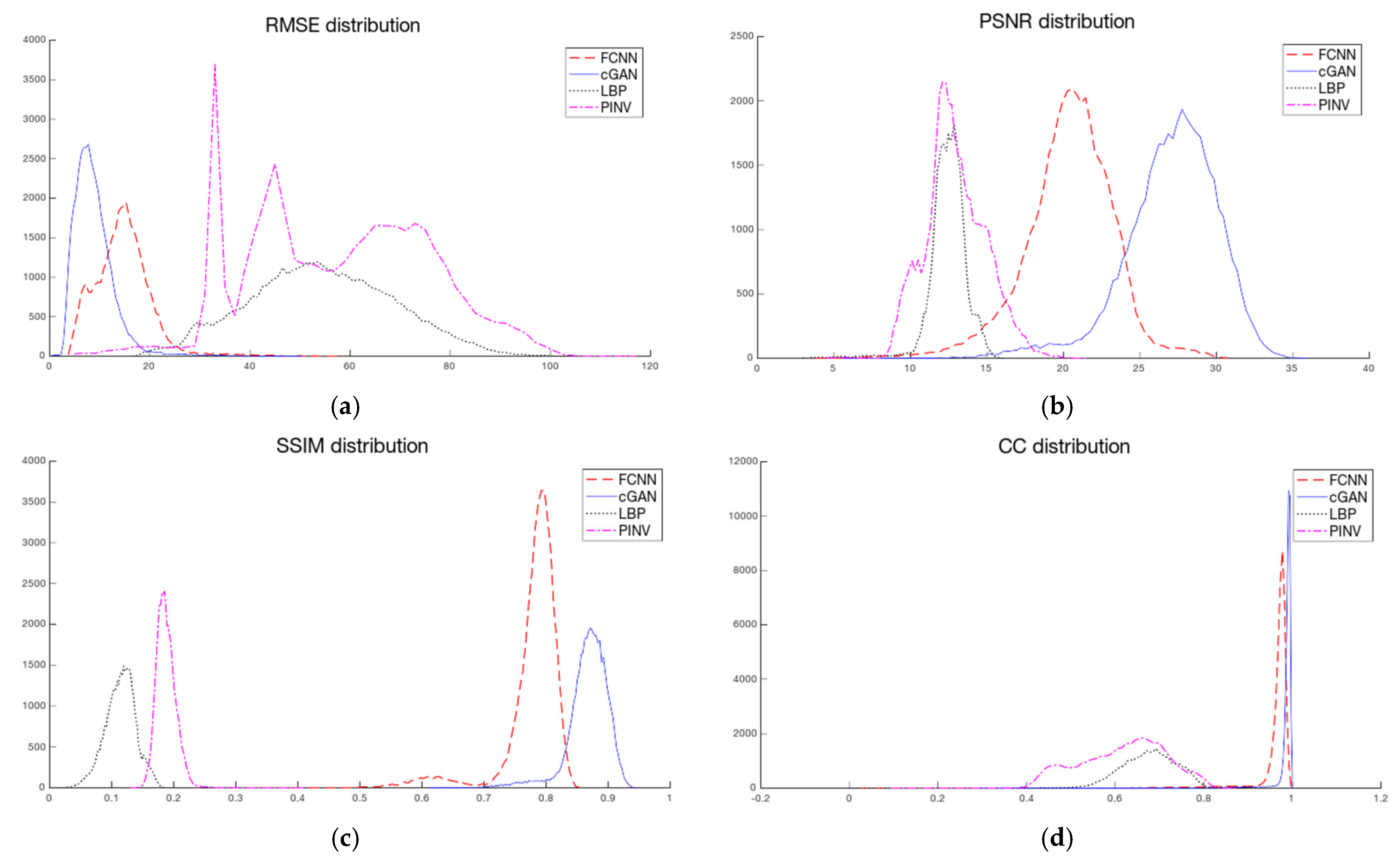
2.5. Reconstruction Quality Assessment
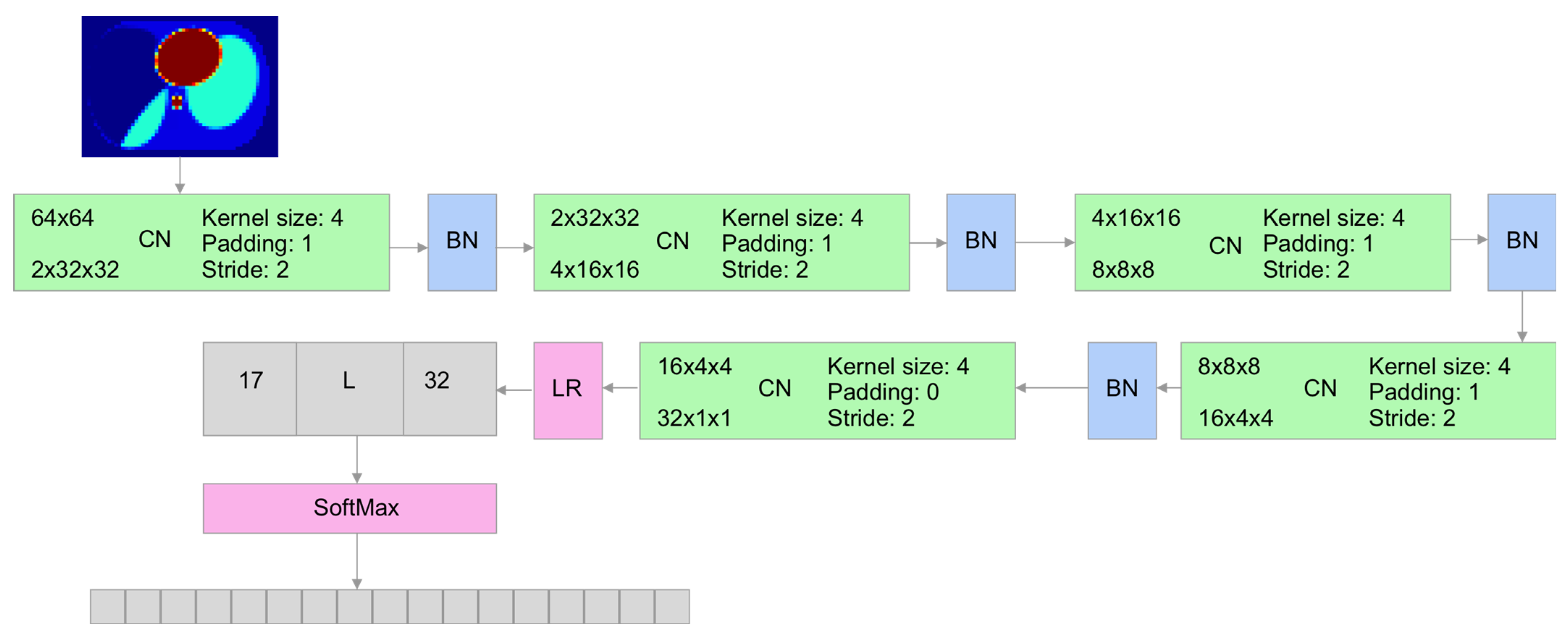
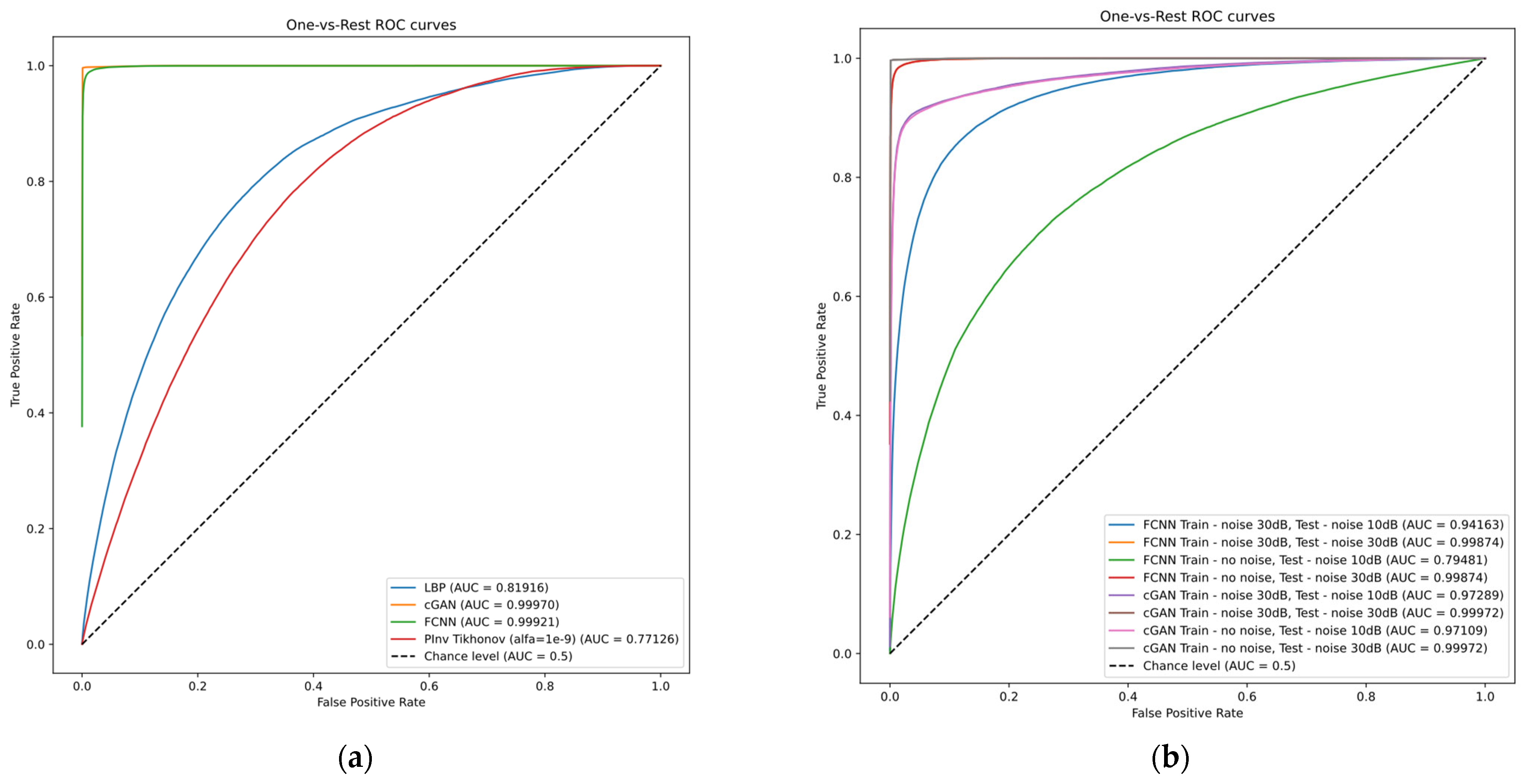
2.6. Image Diagnostical Value Evaluation Using ANN Classifier
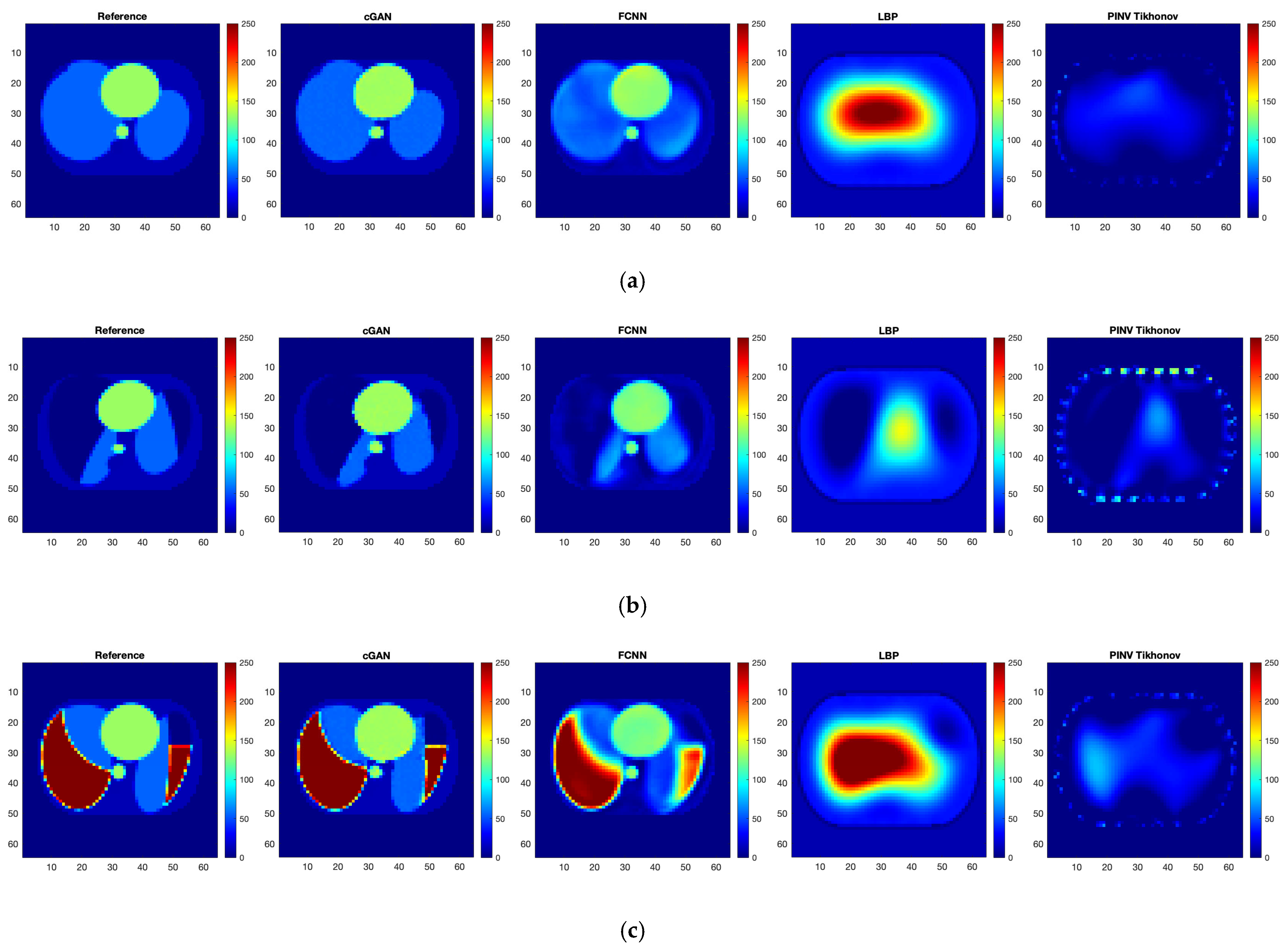
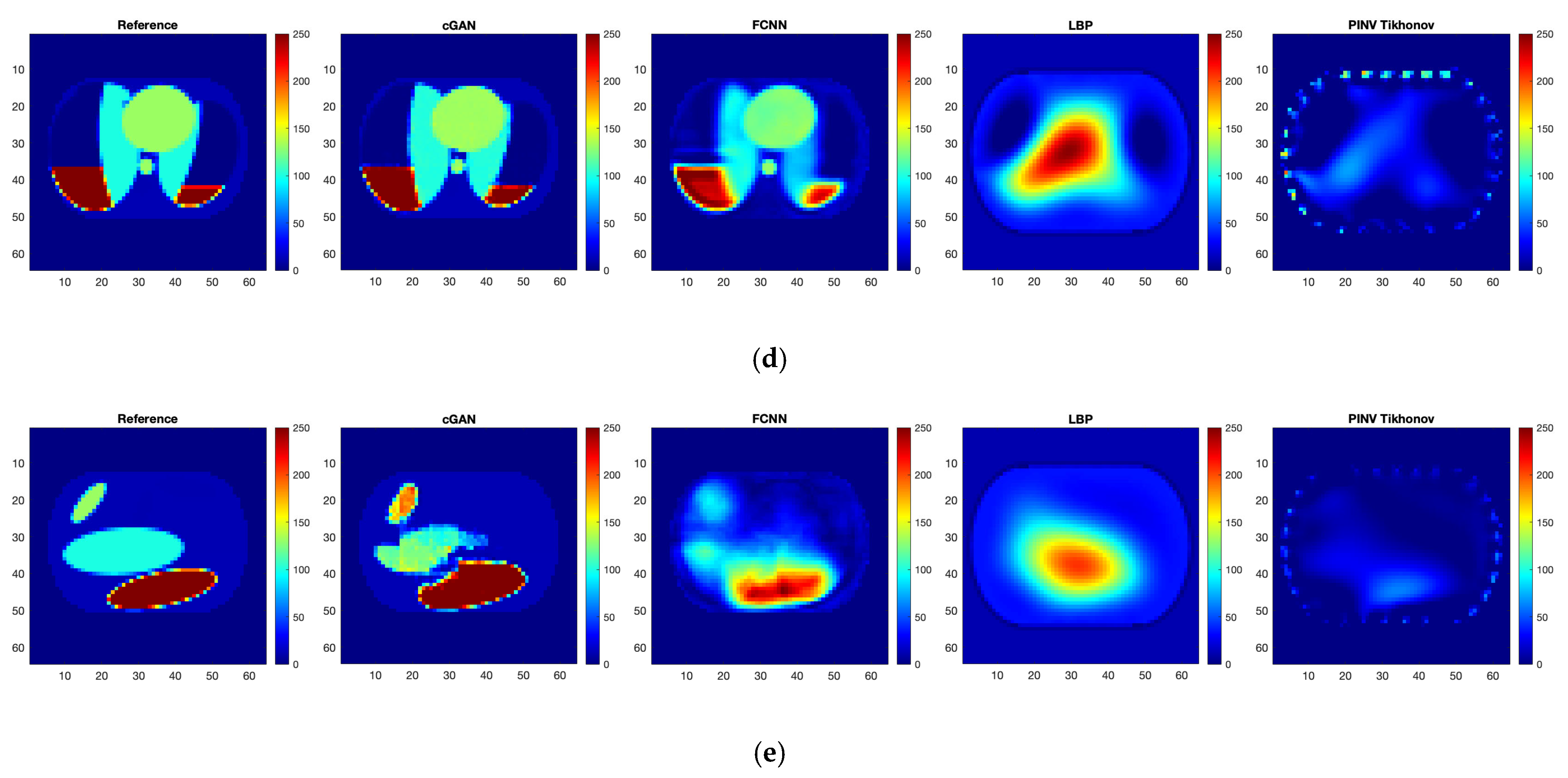
3. Results
- The linear back projection (LBP) given bywhere is a transpose of the normalized sensitivity matrix and is a vector of normalized measurements.
- The pseudoinverse with Tikhonov regularization (TPINV) given by
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Holder, D.S. Introduction to biomedical electrical impedance tomography. In Electrical Impedance Tomography: Methods, History and Applications (Series in Medical Physics and Biomedical Engineering); Holder, D.S., Ed.; Institute of Physics Publishing: Bristol, UK; Philadephia, PA, USA, 2005; pp. 423–450. ISBN 0 7503 0952 0. [Google Scholar]
- Brown, B.H.; Barber, D.C. Electrical Impedance Tomography; the Construction and Application to Physiological Measurement of Electrical Impedance Images. Med. Prog. Technol. 1987, 13, 69–75. [Google Scholar]
- Adler, A.; Arnold, J.H.; Bayford, R.; Borsic, A.; Brown, B.; Dixon, P.; Faes, T.J.C.; Frerichs, I.; Gagnon, H.; Gärber, Y.; et al. GREIT: A unified approach to 2D linear EIT reconstruction of lung images. Physiol. Meas. 2009, 30. [Google Scholar] [CrossRef] [PubMed]
- Sapuan, I.; Yasin, M.; Ain, K.; Apsari, R. Anomaly Detection Using Electric Impedance Tomography Based on Real and Imaginary Images. Sensors 2020, 20, 1907. [Google Scholar] [CrossRef] [PubMed]
- Peyman, A.; Gabriel, C.; Grant, E.H.; Vermeeren, G.; Martens, L. Variation of the dielectric properties of tissues with age: The effect on the values of SAR in children when exposed to walkie–talkie devices. Phys. Med. Biol. 2008, 54, 227. [Google Scholar] [CrossRef]
- Kay, C.F.; Schwan, H.P. Specific Resistance of Body Tissues. Circ. Res. 1956, 4, 664–670. [Google Scholar] [CrossRef] [PubMed]
- Shi, Y.; Yang, Z.G.; Xie, F.; Ren, S.; Xu, S.F. The Research Progress of Electrical Impedance Tomography for Lung Monitoring. Front. Bioeng. Biotechnol. 2021, 9, 1–16. [Google Scholar] [CrossRef]
- Christanto, A.; Darina, I. The Role of Electrical Impedance Tomography in Lung Imaging. Cermin Dunia Kedokt. 2021, 48, 372–375. [Google Scholar] [CrossRef]
- Qu, S.Y.; Dai, M.; Wu, S.; Lv, Z.R.; Ti, X.Y.; Fu, F. System Introduction and Evaluation of the First Chinese Chest EIT Device for ICU Applications. Sci. Rep. 2021, 11, 19273. [Google Scholar] [CrossRef]
- Adler, A.; Amato, M.B.; Arnold, J.H.; Bayford, R.; Bodenstein, M.; Böhm, S.H.; Brown, B.H.; Frerichs, I.; Stenqvist, O.; Weiler, N.; et al. Whither Lung EIT: Where Are We, Where Do We Want to Go and What Do We Need to Get There? Physiol. Meas. 2012, 33, 679–694. [Google Scholar] [CrossRef]
- Jiang, Y.D.; Soleimani, M. Capacitively Coupled Electrical Impedance Tomography for Brain Imaging. IEEE Trans. Med. Imaging 2019, 38, 2104–2113. [Google Scholar] [CrossRef]
- Min Hyun, C.; Jun Jang, T.; Nam, J.; Kwon, H.; Jeon, K.; Lee, K. Machine Learning-Based Signal Quality Assessment for Cardiac Volume Monitoring in Electrical Impedance Tomography. Mach. Learn. Sci. Technol. 2023, 4, 015034. [Google Scholar] [CrossRef]
- Huerta-Franco, M.R. Electrical Bioimpedance and Other Techniques for Gastric Emptying and Motility Evaluation. World J. Gastrointest. Pathophysiol. 2012, 3, 10. [Google Scholar] [CrossRef]
- Mansouri, S.; Alharbi, Y.; Haddad, F.; Chabcoub, S.; Alshrouf, A.; Abd-Elghany, A.A. Electrical Impedance Tomography—Recent Applications and Developments. J. Electr. Bioimpedance 2021, 12, 50–62. [Google Scholar] [CrossRef] [PubMed]
- Pennati, F.; Angelucci, A.; Morelli, L.; Bardini, S.; Barzanti, E.; Cavallini, F.; Conelli, A.; Di Federico, G.; Paganelli, C.; Aliverti, A. Electrical Impedance Tomography: From the Traditional Design to the Novel Frontier of Wearables. Sensors 2023, 23, 1182. [Google Scholar] [CrossRef]
- Wu, Y.; Jiang, D.; Bardill, A.; De Gelidi, S.; Bayford, R.; Demosthenous, A. A High Frame Rate Wearable EIT System Using Active Electrode ASICs for Lung Respiration and Heart Rate Monitoring. IEEE Trans. Circuits Syst. I Regul. Pap. 2018, 65, 3810–3820. [Google Scholar] [CrossRef]
- Isaacson, D.; Mueller, J.L.; Newell, J.C.; Siltanen, S. Reconstructions of Chest Phantoms by the D-Bar Method for Electrical Impedance Tomography. IEEE Trans. Med. Imaging 2004, 23, 821–828. [Google Scholar] [CrossRef] [PubMed]
- Knudsen, K.; Lassas, M.; Mueller, J.L.; Siltanen, S. D-Bar Method for Electrical Impedance Tomography with Discontinuous Conductivities. SIAM J. Appl. Math. 2007, 67, 893–913. [Google Scholar] [CrossRef]
- Vauhkonen, M.; Vadâsz, D.; Karjalainen, P.A.; Somersalo, E.; Kaipio, J.P. Tikhonov Regularization and Prior Information in Electrical Impedance Tomography. IEEE Trans. Med. Imaging 1998, 17, 285–293. [Google Scholar] [CrossRef]
- Jiang, M.; Xia, L.; Shou, G.; Liu, F.; Crozier, S. Two Hybrid Regularization Frameworks for Solving the Electrocardiography Inverse Problem. Phys. Med. Biol. 2008, 53, 5151–5164. [Google Scholar] [CrossRef]
- Abascal, J.F.P.J.; Arridge, S.R.; Bayford, R.H.; Holder, D.S. Comparison of Methods for Optimal Choice of the Regularization Parameter for Linear Electrical Impedance Tomography of Brain Function. Physiol. Meas. 2008, 29, 1319–1334. [Google Scholar] [CrossRef] [PubMed]
- Latourette, K. A Comparison of The Levenberg-Marquardt Method with Standard Optimization Algorithms, in Minimizing the Tikhonov-Total Variational Functional. In 2.1. The Steepest Descent 4. Final Remarks Appendix A. Quadratic Convergence Rate of the Levenberg-Marquard; University of Arizona: Tucson, AZ, USA, 2008. [Google Scholar]
- Colibazzi, F.; Lazzaro, D.; Morigi, S.; Samoré, A. Learning Nonlinear Electrical Impedance Tomography. J. Sci. Comput. 2022, 90, 58. [Google Scholar] [CrossRef]
- Gamio, J.C.; Ortiz-Aleman, C.; Martin, R. Electrical Capacitance Tomography Two-Phase Oil-Gas Pipe Flow Imaging by the Linear Back-Projection Algorithm. Geofísic. Int. 2005, 44, 265–273. [Google Scholar]
- Smolik, W.T. Rekonstrukcja Obrazów w Elektrycznej Tomografii Pojemnościowej; Oficyna Wydawnicza Politechniki Warszawskiej: Warszawa, Poland, 2013; ISBN 978-83-7814-097-9. [Google Scholar]
- Aller, M.; Mera, D.; Cotos, J.M.; Villaroya, S. Study and Comparison of Different Machine Learning-Based Approaches to Solve the Inverse Problem in Electrical Impedance Tomographies. Neural Comput. Appl. 2023, 35, 5465–5477. [Google Scholar] [CrossRef]
- Wang, G.; Ye, J.C.; Mueller, K.; Fessler, J.A. Image Reconstruction Is a New Frontier of Machine Learning. IEEE Trans. Med. Imaging 2018, 37, 1289–1296. [Google Scholar] [CrossRef]
- Ongie, G.; Jalal, A.; Metzler, C.A.; Baraniuk, R.G.; Dimakis, A.G.; Willett, R. Deep Learning Techniques for Inverse Problems in Imaging. IEEE J. Sel. Areas Inf. Theory 2020, 1, 39–56. [Google Scholar] [CrossRef]
- Adler, A.; Guardo, R. A Neural Network Image Reconstruction Technique for Electrical Impedance Tomography. IEEE Trans. Med. Imaging 1994, 13, 594–600. [Google Scholar] [CrossRef]
- Adler, J.; Öktem, O. Solving Ill-Posed Inverse Problems Using Iterative Deep Neural Networks. Inverse Probl. 2017, 33, 124007. [Google Scholar] [CrossRef]
- Khan, T.A.; Ling, S.H. Review on Electrical Impedance Tomography: Artificial Intelligence Methods and Its Applications. Algorithms 2019, 12, 88. [Google Scholar] [CrossRef]
- Zhang, T.; Tian, X.; Liu, X.C.; Ye, J.A.; Fu, F.; Shi, X.T.; Liu, R.G.; Xu, C.H. Advances of Deep Learning in Electrical Impedance Tomography Image Reconstruction. Front. Bioeng. Biotechnol. 2022, 10, 1019531. [Google Scholar] [CrossRef]
- Yang, X.; Zhao, C.; Chen, B.; Zhang, M.; Li, Y. Big Data Driven U-Net Based Electrical Capacitance Image Reconstruction Algorithm. In Proceedings of the 2019 IEEE International Conference on Imaging Systems and Techniques (IST), Abu Dhabi, United Arab, 9–10 December 2019. [Google Scholar] [CrossRef]
- Genzel, M.; Macdonald, J.; Marz, M. Solving Inverse Problems With Deep Neural Networks—Robustness Included. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 8828, 1119–1134. [Google Scholar] [CrossRef]
- Kłosowski, G.; Rymarczyk, T.; Cieplak, T.; Niderla, K.; Skowron, Ł. Quality Assessment of the Neural Algorithms on the Example of EIT-UST Hybrid Tomography. Sensors 2020, 20, 3324. [Google Scholar] [CrossRef] [PubMed]
- Rymarczyk, T.; Klosowski, G.; Kozlowski, E.; Tchórzewski, P. Comparison of Selected Machine Learning Algorithms for Industrial Electrical Tomography. Sensors 2019, 19, 1521. [Google Scholar] [CrossRef] [PubMed]
- Marashdeh, Q.; Warsito, W.; Fan, L.S.; Teixeira, F.L. Nonlinear Forward Problem Solution for Electrical Capacitance Tomography Using Feed-Forward Neural Network. IEEE Sens. J. 2006, 6, 441–448. [Google Scholar] [CrossRef]
- Marashdeh, Q.; Warsito, W.; Fan, L.S.; Teixeira, F.L. A Nonlinear Image Reconstruction Technique for ECT Using a Combined Neural Network Approach. Meas. Sci. Technol. 2006, 17, 2097–2103. [Google Scholar] [CrossRef]
- Zhang, X.; Chen, X.; Wang, Z.; Zhang, M. EIT-4LDNN: A Novel Neural Network for Electrical Impedance Tomography. J. Phys. Conf. Ser. 2021, 1757, 012013. [Google Scholar] [CrossRef]
- Fu, R.; Wang, Z.; Zhang, X.; Wang, D.; Chen, X.; Wang, H. A Regularization-Guided Deep Imaging Method for Electrical Impedance Tomography. IEEE Sens. J. 2022, 22, 8760–8771. [Google Scholar] [CrossRef]
- Coxson, A.; Mihov, I.; Wang, Z.; Avramov, V.; Barnes, F.B.; Slizovskiy, S.; Mullan, C.; Timokhin, I.; Sanderson, D.; Kretinin, A.; et al. Machine Learning Enhanced Electrical Impedance Tomography for 2D Materials. Inverse Probl. 2022, 38, 085007. [Google Scholar] [CrossRef]
- Deabes, W.; Abdel-Hakim, A.E.; Bouazza, K.E.; Althobaiti, H. Adversarial Resolution Enhancement for Electrical Capacitance Tomography Image Reconstruction. Sensors 2022, 22, 3142. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, Q.; Zhang, R.; Li, X.; Duan, X.; Sun, Y.; Wang, J.; Jia, J. Image Reconstruction for Electrical Impedance Tomography (EIT) With Improved Wasserstein Generative Adversarial Network (WGAN). IEEE Sens. J. 2023, 23, 4466–4475. [Google Scholar] [CrossRef]
- Vu, M.T.; Jardani, A. Convolutional Neural Networks with SegNet Architecture Applied to Three-Dimensional Tomography of Subsurface Electrical Resistivity: CNN-3D-ERT. Geophys. J. Int. 2021, 225, 1319–1331. [Google Scholar] [CrossRef]
- Chen, Z.; Ma, G.; Jiang, Y.; Wang, B.; Soleimani, M. Application of Deep Neural Network to the Reconstruction of Two-Phase Material Imaging by Capacitively Coupled Electrical Resistance Tomography. Electronics 2021, 10, 1058. [Google Scholar] [CrossRef]
- Fernández-Fuentes, X.; Mera, D.; Gómez, A.; Vidal-Franco, I. Towards a Fast and Accurate EIT Inverse Problem Solver: A Machine Learning Approach. Electronics 2018, 7, 422. [Google Scholar] [CrossRef]
- Ren, S.; Guan, R.; Liang, G.; Dong, F. RCRC: A Deep Neural Network for Dynamic Image Reconstruction of Electrical Impedance Tomography. IEEE Trans. Instrum. Meas. 2021, 70, 4505311. [Google Scholar] [CrossRef]
- Cheng, Y.; Fan, W. R-UNet Deep Learning-Based Damage Detection of CFRP With Electrical Impedance Tomography. IEEE Trans. Instrum. Meas. 2022, 71, 4506308. [Google Scholar] [CrossRef]
- Zhu, L.; Lu, W.; Soleimani, M.; Li, Z.; Zhang, M. Electrical Impedance Tomography Guided by Digital Twins and Deep Learning for Lung Monitoring. IEEE Trans. Instrum. Meas. 2023, 72, 4009309. [Google Scholar] [CrossRef]
- Liu, D.; Wang, J.; Shan, Q.; Smyl, D.; Deng, J.; Du, J. DeepEIT: Deep Image Prior Enabled Electrical Impedance Tomography. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 9627–9638. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Zhang, R.; Wang, Q.; Duan, X.; Sun, Y.; Wang, J. SAR-CGAN: Improved Generative Adversarial Network for EIT Reconstruction of Lung Diseases. Biomed. Signal Process. Control 2023, 81, 104421. [Google Scholar] [CrossRef]
- Tian, X.; Liu, X.; Zhang, T.; Ye, J.; Zhang, W.; Zhang, L.; Shi, X.; Fu, F.; Li, Z.; Xu, C. Effective Electrical Impedance Tomography Based on Enhanced Encoder-Decoder Using Atrous Spatial Pyramid Pooling Module. IEEE J. Biomed. Health Inform. 2023, 27, 3282–3291. [Google Scholar] [CrossRef]
- Herzberg, W.; Rowe, D.B.; Hauptmann, A.; Hamilton, S.J. Graph Convolutional Networks for Model-Based Learning in Nonlinear Inverse Problems. IEEE Trans. Comput. Imaging 2021, 7, 1341–1353. [Google Scholar] [CrossRef]
- Minhas, A.S.; Reddy, M.R. Neural Network Based Approach for Anomaly Detection in the Lungs Region by Electrical Impedance Tomography. Physiol. Meas. 2005, 26, 489. [Google Scholar] [CrossRef]
- Becher, T.; Bußmeyer, M.; Lautenschläger, I.; Schädler, D.; Weiler, N.; Frerichs, I. Characteristic Pattern of Pleural Effusion in Electrical Impedance Tomography Images of Critically Ill Patients. Br. J. Anaesth. 2018, 120, 1219–1228. [Google Scholar] [CrossRef]
- Hamilton, S.J.; Mueller, J.L.; Alsaker, M. Incorporating a Spatial Prior into Nonlinear D-Bar EIT Imaging for Complex Admittivities. IEEE Trans. Med. Imaging 2017, 36, 457–466. [Google Scholar] [CrossRef] [PubMed]
- Wei, Z.; Liu, D.; Chen, X. Dominant-Current Deep Learning Scheme for Electrical Impedance Tomography. IEEE Trans. Biomed. Eng. 2019, 66, 2546–2555. [Google Scholar] [CrossRef] [PubMed]
- Shin, K.; Mueller, J.L. Calderón’s Method with a Spatial Prior for 2-d Eit Imaging of Ventilation and Perfusion. Sensors 2021, 21, 5635. [Google Scholar] [CrossRef]
- Schullcke, B.; Gong, B.; Krueger-Ziolek, S.; Moeller, K. Reconstruction of Conductivity Change in Lung Lobes Utilizing Electrical Impedance Tomography. Curr. Dir. Biomed. Eng. 2017, 3, 513–516. [Google Scholar] [CrossRef]
- Wanta, D.; Makowiecka, O.; Smolik, W.T.; Kryszyn, J.; Domański, G.; Midura, M.; Wróblewski, P. Numerical Evaluation of Complex Capacitance Measurement Using Pulse Excitation in Electrical Capacitance Tomography. Electronics 2022, 11, 1864. [Google Scholar] [CrossRef]
- Kryszyn, J.; Smolik, W. 2D Modelling of a Sensor for Electrical Capacitance Tomography in Ectsim Toolbox. Inform. Control. Meas. Econ. Environ. Prot. 2017, 7, 146–149. [Google Scholar] [CrossRef]
- Wanta, D.; Smolik, W.T.; Kryszyn, J.; Wróblewski, P.; Midura, M. A Finite Volume Method Using a Quadtree Non-Uniform Structured Mesh for Modeling in Electrical Capacitance Tomography. Proc. Natl. Acad. Sci. India Sect. A Phys. Sci. 2022, 92, 443–452. [Google Scholar] [CrossRef]
- Imran, A.A.Z.; Hatamizadeh, A.; Ananth, S.P.; Ding, X.; Tajbakhsh, N.; Terzopoulos, D. Fast and Automatic Segmentation of Pulmonary Lobes from Chest CT Using a Progressive Dense V-Network. Comput. Methods Biomech. Biomed. Eng. Imaging Vis. 2020, 8, 509–518. [Google Scholar] [CrossRef]
- Jaspard, F.; Nadi, M.; Rouane, A. Dielectric Properties of Blood: An Investigation of Haematocrit Dependence. Physiol. Meas. 2003, 24, 137–147. [Google Scholar] [CrossRef]
- Treo, E.F.; Felice, C.J.; Tirado, M.C.; Valentinuzzi, M.E.; Cervantes, D.O. Comparative Analysis of Hematocrit Measurements by Dielectric and Impedance Techniques. IEEE Trans. Biomed. Eng. 2005, 52, 549–552. [Google Scholar] [CrossRef]
- Deabes, W.; Jamil Khayyat, K.M. Image Reconstruction in Electrical Capacitance Tomography Based on Deep Neural Networks. IEEE Sens. J. 2021, 21, 25818–25830. [Google Scholar] [CrossRef]
- Ye, Y.; Wang, H. Wuqiang Yang Image Reconstruction for Electrical Capacitance Tomography Based on Sparse Representation. IEEE Trans. Instrum. Meas. 2015, 64, 89–102. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J.L. Adam: A Method for Stochastic Optimization. In Proceedings of the 3rd International Conference on Learning Representations, ICLR 2015—Conference Track Proceedings, Diego, CA, USA, 22 December 2015. [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift. In Proceedings of the 32nd International Conference on Machine Learning, Lile, France, 6–11 July 2015; Volume 1, pp. 448–456. [Google Scholar]
- Deabes, W.; Abdel-Hakim, A.E. CGAN-ECT: Tomography Image Reconstruction from Electrical Capacitance Measurements Using CGANs. arXiv 2022, arXiv:2209.03737. [Google Scholar]
- Isola, P.; Zhu, J.Y.; Zhou, T.; Efros, A.A. Image-to-Image Translation with Conditional Adversarial Networks. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 5967–5976. [Google Scholar] [CrossRef]
- DeVries, T.; Romero, A.; Pineda, L.; Taylor, G.W.; Drozdzal, M. On the Evaluation of Conditional GANs. arXiv 2019, arXiv:1907.08175. [Google Scholar]
- Rashidi, H.H.; Albahra, S.; Robertson, S.; Tran, N.K.; Hu, B. Common Statistical Concepts in the Supervised Machine Learning Arena. Front. Oncol. 2023, 13, 1130229. [Google Scholar] [CrossRef]
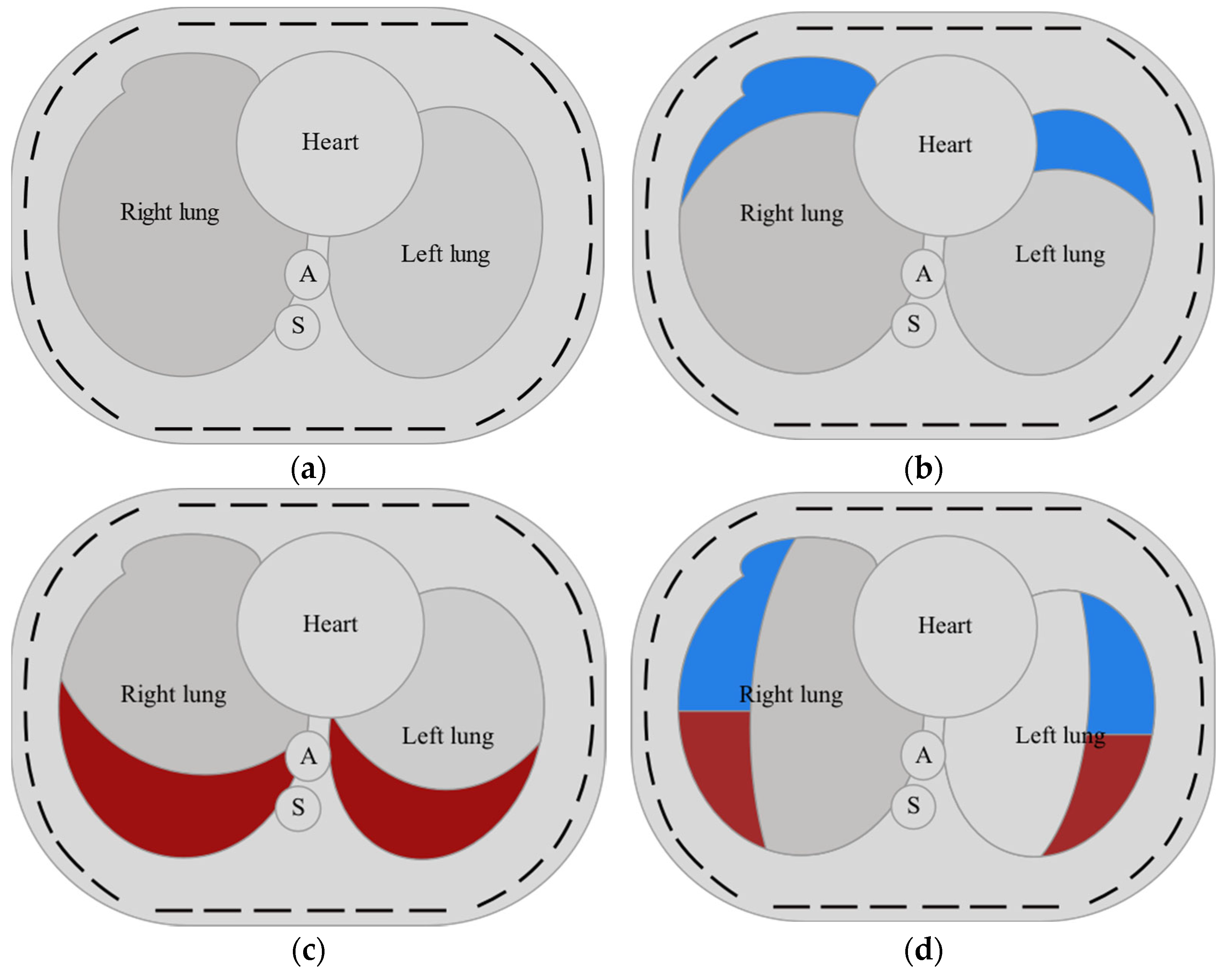
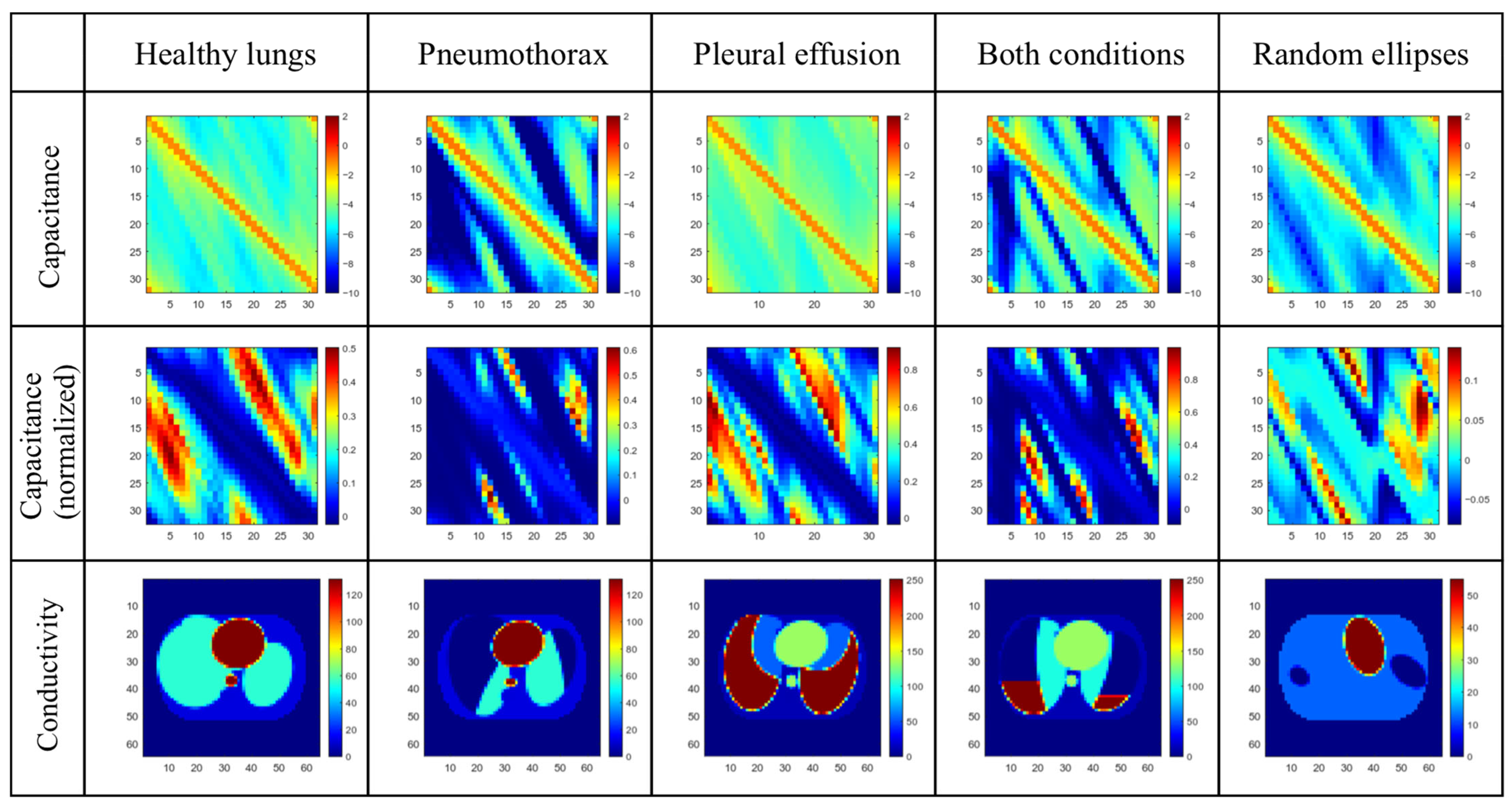

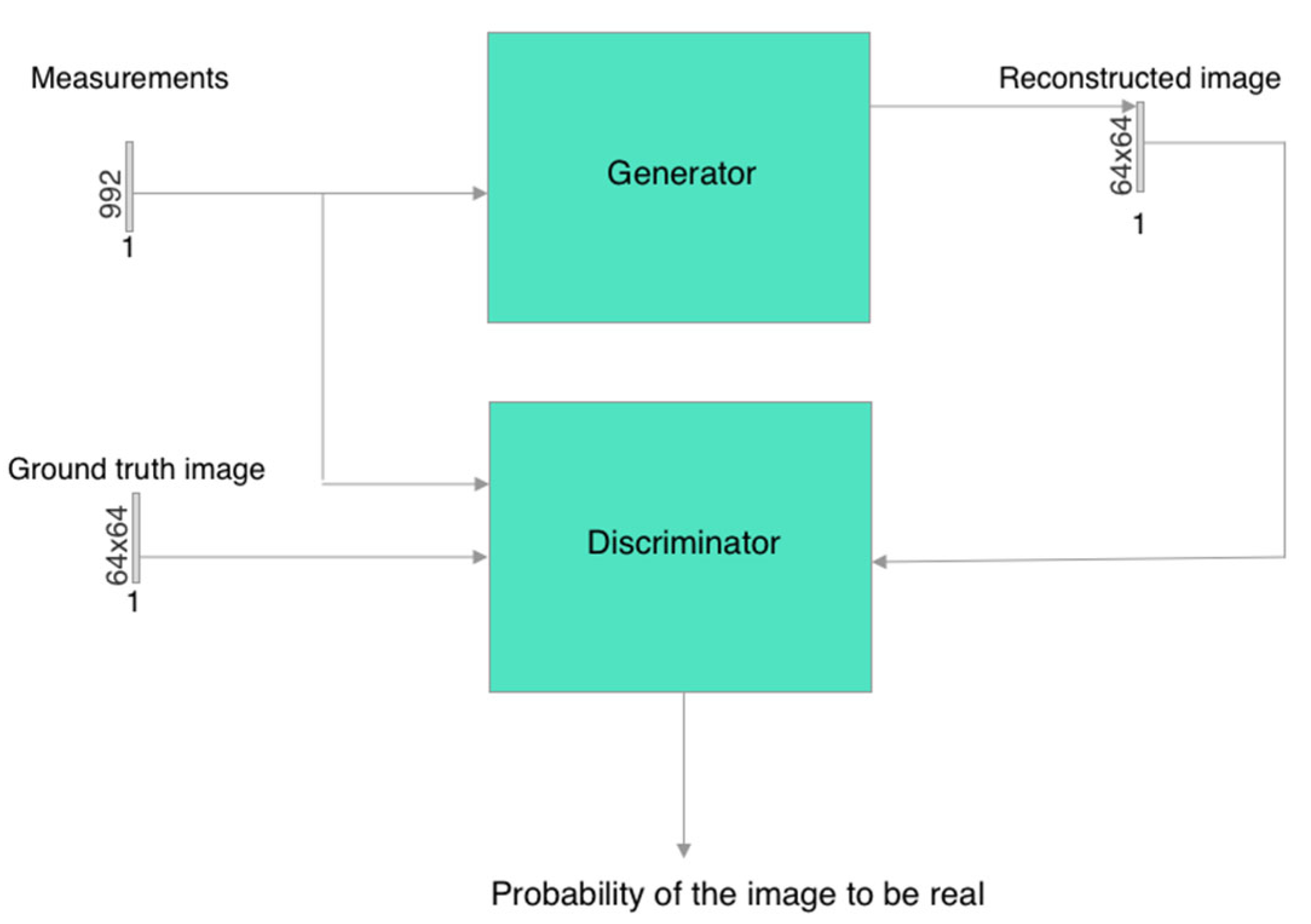
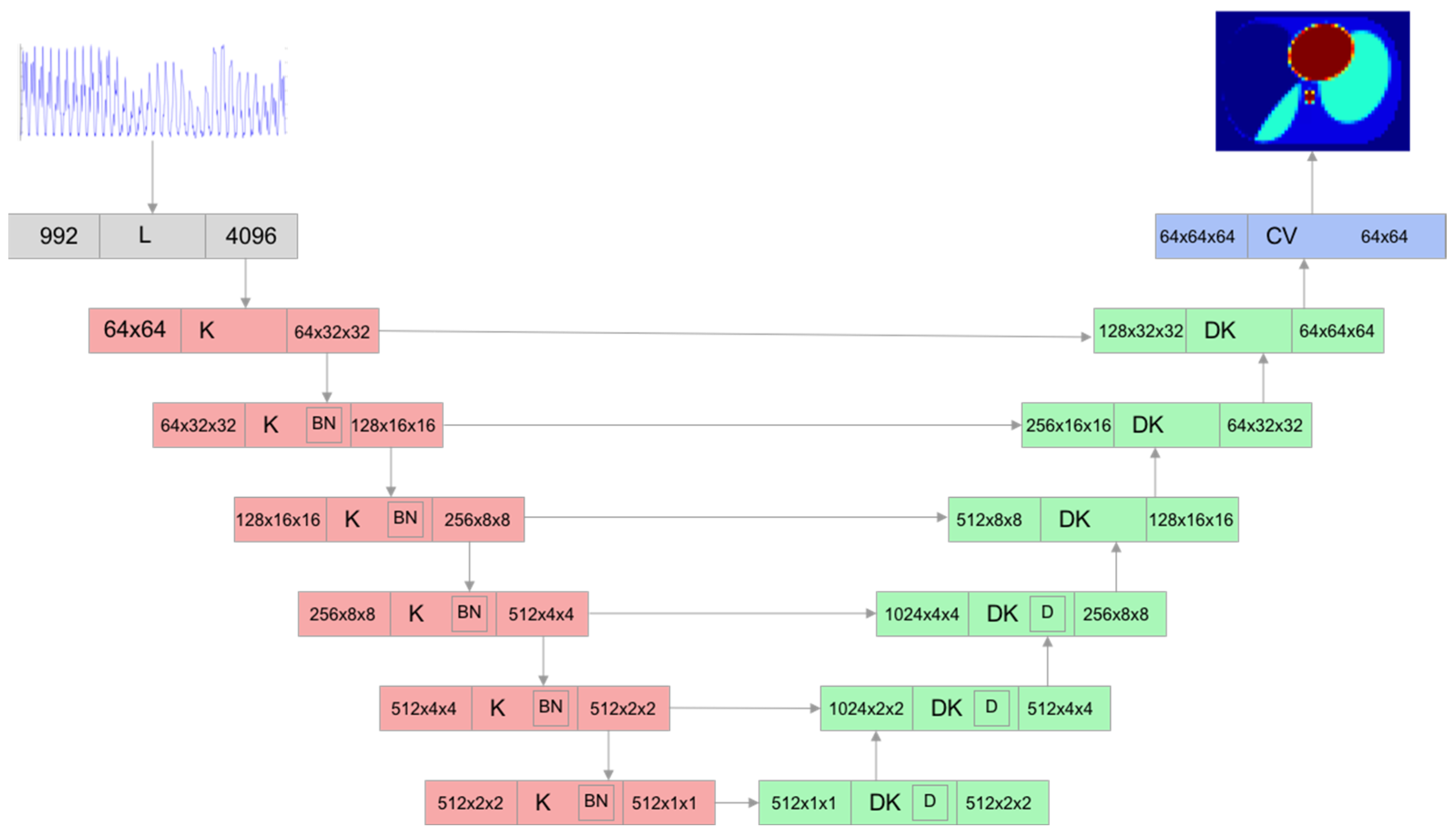
| Healthy Lungs | Pneumothorax | Pleural Effusion | ||
|---|---|---|---|---|
| Inspiration | Expiration | |||
| Relative permittivity | 31.6 | 67.1 | 1 | 70 |
| Conductivity, S/m | 0.306 | 0.559 | 10−15 | 1.4 |
| Component | Permittivity | Conductivity |
|---|---|---|
| Electrodes (metal) | 1 | 0.0643 |
| Isolation (plastic) | 2 | 10−21 |
| Spine | 10.53 | 0.0643 |
| Heart, Aorta | 90.8 | 0.733 |
| Fat | 12.7 | 0.068 |
| Method | RMSE | PSNR | SSIM | CC | DV | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| µ | M | σ | µ | M | σ | µ | M | σ | µ | M | σ | AUC | |
| FCNN | 14.61 | 14.49 | 5.49 | 20.37 | 20.55 | 2.92 | 0.78 | 0.79 | 0.05 | 0.96 | 0.97 | 0.05 | 0.99 |
| cGAN | 8.86 | 8.17 | 4.13 | 27.06 | 27.39 | 3.07 | 0.87 | 0.87 | 0.03 | 0.98 | 0.99 | 0.03 | 0.99 |
| LBP | 54.37 | 53.94 | 14.4 | 12.45 | 12.52 | 1.23 | 0.11 | 0.12 | 0.02 | 0.68 | 0.68 | 0.06 | 0.82 |
| TPINV | 57.22 | 57.48 | 18.16 | 12.93 | 12.73 | 1.97 | 0.19 | 0.19 | 0.02 | 0.62 | 0.63 | 0.1 | 0.77 |
| Method | RMSE | PSNR | SSIM | CC | DV | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| µ | M | σ | µ | M | σ | µ | M | σ | µ | M | σ | AUC | |
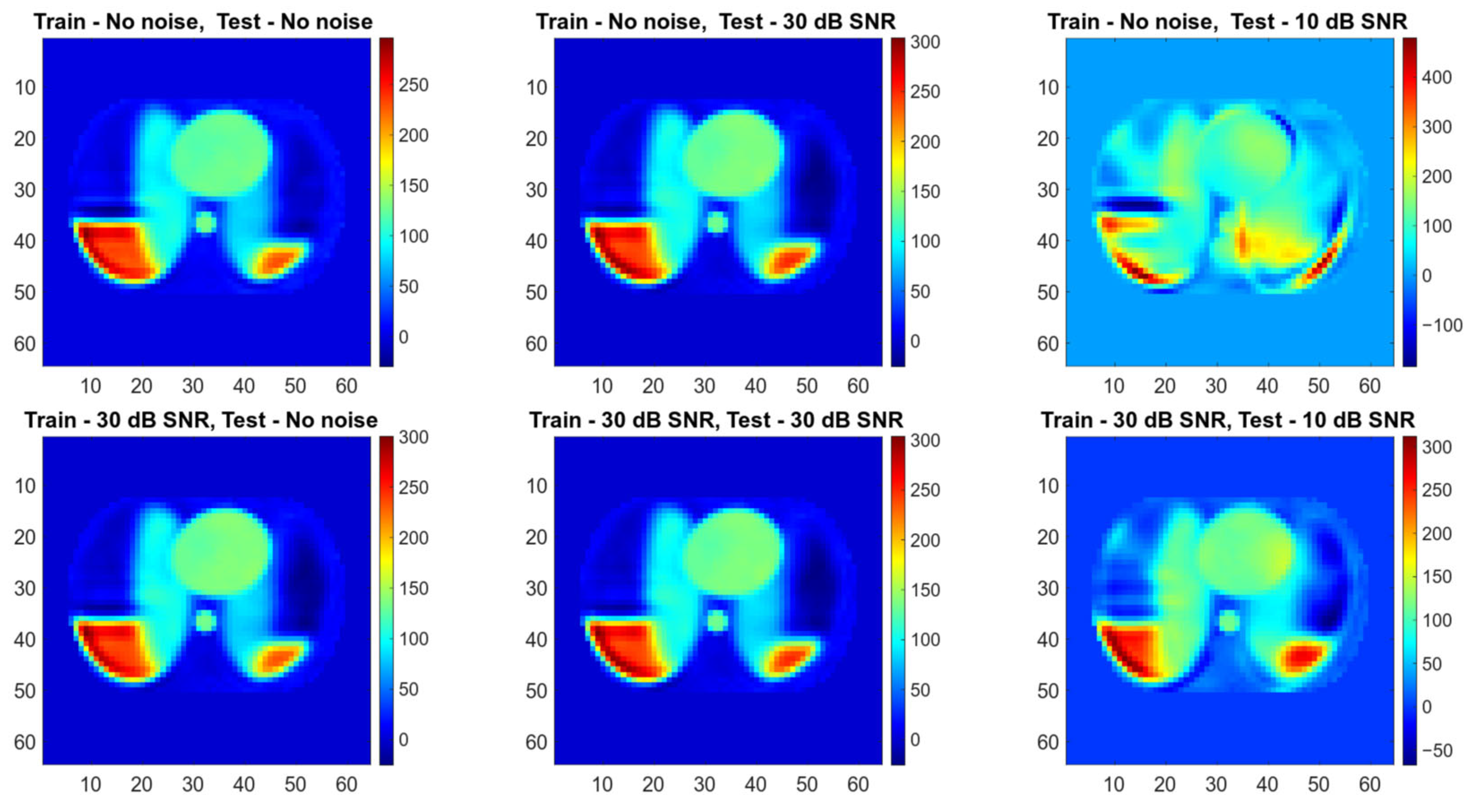
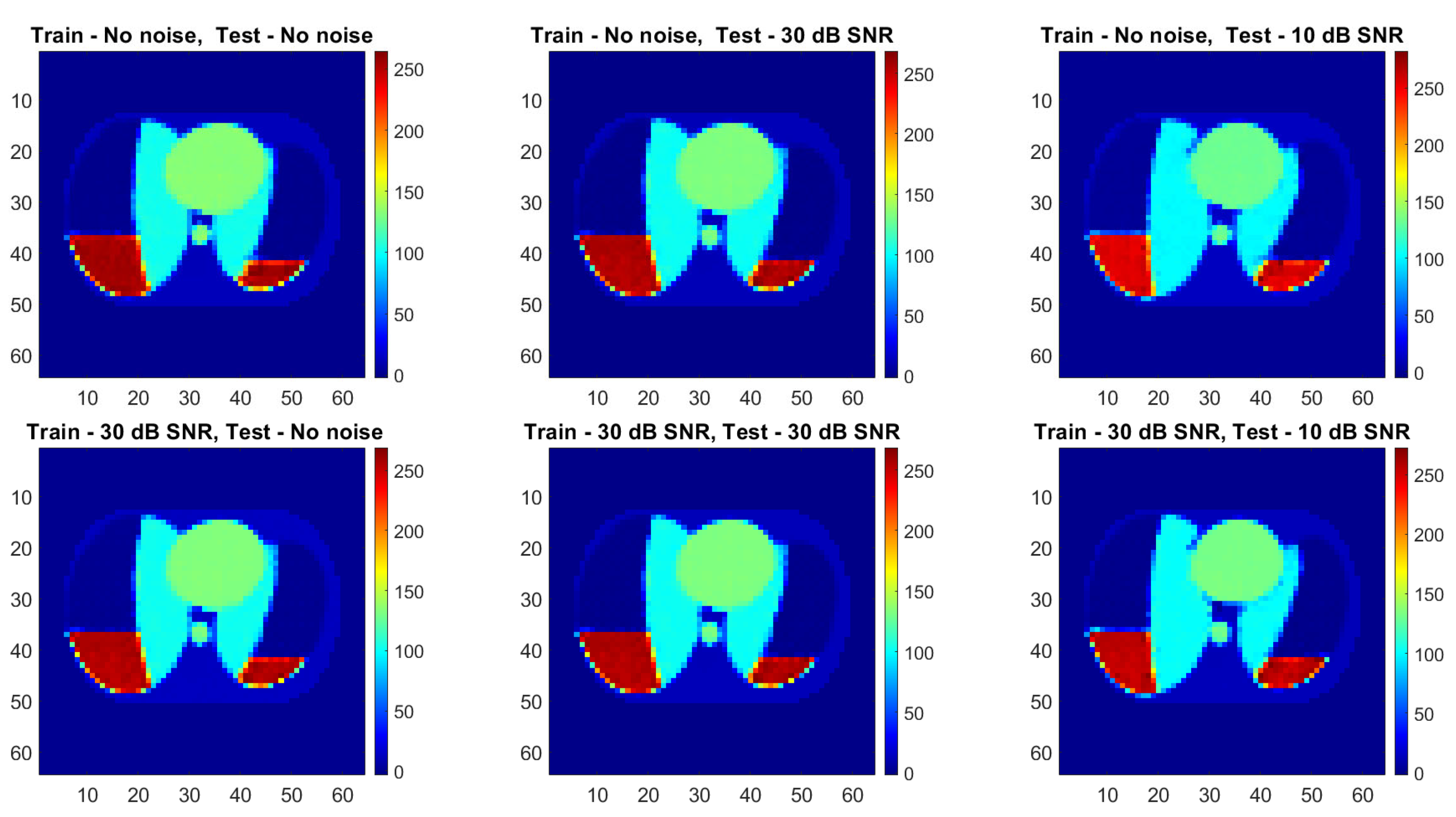
| Training—no noise, Testing—30 dB SNR | |||||||||||||
| FCNN | 14.84 | 14.76 | 5.53 | 20.44 | 20.66 | 3.02 | 0.78 | 0.79 | 0.05 | 0.96 | 0.97 | 0.05 | 0.99 |
| cGAN | 9.45 | 8.96 | 4.37 | 26.9 | 27.17 | 2.96 | 0.87 | 0.87 | 0.03 | 0.98 | 0.99 | 0.03 | 0.99 |
| Training—no noise, Testing—10 dB SNR | |||||||||||||
| FCNN | 62.51 | 61.18 | 14.17 | 11.2 | 11.22 | 1.83 | 0.48 | 0.48 | 0.05 | 0.68 | 0.7 | 0.13 | 0.79 |
| cGAN | 18.00 | 17.36 | 7.37 | 21.67 | 22.01 | 3.67 | 0.81 | 0.82 | 0.04 | 0.95 | 0.96 | 0.06 | 0.97 |
| Training—30 dB SNR, Testing—30 dB SNR | |||||||||||||
| FCNN | 15.01 | 14.92 | 5.52 | 20.28 | 20.5 | 2.97 | 0.77 | 0.79 | 0.05 | 0.96 | 0.97 | 0.05 | 0.99 |
| cGAN | 9.58 | 9.07 | 4.43 | 26.8 | 27.06 | 2.98 | 0.87 | 0.87 | 0.03 | 0.98 | 0.99 | 0.03 | 0.99 |
| Training—30 dB SNR, Testing—10 dB SNR | |||||||||||||
| FCNN | 27.55 | 27.13 | 6.61 | 14.96 | 15.12 | 2.38 | 0.64 | 0.65 | 0.06 | 0.89 | 0.91 | 0.08 | 0.94 |
| cGAN | 17.54 | 16.86 | 7.29 | 22.03 | 22.41 | 3.74 | 0.82 | 0.82 | 0.04 | 0.95 | 0.97 | 0.06 | 0.97 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ivanenko, M.; Smolik, W.T.; Wanta, D.; Midura, M.; Wróblewski, P.; Hou, X.; Yan, X. Image Reconstruction Using Supervised Learning in Wearable Electrical Impedance Tomography of the Thorax. Sensors 2023, 23, 7774. https://doi.org/10.3390/s23187774
Ivanenko M, Smolik WT, Wanta D, Midura M, Wróblewski P, Hou X, Yan X. Image Reconstruction Using Supervised Learning in Wearable Electrical Impedance Tomography of the Thorax. Sensors. 2023; 23(18):7774. https://doi.org/10.3390/s23187774
Chicago/Turabian StyleIvanenko, Mikhail, Waldemar T. Smolik, Damian Wanta, Mateusz Midura, Przemysław Wróblewski, Xiaohan Hou, and Xiaoheng Yan. 2023. "Image Reconstruction Using Supervised Learning in Wearable Electrical Impedance Tomography of the Thorax" Sensors 23, no. 18: 7774. https://doi.org/10.3390/s23187774
APA StyleIvanenko, M., Smolik, W. T., Wanta, D., Midura, M., Wróblewski, P., Hou, X., & Yan, X. (2023). Image Reconstruction Using Supervised Learning in Wearable Electrical Impedance Tomography of the Thorax. Sensors, 23(18), 7774. https://doi.org/10.3390/s23187774







