ADSTGCN: A Dynamic Adaptive Deeper Spatio-Temporal Graph Convolutional Network for Multi-Step Traffic Forecasting
Abstract
1. Introduction
- To address the over-smoothing problem arising from deepening the network layers in multi-step traffic forecasting with Graph Convolutional Networks, we employ a technique of dynamically adjusting hidden layer connections and adaptively modifying the hidden layer weights to prevent model degradation.
- We propose a parameter-sharing adaptive graph convolution method for multi-step traffic forecasting, which considers the ever-changing complex spatio-temporal relationships within the traffic network. This is able to adaptively learn and adjust the spatial dependencies and structures within the traffic network by building the adaptive matrix for parameter sharing.
- We propose Dynamic Adaptive Deeper Spatio-Temporal Graph Convolutional Networks (ADSTGCN), a new traffic forecasting model. It uses the diffusion graph convolutional network to obtain spatial dependencies in traffic and the temporal convolutional network to obtain temporal dependencies for better traffic forecasting.
- We validate our model on two traffic datasets and show better traffic forecasting results than existing advanced baselines.
2. Related Work
3. Methodology
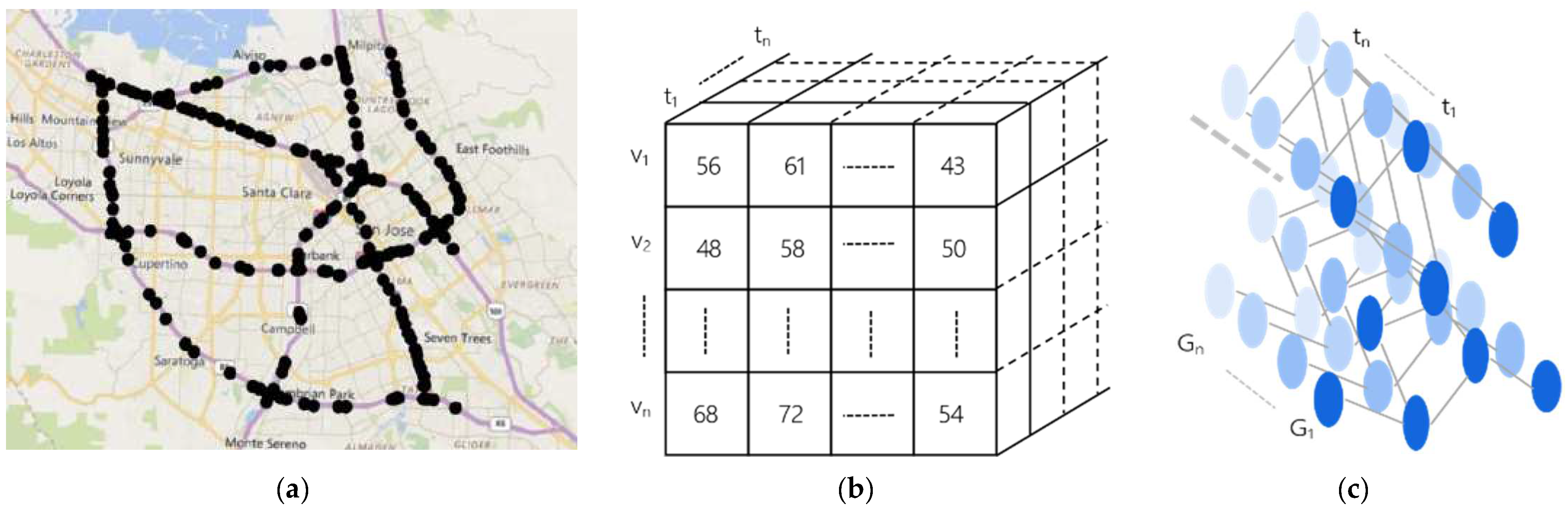
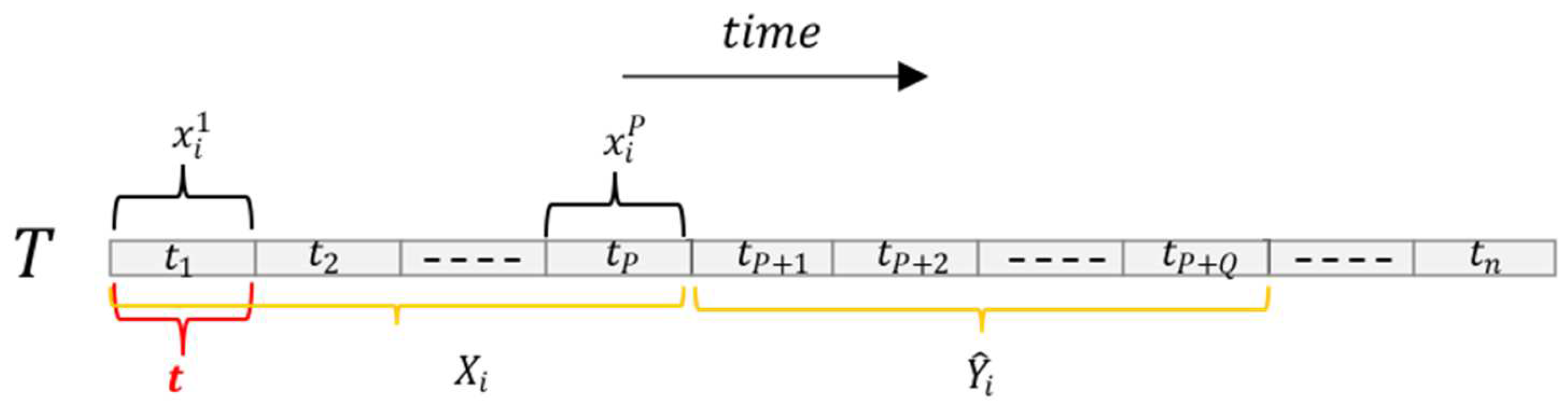
3.1. Problem Definition
3.2. Overall Architecture
3.3. Input Data Processing
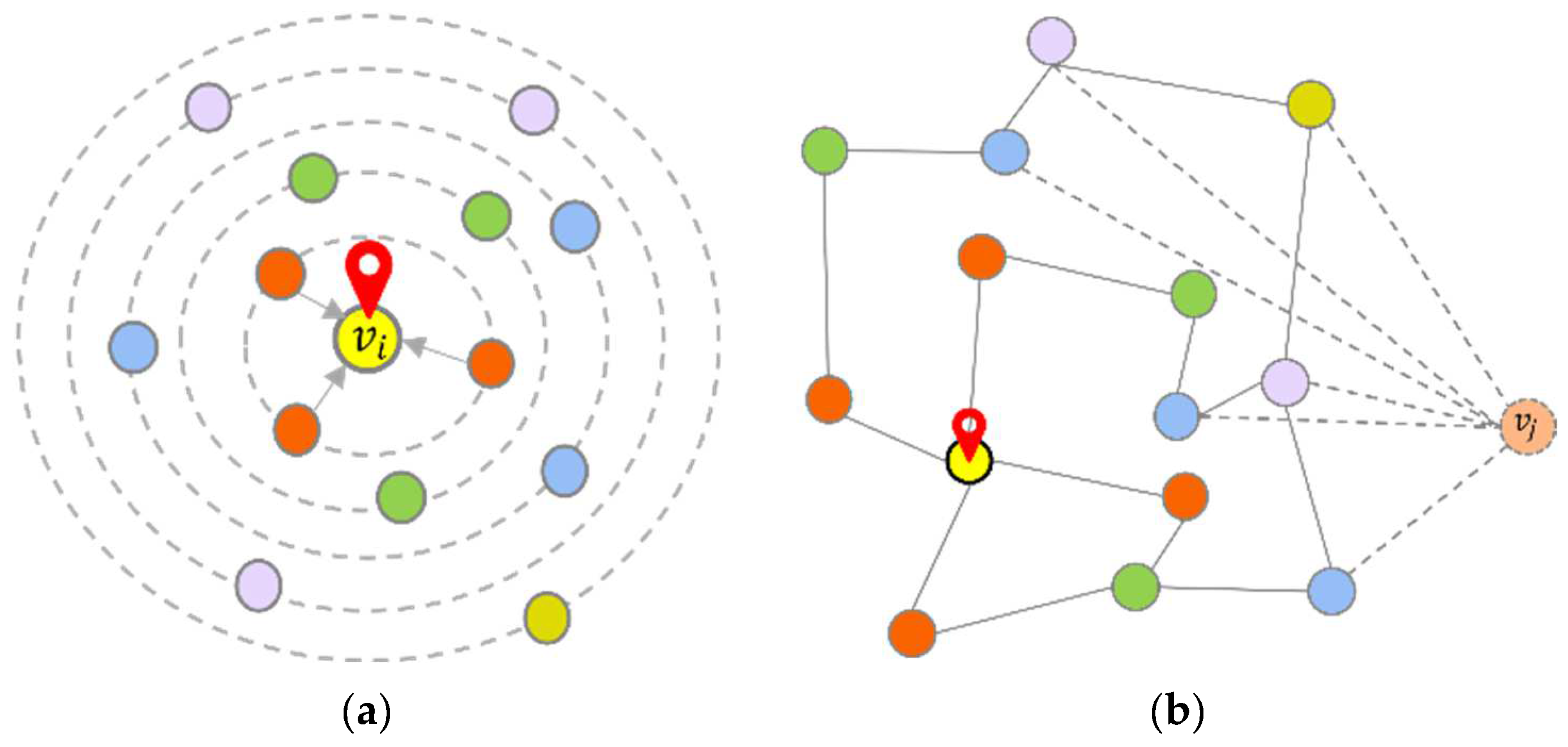
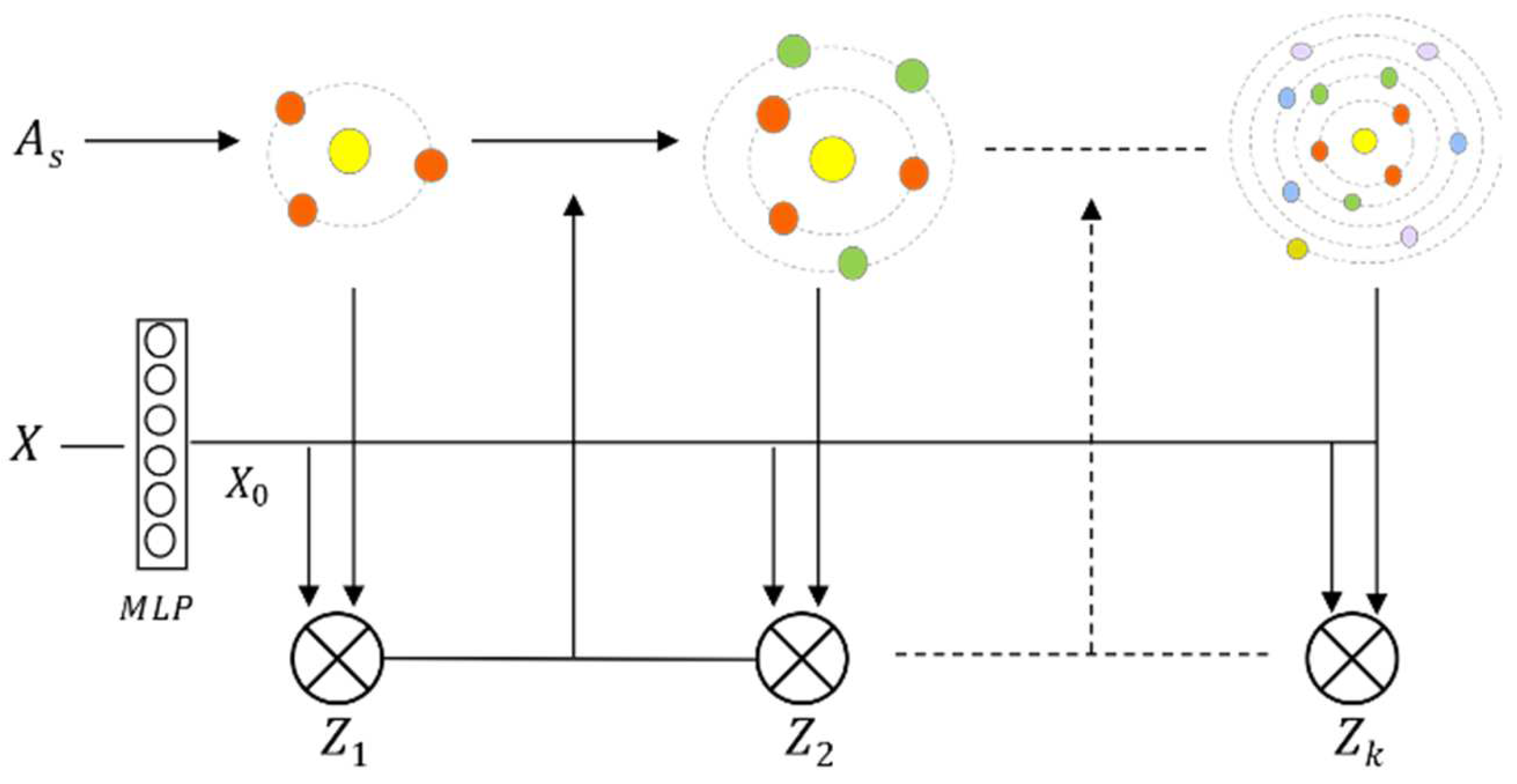
3.4. Deep Diffusion Graph Convolution
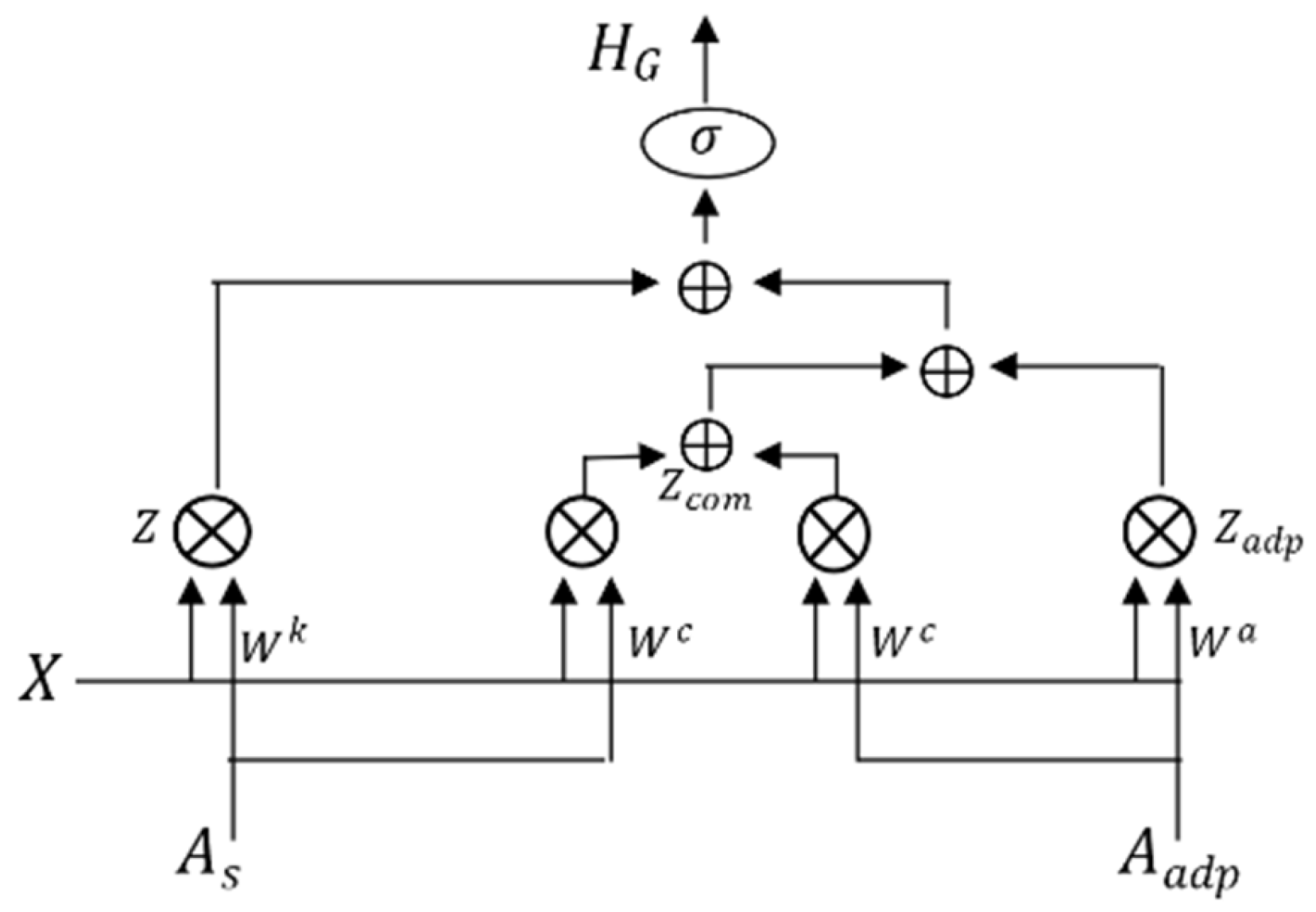
3.5. Adaptive Deep Graph Convolution
3.6. Dilated Causal Temporal Convolution
3.7. Attention Mechanism
4. Experiments
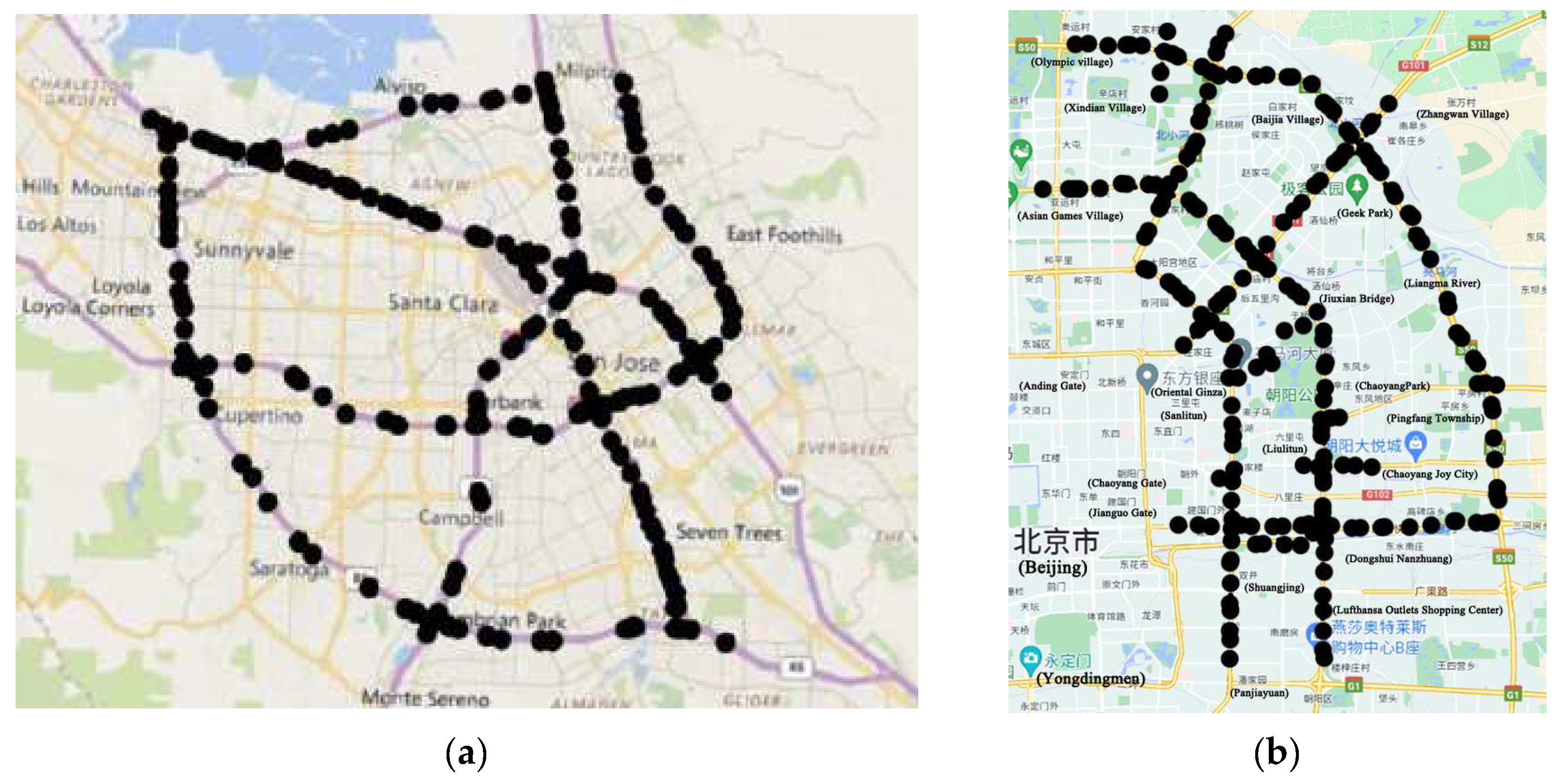
4.1. DataSets
4.2. Experimental Settings
4.3. Baselines
4.4. Experimental Results
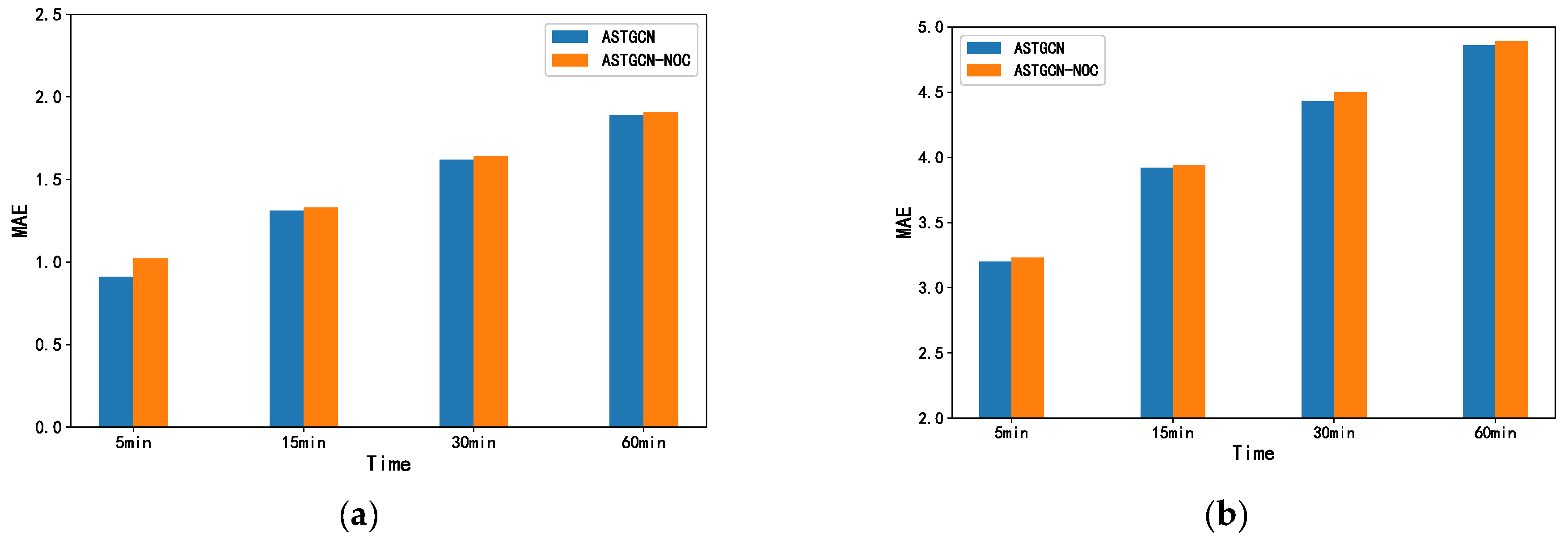
4.5. Ablation Study
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bui, K.-H.N.; Cho, J.; Yi, H. Spatial-Temporal Graph Neural Network for Traffic Forecasting: An Overview and Open Research Issues. Appl. Intell. 2022, 52, 2763–2774. [Google Scholar] [CrossRef]
- Xu, Y.; Cai, X.; Wang, E.; Liu, W.; Yang, Y.; Yang, F. Dynamic Traffic Correlations Based Spatio-Temporal Graph Convolutional Network for Urban Traffic Prediction. Inf. Sci. 2022, 621, 580–595. [Google Scholar] [CrossRef]
- Song, C.; Lin, Y.; Guo, S.; Wan, H. Spatial-Temporal Synchronous Graph Convolutional Networks: A New Framework for Spatial-Temporal Network Data Forecasting. Proc. AAAI Conf. Artif. Intell. 2020, 34, 914–921. [Google Scholar] [CrossRef]
- Zhang, X.; Huang, C.; Xu, Y.; Xia, L.; Dai, P.; Bo, L.; Zhang, J.; Zheng, Y. Traffic Flow Forecasting with Spatial-Temporal Graph Diffusion Network. Proc. AAAI Conf. Artif. Intell. 2021, 35, 15008–15015. [Google Scholar] [CrossRef]
- Chen, W.; Chen, L.; Xie, Y.; Cao, W.; Gao, Y.; Feng, X. Multi-Range Attentive Bicomponent Graph Convolutional Network for Traffic Forecasting. Proc. AAAI Conf. Artif. Intell. 2020, 34, 3529–3536. [Google Scholar] [CrossRef]
- Zhou, Z.; Yang, Z.; Zhang, Y.; Huang, Y.; Chen, H.; Yu, Z. A Comprehensive Study of Speed Prediction in Transportation System: From Vehicle to Traffic. iScience 2022, 25, 103909. [Google Scholar] [CrossRef]
- Li, Y.; Yu, R.; Shahabi, C.; Liu, Y. Diffusion Convolutional Recurrent Neural Network: Data-Driven Traffic Forecasting. In Proceedings of the International Conference on Learning Representations, ICLR, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Yu, B.; Yin, H.; Zhu, Z. Spatio-Temporal Graph Convolutional Networks: A Deep Learning Framework for Traffic Forecasting. In Proceedings of the International Joint Conference on Artificial Intelligence, IJCAI, Stockholm, Sweden, 13–19 July 2018; pp. 3634–3640. [Google Scholar]
- Huang, R.; Huang, C.; Liu, Y.; Dai, G.; Kong, W. LSGCN: Long Short-Term Traffic Prediction with Graph Convolutional Networks. In Proceedings of the Twenty-Ninth International Joint Conference on Artificial Intelligence, Yokohama, Japan, 7–15 January 2021; International Joint Conferences on Artificial Intelligence Organization: Yokohama, Japan, 2020; pp. 2355–2361. [Google Scholar]
- Guo, K.; Hu, Y.; Sun, Y.; Qian, S.; Gao, J.; Yin, B. Hierarchical Graph Convolution Network for Traffic Forecasting. Proc. AAAI Conf. Artif. Intell. 2021, 35, 151–159. [Google Scholar] [CrossRef]
- Wu, Z.; Pan, S.; Long, G.; Jiang, J.; Zhang, C. Graph WaveNet for Deep Spatial-Temporal Graph Modeling. arXiv 2019, arXiv:1906.00121. [Google Scholar]
- Chen, T.; Zhou, K.; Duan, K.; Zheng, W.; Wang, P.; Hu, X.; Wang, Z. Bag of Tricks for Training Deeper Graph Neural Networks: A Comprehensive Benchmark Study. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 45, 2769–2781. [Google Scholar] [CrossRef] [PubMed]
- Rong, Y.; Huang, W.; Xu, T.; Huang, J. DropEdge: Towards Deep Graph Convolutional Networks on Node Classification. arXiv 2019, arXiv:1907.10903. [Google Scholar]
- Oono, K.; Suzuki, T. Graph Neural Networks Exponentially Lose Expressive Power for Node Classification. arXiv 2019, arXiv:1905.10947. [Google Scholar]
- Park, C.; Lee, C.; Bahng, H.; Tae, Y.; Jin, S.; Kim, K.; Ko, S.; Choo, J. ST-GRAT: A Novel Spatio-Temporal Graph Attention Networks for Accurately Forecasting Dynamically Changing Road Speed. In Proceedings of the 29th ACM International Conference on Information & Knowledge Management, Virtual Conference, 19–23 October 2020; pp. 1215–1224. [Google Scholar]
- Han, L.; Du, B.; Sun, L.; Fu, Y.; Lv, Y.; Xiong, H. Dynamic and Multi-Faceted Spatio-Temporal Deep Learning for Traffic Speed Forecasting. In Proceedings of the 27th ACM SIGKDD Conference on Knowledge Discovery & Data Mining, Singapore, 14–18 August 2021; pp. 547–555. [Google Scholar]
- Cao, D.; Wang, Y.; Duan, J.; Zhang, C.; Zhu, X.; Huang, C.; Tong, Y.; Xu, B.; Bai, J.; Tong, J.; et al. Spectral Temporal Graph Neural Network for Multivariate Time-Series Forecasting. In Advances in Neural Information Processing Systems; Larochelle, H., Ranzato, M., Hadsell, R., Balcan, M.F., Lin, H., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2020; Volume 33, pp. 17766–17778. [Google Scholar]
- Bai, L.; Yao, L.; Li, C.; Wang, X.; Wang, C. Adaptive Graph Convolutional Recurrent Network for Traffic Forecasting. Adv. Neural Inf. Process. Syst. 2020, 33, 17804–17815. [Google Scholar] [CrossRef]
- Ye, J.; Xue, S.; Jiang, A. Attention-Based Spatio-Temporal Graph Convolutional Network Considering External Factors for Multi-Step Traffic Flow Prediction. Digit. Commun. Netw. 2021, 8, 343–350. [Google Scholar] [CrossRef]
- Guo, S.; Lin, Y.; Feng, N.; Song, C.; Wan, H. Attention Based Spatial-Temporal Graph Convolutional Networks for Traffic Flow Forecasting. Proc. AAAI Conf. Artif. Intell. 2019, 33, 922–929. [Google Scholar] [CrossRef]
- Zheng, C.; Fan, X.; Wang, C.; Qi, J. GMAN: A Graph Multi-Attention Network for Traffic Prediction. arXiv 2019, arXiv:1911.08415. [Google Scholar] [CrossRef]
- Cui, Z.; Henrickson, K.; Ke, R.; Wang, Y. Traffic Graph Convolutional Recurrent Neural Network: A Deep Learning Framework for Network-Scale Traffic Learning and Forecasting. IEEE Trans. Intell. Transp. Syst. 2020, 21, 4883–4894. [Google Scholar] [CrossRef]
- Kipf, T.; Welling, M. Semi-Supervised Classification with Graph Convolutional Networks. arXiv 2017, arXiv:1609.02907. [Google Scholar]
- Atwood, J.; Towsley, D. Diffusion-Convolutional Neural Networks. In Advances in Neural Information Processing Systems; Curran Associates, Inc.: Red Hook, NY, USA, 2016; Volume 29, pp. 2001–2009. [Google Scholar]
- Veličković, P.; Cucurull, G.; Casanova, A.; Romero, A.; Liò, P.; Bengio, Y. Graph Attention Networks. In Proceedings of the International Conference on Learning Representations, ICLR, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Niepert, M.; Ahmed, M.; Kutzkov, K. Learning Convolutional Neural Networks for Graphs. In Proceedings of the 33rd International Conference on International Conference on Machine Learning, JMLR.org, New York, NY, USA, 19–24 June 2016; Volume 48, pp. 2014–2023. [Google Scholar]
- Defferrard, M.; Bresson, X.; Vandergheynst, P. Convolutional Neural Networks on Graphs with Fast Localized Spectral Filtering. Adv. Neural Inf. Process. Syst. 2016, 29, 3844–3852. [Google Scholar]
- Huang, J.; Luo, K.; Cao, L.; Wen, Y.; Zhong, S. Learning Multiaspect Traffic Couplings by Multirelational Graph Attention Networks for Traffic Prediction. IEEE Trans. Intell. Transp. Syst. 2022, 23, 20681–20695. [Google Scholar] [CrossRef]
- Zhang, K.; He, F.; Zhang, Z.; Lin, X.; Li, M. Graph Attention Temporal Convolutional Network for Traffic Speed Forecasting on Road Networks. Transp. B Transp. Dyn. 2021, 9, 153–171. [Google Scholar] [CrossRef]
- Zhu, J.; Wang, Q.; Tao, C.; Deng, H.; Zhao, L.; Li, H. AST-GCN: Attribute-Augmented Spatiotemporal Graph Convolutional Network for Traffic Forecasting. IEEE Access 2021, 9, 35973–35983. [Google Scholar] [CrossRef]
- Zhang, S.; Guo, Y.; Zhao, P.; Zheng, C.; Chen, X. A Graph-Based Temporal Attention Framework for Multi-Sensor Traffic Flow Forecasting. IEEE Trans. Intell. Transport. Syst. 2021, 23, 7743–7758. [Google Scholar] [CrossRef]
- Huang, X.; Tang, J.; Yang, X.; Xiong, L. A Time-Dependent Attention Convolutional LSTM Method for Traffic Flow Prediction. Appl. Intell. 2022, 52, 17371–17386. [Google Scholar] [CrossRef]
- Sserwadda, A.; Ozcan, A.; Yaslan, Y. Structural and Topological Guided GCN for Link Prediction in Temporal Networks. J. Ambient. Intell. Humaniz. Comput. 2023, 14, 9667–9675. [Google Scholar] [CrossRef]
- Ni, Q.; Zhang, M. STGMN: A Gated Multi-Graph Convolutional Network Framework for Traffic Flow Prediction. Appl. Intell. 2022, 52, 15026–15039. [Google Scholar] [CrossRef]
- Chen, Y.; Xie, Z. Multi-Channel Fusion Graph Neural Network for Multivariate Time Series Forecasting. J. Comput. Sci. 2022, 64, 101862. [Google Scholar] [CrossRef]
- Bai, S.; Kolter, J.Z.; Koltun, V. An Empirical Evaluation of Generic Convolutional and Recurrent Networks for Sequence Modeling. arXiv 2018, arXiv:1803.01271. [Google Scholar]
- Cui, Z.; Zhang, J.; Noh, G.; Park, H.J. MFDGCN: Multi-Stage Spatio-Temporal Fusion Diffusion Graph Convolutional Network for Traffic Prediction. Appl. Sci. 2022, 12, 2688. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention Is All You Need. arXiv 2017, arXiv:1706.03762. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Grover, A.; Leskovec, J. Node2vec: Scalable Feature Learning for Networks. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining; Association for Computing Machinery: New York, NY, USA, 2016; pp. 855–864. [Google Scholar]
- Zhou, K.; Dong, Y.; Wang, K.; Lee, W.S.; Hooi, B.; Xu, H.; Feng, J. Understanding and Resolving Performance Degradation in Deep Graph Convolutional Networks. In Proceedings of the 30th ACM International Conference on Information & Knowledge Management, Queensland, Australia, 1–5 November 2021; pp. 2728–2737. [Google Scholar]
- Liu, M.; Gao, H.; Ji, S. Towards Deeper Graph Neural Networks. In Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining; Association for Computing Machinery, San Francisco, CA, USA, 6–10 July 2020; pp. 338–348. [Google Scholar]
- Smith, B.L.; Demetsky, M.J. Traffic Flow Forecasting: Comparison of Modeling Approaches. J. Transp. Eng. 1997, 123, 261–266. [Google Scholar] [CrossRef]
- Ang, A.; Piazzesi, M. A No-Arbitrage Vector Autoregression of Term Structure Dynamics with Macroeconomic and Latent Variables. J. Monet. Econ. 2003, 50, 745–787. [Google Scholar] [CrossRef]
- Sutskever, I.; Vinyals, O.; Le, Q.V. Sequence to Sequence Learning with Neural Networks. In Proceedings of the 27th International Conference on Neural Information Processing Systems, Montreal, QC, Canada, 8–13 December 2014; MIT Press: Cambridge, MA, USA, 2014; Volume 2, pp. 3104–3112. [Google Scholar]
- Wu, Z.; Pan, S.; Long, G.; Jiang, J.; Chang, X.; Zhang, C. Connecting the Dots: Multivariate Time Series Forecasting with Graph Neural Networks. In Proceedings of the 26th ACM SIGKDD Conference on Knowledge Discovery and Data Mining (KDD ’20), Virtual Event, CA, USA, 23–27 August 2020; ACM: New York, NY, USA, 2020. [Google Scholar] [CrossRef]






| Method | 15 min | 30 min | 60 min | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| MAE | RMSE | MAPE | MAE | RMSE | MAPE | MAE | RMSE | MAPE | ||
| PEMS_BAY | HA [43] | 2.88 | 5.59 | 6.80% | 2.88 | 5.59 | 6.80% | 2.88 | 5.59 | 6.80% |
| VAR [44] | 1.74 | 3.16 | 3.60% | 2.32 | 4.25 | 5.00% | 2.93 | 5.44 | 6.50% | |
| FC-LSTM [45] | 2.05 | 4.19 | 4.80% | 2.20 | 4.55 | 5.20% | 2.37 | 4.96 | 5.70% | |
| DCRNN [7] | 1.38 | 2.95 | 2.90% | 1.74 | 3.97 | 3.90% | 2.07 | 4.74 | 4.90% | |
| STGCN [8] | 1.36 | 2.96 | 2.90% | 1.81 | 4.27 | 4.17% | 2.49 | 5.69 | 5.79% | |
| GWnet [11] | 1.30 | 2.74 | 2.73% | 1.63 | 3.70 | 3.67% | 1.95 | 4.52 | 4.63% | |
| AGCRN [18] | 1.37 | 2.87 | 2.94% | 1.69 | 3.85 | 3.87% | 1.96 | 4.54 | 4.64% | |
| GMAN [21] | 1.34 | 2.82 | 2.81% | 1.62 | 3.72 | 3.63% | 1.86 | 4.32 | 4.31% | |
| MTGNN [46] | 1.32 | 2.79 | 2.77% | 1.65 | 3.74 | 3.69% | 1.94 | 4.49 | 4.53% | |
| ADSTGCN | 1.28 | 2.71 | 2.70% | 1.60 | 3.63 | 3.60% | 1.86 | 4.26 | 4.31% | |
| NE_BJ | HA [43] | 6.00 | 10.95 | 26.40% | 6.00 | 10.95 | 26.40% | 6.00 | 10.95 | 26.40% |
| VAR [44] | 5.42 | 8.16 | 19.28% | 5.76 | 9.07 | 21.53% | 6.14 | 9.65 | 23.33% | |
| FC-LSTM [45] | 3.97 | 7.05 | 13.05% | 4.93 | 9.04 | 17.74% | 6.06 | 10.88 | 23.52% | |
| DCRNN [7] | 3.84 | 6.84 | 12.82% | 4.51 | 8.49 | 15.84% | 5.15 | 9.77 | 19.08% | |
| STGCN [8] | 5.02 | 8.34 | 19.31% | 5.10 | 8.55 | 19.82% | 5.39 | 9.09 | 22.14% | |
| GWnet [11] | 3.74 | 6.54 | 12.49% | 4.41 | 8.08 | 15.79% | 4.99 | 9.20 | 19.45% | |
| AGCRN [18] | 3.84 | 6.75 | 13.80% | 4.48 | 8.41 | 16.70% | 4.99 | 9.44 | 19.94% | |
| GMAN [21] | 4.08 | 7.63 | 14.94% | 4.42 | 8.45 | 16.51% | 4.80 | 9.18 | 18.36% | |
| MTGNN [46] | 3.75 | 6.71 | 12.91% | 4.39 | 8.33 | 16.07% | 4.90 | 9.38 | 19.79% | |
| ADSTGCN | 3.78 | 6.75 | 12.95% | 4.32 | 8.16 | 15.70% | 4.73 | 9.02 | 18.42% | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cui, Z.; Zhang, J.; Noh, G.; Park, H.J. ADSTGCN: A Dynamic Adaptive Deeper Spatio-Temporal Graph Convolutional Network for Multi-Step Traffic Forecasting. Sensors 2023, 23, 6950. https://doi.org/10.3390/s23156950
Cui Z, Zhang J, Noh G, Park HJ. ADSTGCN: A Dynamic Adaptive Deeper Spatio-Temporal Graph Convolutional Network for Multi-Step Traffic Forecasting. Sensors. 2023; 23(15):6950. https://doi.org/10.3390/s23156950
Chicago/Turabian StyleCui, Zhengyan, Junjun Zhang, Giseop Noh, and Hyun Jun Park. 2023. "ADSTGCN: A Dynamic Adaptive Deeper Spatio-Temporal Graph Convolutional Network for Multi-Step Traffic Forecasting" Sensors 23, no. 15: 6950. https://doi.org/10.3390/s23156950
APA StyleCui, Z., Zhang, J., Noh, G., & Park, H. J. (2023). ADSTGCN: A Dynamic Adaptive Deeper Spatio-Temporal Graph Convolutional Network for Multi-Step Traffic Forecasting. Sensors, 23(15), 6950. https://doi.org/10.3390/s23156950





