Exploration of Damage Identification Method for a Large-Span Timber Lattice Shell Structure in Taiyuan Botanical Garden based on Structural Health Monitoring
Abstract
:1. Introduction
2. Research Background
3. Methodology
3.1. Time Series Analysis Modeling
3.1.1. Basic Theory of ARMA Model
3.1.2. Determination of ARMA Order
3.1.3. Estimation of ARMA Parameter
3.1.4. Principal Component Analysis
3.2. Damage Sensitive Feature
3.2.1. Mahalanobis Distance
3.2.2. Construction of DSF
4. Results and Discussions
4.1. Damage Identification Based on Numerical Models
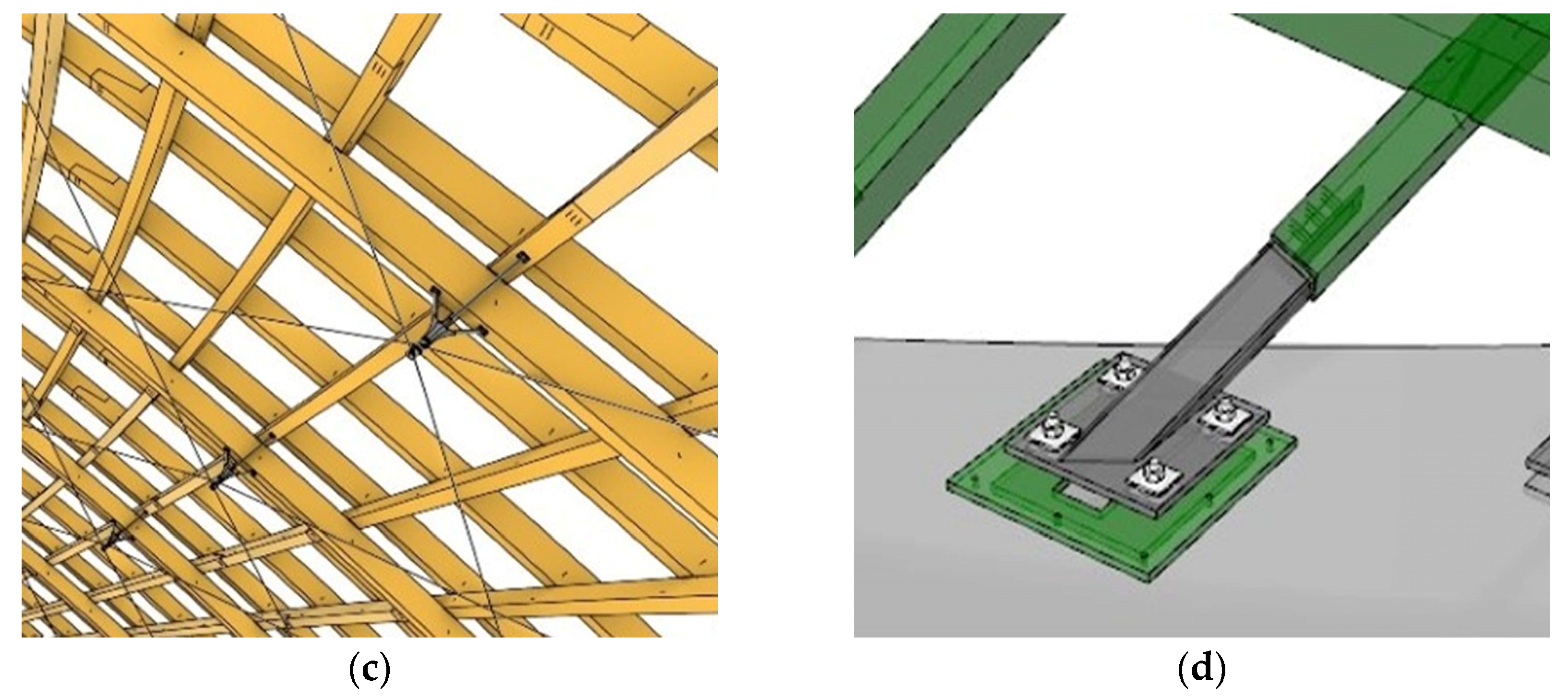
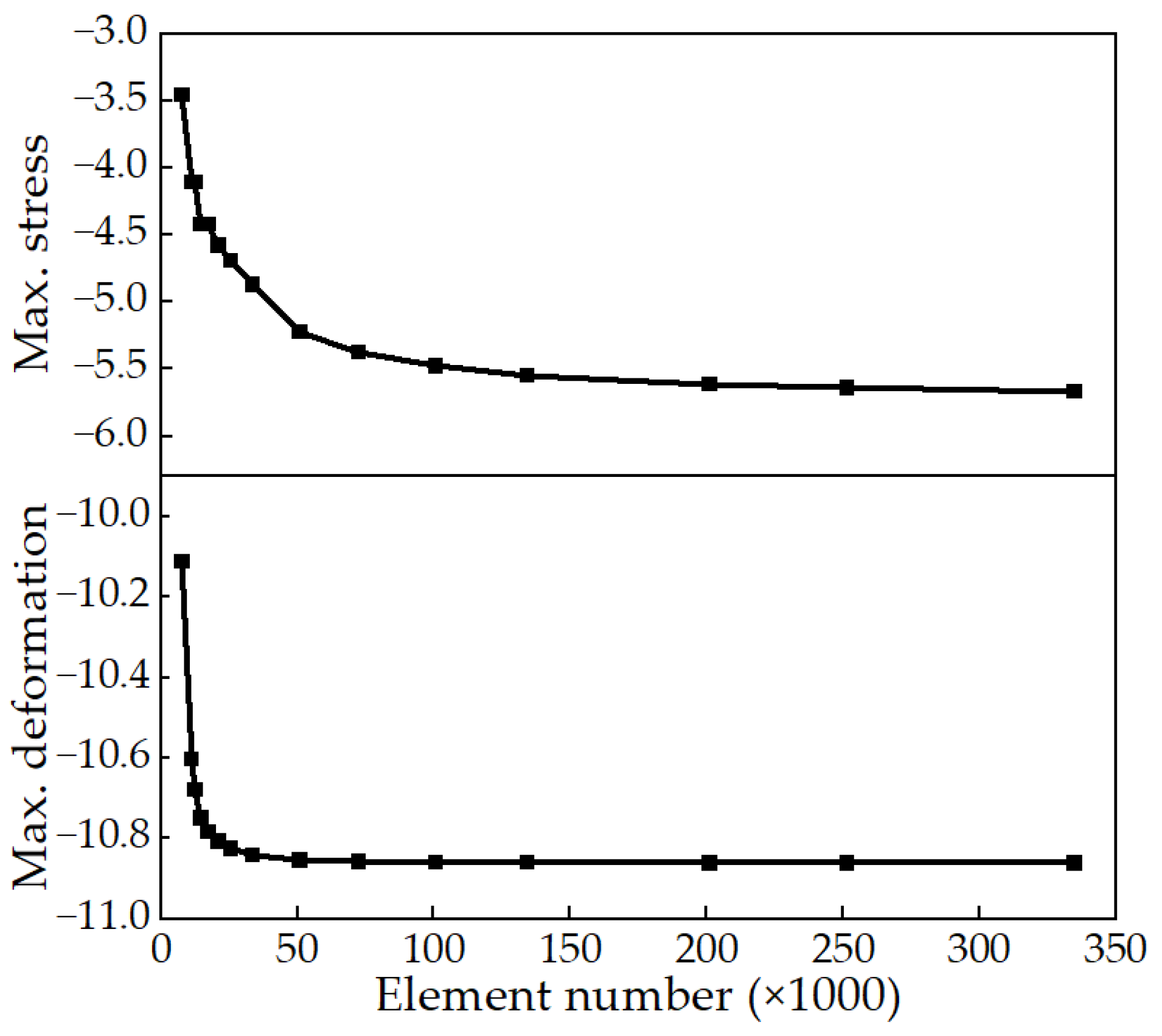
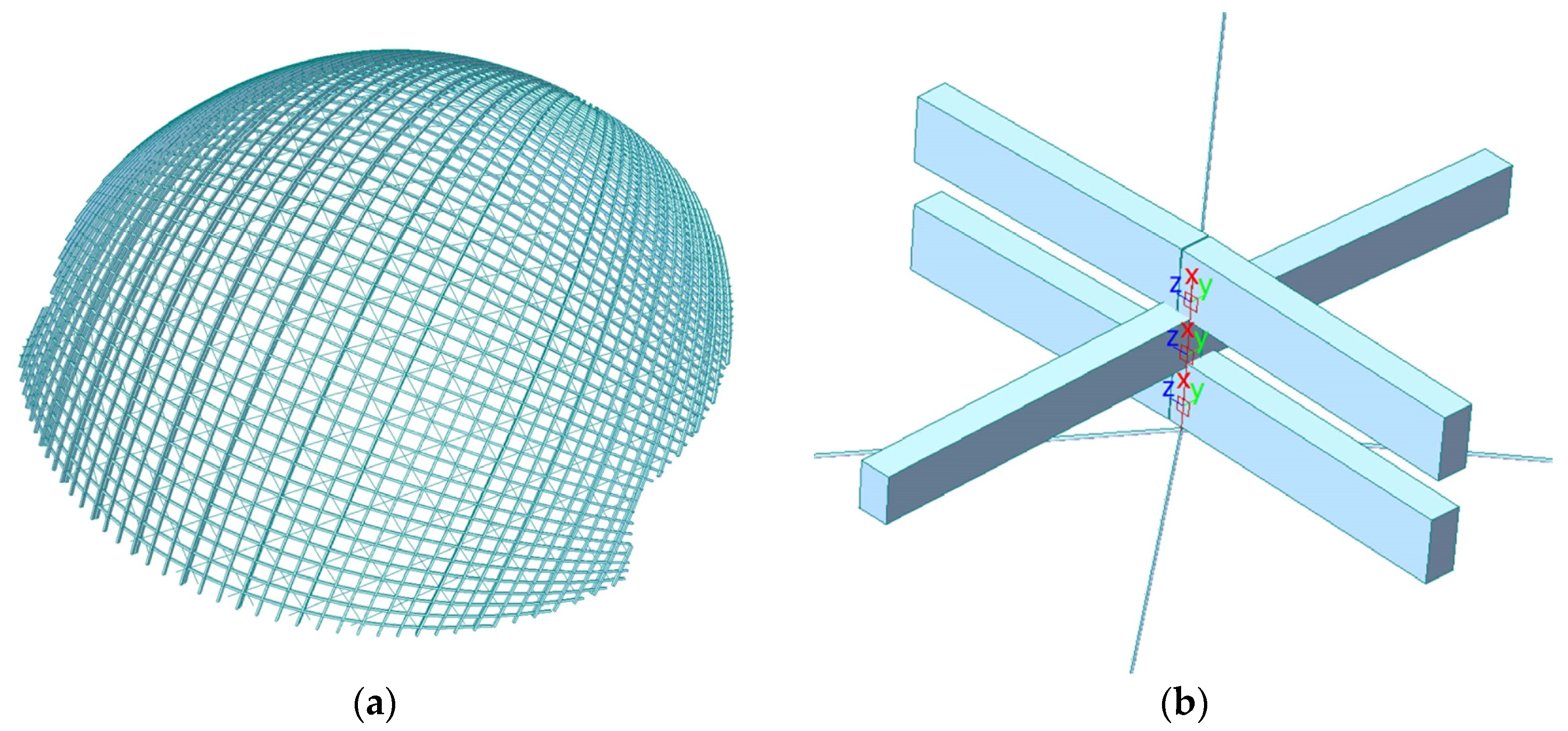
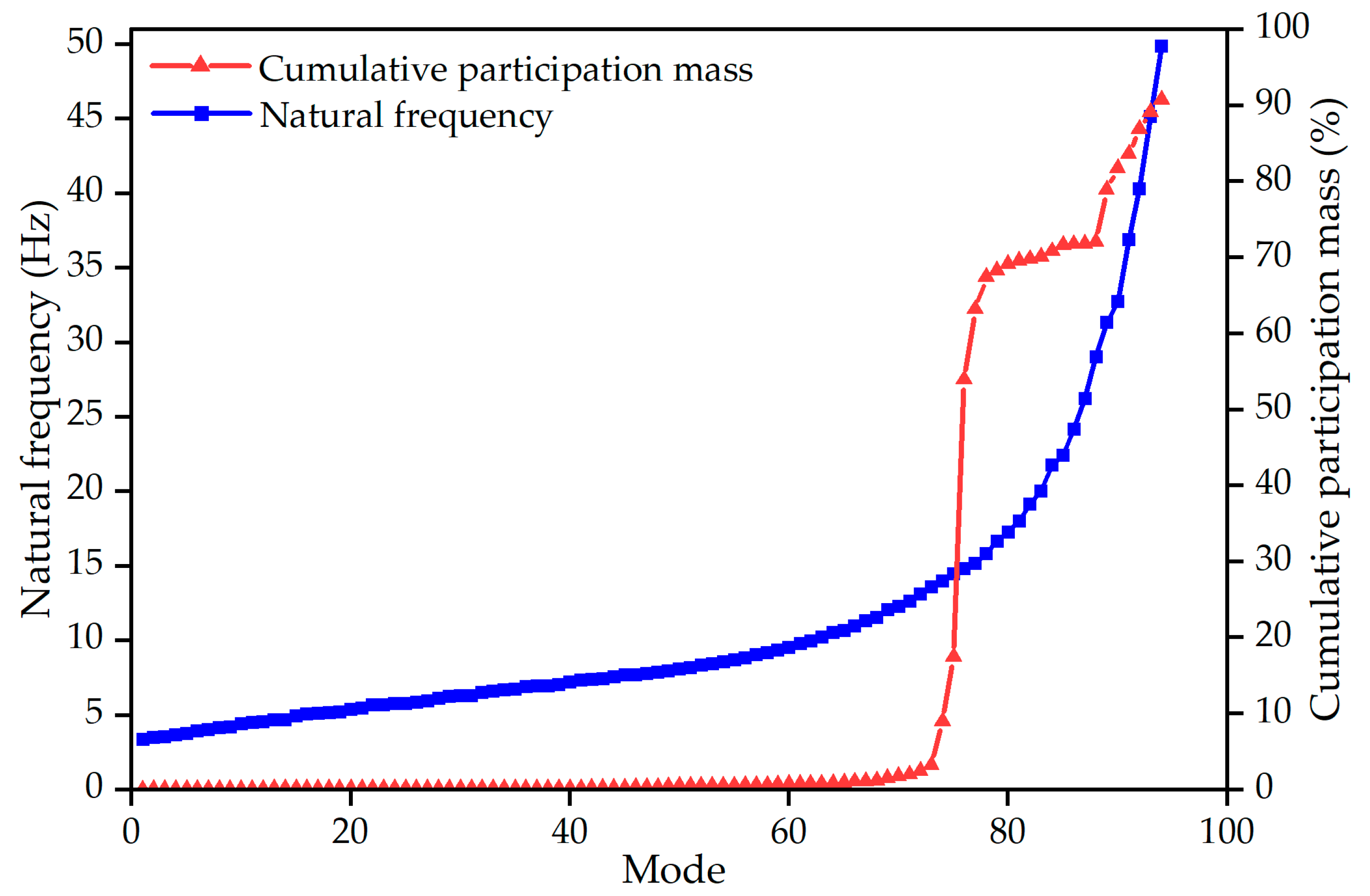
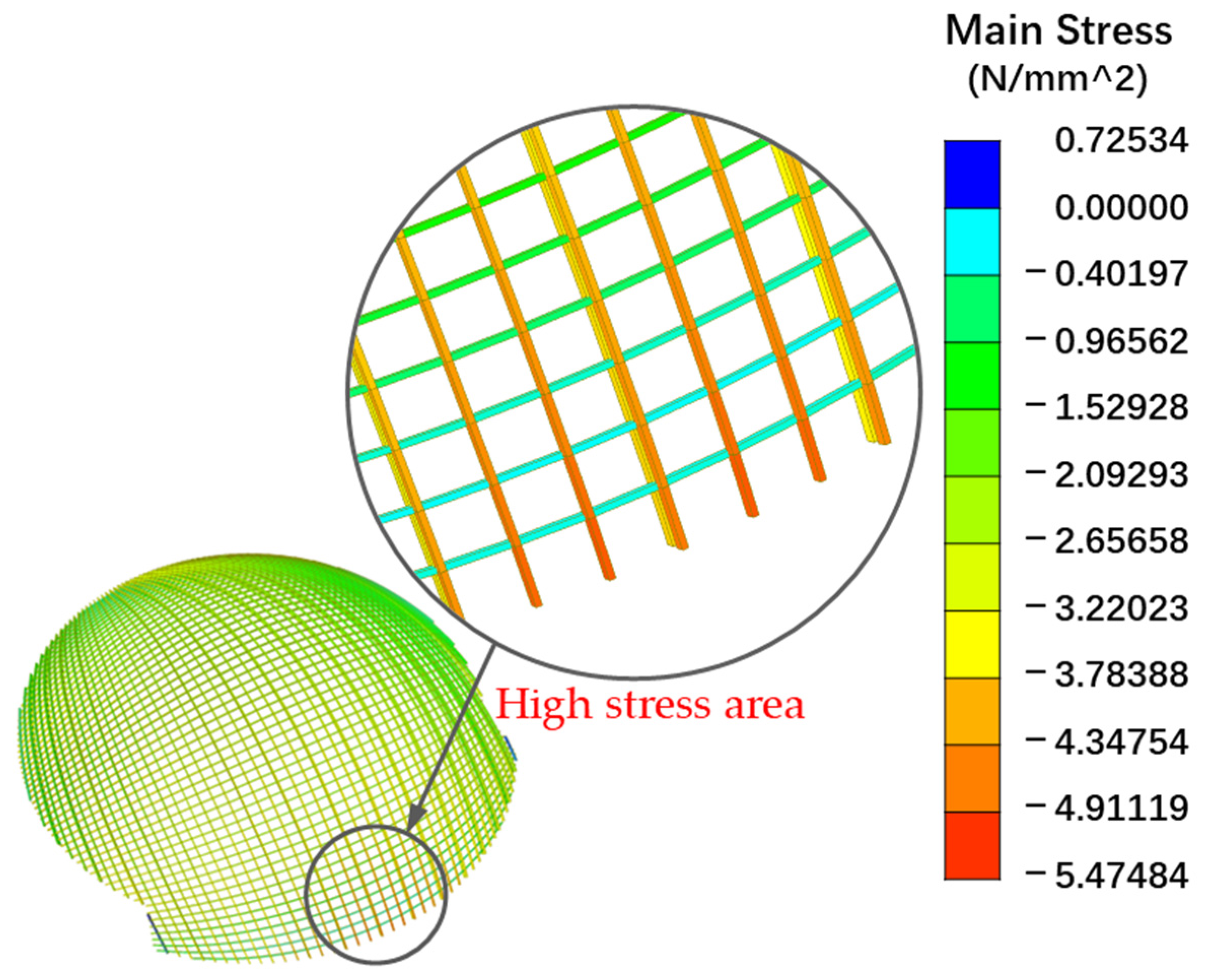
4.1.1. Finite Element Model
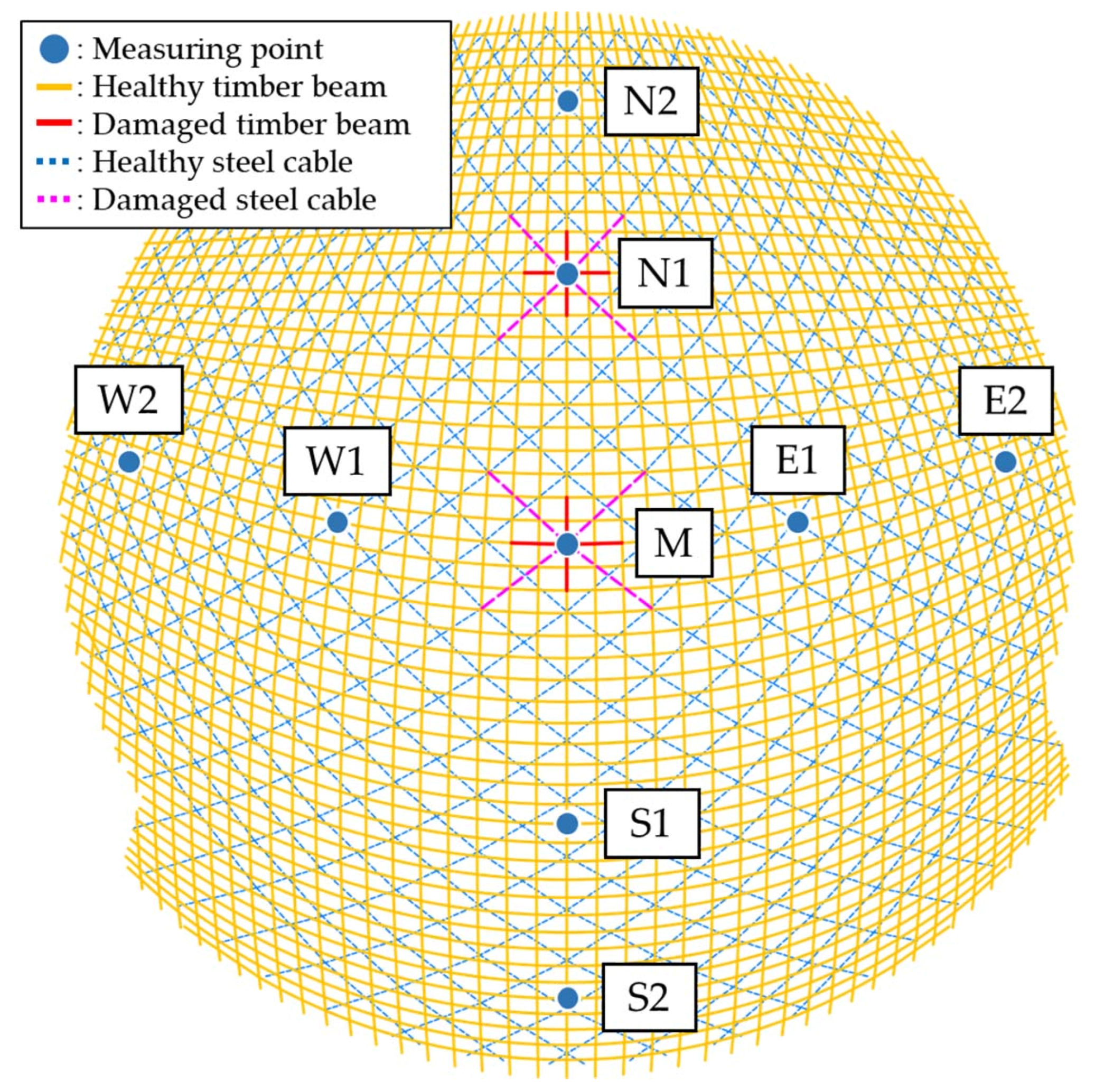
4.1.2. Damage Conditions
4.1.3. Establishment of ARMA Model
4.1.4. Damage Identification of FE Models
- (1)
- When the damage of the timber beam at MP M was 40% (DC 2), the DSF at M was 2.1799, which was significantly higher than the DSF at other MPs, not exceeding 1.15. As the damage increased to 80% (DC 3), the DSF at M increased to 3.5720, while the average DSF at other MPs was 1.1450. This represented a 63.9% increase in DSF compared to the 40% damage level. When both the timber beam and steel cable at M were damaged simultaneously (DC 4), the DSF further increased to 4.0281, which was approximately 12.77% higher than the previous DC. The average DSF value at other MPs was 1.1773. These results demonstrate that the DSF constructed using PCA and MD is highly sensitive to component damage, capable of identifying and locating damage to timber beams and steel cables, and positively correlates with the degree of damage. Therefore, it could reflect the degree of damage to the damaged components to a certain extent.
- (2)
- When the timber beam and steel cable at MPs M and N1 were simultaneously damaged by 80% (DC 5), the DSF of M and N1 were 4.1645 and 3.9983, respectively, which were significantly higher than the DSF values of other MPs, ranging from 1.07 to 1.38. This demonstrates that the proposed damage identification model can effectively identify conditions where multiple components are damaged simultaneously.
- (3)
- As the damage at MP M intensified from DC 2 to 4, the DSF of M significantly increased, while the DSF of adjacent MPs N1, E1, S1, and W1 also slightly increased, with an average increase of approximately 0.19. However, the DSF of MPs N2, E2, S2, and W2 did not increase significantly, with an average increase of no more than 0.1. Under DC 5, further damage occurred at MP N1. During this process, the DSF of N2 and M, which were closest to N1, increased the most, with values of 0.2070 and 0.1364, respectively. However, the DSF of S2, W2, and E2, which were farthest from N1, remained almost unchanged, with values of 0.049, 0.074, and 0.054, respectively. This suggests that structural damage at a specific location can cause an increase in the DSF of surrounding MPs, and the degree of increase is inversely proportional to the distance. This phenomenon may be attributed to the changes in the local natural vibration characteristics caused by component damage, which were not significantly far from the damage location.
- (4)
- Assuming that no MPs are set at M and N1, meaning that the DSF of M and N1 were not taken into account, under DC 4, the DSF values of E1, W1, and S1 experienced a significant increase, ranging from 1.25 to 1.35, while the DSF of the remaining MPs showed no noticeable changes. This suggests that the damage occurred in areas near E1, W1, and S1. It can be inferred that the damage may have occurred around M, which aligns with the severe damage observed at M under DC 4. From DC 4 to 5, the DSF of N2 increased significantly, while the DSF of the other MPs increased slightly and to a similar extent. This implies that the damage may have occurred in a location close to N2. As determined, N1 sustained damage during the transition from DC 4 to 5, which is consistent with this characteristic. The aforementioned statement indicates that even if the damage does not occur at MPs, the approximate location of the damage can be determined based on the DSF of the existing MPs, thereby achieving the objective of damage monitoring. This is advantageous for optimizing the number of MPs.
4.2. Damage Identification Based on SHM Data
5. Conclusions
- (1)
- This article was based on a time series model and introduced PCA for extracting principal components. In this study, only the first three AR coefficients were required to achieve damage identification and it demonstrated high accuracy.
- (2)
- The MD is advantageous compared to other distance methods in constructing DSF because it considers the differences and correlations in the variability of variables for each observation. Additionally, it can effectively calculate the influence of scale on different measurement values.
- (3)
- Verified by the FE model, the damage identification method proposed in this article was found to be sensitive to structural damage. It could, to a certain extent, accurately locate the site of structural damage and reflect the extent of the damage. Therefore, it can be effectively utilized for practical structural damage identification.
- (4)
- Based on SHM data, the paper identified the damage of the structure after two years of service. The results indicated that the structure is in a relatively healthy state, but the DSF of MP S2 is slightly higher than those of other MPs. In the future, it is necessary to pay attention and give timely warnings if necessary.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhao, Y.; Gong, M.; Yang, Y. A review of structural damage identification methods. World Earthq. Eng. 2020, 36, 73–84. [Google Scholar]
- Yan, G.; Duan, Z.; Ou, J. Review on structural damage detection based on vibration data. J. Earthq. Eng. Eng. Vib. 2007, 27, 95–103. [Google Scholar] [CrossRef]
- Lakshmi, K.; Rao, A.R.M. Damage identification technique based on time series models for LANL and ASCE benchmark structures. Insight-Non-Destr. Test. Cond. Monit. 2015, 57, 580–587. [Google Scholar] [CrossRef]
- Razavi, B.S.; Mahmoudkelayeh, M.R.; Razavi, S.S. Damage Identification under Ambient Vibration and Unpredictable Signal Nature. J Civ. Struct Health Monit 2021, 11, 1253–1273. [Google Scholar] [CrossRef]
- Box, G.E.P.; Jenkins, G.M. Time Series Analysis, Forecasting and Control; John Wiley & Sons: Hoboken, NJ, USA, 1971; Volume 134. [Google Scholar]
- Bao, C.; Hao, H.; Li, Z.-X. Integrated ARMA Model Method for Damage Detection of Subsea Pipeline System. Eng. Struct. 2013, 48, 176–192. [Google Scholar] [CrossRef]
- Liu, Y.; Li, A.; Ding, Y.; Fei, Q. Time Series Analysis with Structural Damage Feature Extraction and Alarming Method. Chin. J. Appl. Mech. 2008, 25, 253–257+357. [Google Scholar]
- Zuo, H.; Guo, H. Structural Nonlinear Damage Identification Method Based on the Kullback-Leibler Distance of Time Domain Model Residuals. Remote Sens. 2023, 15, 1135. [Google Scholar] [CrossRef]
- Zhu, H.; Yu, H.; Gao, F.; Weng, S.; Sun, Y.; Hu, Q. Damage Identification Using Time Series Analysis and Sparse Regularization. Struct. Control Health Monit. 2020, 27, e2554. [Google Scholar] [CrossRef]
- Chen, L.; Yu, L.; Fu, J.; Ng, C.-T. Nonlinear Damage Detection Using Linear ARMA Models with Classification Algorithms. Smart Struct. Syst. 2020, 26, 23–33. [Google Scholar] [CrossRef]
- Zeng, Y.; Yan, Y.; Weng, S.; Sun, Y.; Tian, W.; Yu, H. Fuzzy Clustering of Time-Series Model to Damage Identification of Structures. Adv. Struct. Eng. 2019, 22, 868–881. [Google Scholar] [CrossRef]
- Diao, Y.; Cao, Y.; Sun, Y. Structural Damage Identification based on AR Model Coefficients and Cointegration for Offshore Platform Under Environmental Variations. Eng. Mech. 2017, 34, 179–188. [Google Scholar]
- Hu, M.-H.; Tu, S.-T.; Xuan, F.-Z. Statistical Moments of ARMA(n,m) Model Residuals for Damage Detection. Procedia Eng. 2015, 130, 1622–1641. [Google Scholar] [CrossRef]
- Tang, Q.; Xin, J.; Zhou, J.; Fu, L.; Zhou, B. Structural damage identification method based on AR-GP model. J. Vib. Shock 2021, 40, 102–109. [Google Scholar] [CrossRef]
- Sui, Z.; Wang, Q.; Jia, D.; Yang, Y. Structural Damage Identification based on AR Model and Bayesian Optimization SVM. Low Temp. Archit. Technol. 2020, 42, 74–76. [Google Scholar] [CrossRef]
- Xu, J.; Guo, W.; Wang, X.; Cui, S. Study on the damage detection method for latticed shell structures based on AR model and BP neural network. Spat. Struct. 2015, 21, 66–71. [Google Scholar] [CrossRef]
- Wang, C.; Guan, W.; Gou, J.; Hou, F.; Bai, J.; Yan, G. Principal Component Analysis Based Three-Dimensional Operational Modal Analysis. Int. J. Appl. Electromagn. Mech. 2014, 45, 137–144. [Google Scholar] [CrossRef]
- Jia, S. Research on key technologies of large-span glued laminated timber reticulated shell structure design in Taiyuan Botanical Garden. Build. Struct. 2022, 52, 1–5+62. [Google Scholar] [CrossRef]
- Liu, Z. Spatial Steel Structural Damage Alarming Based on Statistical Pattern Recognition. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2010. [Google Scholar]
- Zhou, X. Research on the Damage Identification of Girder Bridge Structures Based on Auto-Regressive Moving Average Model. Master’s Thesis, Southwest Jiaotong University, Chengdu, China, 2008. [Google Scholar]
- Du, Y.; Li, W.; Li, H.; Liu, D. Structural damage identification based on time series analysis. J. Vib. Shock 2012, 31, 108–111. [Google Scholar] [CrossRef]
- Burnham, K.; Anderson, D. Model Selection and Multimodel Inference: A Practical Information-Theoretic Approach, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2002; Volume 67, ISBN 978-0-387-95364-9. [Google Scholar]
- Ljung, L. System Identification: Theory for the User. In System Identification: Theory for the User; Prentice-Hall: Hoboken, NJ, USA, 1999. [Google Scholar]
- Yang, S. Time Series Analysis in Engineering Application, 2nd ed.; Huazhong University of Science & Technology Press: Wuhan, China, 1991. [Google Scholar]
- Zhou, Y.; Liu, Z.; Zhang, G.; Zhou, L.; Liu, Y.; Tang, L.; Jiang, Z.; Yang, B. Structural Damage Identification Method Based on Moving Principal Component Analysis and Ensemble Learning. J. Univ. Jinan Sci. Technol. 2023, 37, 116–126. [Google Scholar] [CrossRef]
- Kumar, K.; Biswas, P.K.; Dhang, N. Time Series-Based SHM Using PCA with Application to ASCE Benchmark Structure. J. Civ. Struct. Health Monit. 2020, 10, 899–911. [Google Scholar] [CrossRef]
- Jia, S.; Li, R.; Li, Y. Research on material properties test and application of imported glued laminated timber in Taiyuan Botanical Garden. Build. Struct. 2022, 52, 17–21. [Google Scholar] [CrossRef]
- Zhang, L.; Xie, Q.; Wu, Y.; Zhang, B. Research on the mechanical properties and constitutive model of wood under parallel-to-grain cyclic loading. China Civ. Eng. J. 2023, 44, 286–304. [Google Scholar]
- Wang, M.; Song, X.; Gu, X. Nonlinear analysis of wood based on three-dimensional combined elastic-plastic and damage model. China Civ. Eng. J. 2018, 51, 22–28+49. [Google Scholar] [CrossRef]
- Wang, M.; Gu, X.; Song, X.; Tang, J. State-of-the-art for description methods of nonlinear mechanical behavior of wood. J. Build. Struct. 2021, 42, 76–86. [Google Scholar] [CrossRef]
- Xu, B.-H.; Bouchaïr, A.; Racher, P. Appropriate Wood Constitutive Law for Simulation of Nonlinear Behavior of Timber Joints. J. Mater. Civ. Eng. 2014, 26, 04014004. [Google Scholar] [CrossRef]
- Shannon, C.E. Communication in the Presence of Noise. Proc. IEEE 1998, 86, 447–457. [Google Scholar] [CrossRef]


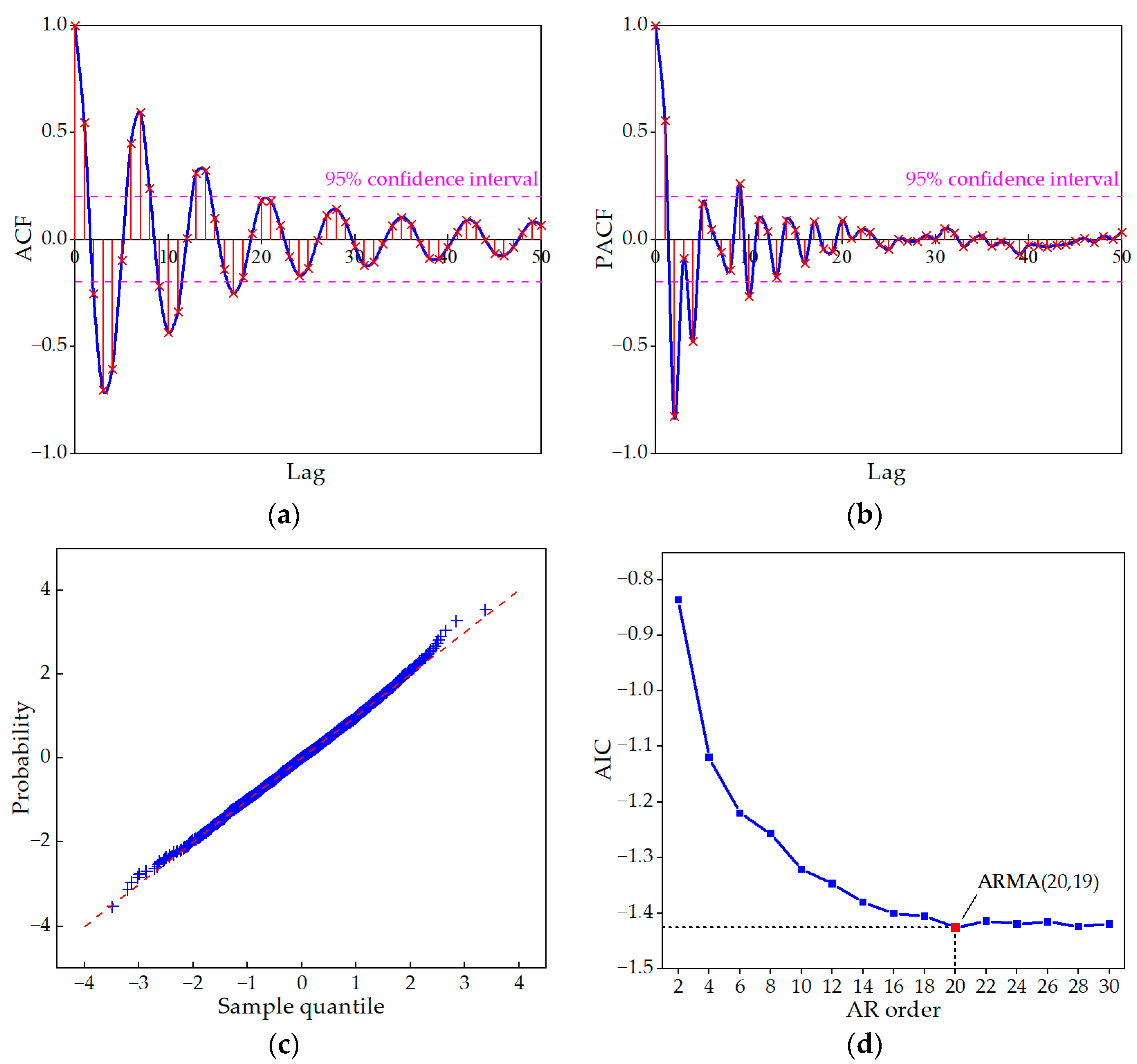




| Model Type | Autocorrelation Function (ACF) | Partial Autocorrelation Function (PACF) |
|---|---|---|
| AR | Tailing | Truncation |
| MA | Truncation | Tailing |
| ARMA | Tailing | Tailing |
| Ec,0 (MPa) | Et,0 (MPa) | Ec,90 (MPa) | fc,0 (MPa) | ft,0 (MPa) | fc,90 (MPa) |
|---|---|---|---|---|---|
| 13,901 | 7438 | 185 | 29.6 | 77.5 | 5.0 |
| Mode Order | Frequency (Hz) | Mode Order | Frequency (Hz) | Mode Order | Frequency (Hz) | Mode Order | Frequency (Hz) |
|---|---|---|---|---|---|---|---|
| 1 | 3.3537 | 26 | 5.8696 | 51 | 8.2039 | 76 | 14.8373 |
| 2 | 3.5002 | 27 | 5.9719 | 52 | 8.3625 | 77 | 15.1701 |
| 3 | 3.5525 | 28 | 6.134 | 53 | 8.4575 | 78 | 15.8307 |
| 4 | 3.6825 | 29 | 6.2517 | 54 | 8.5635 | 79 | 16.6591 |
| 5 | 3.7451 | 30 | 6.2953 | 55 | 8.7213 | 80 | 17.2487 |
| 6 | 3.9603 | 31 | 6.3233 | 56 | 8.847 | 81 | 17.9974 |
| 7 | 4.0067 | 32 | 6.5079 | 57 | 9.0585 | 82 | 19.1284 |
| 8 | 4.1308 | 33 | 6.6175 | 58 | 9.1913 | 83 | 20.0353 |
| 9 | 4.2118 | 34 | 6.6899 | 59 | 9.3714 | 84 | 21.7652 |
| 10 | 4.431 | 35 | 6.7379 | 60 | 9.5392 | 85 | 22.4354 |
| 11 | 4.4916 | 36 | 6.9291 | 61 | 9.7873 | 86 | 24.1665 |
| 12 | 4.5736 | 37 | 6.9573 | 62 | 9.9823 | 87 | 26.2336 |
| 13 | 4.6526 | 38 | 6.9682 | 63 | 10.2407 | 88 | 29.05 |
| 14 | 4.6659 | 39 | 7.0649 | 64 | 10.5235 | 89 | 31.3453 |
| 15 | 4.9154 | 40 | 7.2344 | 65 | 10.6672 | 90 | 32.7382 |
| 16 | 5.0791 | 41 | 7.3614 | 66 | 10.9764 | 91 | 36.9209 |
| 17 | 5.1145 | 42 | 7.3811 | 67 | 11.3259 | 92 | 40.3238 |
| 18 | 5.1646 | 43 | 7.4171 | 68 | 11.5494 | 93 | 45.1509 |
| 19 | 5.2276 | 44 | 7.5568 | 69 | 12.0646 | 94 | 49.8536 |
| 20 | 5.3595 | 45 | 7.6886 | 70 | 12.2717 | 95 | 59.3389 |
| 21 | 5.4691 | 46 | 7.7193 | 71 | 12.6162 | 96 | 72.188 |
| 22 | 5.6584 | 47 | 7.7773 | 72 | 13.0992 | 97 | 88.9345 |
| 23 | 5.6804 | 48 | 7.8668 | 73 | 13.6149 | 98 | 121.4361 |
| 24 | 5.7494 | 49 | 7.9797 | 74 | 13.9864 | 99 | 180.6925 |
| 25 | 5.7668 | 50 | 8.1043 | 75 | 14.4609 | 100 | 349.0827 |
| Condition No. | MP M | MP N1 | ||
|---|---|---|---|---|
| Beam | Cable | Beam | Cable | |
| 1 |  |  |  |  |
| 2 |  |  |  |  |
| 3 |  |  |  |  |
| 4 |  |  |  |  |
| 5 |  |  |  |  |
 : in a healthy state;
: in a healthy state;  : damaged by 40%;
: damaged by 40%;  : damaged by 80%.
: damaged by 80%.| Order | AR Coef. | MA Coef. | Order | AR Coef. | MA Coef. |
|---|---|---|---|---|---|
| 1 | 0.1956 | 0.9294 | 11 | 0.0487 | −0.3235 |
| 2 | −0.3641 | 0.1359 | 12 | −0.0731 | −0.1088 |
| 3 | −0.0754 | −0.3965 | 13 | −0.0082 | 0.3625 |
| 4 | −0.2056 | −0.4014 | 14 | −0.4730 | 0.8166 |
| 5 | −0.1359 | −0.0875 | 15 | 0.1008 | 0.4343 |
| 6 | −0.1749 | 0.1776 | 16 | −0.2690 | −0.0291 |
| 7 | 0.2484 | 0.4023 | 17 | −0.1583 | −0.1125 |
| 8 | −0.1414 | 0.1495 | 18 | −0.3139 | 0.0210 |
| 9 | 0.0141 | −0.2229 | 19 | 0.0208 | 0.1027 |
| 10 | 0.0242 | −0.2021 | 20 | 0.0635 | - |
| Principal Component | M | E1 | E2 | |||
| Eigenvalue | ACR | Eigenvalue | ACR | Eigenvalue | ACR | |
| 1 | 10.3245 | 51.62% | 14.4691 | 72.35% | 13.7320 | 68.66% |
| 2 | 4.6304 | 74.77% | 3.2225 | 88.46% | 3.1710 | 84.52% |
| 3 | 3.8133 | 93.84% | 1.2549 | 94.73% | 1.9219 | 94.12% |
| 4 | 0.8551 | 98.12% | 1.0002 | 99.73% | 1.0343 | 99.30% |
| 5 | 0.3768 | 100.00% | 0.0532 | 100.00% | 0.1407 | 100.00% |
| Principal Component | W1 | W2 | S1 | |||
| Eigenvalue | ACR | Eigenvalue | ACR | Eigenvalue | ACR | |
| 1 | 15.0565 | 75.28% | 10.4912 | 52.46% | 12.8791 | 64.40% |
| 2 | 4.0753 | 95.66% | 6.4063 | 84.49% | 4.0294 | 84.54% |
| 3 | 0.7505 | 99.41% | 1.8273 | 93.62% | 2.8699 | 98.89% |
| 4 | 0.1117 | 99.97% | 1.0842 | 99.05% | 0.2155 | 99.97% |
| 5 | 0.0060 | 100.00% | 0.1909 | 100.00% | 0.0061 | 100.00% |
| Principal Component | S2 | N1 | N2 | |||
| Eigenvalue | ACR | Eigenvalue | ACR | Eigenvalue | ACR | |
| 1 | 10.8759 | 54.38% | 8.3965 | 41.98% | 11.1385 | 55.69% |
| 2 | 4.3566 | 76.16% | 7.4009 | 78.99% | 7.1796 | 91.59% |
| 3 | 2.7723 | 90.02% | 2.4547 | 91.26% | 1.1040 | 97.11% |
| 4 | 1.9425 | 99.74% | 1.2340 | 97.43% | 0.4086 | 99.15% |
| 5 | 0.0527 | 100.00% | 0.5139 | 100.00% | 0.1693 | 100.00% |
| Mode | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| Parameter | Acceleration | Low Velocity | Medium Velocity | High Velocity |
| Sensitivity | 0.3 V/m·s−2 | 20 V/m·s−1 | 5 V/m·s−1 | 0.3 V/m·s−1 |
| Capacity | 20 m·s−2 | 0.125 m·s−1 | 0.3 m·s−1 | 0.6 m·s−1 |
| Bandwidth (−3–+1 dB) | (0.25–100) Hz | (1–100) Hz | (0.5–100) Hz | (0.17–80) Hz |
| Output Impedance | 50 kΩ | |||
| Working Temperature | (−20–80) °C | |||
| Dimensions | 63 mm × 63 mm × 63 mm | |||
| Weight | 0.6 kg | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, G.; Xu, C.; Zhang, S.; Zhou, Z.; Zhang, L.; Qiu, B.; Wan, J.; Lei, H. Exploration of Damage Identification Method for a Large-Span Timber Lattice Shell Structure in Taiyuan Botanical Garden based on Structural Health Monitoring. Sensors 2023, 23, 6710. https://doi.org/10.3390/s23156710
Wang G, Xu C, Zhang S, Zhou Z, Zhang L, Qiu B, Wan J, Lei H. Exploration of Damage Identification Method for a Large-Span Timber Lattice Shell Structure in Taiyuan Botanical Garden based on Structural Health Monitoring. Sensors. 2023; 23(15):6710. https://doi.org/10.3390/s23156710
Chicago/Turabian StyleWang, Guoqing, Chenjia Xu, Shujia Zhang, Zichun Zhou, Liang Zhang, Bin Qiu, Jia Wan, and Honggang Lei. 2023. "Exploration of Damage Identification Method for a Large-Span Timber Lattice Shell Structure in Taiyuan Botanical Garden based on Structural Health Monitoring" Sensors 23, no. 15: 6710. https://doi.org/10.3390/s23156710
APA StyleWang, G., Xu, C., Zhang, S., Zhou, Z., Zhang, L., Qiu, B., Wan, J., & Lei, H. (2023). Exploration of Damage Identification Method for a Large-Span Timber Lattice Shell Structure in Taiyuan Botanical Garden based on Structural Health Monitoring. Sensors, 23(15), 6710. https://doi.org/10.3390/s23156710






