Classification of Alzheimer’s Progression Using fMRI Data
Abstract
1. Introduction
2. Related Works
2.1. Alzheimer’s Disease
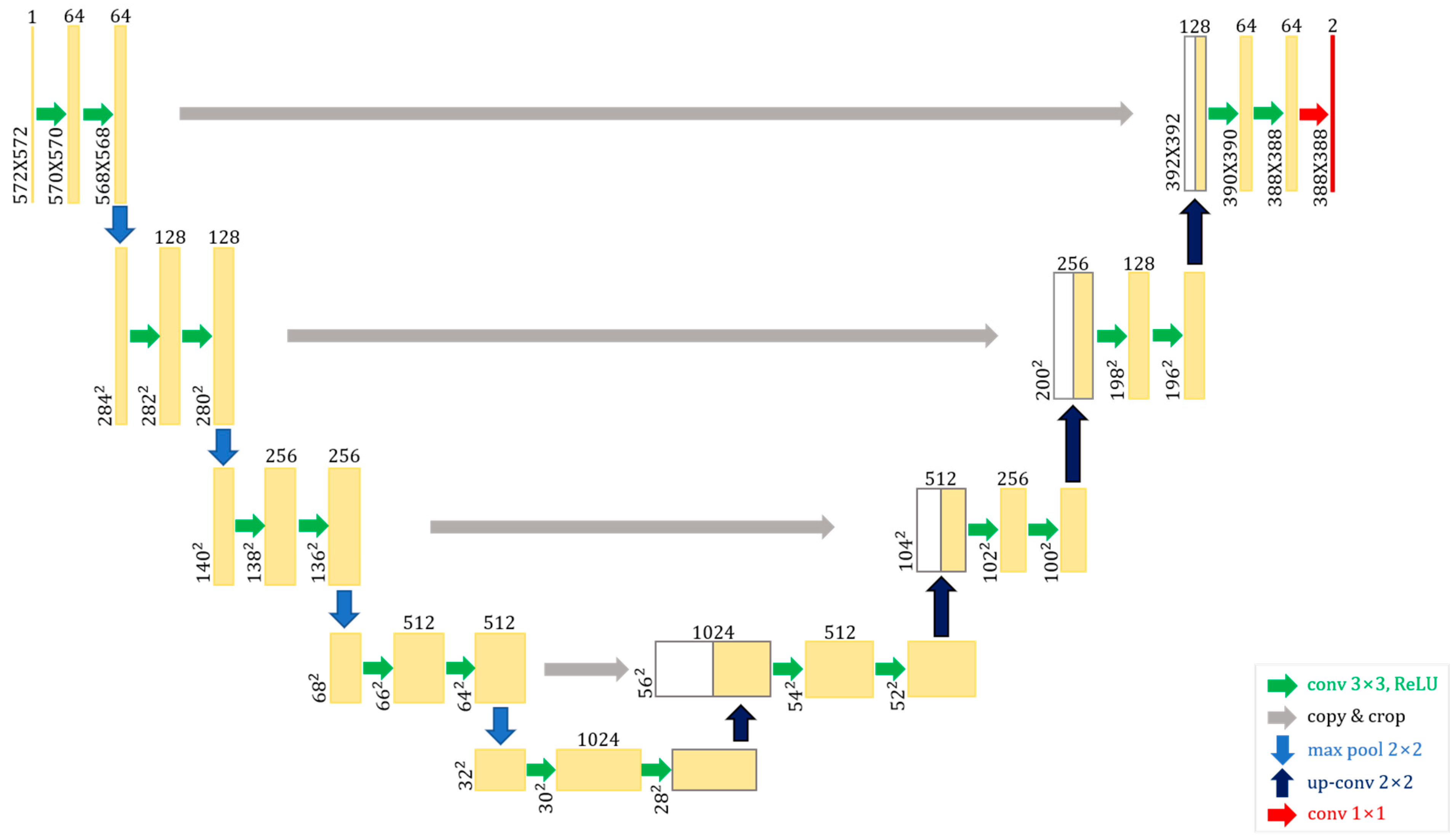
2.2. U-Net
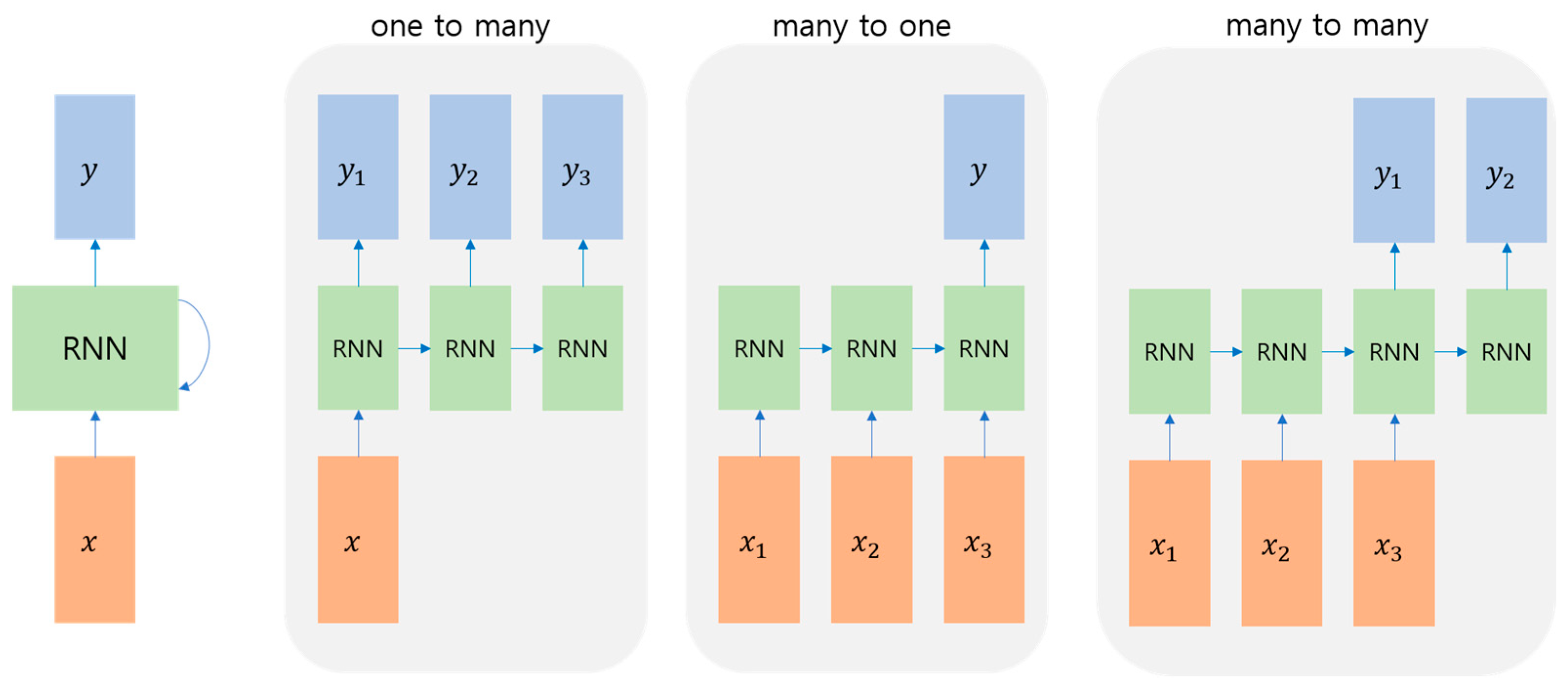
2.3. Time-Series Network
3. Materials and Methods
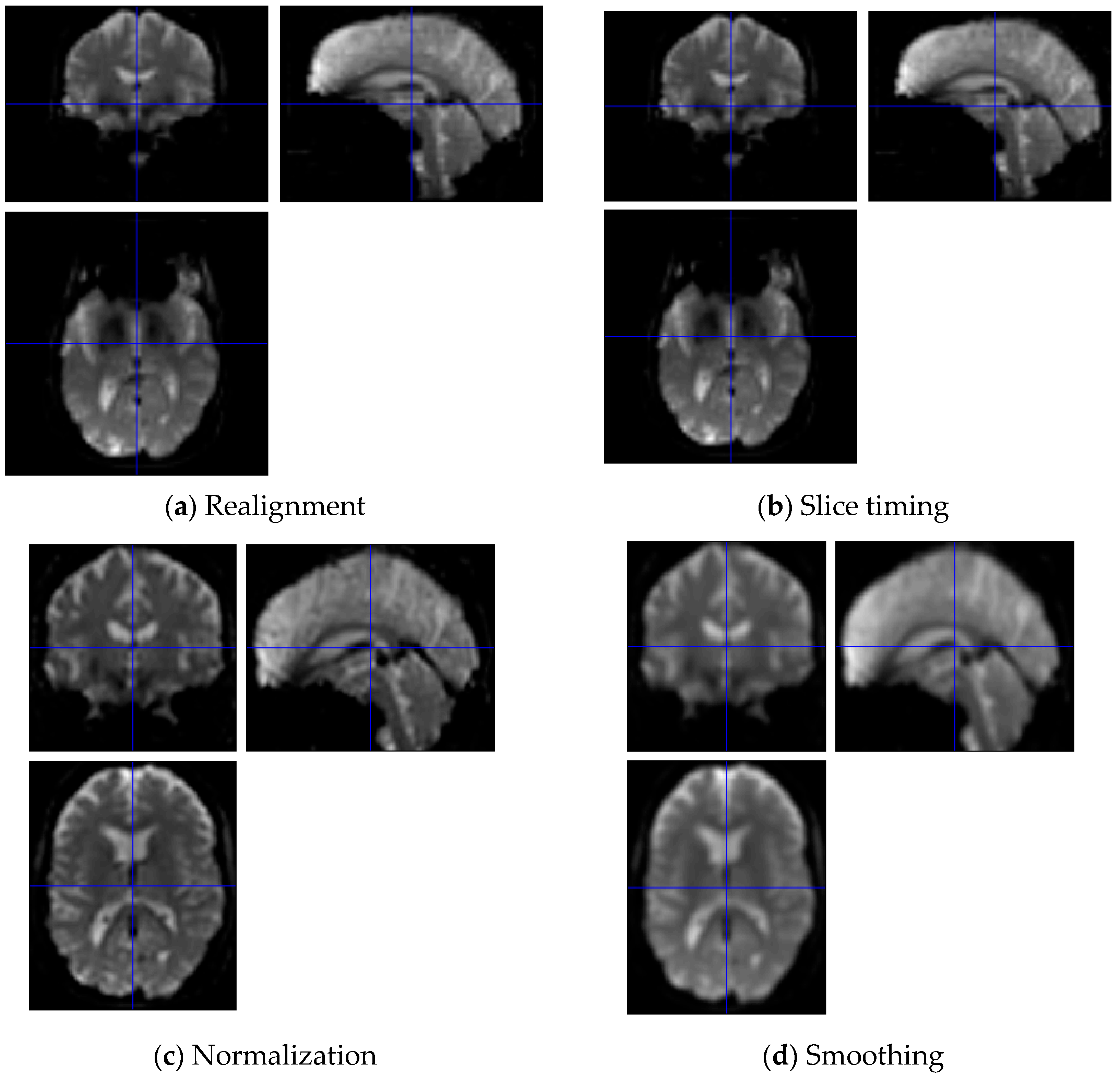
3.1. Pre-Processing
- CN—108F/89M, age: 65–96
- EMCI—142F/96M, age: 56–90
- LMCI—58F/101M, age: 57–88
- AD—56F/62M, age: 56–89
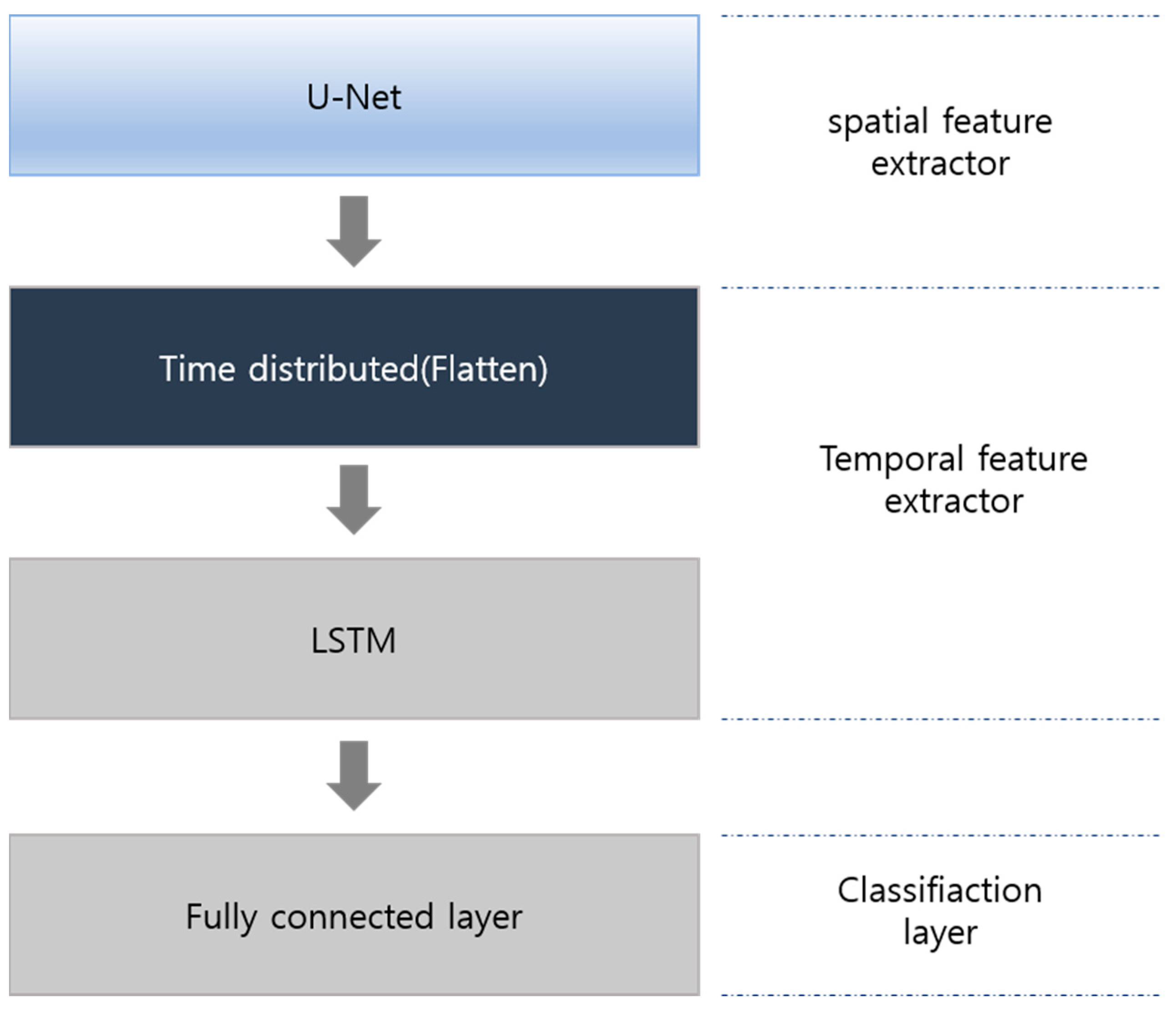
3.2. Model
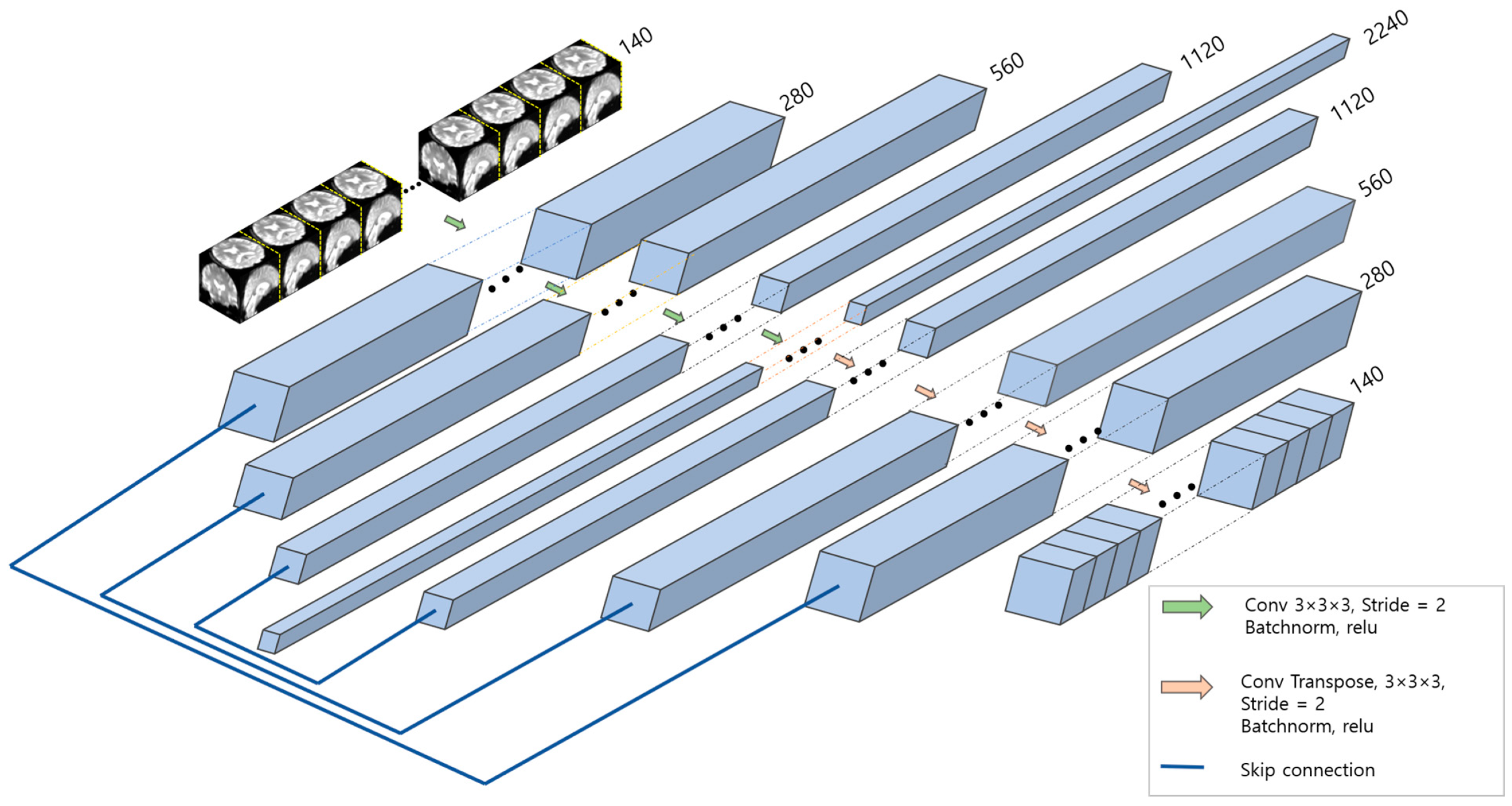
3.3. Spatial Feature Extraction
3.4. Temporal Feature Extractor and Classifier
3.5. Hyperparameters
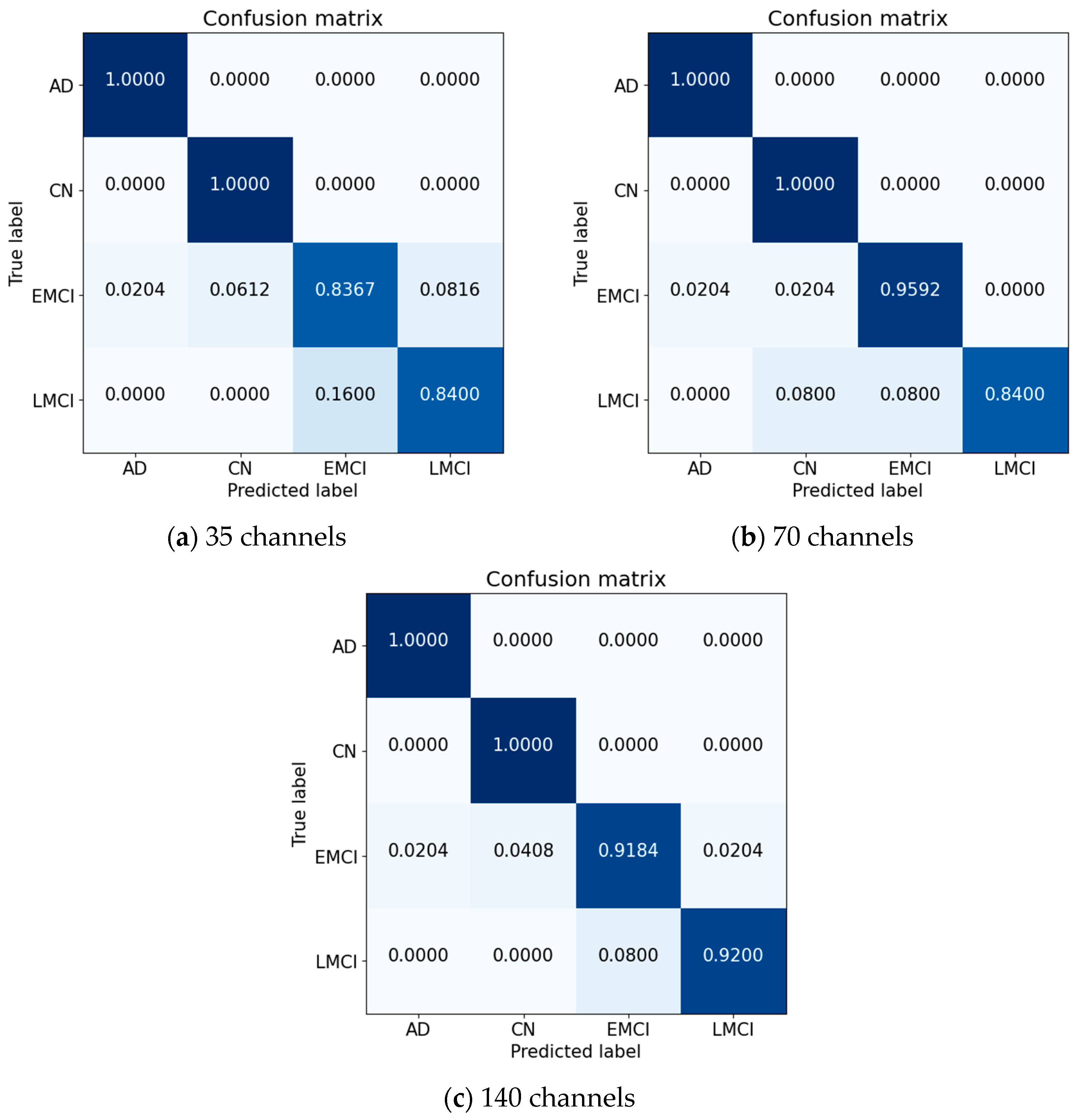
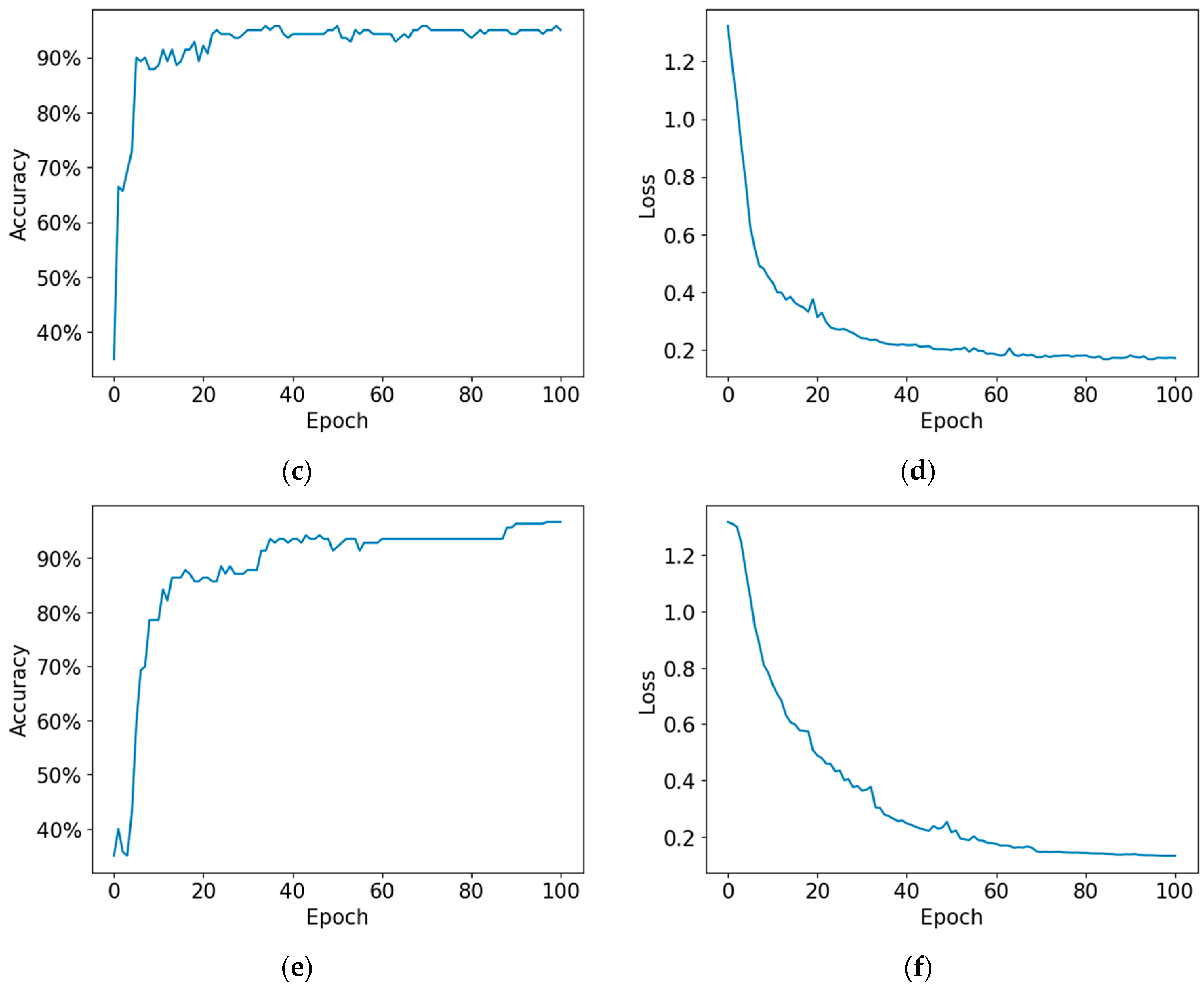
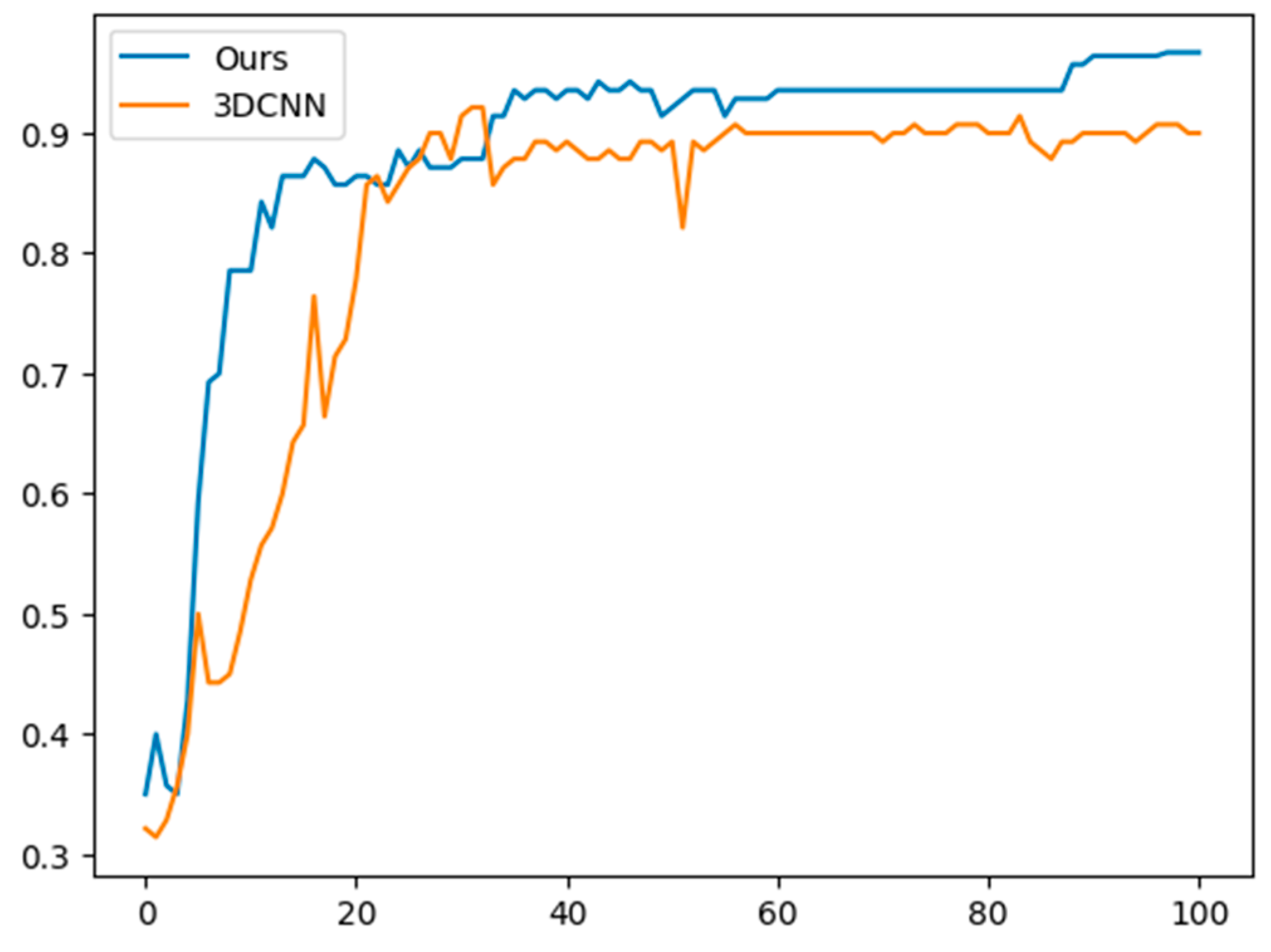
4. Experimental Results
4.1. Proposed Model
4.2. Performance Metrics
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ott, A.; Breteler, M.M.B.; Van Harskamp, F.; Stijnen, T.; Hofman, A. Incidence and Risk of Dementia: The Rotterdam Study. Am. J. Epidemiol. 1998, 147, 574–580. [Google Scholar] [CrossRef]
- Seshadri, S.; Beiser, A.; Au, R.; Wolf, P.A.; Evans, D.A.; Wilson, R.S.; Petersen, R.C.; Knopman, D.S.; Rocca, W.A.; Kawas, C.H.; et al. Operationalizing Diagnostic Criteria for Alzheimer’s Disease and Other Age-Related Cognitive Impairment—Part 2. Alzheimer’s Dement. 2011, 7, 35–52. [Google Scholar] [CrossRef] [PubMed]
- Serrano-Pozo, A.; Frosch, M.P.; Masliah, E.; Hyman, B.T. Neuropathological Alterations in Alzheimer Disease. Cold Spring Harb. Perspect. Med. 2011, 1, a006189. [Google Scholar] [CrossRef] [PubMed]
- McKhann, G.; Drachman, D.; Folstein, M.; Katzman, R.; Price, D.; Stadlan, E.M. Clinical Diagnosis of Alzheimer’s Disease. Neurology 1984, 34, 939. [Google Scholar] [CrossRef] [PubMed]
- Petersen, R.C.; Roberts, R.O.; Knopman, D.S.; Boeve, B.F.; Geda, Y.E.; Ivnik, R.J.; Smith, G.E.; Jack, C.R. Mild Cognitive Impairment: Ten Years Later. Arch. Neurol. 2009, 66, 1447–1455. [Google Scholar] [CrossRef]
- Farlow, M.R. Treatment of mild cognitive impairment. Curr. Alzheimer Res. 2009, 6, 362–367. [Google Scholar] [CrossRef]
- Eskildsen, S.F.; Coupé, P.; García-Lorenzo, D.; Fonov, V.; Pruessner, J.C.; Collins, D.L. Prediction of Alzheimer’s Disease in Subjects with Mild Cognitive Impairment from the ADNI Cohort Using Patterns of Cortical Thinning. Neuroimage 2013, 65, 511–521. [Google Scholar] [CrossRef]
- Beheshti, I.; Demirel, H.; Matsuda, H. Classification of Alzheimer’s Disease and Prediction of Mild Cognitive Impairment-to-Alzheimer’s Conversion from Structural Magnetic Resource Imaging Using Feature Ranking and a Genetic Algorithm. Comput. Biol. Med. 2017, 83, 109–119. [Google Scholar] [CrossRef]
- Syaifullah, A.H.; Shiino, A.; Kitahara, H.; Ito, R.; Ishida, M.; Tanigaki, K. Machine Learning for Diagnosis of AD and Prediction of MCI Progression from Brain MRI Using Brain Anatomical Analysis Using Diffeomorphic Deformation. Front. Neurol. 2021, 11, 576029. [Google Scholar] [CrossRef]
- Nanni, L.; Interlenghi, M.; Brahnam, S.; Salvatore, C.; Papa, S.; Nemni, R.; Castiglioni, I. Comparison of Transfer Learning and Conventional Machine Learning Applied to Structural Brain MRI for the Early Diagnosis and Prognosis of Alzheimer’s Disease. Front. Neurol. 2020, 11, 576194. [Google Scholar] [CrossRef]
- Dhinagar, N.J.; Thomopoulos, S.I.; Laltoo, E.; Thompson, P.M. Efficiently Training Vision Transformers on Structural MRI Scans for Alzheimer’s Disease Detection. arXiv 2023, arXiv:2303.08216. [Google Scholar]
- Gauthier, S.; Reisberg, B.; Zaudig, M.; Petersen, R.C.; Ritchie, K.; Broich, K.; Belleville, S.; Brodaty, H.; Bennett, D.; Chertkow, H.; et al. Mild Cognitive Impairment. Lancet 2006, 367, 1262–1270. [Google Scholar] [CrossRef]
- Grieder, M.; Wang, D.J.J.; Dierks, T.; Wahlund, L.O.; Jann, K. Default Mode Network Complexity and Cognitive Decline in Mild Alzheimer’s Disease. Front. Neurosci. 2018, 12, 388987. [Google Scholar] [CrossRef]
- Vemuri, P.; Jones, D.T.; Jack, C.R. Resting State Functional MRI in Alzheimer’s Disease. Alzheimers Res. Ther. 2012, 4, 2. [Google Scholar] [CrossRef]
- Ogawa, S.; Lee, T.-M.; Nayak, A.S.; Glynn, P. Oxygenation-Sensitive Contrast in Magnetic Resonance Image of Rodent Brain at High Magnetic Fields. Magn. Reson. Med. 1990, 14, 68–78. [Google Scholar] [CrossRef]
- Hojjati, S.H.; Ebrahimzadeh, A.; Khazaee, A.; Babajani-Feremi, A. Predicting Conversion from MCI to AD by Integrating Rs-FMRI and Structural MRI. Comput. Biol. Med. 2018, 102, 30–39. [Google Scholar] [CrossRef]
- Khazaee, A.; Ebrahimzadeh, A.; Babajani-Feremi, A. Classification of Patients with MCI and AD from Healthy Controls Using Directed Graph Measures of Resting-State FMRI. Behav. Brain Res. 2017, 322, 339–350. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. Lect. Notes Comput. Sci. 2015, 9351, 234–241. [Google Scholar] [CrossRef]
- Gao, Y.; No, A. Age Estimation from FMRI Data Using Recurrent Neural Network. Appl. Sci. 2022, 12, 749. [Google Scholar] [CrossRef]
- Li, H.; Fan, Y. Brain Decoding from Functional Mri Using Long Short-Term Memory Recurrent Neural Networks. Lect. Notes Comput. Sci. 2018, 11072, 320–328. [Google Scholar] [CrossRef]
- Parmar, H.; Nutter, B.; Long, R.; Antani, S.; Mitra, S. Spatiotemporal Feature Extraction and Classification of Alzheimer’s Disease Using Deep Learning 3D-CNN for FMRI Data. J. Med. Imaging 2020, 7, 056001. [Google Scholar] [CrossRef]
- Jack, C.R.; Bernstein, M.A.; Fox, N.C.; Thompson, P.; Alexander, G.; Harvey, D.; Borowski, B.; Britson, P.J.; Whitwell, J.L.; Ward, C.; et al. The Alzheimer’s Disease Neuroimaging Initiative (ADNI): MRI Methods. J. Magn. Reson. Imaging 2008, 27, 685–691. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J.L. Adam: A Method for Stochastic Optimization. In Proceedings of the 3rd International Conference on Learning Representations, ICLR 2015—Conference Track Proceedings, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Sarraf, S.; Tofighi, G. Deep Learning-Based Pipeline to Recognize Alzheimer’s Disease Using FMRI Data. In Proceedings of the FTC 2016—Proceedings of Future Technologies Conference, San Francisco, CA, USA, 6–7 December 2016; pp. 816–820. [Google Scholar] [CrossRef]
- Billones, C.D.; Demetria, O.J.L.D.; Hostallero, D.E.D.; Naval, P.C. DemNet: A Convolutional Neural Network for the Detection of Alzheimer’s Disease and Mild Cognitive Impairment. In Proceedings of the 2016 IEEE region 10 conference (TENCON), Marina Bay Sands, Singapore, 22–25 November 2016; pp. 3724–3727. [Google Scholar] [CrossRef]
- Jain, R.; Jain, N.; Aggarwal, A.; Hemanth, D.J. Convolutional Neural Network Based Alzheimer’s Disease Classification from Magnetic Resonance Brain Images. Cogn. Syst. Res. 2019, 57, 147–159. [Google Scholar] [CrossRef]
- Li, W.; Lin, X.; Chen, X. Detecting Alzheimer’s Disease Based on 4D FMRI: An Exploration under Deep Learning Framework. Neurocomputing 2020, 388, 280–287. [Google Scholar] [CrossRef]
- Kazemi, Y.; Houghten, S. A Deep Learning Pipeline to Classify Different Stages of Alzheimer’s Disease from FMRI Data. In Proceedings of the 2018 IEEE Conference on Computational Intelligence in Bioinformatics and Computational Biology, CIBCB, Saint Louis, MO, USA, 30 May–2 June 2018; pp. 1–8. [Google Scholar] [CrossRef]



| CN | EMCI | LMCI | AD |
|---|---|---|---|
| 197 | 238 | 159 | 118 |
| Spatial Feature Extractor | Intact | Reduced 1/2 | Reduced 1/4 |
|---|---|---|---|
| Input | 128 × 128 × 128 × 140 | 128 × 128 × 128 × 70 | 128 × 128 × 128 × 35 |
| Layer 1 | 64 × 64 × 64 × 280 | 64 × 64 × 64 × 140 | 64 × 64 × 64 × 70 |
| Layer 2 | 32 × 32 × 32 × 560 | 32 × 32 × 32 × 280 | 32 × 32 × 32 × 140 |
| Layer 3 | 16 × 16 × 16 × 1120 | 16 × 16 × 16 × 560 | 16 × 16 × 16 × 280 |
| Layer 4 | 8 × 8 × 8 × 2240 | 8 × 8 × 8 × 1120 | 8 × 8 × 8 × 560 |
| Layer 5 | 16 × 16 × 16 × 1120 | 4 × 4 × 4 × 2240 | 4 × 4 × 4 × 1120 |
| Layer 6 | 32 × 32 × 32 × 560 | 8 × 8 × 8 × 1120 | 2 × 2 × 2 × 2240 |
| Layer 7 | 64 × 64 × 64 × 280 | 16 × 16 × 16 × 560 | 4 × 4 × 4 × 1120 |
| Layer 8 | 128 × 128 × 128 × 140 | 32 × 32 × 32 × 280 | 8 × 8 × 8 × 560 |
| Layer 9 | - | 64 × 64 × 64 × 140 | 16 × 16 × 16 × 280 |
| Layer 10 | - | 128 × 128 × 128 × 70 | 32 × 32 × 32 × 140 |
| Layer 11 | - | - | 64 × 64 × 64 × 70 |
| Layer 12 | - | - | 128 × 128 × 128 × 35 |
| Intact | Reduced 1/2 | Reduced 1/4 |
|---|---|---|
| CB Unit | ||
| CB Unit | ||
| CB Unit | ||
| CB Unit | ||
| CTB Unit | CB Unit | |
| CTB Unit | CB Unit | |
| CTB Unit | ||
| CTB Unit | ||
| - | CTB Unit | |
| - | CTB Unit | |
| - | - | CTB Unit |
| - | - | CTB Unit |
| 140 Channel (%) | 70 Channel (%) | 35 Channel (%) | |
|---|---|---|---|
| Test 1 | 96.1 | 95.7 | 92.4 |
| Test 2 | 96.4 | 94.8 | 92.2 |
| Test 3 | 95.8 | 95.4 | 92.3 |
| Test 4 | 96.7 | 95.1 | 91.6 |
| Test 5 | 96.4 | 95.1 | 91.4 |
| Average | 96.28 | 95.22 | 91.8 |
| Research | Modality | Type | Accuracy (%) |
|---|---|---|---|
| Sarraf et al. [24] | fMRI-2D | Binary | 96.8 |
| Billones et al. [25] | fMRI-2D | Binary | 98.3 |
| Jain et al. [26] | MRI-2D | Binary | 99.1 |
| Li et al. [27] | fMRI-4D | Binary | 97.3 |
| Parmar et al. [21] | fMRI-4D | Binary | 94.5 |
| Billones et al. [25] | fMRI-2D | Multi-class | 91.8 |
| Kazemi et al. [28] | fMRI-2D | Multi-class | 97.6 |
| Li et al. [27] | fMRI-4D | Multi-class | 89.4 |
| Harshit et al. [21] | fMRI-4D | Multi-class | 94.5 |
| Ours | fMRI-4D | Multi-class | 96.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Noh, J.-H.; Kim, J.-H.; Yang, H.-D. Classification of Alzheimer’s Progression Using fMRI Data. Sensors 2023, 23, 6330. https://doi.org/10.3390/s23146330
Noh J-H, Kim J-H, Yang H-D. Classification of Alzheimer’s Progression Using fMRI Data. Sensors. 2023; 23(14):6330. https://doi.org/10.3390/s23146330
Chicago/Turabian StyleNoh, Ju-Hyeon, Jun-Hyeok Kim, and Hee-Deok Yang. 2023. "Classification of Alzheimer’s Progression Using fMRI Data" Sensors 23, no. 14: 6330. https://doi.org/10.3390/s23146330
APA StyleNoh, J.-H., Kim, J.-H., & Yang, H.-D. (2023). Classification of Alzheimer’s Progression Using fMRI Data. Sensors, 23(14), 6330. https://doi.org/10.3390/s23146330






