Boosting 3D Object Detection with Density-Aware Semantics-Augmented Set Abstraction
Abstract
1. Introduction
- We propose the DSASA framework, which includes the DS-FPS and the RCE module to balance the foreground points sampling and enhance the point features.
- We conduct experiments to verify that the DS-FPS can alleviate sampling imbalance, and the RCE module can improve performance with negligible increases in computing resources.
- The evaluation conducted on KITTI [12] 3D benchmarks shows that DSASA outperforms other single-staged point-based detectors under the same experimental environment in the outdoor scenarios.
2. Related Work
2.1. Point Cloud-Based 3D Detectors
2.2. Point Sampling in Point Cloud Processing
2.3. Point Density in 3D Object Detection
2.4. Learning from Raw Points Coordinates
3. Methods
3.1. Preliminary
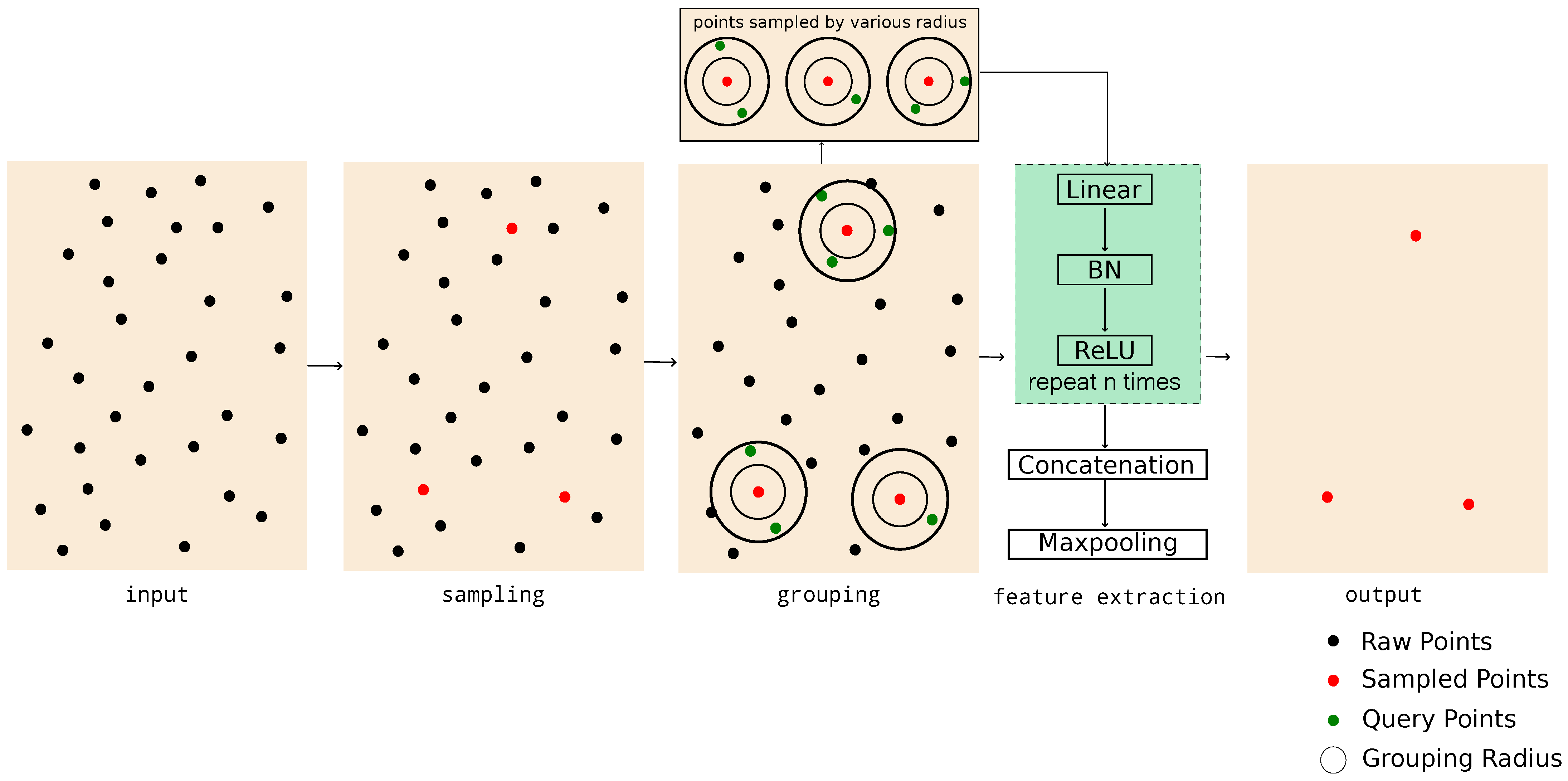
3.1.1. Sampling
| Algorithm 1: Generalized Farthest Point Sampling |
| Input: (required): coordinates (optional): features foreground scores Output: sampled key point set 1: initialize an empty sampling point set K; 2: initialize a distance array d of length N with all 3: initialize a visit array v of length N with all zeros; 4: for to M do 5: if then 6: 7: else 8: 9: 10: end if 11: add to K, 12: for to N do 13: 14: end for 15: end for |
3.1.2. Grouping
3.1.3. Feature Extraction
3.2. Density-Aware Semantics-Augmented Set Abstraction
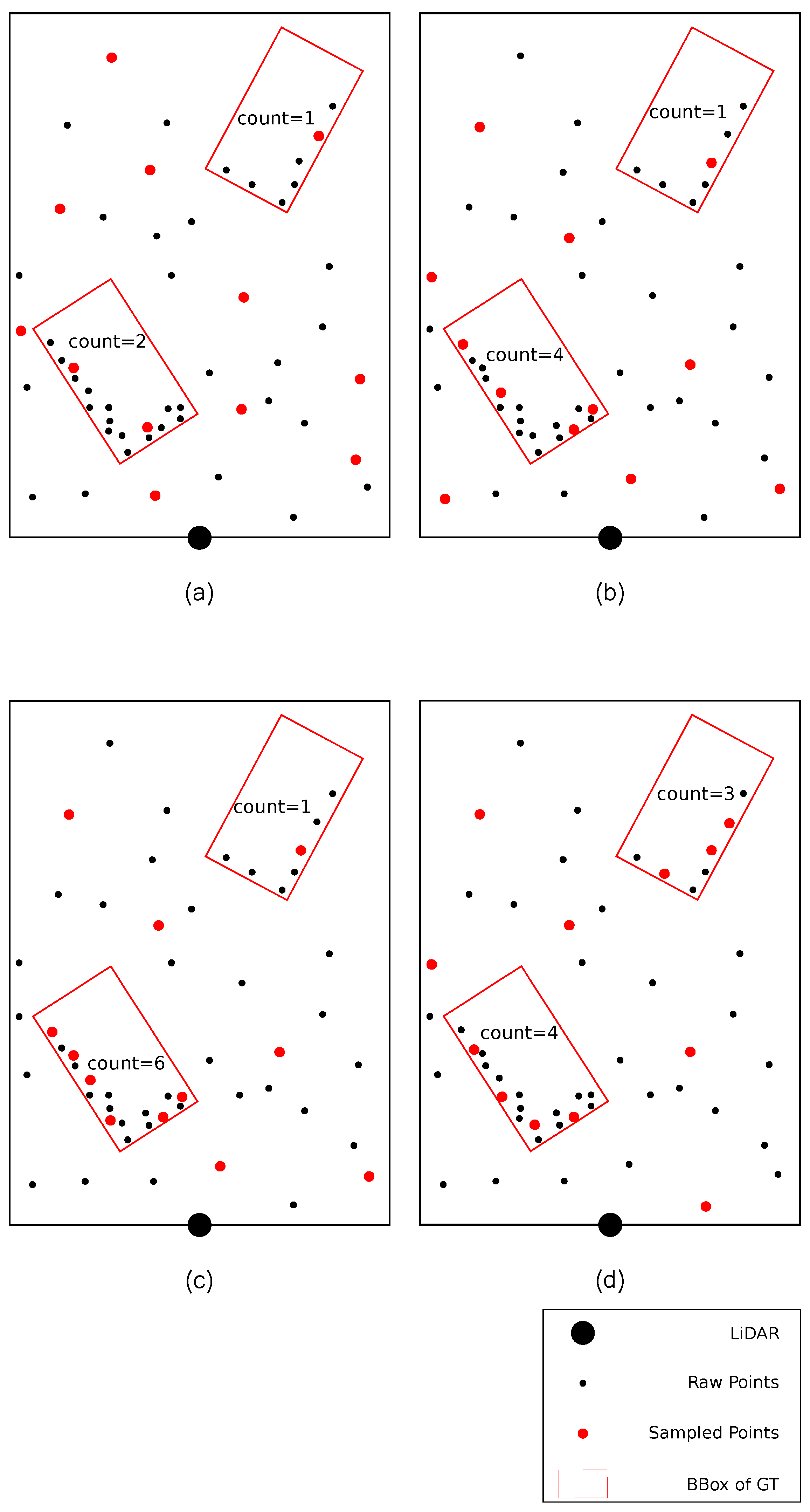
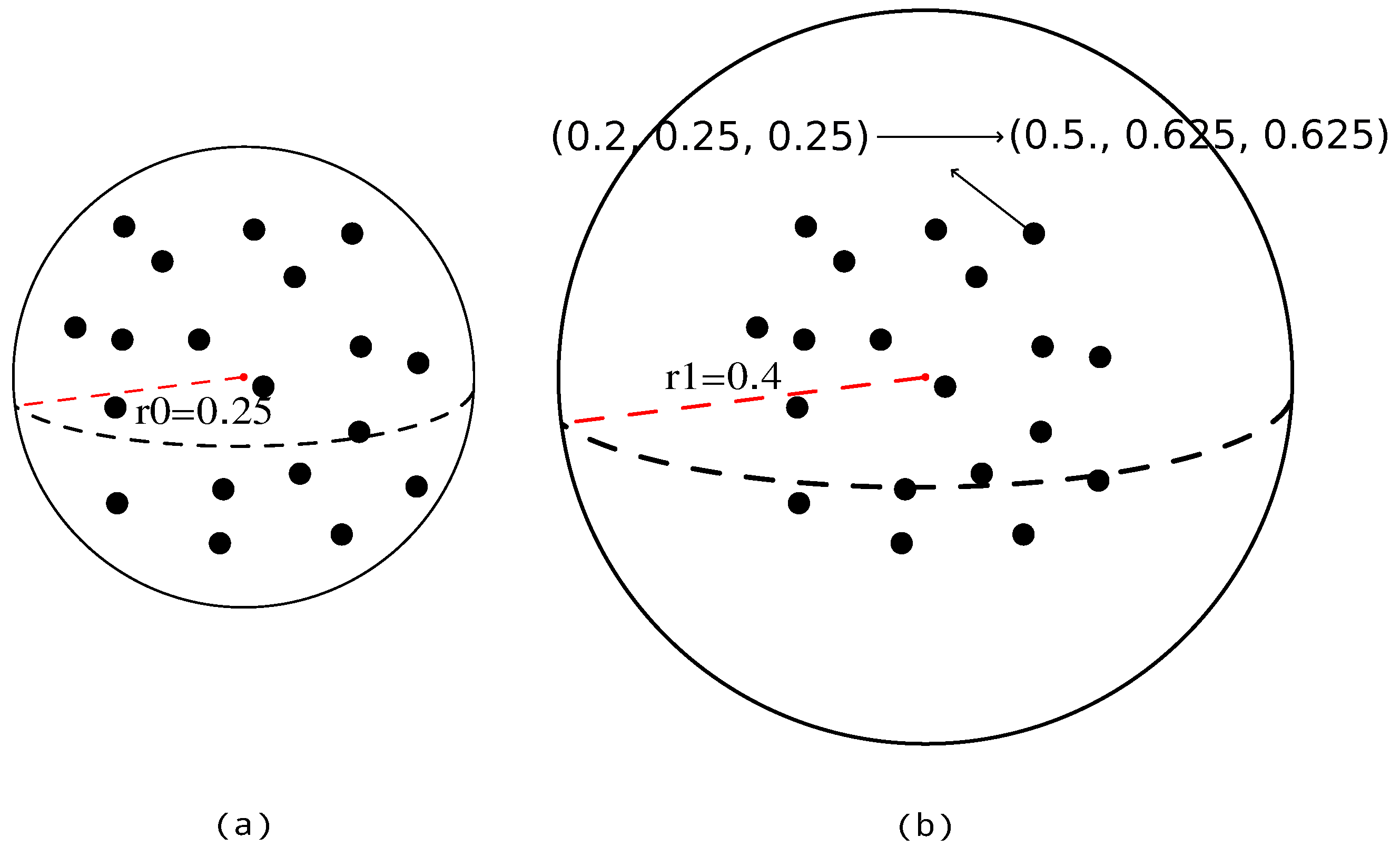
3.2.1. Density-Aware Semantic Farthest Point Sampling
3.2.2. Raw Coordinate Enhancement
4. Experiments
4.1. Datasets
4.2. Implementation Details
4.3. Main Results
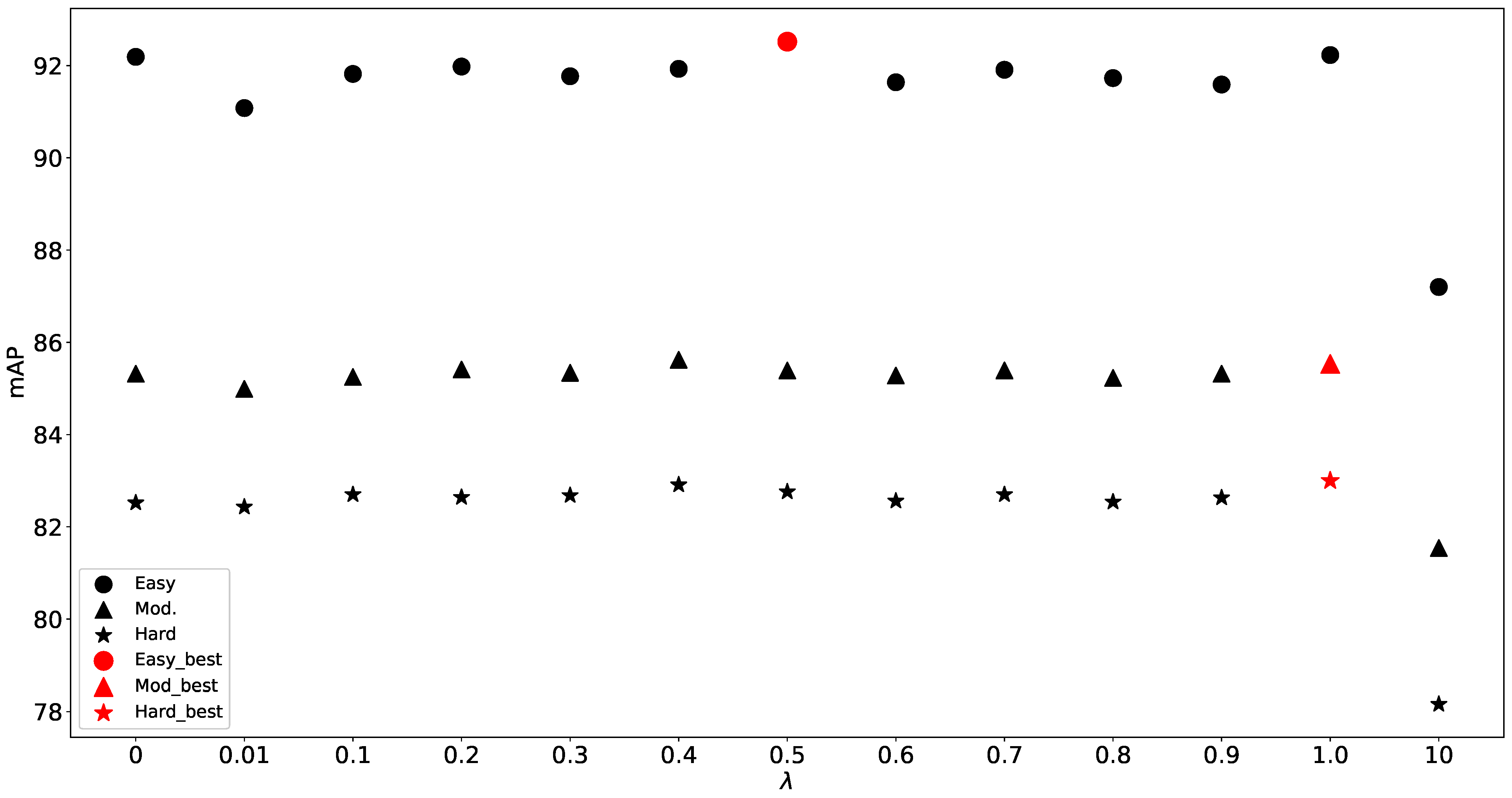
4.4. Ablation Study
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DSASA | Density-Aware Semantics-Augmented Set Abstraction |
| SA | Set Abstraction |
| FPS | Farthest Point Sampling |
| DS-FPS | Density-Semantics-Aware Farthest Point Sampling |
| S-FPS | Semantic-aware FPS |
| RCE | Raw Coordinate Enhancement |
| FP | Feature Propagation |
| D-FPS | Distance-Based FPS |
| F-FPS | Feature-Based FPS |
| GNN | Graph Neural Network |
| KDE | Kernel Density Estimation |
| KNN | K-Nearest Neighborhood |
| MLP | Multi-Layer Perceptron |
| RDA | Relative Direction Angle |
| ADA | Absolute Direction Angle |
| RPQB | Relative Position in Query Ball |
| BBox | Bounding Box |
| Std | Standard Deviation |
| GT | Ground Truth |
| BEV | Bird’s-Eye View |
References
- Graham, B.; Van der Maaten, L. Submanifold sparse convolutional networks. arXiv 2017, arXiv:1706.01307. [Google Scholar]
- Yan, Y.; Mao, Y.; Li, B. Second: Sparsely embedded convolutional detection. Sensors 2018, 18, 3337. [Google Scholar] [CrossRef] [PubMed]
- Qi, C.R.; Su, H.; Mo, K.; Guibas, L.J. Pointnet: Deep learning on point sets for 3d classification and segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 652–660. [Google Scholar]
- Qi, C.R.; Yi, L.; Su, H.; Guibas, L.J. Pointnet++: Deep hierarchical feature learning on point sets in a metric space. Adv. Neural Inf. Process. Syst. 2017, 30, 5099–5108. [Google Scholar]
- Qian, G.; Li, Y.; Peng, H.; Mai, J.; Hammoud, H.; Elhoseiny, M.; Ghanem, B. Pointnext: Revisiting pointnet++ with improved training and scaling strategies. Adv. Neural Inf. Process. Syst. 2022, 35, 23192–23204. [Google Scholar]
- Shi, S.; Guo, C.; Jiang, L.; Wang, Z.; Shi, J.; Wang, X.; Li, H. Pv-rcnn: Point-voxel feature set abstraction for 3d object detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 10529–10538. [Google Scholar]
- Shi, S.; Jiang, L.; Deng, J.; Wang, Z.; Guo, C.; Shi, J.; Wang, X.; Li, H. PV-RCNN++: Point-voxel feature set abstraction with local vector representation for 3D object detection. Int. J. Comput. Vis. 2023, 131, 531–551. [Google Scholar] [CrossRef]
- Shi, S.; Wang, X.; Li, H. Pointrcnn: 3d object proposal generation and detection from point cloud. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 770–779. [Google Scholar]
- Yang, Z.; Sun, Y.; Liu, S.; Jia, J. 3dssd: Point-based 3d single stage object detector. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 11040–11048. [Google Scholar]
- Chen, C.; Chen, Z.; Zhang, J.; Tao, D. Sasa: Semantics-augmented set abstraction for point-based 3d object detection. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtual, 22 February–1 March 2022; Volume 36, pp. 221–229. [Google Scholar]
- Zhang, Y.; Hu, Q.; Xu, G.; Ma, Y.; Wan, J.; Guo, Y. Not all points are equal: Learning highly efficient point-based detectors for 3d lidar point clouds. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 18953–18962. [Google Scholar]
- Geiger, A.; Lenz, P.; Urtasun, R. Are we ready for autonomous driving? The kitti vision benchmark suite. In Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012; pp. 3354–3361. [Google Scholar]
- Zhou, Y.; Tuzel, O. Voxelnet: End-to-end learning for point cloud based 3d object detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 4490–4499. [Google Scholar]
- Lang, A.H.; Vora, S.; Caesar, H.; Zhou, L.; Yang, J.; Beijbom, O. Pointpillars: Fast encoders for object detection from point clouds. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 12697–12705. [Google Scholar]
- Mao, J.; Xue, Y.; Niu, M.; Bai, H.; Feng, J.; Liang, X.; Xu, H.; Xu, C. Voxel transformer for 3d object detection. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 3164–3173. [Google Scholar]
- He, C.; Li, R.; Li, S.; Zhang, L. Voxel set transformer: A set-to-set approach to 3d object detection from point clouds. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 8417–8427. [Google Scholar]
- Sheng, H.; Cai, S.; Liu, Y.; Deng, B.; Huang, J.; Hua, X.S.; Zhao, M.J. Improving 3d object detection with channel-wise transformer. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 2743–2752. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30, 5998–6008. [Google Scholar]
- Fan, L.; Pang, Z.; Zhang, T.; Wang, Y.X.; Zhao, H.; Wang, F.; Wang, N.; Zhang, Z. Embracing single stride 3d object detector with sparse transformer. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 8458–8468. [Google Scholar]
- Shi, W.; Rajkumar, R. Point-gnn: Graph neural network for 3d object detection in a point cloud. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 1711–1719. [Google Scholar]
- Qian, R.; Lai, X.; Li, X. BADet: Boundary-aware 3D object detection from point clouds. Pattern Recognit. 2022, 125, 108524. [Google Scholar] [CrossRef]
- Guan, T.; Wang, J.; Lan, S.; Chandra, R.; Wu, Z.; Davis, L.; Manocha, D. M3detr: Multi-representation, multi-scale, mutual-relation 3d object detection with transformers. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Waikoloa, HI, USA, 3–8 January 2022; pp. 772–782. [Google Scholar]
- Hu, J.S.; Kuai, T.; Waslander, S.L. Point density-aware voxels for lidar 3d object detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 8469–8478. [Google Scholar]
- Parzen, E. On estimation of a probability density function and mode. Ann. Math. Stat. 1962, 33, 1065–1076. [Google Scholar] [CrossRef]
- Rosenblatt, M. Remarks on some nonparametric estimates of a density function. Ann. Math. Stat. 1956, 27, 832–837. [Google Scholar] [CrossRef]
- Contributors, M. MMDetection3D: OpenMMLab Next-Generation Platform for General 3D Object Detection. 2020. Available online: https://github.com/open-mmlab/mmdetection3d (accessed on 1 September 2022).
- Li, Z.; Wang, F.; Wang, N. Lidar r-cnn: An efficient and universal 3d object detector. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 7546–7555. [Google Scholar]
- Chen, X.; Ma, H.; Wan, J.; Li, B.; Xia, T. Multi-view 3d object detection network for autonomous driving. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 1907–1915. [Google Scholar]
- Qi, C.R.; Liu, W.; Wu, C.; Su, H.; Guibas, L.J. Frustum pointnets for 3d object detection from rgb-d data. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 918–927. [Google Scholar]
- Chen, Y.; Li, Y.; Zhang, X.; Sun, J.; Jia, J. Focal sparse convolutional networks for 3d object detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 5428–5437. [Google Scholar]
- Wu, H.; Wen, C.; Shi, S.; Li, X.; Wang, C. Virtual Sparse Convolution for Multimodal 3D Object Detection. arXiv 2023, arXiv:2303.02314. [Google Scholar]
- He, C.; Zeng, H.; Huang, J.; Hua, X.S.; Zhang, L. Structure aware single-stage 3d object detection from point cloud. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 11873–11882. [Google Scholar]
- Deng, J.; Shi, S.; Li, P.; Zhou, W.; Zhang, Y.; Li, H. Voxel r-cnn: Towards high performance voxel-based 3d object detection. In Proceedings of the AAAI Conference on Artificial Intelligence, Online, 4–7 February 2021; Volume 35, pp. 1201–1209. [Google Scholar]




| Method | Car (IoU = 0.7) | ||
|---|---|---|---|
| Easy | Mod. | Hard | |
| RGB+LiDAR | |||
| MV3D [28] | 74.97 | 63.63 | 54.00 |
| F-PointNet [29] | 82.19 | 69.79 | 60.59 |
| Focals Conv-F [30] | 90.55 | 82.28 | 77.59 |
| VirConv-T [31] | 92.54 | 86.25 | 81.24 |
| LiDAR only | |||
| Voxel-based | |||
| VoxelNet [13] | 77.47 | 65.11 | 57.73 |
| SECOND [2] | 83.34 | 72.55 | 65.82 |
| PointPillars [14] | 82.58 | 74.31 | 68.99 |
| SA-SSD [32] | 88.75 | 79.9 | 74.16 |
| Voxel-RCNN [33] | 90.90 | 81.62 | 77.06 |
| VoxSeT [16] | 88.53 | 82.06 | 77.46 |
| Hybrid-based | |||
| PV-RCNN [6] | 90.25 | 81.43 | 76.82 |
| PV-RCNN++ [7] | 90.14 | 81.88 | 77.15 |
| Point-based | |||
| PointRCNN [8] | 86.96 | 75.64 | 70.70 |
| 3DSSD [9] | 88.36 | 79.57 | 74.55 |
| IA-SSD [11] | 88.87 | 80.32 | 75.10 |
| SASA (reproduced) [10] | 87.79 | 81.21 | 76.52 |
| DSASA (ours) | 88.64 | 81.72 | 76.73 |
| Method | Car (IoU = 0.7) | Delay (ms) | ||
|---|---|---|---|---|
| Easy | Mod. | Hard | ||
| PointRCNN | 91.57 | 82.24 | 80.45 | 57 |
| PointRCNN+SASA (reproduced) | 92.14 | 83.10 | 80.71 | 48 |
| PointRCNN+DSASA | 92.05 | 84.05 | 82.55 | 50 |
| 3DSSD | 91.54 | 83.46 | 82.18 | 36 |
| 3DSSD+SASA (reproduced) | 91.89 | 85.32 | 82.52 | 36 |
| 3DSSD+DSASA | 92.54 | 85.91 | 83.12 | 37 |
| Method | Car (IoU = 0.7) | Ped. (IoU = 0.5) | Cyc. (IoU = 0.5) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Easy | Mod. | Hard | Easy | Mod. | Hard | Easy | Mod. | Hard | |
| PointRCNN | 91.92 | 80.84 | 78.47 | 67.00 | 58.48 | 51.21 | 93.37 | 75.16 | 70.67 |
| PointRCNN+SASA (reproduced) | 92.13 | 82.76 | 80.39 | 68.34 | 60.48 | 51.92 | 92.30 | 74.13 | 69.71 |
| PointRCNN+DSASA | 92.25 | 82.93 | 80.60 | 71.22 | 63.19 | 55.62 | 94.12 | 76.29 | 71.79 |
| 3DSSD | 91.47 | 83.00 | 81.88 | 57.10 | 52.24 | 48.83 | 89.90 | 71.78 | 68.09 |
| 3DSSD+SASA (reproduced) | 92.02 | 85.32 | 82.55 | 63.28 | 57.98 | 53.45 | 92.20 | 74.37 | 69.74 |
| 3DSSD+DSASA | 92.18 | 85.32 | 82.71 | 67.21 | 59.38 | 52.19 | 92.93 | 75.08 | 70.46 |
| Method | Car (IoU = 0.7) | ||
|---|---|---|---|
| Easy | Mod. | Hard | |
| Baseline (DSASA without RCE) | 92.23 | 85.53 | 83.00 |
| Baseline+RPQB | 92.13 | 85.57 | 82.92 |
| Baseline+RDA | 92.14 | 85.77 | 83.02 |
| Baseline+Density | 92.20 | 85.68 | 82.80 |
| Baseline+ADA | 91.54 | 85.65 | 82.83 |
| Baseline+RPQB+RDA+Density | 92.54 | 85.91 | 83.12 |
| Baseline+RPQB+ADA+Density | 91.72 | 85.69 | 82.77 |
| Method | Car (IoU = 0.7) | ||
|---|---|---|---|
| Easy | Mod. | Hard | |
| RCE | 92.54 | 85.91 | 83.12 |
| Small MLP | 91.64 | 85.66 | 82.97 |
| Large MLP | 91.89 | 85.47 | 82.61 |
| Stage | Mean | Std | |
|---|---|---|---|
| F-FPS | Second SA | 9.23 | 6.42 |
| Third SA | 4.23 | 3.12 | |
| S-FPS | Second SA | 23.31 | 20.89 |
| Third SA | 20.37 | 18.29 | |
| DS-FPS | Second SA | 17.89 | 15.00 |
| Third SA | 16.67 | 13.84 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, T.; Wang, J.; Yang, X. Boosting 3D Object Detection with Density-Aware Semantics-Augmented Set Abstraction. Sensors 2023, 23, 5757. https://doi.org/10.3390/s23125757
Zhang T, Wang J, Yang X. Boosting 3D Object Detection with Density-Aware Semantics-Augmented Set Abstraction. Sensors. 2023; 23(12):5757. https://doi.org/10.3390/s23125757
Chicago/Turabian StyleZhang, Tingyu, Jian Wang, and Xinyu Yang. 2023. "Boosting 3D Object Detection with Density-Aware Semantics-Augmented Set Abstraction" Sensors 23, no. 12: 5757. https://doi.org/10.3390/s23125757
APA StyleZhang, T., Wang, J., & Yang, X. (2023). Boosting 3D Object Detection with Density-Aware Semantics-Augmented Set Abstraction. Sensors, 23(12), 5757. https://doi.org/10.3390/s23125757






