A DFT Study of Phosphate Ion Adsorption on Graphene Nanodots: Implications for Sensing
Abstract
1. Introduction
2. Methods
3. Results and Discussion
4. Conclusions
Supplementary Materials
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Westheimer, F.H. Why Nature Chose Phosphates. Science 1987, 235, 1173–1178. [Google Scholar] [CrossRef]
- Knouse, K.W.; Flood, D.T.; Vantourout, J.C.; Schmidt, M.A.; McDonald, I.M.; Eastgate, M.D.; Baran, P.S. Nature Chose Phosphates and Chemists Should Too: How Emerging P(V) Methods Can Augment Existing Strategies. ACS Cent. Sci. 2021, 7, 1473–1485. [Google Scholar] [CrossRef]
- Bechtaoui, N.; Rabiu, M.K.; Raklami, A.; Oufdou, K.; Hafidi, M.; Jemo, M. Phosphate-Dependent Regulation of Growth and Stresses Management in Plants. Front. Plant Sci. 2021, 12, 679916. [Google Scholar] [CrossRef]
- Penido, M.G.M.G.; Alon, U.S. Phosphate Homeostasis and Its Role in Bone Health. Pediatr. Nephrol. 2012, 27, 2039–2048. [Google Scholar] [CrossRef]
- Gupta, R.; Laxman, S. Cycles, Sources, and Sinks: Conceptualizing How Phosphate Balance Modulates Carbon Flux Using Yeast Metabolic Networks. eLife 2021, 10, e63341. [Google Scholar] [CrossRef]
- Tone, D.; Ode, K.L.; Zhang, Q.; Fujishima, H.; Yamada, R.G.; Nagashima, Y.; Matsumoto, K.; Wen, Z.; Yoshida, S.Y.; Mitani, T.T.; et al. Distinct Phosphorylation States of Mammalian CaMKIIβ Control the Induction and Maintenance of Sleep. PLoS Biol. 2022, 20, e3001813. [Google Scholar] [CrossRef]
- Carpenter, S.R. Eutrophication of Aquatic Ecosystems: Bistability and Soil Phosphorus. Proc. Natl. Acad. Sci. USA 2005, 102, 10002–10005. [Google Scholar] [CrossRef]
- McCutcheon, J.; Lutz, S.; Williamson, C.; Cook, J.M.; Tedstone, A.J.; Vanderstraeten, A.; Wilson, S.A.; Stockdale, A.; Bonneville, S.; Anesio, A.M.; et al. Mineral Phosphorus Drives Glacier Algal Blooms on the Greenland Ice Sheet. Nat. Commun. 2021, 12, 570. [Google Scholar] [CrossRef]
- Nadkarni, G.N.; Uribarri, J. Phosphorus and the Kidney: What Is Known and What Is Needed. Adv. Nutr. 2014, 5, 98–103. [Google Scholar] [CrossRef]
- Carpenter, T.O. Primary Disorders of Phosphate Metabolism. In Endotext; Feingold, K.R., Anawalt, B., Blackman, M.R., Boyce, A., Chrousos, G., Corpas, E., de Herder, W.W., Dhatariya, K., Dungan, K., Hofland, J., et al., Eds.; MDText.com, Inc.: South Dartmouth, MA, USA, 2000–2022. [Google Scholar]
- Ray, A.; Esparza, S.; Wu, D.; Hanudel, M.R.; Joung, H.-A.; Gales, B.; Tseng, D.; Salusky, I.B.; Ozcan, A. Measurement of Serum Phosphate Levels Using a Mobile Sensor. Analyst 2020, 145, 1841–1848. [Google Scholar] [CrossRef]
- Haberer, J.L.; Brandes, J.A. A High Sensitivity, Low Volume HPLC Method to Determine Soluble Reactive Phosphate in Freshwater and Saltwater. Mar. Chem. 2003, 82, 185–196. [Google Scholar] [CrossRef]
- Winkler, D.; Banke, S.; Kurz, P. Fluorimetric Detection of Phosphates in Water Using a Disassembly Approach: A Comparison of FeIII-, ZnII-, MnII-, and MnIII-salen Complexes. Z. Anorg. Allg. Chem. 2020, 646, 933–939. [Google Scholar] [CrossRef]
- Zeitoun, R.; Biswas, A. Review—Potentiometric Determination of Phosphate Using Cobalt: A Review. J. Electrochem. Soc. 2020, 167, 127507. [Google Scholar] [CrossRef]
- Gilbert, L.; Jenkins, A.T.; Browning, S.; Hart, J.P. Development of an Amperometric Assay for Phosphate Ions in Urine Based on a Chemically Modified Screen-Printed Carbon Electrode. Anal. Biochem. 2009, 393, 242–247. [Google Scholar] [CrossRef]
- Kulkarni, S.J.; Karve, M.S. Fabrication of Enzyme-Based Optical Biosensor for Estimation of Inorganic Phosphate in a Urine Sample. SN Appl. Sci. 2020, 2, 1118. [Google Scholar] [CrossRef]
- Balbach, S.; Jiang, N.; Moreddu, R.; Dong, X.; Kurz, W.; Wang, C.; Dong, J.; Yin, Y.; Butt, H.; Brischwein, M.; et al. Smartphone-Based Colorimetric Detection System for Portable Health Tracking. Anal. Methods 2021, 13, 4361–4369. [Google Scholar] [CrossRef]
- Crouch, S.R.; Malmstadt, H.V. Mechanistic Investigation of Molybdenum Blue Method for Determination of Phosphate. Anal. Chem. 1967, 39, 1084–1089. [Google Scholar] [CrossRef]
- Ganesh, S.; Khan, F.; Ahmed, M.K.; Velavendan, P.; Pandey, N.K.; Mudali, U.K. Spectrophotometric Determination of Trace Amounts of Phosphate in Water and Soil. Water Sci. Technol. 2012, 66, 2653–2658. [Google Scholar] [CrossRef]
- Bacon, M.; Bradley, S.J.; Nann, T. Graphene Quantum Dots. Part. Part. Syst. Charact. 2014, 31, 415–428. [Google Scholar] [CrossRef]
- Henna, T.K.; Pramod, K. Chapter 16—Biocompatibility of Graphene Quantum Dots and Related Materials. In Handbook of Biomaterials Biocompatibility; Mozafari, M., Ed.; Woodhead Publishing Series in Biomaterials; Woodhead Publishing: Sawston, UK, 2020; pp. 353–367. [Google Scholar] [CrossRef]
- Fasbender, S.; Zimmermann, L.; Cadeddu, R.P.; Luysberg, M.; Moll, B.; Janiak, C.; Heinzel, T.; Haas, R. The Low Toxicity of Graphene Quantum Dots is Reflected by Marginal Gene Expression Changes of Primary Human Hematopoietic Stem Cells. Sci. Rep. 2019, 9, 12028. [Google Scholar] [CrossRef]
- Özönder, Ş.; Ünlü, C.; Güleryüz, C.; Trabzon, L. Doped Graphene Quantum Dots UV–Vis Absorption Spectrum: A High-Throughput TDDFT Study. ACS Omega 2023, 8, 2112–2118. [Google Scholar] [CrossRef] [PubMed]
- Motlagh, S.A.O.; Apalkov, V. Absorption Properties of Graphene Quantum Dots under Ultrashort Optical Pulses. Phys. Rev. B 2021, 104, 045421. [Google Scholar] [CrossRef]
- Shtepliuk, I.; Khranovskyy, V.; Yakimova, R. Insights into the Origin of the Excited Transitions in Graphene Quantum Dots Interacting with Heavy Metals in Different Media. Phys. Chem. Chem. Phys. 2017, 19, 30445–30463. [Google Scholar] [CrossRef]
- Shtepliuk, I.; Caffrey, N.M.; Iakimov, T.; Khranovskyy, V.; Abrikosov, I.A.; Yakimova, R. On the Interaction of Toxic Heavy Metals (Cd, Hg, Pb) with Graphene Quantum Dots and Infinite Graphene. Sci. Rep. 2017, 7, 3934. [Google Scholar] [CrossRef]
- Ye, Z.; Wu, P.; Wang, H.; Jiang, S.; Huang, M.; Lei, D.; Wu, F. Multimode tunable terahertz absorber based on a quarter graphene disk structure. Results Phys. 2023, 48, 106420. [Google Scholar] [CrossRef]
- Lai, R.; Shi, P.; Yi, Z.; Li, H.; Yi, Y. Triple-Band Surface Plasmon Resonance Metamaterial Absorber Based on Open-Ended Prohibited Sign Type Monolayer Graphene. Micromachines 2023, 14, 953. [Google Scholar] [CrossRef]
- Li, W.; Yi, Y.; Yang, H.; Cheng, S.; Yang, W.; Zhang, H.; Yi, Z.; Yi, Y.; Li, H. Active tunable terahertz bandwidth absorber based on single layer graphene. Commun. Theor. Phys. 2023, 75, 045503. [Google Scholar] [CrossRef]
- Tang, B.; Guo, Z.; Jin, G. Polarization-controlled and symmetry-dependent multiple plasmon-induced transparency in graphene-based metasurfaces. Opt. Express 2022, 30, 35554–35566. [Google Scholar] [CrossRef]
- Ahmadi, H.; Keshipour, S. New Water-Soluble Colorimetric pH and Metal Ion Sensor Based on Graphene Quantum Dot Modified with Alizarin Red S. Sci. Rep. 2020, 10, 14185. [Google Scholar] [CrossRef]
- Nirala, N.R.; Abraham, S.; Kumar, V.; Bansal, A.; Srivastava, A.; Saxena, P.S. Colorimetric Detection of Cholesterol Based on Highly Efficient Peroxidase Mimetic Activity of Graphene Quantum Dots. Sens. Actuators B Chem. 2015, 218, 42–50. [Google Scholar] [CrossRef]
- Facure, M.H.M.; Andre, R.S.; Mercante, L.A.; Correa, D.S. Colorimetric Detection of Antioxidants in Food Samples Using MnO2/Graphene Quantum Dot Composites with Oxidase-Like Activity. ACS Appl. Nano Mater. 2022, 5, 15211–15219. [Google Scholar] [CrossRef]
- Abolghasemi-Fakhri, Z.; Amjadi, M. Gold Nanostar@Graphene Quantum Dot as a New Colorimetric Sensing Platform for Detection of Cysteine. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2021, 261, 120010. [Google Scholar] [CrossRef] [PubMed]
- Chatterjee, M.; Nath, P.; Kadian, S.; Kumar, A.; Kumar, V.; Roy, P.; Manik, G.; Satapathi, S. Highly Sensitive and Selective Detection of Dopamine with Boron and Sulfur Co-Doped Graphene Quantum Dots. Sci. Rep. 2022, 12, 9061. [Google Scholar] [CrossRef] [PubMed]
- Shtepliuk, I.; Yakimova, R. Interband Absorption in Few-Layer Graphene Quantum Dots: Effect of Heavy Metals. Materials 2018, 11, 1217. [Google Scholar] [CrossRef]
- Shtepliuk, I.; Yakimova, R. Interband Transitions in Closed-Shell Vacancy Containing Graphene Quantum Dots Complexed with Heavy Metals. Phys. Chem. Chem. Phys. 2018, 20, 21528–21543. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.; Zhang, G.; Ni, P.; Lu, Y.; Lu, Z. Fluorometric and Colorimetric Dual-Readout Alkaline Phosphatase Activity Assay Based on Enzymatically Induced Formation of Colored Au@Ag Nanoparticles and an Inner Filter Effect. Microchim. Acta 2019, 186, 348. [Google Scholar] [CrossRef]
- Upadhyay, L.S.B.; Verma, N. Alkaline Phosphatase Inhibition Based Conductometric Biosensor for Phosphate Estimation in Biological Fluids. Biosens. Bioelectron. 2015, 68, 611–616. [Google Scholar] [CrossRef]
- Chen, B.B.; Li, R.S.; Liu, M.L.; Zou, H.Y.; Liu, H.; Huang, C.Z. Highly Selective Detection of Phosphate Ion Based on a Single-Layered Graphene Quantum Dots-Al3+ Strategy. Talanta 2018, 178, 172–177. [Google Scholar] [CrossRef]
- Bai, J.-M.; Zhang, L.; Liang, R.-P.; Qiu, J.-D. Graphene Quantum Dots Combined with Europium Ions as Photoluminescent Probes for Phosphate Sensing. Chem. Eur. J. 2013, 19, 3822–3826. [Google Scholar] [CrossRef] [PubMed]
- Lia, S.; Xiao, D.; Liu, D.; He, H. Calcium-doped fluorescent carbon nanoparticles: Spontaneousthermal synthesis, pH-sensitive fluorescence off-on, and mechanism. Sens. Actuators B 2018, 266, 594–602. [Google Scholar] [CrossRef]
- Peng, X.; Liu, D.; Zhao, F.; Tang, C. Gas sensing properties of Mg-doped graphene for H2S, SO2, SOF2, and SO2F2 based on DFT. Int. J. Quantum Chem. 2022, 122, e26989. [Google Scholar] [CrossRef]
- Yin, Q.; Liu, M.; Li, Y.; Li, H.; Wen, Z. Computational study of phosphate adsorption on Mg/Ca modified biochar structure in aqueous solution. Chemosphere 2021, 269, 129374. [Google Scholar] [CrossRef] [PubMed]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16, Revision C.01; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- PubChem Compound Database; CID = 24890634, Circumcircumcoronene. Available online: https://pubchem.ncbi.nlm.nih.gov/compound/24890634 (accessed on 26 May 2023).
- Shtepliuk, I.; Yakimova, R. Nature of Photoexcited States in ZnO-Embedded Graphene Quantum Dots. Phys. Chem. Chem. Phys. 2023, 25, 10525–10535. [Google Scholar] [CrossRef]
- Shtepliuk, I.; Santangelo, M.F.; Vagin, M.; Ivanov, I.G.; Khranovskyy, V.; Iakimov, T.; Eriksson, J.; Yakimova, R. Understanding Graphene Response to Neutral and Charged Lead Species: Theory and Experiment. Materials 2018, 11, 2059. [Google Scholar] [CrossRef] [PubMed]
- Santangelo, M.F.; Shtepliuk, I.; Filippini, D.; Puglisi, D.; Vagin, M.; Yakimova, R.; Eriksson, J. Epitaxial Graphene Sensors Combined with 3D-Printed Microfluidic Chip for Heavy Metals Detection. Sensors 2019, 19, 2393. [Google Scholar] [CrossRef] [PubMed]
- GaussView 6; Semichem Inc.: Shawnee Mission, KS, USA, 2019. Available online: https://gaussian.com/gaussview6/ (accessed on 26 May 2023).
- Da Silva, S.; Basséguy, R.; Bergel, A. Electrochemical deprotonation of phosphate on stainless steel. Electrochim. Acta 2004, 49, 4553–4561. [Google Scholar] [CrossRef]
- Zahn, D. Mechanisms of Calcium and Phosphate Ion Association in Aqueous Solution. Z. Anorg. Allg. Chem. 2004, 630, 1507–1511. [Google Scholar] [CrossRef]
- Persson, I.; Trublet, M.; Klysubun, W. Structure Determination of Phosphoric Acid and Phosphate Ions in Aqueous Solution Using EXAFS Spectroscopy and Large Angle X-ray Scattering. J. Phys. Chem. A 2018, 122, 7413–7420. [Google Scholar] [CrossRef]
- Yanai, T.; Tew, D.; Handy, N. A New Hybrid Exchange-Correlation Functional Using the Coulomb-Attenuating Method (CAM-B3LYP). Chem. Phys. Lett. 2004, 393, 51–57. [Google Scholar] [CrossRef]
- Petersson, G.A.; Bennett, A.; Tensfeldt, T.G.; Al-Laham, M.A.; Shirley, W.A.; Mantzaris, J. A Complete Basis Set Model Chemistry. I. The Total Energies of Closed-Shell Atoms and Hydrides of the First-Row Atoms. J. Chem. Phys. 1988, 89, 2193–2218. [Google Scholar] [CrossRef]
- Wang, J.; Cao, S.; Ding, Y.; Ma, F.; Lu, W.; Sun, M. Theoretical Investigations of Optical Origins of Fluorescent Graphene Quantum Dots. Sci. Rep. 2016, 6, 24850. [Google Scholar] [CrossRef] [PubMed]
- Osella, S.; Knippenberg, S. Environmental Effects on the Charge Transfer Properties of Graphene Quantum Dot Based Interfaces. Int. J. Quantum Chem. 2019, 119, e25882. [Google Scholar] [CrossRef]
- Li, M.; Reimers, J.R.; Ford, M.J.; Kobayashi, R.; Amos, R.D. Accurate prediction of the properties of materials using the CAM-B3LYP density functional. J. Comput. Chem. 2021, 42, 1486–1497. [Google Scholar] [CrossRef] [PubMed]
- Sheely, A.; Gifford, B.; Tretiak, S.; Bishop, A. Tunable Optical Features of Graphene Quantum Dots from Edge Functionalization. J. Phys. Chem. C 2021, 125, 9244–9252. [Google Scholar] [CrossRef]
- Otero, N.; Karamanis, P.; El-Kelany, K.E.; Rérat, M.; Maschio, L.; Civalleri, B.; Kirtman, B. Exploring the Linear Optical Properties of Borazine (B3N3) Doped Graphenes: 0D Flakes vs 2D Sheets. J. Phys. Chem. C 2017, 121, 709–722. [Google Scholar] [CrossRef]
- Xie, X.; Liu, Z.H.; Bai, F.Q.; Zhang, H.X. Performance Regulation of Thieno[3,2-b]benzothiophene π-Spacer-Based D-π-A Organic Dyes for Dye-Sensitized Solar Cell Applications: Insights from Computational Study. Front. Chem. 2019, 6, 676. [Google Scholar] [CrossRef]
- Shi, W.; Xia, M.; Wang, F.; Dong, L.; Zhu, S. Efficient absorption properties of surface grafted HEDP-HAP composites for Pb2+ and Cu2+: Experimental study and visualization study of interaction based on Becke surface analysis and independent gradient model. J. Hazard. Mater. 2021, 401, 123748. [Google Scholar] [CrossRef]
- Pascual-Ahuir, J.L.; Silla, E.; Tuñón, I. GEPOL: An Improved Description of Molecular Surfaces. 3. A New Algorithm for the Computation of a Solvent-Excluding Surface. J. Comp. Chem. 1994, 15, 1127–1138. [Google Scholar] [CrossRef]
- Scalmani, G.; Frisch, M.J.; Mennucci, B.; Tomasi, J.; Cammi, R.; Barone, V. Geometries and Properties of Excited States in the Gas Phase and in Solution: Theory and Application of a Time-Dependent Density Functional Theory Polarizable Continuum Model. J. Chem. Phys. 2006, 124, 094107. [Google Scholar] [CrossRef]
- Gaussian, Inc. Creating UV/Visible Plots from the Results of Excited States Calculations. Available online: https://gaussian.com/uvvisplot/ (accessed on 12 June 2023).
- Lu, T.; Chen, F.W. Atomic Dipole Moment Corrected Hirshfeld Population Method. J. Theor. Comput. Chem. 2012, 11, 163–183. [Google Scholar] [CrossRef]
- Shannon, R.D. Revised Effective Ionic Radii and Systematic Studies of Interatomic Distances in Halides and Chalcogenides. Acta Crystallogr. Sect. A 1976, 32, 751–767. [Google Scholar] [CrossRef]
- Becke, A.D.; Edgecombe, K.E. A simple measure of electron localization in atomic and molecular systems. J. Chem. Phys. 1990, 92, 5397–5403. [Google Scholar] [CrossRef]
- Lu, T.; Chen, F. Multiwfn: A Multifunctional Wavefunction Analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef]
- Zhu, S.; Chen, Y.; Khan, M.A.; Xu, H.; Wang, F.; Xia, M. In-Depth Study of Heavy Metal Removal by an Etidronic Acid-Functionalized Layered Double Hydroxide. ACS Appl. Mater. Interfaces 2022, 14, 7450–7463. [Google Scholar] [CrossRef]
- Geng, X.; Li, S.; Mawella-Vithanage, L.; Ma, T.; Kilani, M.; Wang, B.; Ma, L.; Hewa-Rahinduwage, C.C.; Shafikova, A.; Nikolla, E.; et al. Atomically Dispersed Pb Ionic Sites in PbCdSe Quantum Dot Gels Enhance Room-Temperature NO2 Sensing. Nat. Commun. 2021, 12, 4895. [Google Scholar] [CrossRef] [PubMed]
- Raeker, T. Physical Adsorption: Forces and Phenomena. J. Chem. Educ. 1998, 75, 1557. [Google Scholar] [CrossRef]
- Wang, Y.; Weng, W.; Xu, H.; Luo, Y.; Guo, D.; Li, D.; Li, D. Negatively charged molybdate mediated nitrogen-doped graphene quantum dots as a fluorescence turn on probe for phosphate ion in aqueous media and living cells. Anal. Chim. Acta 2019, 1080, 196–205. [Google Scholar] [CrossRef]
- Kim, J.; Wang, L.; Bourouina, T.; Cui, T. Ion sensitive field effect transistor based on graphene and ionophore hybrid membrane for phosphate detection. Microsyst. Technol. 2019, 25, 3357–3364. [Google Scholar] [CrossRef]
- Chai, S.Q.; He, J.H.; Zhan, L.; Li, Y.F.; Li, C.M.; Huang, C.Z. Dy(III)-induced aggregation emission quenching effect of single-layered graphene quantum dots for selective detection of phosphate in the artificial wetlands. Talanta 2019, 196, 100–108. [Google Scholar] [CrossRef]
- Ge, S.; He, J.; Ma, C.; Liu, J.; Xi, F.; Dong, X. One-step synthesis of boron-doped graphene quantum dots for fluorescent sensors and biosensor. Talanta 2019, 199, 581–589. [Google Scholar] [CrossRef]
- Sun, S.; Jiang, K.; Qian, S.; Wang, Y.; Lin, H. Applying Carbon Dots-Metal Ions Ensembles as a Multichannel Fluorescent Sensor Array: Detection and Discrimination of Phosphate Anions. Anal. Chem. 2017, 89, 5542–5548. [Google Scholar] [CrossRef] [PubMed]
- Bhat, K.S.; Nakate, U.T.; Yoo, J.-Y.; Wang, Y.; Mahmoudi, T.; Hahn, Y.-B. Nozzle-Jet-Printed Silver/Graphene Composite-Based Field-Effect Transistor Sensor for Phosphate Ion Detection. ACS Omega 2019, 4, 8373–8380. [Google Scholar] [CrossRef] [PubMed]
- Patella, B.; Gitto, F.; Russo, M.; Aiello, G.; O’Riordan, A.; Inguanta, R. Electrochemical sensor for phosphate ions based on laser scriber reduced graphene oxide. In Proceedings of the 2022 IEEE International Conference on Flexible and Printable Sensors and Systems (FLEPS), Vienna, Austria, 10–13 July 2022. [Google Scholar] [CrossRef]
- Zhuo, S.; Chen, L.; Zhang, Y.; Jin, G. Luminescent phosphate sensor based on upconverting graphene quantum dots. Spectrosc. Lett. 2016, 49, 1–4. [Google Scholar] [CrossRef]
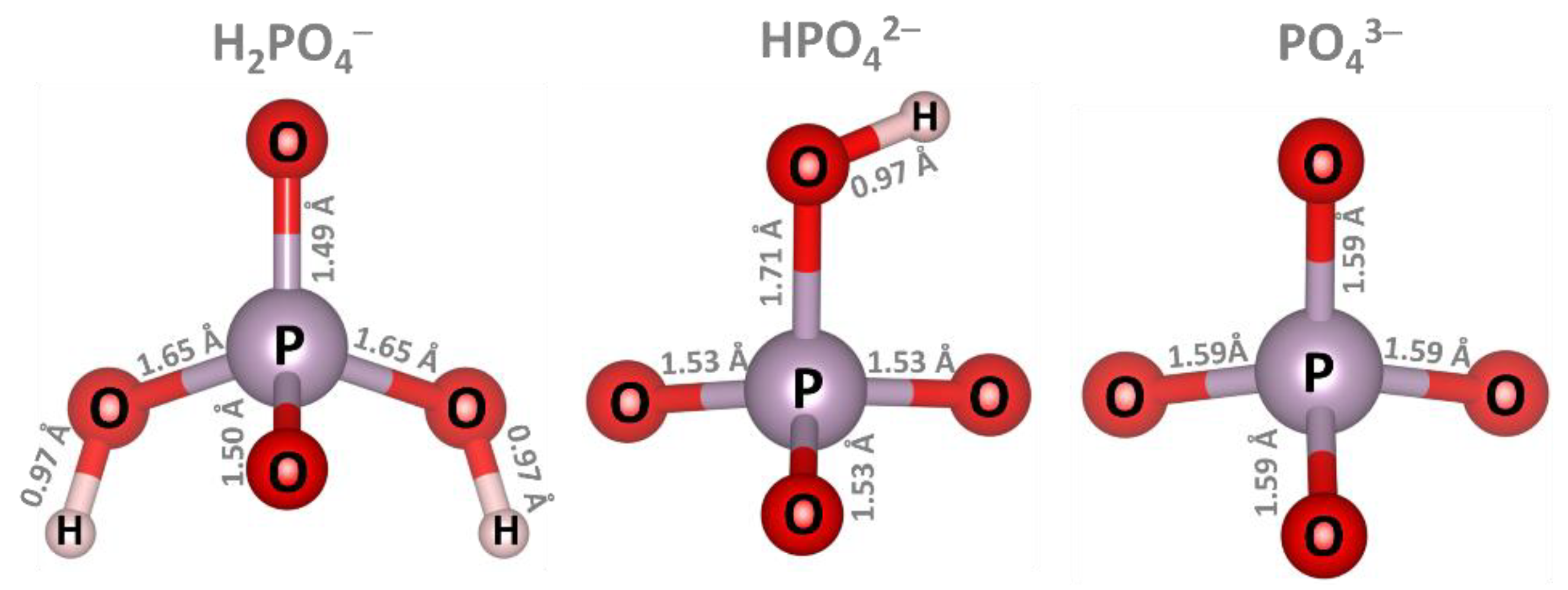

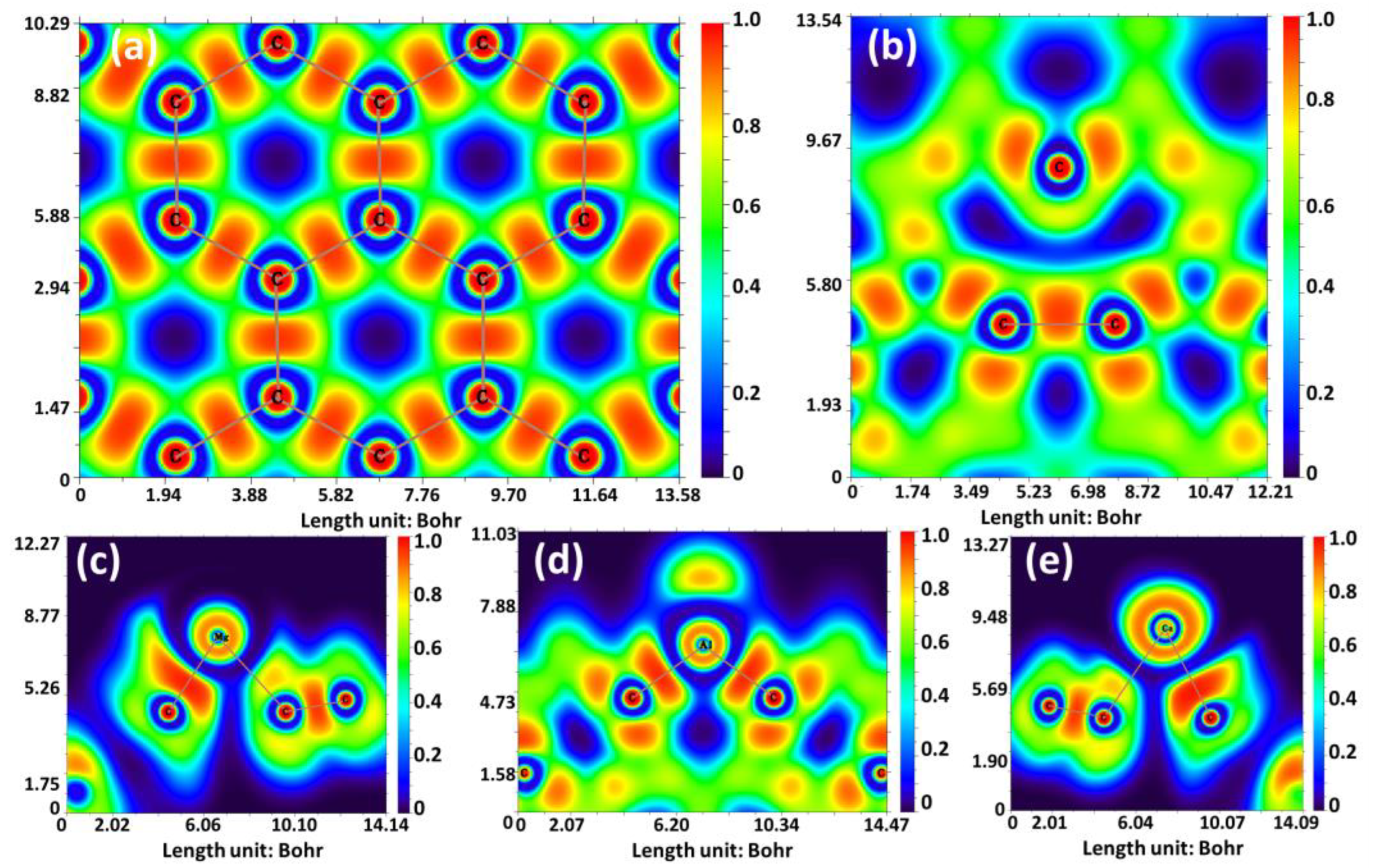

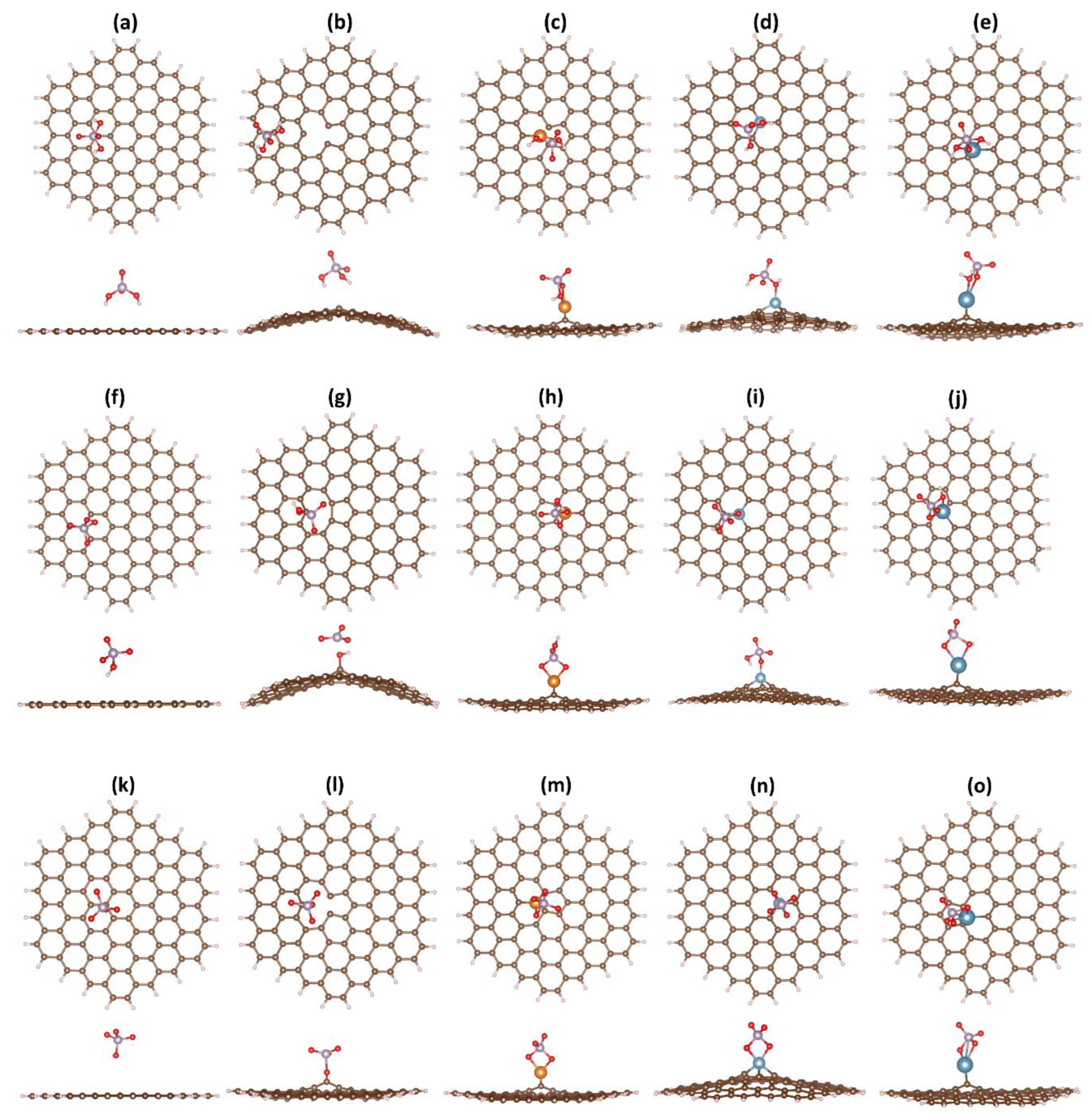
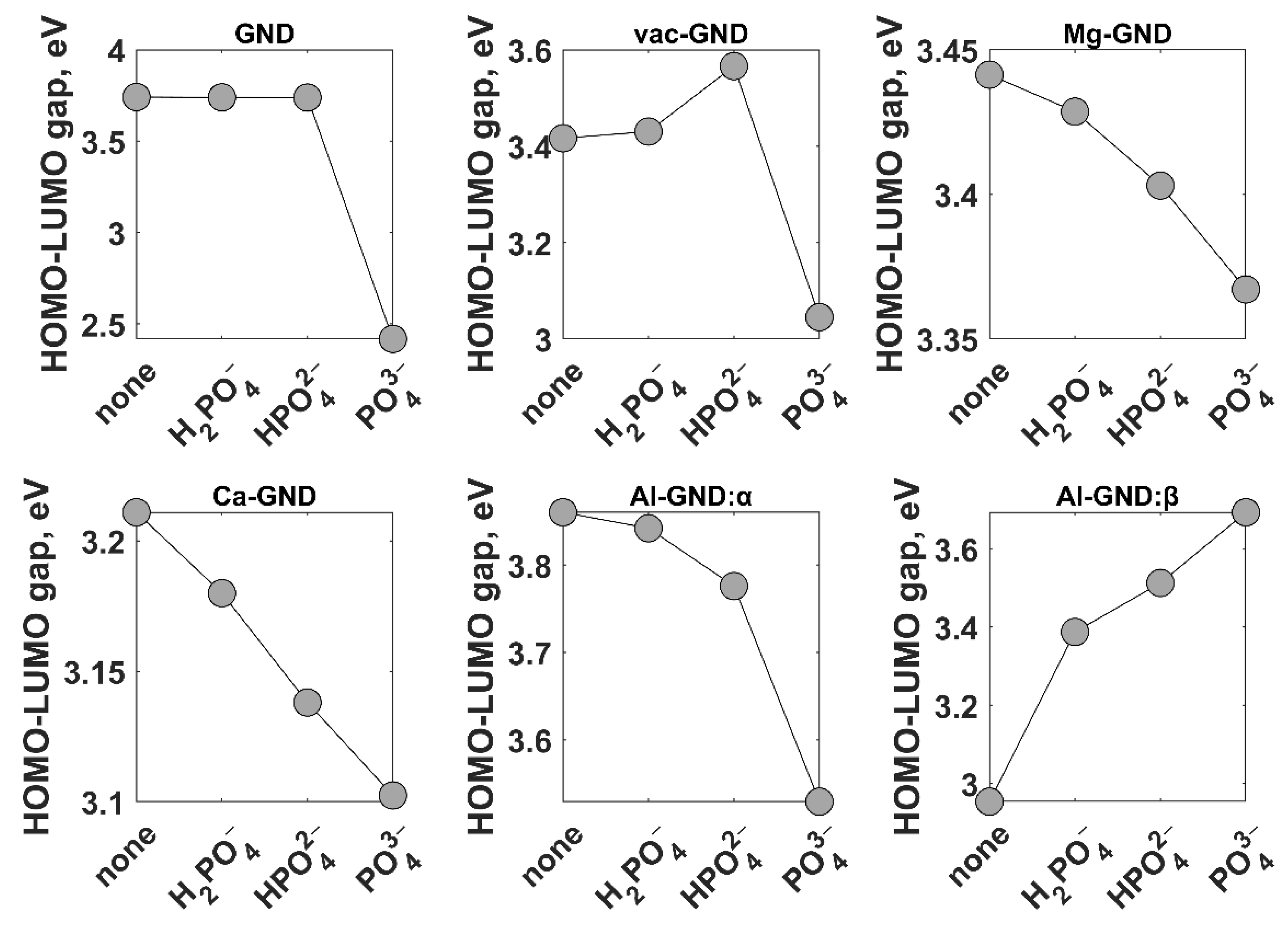


| Ion | GND | vac-GND | Ca-GND | Mg-GND | Al-GND | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Δz1, Å | Δz2, Å | Δz1, Å | Δz2, Å | Δz1, Å | Δz2, Å | Δz1, Å | Δz2, Å | Δz1, Å | Δz2, Å | |
| none | 0.004 | 0.004 | 1.364 | 1.364 | 2.589 | 2.786 | 2.131 | 2.227 | 1.703 | 1.939 |
| H2PO4− | 0.389 | 0.390 | 1.556 | 1.556 | 1.724 | 2.747 | 1.436 | 2.216 | 1.126 | 2.056 |
| HPO42− | 0.540 | 0.542 | 1.894 | 1.894 | 1.738 | 2.699 | 1.477 | 2.252 | 1.183 | 2.081 |
| PO43− | 0.333 | 0.334 | 0.956 | 1.052 | 1.832 | 2.760 | 1.541 | 2.304 | 1.363 | 2.248 |
| Structure | H2PO4− | HPO42− | PO43− | |||
|---|---|---|---|---|---|---|
| ΔEads, eV | Charge, e− | ΔEads, eV | Charge, e− | ΔEads, eV | Charge, e− | |
| GND | −0.0027 | −1.0472 | −0.0001 | −2.0144 | 0.0011 | −2.9916 |
| vac-GND | −0.0039 | −1.0481 | −0.0016 | −1.3113 | −0.1614 | −1.8274 |
| Ca-GND | −0.0267 | −0.6695 | −0.0674 | −1.4328 | −0.1160 | −2.3799 |
| Mg-GND | −0.0441 | −0.4845 | −0.1147 | −1.2604 | −0.1669 | −2.1696 |
| Al-GND | −0.0709 | −0.4487 | −0.1389 | −1.3032 | −0.2001 | −1.9408 |
| Structures | State | λ, nm | f | Assignment |
|---|---|---|---|---|
| GND | S3,4 | 461.81 | 2.818 | H-1→LUMO (21%), H-1→L + 1 (28%), HOMO→LUMO (28%), HOMO→L + 1 (21%) [H-1→LUMO (28%), H-1→L + 1 (21%), HOMO→LUMO (21%), HOMO→L + 1 (28%)] |
| S47,48 | 271.93 | 0.648 | H-9→L + 1 (12%), H-4→L + 2 (17%), H-3→L + 3 (17%), H-2→L + 2 (13%), HOMO→L + 8 (10%) [H-9→LUMO (12%), H-4→L + 3 (17%), H-3→L + 2 (17%), H-2→L + 3 (13%), H-1→L + 8 (10%)] | |
| S69,70 | 251.99 | 0.932 | H-3→L + 5 (18%), H-3→L + 12 (12%) [H-4→L + 5 (18%), H-4→L + 12 (12%)] | |
| S81,82 | 244.70 | 0.814 | H-3→L + 12 (27%) [H-4→L + 12 )27%] | |
| S99,100 | 229.12 | 0.784 | H-18→LUMO (10%), H-3→L + 5 (10%), H-2→L + 10 (13%) [H-18→L + 1 (10%), H-4→L + 5 (10%), H-2→L + 11 (13%)] | |
| vac-GND | S7 | 454.13 | 2.477 | H-1→L + 2 (52%), HOMO→L + 1 (38%) |
| S8 | 449.85 | 1.016 | H-6→LUMO (11%), H-1→L + 1 (14%), HOMO→L + 2 (29%) | |
| S9 | 440.73 | 1.607 | H-2→LUMO (26%), H-1→L + 1 (30%), HOMO→L + 2 (17%) | |
| S93 | 247.56 | 0.804 | H-3→L + 11 (11%) | |
| S99 | 242.28 | 0.528 | H-13→L + 1 (16%) | |
| Ca-GND | S5 | 477.76 | 0.759 | H-2→LUMO (24%), HOMO→L + 2 (10%), HOMO→L + 3 (35%) |
| S6 | 461.45 | 1.835 | H-2→L + 1 (31%), H-1→LUMO (36%) | |
| S7 | 457.67 | 1.566 | H-1→L + 1 (28%), HOMO→L + 3 (24%) | |
| S95 | 249.54 | 0.322 | H-17→L + 1 (2%), H-7→L + 10 (2%), H-6→L + 4 (4%), H-2→L + 15 (2%), H-2→L + 17 (2%), H-2→L + 18 (3%), H-1→L + 14 (2%), HOMO→L + 17 (3%), HOMO→L + 19 (9%) | |
| S98 | 247.30 | 0.366 | H-15→L + 1 (3%), H-12→LUMO (3%), H-12→L + 3 (2%), H-10→L + 3 (3%), H-8→L + 3 (2%), H-6→L + 4 (6%), H-5→L + 6 (4%), H-5→L + 7 (3%), H-4→L + 8 (4%), H-3→L + 5 (2%), H-3→L + 6 (3%), H-3→L + 8 (2%), H-3→L + 9 (9%) | |
| Mg-GND | S3 | 543.28 | 0.930 | H-2→L + 1 (11%), H-1→LUMO (68%), HOMO→L + 1 (12%) |
| S4 | 525.78 | 1.202 | H-1→L + 1 (80%) | |
| S9 | 436.51 | 0.909 | H-3→LUMO (31%), H-2→L + 1 (40%) | |
| S92 | 249.74 | 0.524 | H-3→L + 12 (12%), H-1→L + 13 (10%) | |
| S99 | 245.58 | 0.626 | HOMO→L + 22 (14%) | |
| Al-GND | S13 | 507.01 | 0.694 | H-2(A)→L + 1(A) (14%), H-1(A)→L + 1(A) (16%), HOMO(A)→LUMO(A) (20%), H-2(B)→LUMO(B) (19%) |
| S21 | 438.10 | 0.299 | H-2(A)→L + 1(A) (19%) | |
| S23 | 434.49 | 1.168 | H-9(B)→LUMO(B) (10%), H-1(B)→L + 1(B) (12%), HOMO(B)→L + 2(B) (29%) | |
| S24 | 433.61 | 1.058 | H-2(A)→LUMO(A) (13%), HOMO(B)→L + 1(B) (16%) | |
| S25 | 429.48 | 0.663 | H-1(A)→L + 2(A) (14%), H-5(B)→LUMO(B) (24%) |
| Structure | Ref. | Sensor Concept | Limit of Detection | [(F − F0)/F0] × 100% |
|---|---|---|---|---|
| CVD graphene | [74] | Ion-sensitive field effect transistor with graphene/ionophore hybrid membrane for PO43− detection | 0.1 mg/L | - |
| Mo7O246−-mediated N-GQDs | [73] | A fluorescence turn-on probe for phosphate (PO43−) ion detection | 50 nM | 30 at [1 μM)] |
| Single-layered s-GQDs-Al3+ system | [40] | Photoluminescence probe for highly selective PO43− detection | 0.1 μM | 13 at [7.5 μM)] |
| s-GQDs-Dy3+ complex | [75] | Off–on fluorescent strategy detection of PO43− | 0.1 μM | 28 [at 0.2 μM] |
| Boron-doped GQDs with Fe3+ (B-GQDs) | [76] | Indirect fluorescent detection of PO43− (turn-off-on model) | 340 nM | 7 [at 3 μM] |
| Carbon dots (CDs)-Ce3+ ions ensembles | [77] | Triple-channel fluorescent sensor array for the identification of various phosphate anions (PO43−) | 10 μM | 27 [at 10 μM] |
| Carbon dots (CDs)-Fe3+ ions ensembles | [77] | Triple-channel fluorescent sensor array for the identification of phosphate anions (PO43−) | 10 μM | 6 [at 10 μM] |
| Nozzle-jet-printed silver/reduced graphene oxide (Ag/rGO) | [78] | Field-effect transistor phosphate ion (PO43−) sensor | 0.20 μM | - |
| Graphene quantum dots combined with Europium ions | [41] | Off–on photoluminescent probes for phosphate (PO43−) sensing | 0.1 μM | 10 [at 0.5 μm] |
| Laser scribed reduced graphene oxide (LSGO) | [79] | Electrochemical PO43− sensing based on molybdenum blue method | 0.0004 mM | - |
| Graphene quantum dots-Eu3+ | [80] | Luminescent phosphate (PO43−) sensor | 100 nM | 53 [at 1 μm] |
| vac-GND | this work | UV–vis spectroscopic method for detection of PO43− | - | 26 |
| Mg-GND | this work | UV–vis spectroscopic method for detection of PO43− | - | 21 |
| Al-GND | this work | UV–vis spectroscopic method for detection of PO43− | - | 11 |
| Ca-GND | this work | UV–vis spectroscopic method for detection of PO43− | - | 33 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shtepliuk, I. A DFT Study of Phosphate Ion Adsorption on Graphene Nanodots: Implications for Sensing. Sensors 2023, 23, 5631. https://doi.org/10.3390/s23125631
Shtepliuk I. A DFT Study of Phosphate Ion Adsorption on Graphene Nanodots: Implications for Sensing. Sensors. 2023; 23(12):5631. https://doi.org/10.3390/s23125631
Chicago/Turabian StyleShtepliuk, Ivan. 2023. "A DFT Study of Phosphate Ion Adsorption on Graphene Nanodots: Implications for Sensing" Sensors 23, no. 12: 5631. https://doi.org/10.3390/s23125631
APA StyleShtepliuk, I. (2023). A DFT Study of Phosphate Ion Adsorption on Graphene Nanodots: Implications for Sensing. Sensors, 23(12), 5631. https://doi.org/10.3390/s23125631






