A Self-Coordinating Controller with Balance-Guiding Ability for Lower-Limb Rehabilitation Exoskeleton Robot
Abstract
1. Introduction
2. Design of SCVV Controller
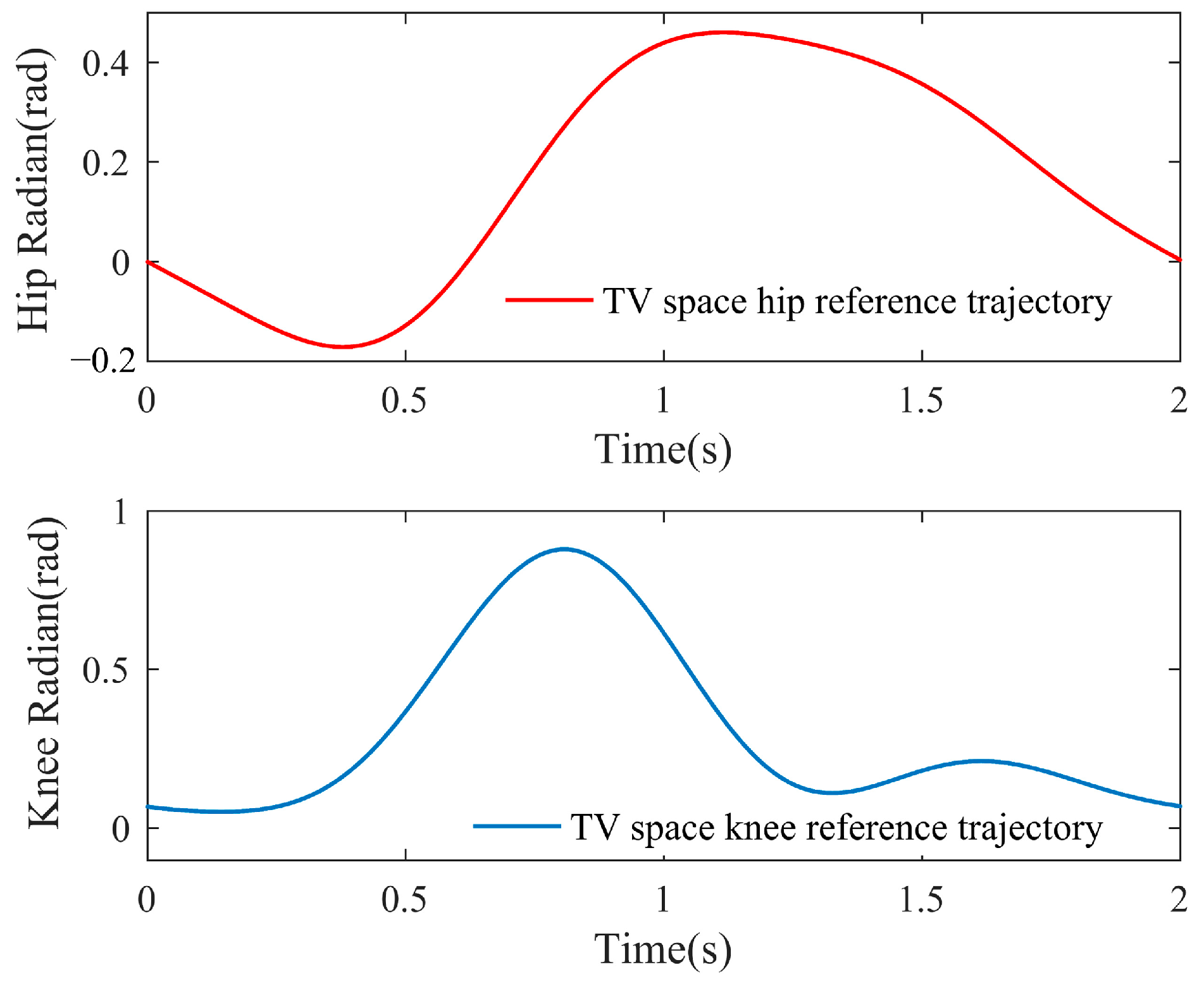
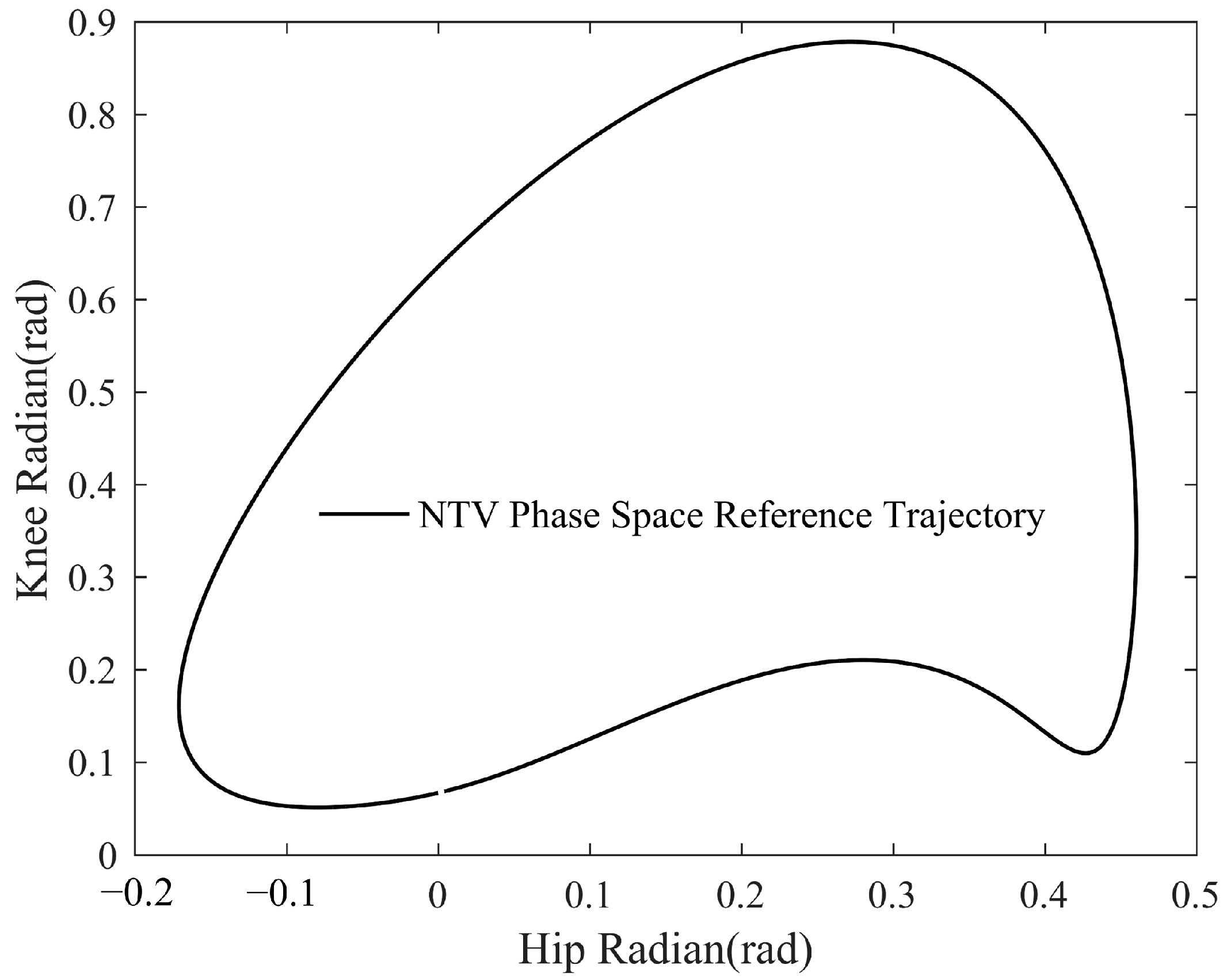
2.1. Outer Loop of the Controller
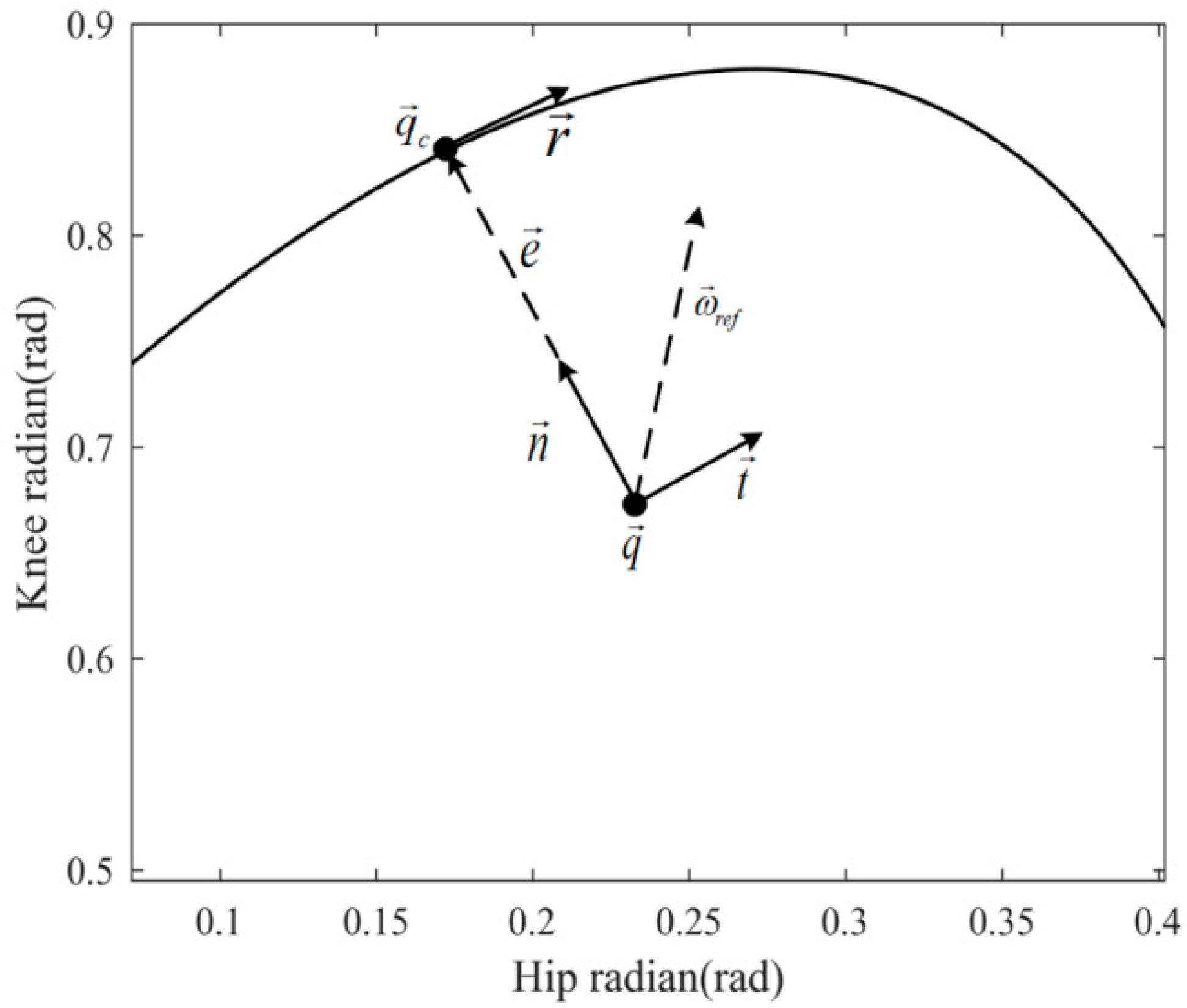
2.2. Inner Loop of the Controller
3. Simulation Model and Result
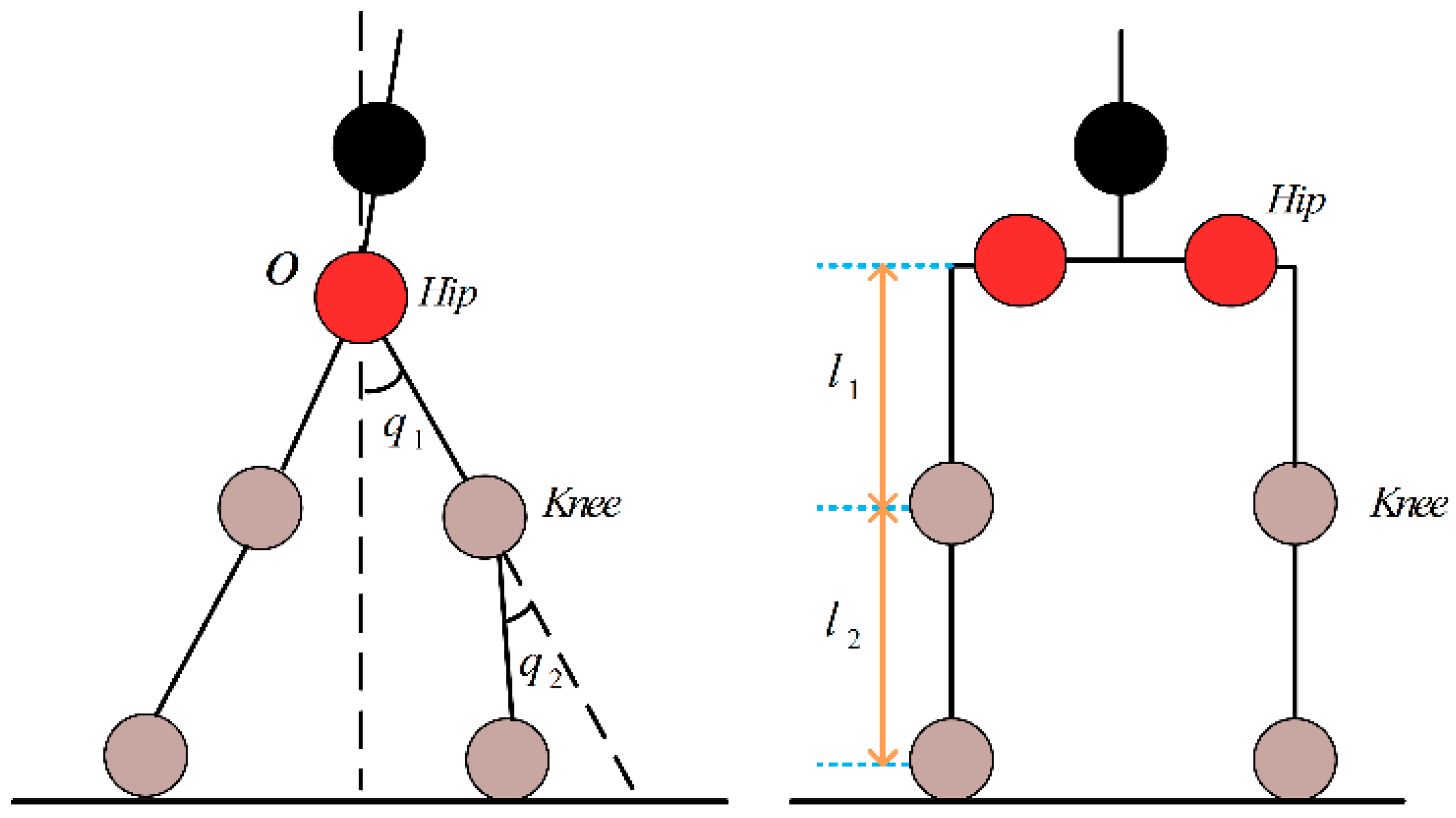
3.1. Simulation Model
3.2. Control Framework and Simulation Setup
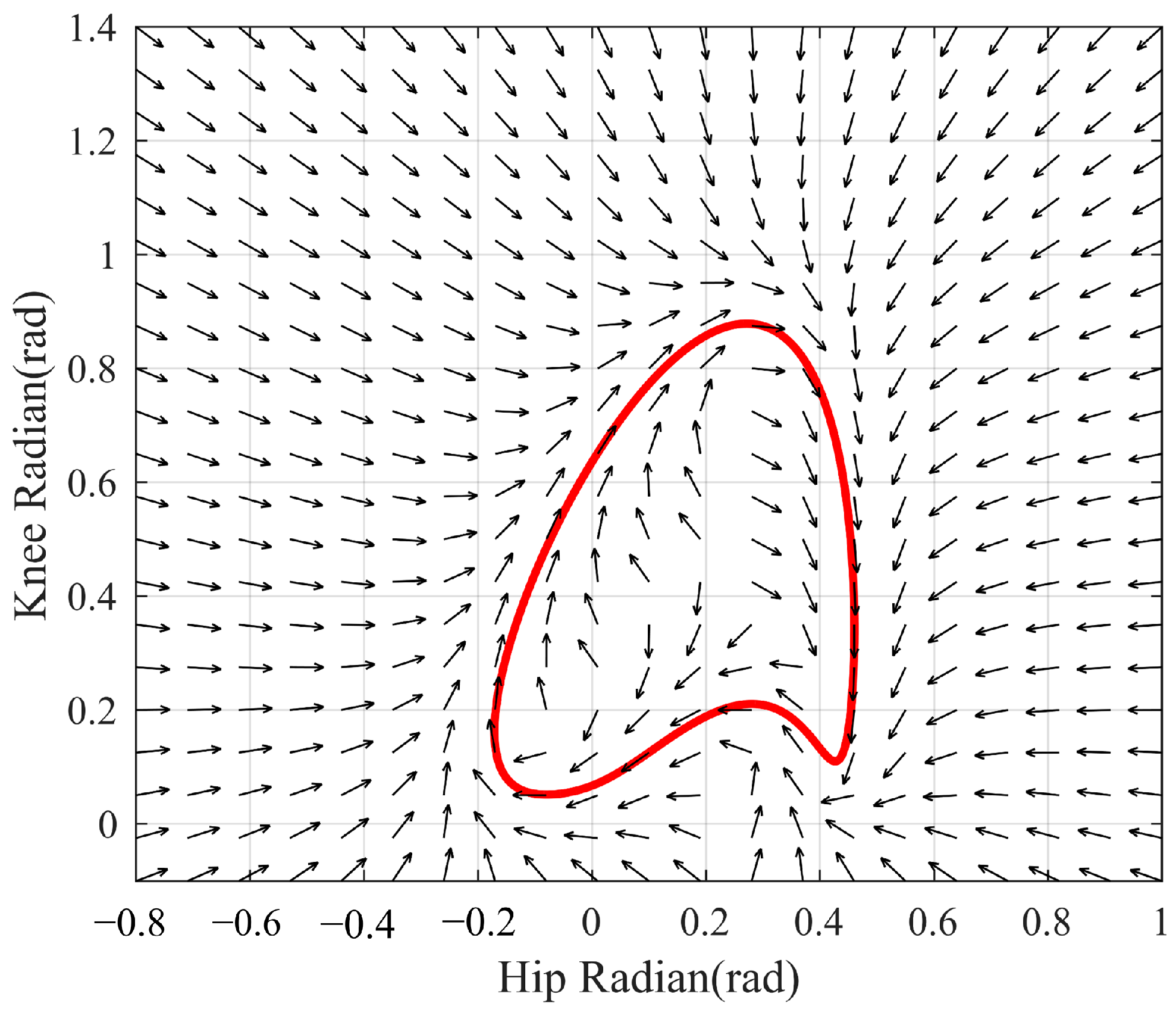
3.3. Simulation Results of Adaptive Gait Generation
3.4. Simulation Results of the Self-Coordination Balance Guiding
4. Units Experimental Implementation and Evaluation
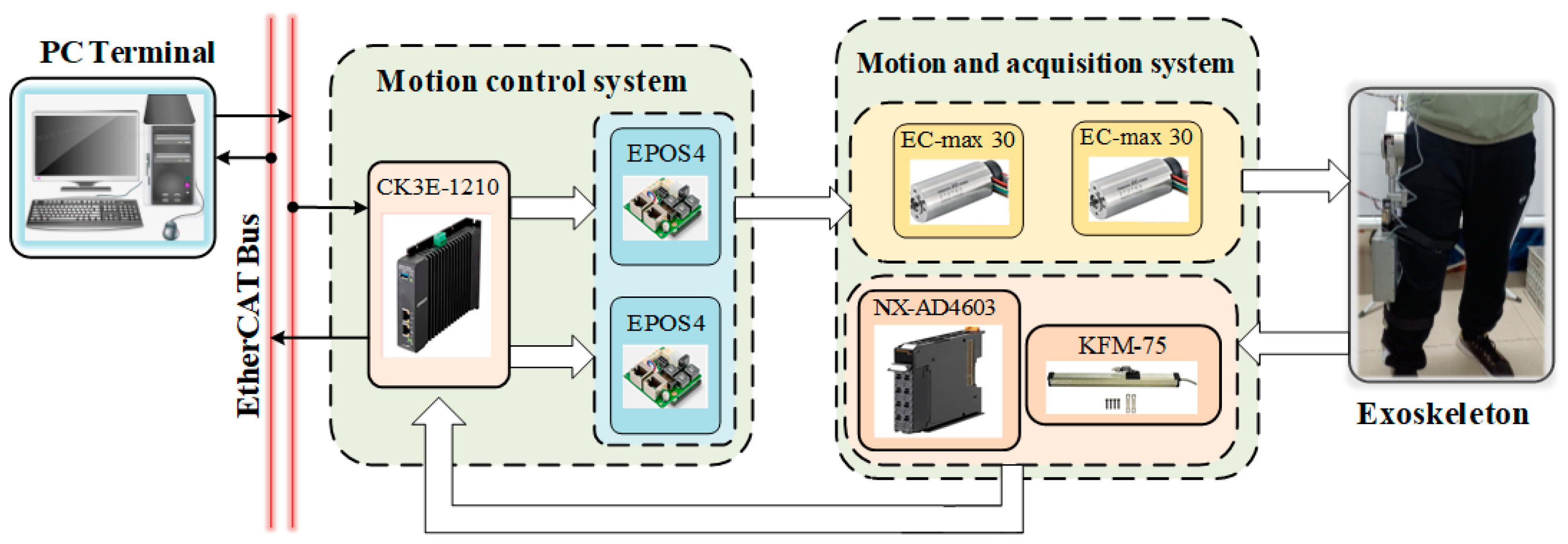
4.1. Exoskeleton Hardware and Experimental Setup
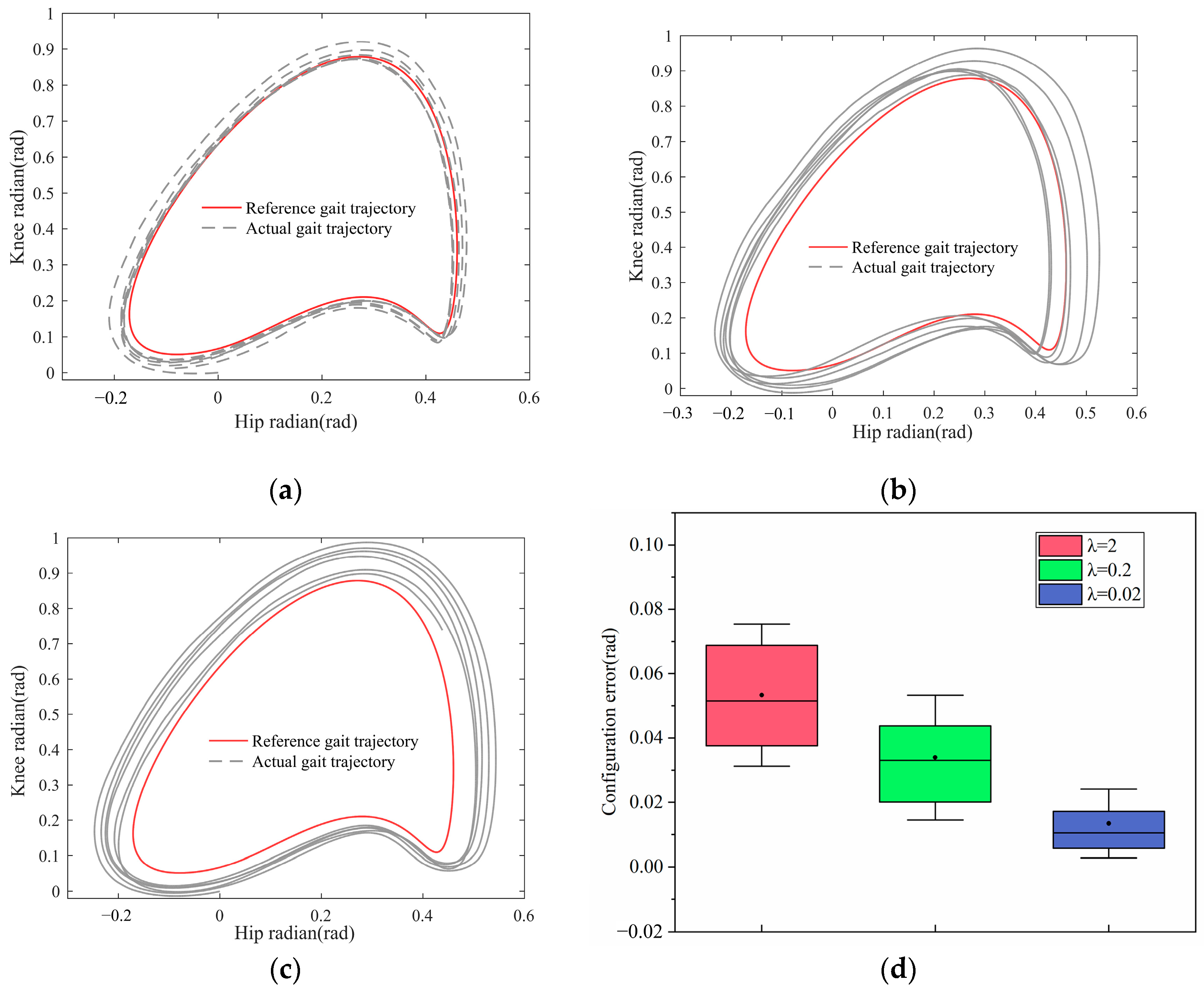
4.2. Self-Coordinated Experimental Evaluation
- Experimental Preparation: Prepare and lay out a spacious and flat pathway. Participants wear and familiarize themselves with the LLRER exoskeleton device.
- Experimental Procedure: Three participants sequentially wear the LLRER exoskeleton device and repeat walking on the predetermined pathway. Each participant performs three sets of walks, with a duration of 20 s per set.
- Condition Control: Among the sets performed by each participant, the only differing factor is the control parameter, while all other parameters and conditions remain consistent. The values of the parameter for the three sets of experiments are 0.02, 0.2, and 2, respectively.
- Participant Awareness: Participants are not informed that the experiment’s outcomes are influenced by their own actions, nor are they informed of any changes in the control parameters.
- Data Collection: Collect position trajectories of the participants’ knee and hip joints, as well as motor speed profiles.
4.3. Balance Guiding Experimental Evaluation
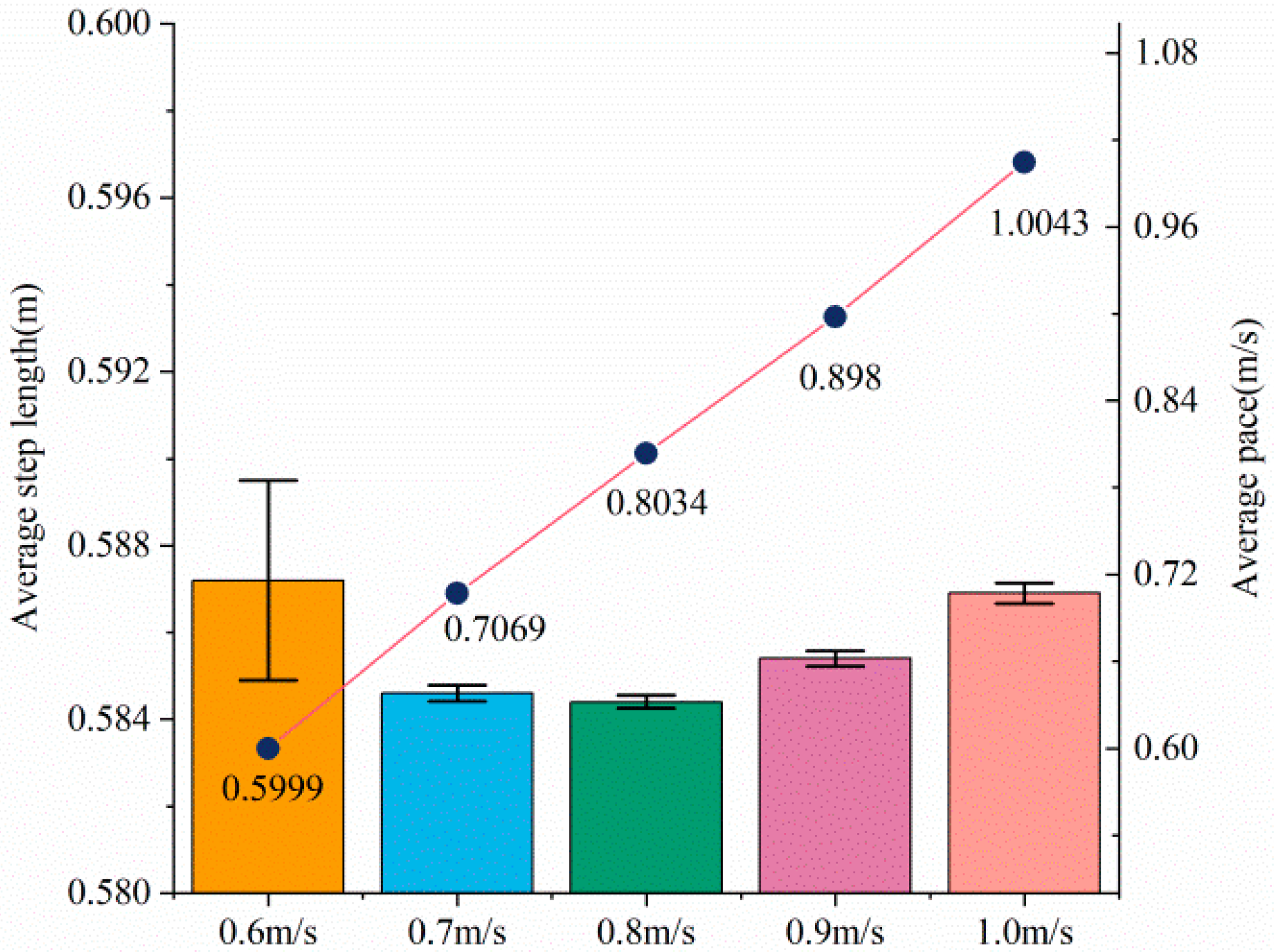
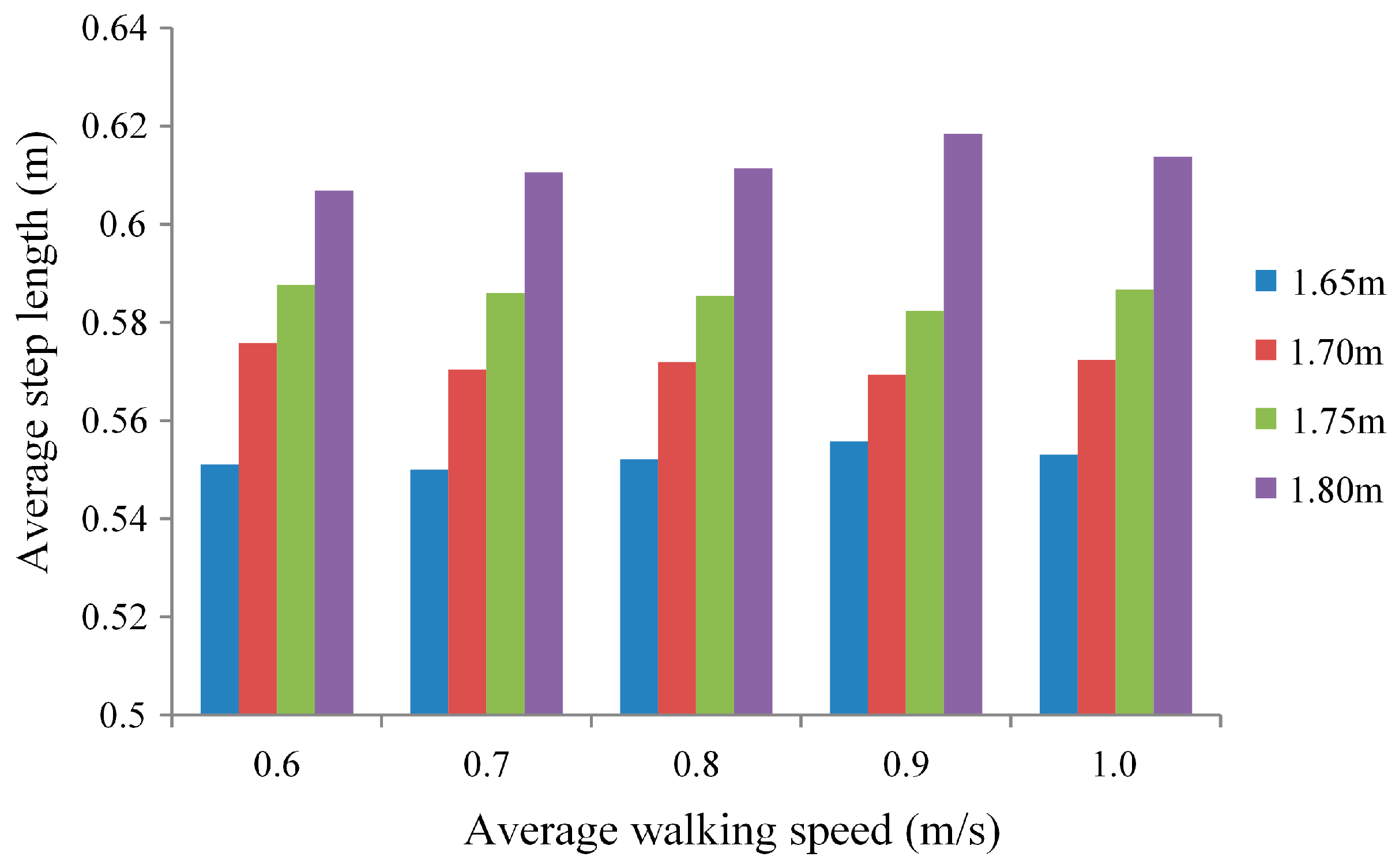
4.4. Step Size and Pace Experiment
- Experimental Preparation: Prepare and lay out a spacious and flat walkway with a length of 25 m.
- Experimental Procedure: Three participants sequentially wear the LLRER exoskeleton device and walk a distance of 20 m on the designated walkway. Each participant performs five sets of walks.
- Condition Control: Within each set of experiments, participants are instructed to maintain the required speed as closely as possible. Among different sets of experiments for the same participant, only the walking speed varies. The walking speeds for the five sets of experiments are: 0.6 m/s, 0.7 m/s, 0.8 m/s, 0.9 m/s, and 1 m/s, respectively.
- Data Collection: Measure the stride length of each step taken by the participants and record the walking speeds of the participants.
- Subject Information: Four healthy adult males with heights of 1.65 m, 1.7 m, 1.75 m, and 1.8 m, corresponding to body weights of 60 kg, 68 kg, 75 kg, and 80 kg, respectively.
- Experimental Procedure: The four subjects sequentially wore LLRER exoskeleton devices and walked back and forth on a predetermined 25 m pathway. This constituted one experimental group, and a total of five groups were conducted.
- Condition Control: Within each group, the subjects were instructed to maintain the required speed, while different groups varied only in walking speed. The control parameters remained the same across all groups. The walking speeds for the five groups were 0.6 m/s, 0.7 m/s, 0.8 m/s, 0.9 m/s, and 1 m/s, respectively.
- Data Collection: The stride length of each step and the walking speed of the subjects were measured. To minimize the influence of starting and stopping on the experimental results, the first and last two steps near the beginning and end of the pathway were excluded from the statistical analysis.
5. Conclusions
- In the inner loop self-coordinated velocity vector control of the controller, both control parameters need to be determined prior to control and cannot be adapted based on the user’s current condition. Subsequent research will investigate how to achieve adaptive control parameters.
- The mentioned hierarchical balance-guided control strategy heavily relies on the phase space reference gait trajectory generated by the outer loop. To address this issue, future considerations will involve the use of intelligent optimization algorithms to modify the reference gait trajectory, thereby further ensuring the balancing performance of the controller.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Geng, T.; Jia, X.; Guo, Y. Lower Limb Joint Nursing and Rehabilitation System Based on Intelligent Medical Treatment. J. Healthc. Eng. 2021, 2021, 6646977. [Google Scholar] [CrossRef] [PubMed]
- Correa-de-Araujo, R.; Bhasin, S. Public Health Need, Molecular Targets, and Opportunities for the Accelerated Development of Function-Promoting Therapies: Proceedings of a National Institute on Aging Workshop. J. Gerontol. Ser. A 2022, 77, 2227–2237. [Google Scholar] [CrossRef] [PubMed]
- Tsai, T.C.; Chiang, M.H. A Lower Limb Rehabilitation Assistance Training Robot System Driven by an Innovative Pneumatic Artificial Muscle System. Soft Robot. 2023, 10, 1–16. [Google Scholar] [CrossRef] [PubMed]
- Zhang, M.K.; Wei, J.N.; Wu, X.P. Effects of whole-body vibration training on lower limb motor function and neural plasticity in patients with stroke: Protocol for a randomised controlled clinical trial. BMJ Open 2022, 12, e060796. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Wang, H.P.; Tian, Y. Adaptive interaction torque-based AAN control for lower limb rehabilitation exoskeleton. ISA Trans. 2022, 128, 184–197. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Wang, Z.; Lei, H.; Gu, W. Gait phase recognition of lower limb exoskeleton system based on the integrated network model. Biomed. Signal Process. Control. 2022, 76, 103693. [Google Scholar] [CrossRef]
- Lin, J.; Hu, G.; Ran, J.; Chen, L.; Zhang, X.; Zhang, Y. Effects of bodyweight support and guidance force on muscle activation during Locomat walking in people with stroke: A cross-sectional study. J. NeuroEngineering Rehabil. 2020, 17, 5. [Google Scholar] [CrossRef]
- Kwon, S.H.; Lee, B.S.; Lee, H.J.; Kim, E.J.; Lee, J.A.; Yang, S.P.; Kim, T.Y.; Pak, H.R.; Kim, H.K.; Kim, H.Y.; et al. Energy Efficiency and Patient Satisfaction of Gait with Knee-Ankle-Foot Orthosis and Robot (ReWalk)-Assisted Gait in Patients with Spinal Cord Injury. Ann. Rehabil. Med. 2020, 44, 131–141. [Google Scholar] [CrossRef]
- Yoshikawa, K.; Mizukami, M.; Kawamoto, H.; Sano, A.; Koseki, K.; Sano, K.; Asakawa, Y.; Kohno, Y.; Nakai, K.; Gosho, M.; et al. Gait training with Hybrid Assistive Limb enhances the gait functions in subacute stroke patients: A pilot study. Neurorehabilitation 2017, 40, 87–97. [Google Scholar] [CrossRef]
- Kang, I.; Kunapuli, P.; Hsu, H.; Young, A.J. Electromyography (EMG) Signal Contributions in Speed and Slope Estimation Using Robotic Exoskeletons. In Proceedings of the 2019 IEEE 16th International Conference on Rehabilitation Robotics (ICORR), Toronto, ON, Canada, 24–28 June 2019; pp. 548–553. [Google Scholar]
- Shushtari, M.; Nasiri, R.; Arami, A. Online Reference Trajectory Adaptation: A Personalized Control Strategy for Lower Limb Exoskeletons. IEEE Robot. Autom. Lett. 2021, 7, 128–134. [Google Scholar] [CrossRef]
- Yang, W.; Zhang, J.; Zhang, S.; Yang, C. Lower Limb Exoskeleton Gait Planning Based on Crutch and Human-Machine Foot Combined Center of Pressure. Sensors 2020, 20, 7216. [Google Scholar] [CrossRef] [PubMed]
- Gui, K.; Liu, H.; Zhang, D. A Practical and Adaptive Method to Achieve EMG-Based Torque Estimation for a Robotic Exoskeleton. IEEE/ASME Trans. Mechatron. 2019, 24, 483–494. [Google Scholar] [CrossRef]
- Li, Z.; Yuan, Y.; Luo, L.; Su, W.; Zhao, K.; Xu, C.; Huang, J.; Pi, M. Hybrid Brain/Muscle Signals Powered Wearable Walking Exoskeleton Enhancing Motor Ability in Climbing Stairs Activity. IEEE Trans. Med. Robot. Bionics 2019, 1, 218–227. [Google Scholar] [CrossRef]
- Amiri, M.S.; Ramli, R.; Ibrahim, M.F. Genetically optimized parameter estimation of mathematical model for multi-joints hip–knee exoskeleton. Robot. Auton. Syst. 2020, 125, 103425. [Google Scholar] [CrossRef]
- Beck, O.N.; Shepherd, M.K.; Rastogi, R.; Martino, G.; Ting, L.H.; Sawicki, G.S. Exoskeletons need to react faster than physiological responses to improve standing balance. Sci. Robot. 2023, 8, eadf1080. [Google Scholar] [CrossRef] [PubMed]
- Modares, H.; Ranatunga, I.; Lewis, F.L.; Popa, D.O. Optimized Assistive Human–Robot Interaction Using Reinforcement Learning. IEEE Trans. Cybern. 2016, 46, 655–667. [Google Scholar] [CrossRef]
- Zhang, T.; Tran, M.; Huang, H. Design and Experimental Verification of Hip Exoskeleton With Balance Capacities for Walking Assistance. IEEE/ASME Trans. Mechatron. 2018, 23, 274–285. [Google Scholar] [CrossRef]
- Nelson, B.J.; Nelson, B.J.; Goldfarb, M.; Hannaford, B.; Menciassi, A.; O’malley, M.K.; Simaan, N.; Valdastri, P.; Yang, G.-Z. A decade retrospective of medical robotics research from 2010 to 2020. Sci. Robot. 2021, 6, eabi8017. [Google Scholar]
- Zheng, Y.; Zhong, P.; Liu, K.; Yang, K.; Yue, Q. Human Motion Capture System Based 3D Reconstruction on Rehabilitation Assistance Stability of Lower Limb Exoskeleton Robot Climbing Upstairs Posture. IEEE Sens. J. 2020, 20, 11778–11786. [Google Scholar] [CrossRef]
- Xu, Y.; Xiao, Y.; Ma, Y.; Zheng, L.; He, Y. The Measuring ZMP of Self-Balancing Exoskeleton Robot is Calibrated by Using The Neural Network. In Proceedings of the 2021 IEEE International Conference on Real-time Computing and Robotics (RCAR), Xining, China, 15–19 July 2021; pp. 1087–1092. [Google Scholar]
- Kim, I.-S.; Han, Y.-J.; Hong, Y.-D. Stability Control for Dynamic Walking of Bipedal Robot with Real-time Capture Point Trajectory Optimization. J. Intell. Robot. Syst. 2019, 96, 345–361. [Google Scholar] [CrossRef]
- Caulcrick, C.; Huo, W.; Hoult, W.; Vaidyanathan, R. Human Joint Torque Modelling With MMG and EMG During Lower Limb Human-Exoskeleton Interaction. IEEE Robot. Autom. Lett. 2021, 6, 7185–7192. [Google Scholar] [CrossRef]
- Wang, W.A.; Li, H.A.; Xiao, M.A.; Yang, C.; Xiaoqing, Y.; Xing, M.; Bing, Z. Design and verification of a human–robot interaction system for upper limb exoskeleton rehabilitation—ScienceDirect. Med. Eng. Phys. 2020, 79, 19–25. [Google Scholar]
- Martínez, A.; Lawson, B.; Durrough, C.; Goldfarb, M. A Velocity-Field-Based Controller for Assisting Leg Movement During Walking With a Bilateral Hip and Knee Lower Limb Exoskeleton. IEEE Trans. Robot. 2019, 35, 307–316. [Google Scholar] [CrossRef]

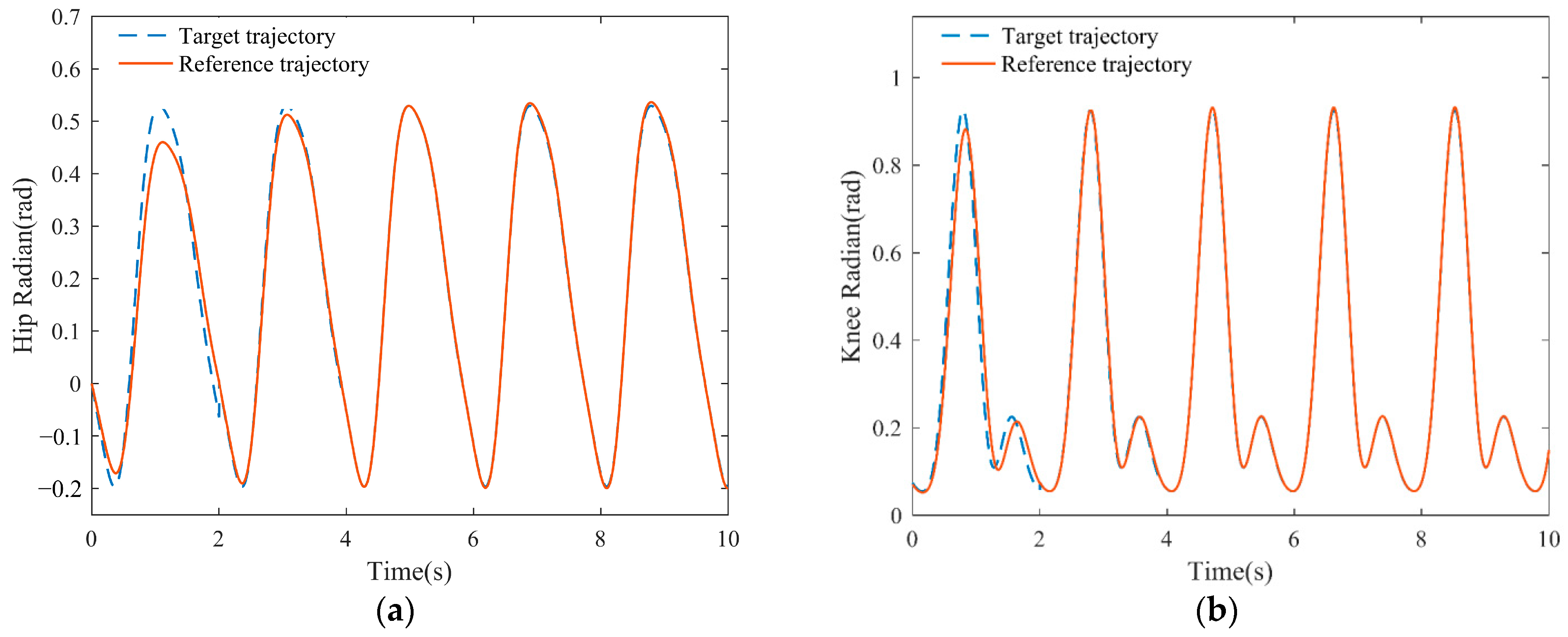
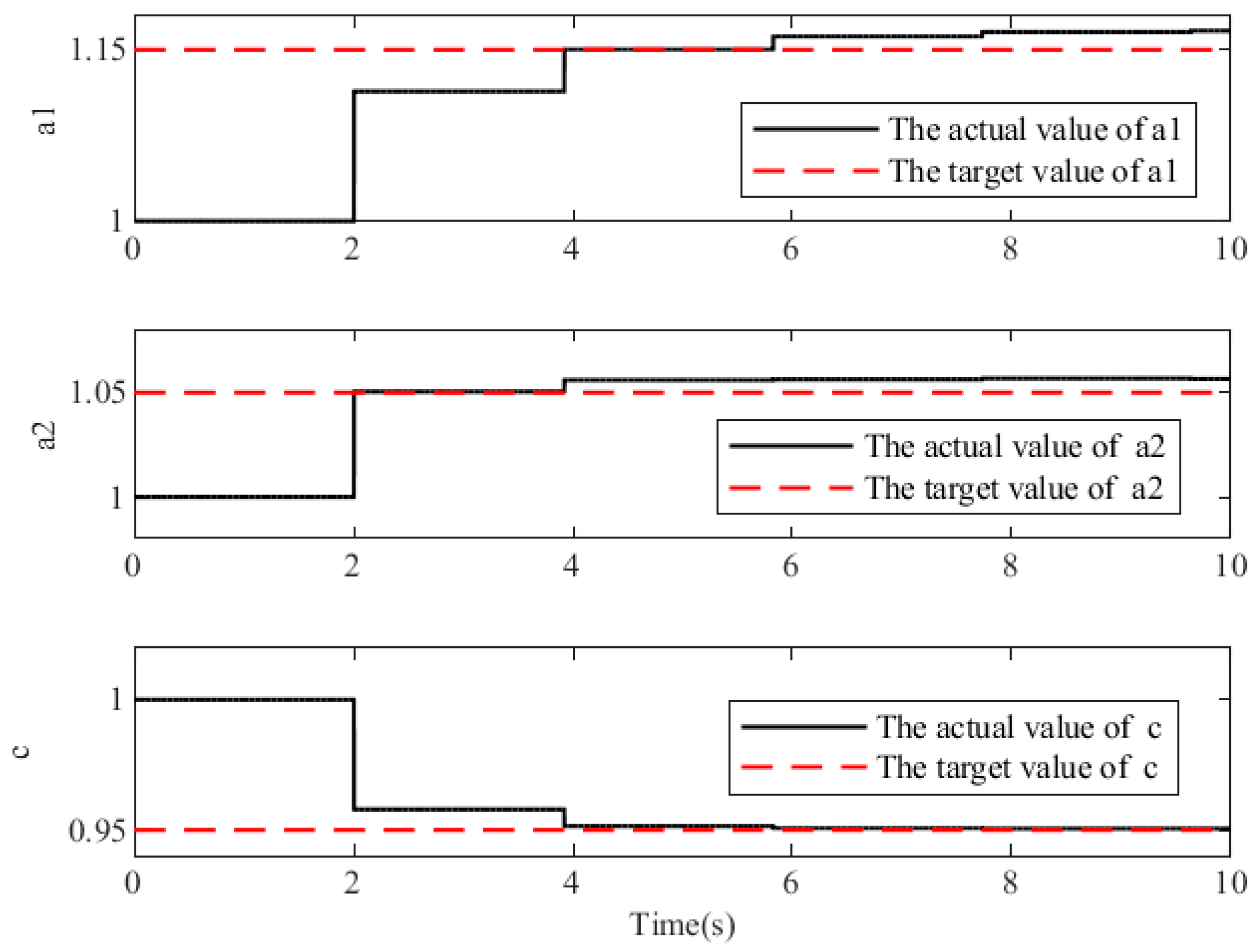
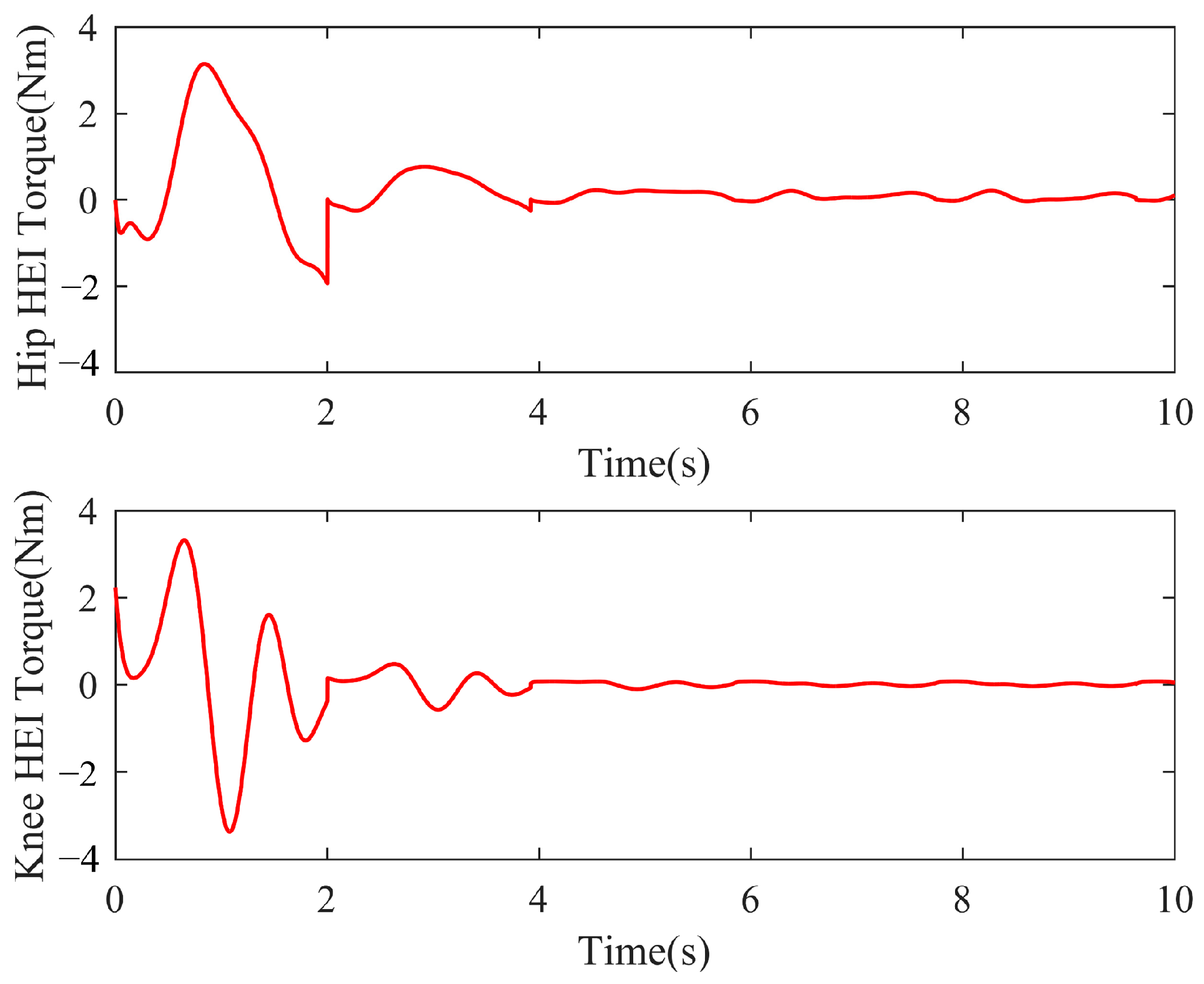
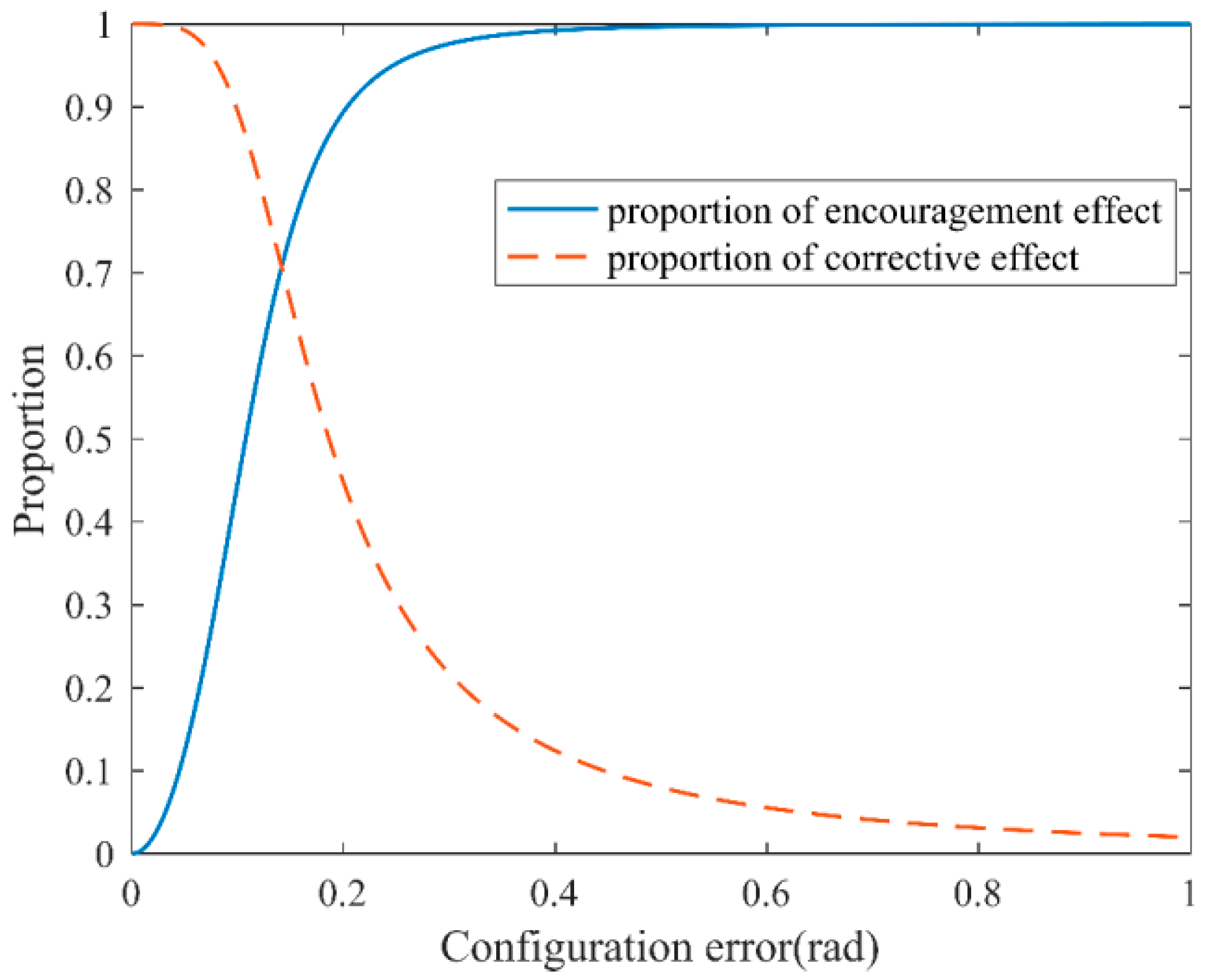







| Projects | Value | Projects | Value |
|---|---|---|---|
| Total body weight | 70 kg | Exoskeleton unilateral thigh | 6 kg |
| Human unilateral thigh | 7 kg | Exoskeleton unilateral calf | 5 kg |
| Human unilateral calf | 4.41 kg | Thigh linkage length | 0.48 m |
| Total exoskeleton weight | 22 kg | Calf linkage length | 0.35 m |
| Joint | Controller | Absolute Average (Nm) | Standard Deviation (Nm) | Maximum (Nm) | Minimum (Nm) |
|---|---|---|---|---|---|
| HIP | Position | 6.4603 | 8.2309 | 15.6984 | −14.7982 |
| HIP | Impedance | 0.8743 | 0.9622 | 2.0702 | −0.7719 |
| HIP | SCVV | 1.1912 | 2.1218 | 4.1338 | −3.0231 |
| Knee | Position | 8.4505 | 11.3968 | 26.4005 | −15.2920 |
| Knee | Impedance | 1.1877 | 1.3801 | 2.0702 | −0.7719 |
| Knee | SCVV | 3.0487 | 2.1289 | 2.2312 | −3.0231 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qin, L.; Ji, H.; Chen, M.; Wang, K. A Self-Coordinating Controller with Balance-Guiding Ability for Lower-Limb Rehabilitation Exoskeleton Robot. Sensors 2023, 23, 5311. https://doi.org/10.3390/s23115311
Qin L, Ji H, Chen M, Wang K. A Self-Coordinating Controller with Balance-Guiding Ability for Lower-Limb Rehabilitation Exoskeleton Robot. Sensors. 2023; 23(11):5311. https://doi.org/10.3390/s23115311
Chicago/Turabian StyleQin, Li, Houzhao Ji, Minghao Chen, and Ke Wang. 2023. "A Self-Coordinating Controller with Balance-Guiding Ability for Lower-Limb Rehabilitation Exoskeleton Robot" Sensors 23, no. 11: 5311. https://doi.org/10.3390/s23115311
APA StyleQin, L., Ji, H., Chen, M., & Wang, K. (2023). A Self-Coordinating Controller with Balance-Guiding Ability for Lower-Limb Rehabilitation Exoskeleton Robot. Sensors, 23(11), 5311. https://doi.org/10.3390/s23115311









