A Cascaded Adaptive Network-Based Fuzzy Inference System for Hydropower Forecasting
Abstract
:1. Introduction
2. Related Works
- Generally, artificial neural network-based algorithms are bulky in the complexity of the calculations.
- The methods are to use when the predictions depend on the uncertainty factors and non-linear inputs.
- The methods are not likely to generate the best possible predictions because the input factors vary depending on the different environments.
- The methods are require enormous amounts of computing power.
- This system uses fuzzy logic approach along with a neural network to address the uncertainty and the non-linearity of the inputs.
- The base algorithm of this system is two-input one-output ANFIS, and the computational power reduces dramatically.
- It is possible to generate a near-zero error in the prediction by increasing the number of levels in the Cascaded ANFIS algorithm.
- This study presents future power generation up to the year 2099 using two different climate models.
- The comparative study presented in this work provides a solid understanding of the potential regarding the Cascaded ANFIS algorithm compared to that of the cutting-edge time series prediction algorithms.
Hydropower in Sri Lanka
3. Study Area
4. Methodology
4.1. Climate Data Extraction for Future
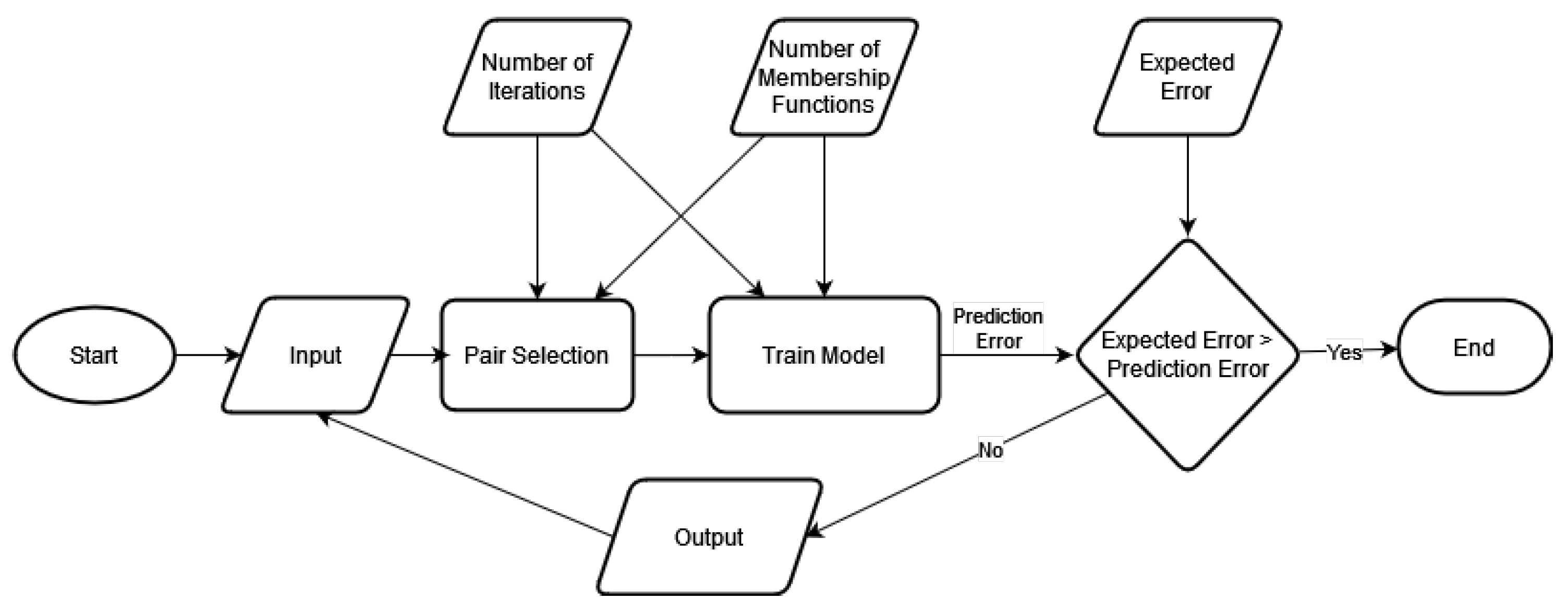
4.1.1. Implementation of the Cascaded ANFIS Algorithm
4.1.2. Parameter Settings for Each Algorithm
- Multilayer Perception (MLP)
- K-Nearest Neighbors (KNN)
- Adaptive Network-based Fuzzy Inference System (ANFIS)
- Particle Swarm Optimization with ANFIS (ANFIS-PSO (Hybrid))
- Genetic algorithms with ANFIS (ANFIS-GA (Hybrid))
- Linear regression
- Lasso regression
- Ridge regression
- Recurrent neural network (RNN)
- Long short-term memory (LSTM)
- Gated recurrent unit (GRU)
- Cascaded ANFIS
5. Results and Discussion
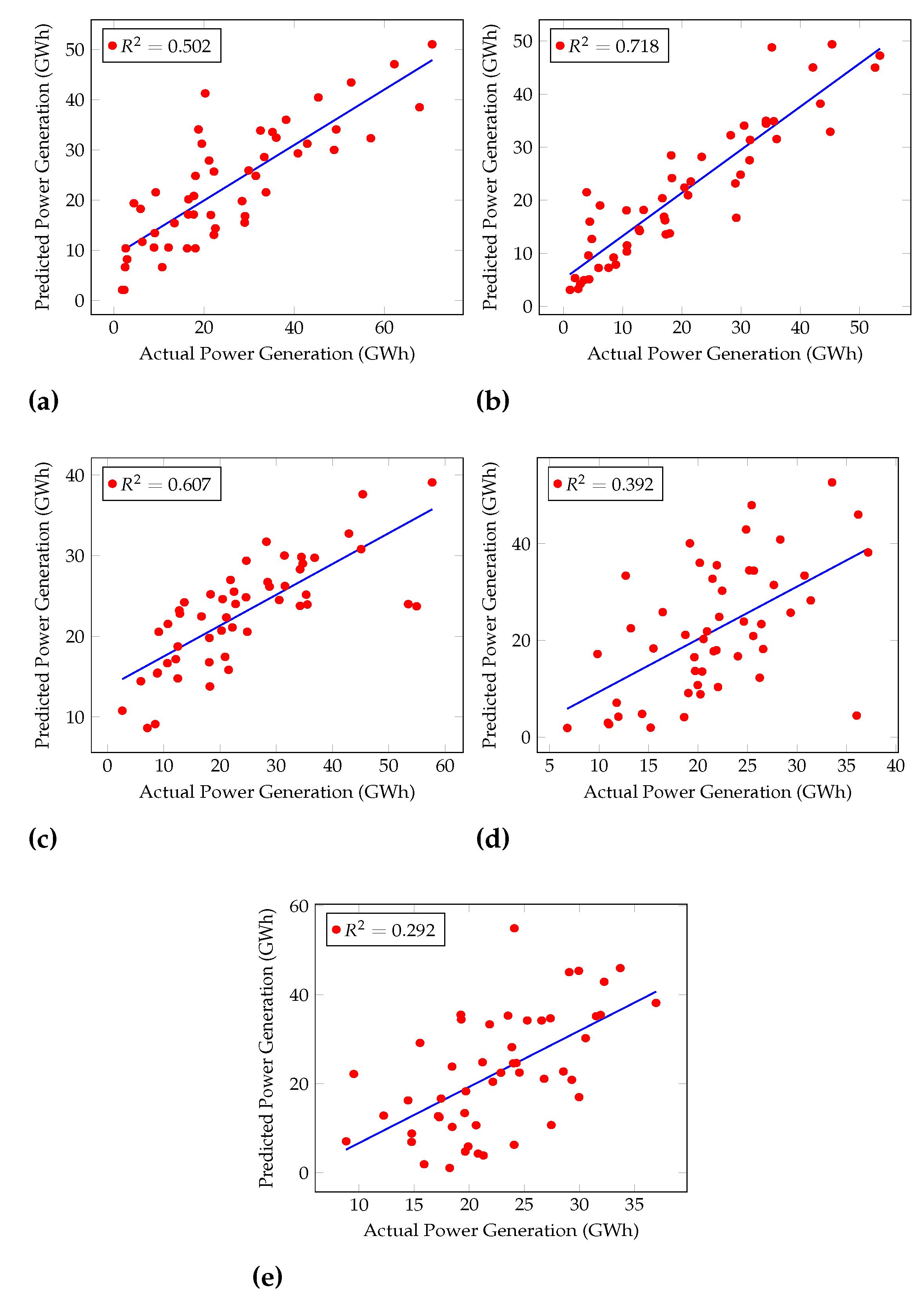
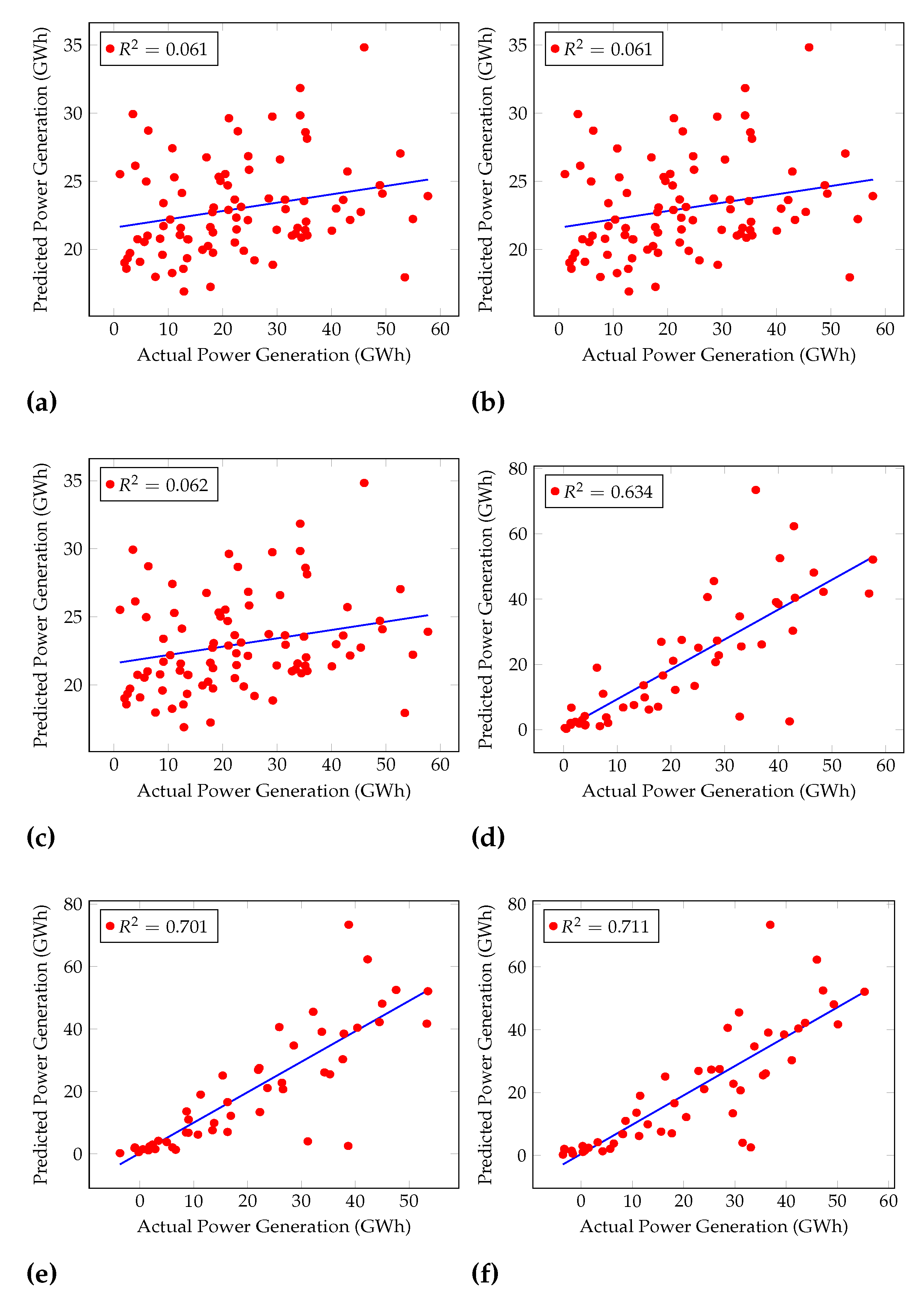
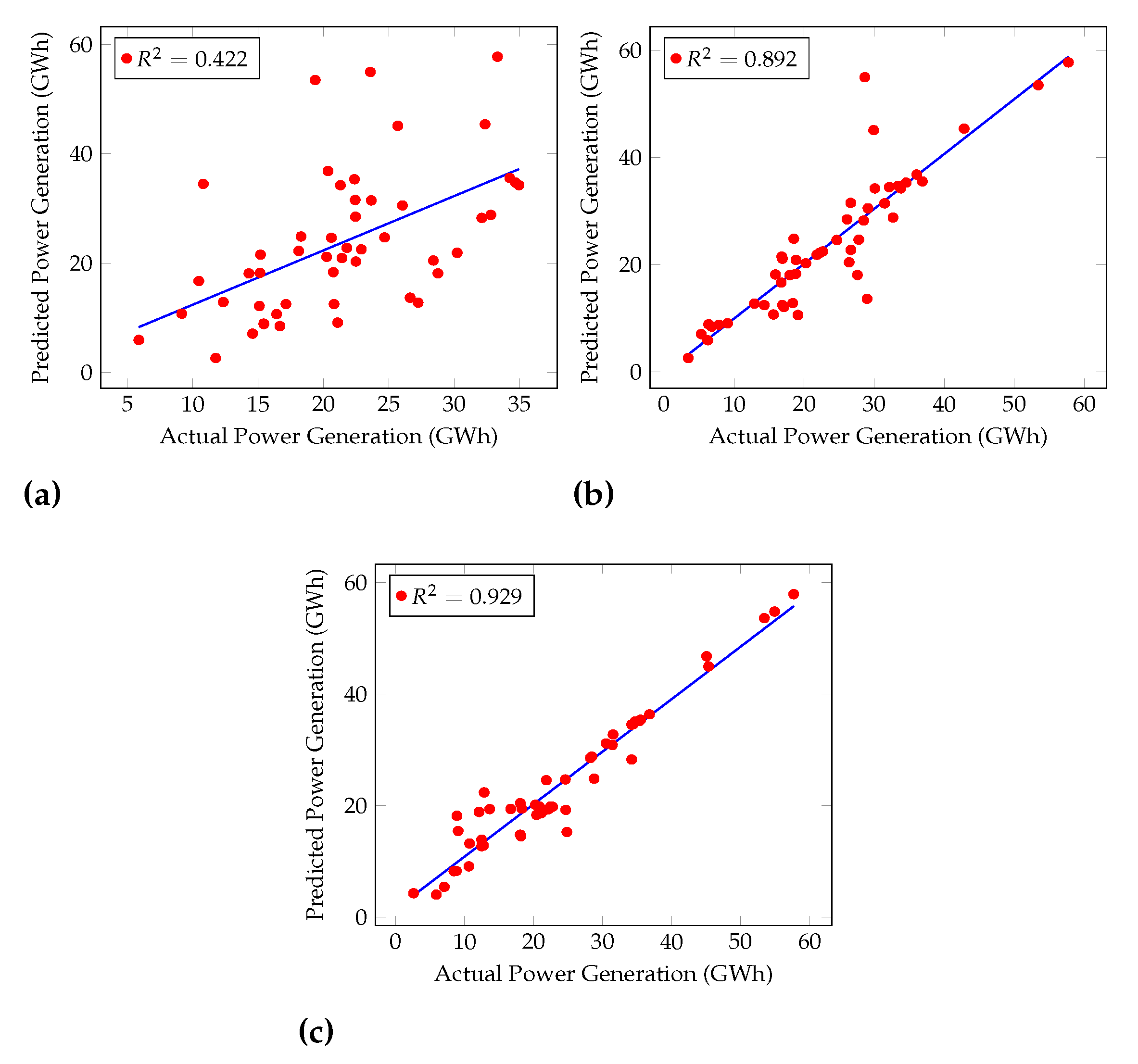
5.1. Comparison of the Algorithms
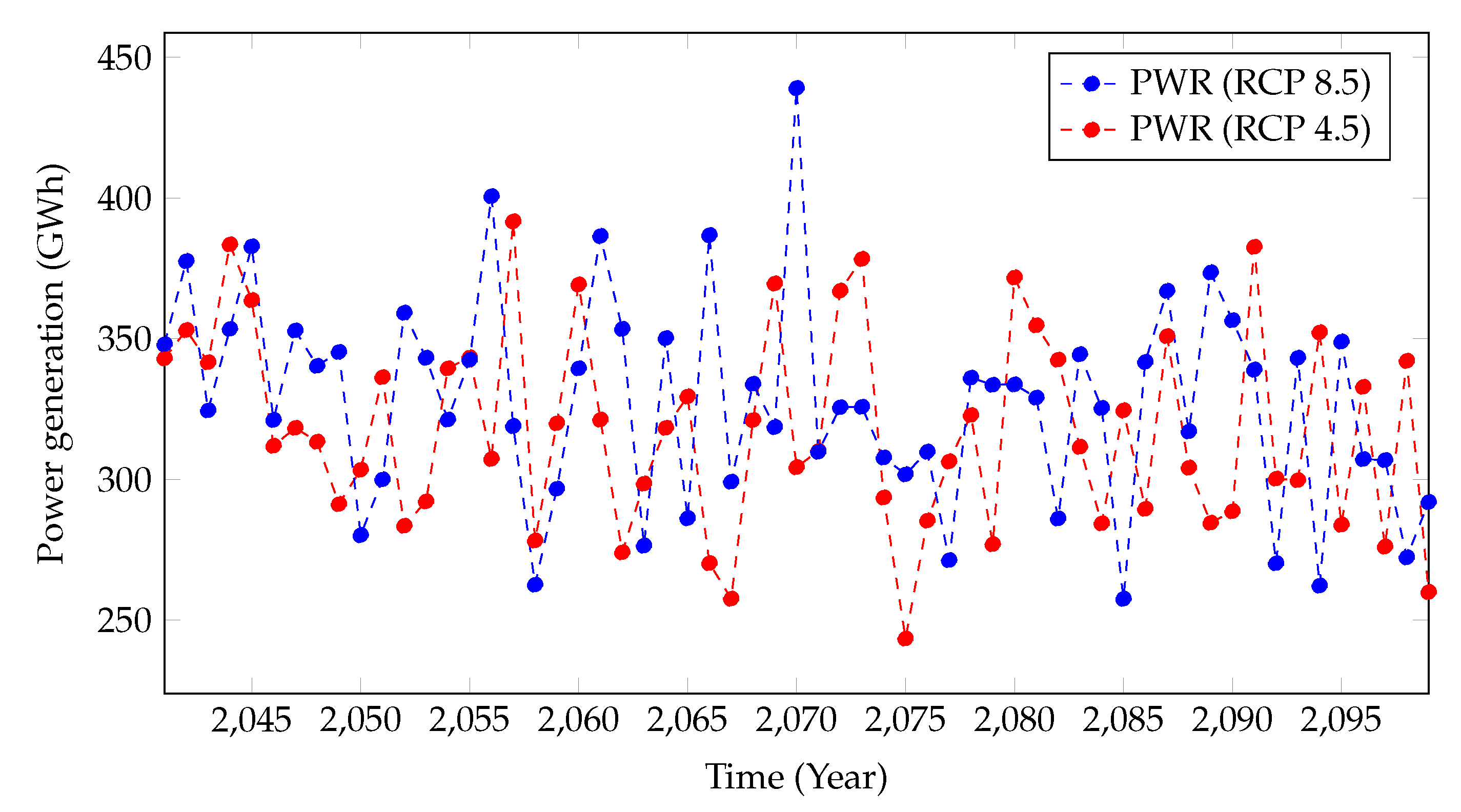
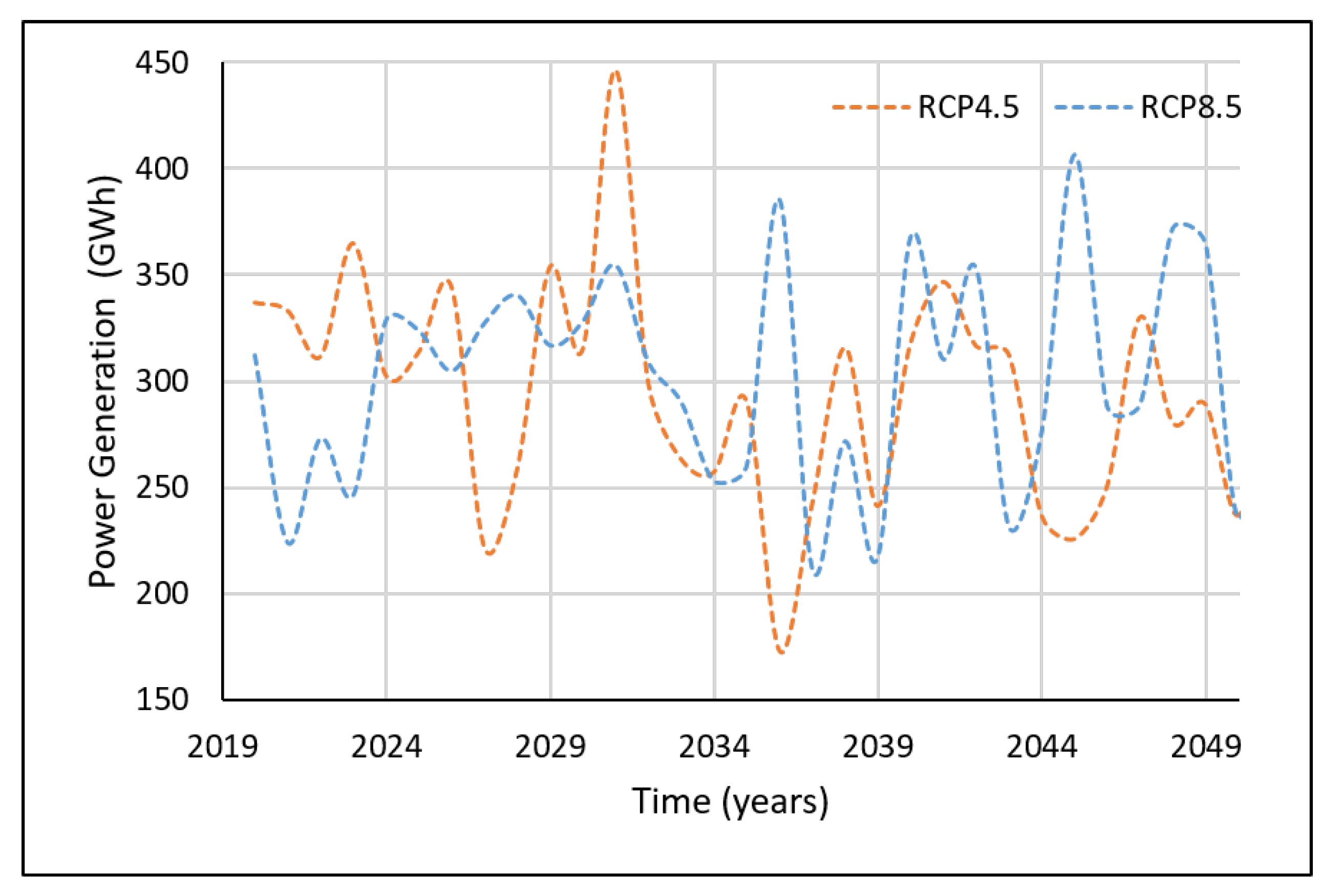
5.2. Forecasting of Hydropower Generation in the Future
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| MDPI | Multidisciplinary Digital Publishing Institute |
| ANFIS | Adaptive Network Based Fuzzy Inference System |
| RNN | Recurrent Neural Network |
| LSTM | Long Short-Term Memory |
| GRU | Gated Recurrent Unit |
| RCP | Representative Concentration Pathway |
| SDG | Sustainable Development Goals |
| GCMs/RCMs | Global/Regional Climate Models |
| ANN | Artificial Neural Network |
| ARIMA | Auto Regressive Integrated Moving Average |
| FIS | Fuzzy Infererence System |
| FL | Fuzzy Logic |
| ML | Machine Learning |
| PSO | Particle Swarm Optimization |
| GA | Genetic Algorithms |
| RMSE | Root Mean Square Error |
References
- Ban, K.M. Sustainable Development Goals. 2016. Available online: https://www.grips.ac.jp/cms/wp-content/uploads/2018/12/190314_penseeSP_en.pdf (accessed on 15 March 2022).
- Chandrasekara, S.; Prasanna, V.; Kwon, H.H. Monitoring water resources over the Kotmale reservoir in Sri Lanka using ENSO phases. Adv. Meteorol. 2017, 2017, 4025964. [Google Scholar]
- Kober, T.; Schiffer, H.W.; Densing, M.; Panos, E. Global energy perspectives to 2060–WEC’s World Energy Scenarios 2019. Energy Strategy Rev. 2020, 31, 100523. [Google Scholar]
- Bank, A.D. Tourism Sector Assessment, Strategy, and Road Map for Cambodia, Lao People’s Democratic Republic, Myanmar, and Vietnam (2016–2018); Asian Development Bank: Mandaluyong, Philippines, 2017. [Google Scholar]
- Shaktawat, A.; Vadhera, S. Risk management of hydropower projects for sustainable development: A review. Environ. Dev. Sustain. 2021, 23, 45–76. [Google Scholar] [CrossRef]
- Hussain, A.; Sarangi, G.K.; Pandit, A.; Ishaq, S.; Mamnun, N.; Ahmad, B.; Jamil, M.K. Hydropower development in the Hindu Kush Himalayan region: Issues, policies and opportunities. Renew. Sust. Energ. Rev. 2019, 107, 446–461. [Google Scholar] [CrossRef]
- Chen, G.; De Costa, G. Climate Change Impacts on Water Resources: Case of Sri Lanka; Horizon Research Publishing: San Jose, CA, USA, 2017. [Google Scholar]
- Naveendrakumar, G.; Vithanage, M.; Kwon, H.H.; Iqbal, M.; Pathmarajah, S.; Obeysekera, J. Five decadal trends in averages and extremes of rainfall and temperature in Sri Lanka. Adv. Meteorol. 2018, 2018, 4217917. [Google Scholar] [CrossRef]
- Zhang, X.; Li, H.Y.; Deng, Z.D.; Ringler, C.; Gao, Y.; Hejazi, M.I.; Leung, L.R. Impacts of climate change, policy and Water-Energy-Food nexus on hydropower development. Renew. Energy 2018, 116, 827–834. [Google Scholar] [CrossRef]
- Yadav, D.; Sharma, N.V. Artificial neural network based hydro electric generation modelling. Int. J. Appl. Eng. Res. 2010, 2, 56–72. [Google Scholar]
- Khan, M.S.; Coulibaly, P.; Dibike, Y. Uncertainty analysis of statistical downscaling methods. J. Hydrol. 2006, 319, 357–382. [Google Scholar] [CrossRef]
- Khaniya, B.; Priyantha, H.G.; Baduge, N.; Azamathulla, H.M.; Rathnayake, U. Impact of climate variability on hydropower generation: A case study from Sri Lanka. ISH J. Hydraul. Eng. 2020, 26, 301–309. [Google Scholar] [CrossRef]
- Qin, P.; Xu, H.; Liu, M.; Du, L.; Xiao, C.; Liu, L.; Tarroja, B. Climate change impacts on Three Gorges Reservoir impoundment and hydropower generation. J. Hydrol. 2020, 580, 123922. [Google Scholar] [CrossRef]
- Abdulkadir, T.; Salami, A.; Anwar, A.; Kareem, A. Modelling of hydropower reservoir variables for energy generation: Neural network approach. EJESM 2013, 6, 310–316. [Google Scholar] [CrossRef] [Green Version]
- Uzlu, E.; Akpınar, A.; Özturk, H.T.; Nacar, S.; Kankal, M. Estimates of hydroelectric generation using neural networks with the artificial bee colony algorithm for Turkey. Energy 2014, 69, 638–647. [Google Scholar] [CrossRef]
- Patil, M. Stream flow modeling for Ranganadi hydropower project in India considering climate change. Curr. World Environ. 2016, 11, 834. [Google Scholar] [CrossRef] [Green Version]
- Hammid, A.T.; Sulaiman, M.H.B.; Abdalla, A.N. Prediction of small hydropower plant power production in Himreen Lake dam (HLD) using artificial neural network. Alex. Eng. J. 2018, 57, 211–221. [Google Scholar] [CrossRef]
- Khodaverdi, M. Forecasting Future Energy Production Using Hybrid Artificial Neural Network and Arima Model. 2018. Available online: https://researchrepository.wvu.edu/etd/4004/ (accessed on 15 March 2022).
- Ajala, A.L.; Adeyemo, J.; Akanmu, S. The Need for Recurrent Learning Neural Network and Combine Pareto Differential Algorithm for Multi-Objective Optimization of Real Time Reservoir Operations. J. Soft Comput. Civ. Eng. 2020, 4, 52–64. [Google Scholar]
- Anuar, N.; Khan, M.; Pasupuleti, J.; Ramli, A. Flood risk prediction for a hydropower system using artificial neural network. Int. J. Recent Technol. Eng. 2019, 8, 6177–6181. [Google Scholar]
- Sessa, V.; Assoumou, E.; Bossy, M. Modeling the climate dependency of the run-of-river based hydro power generation using machine learning techniques: An application to French, Portuguese and Spanish cases. In Proceedings of the EMS 2019 Annual Meeting, Copenhagen, Denmark, 9–13 September 2019; Volume 16. [Google Scholar]
- Karunathilake, S.L.; Nagahamulla, H.R. Artificial neural networks for daily electricity demand prediction of Sri Lanka. In Proceedings of the 2017 Seventeenth International Conference on Advances in ICT for Emerging Regions (ICTer), Colombo, Sri Lanka, 7–8 September 2017; pp. 1–6. [Google Scholar]
- Dehghani, M.; Riahi-Madvar, H.; Hooshyaripor, F.; Mosavi, A.; Shamshirband, S.; Zavadskas, E.K.; Chau, K.W. Prediction of hydropower generation using grey wolf optimization adaptive neuro-fuzzy inference system. Energies 2019, 12, 289. [Google Scholar] [CrossRef] [Green Version]
- Konica, J.A.; Staka, E. Forecasting of a hydropower plant energy production with Fuzzy logic Case for Albania. J. Multidiscip. Eng. Sci. Technol. 2017, 4, 7244–7248. [Google Scholar]
- Suprapty, B.; Malani, R.; Minardi, J. Rainfall prediction using fuzzy inference system for preliminary micro-hydro power plant planning. In IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2018; Volume 144, p. 012005. [Google Scholar]
- Rahman, M.A. Improvement of Rainfall Prediction Model by Using Fuzzy Logic. Am. J. Clim. Chang. 2020, 9, 391. [Google Scholar] [CrossRef]
- Jafari, R.; Yu, W. Fuzzy modeling for uncertainty nonlinear systems with fuzzy equations. Math. Probl. Eng. 2017, 2017, 8594738. [Google Scholar] [CrossRef]
- Rathnayake, N.; Dang, T.L.; Hoshino, Y. A Novel Optimization Algorithm: Cascaded Adaptive Neuro-Fuzzy Inference System. Int. J. Fuzzy Syst. 2021, 23, 1955–1971. [Google Scholar] [CrossRef]
- Gunasekara, C.G.S. Modelling and Simulation of Temperature Variations of Bearings in a Hydropower Generation Unit. 2011. Available online: https://www.diva-portal.org/smash/record.jsf?pid=diva2:439471 (accessed on 15 March 2022).
- Udayakumara, E.; Shrestha, R.; Samarakoon, L.; Schmidt-Vogt, D. Mitigating soil erosion through farm-level adoption of soil and water conservation measures in Samanalawewa Watershed, Sri Lanka. Acta Agric. Scand. B Soil Plant Sci. 2012, 62, 273–285. [Google Scholar] [CrossRef]
- Udayakumara, E.; Gunawardena, U. Reducing Siltation and Increasing Hydropower Generation from the Rantambe Reservoir, Sri Lanka. 2016. Available online: https://ideas.repec.org/p/snd/wpaper/110.html (accessed on 15 March 2022).
- Imbulana, N.; Gunawardana, S.; Shrestha, S.; Datta, A. Projections of extreme precipitation events under climate change scenarios in Mahaweli River Basin of Sri Lanka. Curr. Sci. 2018, 114, 1495–1509. [Google Scholar] [CrossRef]
- Perera, A.; Rathnayake, U. Impact of climate variability on hydropower generation in an un-gauged catchment: Erathna run-of-the-river hydropower plant, Sri Lanka. Appl. Water Sci. 2019, 9, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Khaniya, B.; Jayanayaka, I.; Jayasanka, P.; Rathnayake, U. Rainfall trend analysis in Uma Oya basin, Sri Lanka, and future water scarcity problems in perspective of climate variability. Adv. Meteorol. 2019, 2019, 3636158. [Google Scholar] [CrossRef]
- Udagedara, D.T.; Oguchi, C.T.; Gunatilake, J.K. Evaluation of geomechanical and geochemical properties in weathered metamorphic rocks in tropical environment: A case study from Samanalawewa hydropower project, Sri Lanka. Geosci. J. 2017, 21, 441–452. [Google Scholar] [CrossRef]
- Laksiri, K.; Gunathilake, J.; Iwao, Y. A case study of the Samanalawewa reservoir on the Walawe river in an area of Karst in Sri Lanka. In Proceedings of the 10th Multidisciplinary Conference on Sinkholes and the Engineering and Environmental Impacts of Karst, San Antonio, TX, USA, 24–28 September 2005; pp. 253–262. [Google Scholar]
- Wijesinghe, D. Optimization of Hydropower Potential of Samanalawewa Project. 2006. Available online: https://pdfs.semanticscholar.org/441a/518388b85c6d8ad1384194922cefa7728faa.pdf (accessed on 15 March 2022).
- Pathiraja, M.; Wijayapala, W. Optimization of the usage of Samanalawewa water resource for power generation. In Proceedings of the 2016 Electrical Engineering Conference (EECon), Colombo, Sri Lanka, 15 December 2016; pp. 86–90. [Google Scholar]
- Udayakumara, E.; Gunawardena, U. Cost–benefit analysis of Samanalawewa Hydroelectric Project in Sri Lanka: An ex post analysis. Earth Syst. Environ. 2018, 2, 401–412. [Google Scholar] [CrossRef]
- Jakob Themeßl, M.; Gobiet, A.; Leuprecht, A. Empirical-statistical downscaling and error correction of daily precipitation from regional climate models. Int. J. Climatol. 2011, 31, 1530–1544. [Google Scholar] [CrossRef]
- Glossary, I. Climate Change 2014 Report Fifth Assessment Report; IPCC: Geneva, Switzerland, 2014. [Google Scholar]
- Christensen, J.H.; Boberg, F.; Christensen, O.B.; Lucas-Picher, P. On the need for bias correction of regional climate change projections of temperature and precipitation. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef]
- Piani, C.; Haerter, J.; Coppola, E. Statistical bias correction for daily precipitation in regional climate models over Europe. Theor. Appl. 2010, 99, 187–192. [Google Scholar] [CrossRef] [Green Version]
- Teutschbein, C.; Seibert, J. Bias correction of regional climate model simulations for hydrological climate-change impact studies: Review and evaluation of different methods. J. Hydrol. 2012, 456, 12–29. [Google Scholar] [CrossRef]
- Lenderink, G.; Buishand, A.; Deursen, W.V. Estimates of future discharges of the river Rhine using two scenario methodologies: Direct versus delta approach. Hydrol. Earth Syst. Sci. 2007, 11, 1145–1159. [Google Scholar] [CrossRef]
- Ghimire, U.; Srinivasan, G.; Agarwal, A. Assessment of rainfall bias correction techniques for improved hydrological simulation. Int. J. Climatol. 2019, 39, 2386–2399. [Google Scholar] [CrossRef]
- Lafon, T.; Dadson, S.; Buys, G.; Prudhomme, C. Bias correction of daily precipitation simulated by a regional climate model: A comparison of methods. Int. J. Climatol. 2013, 33, 1367–1381. [Google Scholar] [CrossRef] [Green Version]
- Luo, M.; Liu, T.; Meng, F.; Duan, Y.; Frankl, A.; Bao, A.; De Maeyer, P. Comparing bias correction methods used in downscaling precipitation and temperature from regional climate models: A case study from the Kaidu River Basin in Western China. Water 2018, 10, 1046. [Google Scholar] [CrossRef] [Green Version]
- Mahmood, R.; Jia, S.; Tripathi, N.K.; Shrestha, S. Precipitation extended linear scaling method for correcting GCM precipitation and its evaluation and implication in the transboundary Jhelum River basin. Atmosphere 2018, 9, 160. [Google Scholar] [CrossRef] [Green Version]
- Jang, J.S. ANFIS: Adaptive-network-based fuzzy inference system. IEEE Trans. Syst. Man Cybern. Syst. 1993, 23, 665–685. [Google Scholar] [CrossRef]

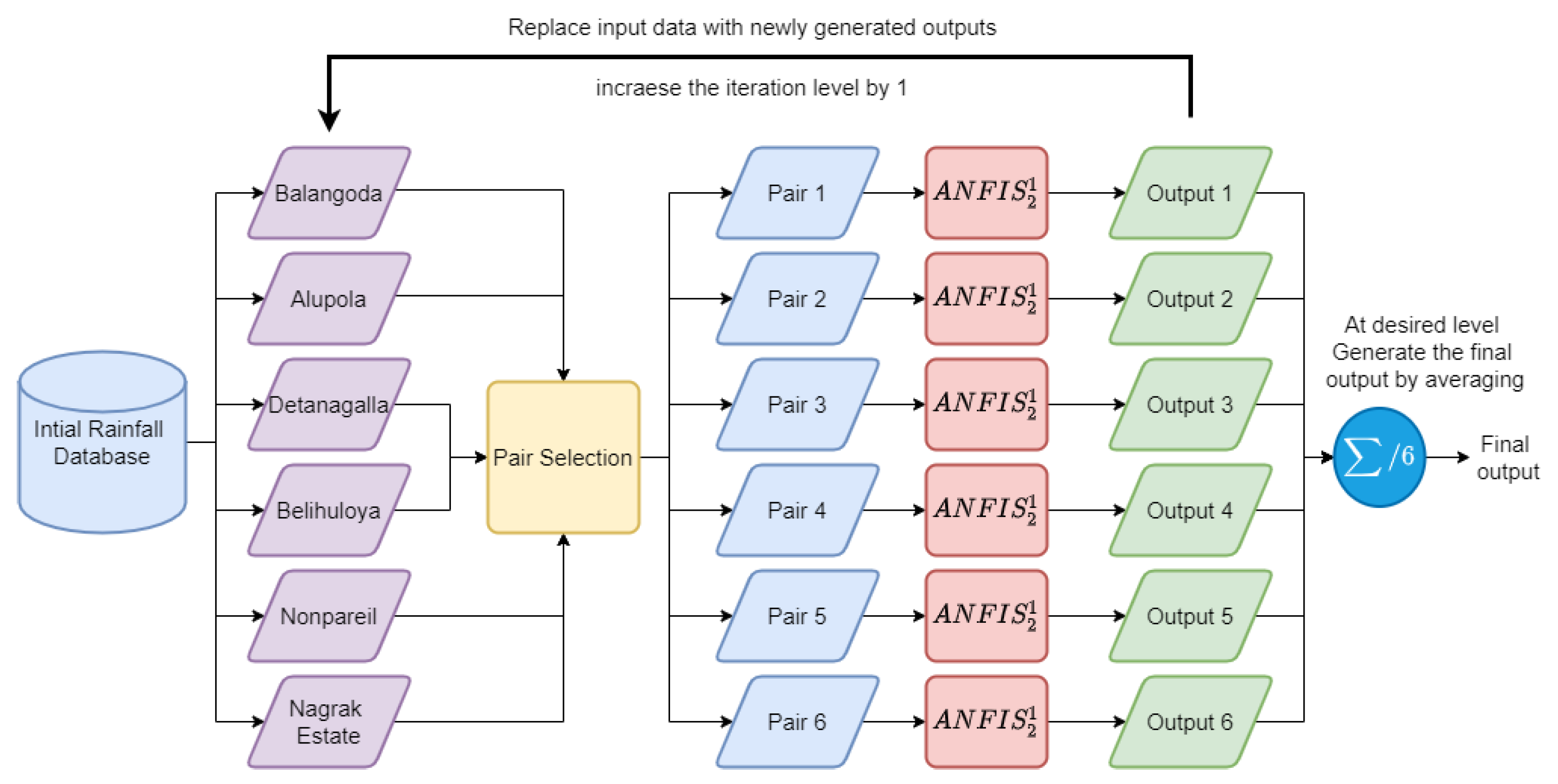

| Balangoda | Alupola | Detanagalla | Belihuloya | Nonpareil | Nagrak Estate | Power | |
|---|---|---|---|---|---|---|---|
| count | 127.00 | 127.00 | 127.00 | 127.00 | 127.00 | 127.00 | 127.00 |
| mean | 377.88 | 190.57 | 221.81 | 240.77 | 183.42 | 187.65 | 22.86 |
| std | 224.50 | 161.46 | 215.17 | 218.55 | 156.57 | 183.21 | 14.69 |
| min | 27.40 | 7.50 | 0.00 | 2.70 | 0.00 | 0.67 | 1.10 |
| 25% | 205.35 | 61.35 | 50.55 | 83.30 | 54.54 | 40.31 | 10.72 |
| 50% | 348.10 | 136.60 | 144.50 | 160.20 | 132.20 | 124.95 | 21.04 |
| 75% | 509.05 | 308.05 | 349.90 | 353.95 | 289.53 | 282.10 | 34.00 |
| max | 1159.90 | 734.70 | 926.10 | 1371.00 | 661.30 | 930.30 | 67.85 |
| Algorithm | Parameters | |
|---|---|---|
| MLP | Hidden layer size | 50, 50, 50 |
| Activation | tanh | |
| Solver | adam | |
| alpha | 0.05 | |
| learning rate | constant | |
| KNN | Weights | Uniform |
| n_neighbors | 1 | |
| ANFIS | Iteration | 100 |
| Membership Functions | 3 | |
| Step Size | 0.1 | |
| Decrease rate | 0.9 | |
| Increase rate | 1.1 | |
| ANFIS-PSO | Inertia Weight | 1 |
| Inertia weight damping ratio | 0.99 | |
| Personal Learning Coefficient | 1 | |
| Global Learning Coefficient | 2 | |
| ANFIS-GA | Crossover Percentage | 0.7 |
| Mutation Percentage | 0.5 | |
| Mutation Rate | 0.1 | |
| Selection Pressure | 8 | |
| Gamma | 0.2 | |
| RNN/LSTM/GRU | Optimizer | adam |
| Learning rate | 0.0001 | |
| Activation | relu | |
| batch size | 30 | |
| epochs | 100 | |
| Cascaded ANFIS | Iteration | 100 |
| Membership Functions | 3 | |
| Step Size | 0.1 | |
| Decrease rate | 0.9 | |
| Increase rate | 1.1 | |
| Algorithm | RMSE (Train) | RMSE (Test) |
|---|---|---|
| MLP | 7.52 | 25.26 |
| KNN | 9.73 | 19.33 |
| ANFIS | 10.47 | 18.06 |
| ANFIS-PSO | 10.99 | 16.61 |
| ANFIS-GA | 11.88 | 16.87 |
| Linear Regression | 13.74 | 14.85 |
| Lasso Regression | 13.72 | 14.82 |
| Ridge Regression | 13.70 | 14.88 |
| RNN | 7.85 | 11.62 |
| GRU | 6.50 | 8.33 |
| LSTM | 6.03 | 6.88 |
| Cascaded ANFIS | 1.01 | 1.80 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rathnayake, N.; Rathnayake, U.; Dang, T.L.; Hoshino, Y. A Cascaded Adaptive Network-Based Fuzzy Inference System for Hydropower Forecasting. Sensors 2022, 22, 2905. https://doi.org/10.3390/s22082905
Rathnayake N, Rathnayake U, Dang TL, Hoshino Y. A Cascaded Adaptive Network-Based Fuzzy Inference System for Hydropower Forecasting. Sensors. 2022; 22(8):2905. https://doi.org/10.3390/s22082905
Chicago/Turabian StyleRathnayake, Namal, Upaka Rathnayake, Tuan Linh Dang, and Yukinobu Hoshino. 2022. "A Cascaded Adaptive Network-Based Fuzzy Inference System for Hydropower Forecasting" Sensors 22, no. 8: 2905. https://doi.org/10.3390/s22082905
APA StyleRathnayake, N., Rathnayake, U., Dang, T. L., & Hoshino, Y. (2022). A Cascaded Adaptive Network-Based Fuzzy Inference System for Hydropower Forecasting. Sensors, 22(8), 2905. https://doi.org/10.3390/s22082905






