Cascade Brillouin Lasing in a Tellurite-Glass Microsphere Resonator with Whispering Gallery Modes
Abstract
:1. Introduction
2. Materials and Methods
2.1. Fabrication and Characterization of Tellurite Glass
2.2. Fabrication of Tellurite Microsphere Resonators
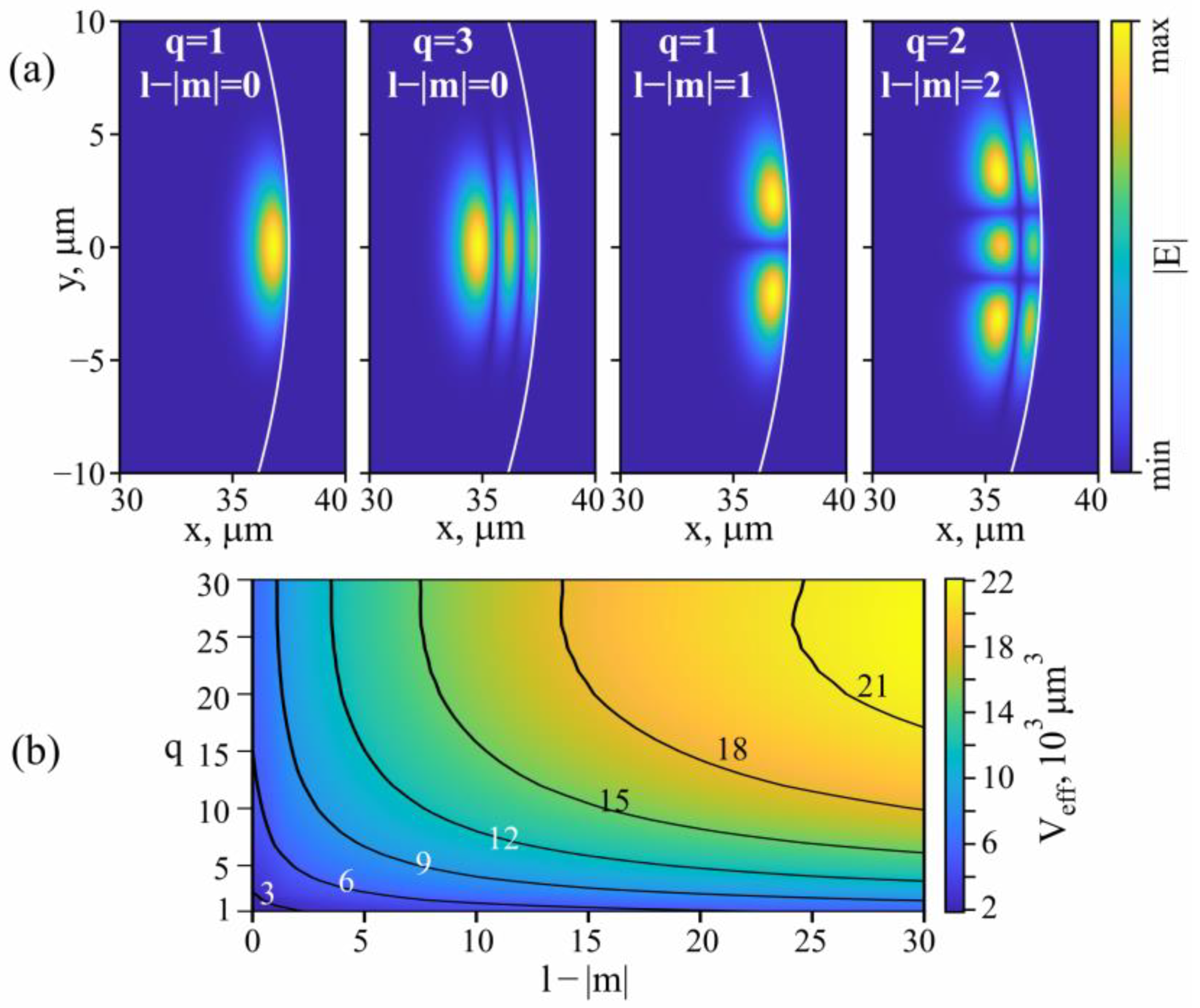
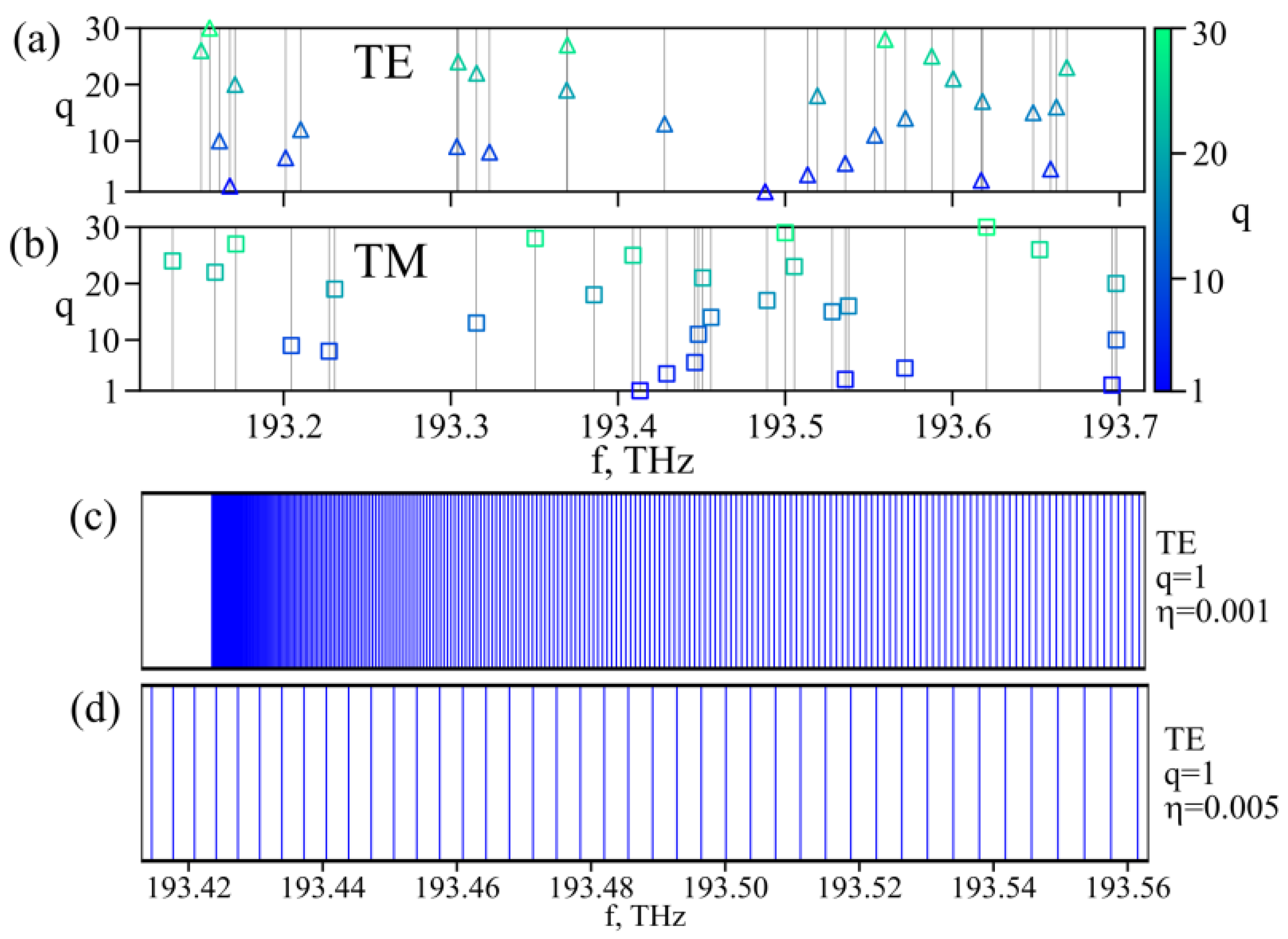
2.3. Theoretical Description of Microsphere Characteristics
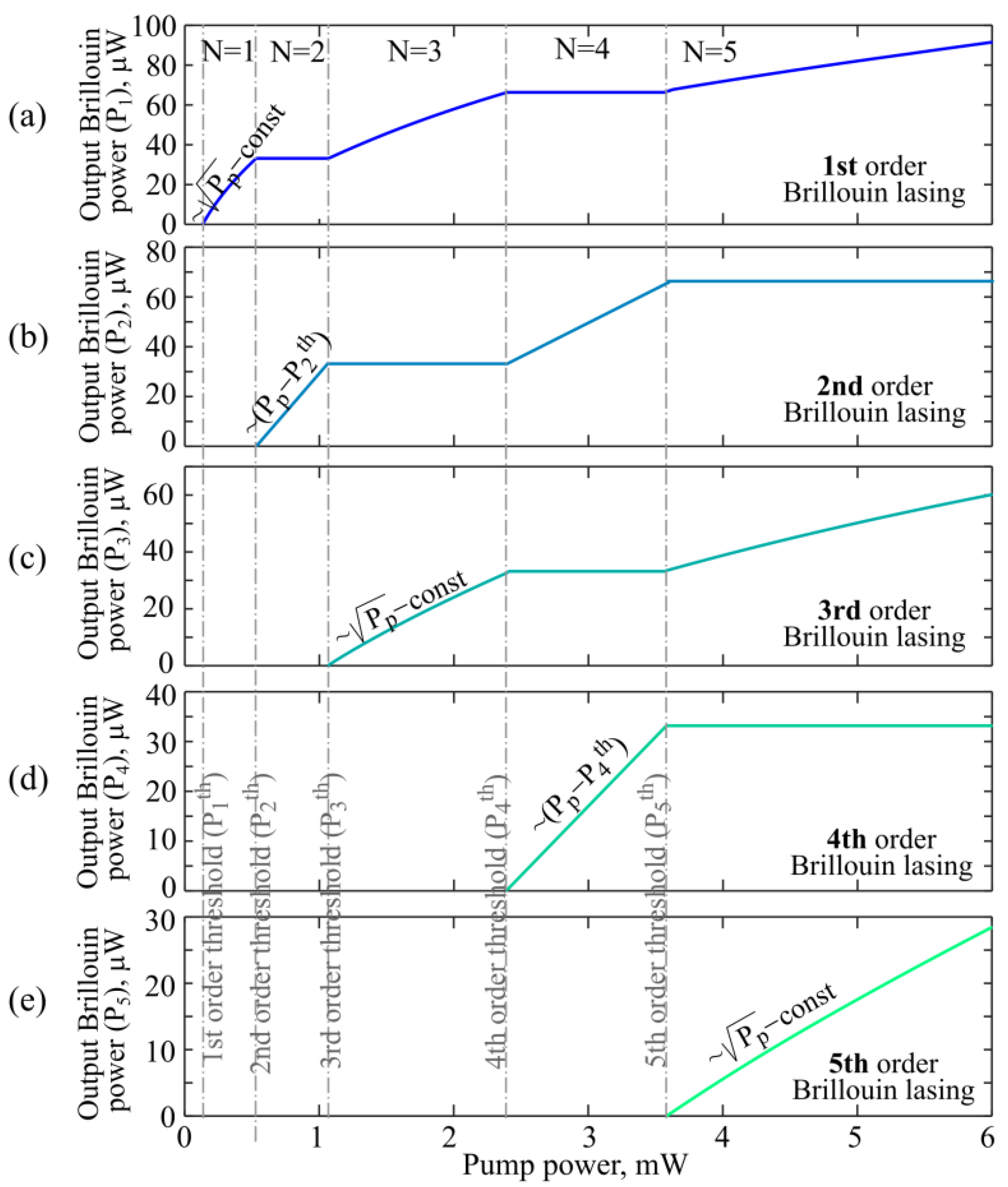
2.4. Theoretical Model of Cascade Brillouin Lasing
3. Results
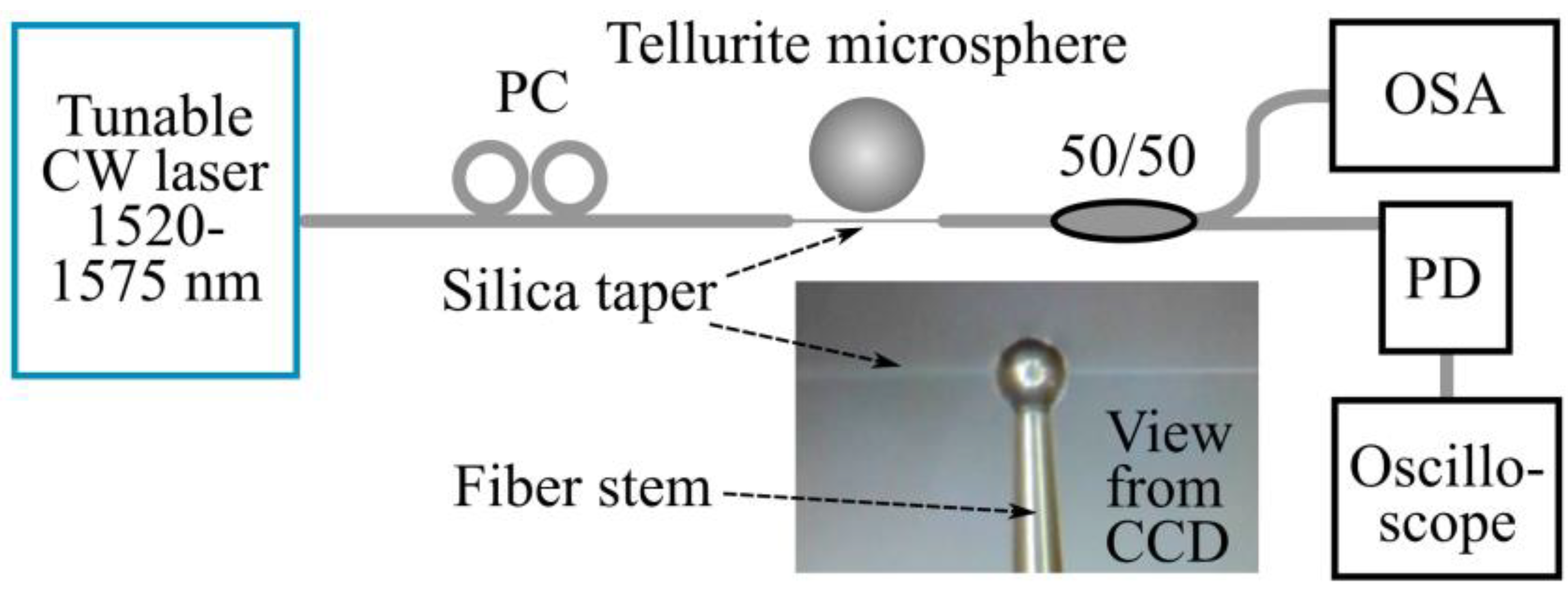
3.1. Experimental Results
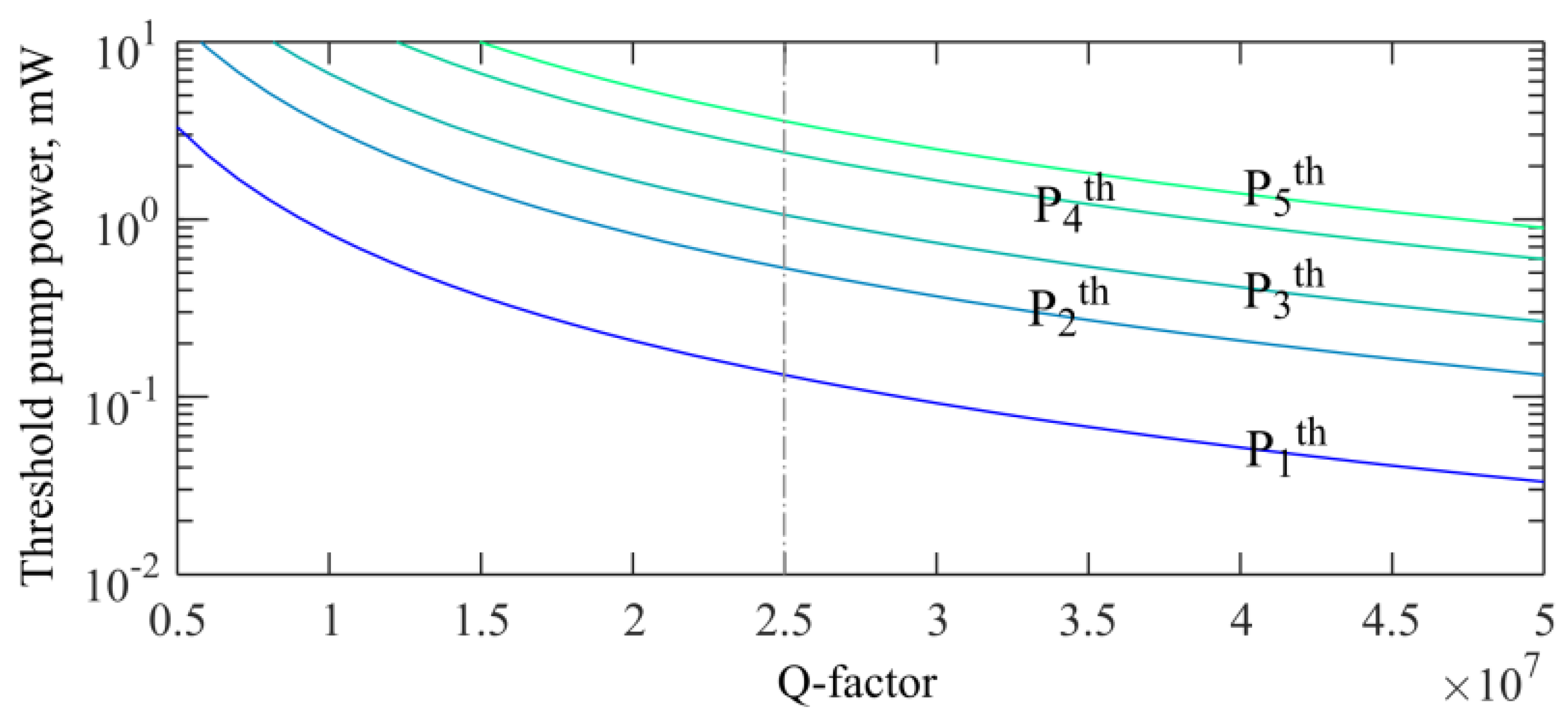
3.2. Theoretical Results
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Reynolds, T.; Riesen, N.; Meldrum, A.; Fan, X.; Hall, J.M.M.; Monro, T.M.; François, A. Fluorescent and lasing whispering gallery mode microresonators for sensing applications. Laser Photonics Rev. 2017, 11, 1600265. [Google Scholar] [CrossRef]
- Yu, D.; Humar, M.; Meserve, K.; Bailey, R.C.; Nic Chormaic, S.; Vollmer, F. Whispering-gallery-mode sensors for biological and physical sensing. Nat. Rev. Methods Primers 2021, 1, 83. [Google Scholar] [CrossRef]
- Jiang, X.; Qavi, A.J.; Huang, S.H.; Yang, L. Whispering-gallery sensors. Matter 2020, 3, 371–392. [Google Scholar] [CrossRef] [PubMed]
- Tan, T.; Yuan, Z.; Zhang, H.; Yan, G.; Zhou, S.; An, N.; Peng, B.; Soavi, G.; Rao, Y.; Yao, B. Multispecies and individual gas molecule detection using stokes solitons in a graphene over-modal microresonator. Nat. Commun. 2021, 12, 6716. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.; Chen, Y.-L.; Tang, S.-J.; Vollmer, F.; Xiao, Y.-F. Nonlinear sensing with whispering-gallery mode microcavities: From label-free detection to spectral fingerprinting. Nano Lett. 2020, 21, 1566–1575. [Google Scholar] [CrossRef]
- Brice, I.; Grundsteins, K.; Draguns, K.; Atvars, A.; Alnis, J. Whispering gallery mode resonator temperature compensation and refractive index sensing in glucose droplets. Sensors 2021, 21, 7184. [Google Scholar] [CrossRef]
- Zhivotkov, D.; Ristić, D.; Romanova, E.; Ivanda, M. Refractometric gas sensing using a whispering gallery mode microresonator coated with a supra-micron sol-gel layer. Opt. Mater. 2021, 118, 111286. [Google Scholar] [CrossRef]
- Lin, G.; Song, Q. Kerr frequency comb interaction with Raman, Brillouin, and second order nonlinear effects. Laser Photonics Rev. 2021, 16, 2100184. [Google Scholar] [CrossRef]
- Shen, X.; Beltran, R.C.; Diep, V.M.; Soltani, S.; Armani, A.M. Low-threshold parametric oscillation in organically modified microcavities. Sci. Adv. 2018, 4, eaao450. [Google Scholar] [CrossRef] [Green Version]
- Frigenti, G.; Cavigli, L.; Ratto, F.; Centi, S.; Murzina, T.V.; Farnesi, D.; Pelli, S.; Soria, S.; Nunzi Conti, G. Microbubble resonators for scattering-free absorption spectroscopy of nanoparticles. Opt. Express 2021, 29, 31130–31136. [Google Scholar] [CrossRef]
- Bochek, D.; Toropov, N.; Vatnik, I.; Churkin, D.; Sumetsky, M. SNAP Microresonators introduced by strong bending of optical fibers. Opt. Lett. 2019, 44, 3218–3221. [Google Scholar] [CrossRef] [PubMed]
- Shitikov, A.E.; Bilenko, I.A.; Kondratiev, N.M.; Lobanov, V.E.; Markosyan, A.; Gorodetsky, M.L. Billion Q-factor in silicon WGM resonators. Optica 2018, 5, 1525–1528. [Google Scholar] [CrossRef]
- Smirnov, S.; Andryushkov, V.; Podivilov, E.; Sturman, B.; Breunig, I. Soliton based χ(2) combs in high-Q optical microresonators. Opt. Express 2021, 29, 27434–27449. [Google Scholar] [CrossRef] [PubMed]
- Min, B.; Kippenberg, T.J.; Yang, L.; Vahala, K.J.; Kalkman, J.; Polman, A. Erbium-implanted high-qsilica toroidal microcavity laser on a silicon chip. Phys. Rev. A 2004, 70, 033803. [Google Scholar] [CrossRef] [Green Version]
- Spillane, S.M.; Kippenberg, T.J.; Vahala, K.J. Ultralow-threshold raman laser using a spherical dielectric microcavity. Nature 2002, 415, 621–623. [Google Scholar] [CrossRef] [PubMed]
- Zhu, S.; Xiao, B.; Jiang, B.; Shi, L.; Zhang, X. Tunable brillouin and raman microlasers using hybrid microbottle resonators. Nanophotonics 2019, 8, 931–940. [Google Scholar] [CrossRef]
- Yao, B.; Yu, C.; Wu, Y.; Huang, S.-W.; Wu, H.; Gong, Y.; Chen, Y.; Li, Y.; Wong, C.W.; Fan, X.; et al. Graphene-enhanced brillouin optomechanical microresonator for ultrasensitive gas detection. Nano Lett. 2017, 17, 4996–5002. [Google Scholar] [CrossRef]
- Yang, J.; Qin, T.; Zhang, F.; Chen, X.; Jiang, X.; Wan, W. Multiphysical sensing of light, sound and microwave in a microcavity Brillouin laser. Nanophotonics 2020, 9, 2915–2925. [Google Scholar] [CrossRef]
- Qin, G.-Q.; Wang, M.; Wen, J.-W.; Ruan, D.; Long, G.-L. Brillouin cavity optomechanics sensing with enhanced dynamical Backaction. Photon. Res. 2019, 7, 1440–1446. [Google Scholar] [CrossRef]
- Eggleton, B.J.; Poulton, C.G.; Rakich, P.T.; Steel, M.J.; Bahl, G. Brillouin integrated photonics. Nat. Photonics 2019, 13, 664–677. [Google Scholar] [CrossRef]
- Li, J.; Suh, M.-G.; Vahala, K. Microresonator brillouin gyroscope. Optica 2017, 4, 346–348. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.; Lai, Y.-H.; Yuan, Z.; Suh, M.-G.; Vahala, K. Petermann-factor sensitivity limit near an exceptional point in a Brillouin ring laser gyroscope. Nat. Commun. 2020, 11, 1610. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Enzian, G.; Szczykulska, M.; Silver, J.; Del Bino, L.; Zhang, S.; Walmsley, I.A.; Del’Haye, P.; Vanner, M.R. Observation of Brillouin optomechanical strong coupling with an 11 GHz mechanical Mode. Optica 2018, 6, 7–14. [Google Scholar] [CrossRef]
- Feng, C.; Schneider, T. Benefits of spectral property engineering in distributed Brillouin fiber sensing. Sensors 2021, 21, 1881. [Google Scholar] [CrossRef] [PubMed]
- Hu, D.J.J.; Humbert, G.; Dong, H.; Zhang, H.; Hao, J.; Sun, Q. Review of specialty fiber based Brillouin optical time domain analysis technology. Photonics 2021, 8, 421. [Google Scholar] [CrossRef]
- Gorshkov, B.G.; Yüksel, K.; Fotiadi, A.A.; Wuilpart, M.; Korobko, D.A.; Zhirnov, A.A.; Stepanov, K.V.; Turov, A.T.; Konstantinov, Y.A.; Lobach, I.A. Scientific applications of distributed acoustic sensing: State-of-the-art review and perspective. Sensors 2022, 22, 1033. [Google Scholar] [CrossRef]
- Tkachenko, A.Y.; Lobach, I.A.; Kablukov, S.I. All-fiber Brillouin optical spectrum analyzer based on self-sweeping fiber laser. Opt. Express 2017, 25, 17600–17605. [Google Scholar] [CrossRef]
- Lopez-Mercado, C.A.; Korobko, D.A.; Zolotovskii, I.O.; Fotiadi, A.A. Application of dual-frequency self-injection locked DFB laser for Brillouin optical time domain analysis. Sensors 2021, 21, 6859. [Google Scholar] [CrossRef]
- Kovach, A.; Chen, D.; He, J.; Choi, H.; Dogan, A.H.; Ghasemkhani, M.; Taheri, H.; Armani, A.M. Emerging material systems for integrated optical kerr frequency combs. Adv. Opt. Photonics 2020, 12, 135–222. [Google Scholar] [CrossRef] [Green Version]
- Tao, G.; Ebendorff-Heidepriem, H.; Stolyarov, A.M.; Danto, S.; Badding, J.V.; Fink, Y.; Ballato, J.; Abouraddy, A.F. Infrared fibers. Adv. Opt. Photonics 2015, 7, 379–458. [Google Scholar] [CrossRef]
- Deroh, M.; Beugnot, J.-C.; Hammani, K.; Finot, C.; Fatome, J.; Smektala, F.; Maillotte, H.; Sylvestre, T.; Kibler, B. Comparative analysis of stimulated Brillouin scattering at 2 µm in various infrared glass-based optical fibers. J. Opt. Soc. Am. B 2020, 37, 3792–3800. [Google Scholar] [CrossRef]
- Wolff, C.; Smith, M.J.A.; Stiller, B.; Poulton, C.G. Brillouin scattering—Theory and experiment: Tutorial. J. Opt. Soc. Am. B 2021, 38, 1243–1269. [Google Scholar] [CrossRef]
- Qin, G.; Sotobayashi, H.; Tsuchiya, M.; Mori, A.; Suzuki, T.; Ohishi, Y. Stimulated Brillouin scattering in a single-mode tellurite fiber for amplification, lasing, and slow light generation. J. Lightwave Technol. 2008, 26, 492–498. [Google Scholar] [CrossRef]
- Domachuk, P.; Wolchover, N.A.; Cronin-Golomb, M.; Wang, A.; George, A.K.; Cordeiro, C.M.B.; Knight, J.C.; Omenetto, F.G. Over 4000 nm bandwidth of mid-IR supercontinuum generation in sub-centimeter segments of highly nonlinear tellurite PCFs. Opt. Express 2008, 16, 7161–7168. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kibler, B.; Lemière, A.; Gomes, J.-T.; Gaponov, D.; Lavoute, L.; Désévédavy, F.; Smektala, F. Octave-spanning coherent supercontinuum generation in a step-index tellurite fiber and towards few-cycle pulse compression at 2 µm. Opt. Commun. 2021, 488, 126853. [Google Scholar] [CrossRef]
- Kedenburg, S.; Steinle, T.; Mörz, F.; Steinmann, A.; Nguyen, D.; Rhonehouse, D.; Zong, J.; Chavez-Pirson, A.; Giessen, H. Solitonic supercontinuum of femtosecond mid-IR pulses in W-type index tellurite fibers with two zero dispersion wavelengths. APL Photonics 2016, 1, 086101. [Google Scholar] [CrossRef] [Green Version]
- Okhrimchuk, A.G.; Pryamikov, A.D.; Gladyshev, A.V.; Alagashev, G.K.; Smayev, M.P.; Likhov, V.V.; Dorofeev, V.V.; Motorin, S.E.; Yatsenko, Y.P. Direct laser written waveguide in tellurite glass for supercontinuum generation in 2 µm spectral range. J. Lightwave Technol. 2020, 38, 1492–1500. [Google Scholar] [CrossRef]
- Anashkina, E.A. Laser sources based on rare-earth ion doped tellurite glass fibers and microspheres. Fibers 2020, 8, 30. [Google Scholar] [CrossRef]
- Guo, C.; Che, K.; Zhang, P.; Wu, J.; Huang, Y.; Xu, H.; Cai, Z. Low-threshold stimulated brillouin scattering in high-Q whispering gallery mode tellurite microspheres. Opt. Express 2015, 23, 32261–32266. [Google Scholar] [CrossRef]
- Dorofeev, V.V.; Koltashev, V.V.; Motorin, S.E.; Plekhovich, A.D.; Kim, A.V. Thermal, optical, and IR-emission properties of extremely low Hydroxyl TeO2-WO3-Bi2O3-La2O3-xEr2O3 glasses for mid-infrared photonics. Photonics 2021, 8, 320. [Google Scholar] [CrossRef]
- Anashkina, E.A.; Dorofeev, V.V.; Koltashev, V.V.; Kim, A.V. Development of Er3+-doped high-purity tellurite glass fibers for gain-switched laser operation at 2.7 µm. Opt. Mater. Express 2017, 7, 4337–4351. [Google Scholar] [CrossRef]
- Moiseev, A.N.; Dorofeev, V.V.; Chilyasov, A.V.; Pimenov, V.G.; Kotereva, T.V.; Kraev, I.A.; Ketkova, L.A.; Kosolapov, A.F.; Plotnichenko, V.G.; Koltashev, V.V. Low-loss, high-purity (TeO2)0.75(WO3)0.25 glass. Inorg. Mater. 2011, 47, 665–669. [Google Scholar] [CrossRef]
- Dorofeev, V.V.; Moiseev, A.N.; Churbanov, M.F.; Snopatin, G.E.; Chilyasov, A.V.; Kraev, I.A.; Lobanov, A.S.; Kotereva, T.V.; Ketkova, L.A.; Pushkin, A.A.; et al. High-purity TeO2–WO3–(La2O3,Bi2O3) glasses for fiber-optics. Opt. Mater. 2011, 33, 1911–1915. [Google Scholar] [CrossRef]
- Anashkina, E.A.; Andrianov, A. Erbium-doped tellurite glass microlaser in C-band and L-band. J. Lightwave Technol. 2021, 39, 3568–3574. [Google Scholar] [CrossRef]
- Anashkina, E.A.; Dorofeev, V.V.; Andrianov, A.V. In-band pumped thulium-doped tellurite glass microsphere laser. Appl. Sci. 2021, 11, 5440. [Google Scholar] [CrossRef]
- Oraevsky, A.N. Whispering-gallery waves. Quantum Electron. 2002, 32, 377–400. [Google Scholar] [CrossRef]
- Schiller, S. Asymptotic expansion of morphological resonance frequencies in mie scattering. Appl. Opt. 1993, 32, 2181–2185. [Google Scholar] [CrossRef]
- Teraoka, I.; Arnold, S. Whispering-gallery modes in a microsphere coated with a high-refractive index layer: Polarization-dependent sensitivity enhancement of the resonance-shift sensor and TE-TM resonance matching. J. Opt. Soc. Am. B 2007, 24, 653–659. [Google Scholar] [CrossRef] [Green Version]
- Kher-Alden, J.; Maayani, S.; Martin, L.L.; Douvidzon, M.; Deych, L.; Carmon, T. Microspheres with atomic-scale tolerances generate hyperdegeneracy. Phys. Rev. X 2020, 10, 031049. [Google Scholar] [CrossRef]
- Korobko, D.A.; Zolotovskii, I.O.; Svetukhin, V.V.; Zhukov, A.V.; Fomin, A.N.; Borisova, C.V.; Fotiadi, A.A. Detuning effects in Brillouin ring microresonator laser. Opt. Express 2020, 28, 4962–4972. [Google Scholar] [CrossRef]
- Che, K.; Tang, D.; Ren, C.; Xu, H.; Chen, L.; Jin, C.; Cai, Z. Thermal characteristics of Brillouin microsphere lasers. IEEE J. Quantum Electron. 2018, 54, 1000108. [Google Scholar] [CrossRef]
- Anashkina, E.A.; Marisova, M.P.; Salgals, T.; Alnis, J.; Lyashuk, I.; Leuchs, G.; Spolitis, S.; Bobrovs, V.; Andrianov, A.V. Optical frequency combs generated in silica microspheres in the telecommunication C-, U-, and E-bands. Photonics 2021, 8, 345. [Google Scholar] [CrossRef]
- Spolitis, S.; Murnieks, R.; Skladova, L.; Salgals, T.; Andrianov, A.V.; Marisova, M.P.; Leuchs, G.; Anashkina, E.A.; Bobrovs, V. IM/DD WDM-PON communication system based on optical frequency comb generated in silica whispering gallery mode resonator. IEEE Access 2021, 9, 66335–66345. [Google Scholar] [CrossRef]
- Suzuki, R.; Kubota, A.; Hori, A.; Fujii, S.; Tanabe, T. Broadband gain induced raman comb formation in a silica microresonator. J. Opt. Soc. Am. B 2018, 35, 933–938. [Google Scholar] [CrossRef] [Green Version]







Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Anashkina, E.A.; Marisova, M.P.; Dorofeev, V.V.; Andrianov, A.V. Cascade Brillouin Lasing in a Tellurite-Glass Microsphere Resonator with Whispering Gallery Modes. Sensors 2022, 22, 2866. https://doi.org/10.3390/s22082866
Anashkina EA, Marisova MP, Dorofeev VV, Andrianov AV. Cascade Brillouin Lasing in a Tellurite-Glass Microsphere Resonator with Whispering Gallery Modes. Sensors. 2022; 22(8):2866. https://doi.org/10.3390/s22082866
Chicago/Turabian StyleAnashkina, Elena A., Maria P. Marisova, Vitaly V. Dorofeev, and Alexey V. Andrianov. 2022. "Cascade Brillouin Lasing in a Tellurite-Glass Microsphere Resonator with Whispering Gallery Modes" Sensors 22, no. 8: 2866. https://doi.org/10.3390/s22082866
APA StyleAnashkina, E. A., Marisova, M. P., Dorofeev, V. V., & Andrianov, A. V. (2022). Cascade Brillouin Lasing in a Tellurite-Glass Microsphere Resonator with Whispering Gallery Modes. Sensors, 22(8), 2866. https://doi.org/10.3390/s22082866







