Bipartite Consensus of Nonlinear Agents in the Presence of Communication Noise
Abstract
:1. Introduction
- Feedback linearization theory is used to cancel the nonlinearities in the plant. Moreover, the closed-loop response of the plant is similar to a stable linear system.
- The NDI controller has many advantages. Examples of these advantages include (1) simple and closed-form control expression, (2) easily implementable, global exponential stability of the tracking error, (3) use of nonlinear kinematics in the plant inversion and (4) minimize the need for individual gain tuning, etc.
- Distributed Nonlinear Dynamic Inversion (DNDI) control protocol is used for bipartite consensus of nonlinear agents for the first time. This is a unique idea because the advantages of NDI are inherited in DNDI and applied to bipartite problems.
- The mathematical details for the convergence study are presented, which gives a solid theoretical base.
- The effect of communication noise is studied, which is a practical consideration in the context of multi-agent operation.
- The detailed simulation study considering the noise separately gives a clear understanding regarding the effectiveness of the proposed consensus protocol.
2. Preliminaries
2.1. Bipartite Consensus of MASs
2.2. Graph Theory
2.3. Communication Noise
2.4. Theorems and Lemmas
- is structurally balanced.
- and the associated undirected graph is structurally balanced, where .
- , such that is a nonnegative matrix.
- either there are no directed semicycles, or all directed semicycles are positive.
3. Problem Description
4. Distributed Nonlinear Dynamic Inversion (DNDI) Controller for Bipartite Consensus
5. Convergence Study of DNDI for Bipartite Consensus
6. Simulation Study
- Case 1: Bipartite consensus without noise
- Case 2: Bipartite consensus with noise
6.1. Agent Dynamics and Control Calculation
6.2. Communication Topology
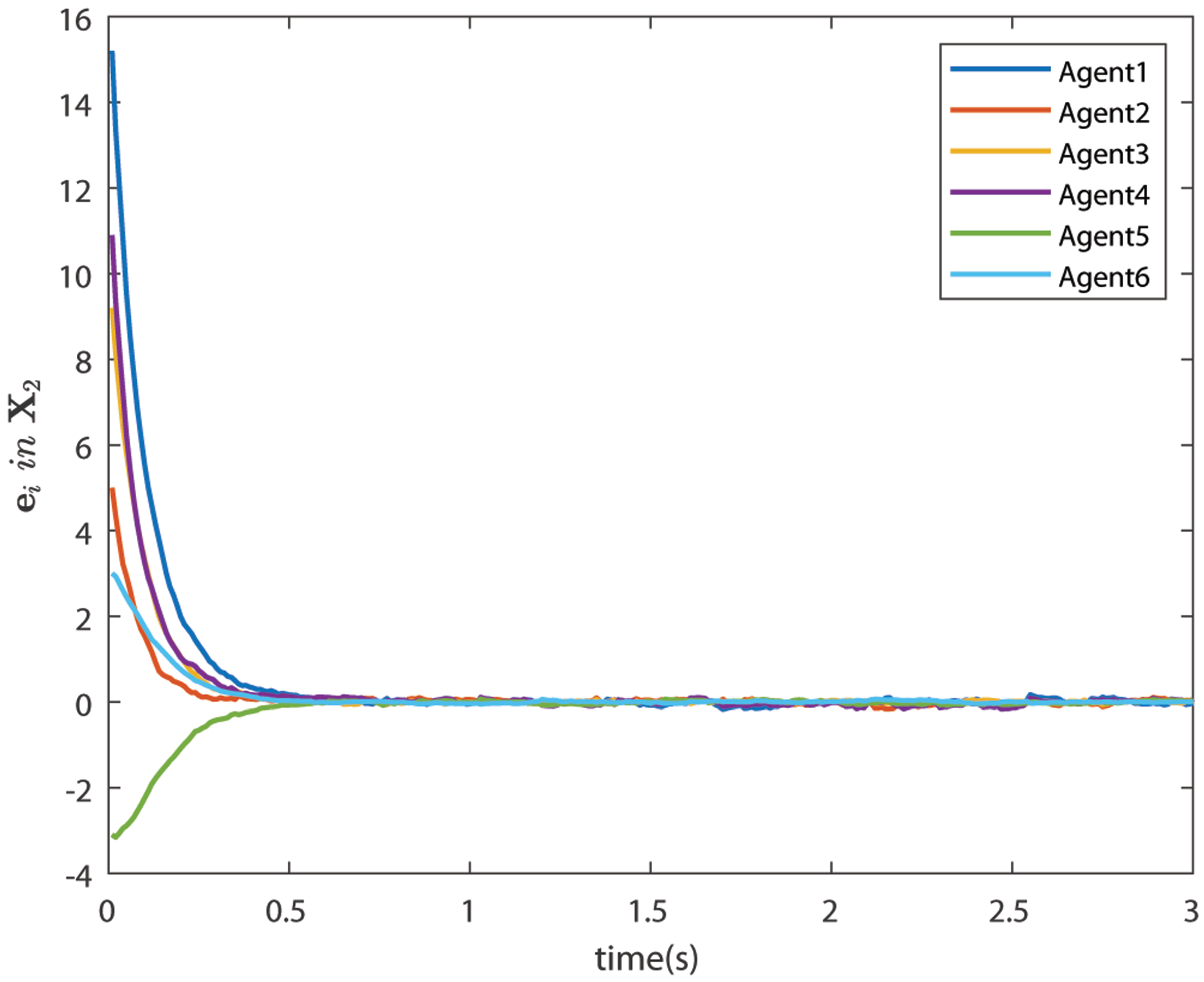
6.3. Case 1: Bipartite Consensus without Noise
6.4. Case 2: Bipartite Consensus with Noise
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| DNDI | Distributed Nonlinear Dynamic Inversion |
| N-DNDI | Neuro-adaptive augmented DNDI |
References
- Cao, Y.U.; Kahng, A.B.; Fukunaga, A.S. Cooperative mobile robotics: Antecedents and directions. In Robot Colonies; Springer: Dordrecht, The Netherlands, 1997; pp. 7–27. [Google Scholar]
- Florens, C.; Franceschetti, M.; McEliece, R.J. Lower bounds on data collection time in sensory networks. IEEE J. Sel. Areas Commun. 2004, 22, 1110–1120. [Google Scholar] [CrossRef]
- Olfati-Saber, R. Flocking for multi-agent dynamic systems: Algorithms and theory. IEEE Trans. Autom. Control 2006, 51, 401–420. [Google Scholar] [CrossRef] [Green Version]
- Ren, W.; Beard, R.W. Distributed Consensus in Multi-Vehicle Cooperative Control; Springer: London, UK, 2008. [Google Scholar]
- Gao, H.; Yang, X.; Shi, P. Multi-objective robust H∞ Control of spacecraft rendezvous. IEEE Trans. Control Syst. Technol. 2009, 17, 794–802. [Google Scholar]
- Das, A.; Lewis, F.L. Distributed adaptive control for synchronization of unknown nonlinear networked systems. Automatica 2010, 46, 2014–2021. [Google Scholar] [CrossRef]
- Park, M.; Kwon, O.; Park, J.H.; Lee, S.A.; Cha, E. Randomly changing leader-following consensus control for Markovian switching multi-agent systems with interval time-varying delays. Nonlinear Anal. Hybrid Syst. 2014, 12, 117–131. [Google Scholar] [CrossRef]
- Wen, G.; Duan, Z.; Chen, G.; Yu, W. Consensus tracking of multi-agent systems with Lipschitz-type node dynamics and switching topologies. IEEE Trans. Circuits Syst. I Regul. Pap. 2013, 61, 499–511. [Google Scholar] [CrossRef]
- Kim, J.M.; Park, J.B.; Choi, Y.H. Leaderless and leader-following consensus for heterogeneous multi-agent systems with random link failures. IET Control Theory Appl. 2014, 8, 51–60. [Google Scholar] [CrossRef]
- Song, C.; Cao, J.; Liu, Y. Robust consensus of fractional-order multi-agent systems with positive real uncertainty via second-order neighbors information. Neurocomputing 2015, 165, 293–299. [Google Scholar] [CrossRef]
- Wen, G.; Yu, Y.; Peng, Z.; Rahmani, A. Consensus tracking for second-order nonlinear multi-agent systems with switching topologies and a time-varying reference state. Int. J. Control 2016, 89, 2096–2106. [Google Scholar] [CrossRef]
- Liu, W.; Zhou, S.; Qi, Y.; Wu, X. Leaderless consensus of multi-agent systems with Lipschitz nonlinear dynamics and switching topologies. Neurocomputing 2016, 173, 1322–1329. [Google Scholar] [CrossRef]
- Wang, A. Event-based consensus control for single-integrator networks with communication time delays. Neurocomputing 2016, 173, 1715–1719. [Google Scholar] [CrossRef]
- Li, Y.; Yan, F.; Liu, W. Distributed consensus protocol for general third-order multi-agent systems with communication delay. In Proceedings of the 2019 Chinese Control And Decision Conference (CCDC), Nanchang, China, 3–5 June 2019; pp. 3436–3441. [Google Scholar]
- Tariverdi, A.; Talebi, H.A.; Shafiee, M. Fault-tolerant consensus of nonlinear multi-agent systems with directed link failures, communication noise and actuator faults. Int. J. Control. 2019, 94, 60–74. [Google Scholar] [CrossRef]
- Li, M.; Deng, F.; Ren, H. Scaled consensus of multi-agent systems with switching topologies and communication noises. Nonlinear Anal. Hybrid Syst. 2020, 36, 100839. [Google Scholar] [CrossRef]
- Li, M.; Deng, F. Necessary and Sufficient Conditions for Consensus of Continuous-Time Multiagent Systems with Markovian Switching Topologies and Communication Noises. IEEE Trans. Cybern. 2019, 50, 3264–3270. [Google Scholar] [CrossRef] [PubMed]
- Shang, Y. Consensus seeking over Markovian switching networks with time-varying delays and uncertain topologies. Appl. Math. Comput. 2016, 273, 1234–1245. [Google Scholar] [CrossRef]
- Zong, X.; Li, T.; Zhang, J.F. Consensus conditions of continuous-time multi-agent systems with time-delays and measurement noises. Automatica 2019, 99, 412–419. [Google Scholar] [CrossRef] [Green Version]
- Ming, P.; Liu, J.; Tan, S.; Li, S.; Shang, L.; Yu, X. Consensus stabilization in stochastic multi-agent systems with Markovian switching topology, noises and delay. Neurocomputing 2016, 200, 1–10. [Google Scholar] [CrossRef]
- Mondal, S.; Tsourdos, A. The consensus of non-linear agents under switching topology using dynamic inversion in the presence of communication noise and delay. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2021, 236, 352–367. [Google Scholar] [CrossRef]
- Altafini, C. Consensus problems on networks with antagonistic interactions. IEEE Trans. Autom. Control 2012, 58, 935–946. [Google Scholar] [CrossRef]
- Altafini, C.; Lini, G. Predictable dynamics of opinion forming for networks with antagonistic interactions. IEEE Trans. Autom. Control 2014, 60, 342–357. [Google Scholar] [CrossRef] [Green Version]
- Qin, J.; Fu, W.; Zheng, W.X.; Gao, H. On the bipartite consensus for generic linear multiagent systems with input saturation. IEEE Trans. Cybern. 2016, 47, 1948–1958. [Google Scholar] [CrossRef]
- Liu, M.; Wang, X.; Li, Z. Robust bipartite consensus and tracking control of high-order multiagent systems with matching uncertainties and antagonistic interactions. IEEE Trans. Syst. Man Cybern. Syst. 2018, 50, 2541–2550. [Google Scholar] [CrossRef]
- Hu, J.; Xiao, Z.; Zhou, Y.; Yu, J. Formation control over antagonistic networks. In Proceedings of the 32nd Chinese Control Conference, Xi’an, China, 26–28 July 2013; pp. 6879–6884. [Google Scholar]
- Li, H. H-infinity bipartite consensus of multi-agent systems with external disturbance and probabilistic actuator faults in signed networks. AIMS Math. 2022, 7, 2019–2043. [Google Scholar] [CrossRef]
- Hu, J.; Zheng, W.X. Bipartite consensus for multi-agent systems on directed signed networks. In Proceedings of the 52nd IEEE Conference on Decision and Control, Firenze, Italy, 10–13 December 2013; pp. 3451–3456. [Google Scholar]
- Valcher, M.E.; Misra, P. On the consensus and bipartite consensus in high-order multi-agent dynamical systems with antagonistic interactions. Syst. Control Lett. 2014, 66, 94–103. [Google Scholar] [CrossRef]
- Zhang, H.; Chen, J. Bipartite consensus of general linear multi-agent systems. In Proceedings of the 2014 American Control Conference, Portland, OR, USA, 4–6 June 2014; pp. 808–812. [Google Scholar]
- Meng, D.; Du, M.; Jia, Y. Interval bipartite consensus of networked agents associated with signed digraphs. IEEE Trans. Autom. Control 2016, 61, 3755–3770. [Google Scholar] [CrossRef]
- Cheng, M.; Zhang, H.; Jiang, Y. Output bipartite consensus of heterogeneous linear multi-agent systems. In Proceedings of the 2016 35th Chinese Control Conference (CCC), Chengdu, China, 27–29 July 2016; pp. 8287–8291. [Google Scholar]
- Zhang, H.; Chen, J. Bipartite consensus of multi-agent systems over signed graphs: State feedback and output feedback control approaches. Int. J. Robust Nonlinear Control 2017, 27, 3–14. [Google Scholar] [CrossRef]
- Bhowmick, S.; Panja, S. Leader–follower bipartite consensus of uncertain linear multiagent systems with external bounded disturbances over signed directed graph. IEEE Control Syst. Lett. 2019, 3, 595–600. [Google Scholar] [CrossRef]
- Yu, T.; Ma, L. Bipartite containment control of nonlinear multi-agent systems with input saturation. In Chinese Intelligent Systems Conference; Springer: Singapore, 2017; pp. 397–406. [Google Scholar]
- Li, H. Event-triggered bipartite consensus of multi-agent systems in signed networks. AIMS Math. 2022, 7, 5499–5526. [Google Scholar] [CrossRef]
- Liang, H.; Guo, X.; Pan, Y.; Huang, T. Event-triggered fuzzy bipartite tracking control for network systems based on distributed reduced-order observers (revised manuscript of TFS-2019-1049). IEEE Trans. Fuzzy Syst. 2020, 29, 1601–1614. [Google Scholar] [CrossRef]
- Wu, Y.; Pan, Y.; Chen, M.; Li, H. Quantized adaptive finite-time bipartite NN tracking control for stochastic multiagent systems. IEEE Trans. Cybern. 2020, 51, 2870–2881. [Google Scholar] [CrossRef]
- Wang, D.; Ma, H.; Liu, D. Distributed control algorithm for bipartite consensus of the nonlinear time-delayed multi-agent systems with neural networks. Neurocomputing 2016, 174, 928–936. [Google Scholar] [CrossRef]
- Zhai, S.; Li, Q. Practical bipartite synchronization via pinning control on a network of nonlinear agents with antagonistic interactions. Nonlinear Dyn. 2017, 87, 207–218. [Google Scholar] [CrossRef]
- Mondai, S.; Padhi, R. Formation Flying using GENEX and Differential geometric guidance law. IFAC-PapersOnLine 2015, 48, 19–24. [Google Scholar] [CrossRef]
- Ma, C.Q.; Qin, Z.Y. Bipartite consensus on networks of agents with antagonistic interactions and measurement noises. IET Control Theory Appl. 2016, 10, 2306–2313. [Google Scholar] [CrossRef]
- Hu, J.; Wu, Y.; Li, T.; Ghosh, B.K. Consensus control of general linear multiagent systems with antagonistic interactions and communication noises. IEEE Trans. Autom. Control 2018, 64, 2122–2127. [Google Scholar] [CrossRef]
- Ma, C.Q.; Xie, L. Necessary and sufficient conditions for leader-following bipartite consensus with measurement noise. IEEE Trans. Syst. Man Cybern. Syst. 2018, 50, 1976–1981. [Google Scholar] [CrossRef]
- Du, Y.; Wang, Y.; Zuo, Z.; Zhang, W. Stochastic bipartite consensus with measurement noises and antagonistic information. J. Frankl. Inst. 2021, 358, 7761–7785. [Google Scholar] [CrossRef]
- Wu, Y.; Liang, Q.; Zhao, Y.; Hu, J.; Xiang, L. Adaptive bipartite consensus control of general linear multi-agent systems using noisy measurements. Eur. J. Control 2021, 59, 123–128. [Google Scholar] [CrossRef]
- Cai, H.; Yuan, F.; Liang, H.; Zhou, Z. Mean Square Consensus under Coopetitive Social Networks with Communication Noise. In Proceedings of the 2021 40th Chinese Control Conference (CCC), Shanghai, China, 26–28 July 2021; pp. 800–805. [Google Scholar]
- Du, Y.; Wang, Y.; Zuo, Z. Bipartite consensus for multi-agent systems with noises over Markovian switching topologies. Neurocomputing 2021, 419, 295–305. [Google Scholar] [CrossRef]
- Harary, F. On the notion of balance of a signed graph. Mich. Math. J. 1953, 2, 143–146. [Google Scholar] [CrossRef]
- Wen, G.; Chen, C.P.; Liu, Y.J.; Liu, Z. Neural network-based adaptive leader-following consensus control for a class of nonlinear multiagent state-delay systems. IEEE Trans. Cybern. 2016, 47, 2151–2160. [Google Scholar] [CrossRef] [PubMed]
- Ren, C.E.; Chen, C.P. Sliding mode leader-following consensus controllers for second-order non-linear multi-agent systems. IET Control Theory Appl. 2015, 9, 1544–1552. [Google Scholar] [CrossRef]
- Lewis, F.L.; Zhang, H.; Hengster-Movric, K.; Das, A. Cooperative Control of Multi-Agent Systems: Optimal and Adaptive Design Approaches; Springer: London, UK, 2013. [Google Scholar]
- Hu, J.; Zheng, W.X. Emergent collective behaviors on coopetition networks. Phys. Lett. A 2014, 378, 1787–1796. [Google Scholar] [CrossRef]
- Ren, W.; Beard, R.W. Consensus seeking in multiagent systems under dynamically changing interaction topologies. IEEE Trans. Autom. Control 2005, 50, 655–661. [Google Scholar] [CrossRef]
- Ma, H.; Wang, Z.; Wang, D.; Liu, D.; Yan, P.; Wei, Q. Neural-network-based distributed adaptive robust control for a class of nonlinear multiagent systems with time delays and external noises. IEEE Trans. Syst. Man Cybern. Syst. 2015, 46, 750–758. [Google Scholar] [CrossRef]
- Ge, S.S.; Wang, C. Adaptive neural control of uncertain MIMO nonlinear systems. IEEE Trans. Neural Netw. 2004, 15, 674–692. [Google Scholar] [CrossRef]
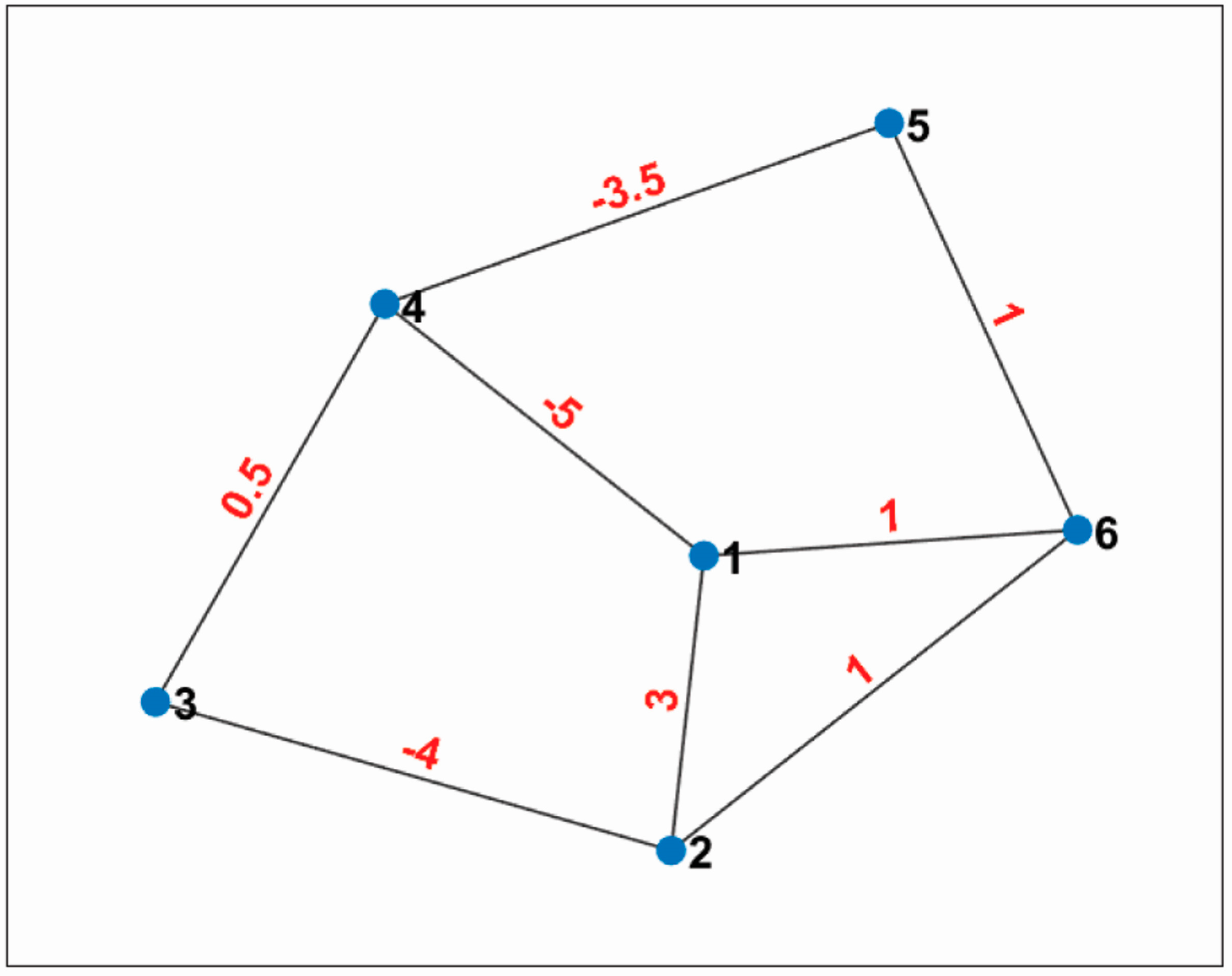
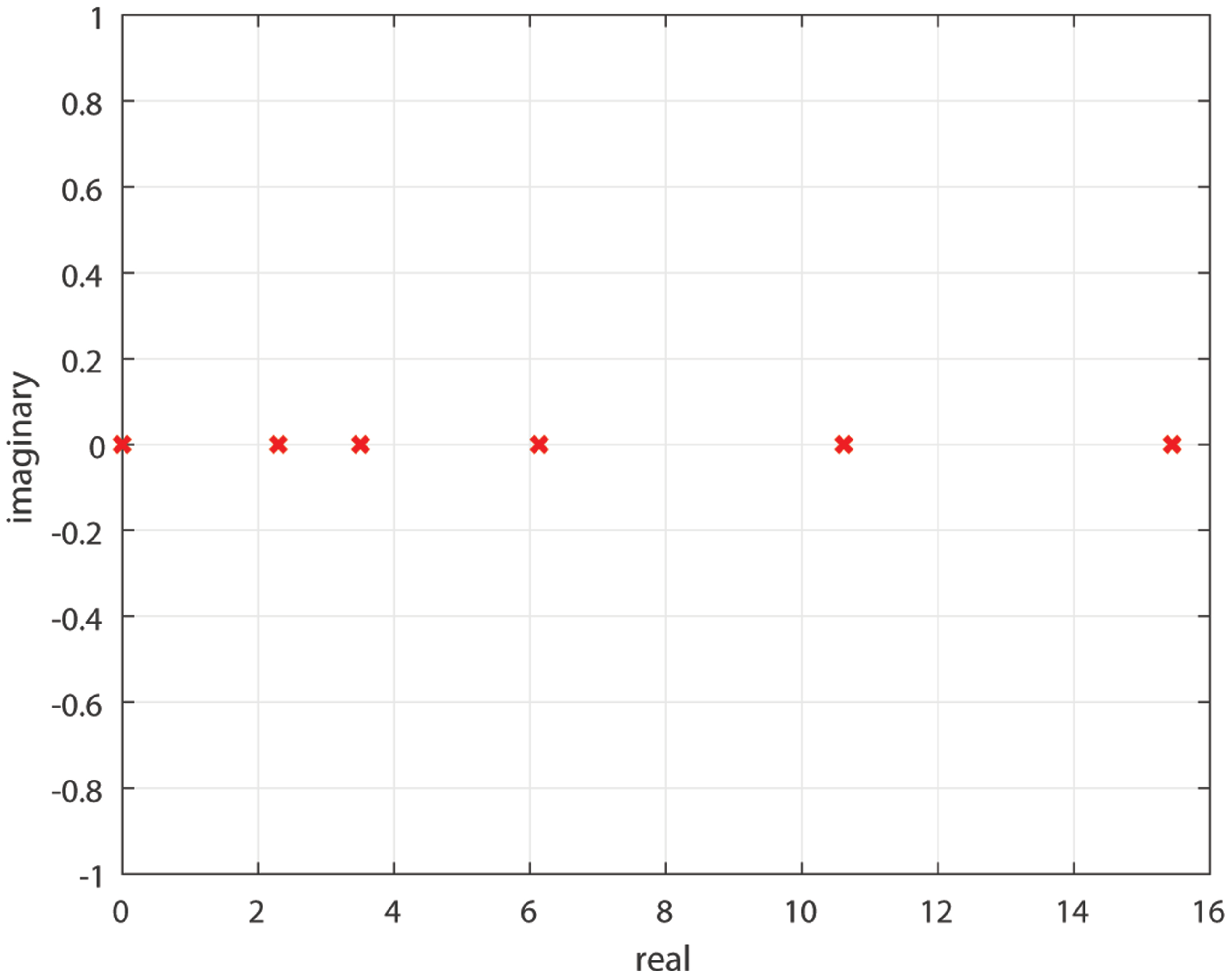

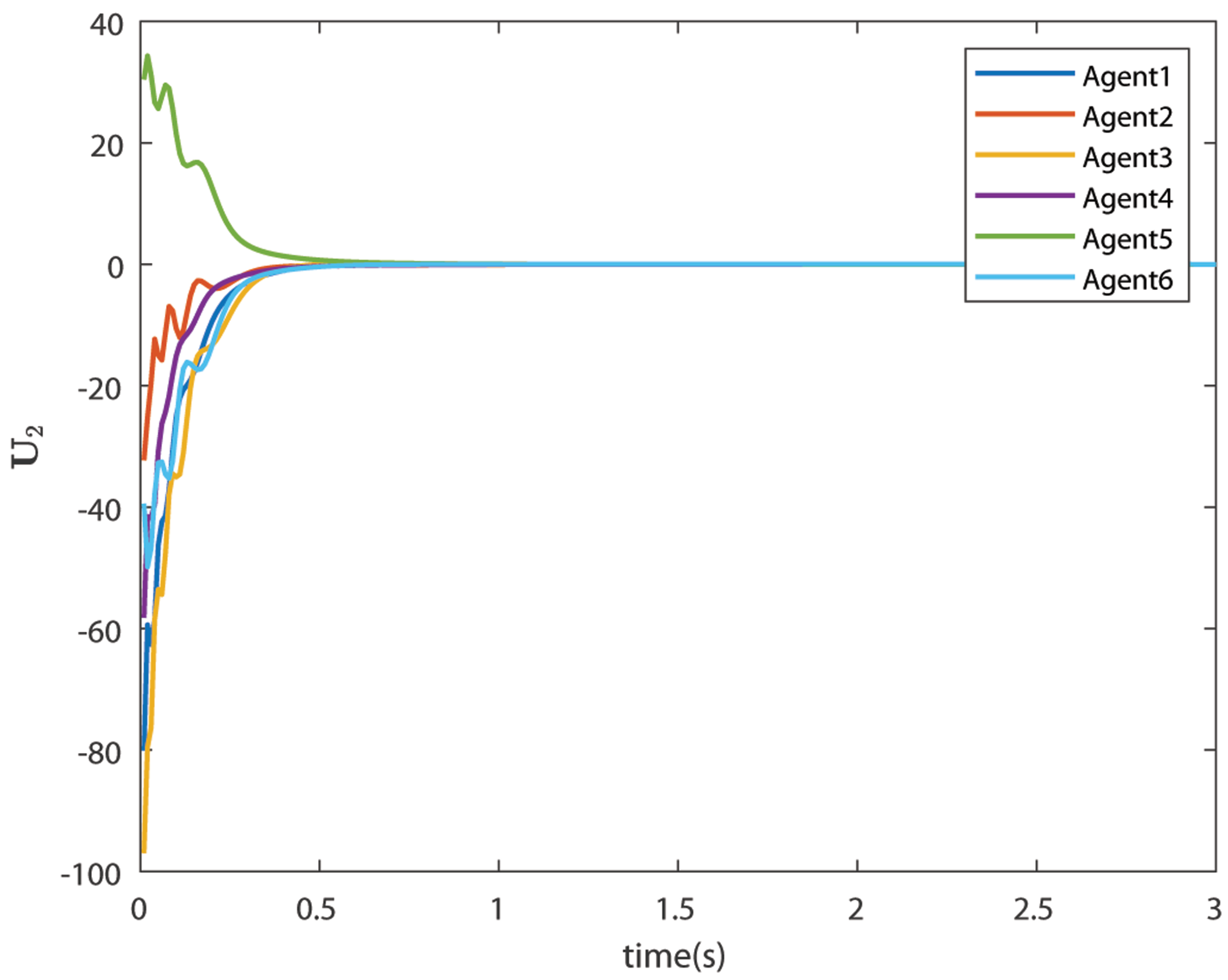
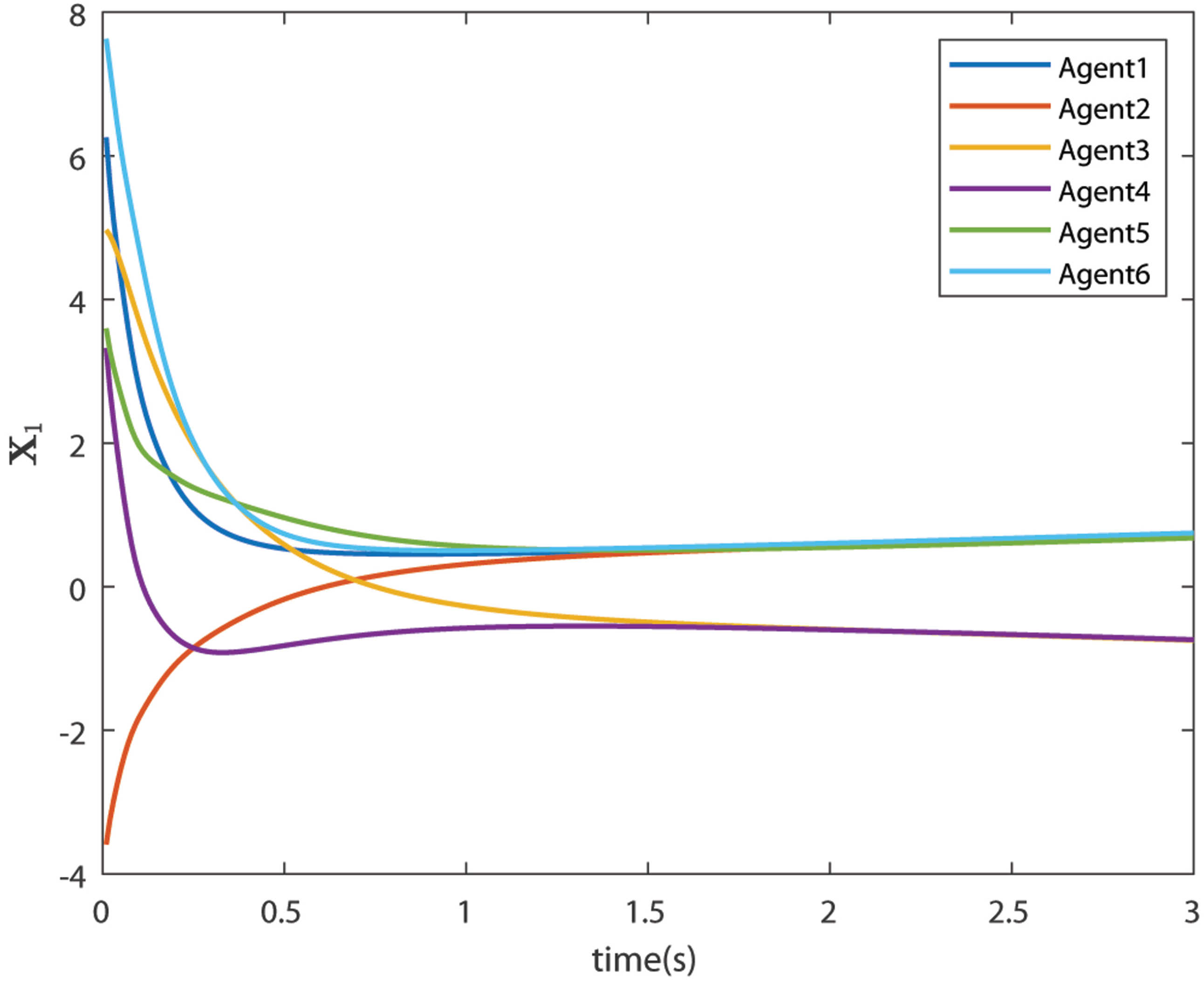


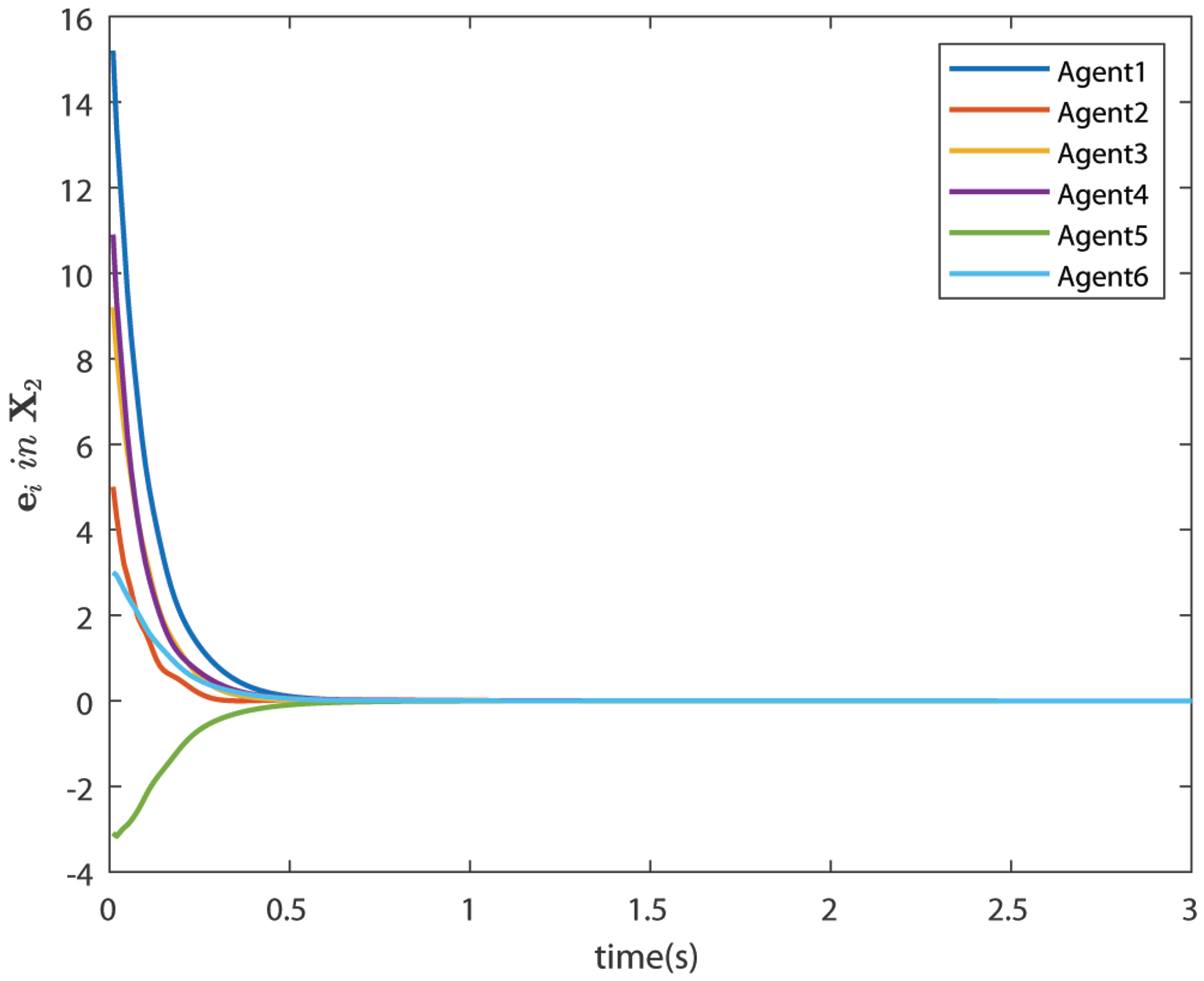
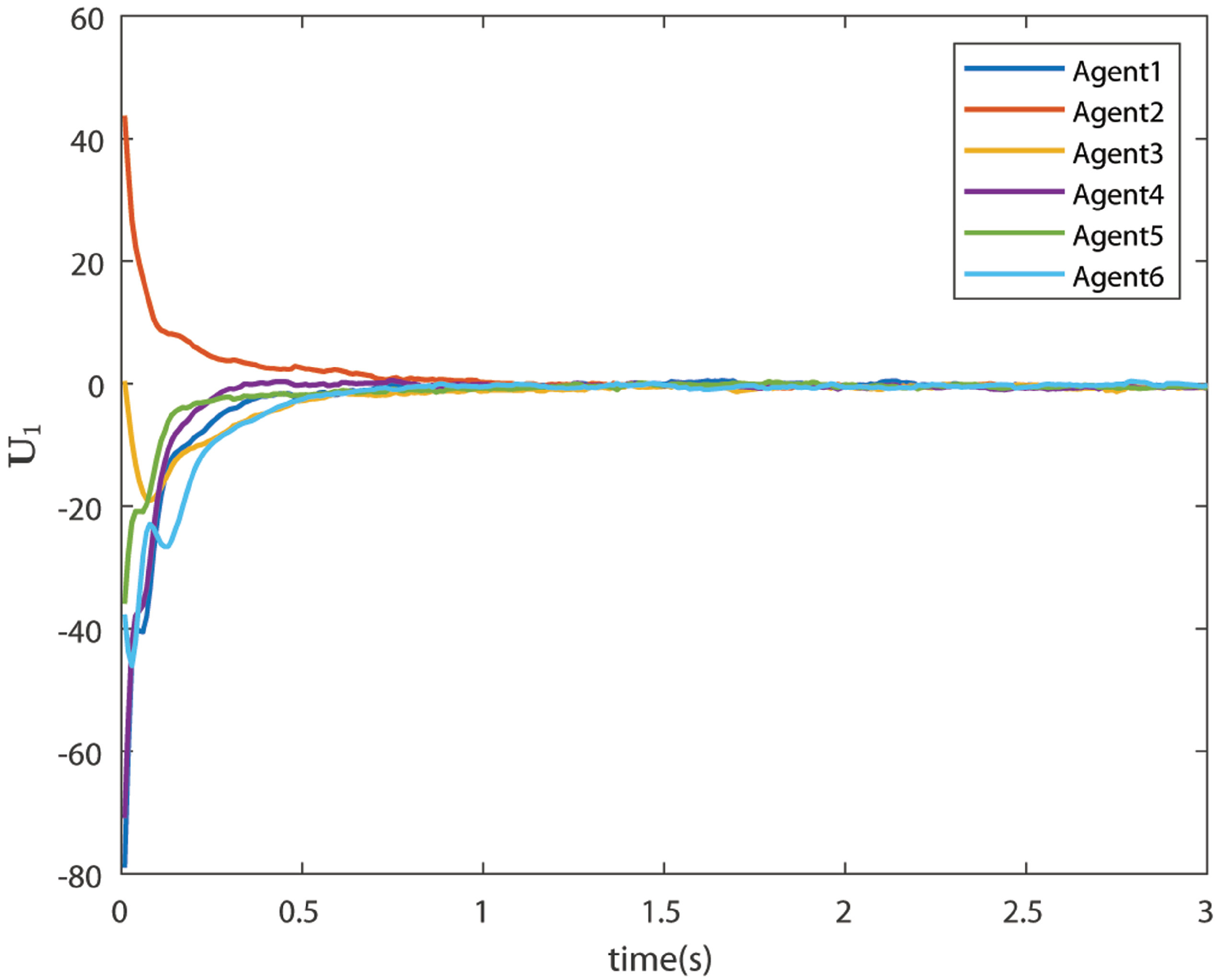
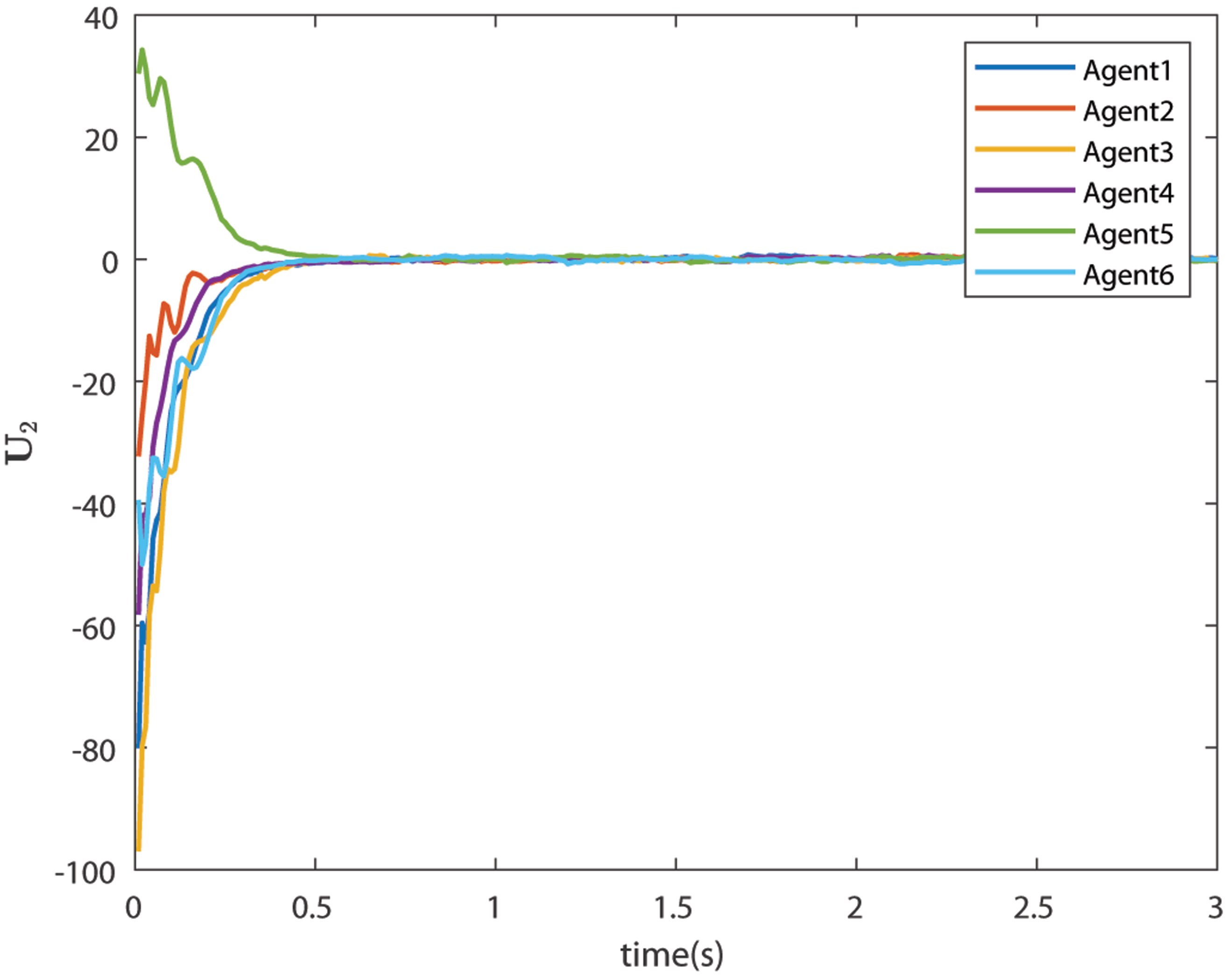


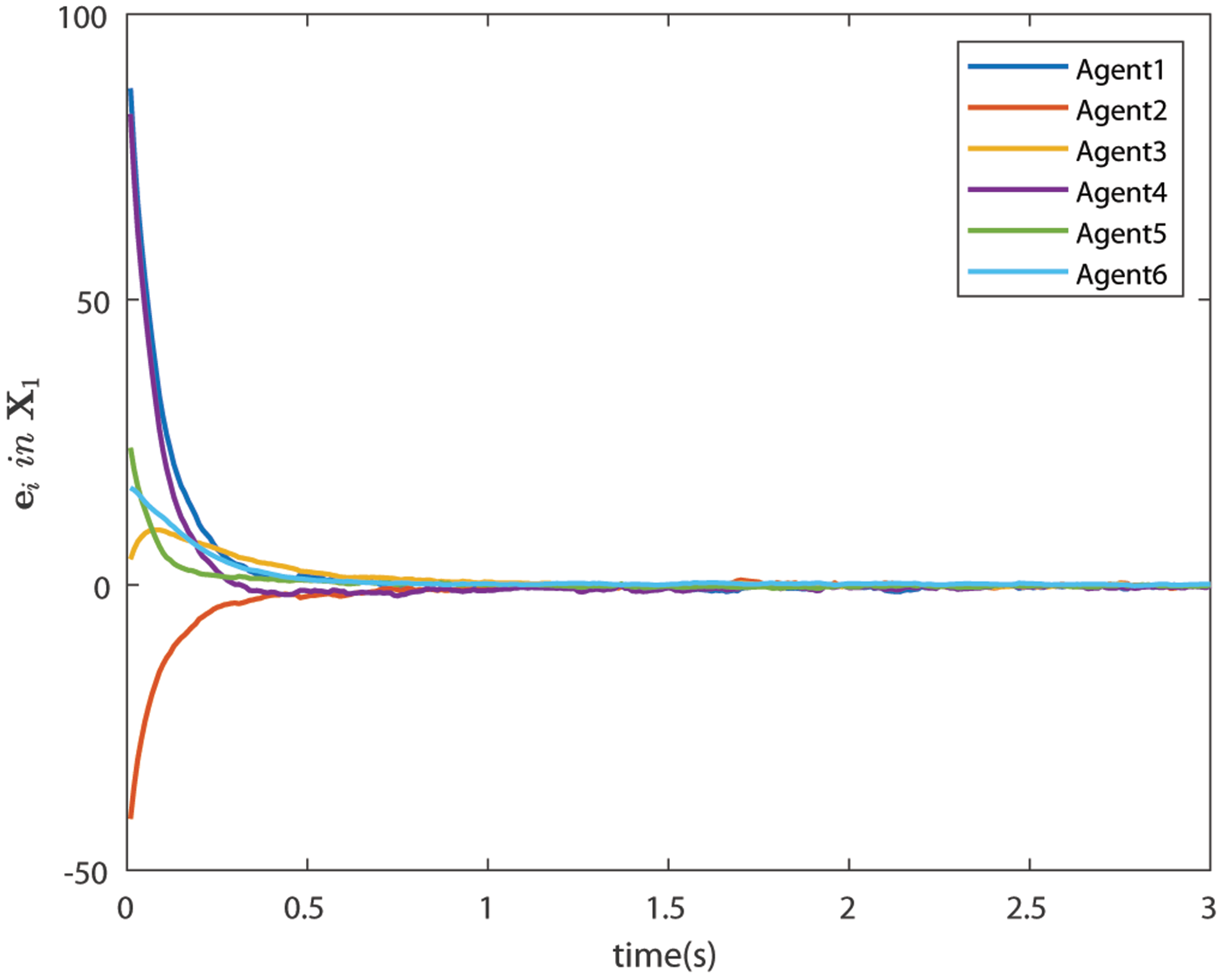
| Agents | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 6.25 | −3.6 | 5 | 3.3 | 3.6 | 7.6 | |
| 7.2 | 2.7 | 7 | 3.4 | −4.7 | 6.6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mondal, S.; Tsourdos, A. Bipartite Consensus of Nonlinear Agents in the Presence of Communication Noise. Sensors 2022, 22, 2357. https://doi.org/10.3390/s22062357
Mondal S, Tsourdos A. Bipartite Consensus of Nonlinear Agents in the Presence of Communication Noise. Sensors. 2022; 22(6):2357. https://doi.org/10.3390/s22062357
Chicago/Turabian StyleMondal, Sabyasachi, and Antonios Tsourdos. 2022. "Bipartite Consensus of Nonlinear Agents in the Presence of Communication Noise" Sensors 22, no. 6: 2357. https://doi.org/10.3390/s22062357
APA StyleMondal, S., & Tsourdos, A. (2022). Bipartite Consensus of Nonlinear Agents in the Presence of Communication Noise. Sensors, 22(6), 2357. https://doi.org/10.3390/s22062357






