A Kalman Filter Approach for Estimating Tendon Wave Speed from Skin-Mounted Accelerometers
Abstract
:1. Introduction
2. Materials and Methods
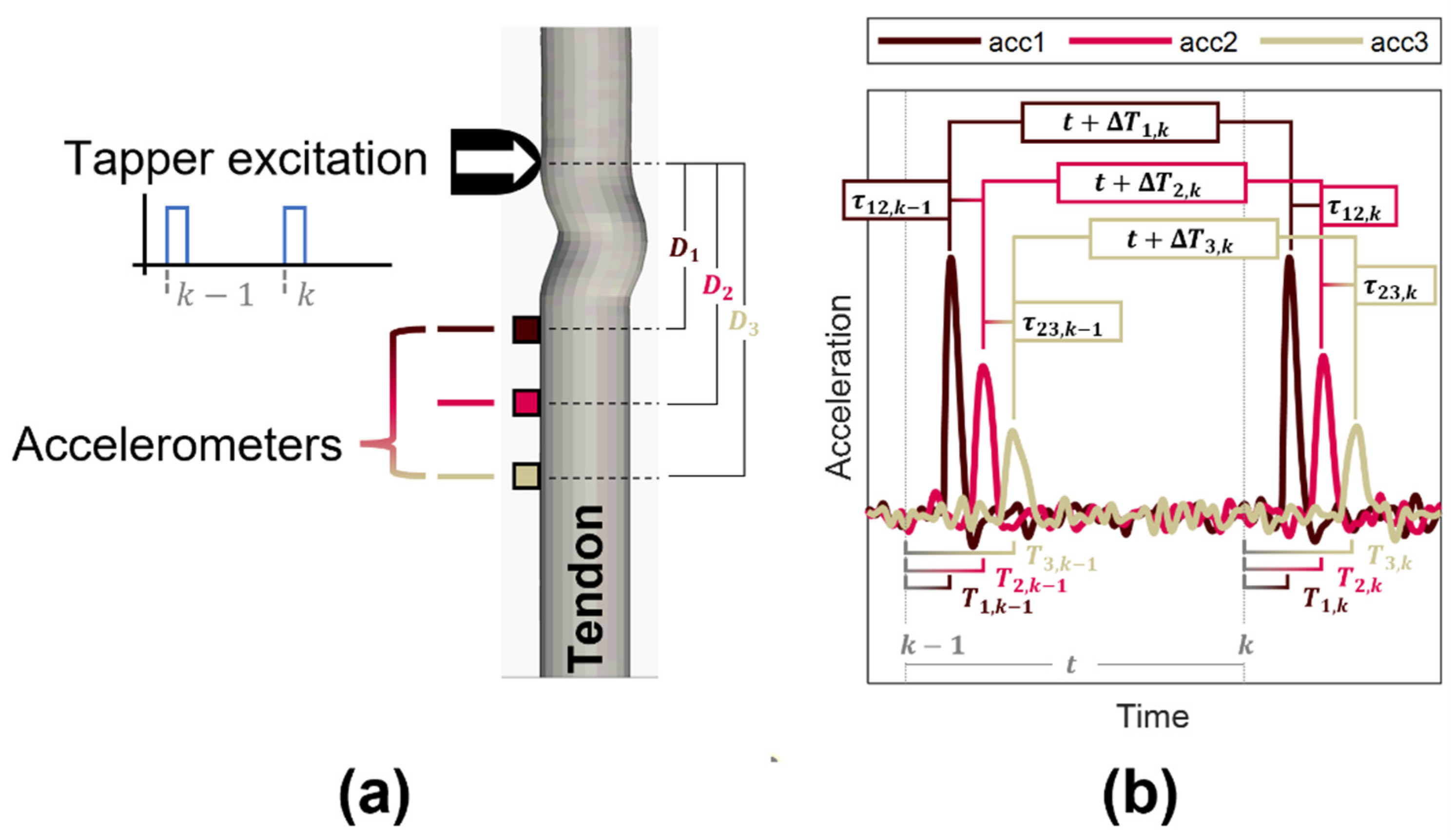
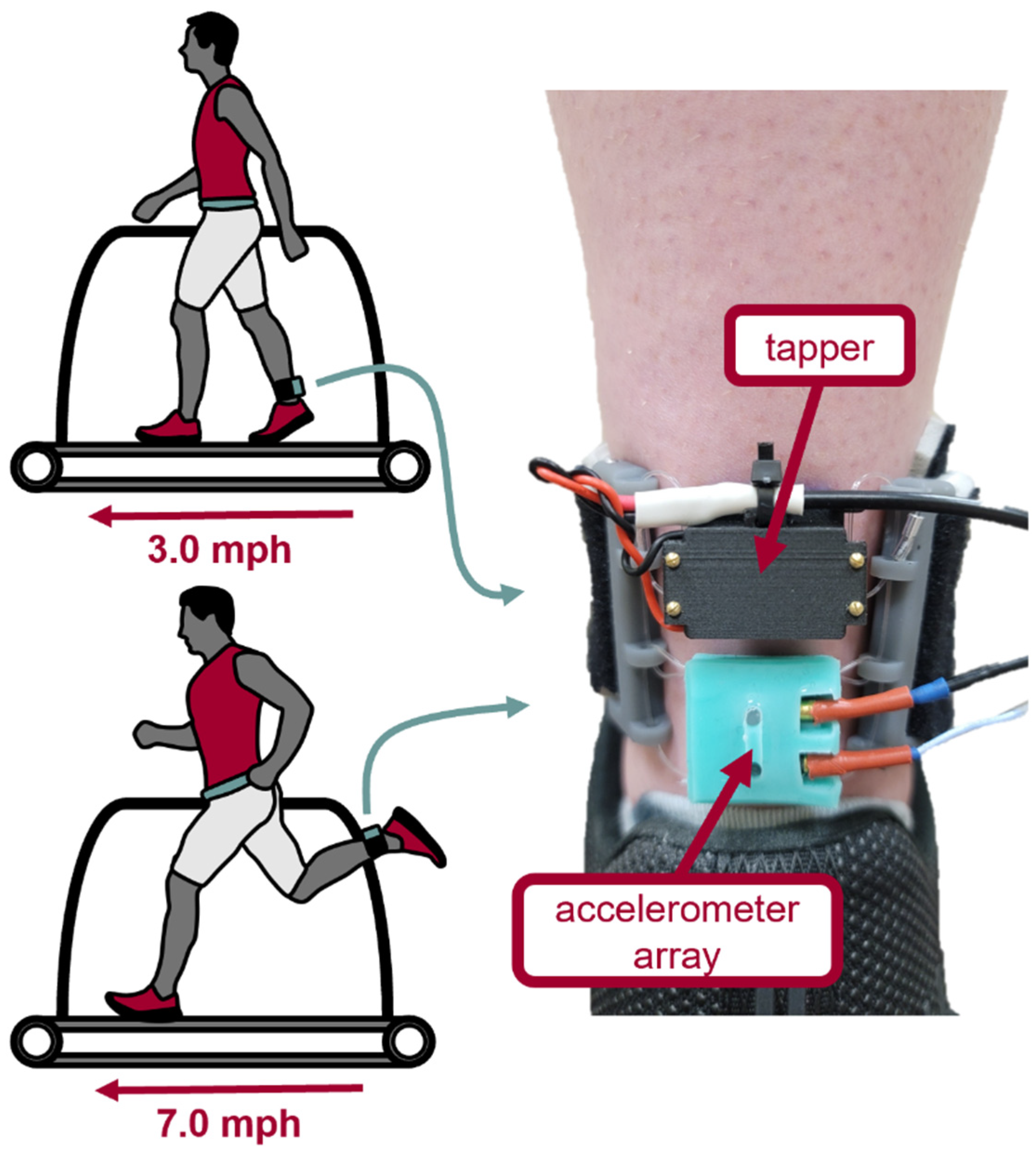
2.1. Shear Wave Tensiometer
2.2. Wave Travel Times
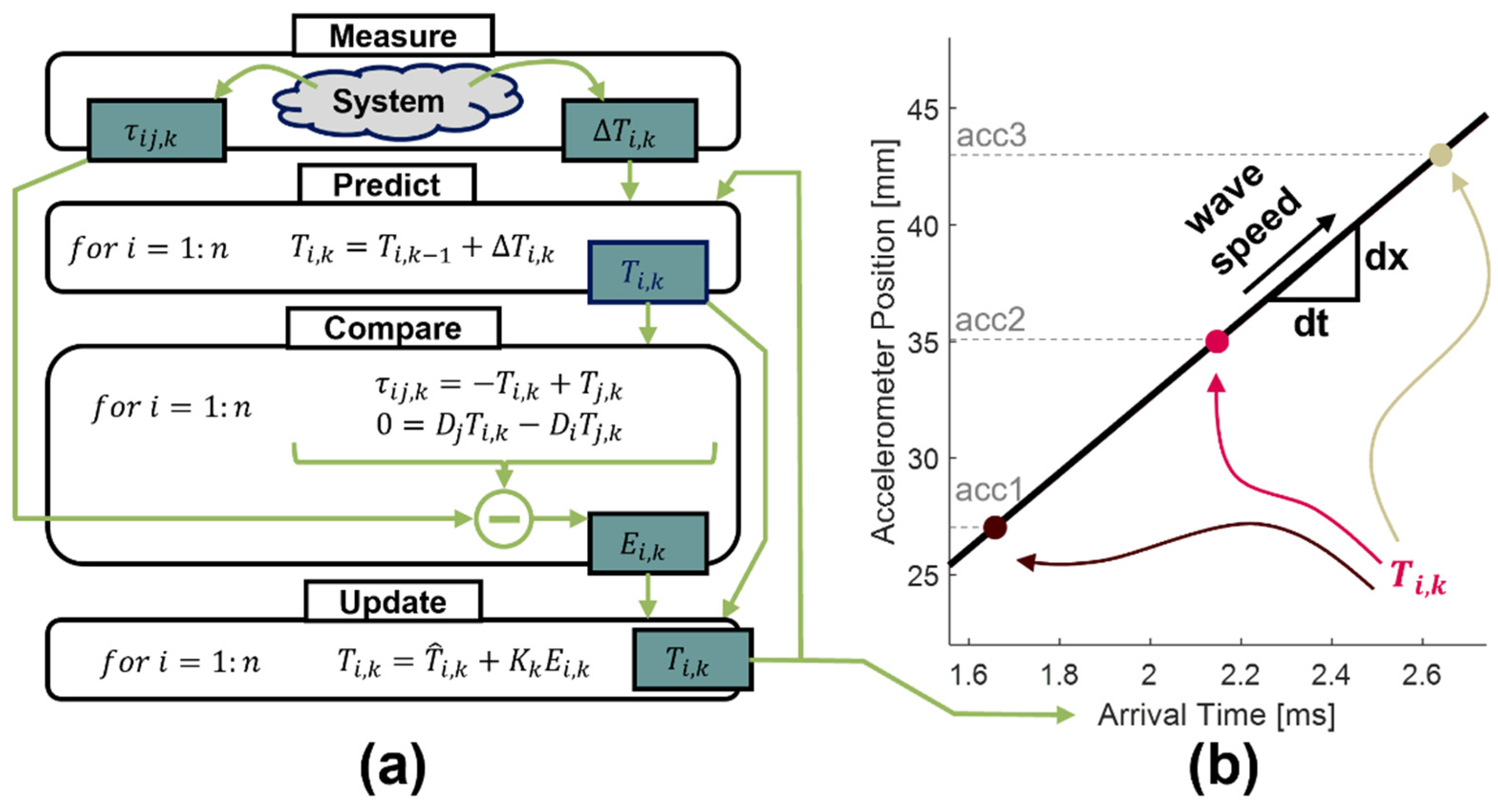
2.3. Kalman Filter
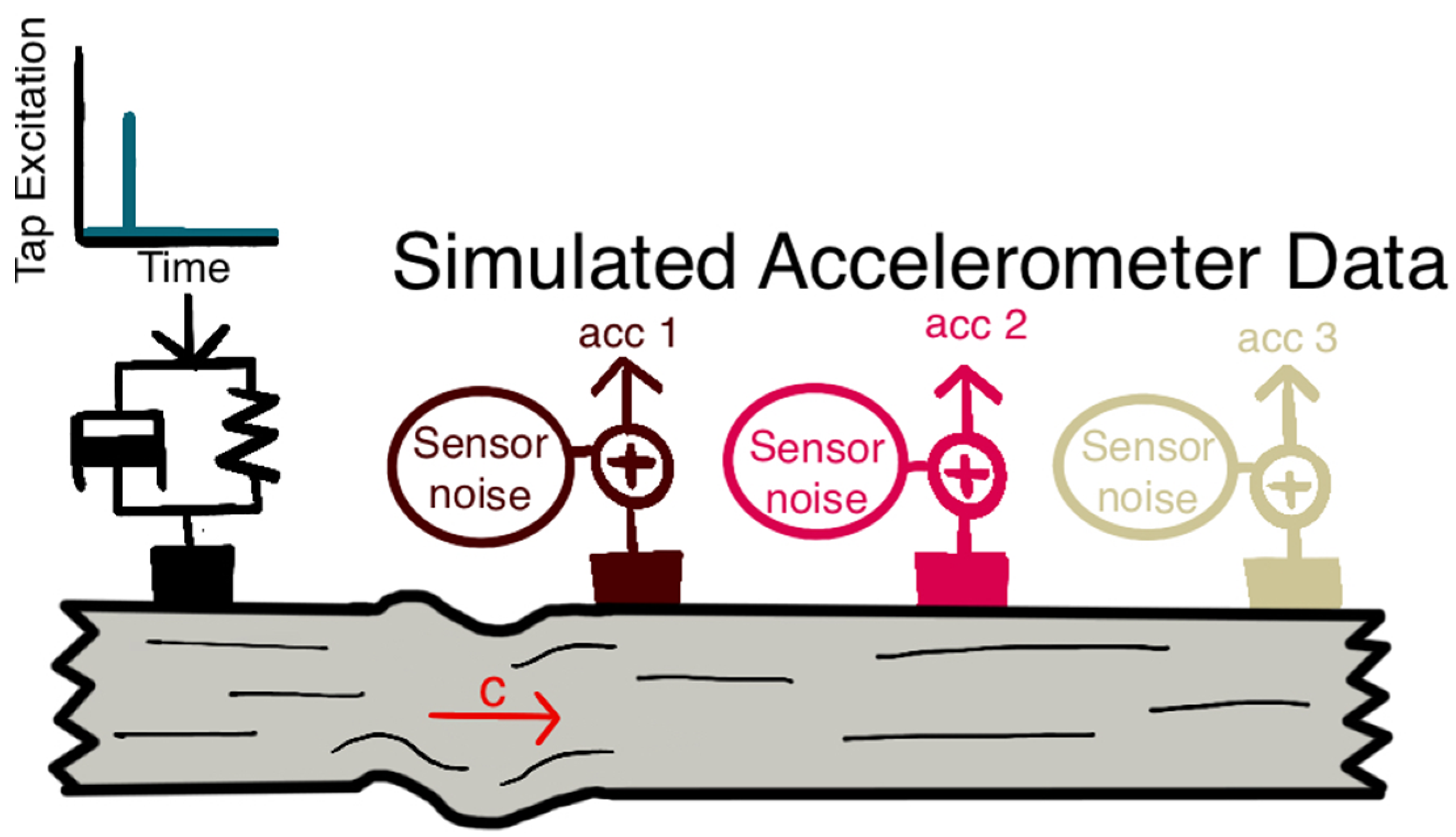
2.4. Shear Wave Tensiometry Simulations
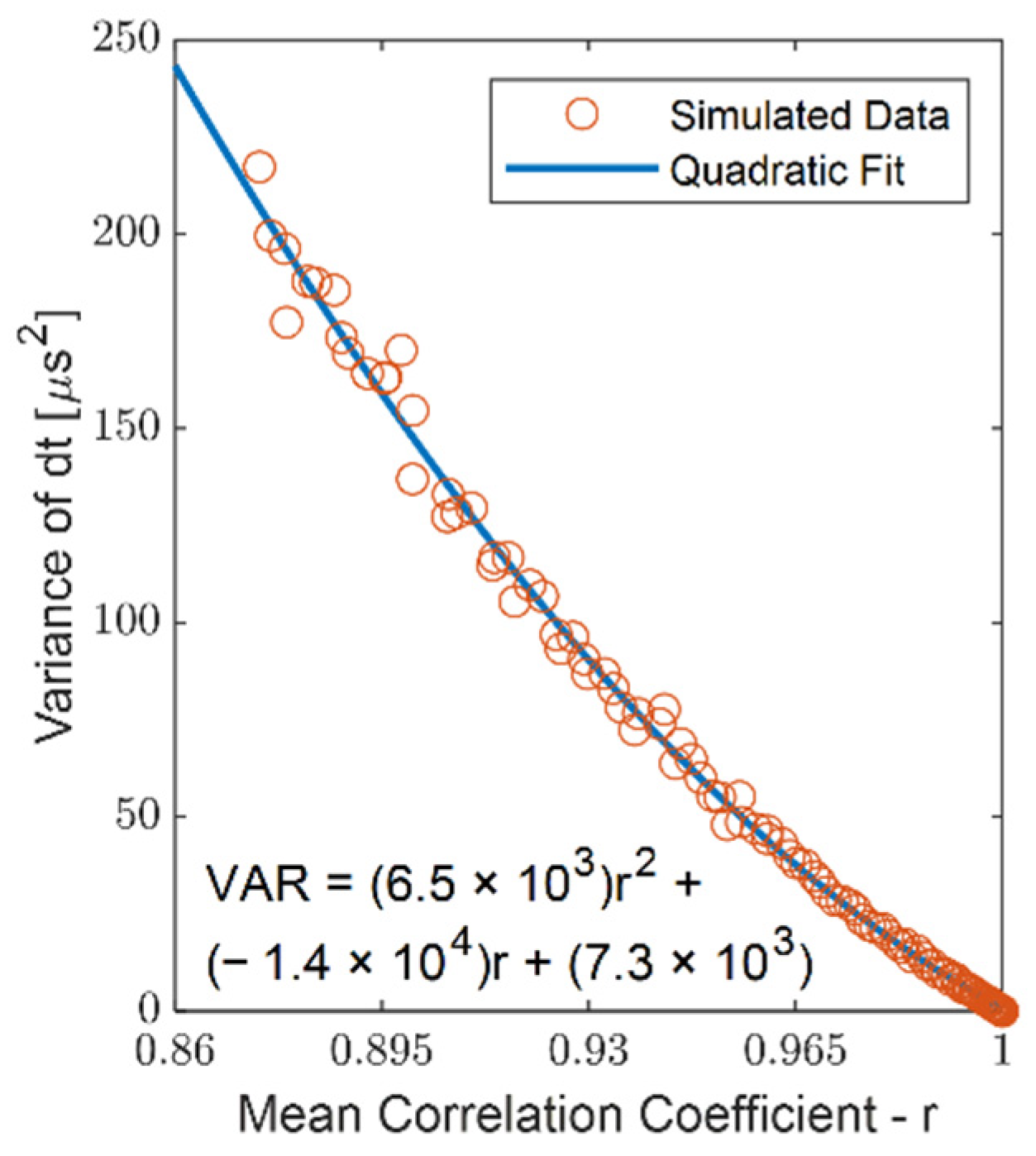
2.5. Noise Covariance
2.6. Tensiometry Simulations during Gait
2.7. Experimental Protocol
3. Results
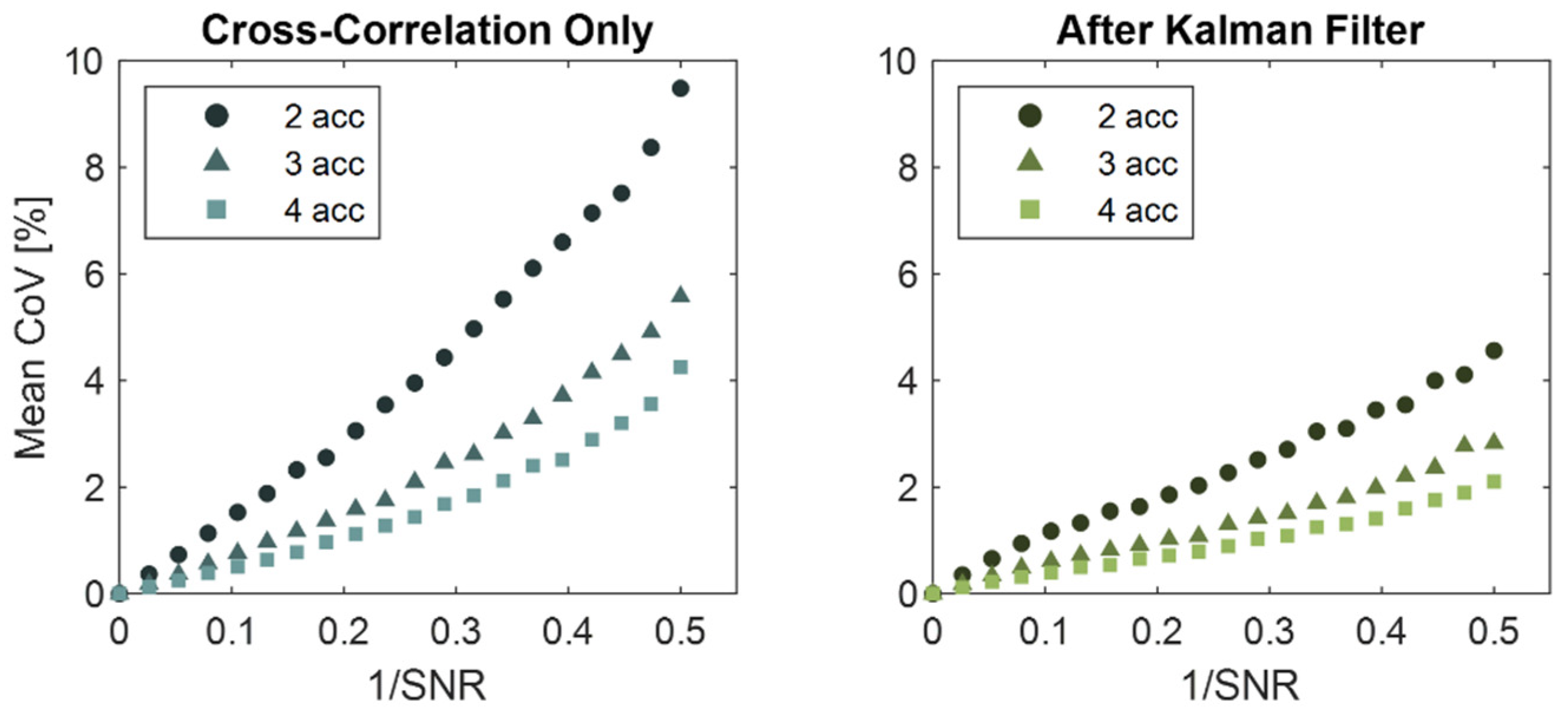
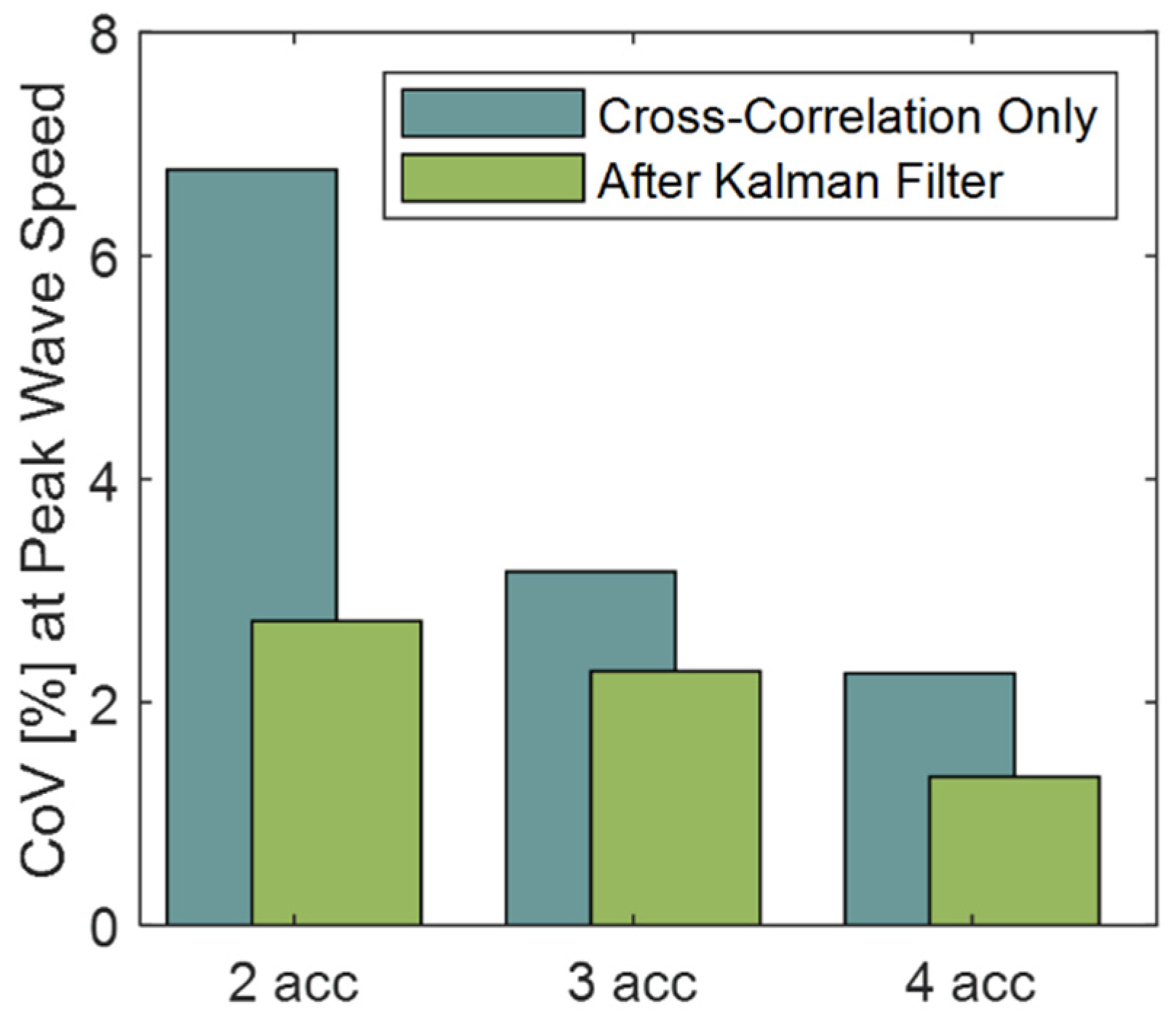
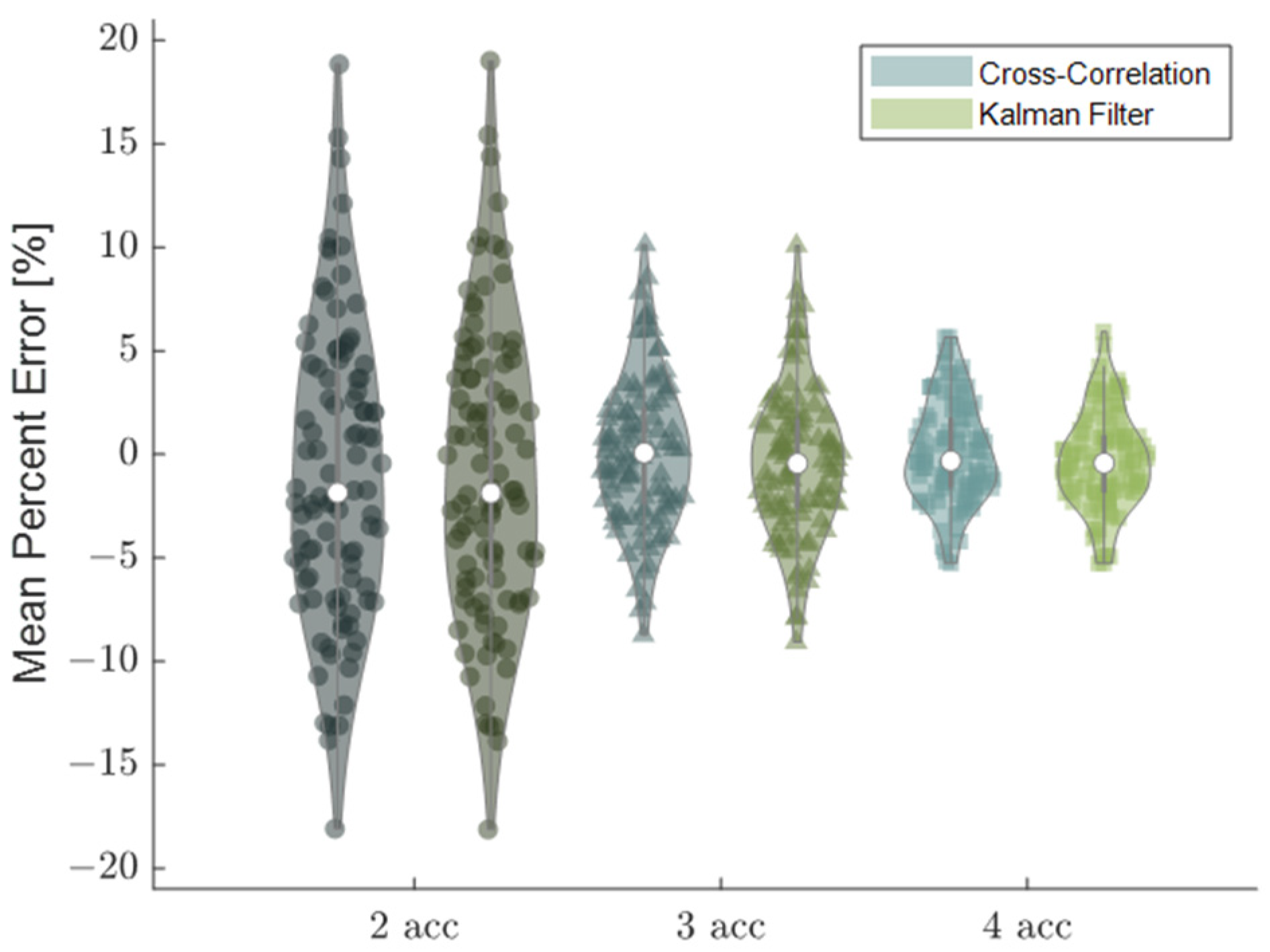
3.1. Sensor Noise
3.2. Sensor Position
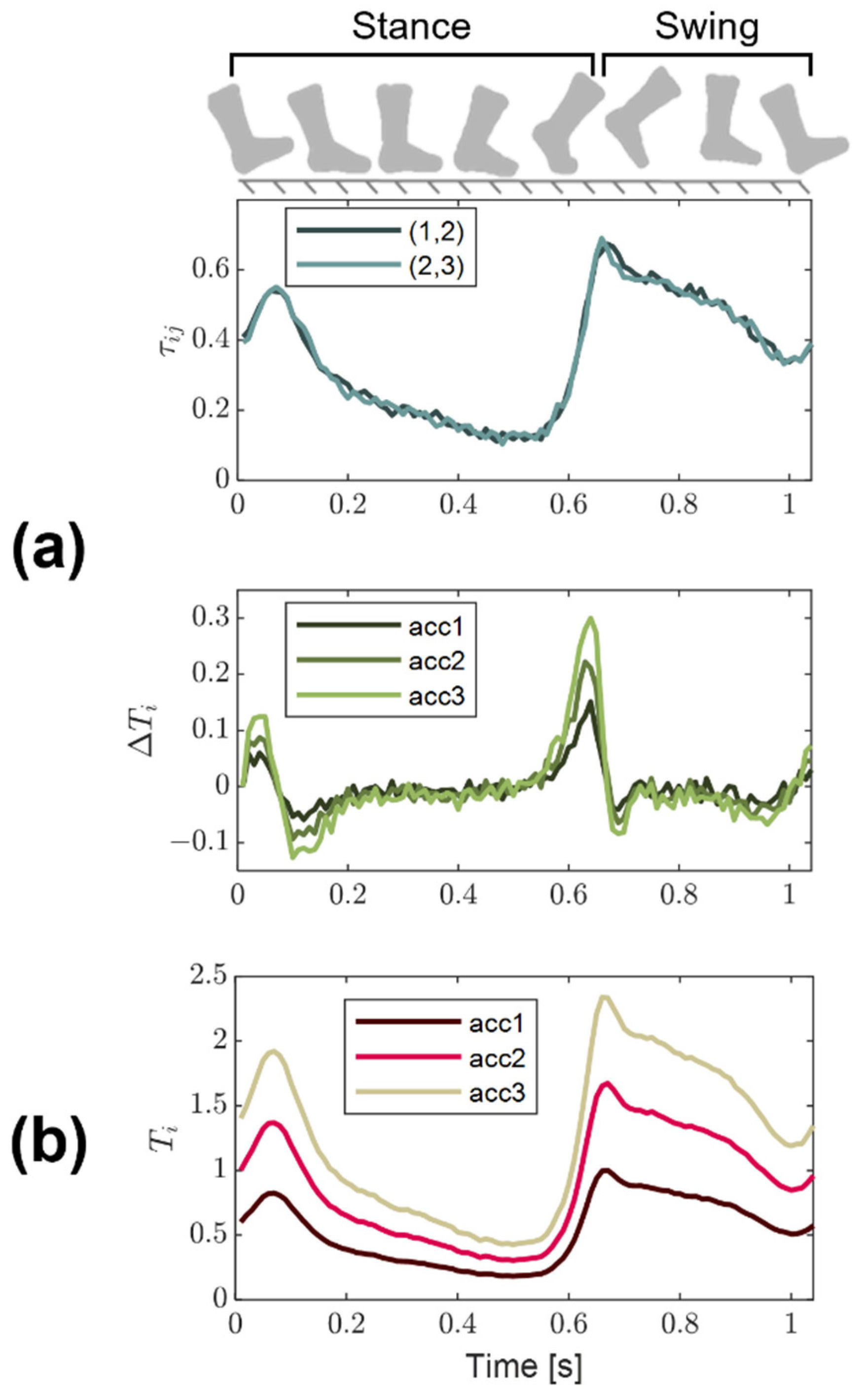
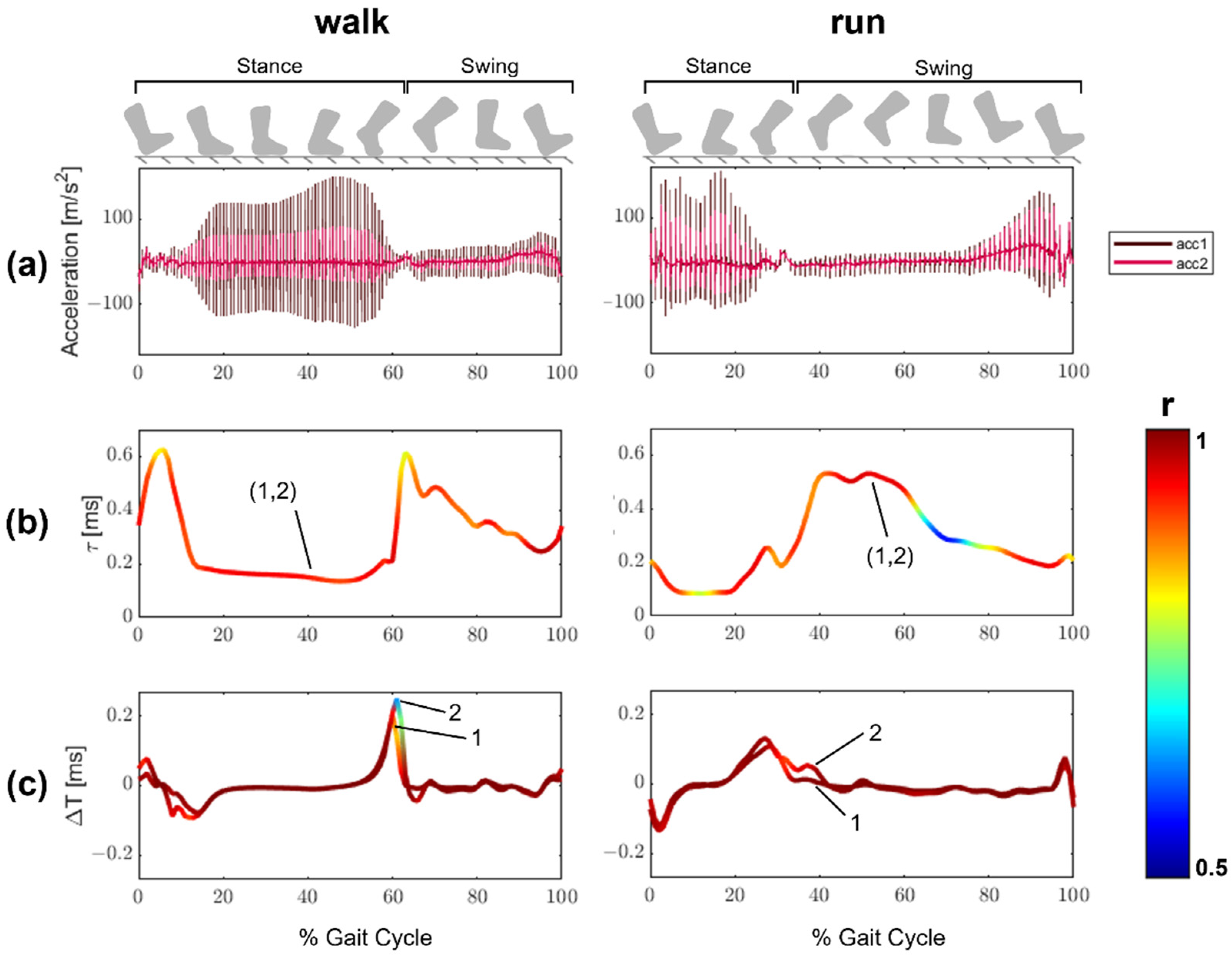
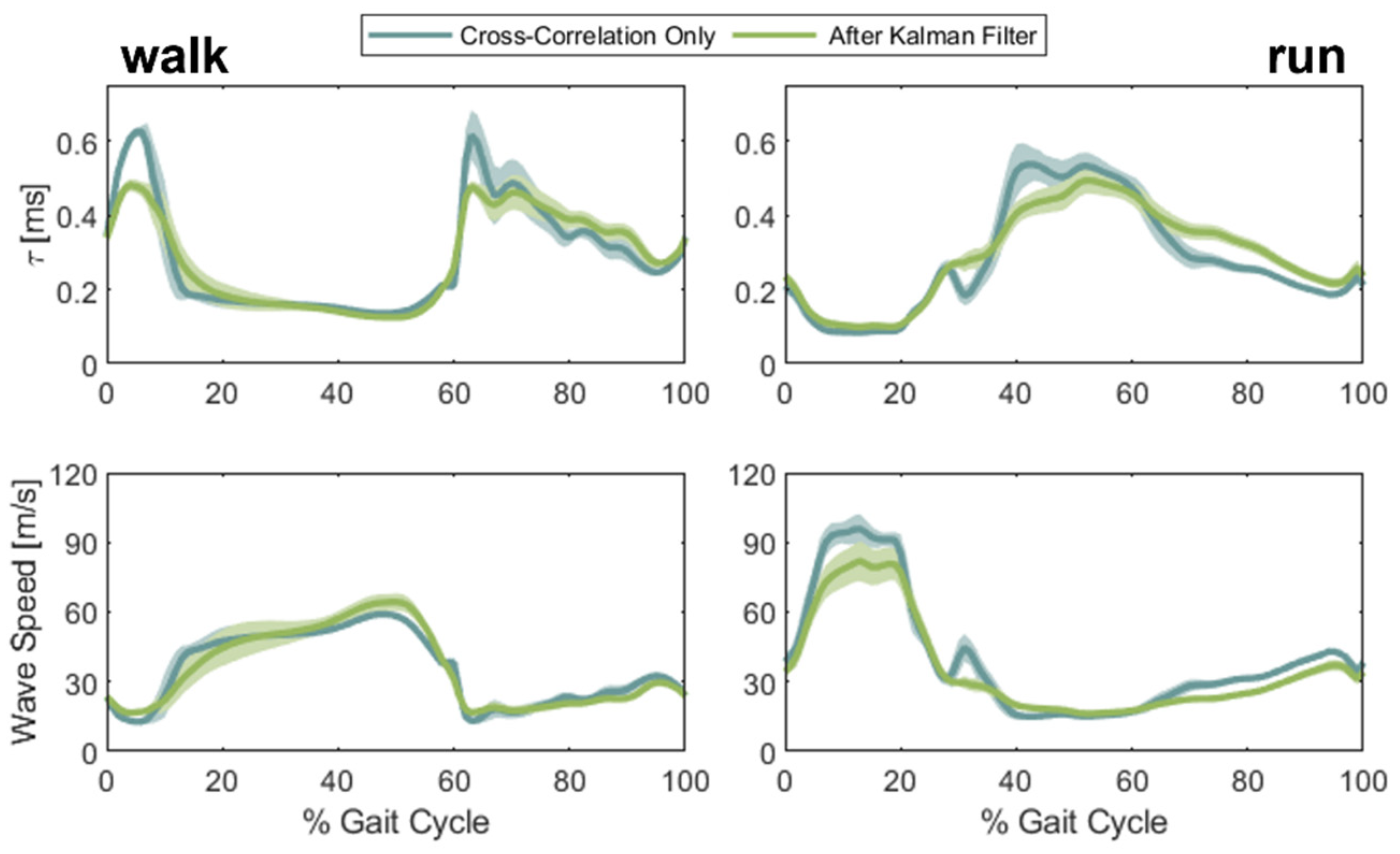
3.3. In Vivo Tensiometry
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Martin, J.A.; Brandon, S.C.E.; Keuler, E.M.; Hermus, J.R.; Ehlers, A.C.; Segalman, D.J.; Allen, M.S.; Thelen, D.G. Gauging force by tapping tendons. Nat. Commun. 2018, 9, 1592. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ebrahimi, A.; Martin, J.A.; Schmitz, D.G.; Thelen, D.G. Shear Wave Tensiometry Reveals an Age-Related Deficit in Triceps Surae Work at Slow and Fast Walking Speeds. Front. Sports Act. Living 2020, 2, 69. [Google Scholar] [CrossRef] [PubMed]
- Harper, S.E.; Roembke, R.A.; Zunker, J.D.; Thelen, D.G.; Adamczyk, P.G. Wearable Tendon Kinetics. Sensors 2020, 20, 4805. [Google Scholar] [CrossRef] [PubMed]
- Keuler, E.M.; Loegering, I.F.; Martin, J.A.; Roth, J.D.; Thelen, D.G. Shear Wave Predictions of Achilles Tendon Loading during Human Walking. Sci. Rep. 2019, 9, 13419. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Palmeri, M.; Wang, M.; Dahl, J.; Frinkley, K.; Nightingale, K. Quantifying Hepatic Shear Modulus In Vivo Using Acoustic Radiation Force. Ultrasound Med. Biol. 2008, 34, 546–558. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Brum, J.; Bernal, M.; Gennisson, J.L.; Tanter, M. In vivo evaluation of the elastic anisotropy of the human Achilles tendon using shear wave dispersion analysis. Phys. Med. Biol. 2014, 59, 505–523. [Google Scholar] [CrossRef] [PubMed]
- Cortes, D.H.; Suydam, S.M.; Silbernagel, K.G.; Buchanan, T.S.; Elliott, D.M. Continuous Shear Wave Elastography: A New Method to Measure Viscoelastic Properties of Tendons in Vivo. Ultrasound Med. Biol. 2015, 41, 1518–1529. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Deffieux, T.; Gennisson, J.-L.; Larrat, B.; Fink, M.; Tanter, M. The variance of quantitative estimates in shear wave imaging: Theory and experiments. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2012, 59, 2390–2410. [Google Scholar] [CrossRef] [PubMed]
- Elegbe, E.C.; McAleavey, S. Single Tracking Location Methods Suppress Speckle Noise in Shear Wave Velocity Estimation. Ultrason. Imaging 2013, 35, 109–125. [Google Scholar] [CrossRef] [PubMed]
- Eby, S.; Song, P.; Chen, S.; Chen, Q.; Greenleaf, J.F.; An, K.-N. Validation of shear wave elastography in skeletal muscle. J. Biomech. 2013, 46, 2381–2387. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Taljanovic, M.S.; Gimber, L.H.; Becker, G.W.; Latt, L.D.; Klauser, A.S.; Melville, D.M.; Gao, L.; Witte, R.S. Shear-Wave Elastography: Basic Physics and Musculoskeletal Applications. RadioGraphics 2017, 37, 855–870. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Corrigan, P.; Zellers, J.A.; Balascio, P.; Silbernagel, K.G.; Cortes, D.H. Quantification of Mechanical Properties in Healthy Achilles Tendon Using Continuous Shear Wave Elas-tography: A Reliability and Validation Study. Ultrasound Med. Biol. 2019, 45, 1574–1585. [Google Scholar] [CrossRef] [PubMed]
- Slane, L.C.; Martin, J.A.; DeWall, R.; Thelen, D.; Lee, K. Quantitative ultrasound mapping of regional variations in shear wave speeds of the aging Achilles tendon. Eur. Radiol. 2017, 27, 474–482. [Google Scholar] [CrossRef]
- Kalman, R.E. A New Approach to Linear Filtering and Prediction Problems. J. Basic Eng. 1960, 82, 35–45. [Google Scholar] [CrossRef] [Green Version]
- Welch, G.; Bishop, G. An Introduction to the Kalman Filter; Univ. of North Carolina: Chapel Hill, NC, USA, 1995. [Google Scholar]
- Cespedes, I.; Huang, Y.; Ophir, J.; Spratt, S. Methods for estimation of subsample time delays of digitized echo signals. Ultrason. Imaging 1995, 17, 142–171. [Google Scholar] [CrossRef]
- Greenleaf, J.F.; Zheng, Y.; Yao, A.; Chen, S. 6G-4 Measurement of Shear Wave Using Ultrasound and Kalman Filter with Large Background Motion for Cardiovascular Studies. In Proceedings of the 2007 IEEE Ultrasonics Symposium Proceedings, Vancouver, BC, Canada, 2–6 October 2006; pp. 718–721. [Google Scholar]
- Quang-Huy, T.; Doan, P.T.; Yen, N.T.H.; Tran, D.-T. Shear wave imaging and classification using extended Kalman filter and decision tree algorithm. Math. Biosci. Eng. 2021, 18, 7631–7647. [Google Scholar] [CrossRef]
- Zheng, Y.; Chen, S.; Tan, W.; Kinnick, R.; Greenleaf, J.F. Detection of tissue harmonic motion induced by ultrasonic radiation force using pulse-echo ultrasound and kalman filter. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2007, 54, 290–300. [Google Scholar] [CrossRef] [PubMed]
- Zheng, Y.; Chen, S.; Zhang, X.; Greenleaf, J.F. Detection of shear wave propagation in an artery using pulse echo ultrasound and Kalman filtering. In Proceedings of the IEEE Ultrasonics Symposium, Montreal, QC, Canada, 23–27 August 2004; pp. 1251–1253. [Google Scholar]
- Wu, S.; Gao, Z.; Liu, Z.; Luo, J.; Zhang, H.; Li, S. Direct Reconstruction of Ultrasound Elastography Using an End-to-End Deep Neural Network. In Swarm, Evolutionary, and Memetic Computing; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Blank, J.L.; Thelen, D.G.; Allen, M.S.; Roth, J.D. Sensitivity of the shear wave speed-stress relationship to soft tissue material properties and fiber alignment. J. Mech. Behav. Biomed. Mater. 2021, 125, 104964. [Google Scholar] [CrossRef] [PubMed]
- Blank, J.L.; Thelen, D.G.; Roth, J.D. Ligament Shear Wave Speeds Are Sensitive to Tensiometer-Tissue Interactions: A Parametric Modeling Study. In International Symposium on Computer Methods in Biomechanics and Biomedical Engineering; Proceedings of the Selected Papers from the 16th International Symposium CMBBE and 4th Conference on Imaging and Visualization, New York, NY, USA, 14–16 August 2019; Springer: Cham, Switzerland, 2019. [Google Scholar]
- Helfenstein-Didier, C.; Andrade, R.J.; Brum, J.; Hug, F.; Tanter, M.; Nordez, A.; Gennisson, J.L. In vivo quantification of the shear modulus of the human Achilles tendon during passive loading using shear wave dispersion analysis. Phys. Med. Biol. 2016, 61, 2485. [Google Scholar] [CrossRef] [Green Version]
- Lee, D.H.; Lee, J.Y.; Bae, J.S.; Yi, N.J.; Lee, K.W.; Suh, K.S.; Kim, H.; Lee, K.B.; Han, J.K. Shear-wave dispersion slope from US shear-wave elastography: Detection of allograft damage after liver transplantation. Radiology 2019, 293, 327–333. [Google Scholar] [CrossRef]
- Urban, M.W.; Chen, J.; Ehman, R.L. Comparison of shear velocity dispersion in viscoelastic phantoms measured by ultra-sound-based shear wave elastography and magnetic resonance elastography. In Proceedings of the 2017 IEEE International Ultrasonics Symposium (IUS), Washington, DC, USA, 2 November 2017. [Google Scholar]
- Mahan, J.; Damodar, D.; Trapana, E.; Barnhill, S.; Nuno, A.U.; Smyth, N.A.; Aiyer, A.; Jose, J. Achilles tendon complex: The anatomy of its insertional footprint on the calcaneus and clinical implications. J. Orthop. 2020, 17, 221–227. [Google Scholar] [CrossRef] [PubMed]
- Martin, J.A.; Thelen, D.G. A Trained Neural Network Model Accurately Predicts Achilles Stress from Shear Wave Propagation. In Proceedings of the 45th Annual Meeting of the American Society of Biomechanics, Virtual Meeting, 13 August 2021. [Google Scholar]
- Blank, J.L.; Thelen, D.G.; Roth, J.D. Shear wave speeds track axial stress in porcine collateral ligaments. J. Mech. Behav. Biomed. Mater. 2020, 105, 103704. [Google Scholar] [CrossRef] [PubMed]
- Ebrahimi, A.; Schwartz, M.H.; Martin, J.A.; Novacheck, T.F.; Thelen, D.G. Atypical triceps surae force and work patterns underlying gait in children with cerebral palsy. J. Orthop. Res. 2022. [Google Scholar] [CrossRef] [PubMed]
| Amplitude of measurement | 20 m/s2 |
| Sample rate | 50,000 Hz |
| Accelerometer locations (relative to excitation) | [15, 25, 35, 45] mm |
| Damping ratio 1 | 0.5 (0.05) |
| Natural frequency of oscillation 1 | 1600 (100) Hz |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schmitz, D.G.; Thelen, D.G.; Cone, S.G. A Kalman Filter Approach for Estimating Tendon Wave Speed from Skin-Mounted Accelerometers. Sensors 2022, 22, 2283. https://doi.org/10.3390/s22062283
Schmitz DG, Thelen DG, Cone SG. A Kalman Filter Approach for Estimating Tendon Wave Speed from Skin-Mounted Accelerometers. Sensors. 2022; 22(6):2283. https://doi.org/10.3390/s22062283
Chicago/Turabian StyleSchmitz, Dylan G., Darryl G. Thelen, and Stephanie G. Cone. 2022. "A Kalman Filter Approach for Estimating Tendon Wave Speed from Skin-Mounted Accelerometers" Sensors 22, no. 6: 2283. https://doi.org/10.3390/s22062283
APA StyleSchmitz, D. G., Thelen, D. G., & Cone, S. G. (2022). A Kalman Filter Approach for Estimating Tendon Wave Speed from Skin-Mounted Accelerometers. Sensors, 22(6), 2283. https://doi.org/10.3390/s22062283






