Query Optimization for Distributed Spatio-Temporal Sensing Data Processing
Abstract
:1. Introduction
- We propose a distributed spatio-temporal polygon range query algorithm STPRQ. The algorithm proposes a polygon range query model based on the global index in the spatial range search stage and refilters the data objects under the spatial and temporal constraints based on the record reader.
- We propose a spatio-temporal k nearest neighbor algorithm STkNNQ, which comprehensively considers the temporal and spatial factors to calculate the spatio-temporal proximity. To improve query efficiency, we propose a spatio-temporal data partition strategy based on the global index. We also propose an adaptive iterative range optimization (AIRO) strategy, which can optimize the iterative range of the algorithm to avoid the time cost caused by querying irrelevant data blocks.
- We conduct extensive experiments on real-world aviation trajectory datasets to evaluate the efficiency and effectiveness of our proposed query algorithms. The experimental results show that the STPRQ algorithm can improve query efficiency by reducing the query cost to 19%. The experimental results also indicate that the STkNNQ algorithm can improve the query efficiency of spatio-temporal data, shortening the response time by 35.6%.
2. Related Work
2.1. Spatio-Temporal Data Management and Processing
2.2. Distributed Spatio-Temporal Query
2.2.1. Spatio-Temporal Range Query
2.2.2. Spatio-Temporal k Nearest Neighbor Query
3. Problem Preliminaries
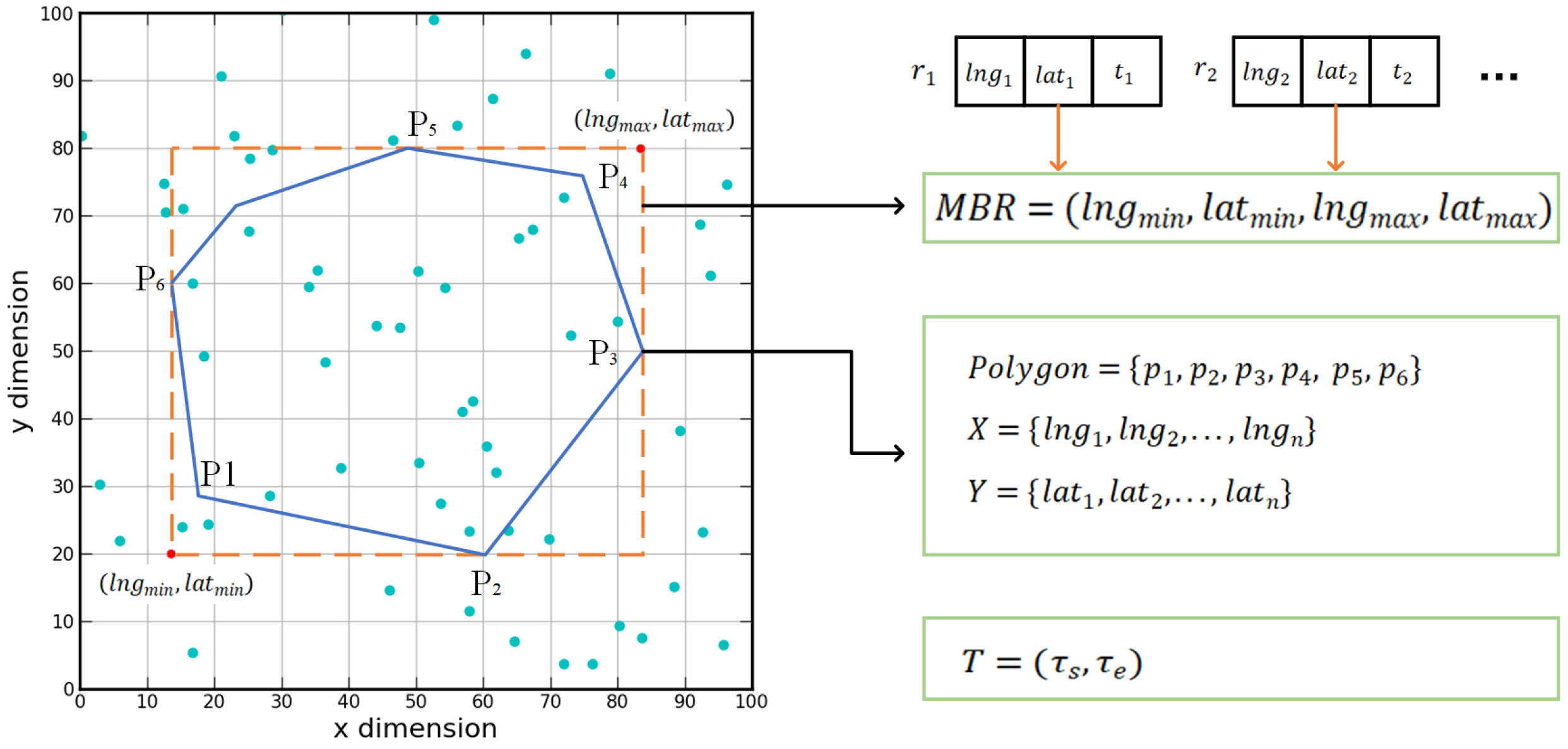
3.1. Spatio-Temporal Data
3.2. Spatio-Temporal Polygon Range Query
3.3. Spatio-Temporal k Nearest Neighbor Query
4. Query Processing Algorithms
4.1. Spatio-Temporal Polygon Range Query
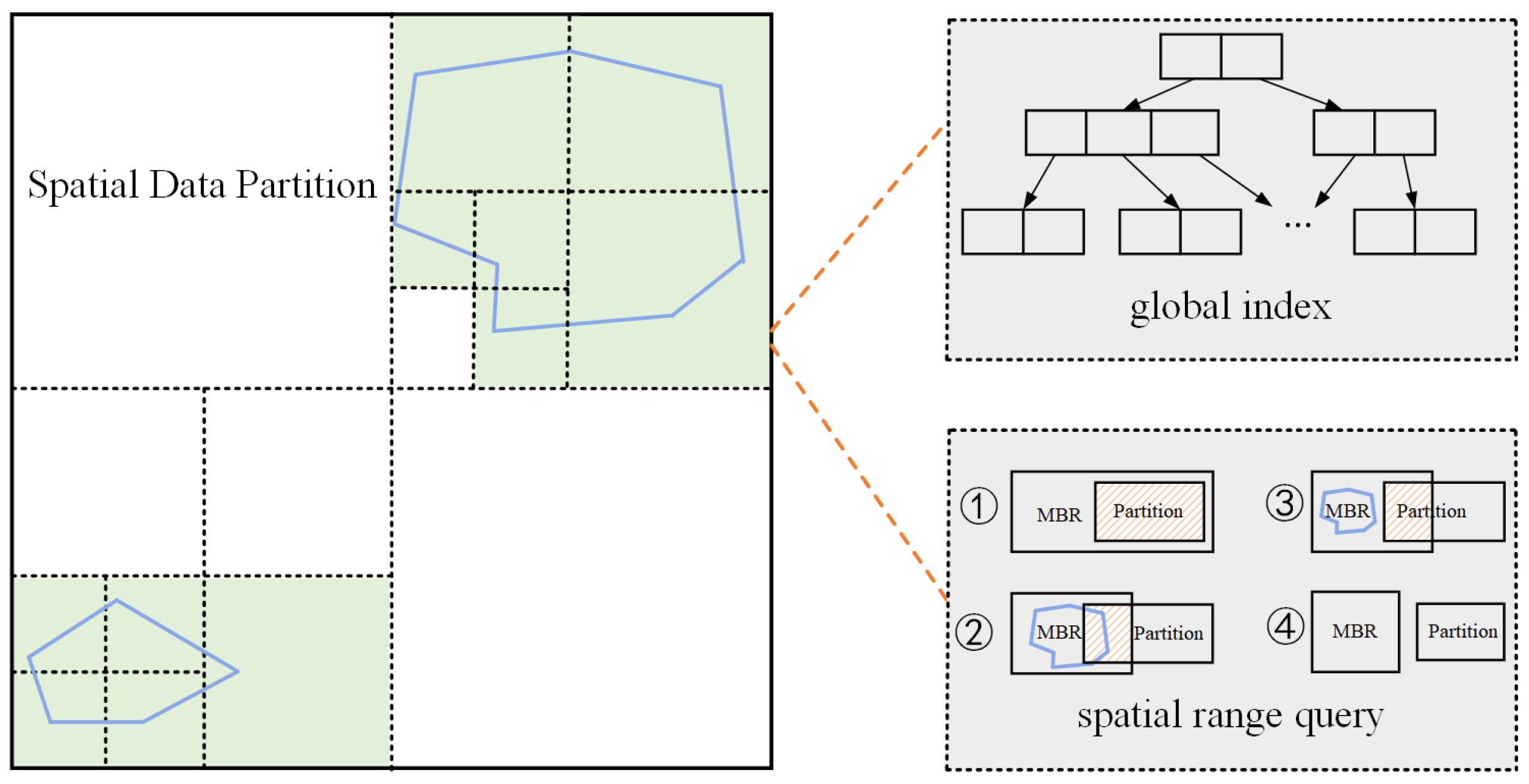
4.1.1. The Framework of Spatio-Temporal Polygon Range Query
- Spatial range search. Spatial search mainly performs a spatial range query on each matching partition and filters data that is not within the spatial range to select data blocks that intersect the query range. We use the global spatial index based on SpatialHadoop to partition the data block, such as grid index, R-tree index, quad-tree index, KD-tree index, space-filling curve, etc. The purpose of a global index is to store spatially adjacent data together to satisfy the principle of spatial locality. Although the space division ideas of diverse indexes are different, their essence is to use different space division algorithms to maximize the preservation of space characteristics and provide fast and efficient query efficiency.As shown in Figure 3, we regard the spatio-temporal dataset as points distributed in the spatial area with time attributes, then build an index for spatial data partitioning. Each index node can be regarded as a uniform data partition, of which the border is a rectangle. Since the boundary information of the partition of the data block is stored on the node of the global index, it is easy to judge the intersection of the partition and the polygon or the MBR of the polygon by using the global index.In combination with the query range for the index metadata, we clip data blocks to filter out all blocks that do not contain the records required by the query information. Since the location coordinates of data change dynamically with time, the data distribution still exhibits uneven characteristics. Therefore, using the spatial pruning strategy, coarse-grained filtering results can be obtained and passed to the next stage for execution.
- Refilter and refine. The spatial range search phase cannot guarantee that every record in the data block is within the query space and time query period. Therefore, it is necessary to perform refiltering and refining for each data block collected after pruning.In each spatial search step, we use the built-in of SpatialHadoop to traverse the data blocks obtained and compare each record’s time attribute with the query’s time interval to select records that match exactly. This step is essential because when a partition is selected, some areas may overlap with the query interval instead of being wholly included in the time interval, so the records need to be refined to delete for records that are not within the time interval. Once the data blocks within the spatial query range are selected, we will filter each matched data block for the precise temporal and spatial range. Finally, we verify whether the queried spatio-temporal records meet the conditions given by the user.
4.1.2. Spatio-Temporal Polygon Range Query Algorithm
| Algorithm 1: STPRQ MapReduce Algorithm |
 |
4.2. Spatio-Temporal k Nearest Neighbors Query
4.2.1. The Framework of Spatio-Temporal k Nearest Neighbors Query
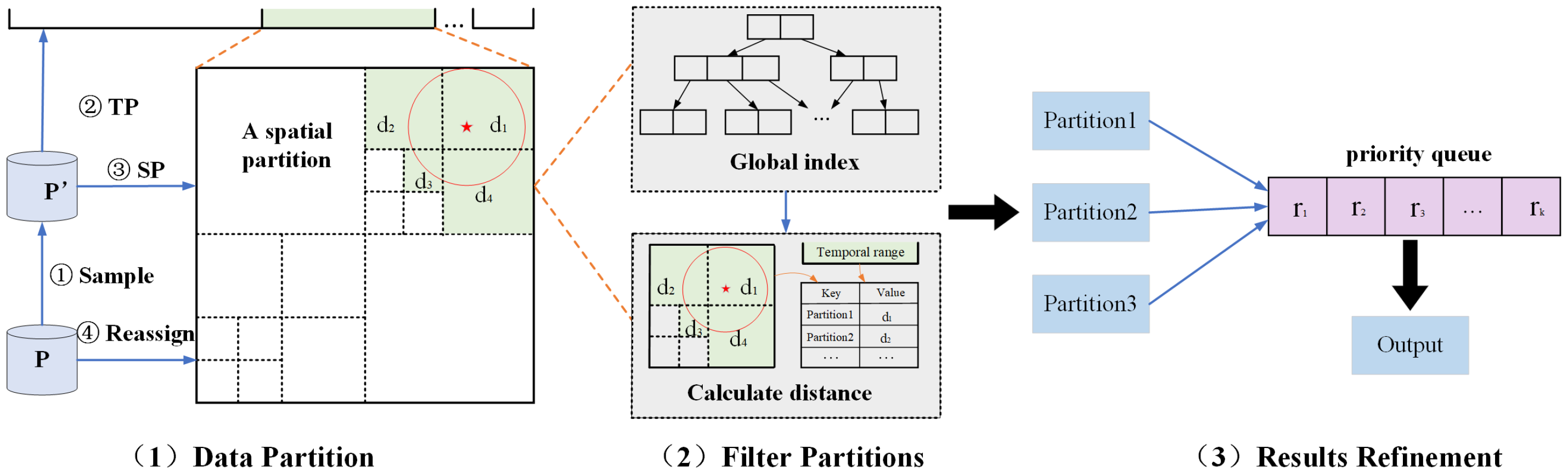
- Data partition. This paper devises a simple but effective spatio-temporal data partition strategy. The partitioning stage is divided into four steps: sampling, time partition, spatial partition, and reassignment. During the sampling phase, a set of random samples are drawn from the dataset at a sampling rate of . Since it is randomly sampled from the original dataset, it maintains its spatio-temporal distribution characteristics. In the spatial partition step, we divide the global spatial range into multiple disjoint data partitions with clear boundary information. The quad tree is generally used to divide the global spatial domain in this paper. Compared with other indexes, quad tree considers all parts of the spatial domain, which can alleviate the problem of unbalanced spatial distribution and make it easier to divide the space. The minimum enclosing rectangle MBR of each object is adopted in this paper because checking the spatial relationship of two MBRs is much faster than checking the spatial relationship of the two records. In the reassignment phase, the global index generated based on the data samples is broadcast to each partition, and all datasets are traversed. For each , if p intersects with some partition of the global index, we inspect the record and update the boundary identifier of the current partition. At last, we repartition according to the bounded identifier.
- Filter partitions. In this step, with the global index, we can query and filter partitions based on the latitude and longitude of the point to be queried. First, we construct the MBR of the query point q, then calculate the distance from each partition to q according to the global index, and then obtain the time range , spatial range , and sorting function according to the input, and the priority of the partition can be obtained. When the number of existing results is less than k, the partition will be selected from the remaining partitions for processing according to the sorting priority.
- Results refinement. After filtering the query partitions, each data partition containing objects that meet the conditions is obtained. This step is mainly to solve the problem of fully considering the time factor in the conventional spatial k nearest neighbor query and improving the query algorithm’s efficiency. Firstly, we scan the partitions to be processed, filter them by time range and spatial range, and deduplicate the duplicate records. Then, the results are redivided into new partitions. Finally, the local results of each partition are merged into global results.A priority queue is then constructed to prioritize each record according to a user-supplied spatio-temporal sorting function. If the results do not satisfy k, it will go back to the second step to continue the diffusion search; if k is satisfied, it is necessary to judge whether the nearest k points are already in the result set. Due to the density of data and the influence of the global index, other untraversed partitions have likely qualified records. Therefore, defining a query test area is necessary to reconfirm whether the k records in the result set are the final result. If the delineated test circle area intersects with other data partitions and the data block has not been processed before, a range query needs to be restarted to scan the data block to obtain closer results.
4.2.2. STkNNQ MapReduce Algorithm
| Algorithm 2: STkNNQ MapReduce algorithm |
 |
4.2.3. Adaptive Iterative Optimization Algorithm
- Set the initial iteration range radius and step size. We select the farthest object from the query point q in the intermediate results O generated by the previous iteration range and calculate its distance to the qand set the initial iteration range radius , and the initial step size . The reason for this setting is that all objects in the previous iteration range may not satisfy the query conditions so that the obtained result set is farther away from the query point than the actual distance.
- Calculate the time impact factor. The larger is, the smaller the influence on the iteration range.denotes the difference between the query point q and the time range T.
- Generate the new radius of the new iteration range. We take the initial iteration range , and combining the time influence factor , and taking the step size into account, the radius of the new iteration range is finally generated.
5. Experiment Results and Analysis
5.1. Experimental Datasets and Setup
5.1.1. Datasets
5.1.2. Experimental Settings
5.2. Experimental Analysis of Spatio-Temporal Polygon Range Query
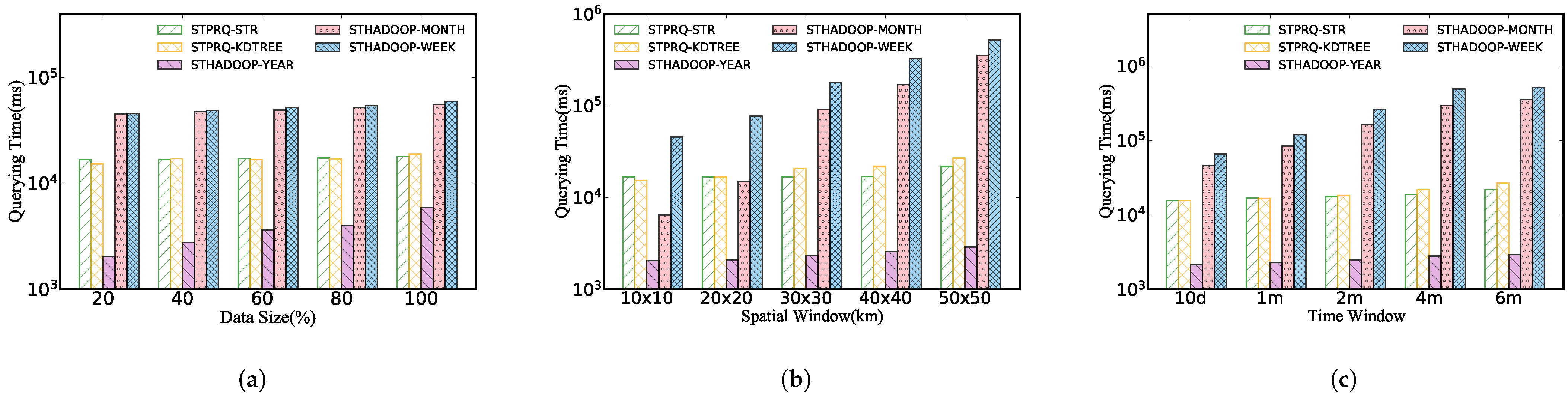
5.2.1. Performance of Spatio-Temporal Polygon Range Query
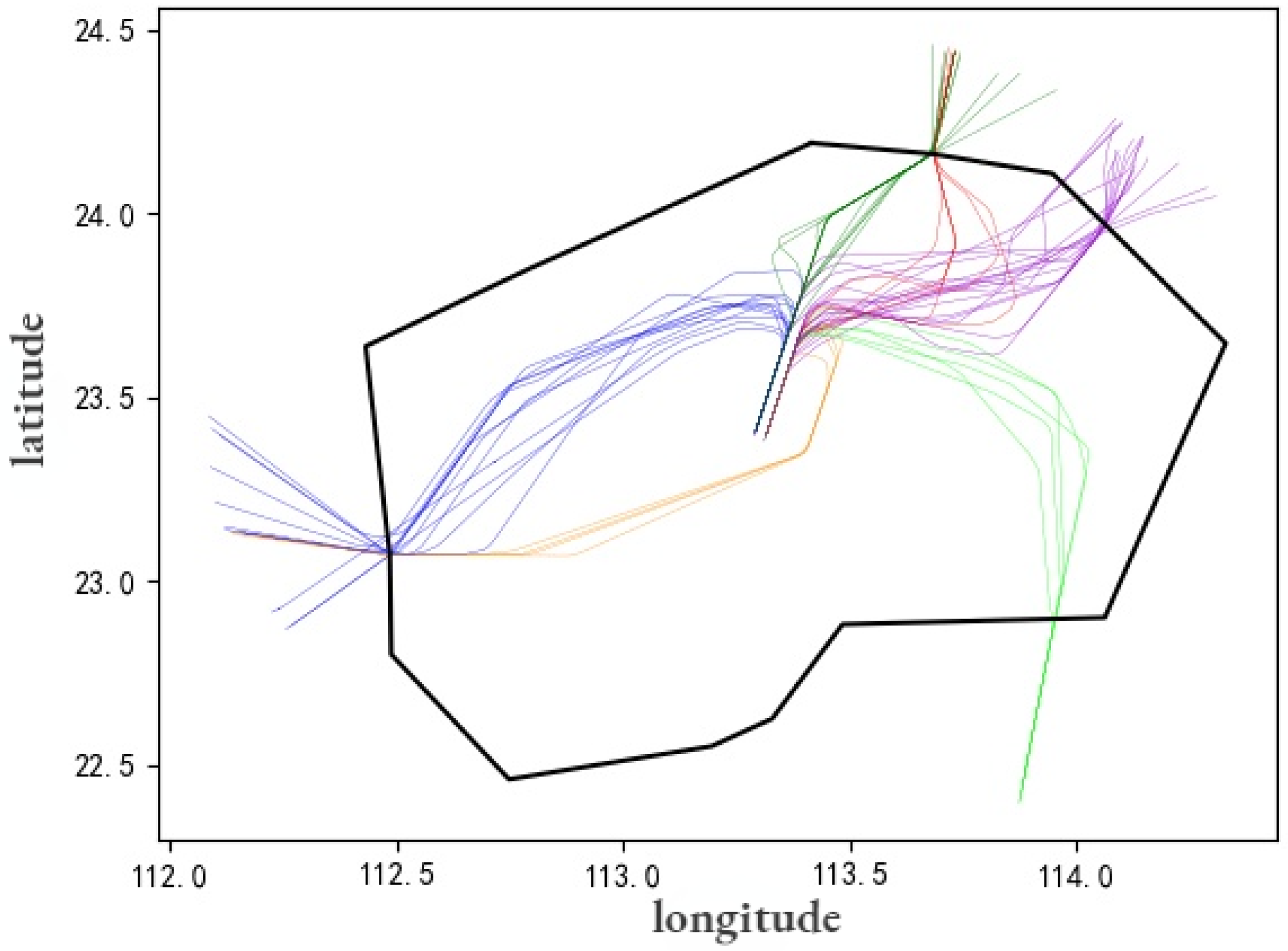
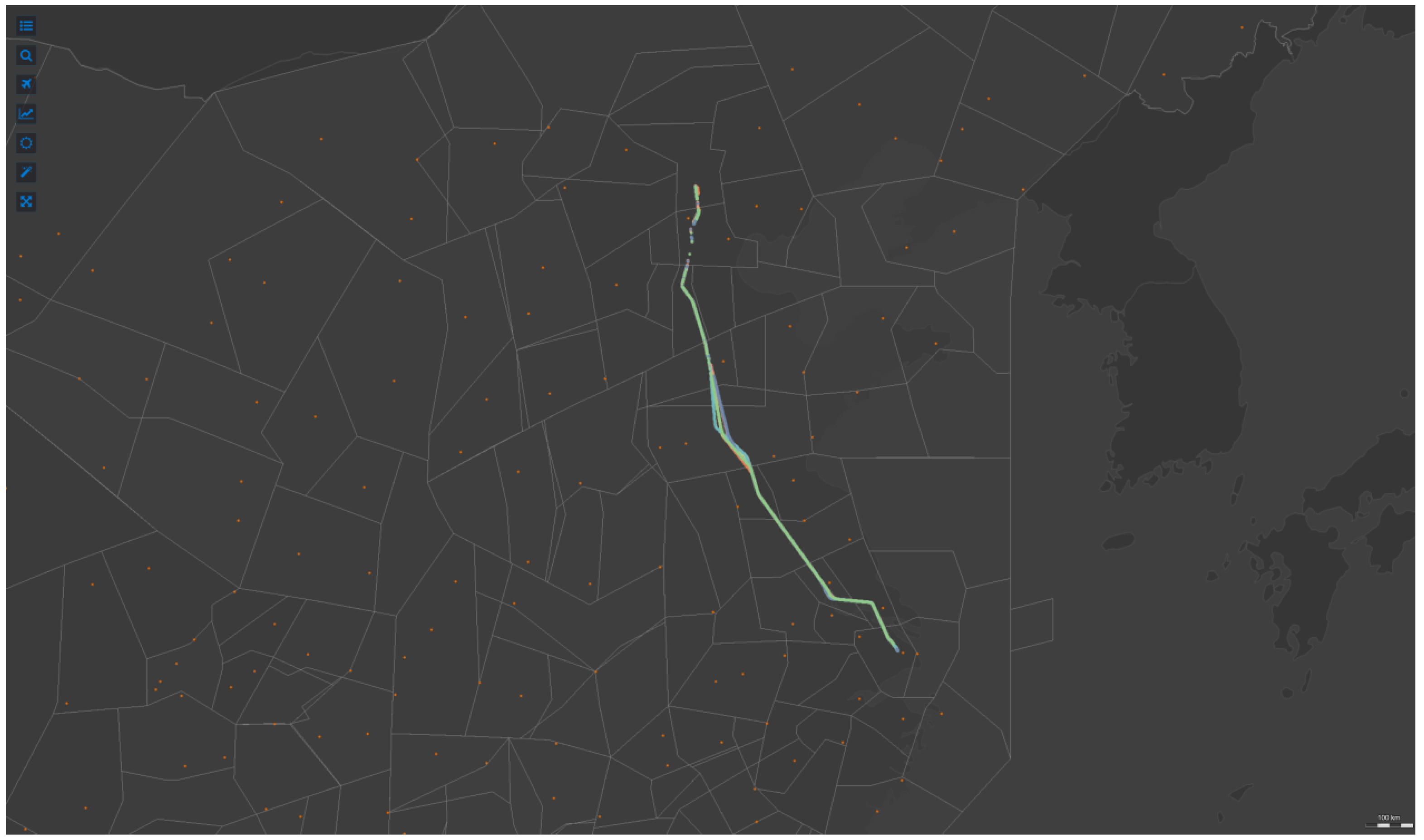
5.2.2. Comparison of STPRQ and STRQ
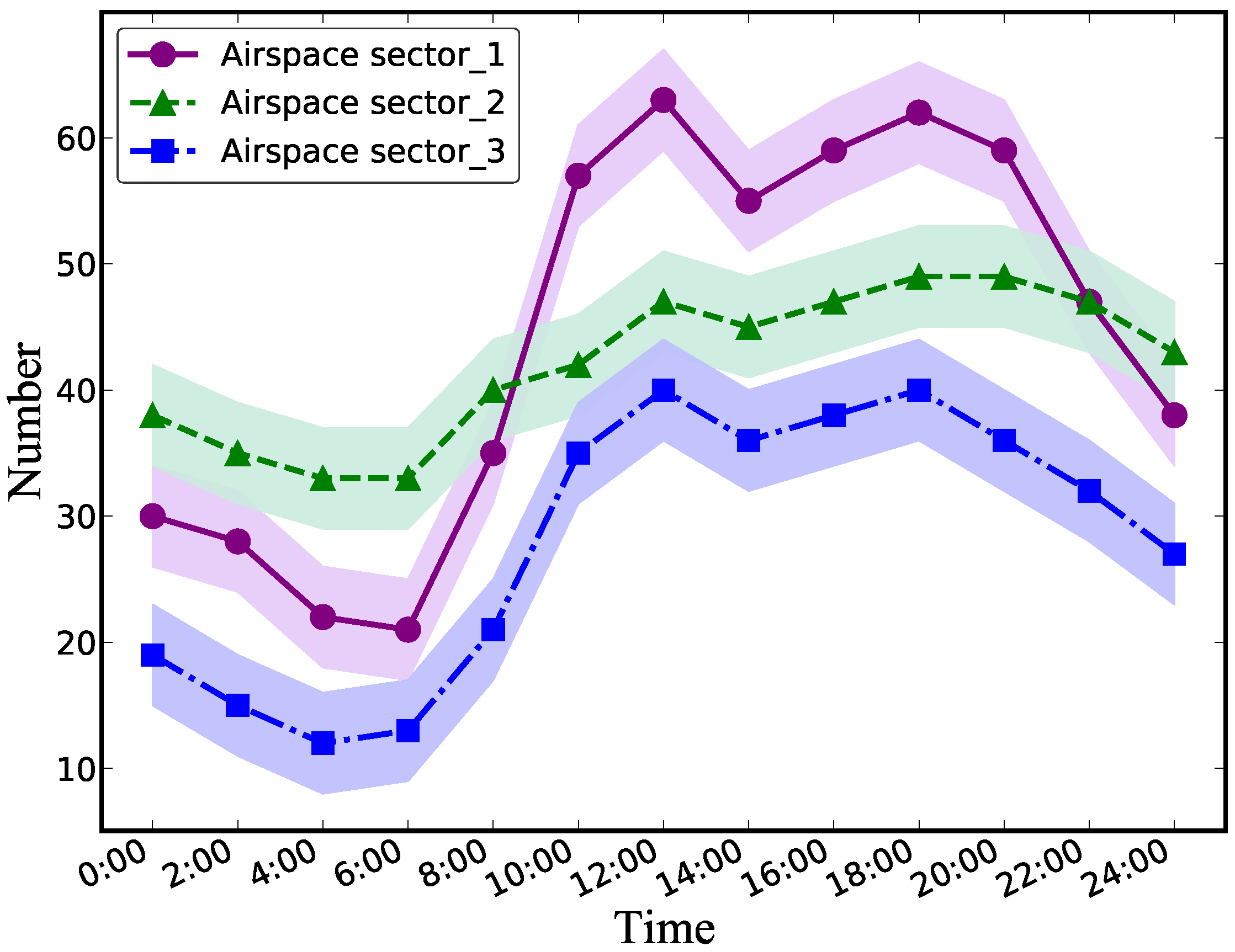
5.2.3. Performance of Air Traffic Flow Statistic
5.3. Experimental Analysis of Spatio-Temporal kNN Query
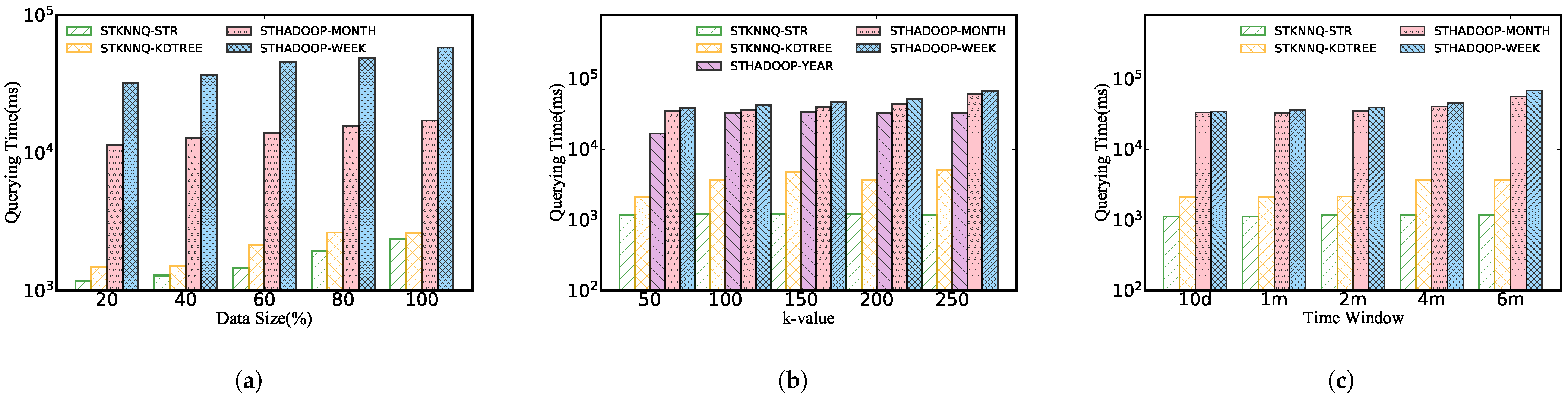
5.3.1. Performance of Spatio-Temporal kNN Query
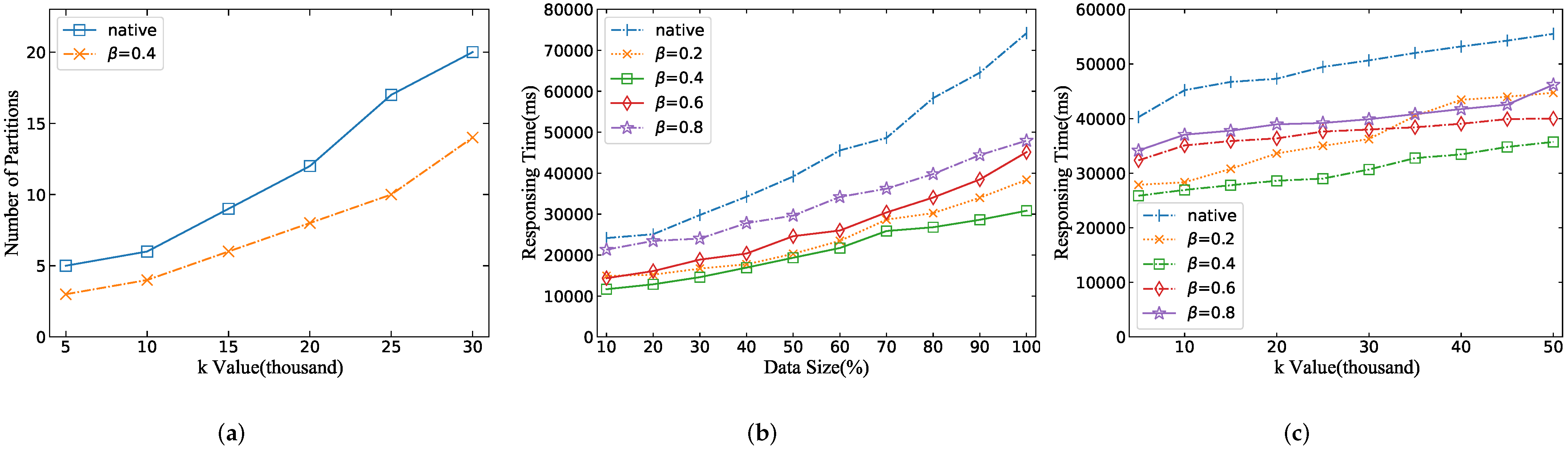
- The varying k makes a slight difference to query performance. We learn that our proposed algorithm keeps steady performance regardless of the parameter change from this result.
- Although STkNNQ and ST-Hadoop kNN query are based on the 100% of the dataset, they achieve a magnitude improvement concerning ST-Hadoop because it is expensive for ST-Hadoop to start a MapReduce job.
5.3.2. Performance of AIRO Algorithm
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xu, F.; Tu, Z.; Li, Y.; Zhang, P.; Fu, X.; Jin, D. Trajectory recovery from ash: User privacy is not preserved in aggregated mobility data. In Proceedings of the 26th International Conference on World Wide Web, Perth, Australia, 3–7 April 2017; pp. 1241–1250. [Google Scholar]
- De Montjoye, Y.A.; Hidalgo, C.A.; Verleysen, M.; Blondel, V.D. Unique in the crowd: The privacy bounds of human mobility. Sci. Rep. 2013, 3, 1376. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yuan, J.; Zheng, Y.; Xie, X.; Sun, G. T-drive: Enhancing driving directions with taxi drivers’ intelligence. IEEE Trans. Knowl. Data Eng. 2011, 25, 220–232. [Google Scholar] [CrossRef]
- He, T.; Bao, J.; Ruan, S.; Li, R.; Li, Y.; He, H.; Zheng, Y. Interactive bike lane planning using sharing bikes’ trajectories. IEEE Trans. Knowl. Data Eng. 2019, 32, 1529–1542. [Google Scholar] [CrossRef]
- Verbesselt, J.; Hyndman, R.; Newnham, G.; Culvenor, D. Detecting trend and seasonal changes in satellite image time series. Remote Sens. Environ. 2010, 114, 106–115. [Google Scholar] [CrossRef]
- Gerber, F.; de Jong, R.; Schaepman, M.E.; Schaepman-Strub, G.; Furrer, R. Predicting missing values in spatio-temporal remote sensing data. IEEE Trans. Geosci. Remote Sens. 2018, 56, 2841–2853. [Google Scholar] [CrossRef] [Green Version]
- Atluri, G.; Karpatne, A.; Kumar, V. Spatio-temporal data mining: A survey of problems and methods. ACM Comput. Surv. (CSUR) 2018, 51, 1–41. [Google Scholar] [CrossRef]
- Wang, X.; Zhou, Z.; Xiao, F.; Xing, K.; Yang, Z.; Liu, Y.; Peng, C. Spatio-temporal analysis and prediction of cellular traffic in metropolis. IEEE Trans. Mob. Comput. 2018, 18, 2190–2202. [Google Scholar] [CrossRef] [Green Version]
- Song, C.; Lin, Y.; Guo, S.; Wan, H. Spatial-temporal synchronous graph convolutional networks: A new framework for spatial-temporal network data forecasting. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; Volume 34, pp. 914–921. [Google Scholar]
- Li, R.; He, H.; Wang, R.; Huang, Y.; Liu, J.; Ruan, S.; He, T.; Bao, J.; Zheng, Y. Just: Jd urban spatio-temporal data engine. In Proceedings of the 2020 IEEE 36th International Conference on Data Engineering (ICDE), Dallas, TX, USA, 20–24 April 2020; pp. 1558–1569. [Google Scholar]
- Gui, G.; Zhou, Z.; Wang, J.; Liu, F.; Sun, J. Machine learning aided air traffic flow analysis based on aviation big data. IEEE Trans. Veh. Technol. 2020, 69, 4817–4826. [Google Scholar] [CrossRef]
- Yu, H.; Li, X.; Yuan, L.; Qin, X. Efficient Spatio-Temporal-Data-Oriented Range Query Processing for Air Traffic Flow Statistics. In Proceedings of the 2021 IEEE Intl Conf on Parallel & Distributed Processing with Applications, Big Data & Cloud Computing, Sustainable Computing & Communications, Social Computing & Networking (ISPA/BDCloud/SocialCom/SustainCom), New York, NY, USA, 30 September–3 October 2021; pp. 1303–1310. [Google Scholar]
- Zhang, J.; Zheng, Y.; Qi, D.; Li, R.; Yi, X.; Li, T. Predicting citywide crowd flows using deep spatio-temporal residual networks. Artif. Intell. 2018, 259, 147–166. [Google Scholar] [CrossRef] [Green Version]
- Sagl, G.; Resch, B.; Hawelka, B.; Beinat, E. From social sensor data to collective human behaviour patterns: Analysing and visualising spatio-temporal dynamics in urban environments. In Proceedings of the GI-Forum, Berlin, Germany, 2–3 July 2012; pp. 54–63. [Google Scholar]
- Yu, J.; Zhang, Z.; Sarwat, M. Spatial data management in apache spark: The geospark perspective and beyond. GeoInformatica 2019, 23, 37–78. [Google Scholar] [CrossRef]
- Wan, S.; Zhao, Y.; Wang, T.; Gu, Z.; Abbasi, Q.H.; Choo, K.K.R. Multi-dimensional data indexing and range query processing via Voronoi diagram for internet of things. Future Gener. Comput. Syst. 2019, 91, 382–391. [Google Scholar] [CrossRef] [Green Version]
- Guo, S.; Lin, Y.; Feng, N.; Song, C.; Wan, H. Attention based spatial-temporal graph convolutional networks for traffic flow forecasting. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; Volume 33, pp. 922–929. [Google Scholar]
- Eldawy, A.; Mokbel, M.F. Spatialhadoop: A mapreduce framework for spatial data. In Proceedings of the 2015 IEEE 31st International Conference on Data Engineering, Seoul, Korea, 13–17 April 2015; pp. 1352–1363. [Google Scholar]
- Aji, A.; Wang, F.; Vo, H.; Lee, R.; Liu, Q.; Zhang, X.; Saltz, J. Hadoop-GIS: A high performance spatial data warehousing system over MapReduce. In Proceedings of the VLDB Endowment International Conference on Very Large Data Bases, Copenhagen, Denmark, 26–30 August 2013; Volume 6. [Google Scholar]
- Yu, J.; Wu, J.; Sarwat, M. Geospark: A cluster computing framework for processing large-scale spatial data. In Proceedings of the 23rd SIGSPATIAL International Conference on Advances in Geographic Information Systems, Seattle, WA, USA, 3–6 November 2015; pp. 1–4. [Google Scholar]
- Xie, D.; Li, F.; Yao, B.; Li, G.; Zhou, L.; Guo, M. Simba: Efficient in-memory spatial analytics. In Proceedings of the 2016 International Conference on Management of Data, San Francisco, CA, USA, 26 June–1 July 2016; pp. 1071–1085. [Google Scholar]
- Hagedorn, S.; Gotze, P.; Sattler, K.U. The STARK framework for spatio-temporal data analytics on spark. In Datenbanksysteme für Business, Technologie und Web (BTW 2017); Gesellschaft für Informatik: Bonn, Germany, 2017. [Google Scholar]
- Nishimura, S.; Das, S.; Agrawal, D.; El Abbadi, A. MD-HBase: A scalable multi-dimensional data infrastructure for location aware services. In Proceedings of the 2011 IEEE 12th International Conference on Mobile Data Management, Lulea, Sweden; 2011; Volume 1, pp. 7–16. [Google Scholar]
- Chen, X.; Zhang, C.; Ge, B.; Xiao, W. Spatio-temporal queries in HBase. In Proceedings of the 2015 IEEE International Conference on Big Data (Big Data), Santa Clara, CA, USA, 29 October–1 November 2015; pp. 1929–1937. [Google Scholar]
- Oh, S.; Jung, H.; Kim, U.M. An efficient processing of range spatial keyword queries over moving objects. In Proceedings of the 2018 International Conference on Information Networking (ICOIN), Chiang Mai, Thailand, 10–12 January 2018; pp. 525–530. [Google Scholar]
- Guttman, A. R-trees: A dynamic index structure for spatial searching. In Proceedings of the 1984 ACM SIGMOD International Conference on Management of Data, Boston, MA, USA, 18–21 June 1984; pp. 47–57. [Google Scholar]
- Finkel, R.A.; Bentley, J.L. Quad trees a data structure for retrieval on composite keys. Acta Inform. 1974, 4, 1–9. [Google Scholar] [CrossRef]
- Bentley, J.L. Multidimensional binary search trees used for associative searching. Commun. ACM 1975, 18, 509–517. [Google Scholar] [CrossRef]
- Wang, D.; Cheng, T. A spatio-temporal data model for activity-based transport demand modelling. Int. J. Geogr. Inf. Sci. 2001, 15, 561–585. [Google Scholar] [CrossRef]
- Vazirgiannis, M.; Wolfson, O. A spatiotemporal model and language for moving objects on road networks. In Proceedings of the International Symposium on Spatial and Temporal Databases, Redondo Beach, CA, USA, 12–15 July 2001; pp. 20–35. [Google Scholar]
- Guting, R.H.; Almeida, V.; Ansorge, D.; Behr, T.; Ding, Z.; Hose, T.; Hoffmann, F.; Spiekermann, M.; Telle, U. Secondo: An extensible dbms platform for research prototyping and teaching. In Proceedings of the 21st International Conference on Data Engineering (ICDE’05), Tokyo, Japan, 5–8 April 2005; pp. 1115–1116. [Google Scholar]
- Theodoridis, Y.; Vazirgiannis, M.; Sellis, T. Spatio-temporal indexing for large multimedia applications. In Proceedings of the Third IEEE International Conference on Multimedia Computing and Systems, Hiroshima, Japan, 17–23 June 1996; pp. 441–448. [Google Scholar]
- Tao, Y.; Papadias, D. The mv3r-tree: A spatio-temporal access method for timestamp and interval queries. In Proceedings of the Very Large Data Bases Conference (VLDB), Rome, Italy, 11–14 September 2001. [Google Scholar]
- Bakli, M.; Sakr, M.; Soliman, T.H.A. HadoopTrajectory: A Hadoop spatiotemporal data processing extension. J. Geogr. Syst. 2019, 21, 211–235. [Google Scholar] [CrossRef]
- Alarabi, L.; Mokbel, M.F.; Musleh, M. St-hadoop: A mapreduce framework for spatio-temporal data. GeoInformatica 2018, 22, 785–813. [Google Scholar] [CrossRef]
- Available online: http://spatialhadoop.cs.umn.edu/ (accessed on 27 January 2022).
- Tang, M.; Yu, Y.; Malluhi, Q.M.; Ouzzani, M.; Aref, W.G. Locationspark: A distributed in-memory data management system for big spatial data. Proc. VLDB Endow. 2016, 9, 1565–1568. [Google Scholar] [CrossRef]
- Zacharatou, E.T.; Doraiswamy, H.; Ailamaki, A.; Silva, C.T.; Freire, J. GPU rasterization for real-time spatial aggregation over arbitrary polygons. Proc. VLDB Endow. 2017, 11, 352–365. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; You, S. Speeding up large-scale point-in-polygon test based spatial join on GPUs. In Proceedings of the 1st ACM SIGSPATIAL International Workshop on Analytics for Big Geospatial Data, Redondo Beach, CA, USA, 6 November 2012; pp. 23–32. [Google Scholar]
- García-García, F.; Corral, A.; Iribarne, L.; Vassilakopoulos, M.; Manolopoulos, Y. Efficient distance join query processing in distributed spatial data management systems. Inf. Sci. 2020, 512, 985–1008. [Google Scholar] [CrossRef]
- Zhang, C.; Li, F.; Jestes, J. Efficient parallel kNN joins for large data in MapReduce. In Proceedings of the 15th International Conference on Extending Database Technology, Berlin, Germany, 27–30 March 2012; pp. 38–49. [Google Scholar]
- Liu, Y.; Jing, N.; Chen, L.; Xiong, W. Algorithm for processing k-nearest join based on r-tree in mapreduce. J. Softw. 2013, 24, 1836–1851. [Google Scholar] [CrossRef]
- Li, R.; Wang, R.; Liu, J.; Yu, Z.; He, H.; He, T.; Ruan, S.; Bao, J.; Chen, C.; Gu, F.; et al. Distributed Spatio-Temporal k Nearest Neighbors Join. In Proceedings of the 29th International Conference on Advances in Geographic Information Systems, Beijing, China, 2–5 November 2021; pp. 435–445. [Google Scholar]
- Available online: https://lbs.amap.com/demo/javascript-api/example/map/map-english/ (accessed on 27 January 2022).



| DSTDMS | Architecture | Query Operation |
|---|---|---|
| Hadoop-GIS | Hadoop | Range query, spatial join |
| SpatialHadoop | Hadoop | Range query, kNN, spatial join |
| ST-Hadoop | Hadoop | ST-range query, ST-join, kNN |
| Hadoop-Trajectory | Hadoop | Pass, Traj, WindowIntersect |
| Simba | Spark | Range query, kNN, spatial join |
| SpatialSpark | Spark | Range query, spatial join |
| GeoSpark | Spark | Range query, kNN |
| STARK | Spark | Range query, kNN, spatial join |
| JUST | NoSQL | ST-range query, kNN |
| Record | Spatio-Temporal Properties | Other Properties | ||||
|---|---|---|---|---|---|---|
| … | … | … | … | … | … | … |
| Attributes | ADS-B Trajectory Data | Synthetic Data |
|---|---|---|
| Records | 10 million | 100 million |
| Raw size | 379 MB | 10.3 GB |
| Timespan | 1 January 2019–1 July 2019 | 1 September 2018–1 September 2019 |
| Parameters | Settings |
|---|---|
| Data size (%) | 20, 40, 60, 80, 100 |
| Time window | 10 d, 1 m, 2 m, 4 m, 6 m |
| Spatial window (km) | 10 × 10, 20 × 20, 30 × 30, 40 × 40, 50 × 50 |
| k value | 50, 100, 150, 200, 250 |
| Factor of range radius () | 0.2, 0.4, 0.6, 0.8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Yu, H.; Yuan, L.; Qin, X. Query Optimization for Distributed Spatio-Temporal Sensing Data Processing. Sensors 2022, 22, 1748. https://doi.org/10.3390/s22051748
Li X, Yu H, Yuan L, Qin X. Query Optimization for Distributed Spatio-Temporal Sensing Data Processing. Sensors. 2022; 22(5):1748. https://doi.org/10.3390/s22051748
Chicago/Turabian StyleLi, Xin, Huayan Yu, Ligang Yuan, and Xiaolin Qin. 2022. "Query Optimization for Distributed Spatio-Temporal Sensing Data Processing" Sensors 22, no. 5: 1748. https://doi.org/10.3390/s22051748
APA StyleLi, X., Yu, H., Yuan, L., & Qin, X. (2022). Query Optimization for Distributed Spatio-Temporal Sensing Data Processing. Sensors, 22(5), 1748. https://doi.org/10.3390/s22051748






