Dependence of Piezoelectric Discs Electrical Impedance on Mechanical Loading Condition
Abstract
:1. Introduction
1.1. Piezoelectric Materials
1.2. Related Work
2. Background
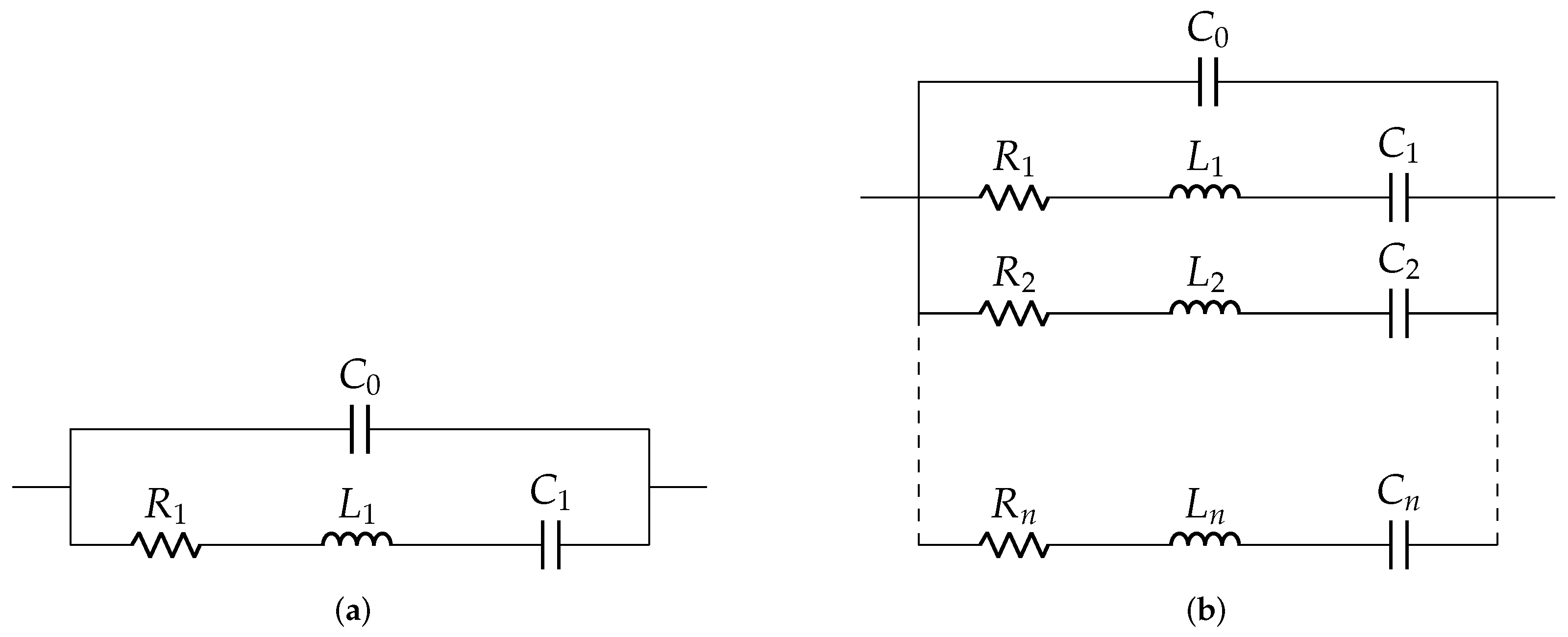
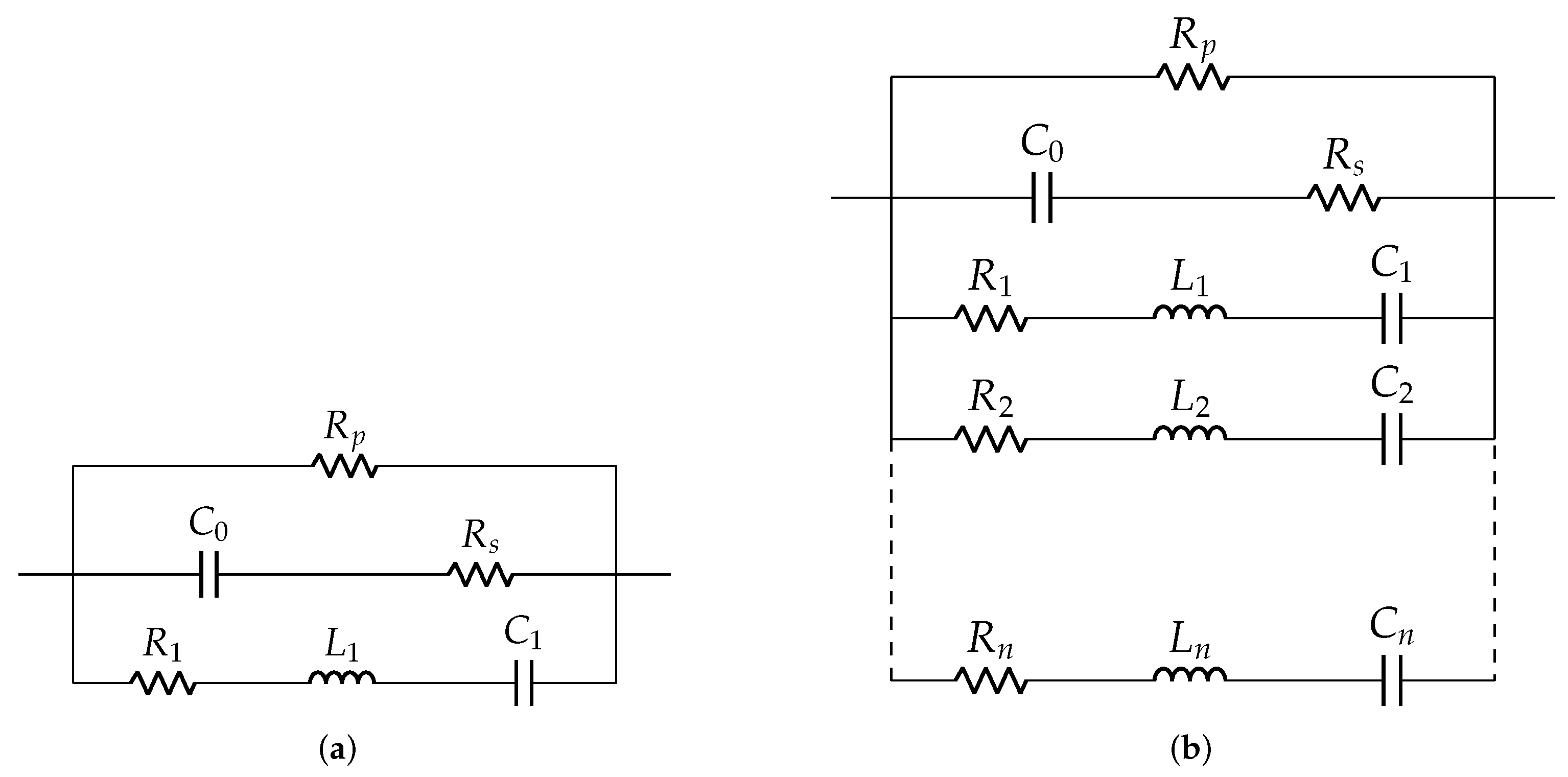
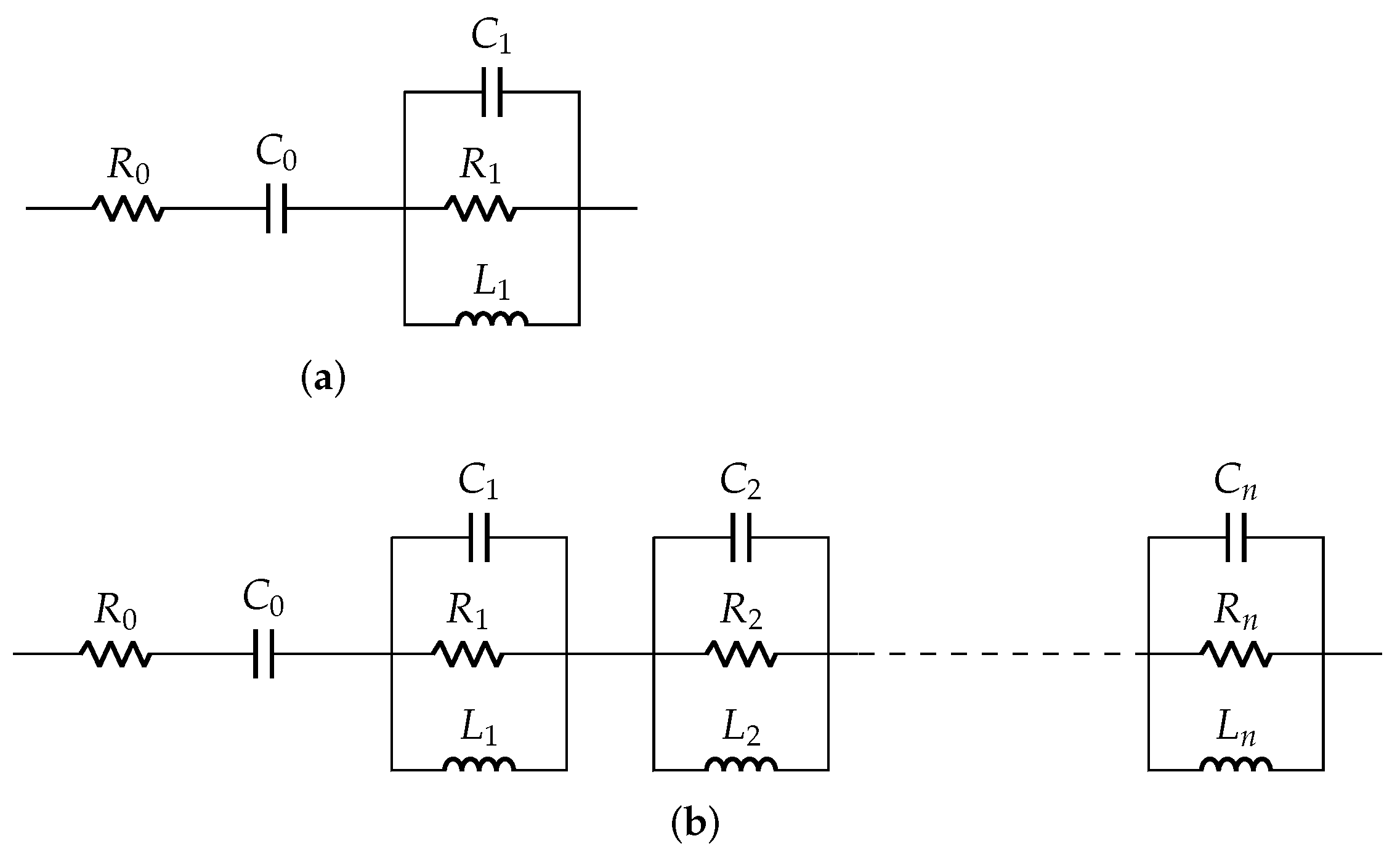
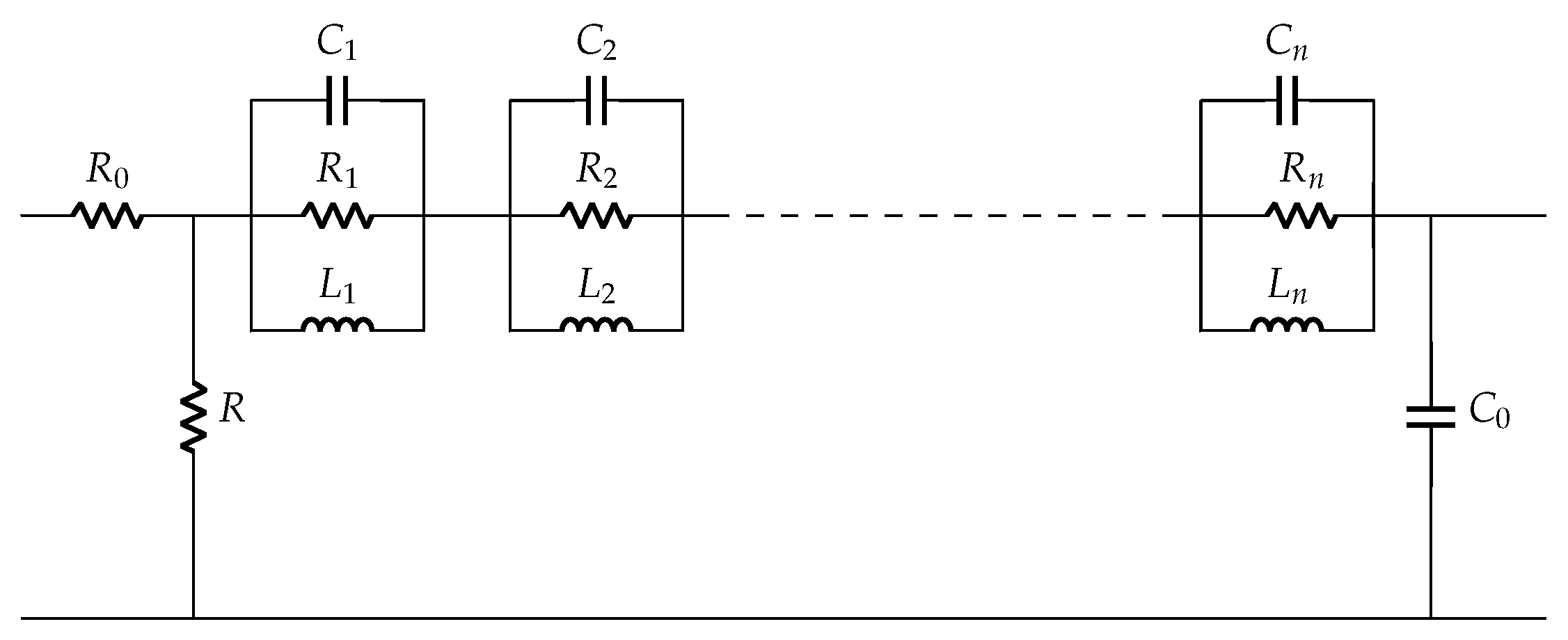
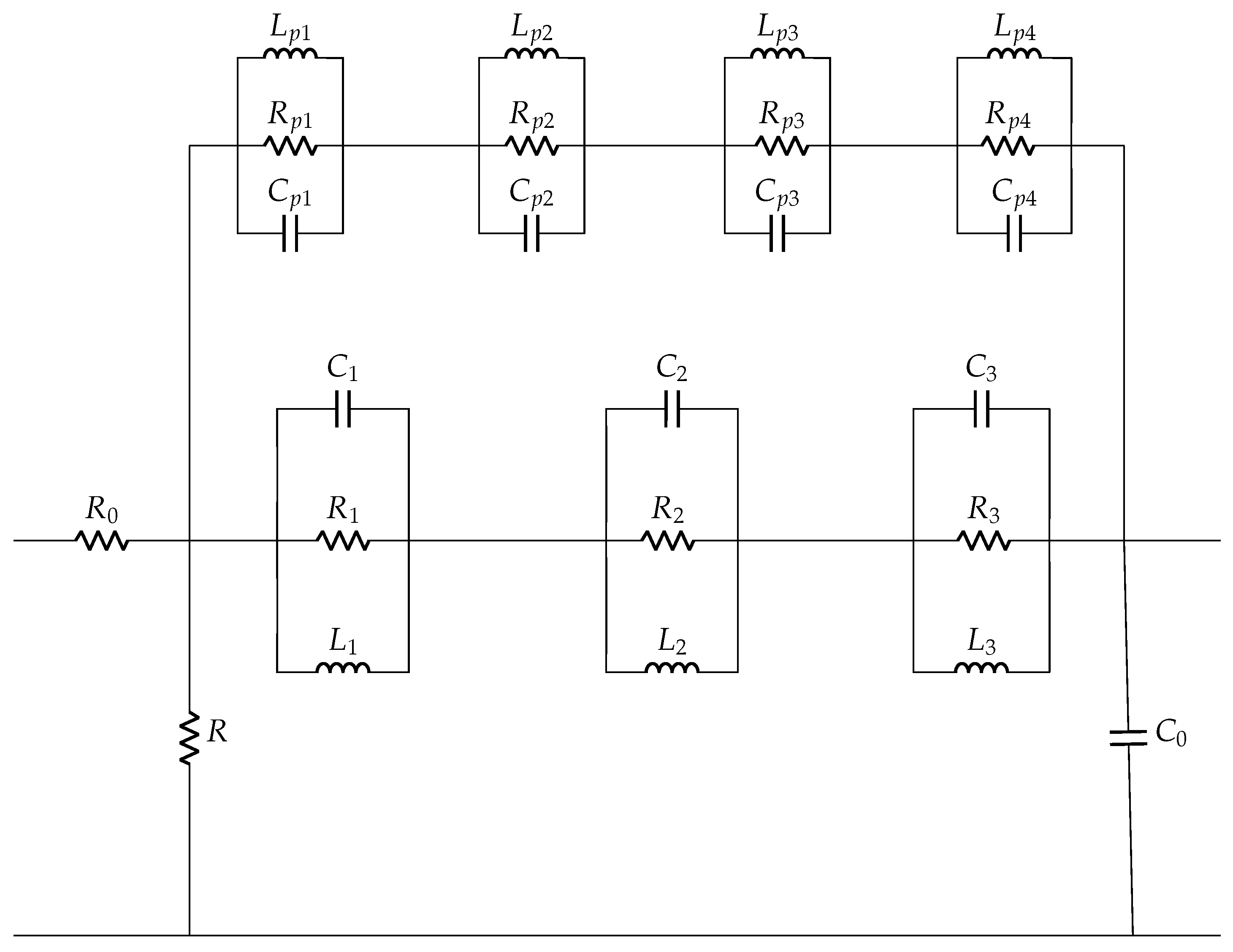
2.1. Existing Electrical Equivalent Models for Piezoelectric Elements
2.2. Fundamental Equations
3. Research Methodology
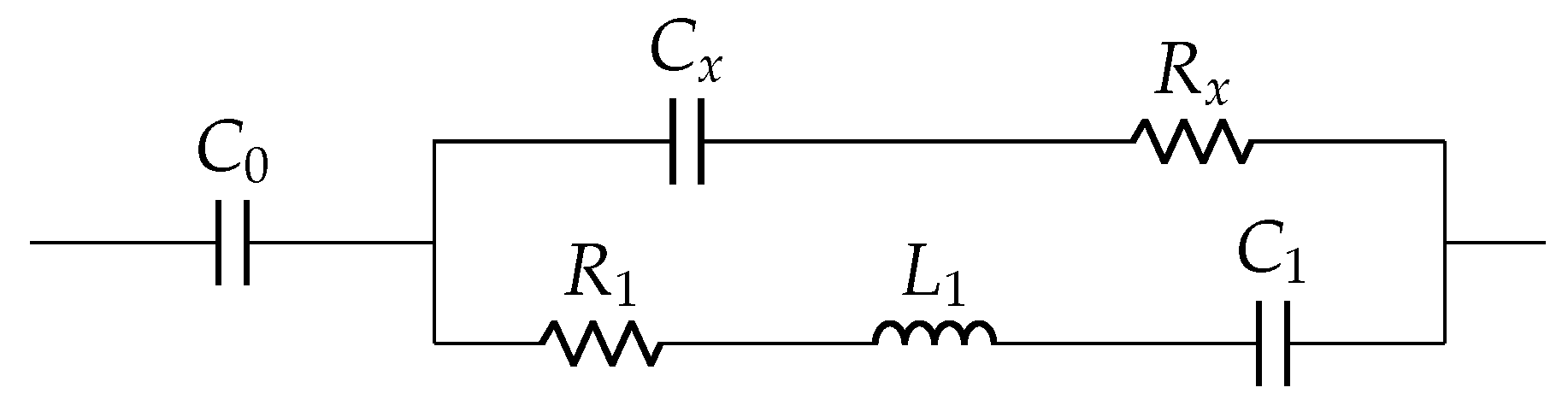
3.1. Proposed Work
3.2. Experimental Details
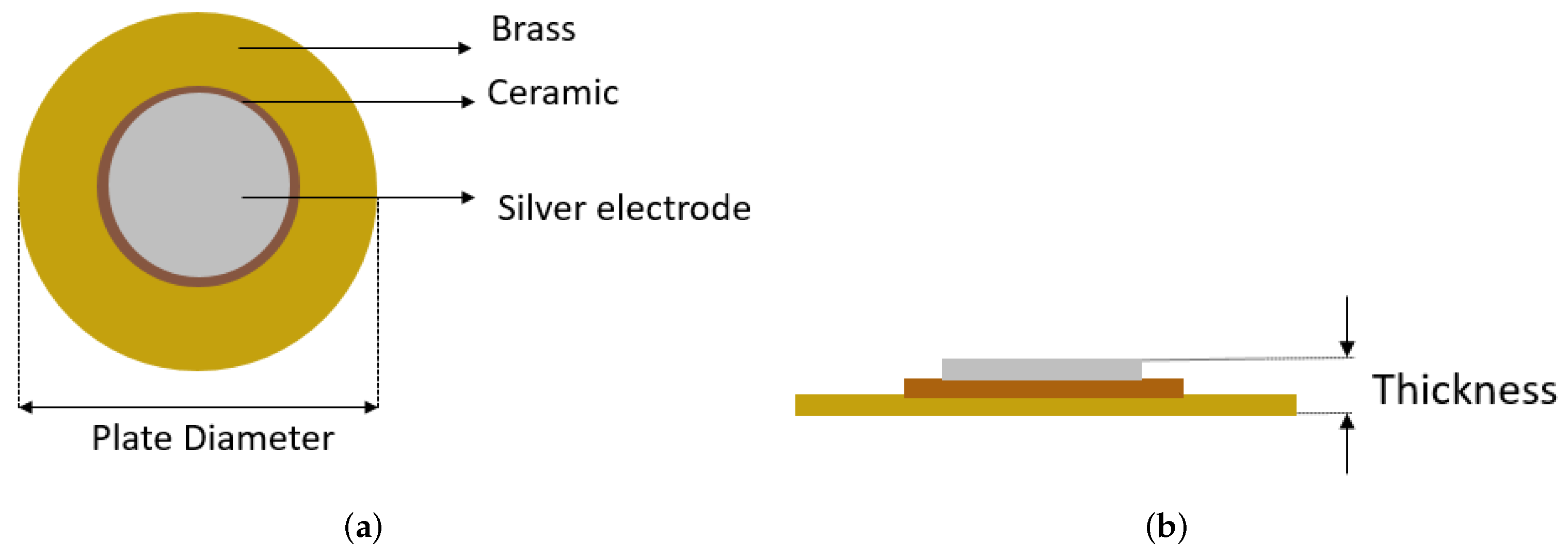
3.2.1. Piezoelectric Discs
3.2.2. Test Equipment
3.3. Method for Electrical Impedance Measurement
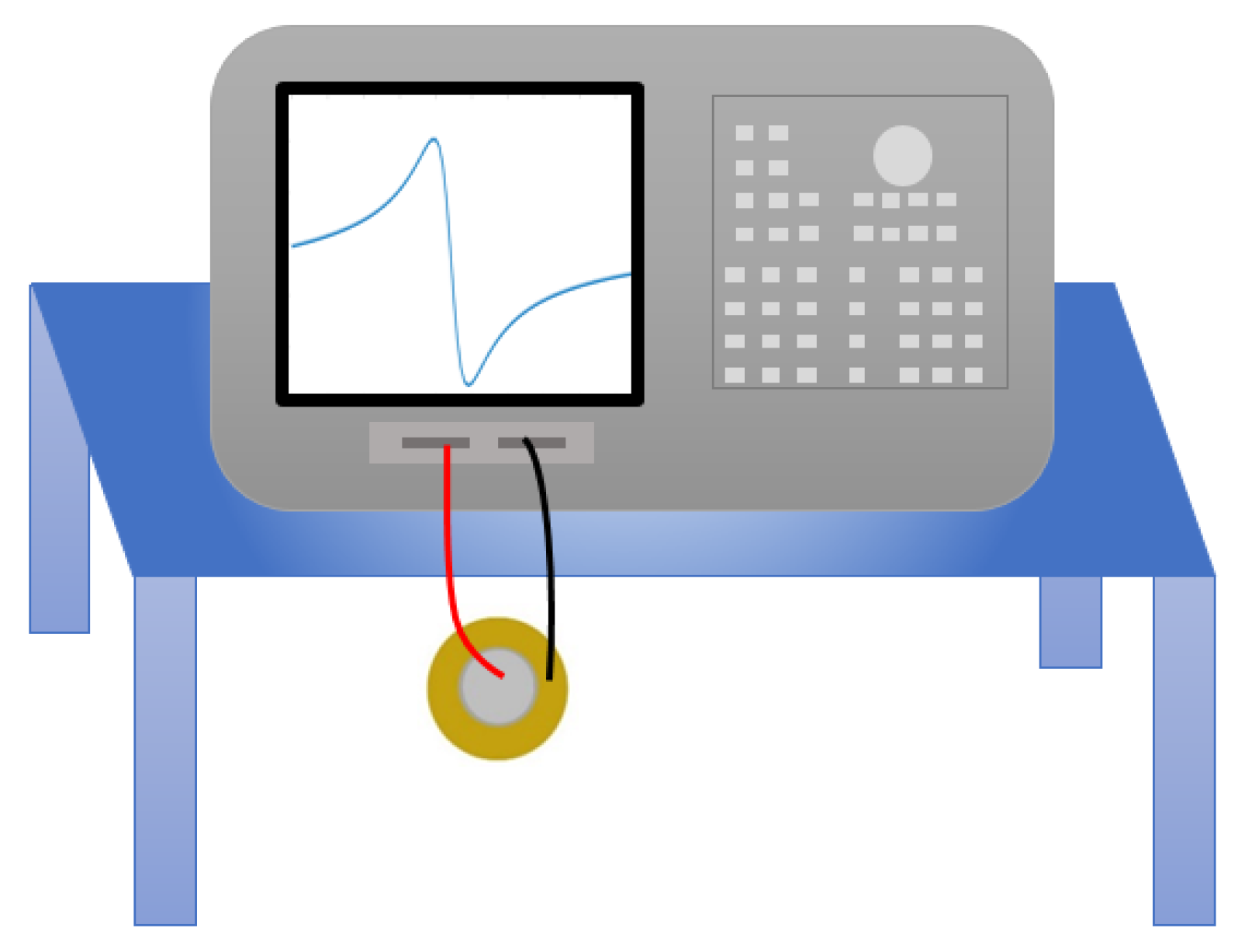
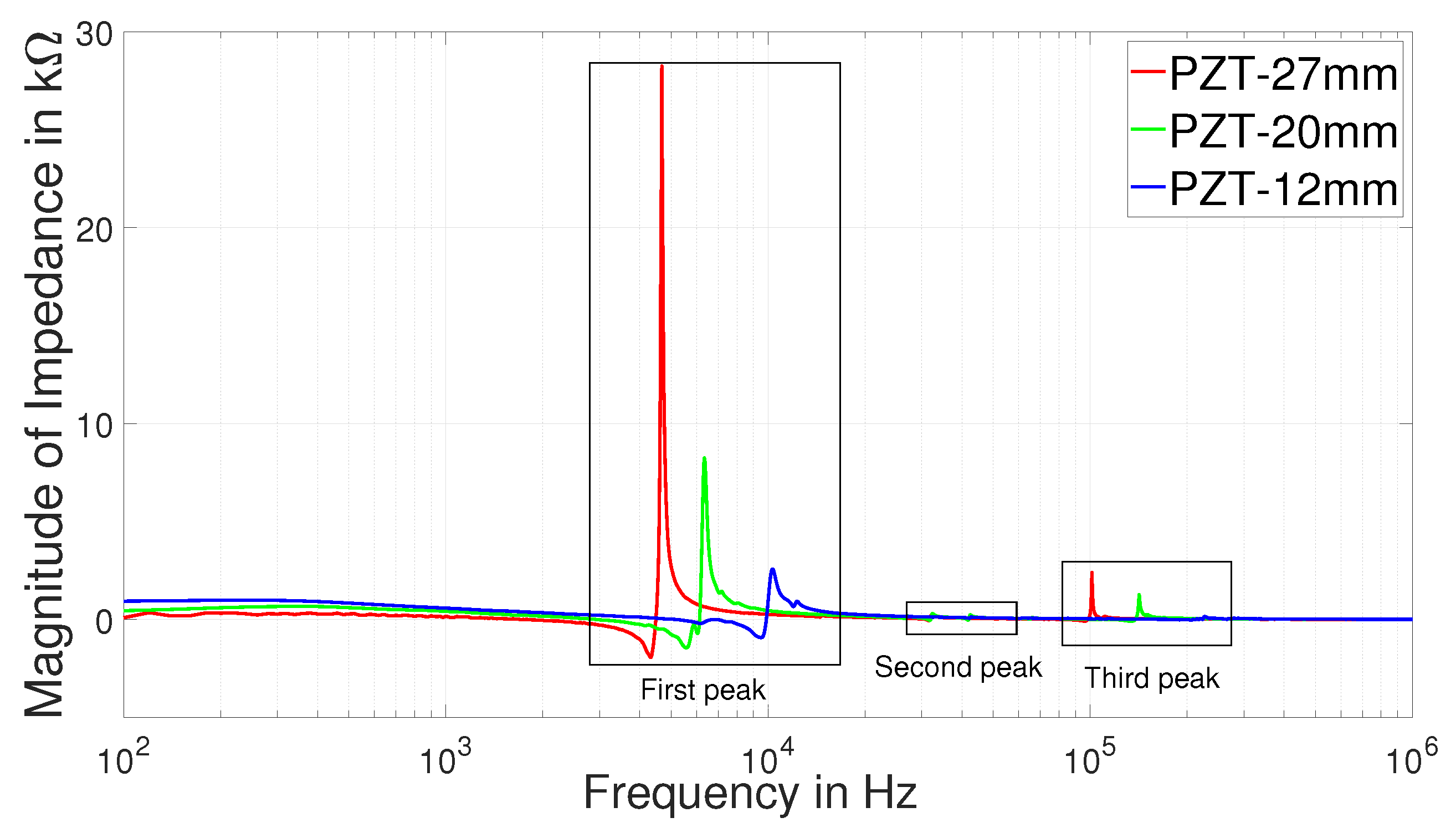
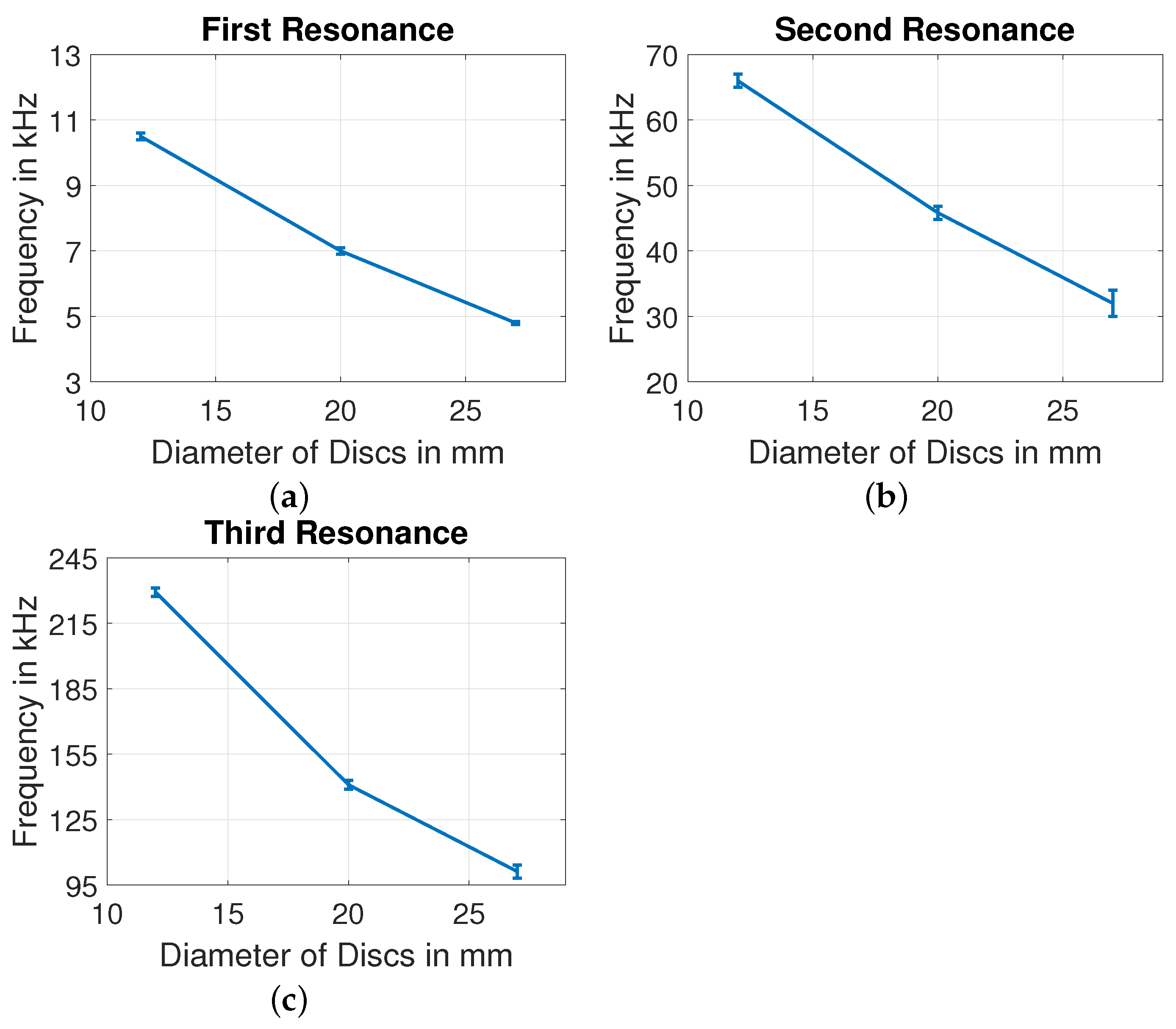
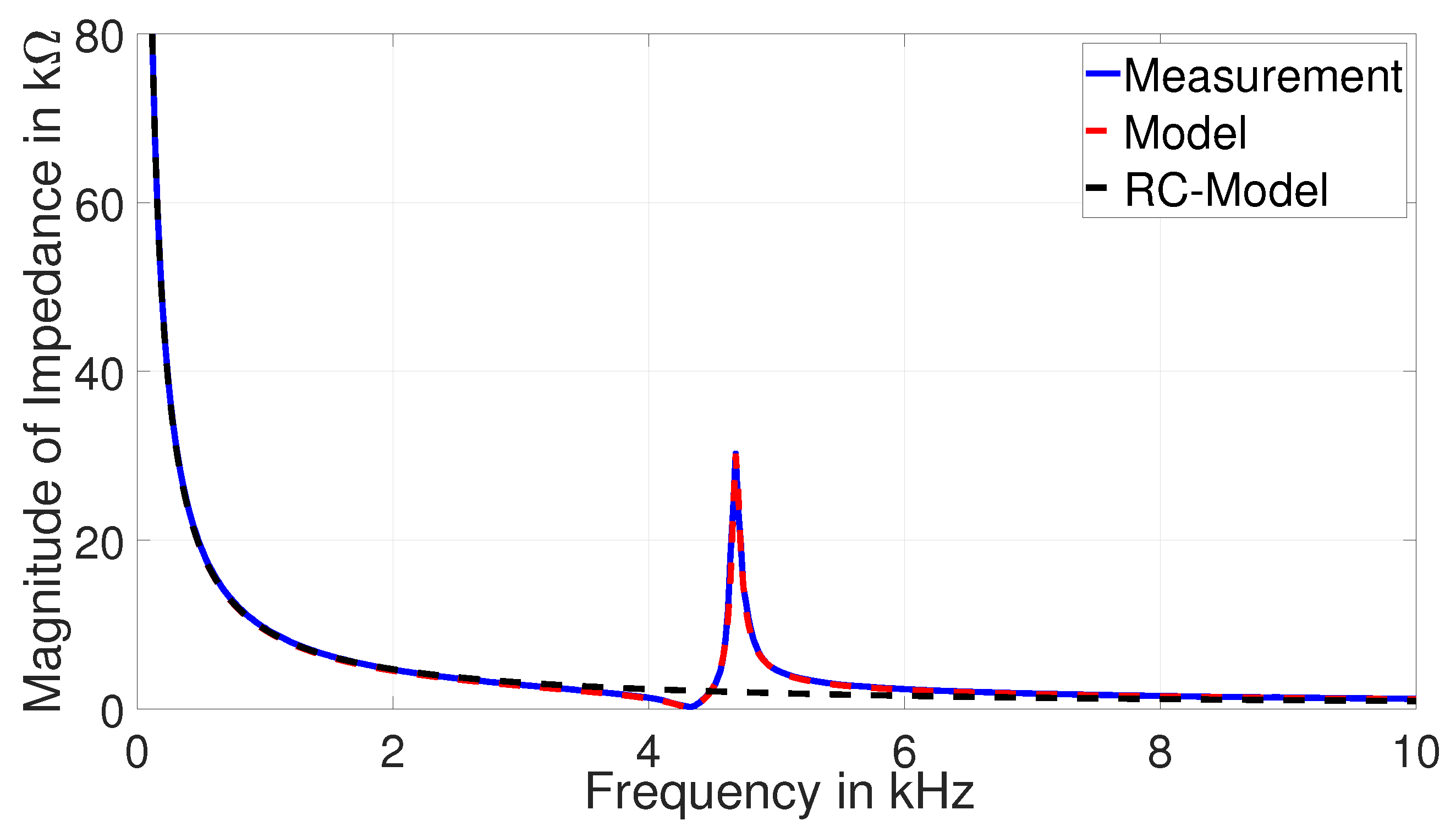
- Without mechanical load: To understand the influence of plate diameters, three PZT discs with diameters of 12 , 20 and 27 are selected for measurement in the frequency range 0.1–1000 with resolution of 20 . PZT discs are suspended in the air as shown in Figure 9, such that they can vibrate freely to obtain the impedance response.
- With mechanical load: To observe the influence of varying mechanical load, the impedance response of three discs are measured over the frequency range 0.1–1000 with a resolution of 20 at different load weights. The disc is placed flat on the table and then on top of it, equal loads are added one after another. Each load has a mass of 1.25 kg, which corresponds to force F = 12.25 N. Therefore, the pressure P equivalent to each mechanical load is derived from Equation (11). The definition of loading for the existing models mean that the piezoelectric element is mounted on a host structure, which we describe as mechanically unloaded in this paper. But in our case of mechanical loading, we apply a known mechanical load on top of the element as shown in Figure 10 below. The mechanical load on the arrangement generates normal displacement on the disc, perpendicular to its plane.
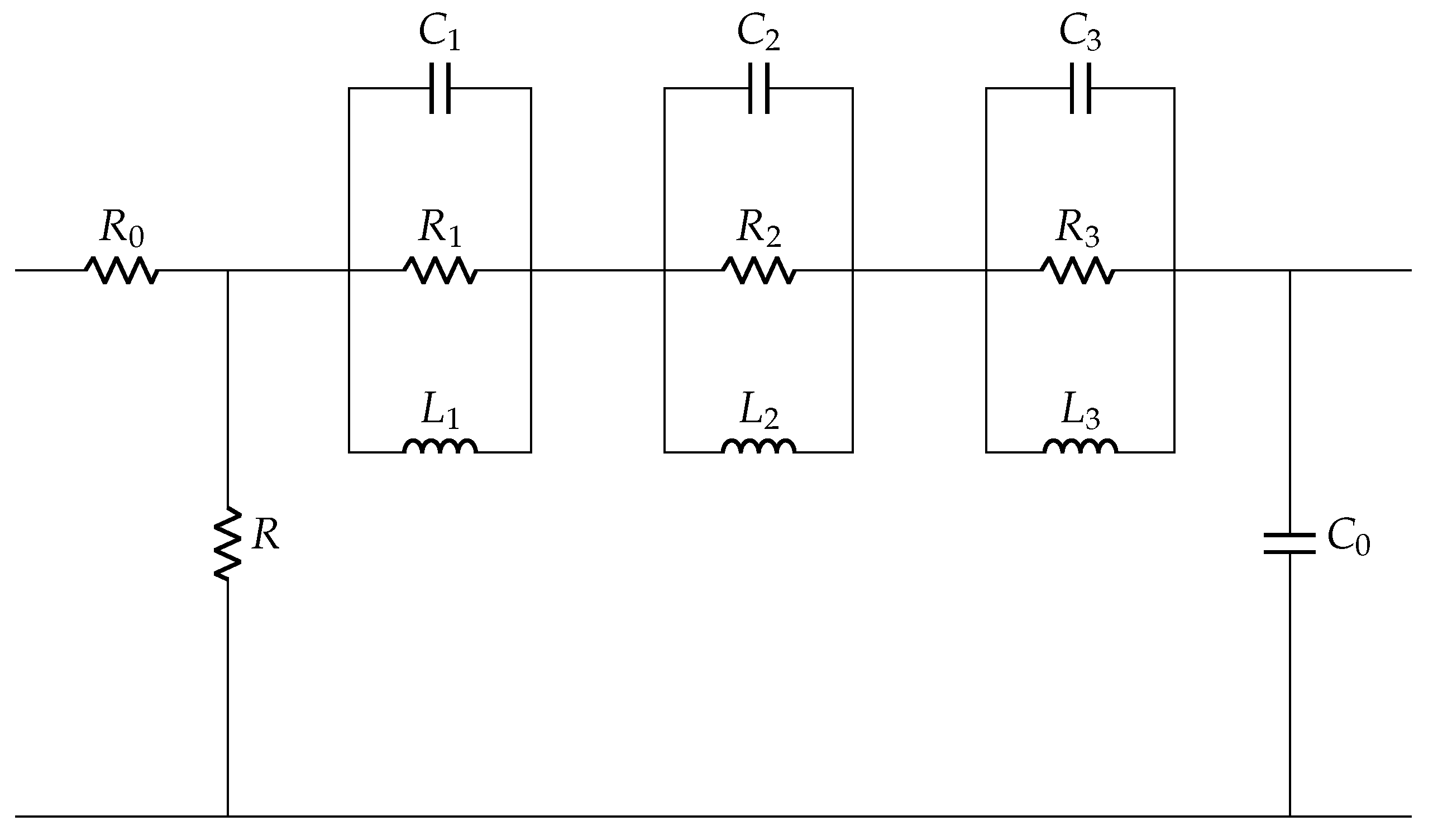
3.4. Derivation of Electrical Model Parameters
4. Results and Discussion
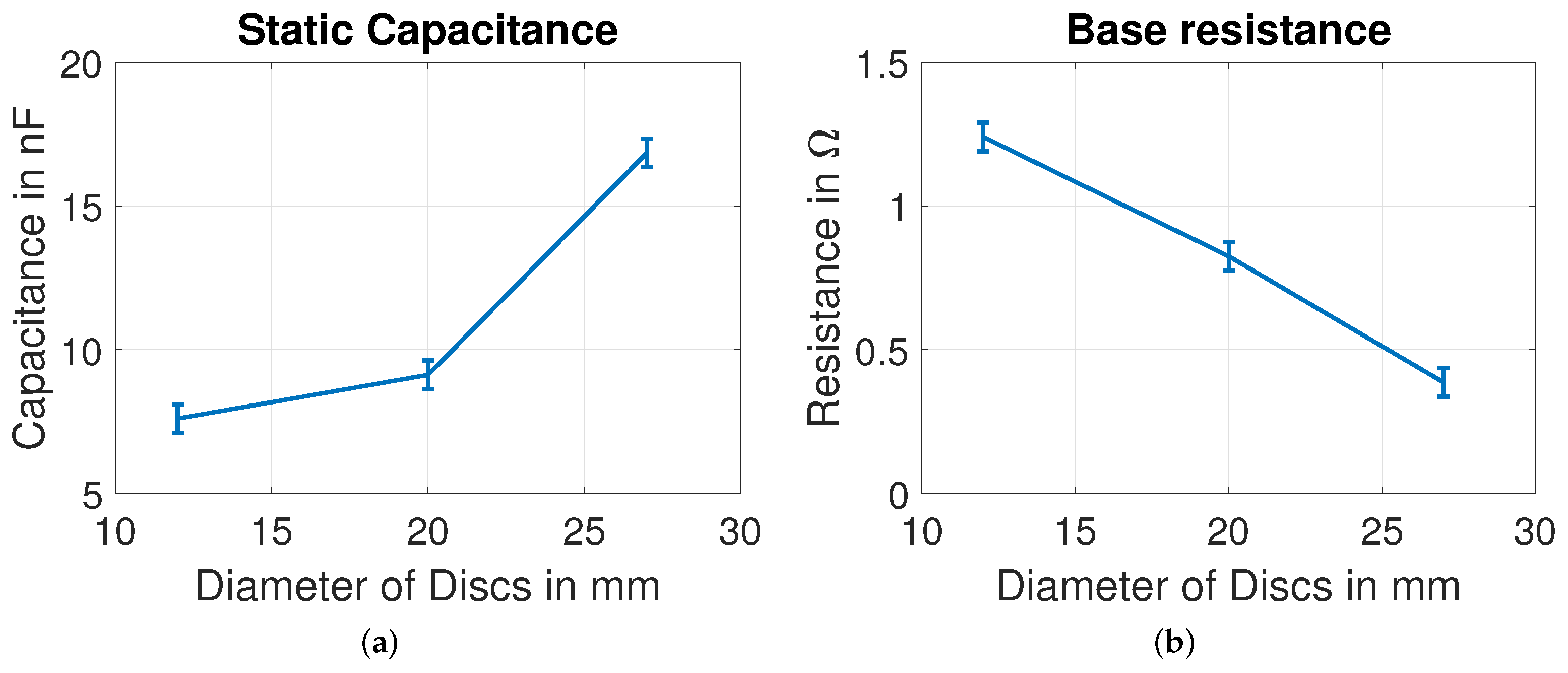
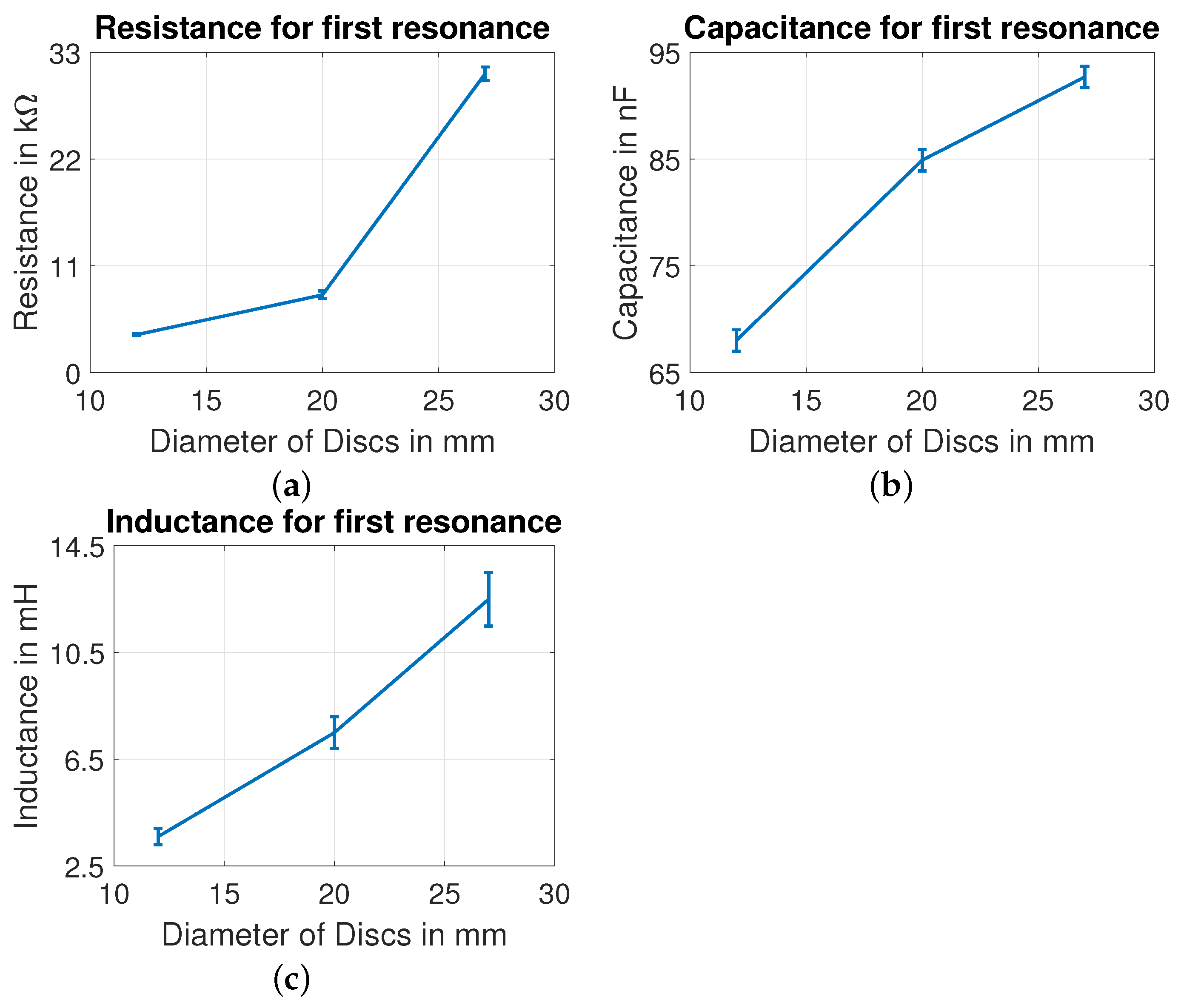
4.1. Without Mechanical Load
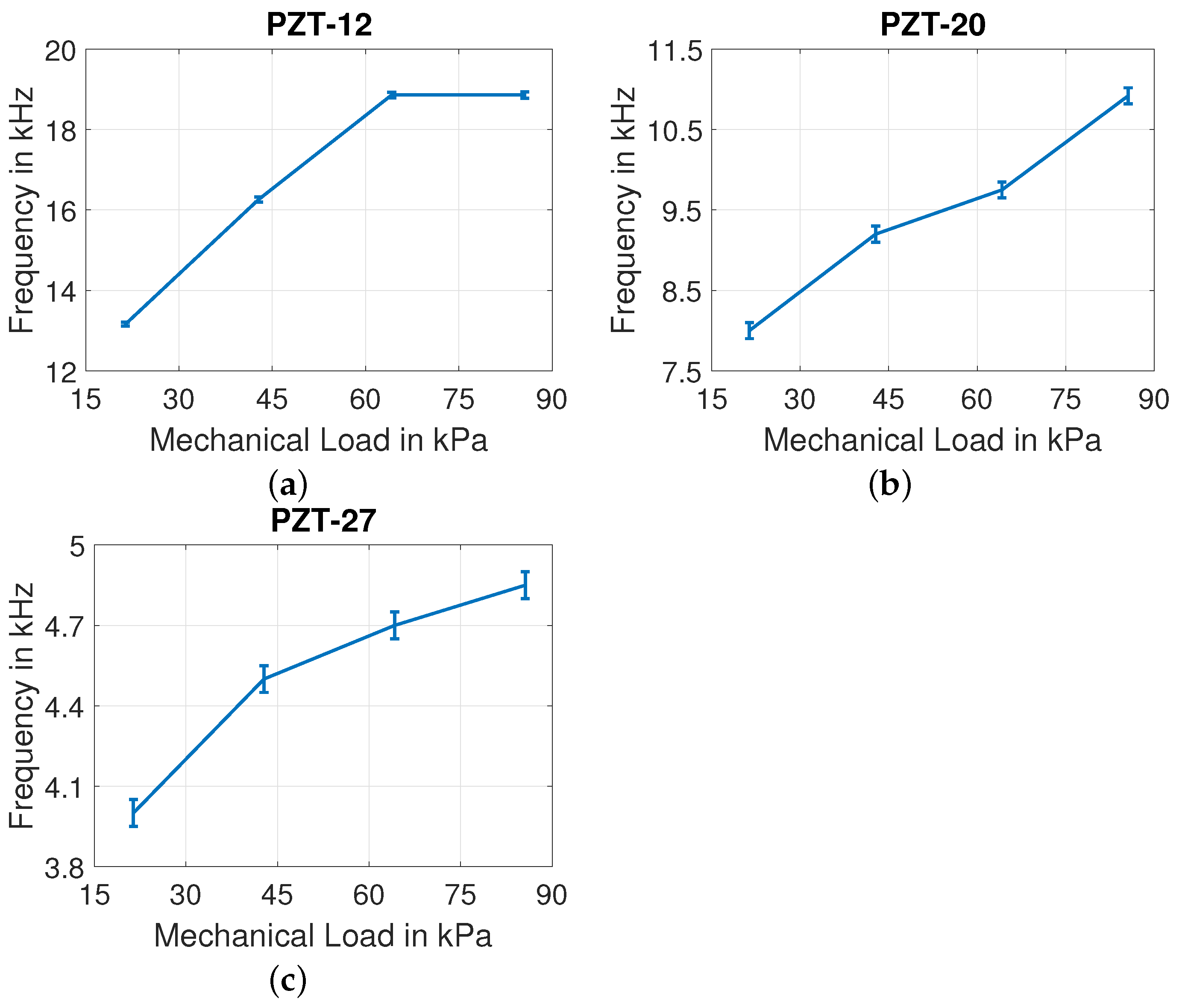
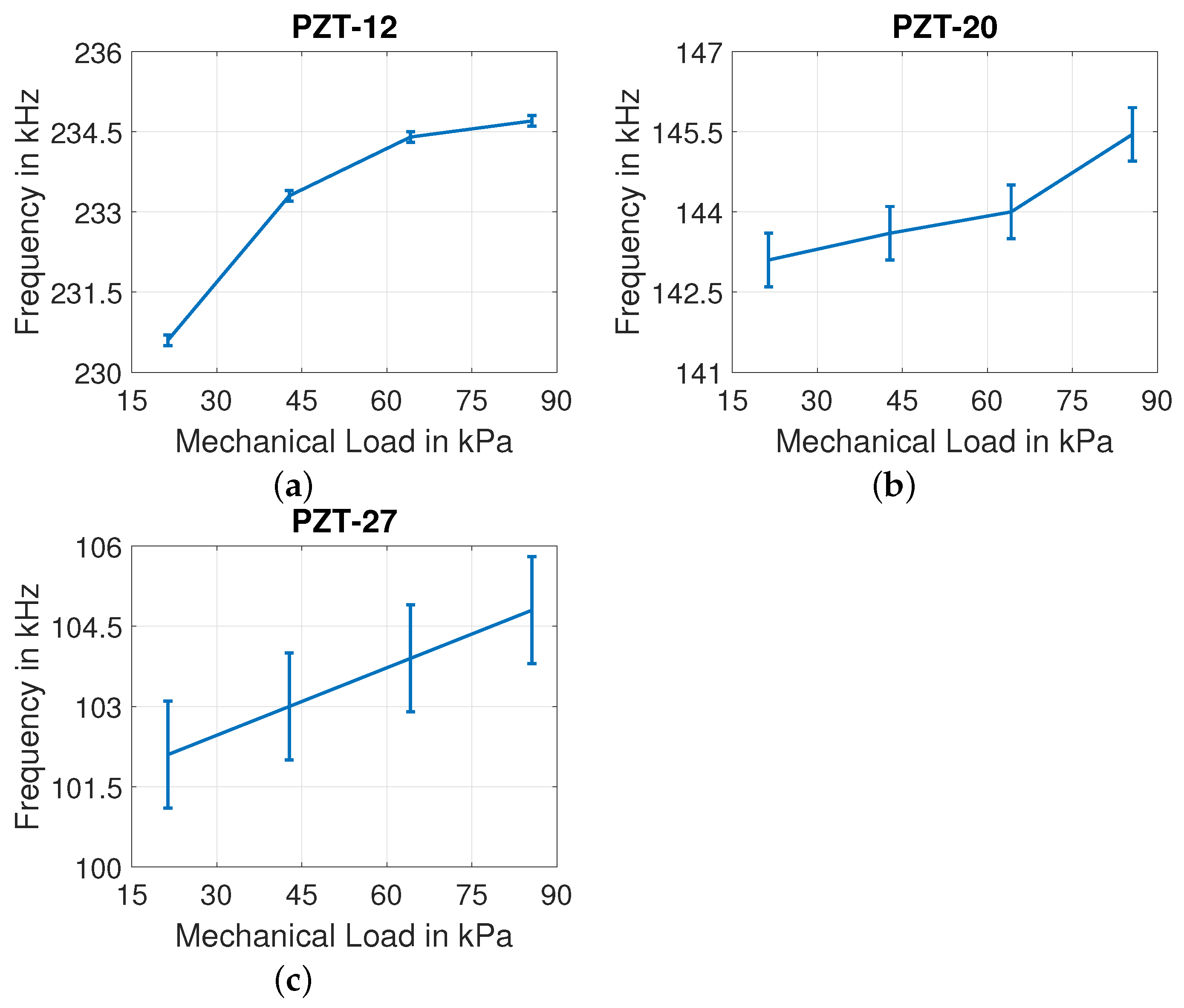
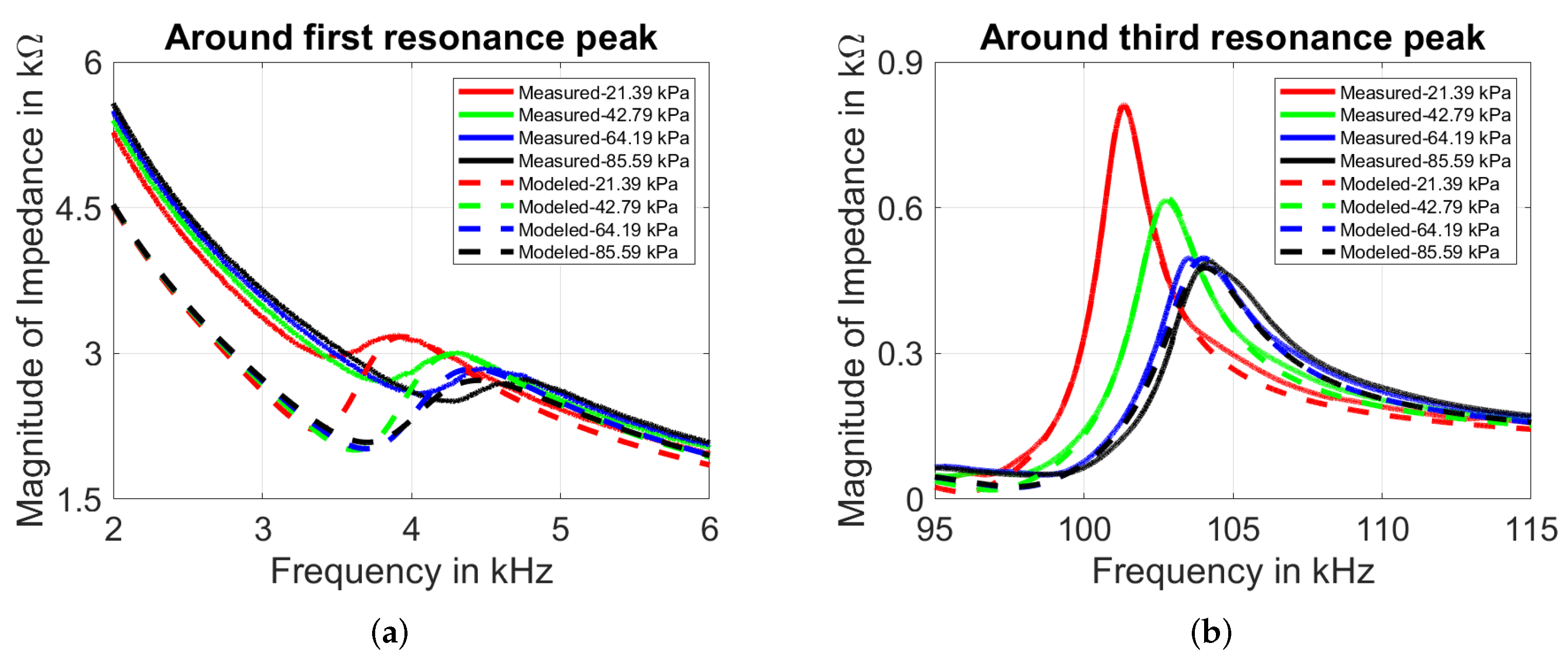
4.2. With Mechanical Load
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Uchino, K. Introduction to Piezoelectric Actuators and Transducers; Technical Report; Pennsylvania State University: State College, PA, USA, 2003. [Google Scholar]
- Yang, Z.; Zhou, S.; Zu, J.; Inman, D. High-performance piezoelectric energy harvesters and their applications. Joule 2018, 2, 642–697. [Google Scholar] [CrossRef] [Green Version]
- Safaei, M.; Sodano, H.A.; Anton, S.R. A review of energy harvesting using piezoelectric materials: State-of-the-art a decade later (2008–2018). Smart Mater. Struct. 2019, 28, 113001. [Google Scholar] [CrossRef]
- Anton, S.R.; Sodano, H.A. A review of power harvesting using piezoelectric materials (2003–2006). Smart Mater. Struct. 2007, 16, R1. [Google Scholar] [CrossRef]
- Shao, J.; Wang, T.; Yin, H.; Yang, D.; Li, Y. Bolt looseness detection based on piezoelectric impedance frequency shift. Appl. Sci. 2016, 6, 298. [Google Scholar] [CrossRef]
- Moreno-Gomez, A.; Perez-Ramirez, C.A.; Dominguez-Gonzalez, A.; Valtierra-Rodriguez, M.; Chavez-Alegria, O.; Amezquita-Sanchez, J.P. Sensors used in structural health monitoring. Arch. Comput. Methods Eng. 2018, 25, 901–918. [Google Scholar] [CrossRef]
- Ellis, T.; Cavanaugh, J.T.; Earhart, G.M.; Ford, M.P.; Foreman, K.B.; Dibble, L.E. Which measures of physical function and motor impairment best predict quality of life in Parkinson’s disease? Park. Relat. Disord. 2011, 17, 693–697. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhao, H.; Wang, Z.; Qiu, S.; Shen, Y.; Wang, J. IMU-based gait analysis for rehabilitation assessment of patients with gait disorders. In Proceedings of the 2017 4th International Conference on Systems and Informatics (ICSAI), Hangzhou, China, 11–13 November 2017; pp. 622–626. [Google Scholar] [CrossRef]
- Qiu, S.; Wang, Z.; Zhao, H.; Liu, L.; Jiang, Y. Using body-worn sensors for preliminary rehabilitation assessment in stroke victims with gait impairment. IEEE Access 2018, 6, 31249–31258. [Google Scholar] [CrossRef]
- Sijobert, B.; Denys, J.; Coste, C.A.; Geny, C. IMU based detection of freezing of gait and festination in Parkinsons disease. In Proceedings of the 2014 IEEE 19th International Functional Electrical Stimulation Society Annual Conference (IFESS), Kuala Lumpur, Malaysia, 17–19 September 2014; pp. 1–3. [Google Scholar] [CrossRef]
- Shu, L.; Hua, T.; Wang, Y.; Li, Q.; Feng, D.D.; Tao, X. In-shoe plantar pressure measurement and analysis system based on fabric pressure sensing array. IEEE Trans. Inf. Technol. Biomed. 2010, 14, 767–775. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mao, Y.; Shen, M.; Liu, B.; Xing, L.; Chen, S.; Xue, X. Self-powered piezoelectric-biosensing textiles for the physiological monitoring and time-motion analysis of individual sports. Sensors 2019, 19, 3310. [Google Scholar] [CrossRef] [Green Version]
- Yu, T.H.; Tsai, F.J.; Lu, T.C. Development of an Immediate Feedback System of Movement Speed and Performance with a Piezoelectric Sensor and its Application in Sport Training. In Proceedings of the 2019 IEEE 2nd International Conference on Knowledge Innovation and Invention (ICKII), Seoul, Korea, 12–15 July 2019; pp. 104–107. [Google Scholar] [CrossRef]
- Xia, H.; Xia, Y.; Ye, Y.; Qian, L.; Shi, G. Simultaneous wireless strain sensing and energy harvesting from multiple piezo-patches for structural health monitoring applications. IEEE Trans. Ind. Electron. 2018, 66, 8235–8243. [Google Scholar] [CrossRef]
- Kim, H.S.; Kim, J.H.; Kim, J. A review of piezoelectric energy harvesting based on vibration. Int. J. Precis. Eng. Manuf. 2011, 12, 1129–1141. [Google Scholar] [CrossRef]
- Shenck, N.S.; Paradiso, J.A. Energy scavenging with shoe-mounted piezoelectrics. IEEE Micro 2001, 21, 30–42. [Google Scholar] [CrossRef]
- Colson, G.; Laurent, P.; Bellier, P.; Stoukatch, S.; Dupont, F.; Kraft, M. Smart-shoe self-powered by walking. In Proceedings of the 2017 IEEE 14th International Conference on Wearable and Implantable Body Sensor Networks (BSN), Eindhoven, The Netherlands, 9–12 May 2017; pp. 35–38. [Google Scholar]
- Lefeuvre, E.; Badel, A.; Benayad, A.; Lebrun, L.; Richard, C.; Guyomar, D. A comparison between several approaches of piezoelectric energy harvesting. J. Phys. IV France 2005, 128, 177–186. [Google Scholar] [CrossRef]
- Ottman, G.; Hofmann, H.; Bhatt, A.; Lesieutre, G. Adaptive piezoelectric energy harvesting circuit for wireless remote power supply. IEEE Trans. Power Electron. 2002, 17, 669–676. [Google Scholar] [CrossRef] [Green Version]
- Moro, L.; Benasciutti, D. Harvested power and sensitivity analysis of vibrating shoe-mounted piezoelectric cantilevers. Smart Mater. Struct. 2010, 19, 115011. [Google Scholar] [CrossRef]
- Zhao, J.; You, Z. A shoe-embedded piezoelectric energy harvester for wearable sensors. Sensors 2014, 14, 12497–12510. [Google Scholar] [CrossRef]
- Asano, S.; Nishimura, S.; Ikeda, Y.; Morita, T.; Hosaka, H. Energy harvester for safety shoes using parallel piezoelectric links. Sens. Actuators A Phys. 2020, 309, 112000. [Google Scholar] [CrossRef]
- Quattrocchi, A.; Montanini, R.; De Caro, S.; Panarello, S.; Scimone, T.; Foti, S.; Testa, A. A new approach for impedance tracking of piezoelectric vibration energy harvesters based on a zeta converter. Sensors 2020, 20, 5862. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Tang, L. Equivalent circuit modeling of piezoelectric energy harvesters. J. Intell. Mater. Syst. Struct. 2009, 20, 2223–2235. [Google Scholar] [CrossRef]
- Banerjee, D.; Banerjee, P.; Goswami, B.; Ghosh, R. Deriving an electrical model of a two terminal piezoelectric buzzer from its impedance response. In Proceedings of the 2018 IEEE Applied Signal Processing Conference (ASPCON), Kolkata, India, 7–9 December 2018; pp. 114–118. [Google Scholar] [CrossRef]
- Staworko, M.; Uhl, T. Modeling and simulation of piezoelectric elements-comparison of available methods and tools. Mech. Univ. Sci. Technol. 2008, 27, 161–171. [Google Scholar]
- Cheng, C.; Chen, Z.; Shi, H.; Liu, Z.; Xiong, Y. System-level coupled modeling of piezoelectric vibration energy harvesting systems by joint finite element and circuit analysis. Shock Vib. 2016. [Google Scholar] [CrossRef]
- Kuznetsova, I.; Zaitsev, B.; Shikhabudinov, A.; Tsivileva, O.; Pankratov, A.; Verona, E. Acousto-electronic gas sensor based on mushroom mycelial extracts. Sens. Actuators B Chem. 2017, 243, 525–531. [Google Scholar] [CrossRef]
- Sherrit, S.; Leary, S.P.; Dolgin, B.P.; Bar-Cohen, Y. Comparison of the Mason and KLM equivalent circuits for piezoelectric resonators in the thickness mode. In Proceedings of the 1999 IEEE Ultrasonics Symposium. Proceedings, International Symposium (Cat. No. 99CH37027), Caesars Tahoe, NV, USA, 17–20 October 1999; Volume 2, pp. 921–926. [Google Scholar]
- Zaitsev, B.; Joshi, S.; Dhuru, V. Elastic properties of dentin bonding agents using bulk acoustic waves. In Proceedings of the 1997 IEEE Ultrasonics Symposium Proceedings. An International Symposium (Cat. No. 97CH36118), Toronto, ON, Canada, 5–8 October 1997; Volume 1, pp. 623–626. [Google Scholar]
- Kuznetsova, I.E.; Zaitsev, B.D.; Shikhabudinov, A.M. Elastic and viscous properties of nanocomposite films based on low-density polyethylene. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2010, 57, 2099–2102. [Google Scholar] [CrossRef] [PubMed]
- Sherrit, S.; Mukherjee, B.K. Characterization of piezoelectric materials for transducers. arXiv 2007, arXiv:0711.2657. [Google Scholar]
- Meitzler, A.; Tiersten, H.; Warner, A.; Berlincourt, D.; Couqin, G.; Welsh III, F. IEEE Standard on Piezoelectricity ANSI/IEEE Std 176–1987; The Institute of Electrical and Electronics Engineers Inc.: New York, NY, USA, 1987. [Google Scholar]
- Sherrit, S.; Wiederick, H.; Mukherjee, B.; Sayer, M. An accurate equivalent circuit for the unloaded piezoelectric vibrator in the thickness mode. J. Phys. D Appl. Phys. 1997, 30, 2354. [Google Scholar] [CrossRef]
- Park, C.H. On the circuit model of piezoceramics. J. Intell. Mater. Syst. Struct. 2001, 12, 515–522. [Google Scholar] [CrossRef]
- Guan, M.; Liao, W.H. Studies on the circuit models of piezoelectric ceramics. In Proceedings of the International Conference on Information Acquisition, Hefei, China, 21–25 June 2004; pp. 26–31. [Google Scholar] [CrossRef]
- Kim, J.; Grisso, B.L.; Kim, J.K.; Ha, D.S.; Inman, D.J. Electrical modeling of piezoelectric ceramics for analysis and evaluation of sensory systems. In Proceedings of the 2008 IEEE Sensors Applications Symposium, Atlanta, GA, USA, 12–14 February 2008; pp. 122–127. [Google Scholar] [CrossRef]
- Koszewnik, A.; Grześ, P.; Walendziuk, W. Mechanical and electrical impedance matching in a piezoelectric beam for Energy Harvesting. Eur. Phys. J. Spec. Top. 2015, 224, 2719–2731. [Google Scholar] [CrossRef]
- Liang, C.; Sun, F.; Rogers, C.A. Electro-mechanical impedance modeling of active material systems. Smart Mater. Struct. 1996, 5, 171. [Google Scholar] [CrossRef]
- Electronics, Murata. 7BB-12-9. PD-SU2-C12-90. Available online: https://www.murata.com/en-eu/products/productdetail?partno=7BB-12-9 (accessed on 20 January 2022).
- Electronics, Murata. 7BB-20-6. PD-SU2-C20-63. Available online: https://www.murata.com/en-eu/products/productdetail?partno=7BB-20-6 (accessed on 20 January 2022).
- Electronics, Murata. 7BB-27-4. PD-SU2-C27-46. Available online: https://www.murata.com/en-eu/products/productdetail?partno=7BB-27-4 (accessed on 20 January 2022).
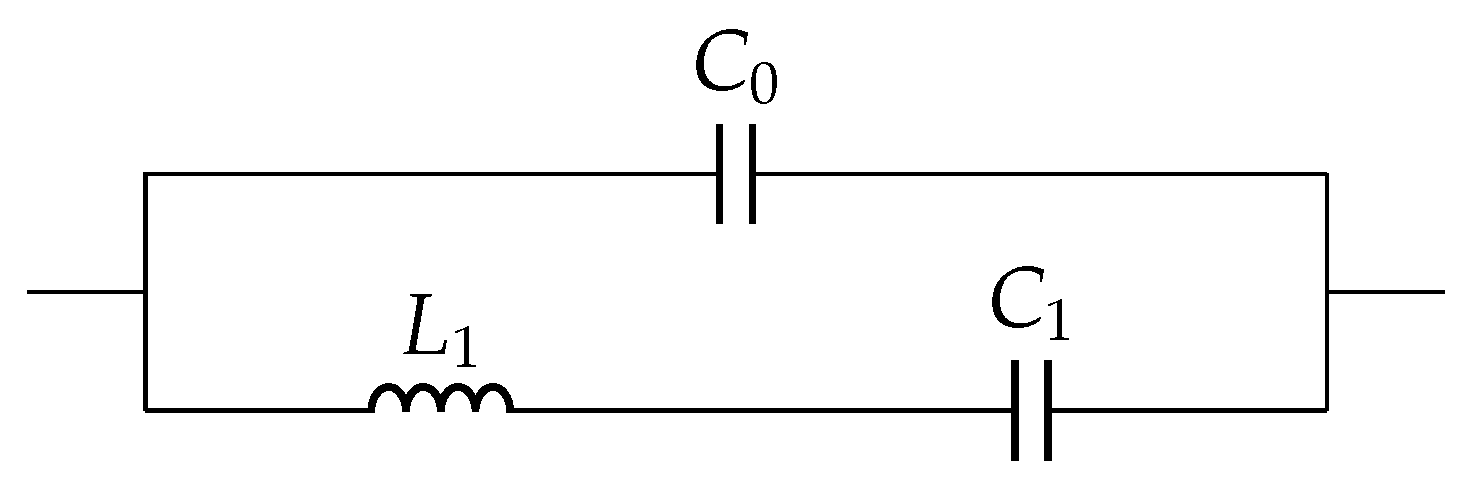
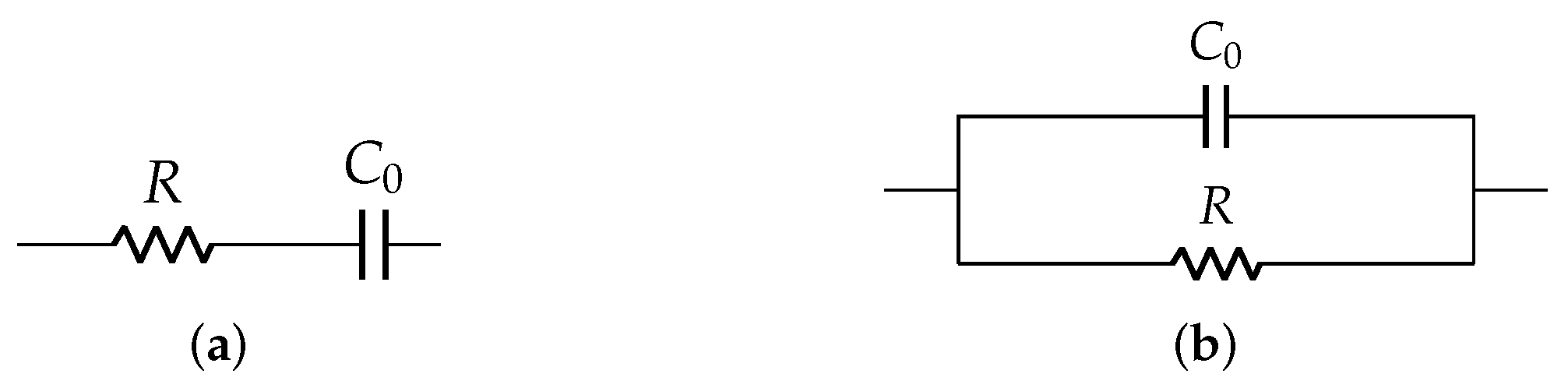

| Name | Based on | Condition | Remarks |
|---|---|---|---|
| Mason | Material constants, field constants, and structure geometry | Both loaded and unloaded condition | Negative capacitance and determination of complex elements for lossy materials |
| Van Dyke | Material constants, field constants, and structure geometry | Both loaded and unloaded condition | Inaccurate in nonresonant frequency range and for lossy materials |
| Sherrit | Material constants, field constants, and structure geometry | Only unloaded condition | Determination of complex elements |
| Park | Impedance response | Only unloaded condition | Below ultrasonic frequency range |
| Guan | Impedance response | Both loaded and unloaded condition | Based on visual inspection, energy dissipation |
| Easy | Impedance response | Both loaded and unloaded condition | Limited frequency range, Simple |
| Banerjee | Impedance response | Only unloaded condition | Limited frequency range, Simple |
| Our model | Impedance response | Both loaded and unloaded condition | Wide frequency range, Simple |
| Product Name | Plate Diameter (mm) | Structure Thickness (mm) | Ceramic Thickness (mm) | Mass (mg) |
|---|---|---|---|---|
| 7BB-12-9 | 12 | 0.22 | 0.12 | 142 |
| 7BB-20-6 | 20 | 0.42 | 0.22 | 776 |
| 7BB-27-4 | 27 | 0.54 | 0.24 | 1968 |
| Resistance | Capacitance | Inductor | Quality Factor |
|---|---|---|---|
| R = e6 | |||
| = 0.4 | = 16.85 | ||
| = 30,300 | = 95.40 | = 12.1 | = 85 |
| = 355 | = 770.56 | = 32.1 | = 55 |
| = 2525 | = 118.34 | = 20.9 | = 190 |
| Load | Resistance | Capacitance | Inductor | |||
|---|---|---|---|---|---|---|
| No load | R = | |||||
| = 0.4 | = 16.85 | |||||
| = 30,300 | = 95.40 | = 12.1 | ||||
| = 355 | = 770.56 | = 32.1 | ||||
| = 2525 | = 118.34 | = 20.9 | ||||
| 21.39 | = 900 | = 14.14 | = 0.7162 | |||
| = 1400 | = 105.2 | = 3.3 | ||||
| = 1180 | = 10.5 | = 230.1 | ||||
| = 470 | = 101.5 | = 11.08 | ||||
| 42.79 | = 400 | = 0.795 | = 0.0141 | |||
| = 1300 | = 65.9 | = 2.526 | ||||
| = 980 | = 9.7 | = 190 | ||||
| = 450 | 47.16 | = 0.9549 | ||||
| 64.19 | = 350 | = 0.641 | = 0.0137 | |||
| = 1000 | = 48.7 | = 2.16 | ||||
| = 920 | = 8.5 | = 181.58 | ||||
| = 370 | = 40.4 | = 0.8660 | ||||
| 85.5 | = 300 | = 0.573 | = 0.0129 | |||
| = 850 | = 44.25 | = 1.89 | ||||
| = 900 | = 8.47 | = 181.51 | ||||
| = 300 | = 40.4 | = 0.5684 |
| Load | Relative Error | Correlation Coefficient |
|---|---|---|
| 0 | 9.46 % | 0.9985 |
| 21.39 () | 11.76 % | 0.9995 |
| 42.79 () | 11.83 % | 0.9995 |
| 64.19 () | 12.76 % | 0.9994 |
| 85.59 () | 14.21 % | 0.9995 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gogoi, N.; Chen, J.; Kirchner, J.; Fischer, G. Dependence of Piezoelectric Discs Electrical Impedance on Mechanical Loading Condition. Sensors 2022, 22, 1710. https://doi.org/10.3390/s22051710
Gogoi N, Chen J, Kirchner J, Fischer G. Dependence of Piezoelectric Discs Electrical Impedance on Mechanical Loading Condition. Sensors. 2022; 22(5):1710. https://doi.org/10.3390/s22051710
Chicago/Turabian StyleGogoi, Niharika, Jie Chen, Jens Kirchner, and Georg Fischer. 2022. "Dependence of Piezoelectric Discs Electrical Impedance on Mechanical Loading Condition" Sensors 22, no. 5: 1710. https://doi.org/10.3390/s22051710
APA StyleGogoi, N., Chen, J., Kirchner, J., & Fischer, G. (2022). Dependence of Piezoelectric Discs Electrical Impedance on Mechanical Loading Condition. Sensors, 22(5), 1710. https://doi.org/10.3390/s22051710








