Delineation of Nitrate Reduction Hotspots in Artificially Drained Areas through Assessment of Small-Scale Spatial Variability of Electrical Conductivity Data
Abstract
1. Introduction
2. Materials and Methods
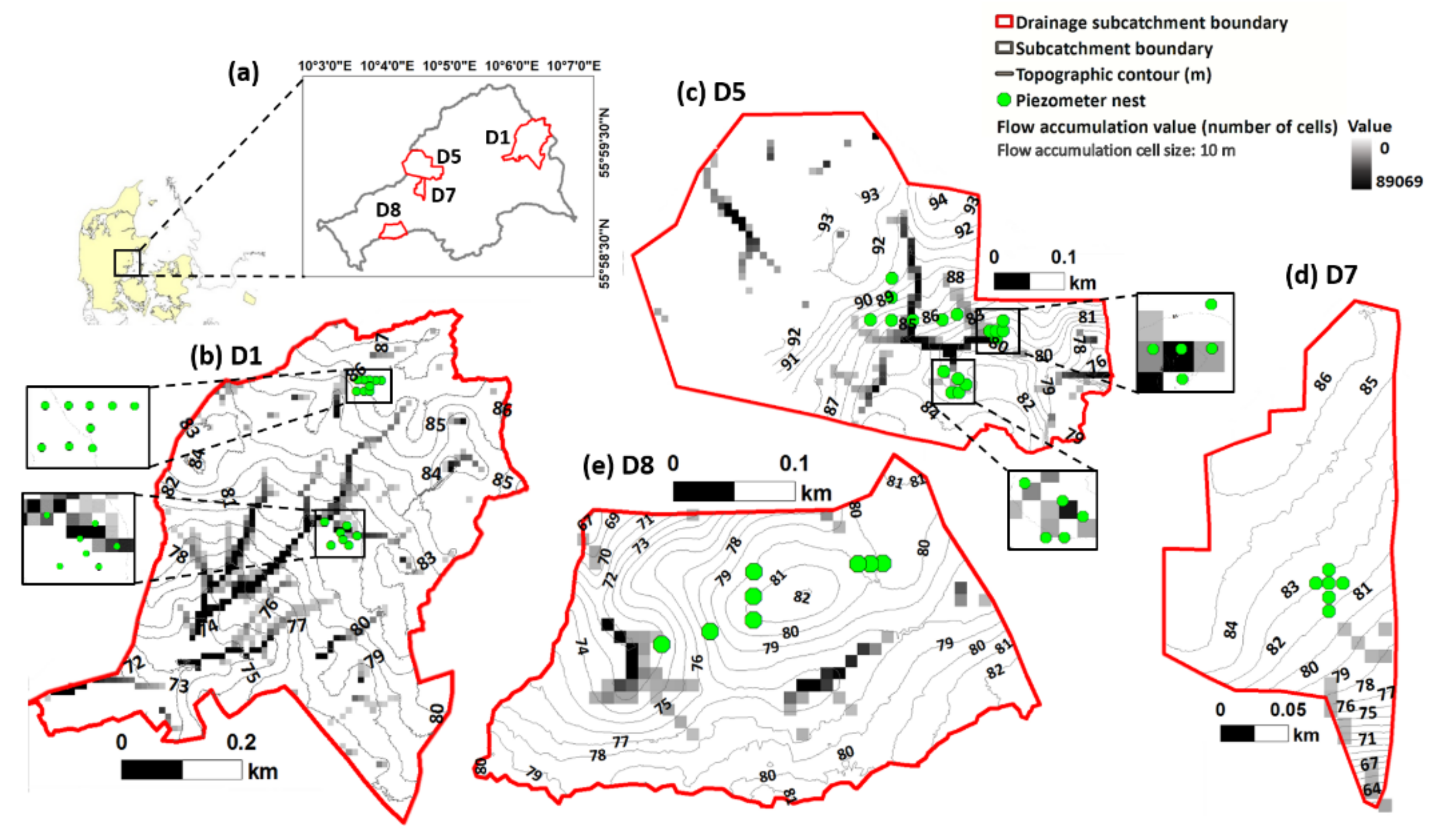
2.1. Study Area
2.2. Flow Accumulation
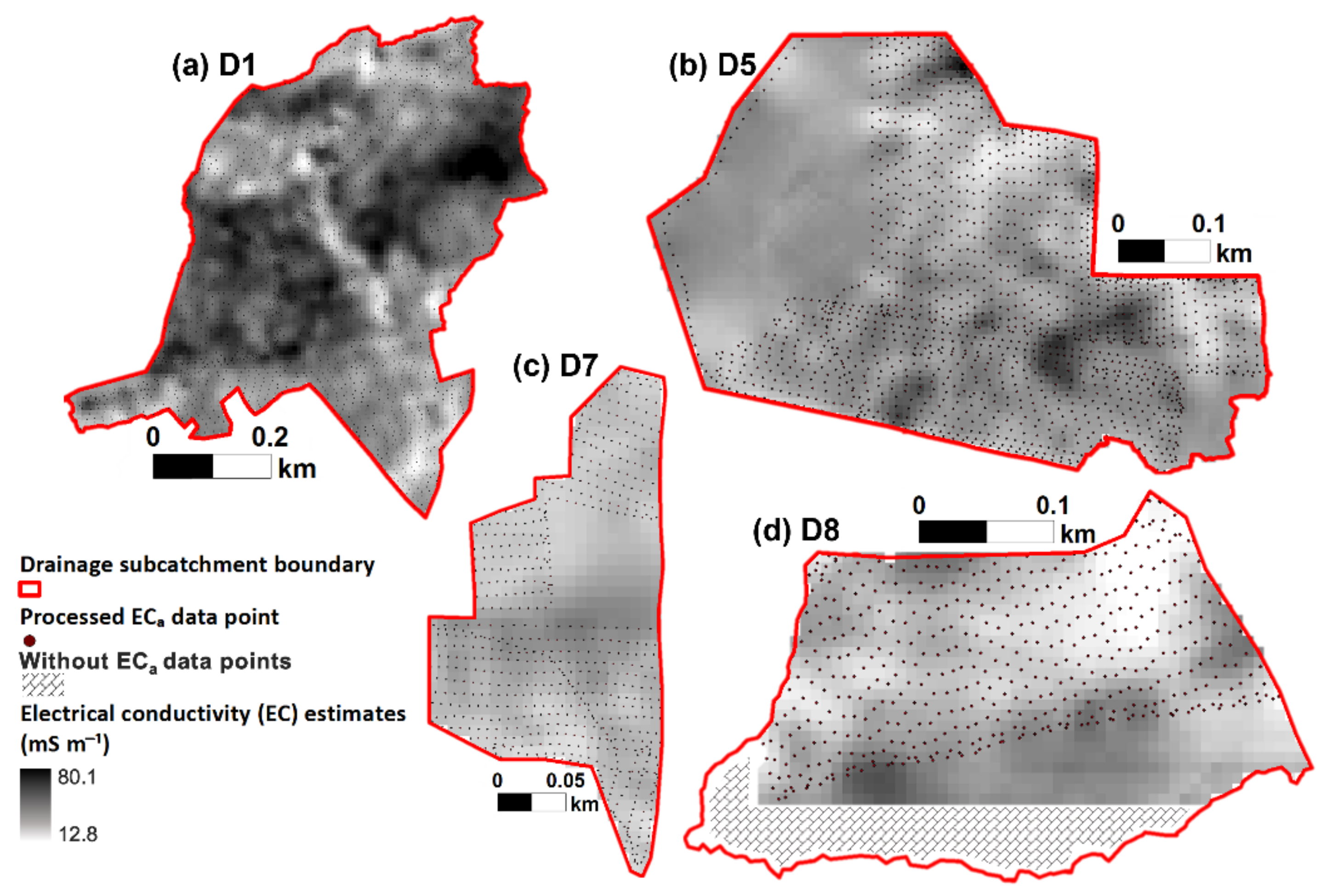
2.3. Electromagnetic Induction Survey, Data Processing, and Inversion
2.4. Measurement of NO3− Concentrations
2.5. Measurement of Redox Potential Values
2.6. Spatial Autocorrelation Using Global Moran’s I Statistic
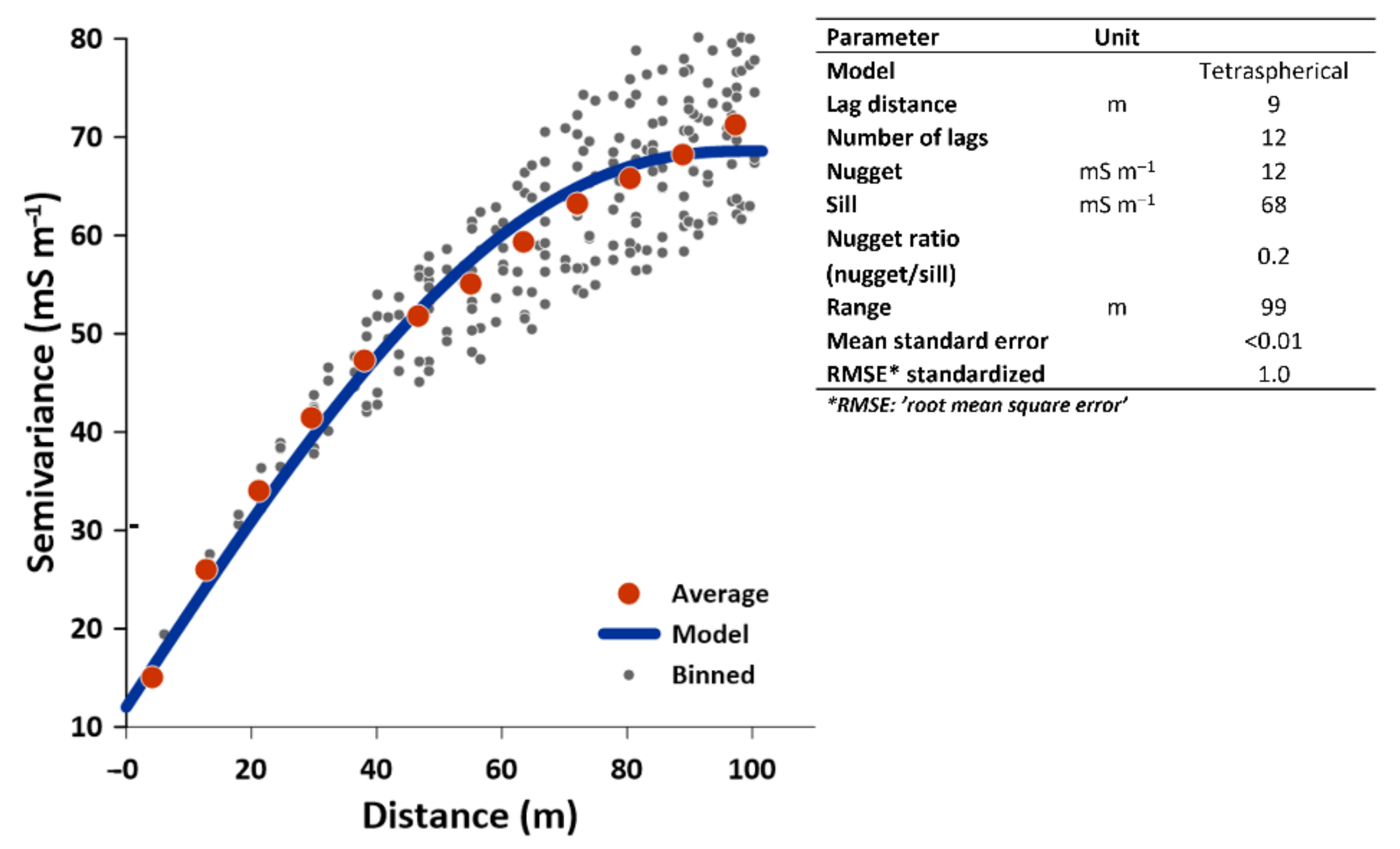
2.7. Geostastistics of EC
2.8. Clustering of EC Values with Optimized Hot Spot Analysis (Getis–Ord Gi* Statistics)
2.9. Clustering of EC Values Using Unsupervised ISODATA Clustering
2.10. Data Analysis
3. Results and Discussion
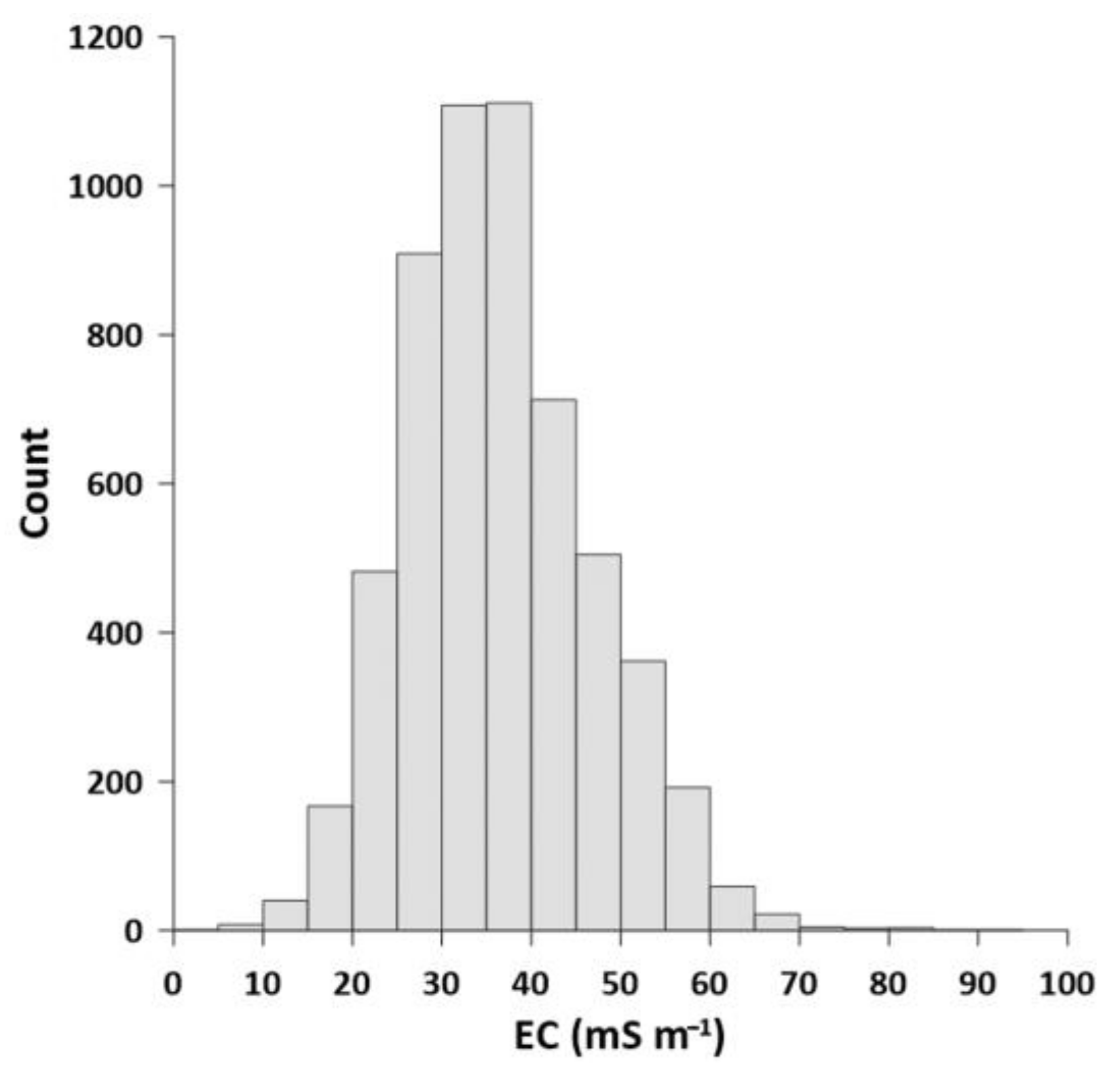
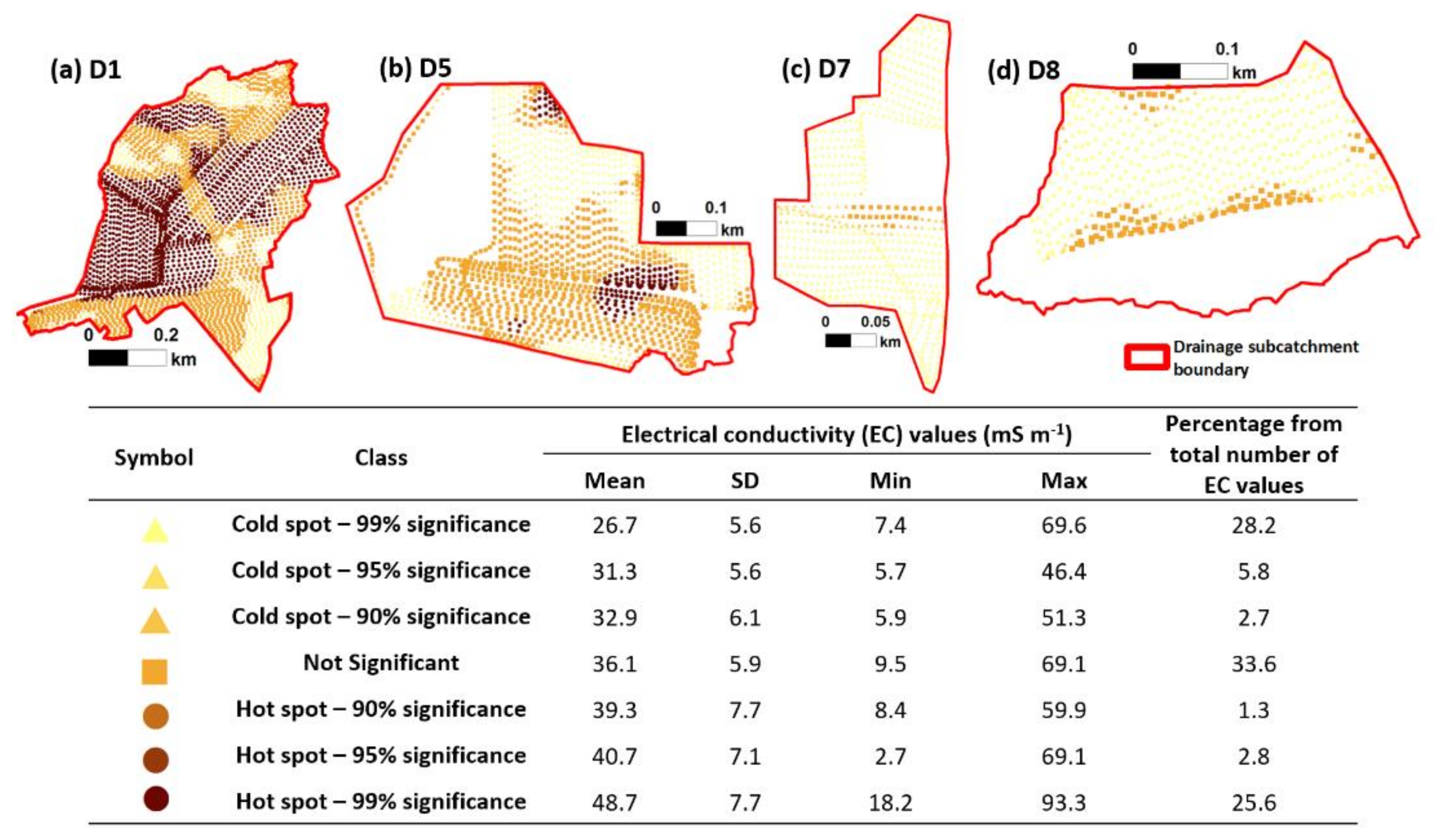
3.1. Distribution and Descriptive Statistics and Spatial Distribution of EC Values
3.2. Clustering of EC Values
3.2.1. Optimized Hot Spot Analysis of EC Values (Getis–Ord Gi* Statistics)
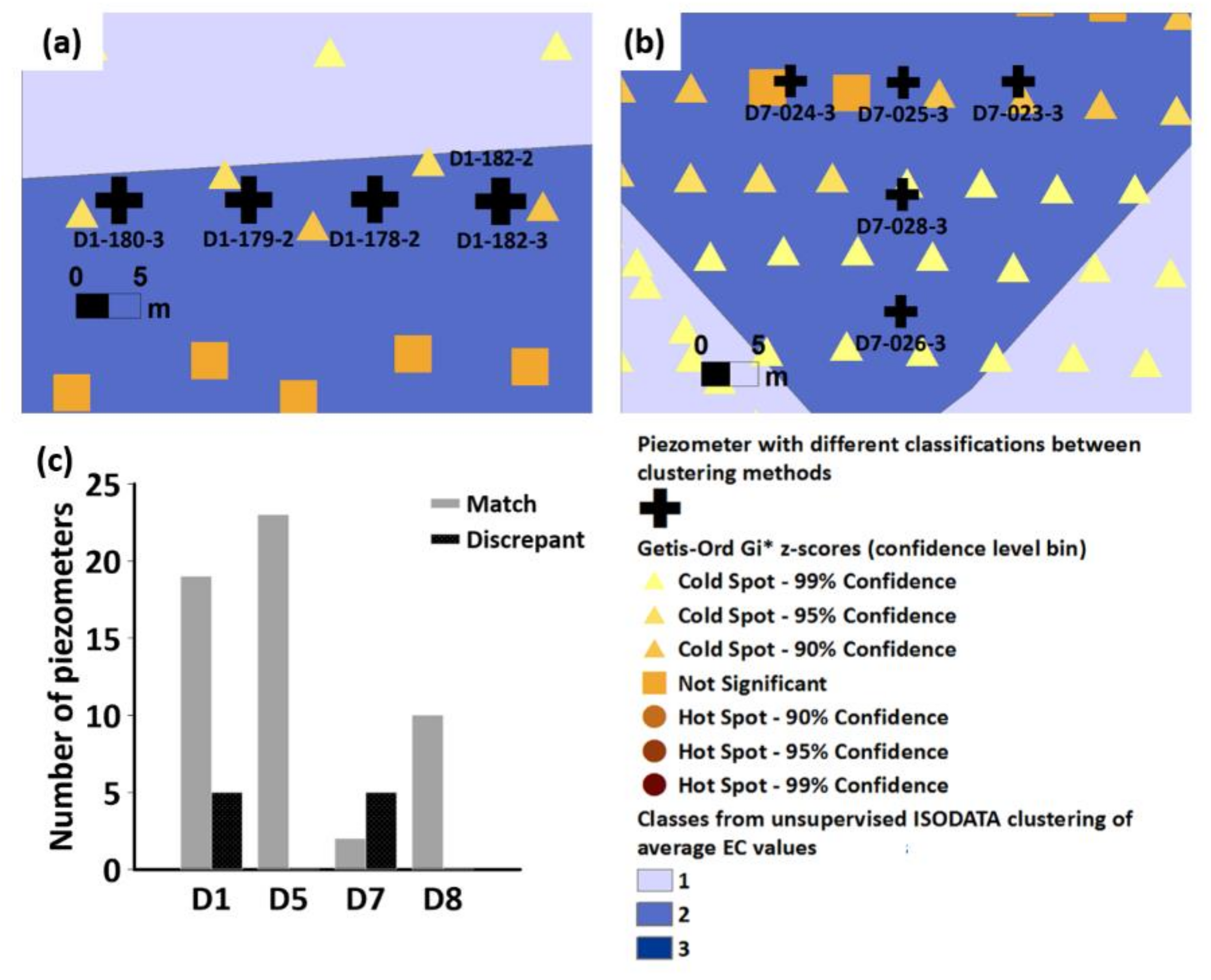
3.2.2. Unsupervised ISODATA Clustering Results
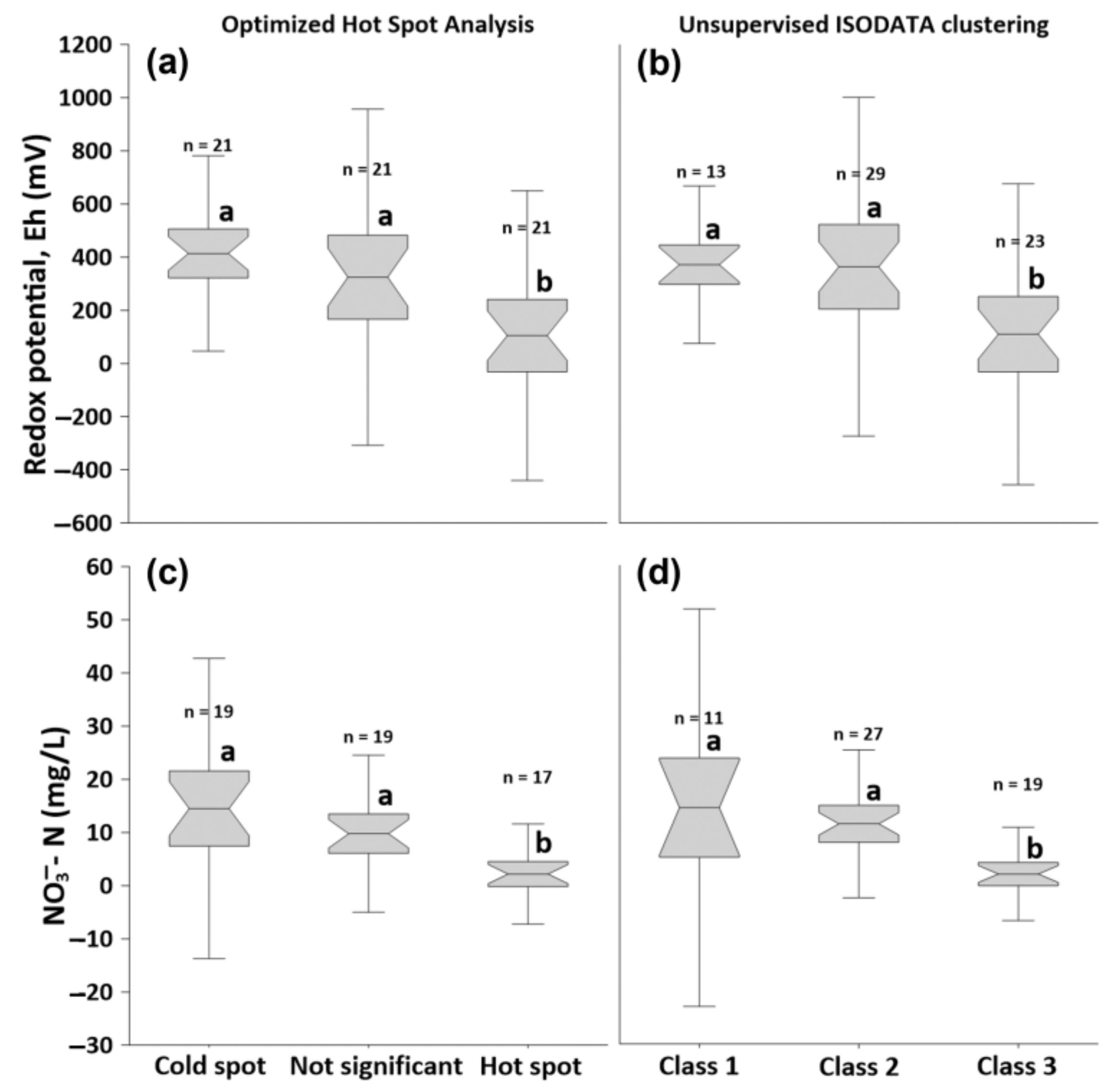
3.3. Comparison of Redox Potential Values and NO3− Concentrations from Classified Piezometers
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Piezometer | X | Y | Installation Depth | ISODATA Class | Gi bin (Confidence Level Bin) | HOTSPOT Class | Do the Classes Match between Two Clustering Methods? |
|---|---|---|---|---|---|---|---|
| D1-013-3 | 568,950.29 | 6,205,760.41 | 135 | 3 | 3 | 99% hotspot | MATCH |
| D1-099-2 | 568,955.31 | 6,205,749.16 | 65 | 3 | 3 | 99% hotspot | MATCH |
| D1-099-3 | 568,955.35 | 6,205,749.61 | 125 | 3 | 3 | 99% hotspot | MATCH |
| D1-100-2 | 568,978.96 | 6,205,754.65 | 135 | 3 | 3 | 99% hotspot | MATCH |
| D1-100-3 | 568,979.10 | 6,205,754.98 | 165 | 3 | 3 | 99% hotspot | MATCH |
| D1-102-2 | 568,925.47 | 6,205,778.52 | 115 | 3 | 3 | 99% hotspot | MATCH |
| D1-102-3 | 568,925.68 | 6,205,778.99 | 145 | 3 | 3 | 99% hotspot | MATCH |
| D1-104-2 | 568,935.25 | 6,205,739.34 | 105 | 2 | 0 | not significant | MATCH |
| D1-104-3 | 568,935.25 | 6,205,739.81 | 145 | 2 | 0 | not significant | MATCH |
| D1-105-2 | 568,965.24 | 6,205,739.08 | 105 | 3 | 3 | 99% hotspot | MATCH |
| D1-105-3 | 568,965.36 | 6,205,739.62 | 165 | 3 | 3 | 99% hotspot | MATCH |
| D1-106-2 | 568,962.35 | 6,205,772.23 | 105 | 3 | 3 | 99% hotspot | MATCH |
| D1-106-3 | 568,962.45 | 6,205,772.60 | 155 | 3 | 3 | 99% hotspot | MATCH |
| D1-178-2 | 568,999.84 | 6,206,013.51 | 125 | 2 | −1 | 90% cold spot | FALSE |
| D1-179-2 | 568,990.00 | 6,206,013.48 | 125 | 2 | −1 | 90% cold spot | FALSE |
| D1-180-3 | 568,979.90 | 6,206,013.46 | 125 | 2 | −2 | 95% cold spot | FALSE |
| D1-181-2 | 569,019.47 | 6,206,013.24 | 85 | 2 | 0 | not significant | MATCH |
| D1-181-3 | 569,019.81 | 6,206,013.23 | 125 | 2 | 0 | not significant | MATCH |
| D1-182-2 | 569,009.52 | 6,206,013.36 | 85 | 2 | −1 | 90% cold spot | FALSE |
| D1-182-3 | 569,009.79 | 6,206,013.38 | 125 | 2 | −1 | 90% cold spot | FALSE |
| D1-183-2 | 568,990.22 | 6,205,995.22 | 125 | 2 | 0 | not significant | MATCH |
| D1-184-2 | 568,978.06 | 6,205,994.69 | 125 | 2 | 0 | not significant | MATCH |
| D1-185-2 | 569,000.79 | 6,205,994.37 | 125 | 2 | 0 | not significant | MATCH |
| D1-186-2 | 568,999.83 | 6,206,003.34 | 125 | 2 | 0 | not significant | MATCH |
| D5-006-3 | 567,286.31 | 6,205,268.42 | 165 | 3 | 3 | 99% hotspot | MATCH |
| D5-034-2 | 567,276.79 | 6,205,277.85 | 85 | 3 | 3 | 99% hotspot | MATCH |
| D5-034-3 | 567,276.74 | 6,205,278.11 | 135 | 3 | 3 | 99% hotspot | MATCH |
| D5-034-4 | 567,276.77 | 6,205,278.42 | 165 | 3 | 3 | 99% hotspot | MATCH |
| D5-035-2 | 567,285.91 | 6,205,277.96 | 85 | 3 | 3 | 99% hotspot | MATCH |
| D5-036-2 | 567,295.93 | 6,205,278.05 | 125 | 3 | 3 | 99% hotspot | MATCH |
| D5-036-3 | 567,295.95 | 6,205,278.46 | 165 | 3 | 3 | 99% hotspot | MATCH |
| D5-037-2 | 567,231.93 | 6,205,209.67 | 85 | 3 | 3 | 99% hotspot | MATCH |
| D5-037-3 | 567,231.86 | 6,205,209.39 | 155 | 3 | 3 | 99% hotspot | MATCH |
| D5-038-3 | 567,230.43 | 6,205,301.69 | 135 | 2 | 0 | not significant | MATCH |
| D5-039-3 | 567,222.71 | 6,205,189.34 | 165 | 2 | 0 | not significant | MATCH |
| D5-040-2 | 567,232.94 | 6,205,189.70 | 85 | 2 | 0 | not significant | MATCH |
| D5-040-3 | 567,232.87 | 6,205,189.31 | 135 | 2 | 0 | not significant | MATCH |
| D5-041-2 | 567,242.74 | 6,205,189.28 | 125 | 2 | 0 | not significant | MATCH |
| D5-042-2 | 567,209.70 | 6,205,293.77 | 105 | 1 | 0 | not significant | MATCH |
| D5-042-3 | 567,209.76 | 6,205,294.20 | 155 | 1 | 0 | not significant | MATCH |
| D5-043-3 | 567,211.24 | 6,205,218.80 | 145 | 3 | 3 | 99% hotspot | MATCH |
| D5-052-3 | 567,137.41 | 6,205,325.90 | 155 | 2 | 0 | not significant | MATCH |
| D5-053-2 | 567,167.57 | 6,205,293.15 | 125 | 2 | 0 | not significant | MATCH |
| D5-053-3 | 567,167.53 | 6,205,293.54 | 155 | 2 | 0 | not significant | MATCH |
| D5-054-3 | 567,137.45 | 6,205,293.54 | 155 | 2 | 0 | not significant | MATCH |
| D5-055-3 | 567,137.68 | 6,205,353.54 | 155 | 2 | 0 | not significant | MATCH |
| D5-068-3 | 567,295.85 | 6,205,292.79 | 165 | 3 | 0 | not significant | MATCH |
| D5-170-3 | 567,243.01 | 6,205,200.79 | 125 | 3 | 1 | 90% hotspot | MATCH |
| D7-023-3 | 567,103.75 | 6,204,929.55 | 135 | 2 | −2 | 95% cold spot | FALSE |
| D7-024-3 | 567,083.62 | 6,204,929.60 | 165 | 2 | −1 | 90% cold spot | FALSE |
| D7-025-3 | 567,093.59 | 6,204,929.46 | 125 | 2 | −1 | 90% cold spot | FALSE |
| D7-026-3 | 567,093.38 | 6,204,909.05 | 145 | 2 | −3 | 99% cold spot | FALSE |
| D7-027-3 | 567,093.28 | 6,204,939.42 | 145 | 2 | 0 | not significant | MATCH |
| D7-028-3 | 567,093.52 | 6,204,919.47 | 145 | 2 | −3 | 99% cold spot | FALSE |
| D7-029-3 | 567,093.64 | 6,204,871.98 | 155 | 1 | −3 | 99% cold spot | MATCH |
| D8-016-3 | 566,615.97 | 6,204,308.57 | 165 | 1 | −3 | 99% cold spot | MATCH |
| D8-017-3 | 566,615.75 | 6,204,288.56 | 165 | 1 | −3 | 99% cold spot | MATCH |
| D8-066-3 | 566,586.07 | 6,204,289.16 | 165 | 1 | −3 | 99% cold spot | MATCH |
| D8-173-3 | 566,711.53 | 6,204,315.16 | 155 | 1 | −3 | 99% cold spot | MATCH |
| D8-174-3 | 566,721.62 | 6,204,315.55 | 145 | 1 | −3 | 99% cold spot | MATCH |
| D8-175-2 | 566,579.78 | 6,204,259.84 | 135 | 1 | −3 | 99% cold spot | MATCH |
| D8-175-3 | 566,580.03 | 6,204,259.92 | 165 | 1 | −3 | 99% cold spot | MATCH |
| D8-176-2 | 566,701.34 | 6,204,315.01 | 105 | 1 | −3 | 99% cold spot | MATCH |
| D8-176-3 | 566,701.67 | 6,204,315.02 | 155 | 1 | −3 | 99% cold spot | MATCH |
| D8-177-3 | 566,540.17 | 6,204,249.21 | 165 | 1 | −3 | 99% cold spot | MATCH |
References
- Kronvang, B.; Blicher-Mathiesen, G.; Windolf, J. 30 Years of Nutrient Management Learnings from Denmark: A Succesful Turnaround and Novel Ideas for the next Generation. In Science and Policy: Nutrient Management Challenges for the Next Generation; Currie, L.D., Hedley, M.J., Eds.; Massey University: Palmerston North, New Zealand, 2017; p. 9. [Google Scholar]
- Kirchmann, H.; Johnston, A.E.J.; Bergström, L.F. Possibilities for Reducing Nitrate Leaching from Agricultural Land. AMBIO J. Hum. Environ. 2002, 31, 404–408. [Google Scholar] [CrossRef] [PubMed]
- Giles, M.; Morley, N.; Baggs, E.; Daniell, T. Soil Nitrate Reducing Processes—Drivers, Mechanisms for Spatial Variation, and Significance for Nitrous Oxide Production. Front. Microbiol. 2012, 3, 407. [Google Scholar] [CrossRef] [PubMed]
- Ministry of Environment and Food of Denmark—Environmental Protection Agency. Overview of the Danish Regulation of Nutrients in Agriculture & the Danish Nitrates Action Programme; Ministry of Environment and Food of Denmark Environmental Protection Agency: Copenhagen, Denmark, 2017. [Google Scholar]
- Højberg, A.; Troldborg, L.; Tornbjerg, H.; Windolf, J.; Blicher-Mathiesen, G.; Thodsen, H.; Kronvang, B.; Børgesen, C. Development of a Danish National Nitrogen Model—Input to a New Spatial Differentiated Regulation. In Proceedings of the LuWQ2015, Land Use and Water Quality: Agricultural Production and the Environment, Vienna, Austria, 21–24 September 2015. [Google Scholar]
- Højberg, A.L.; Windolf, J.; Børgesen, C.D.; Troldborg, L.; Blicher-Mathiesen, G.; Kronvang, B.; Thodsen, H.; Ernstsen, V. National Kvælstofmodel. Oplandsmodel Til Belastning og Virkemidler, Revideret Udgave [National Nitrogen Model-Watershed Model for Estimation of Loading and Measures. Revised Edition] (Methodological Report); De Nationale Geologiske Undersøgelser for Danmark og Grønland; GEUS-the National Danish Geological Survey: Copenhagen, Denmark, 2015; p. 402. [Google Scholar]
- Højberg, A.L.; Hansen, A.L.; Wachniew, P.; Żurek, A.J.; Virtanen, S.; Arustiene, J.; Strömqvist, J.; Rankinen, K.; Refsgaard, J.C. Review and Assessment of Nitrate Reduction in Groundwater in the Baltic Sea Basin. J. Hydrol. Reg. Stud. 2017, 12, 50–68. [Google Scholar] [CrossRef]
- Hansen, A.L.; Christensen, B.S.B.; Ernstsen, V.; He, X.; Refsgaard, J.C. A Concept for Estimating Depth of the Redox Interface for Catchment-Scale Nitrate Modelling in a till Area in Denmark. Hydrogeol. J. 2014, 22, 1639–1655. [Google Scholar] [CrossRef]
- Kim, H.; Høyer, A.-S.; Jakobsen, R.; Thorling, L.; Aamand, J.; Maurya, P.K.; Christiansen, A.V.; Hansen, B. 3D Characterization of the Subsurface Redox Architecture in Complex Geological Settings. Sci. Total Environ. 2019, 693, 133583. [Google Scholar] [CrossRef]
- Hansen, A.L.; Gunderman, D.; He, X.; Refsgaard, J.C. Uncertainty Assessment of Spatially Distributed Nitrate Reduction Potential in Groundwater Using Multiple Geological Realizations. J. Hydrol. 2014, 519, 225–237. [Google Scholar] [CrossRef]
- Ernstsen, V. Nitratreduktion i Den Umætttede Zone, Principper for Beregning Af Nitratreduktion i Jordlagene under Rodzonen; Miljøstyrelsen: Odense, Denmark, 2001. [Google Scholar]
- Murray, R.E.; Feig, Y.S.; Tiedje, J.M. Spatial Heterogeneity in the Distribution of Denitrifying Bacteria Associated with Denitrification Activity Zones. Appl. Environ. Microbiol. 1995, 61, 2791–2793. [Google Scholar] [CrossRef]
- Bruland, G.L.; Richardson, C.J.; Whalen, S.C. Spatial Variability of Denitrification Potential and Related Soil Properties in Created, Restored, and Paired Natural Wetlands. Wetlands 2006, 26, 1042–1056. [Google Scholar] [CrossRef]
- Uchida, Y.; Mogi, H.; Hamamoto, T.; Nagane, M.; Toda, M.; Shimotsuma, M.; Yoshii, Y.; Maeda, Y.; Oka, M. Changes in Denitrification Potentials and Riverbank Soil Bacterial Structures along Shibetsu River, Japan. Appl. Environ. Soil Sci. 2018, 2018, e2530946. [Google Scholar] [CrossRef]
- Butterbach-Bahl, K.; Baggs, E.M.; Dannenmann, M.; Kiese, R.; Zechmeister-Boltenstern, S. Nitrous Oxide Emissions from Soils: How Well Do We Understand the Processes and Their Controls? Philos. Trans. R. Soc. B Biol. Sci. 2013, 368, 20130122. [Google Scholar] [CrossRef]
- Brevik, E.C.; Fenton, T.E. Use of the Geonics EM-38 to Delineate Soils in a Loess over Till Landscape, Southwestern Iowa. Soil Surv. Horiz. 2003, 44, 16–24. [Google Scholar] [CrossRef]
- Doolittle, J.A.; Brevik, E.C. The Use of Electromagnetic Induction Techniques in Soils Studies. Geoderma 2014, 223–225, 33–45. [Google Scholar] [CrossRef]
- Corwin, D.L.; Lesch, S.M. Apparent Soil Electrical Conductivity Measurements in Agriculture. Comput. Electron. Agric. 2005, 46, 11–43. [Google Scholar] [CrossRef]
- Heil, K.; Schmidhalter, U. The Application of EM38: Determination of Soil Parameters, Selection of Soil Sampling Points and Use in Agriculture and Archaeology. Sensors 2017, 17, 2540. [Google Scholar] [CrossRef]
- Corwin, D.L.; Lesch, S.M. Characterizing Soil Spatial Variability with Apparent Soil Electrical Conductivity: I. Survey Protocols. Comput. Electron. Agric. 2005, 46, 103–133. [Google Scholar] [CrossRef]
- Rhoades, J.D.; Manteghi, N.A.; Shouse, P.J.; Alves, W.J. Soil Electrical Conductivity and Soil Salinity: New Formulations and Calibrations. Soil Sci. Soc. Am. J. 1989, 53, 433–439. [Google Scholar] [CrossRef]
- Corwin, D.L.; Lesch, S.M. Application of Soil Electrical Conductivity to Precision Agriculture. Agron. J. 2003, 95, 455–471. [Google Scholar] [CrossRef]
- Huang, J.; Koganti, T.; Santos, F.A.M.; Triantafilis, J. Mapping Soil Salinity and a Fresh-Water Intrusion in Three-Dimensions Using a Quasi-3d Joint-Inversion of DUALEM-421S and EM34 Data. Sci. Total Environ. 2017, 577, 395–404. [Google Scholar] [CrossRef]
- Koganti, T.; Narjary, B.; Zare, E.; Pathan, A.L.; Huang, J.; Triantafilis, J. Quantitative Mapping of Soil Salinity Using the DUALEM-21S Instrument and EM Inversion Software. Land Degrad. Dev. 2018, 29, 1768–1781. [Google Scholar] [CrossRef]
- Triantafilis, J.; Odeh, I.O.A.; McBratney, A.B. Five Geostatistical Models to Predict Soil Salinity from Electromagnetic Induction Data Across Irrigated Cotton. Soil Sci. Soc. Am. J. 2001, 65, 869–878. [Google Scholar] [CrossRef]
- Domsch, H.; Giebel, A. Estimation of Soil Textural Features from Soil Electrical Conductivity Recorded Using the EM38. Precis. Agric. 2004, 5, 389–409. [Google Scholar] [CrossRef]
- Pedrera-Parrilla, A.; Van De Vijver, E.; Van Meirvenne, M.; Espejo-Pérez, A.J.; Giráldez, J.V.; Vanderlinden, K. Apparent Electrical Conductivity Measurements in an Olive Orchard under Wet and Dry Soil Conditions: Significance for Clay and Soil Water Content Mapping. Precis. Agric 2016, 17, 531–545. [Google Scholar] [CrossRef]
- Saey, T.; Van Meirvenne, M.; Vermeersch, H.; Ameloot, N.; Cockx, L. A Pedotransfer Function to Evaluate the Soil Profile Textural Heterogeneity Using Proximally Sensed Apparent Electrical Conductivity. Geoderma 2009, 150, 389–395. [Google Scholar] [CrossRef]
- García-Tomillo, A.; Mirás-Avalos, J.M.; Dafonte-Dafonte, J.; Paz-González, A. Estimating Soil Organic Matter Using Interpolation Methods with a Electromagnetic Induction Sensor and Topographic Parameters: A Case Study in a Humid Region. Precis. Agric. 2017, 18, 882–897. [Google Scholar] [CrossRef]
- Koganti, T.; Moral, F.J.; Rebollo, F.J.; Huang, J.; Triantafilis, J. Mapping Cation Exchange Capacity Using a Veris-3100 Instrument and InvVERIS Modelling Software. Sci. Total Environ. 2017, 599–600, 2156–2165. [Google Scholar] [CrossRef]
- Altdorff, D.; von Hebel, C.; Borchard, N.; van der Kruk, J.; Bogena, H.R.; Vereecken, H.; Huisman, J.A. Potential of Catchment-Wide Soil Water Content Prediction Using Electromagnetic Induction in a Forest Ecosystem. Environ. Earth Sci. 2017, 76, 111. [Google Scholar] [CrossRef]
- Hedley, C.B.; Yule, I.J.; Eastwood, C.R.; Shepherd, T.G.; Arnold, G. Rapid Identification of Soil Textural and Management Zones Using Electromagnetic Induction Sensing of Soils. Soil Res. 2004, 42, 389–400. [Google Scholar] [CrossRef]
- Morari, F.; Castrignanò, A.; Pagliarin, C. Application of Multivariate Geostatistics in Delineating Management Zones within a Gravelly Vineyard Using Geo-Electrical Sensors. Comput. Electron. Agric. 2009, 68, 97–107. [Google Scholar] [CrossRef]
- Peralta, N.R.; Costa, J.L.; Balzarini, M.; Angelini, H. Delineation of Management Zones with Measurements of Soil Apparent Electrical Conductivity in the Southeastern Pampas. Can. J. Soil. Sci. 2013, 93, 205–218. [Google Scholar] [CrossRef]
- McNeill, J. Electromagnetic Terrain Conductivity Measurement at Low Induction Numbers: Technical Note TN-6; Geonics Ltd.: Mississauga, ON, Canada, 1980. [Google Scholar]
- Everett, M.E. Electromagnetic Induction. In Near-Surface Applied Geophysics; Cambridge University Press: Cambridge, UK, 2013; pp. 200–238. ISBN 9781139088435. [Google Scholar]
- Triantafilis, J.; Monteiro Santos, F.A. Electromagnetic Conductivity Imaging (EMCI) of Soil Using a DUALEM-421 and Inversion Modelling Software (EM4Soil). Geoderma 2013, 211–212, 28–38. [Google Scholar] [CrossRef]
- Jouen, T.; Clément, R.; Henine, H.; Chaumont, C.; Vincent, B.; Tournebize, J. Evaluation and Localization of an Artificial Drainage Network by 3D Time-Lapse Electrical Resistivity Tomography. Environ. Sci. Pollut. Res. 2018, 25, 23502–23514. [Google Scholar] [CrossRef] [PubMed]
- Samouëlian, A.; Cousin, I.; Tabbagh, A.; Bruand, A.; Richard, G. Electrical Resistivity Survey in Soil Science: A Review. Soil Tillage Res. 2005, 83, 173–193. [Google Scholar] [CrossRef]
- Senal, M.I.S.; Elsgaard, L.; Petersen, S.O.; Koganti, T.; Iversen, B.V. Assessment of the Spatial Variability of Apparent Electrical Conductivity in a Tile Drained Catchment in Fensholt Subcatchment, Jutland, Denmark for Improved Small-Scale Prediction of Highly Reducing Areas. Geoderma Reg. 2020, 23, e00336. [Google Scholar] [CrossRef]
- Keiluweit, M.; Gee, K.; Denney, A.; Fendorf, S. Anoxic Microsites in Upland Soils Dominantly Controlled by Clay Content. Soil Biol. Biochem. 2018, 118, 42–50. [Google Scholar] [CrossRef]
- Schlüter, S.; Henjes, S.; Zawallich, J.; Bergaust, L.; Horn, M.; Ippisch, O.; Vogel, H.-J.; Dörsch, P. Denitrification in Soil Aggregate Analogues-Effect of Aggregate Size and Oxygen Diffusion. Front. Environ. Sci. 2018, 6, 17. [Google Scholar] [CrossRef]
- Tou, J.T.; Gonzalez, R.C. Pattern Recognition Principles; Addison-Wesley Publishing Company: Boston, MA, USA, 1974; ISBN 9780201075861. [Google Scholar]
- Khosla, R.; Westfall, D.G.; Reich, R.M.; Mahal, J.S.; Gangloff, W.J. Spatial Variation and Site-Specific Management Zones. In Geostatistical Applications for Precision Agriculture; Oliver, M.A., Ed.; Springer: Dordrecht, The Netherlands, 2010; pp. 195–219. ISBN 978-90-481-9133-8. [Google Scholar]
- Guastaferro, F.; Castrignanò, A.; De Benedetto, D.; Sollitto, D.; Troccoli, A.; Cafarelli, B. A Comparison of Different Algorithms for the Delineation of Management Zones. Precis. Agric 2010, 11, 600–620. [Google Scholar] [CrossRef]
- Getis, A.; Ord, J.K. The Analysis of Spatial Association by Use of Distance Statistics. Geogr. Anal. 1992, 24, 189–206. [Google Scholar] [CrossRef]
- Manepalli, U.; Bham, G.; Kandada, S. Evaluation of Hot-Spots Identification Using Kernel Density Estimation and Getis-Ord on I-630. In Proceeding of the 3rd International Conference on Road Safety and Simulation, Indianapolis, IN, USA, 14–16 September 2011. [Google Scholar]
- Songchitruksa, P.; Zeng, X. Getis–Ord Spatial Statistics to Identify Hot Spots by Using Incident Management Data. Transp. Res. Rec. 2010, 2165, 42–51. [Google Scholar] [CrossRef]
- Luo, J.; Chen, G.; Li, C.; Xia, B.; Sun, X.; Chen, S. Use of an E2SFCA Method to Measure and Analyse Spatial Accessibility to Medical Services for Elderly People in Wuhan, China. Int. J. Environ. Res. Public Health 2018, 15, 1503. [Google Scholar] [CrossRef]
- Shifti, D.M.; Chojenta, C.; Holliday, E.G.; Loxton, D. Application of Geographically Weighted Regression Analysis to Assess Predictors of Short Birth Interval Hot Spots in Ethiopia. PLoS ONE 2020, 15, e0233790. [Google Scholar] [CrossRef]
- Yi, H.; Xu, Z.; Song, J.; Wang, P. Optimize the Planning of Ambulance Standby Points by Using Getis-Ord Gi\ast Based on Historical Emergency Data. IOP Conf. Ser. Earth Environ. Sci. 2019, 234, 012034. [Google Scholar] [CrossRef]
- Feng, Y.; Chen, X.; Gao, F.; Liu, Y. Impacts of Changing Scale on Getis-Ord Gi* Hotspots of CPUE: A Case Study of the Neon Flying Squid (Ommastrephes Bartramii) in the Northwest Pacific Ocean. Acta Oceanol. Sin. 2018, 37, 67–76. [Google Scholar] [CrossRef]
- Rossi, F.; Becker, G. Creating Forest Management Units with Hot Spot Analysis (Getis-Ord Gi*) over a Forest Affected by Mixed-Severity Fires. Aust. For. 2019, 82, 166–175. [Google Scholar] [CrossRef]
- Yulianto, J.P.; Nugraheni, W.; Kristoko, D.H.; Bistok, H.S. Geographic Information System for Detecting Spatial Connectivity Brown Planthopper Endemic Areas Using a Combination of Triple Exponential Smoothing—Getis Ord. Comput. Inf. Sci. 2014, 7, 21. [Google Scholar] [CrossRef][Green Version]
- Thanh, L.D.; Jougnot, D.; Van Do, P.; Tuyen, V.P.; Ca, N.X.; Hien, N.T. A Physically Based Model for the Electrical Conductivity of Partially Saturated Porous Media. Geophys. J. Int. 2020, 223, 993–1006. [Google Scholar] [CrossRef]
- Leroy, P.; Revil, A. A Mechanistic Model for the Spectral Induced Polarization of Clay Materials. J. Geophys. Res. Solid Earth 2009, 114. [Google Scholar] [CrossRef]
- Von Hebel, C.; Reynaert, S.; Pauly, K.; Janssens, P.; Piccard, I.; Vanderborght, J.; van der Kruk, J.; Vereecken, H.; Garré, S. Toward High-Resolution Agronomic Soil Information and Management Zones Delineated by Ground-Based Electromagnetic Induction and Aerial Drone Data. Vadose Zone J. 2021, 20, e20099. [Google Scholar] [CrossRef]
- Moral, F.J.; Terrón, J.M.; da Silva, J.R.M. Delineation of Management Zones Using Mobile Measurements of Soil Apparent Electrical Conductivity and Multivariate Geostatistical Techniques. Soil Tillage Res. 2010, 106, 335–343. [Google Scholar] [CrossRef]
- De Schepper, G.; Therrien, R.; Refsgaard, J.C.; He, X.; Kjaergaard, C.; Iversen, B.V. Simulating Seasonal Variations of Tile Drainage Discharge in an Agricultural Catchment. Water Resour. Res. 2017, 53, 3896–3920. [Google Scholar] [CrossRef]
- Prinds, C. Remote and Proximal Sensing of the Geology and Shallow Hydrology in Riparian Lowlands—Research—Aarhus University; Aarhus University: Aarhus, Denmark, 2019. [Google Scholar]
- Varvaris, I.; Børgesen, C.D.; Kjærgaard, C.; Iversen, B.V. Three Two-Dimensional Approaches for Simulating the Water Flow Dynamics in a Heterogeneous Tile-Drained Agricultural Field in Denmark. Soil Sci. Soc. Am. J. 2018, 82, 1367–1383. [Google Scholar] [CrossRef]
- Brenning, A.; Bangs, D.; Becker, M.; Schratz, P.; Polakowski, F. RSAGA: SAGA Geoprocessing and Terrain Analysis (Version 1.3.0). 2018. Available online: https://CRAN.R-project.org/package=RSAGA (accessed on 1 September 2020).
- Seibert, J.; McGlynn, B.L. A New Triangular Multiple Flow Direction Algorithm for Computing Upslope Areas from Gridded Digital Elevation Models. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef]
- Callegary, J.B.; Ferré, T.P.A.; Groom, R.W. Vertical Spatial Sensitivity and Exploration Depth of Low-Induction-Number Electromagnetic-Induction Instruments. Vadose Zone J. 2007, 6, 158–167. [Google Scholar] [CrossRef]
- Callegary, J.B.; Ferré, T.P.A.; Groom, R.W. Three-Dimensional Sensitivity Distribution and Sample Volume of Low-Induction-Number Electromagnetic-Induction Instruments. Soil Sci. Soc. Am. J. 2012, 76, 85–91. [Google Scholar] [CrossRef]
- Dualem, Inc. DUALEM-21S User’s Manual; Dualem, Inc.: Milton, ON, Canada, 2008. [Google Scholar]
- Auken, E.; Viezzoli, A.; Christensen, A. A Single Software for Processing, Inversion, and Presentation of AEM Data of Different Systems: The Aarhus Workbench. ASEG Ext. Abstr. 2009, 2009, 1–5. [Google Scholar] [CrossRef]
- Auken, E.; Christiansen, A.V.; Kirkegaard, C.; Fiandaca, G.; Schamper, C.; Behroozmand, A.A.; Binley, A.; Nielsen, E.; Effersø, F.; Christensen, N.B.; et al. An Overview of a Highly Versatile Forward and Stable Inverse Algorithm for Airborne, Ground-Based and Borehole Electromagnetic and Electric Data. Explor. Geophys. 2015, 46, 223–235. [Google Scholar] [CrossRef]
- Viezzoli, A.; Christiansen, A.V.; Auken, E.; Sørensen, K. Quasi-3D Modeling of Airborne TEM Data by Spatially Constrained Inversion. Geophysics 2008, 73, F105–F113. [Google Scholar] [CrossRef]
- Lindbo, D.L.; Stolt, M.H.; Vepraskas, M.J. 8—Redoximorphic Features. In Interpretation of Micromorphological Features of Soils and Regoliths; Stoops, G., Marcelino, V., Mees, F., Eds.; Elsevier: Amsterdam, The Netherlands, 2010; pp. 129–147. ISBN 9780444531568. [Google Scholar]
- Senal, M.I.; Iversen, B.V. Redox Potential Values and Nitrate Concentrations of Each Classified Piezometer in an Artificially Drained Agricultural Catchment. Mendeley Data. V1. Published on 23 February 2021. 2021. Available online: https://doi.org/10.17632/235yhyjjbt.1 (accessed on 1 September 2020). [CrossRef]
- Wafer, C.C.; Richards, J.B.; Osmond, D.L. Construction of Platinum-Tipped Redox Probes for Determining Soil Redox Potential. J. Environ. Qual. 2004, 33, 2375–2379. [Google Scholar] [CrossRef] [PubMed]
- Boots, B.N.; Getis, A. Point Pattern Analysis; Sage Publications: Newbury Park, CA, USA, 1988; ISBN 9780803922457. [Google Scholar]
- ESRI. Environmental Systems Research Institute ArcGIS Desktop Help 10.3; ESRI: Redlands, CA, USA, 2014. [Google Scholar]
- Herzog, M.H.; Francis, G.; Clarke, A. The Multiple Testing Problem. In Understanding Statistics and Experimental Design: How to Not Lie with Statistics; Herzog, M.H., Francis, G., Clarke, A., Eds.; Learning Materials in Biosciences; Springer International Publishing: Cham, Switzerland, 2019; pp. 63–66. ISBN 9783030034993. [Google Scholar]
- Cambardella, C.A.; Moorman, T.B.; Novak, J.M.; Parkin, T.B.; Karlen, D.L.; Turco, R.F.; Konopka, A.E. Field-Scale Variability of Soil Properties in Central Iowa Soils. Soil Sci. Soc. Am. J. 1994, 58, 1501–1511. [Google Scholar] [CrossRef]
- Trangmar, B.B.; Yost, R.S.; Uehara, G. Application of Geostatistics to Spatial Studies of Soil Properties. In Advances in Agronomy; Brady, N.C., Ed.; Academic Press: Cambridge, MA, USA, 1986; Volume 38, pp. 45–94. [Google Scholar]
- Zhang, Z.; Hu, B.; Hu, G. Spatial Heterogeneity of Soil Chemical Properties in a Subtropical Karst Forest, Southwest China. Sci. World J. 2014, 2014, e473651. [Google Scholar] [CrossRef]
- Yunchao, Z.; Shi-jie, W.; Hong-mei, L.; Liping, X.; De’an, X. Forest Soil Heterogeneity and Soil Sampling Protocols on Limestone Outctops: Example from SW China. Acta Carsologica 2010, 39. [Google Scholar] [CrossRef]
- Negassa, W.; Baum, C.; Schlichting, A.; Müller, J.; Leinweber, P. Small-Scale Spatial Variability of Soil Chemical and Biochemical Properties in a Rewetted Degraded Peatland. Front. Environ. Sci. 2019, 7, 116. [Google Scholar] [CrossRef]
- Molin, J.P.; Faulin, G.D.C. Spatial and Temporal Variability of Soil Electrical Conductivity Related to Soil Moisture. Sci. Agric. 2013, 70, 1–5. [Google Scholar] [CrossRef]
- Senal, M.I.; Iversen, B.V.; Petersen, S.O.; Elsgaard, L. Heterogeneity of Nitrate Reduction Indicators across a Tile-Drained Agricultural Sub-Catchment. 2021; unpublished. [Google Scholar]
- Knight, R.J.; Endres, A.L. An Introduction to Rock Physics Principles for Near-Surface Geophysics. In Near-Surface Geophysics; Investigations in Geophysics; Society of Exploration Geophysicists: Tulsa, OK, USA, 2005; pp. 31–70. ISBN 9781560801306. [Google Scholar]
- Serafini, G.; Davies, J.; Rogers, A. Perched Water Table Mounding between Subsoil Drains in Sand Fill for Urban Development. Hydrol. Water Resour. Symp. 2014, 589–596. [Google Scholar] [CrossRef]
- Cihlar, J.; Xiao, Q.; Chen, J.; Beaubien, J.; Fung, K.; Latifovic, R. Classification by Progressive Generalization: A New Automated Methodology for Remote Sensing Multichannel Data. Int. J. Remote Sens. 1998, 19, 2685–2704. [Google Scholar] [CrossRef]
- Vanderzee, D.; Ehrlich, D. Sensitivity of ISODATA to Changes in Sampling Procedures and Processing Parameters When Applied to AVHRR Time-Series NDV1 Data. Int. J. Remote Sens. 1995, 16, 673–686. [Google Scholar] [CrossRef]
- Harms, T.K.; Wentz, E.A.; Grimm, N.B. Spatial Heterogeneity of Denitrification in Semi-Arid Floodplains. Ecosystems 2009, 12, 129–143. [Google Scholar] [CrossRef]
- Groffman, P.M.; Butterbach-Bahl, K.; Fulweiler, R.W.; Gold, A.J.; Morse, J.L.; Stander, E.K.; Tague, C.; Tonitto, C.; Vidon, P. Challenges to Incorporating Spatially and Temporally Explicit Phenomena (Hotspots and Hot Moments) in Denitrification Models. Biogeochemistry 2009, 93, 49–77. [Google Scholar] [CrossRef]
- Córdoba, M.A.; Bruno, C.I.; Costa, J.L.; Peralta, N.R.; Balzarini, M.G. Protocol for Multivariate Homogeneous Zone Delineation in Precision Agriculture. Biosyst. Eng. 2016, 143, 95–107. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Senal, M.I.; Møller, A.B.; Koganti, T.; Iversen, B.V. Delineation of Nitrate Reduction Hotspots in Artificially Drained Areas through Assessment of Small-Scale Spatial Variability of Electrical Conductivity Data. Sensors 2022, 22, 1508. https://doi.org/10.3390/s22041508
Senal MI, Møller AB, Koganti T, Iversen BV. Delineation of Nitrate Reduction Hotspots in Artificially Drained Areas through Assessment of Small-Scale Spatial Variability of Electrical Conductivity Data. Sensors. 2022; 22(4):1508. https://doi.org/10.3390/s22041508
Chicago/Turabian StyleSenal, Maria Isabel, Anders Bjørn Møller, Triven Koganti, and Bo V. Iversen. 2022. "Delineation of Nitrate Reduction Hotspots in Artificially Drained Areas through Assessment of Small-Scale Spatial Variability of Electrical Conductivity Data" Sensors 22, no. 4: 1508. https://doi.org/10.3390/s22041508
APA StyleSenal, M. I., Møller, A. B., Koganti, T., & Iversen, B. V. (2022). Delineation of Nitrate Reduction Hotspots in Artificially Drained Areas through Assessment of Small-Scale Spatial Variability of Electrical Conductivity Data. Sensors, 22(4), 1508. https://doi.org/10.3390/s22041508








