An End-to-End Deep Learning Pipeline for Football Activity Recognition Based on Wearable Acceleration Sensors
Abstract
:1. Introduction
2. Related Work
2.1. Machine Learning for Football Activity Recognition
2.2. Traditional Machine Learning Approaches
2.3. Deep Learning Approaches
2.4. Background on Deep Learning
2.4.1. Convolutional Neural
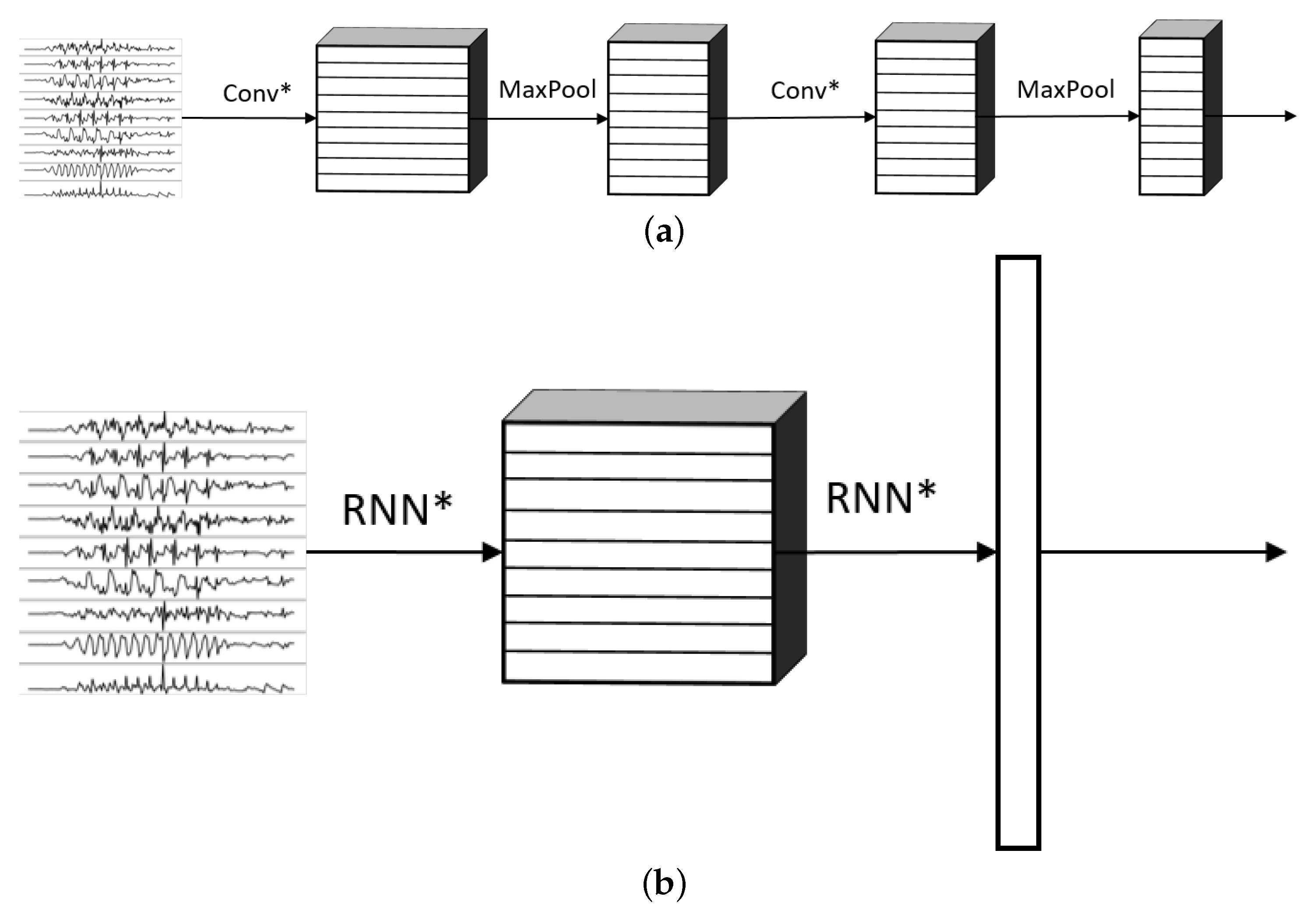
- ConvolutionIn a convolutional layer, the input data are convolved with a certain number of kernels or filters. A filter k is traversed through all the points of the input image (or signal) and on each location, the convolution between the filter and the overlapping area of the data is calculated. The usage of each filter results in a new convolved image (or signal) called a feature map. The combination of all the k filters with different weights then generates a set of k feature maps.
- PoolingIt is a common practice to include pooling layers after convolutional ones. These types of layers condense information from spatially or temporally close points to reduce the data size. In neurology, a receptive field of a neuron is defined as the region in which the presence of a stimulus triggers the response of that particular neuron [23]. Pooling layers introduce the concept of receptive fields into CNNs because they condense information of neighboring points of the convolved data into a single value. Many types of pooling layers can be used, but one of the most common is the max pooling layer. This operation defines a small block (also called a filter) and runs it on top of the input data of the layer. At each point, the maximum of the values contained on the overlapping area of the data and the filter is extracted and the output image (or signal) is built with those maximum values. Pooling layers have the additional property that they reduce the size of the feature maps, which translates into fewer weights to be learned by the model. The outputs of these layers are smaller feature maps, but each element of those maps has information about its neighbors from the previous layer.
2.4.2. Recurrent Neural Networks and LSTM
- Forget gateThis gate is responsible for deciding what information must be forgotten (removed) from the cell state. To do so, it concatenates the hidden state at time () and the current input and calculates a value between 0 (forget) and 1 (keep) for each element of the cell state .
- Input gateThis gate is responsible for deciding what new information will be stored in the cell state and where. It is composed of two parts. The first part calculates candidate values to potentially update the cell state, and the second part decides which parts of the cell state must be updated with those candidate values. This completes the update of into determined by the forget and input gates.
- Output gateThis gate is responsible for deciding which elements of the cell state will be given as the output of the LSTM unit. Only the desired parts of the cell state are output as the new hidden state values .
3. Materials and Methods
3.1. Data and Preparation
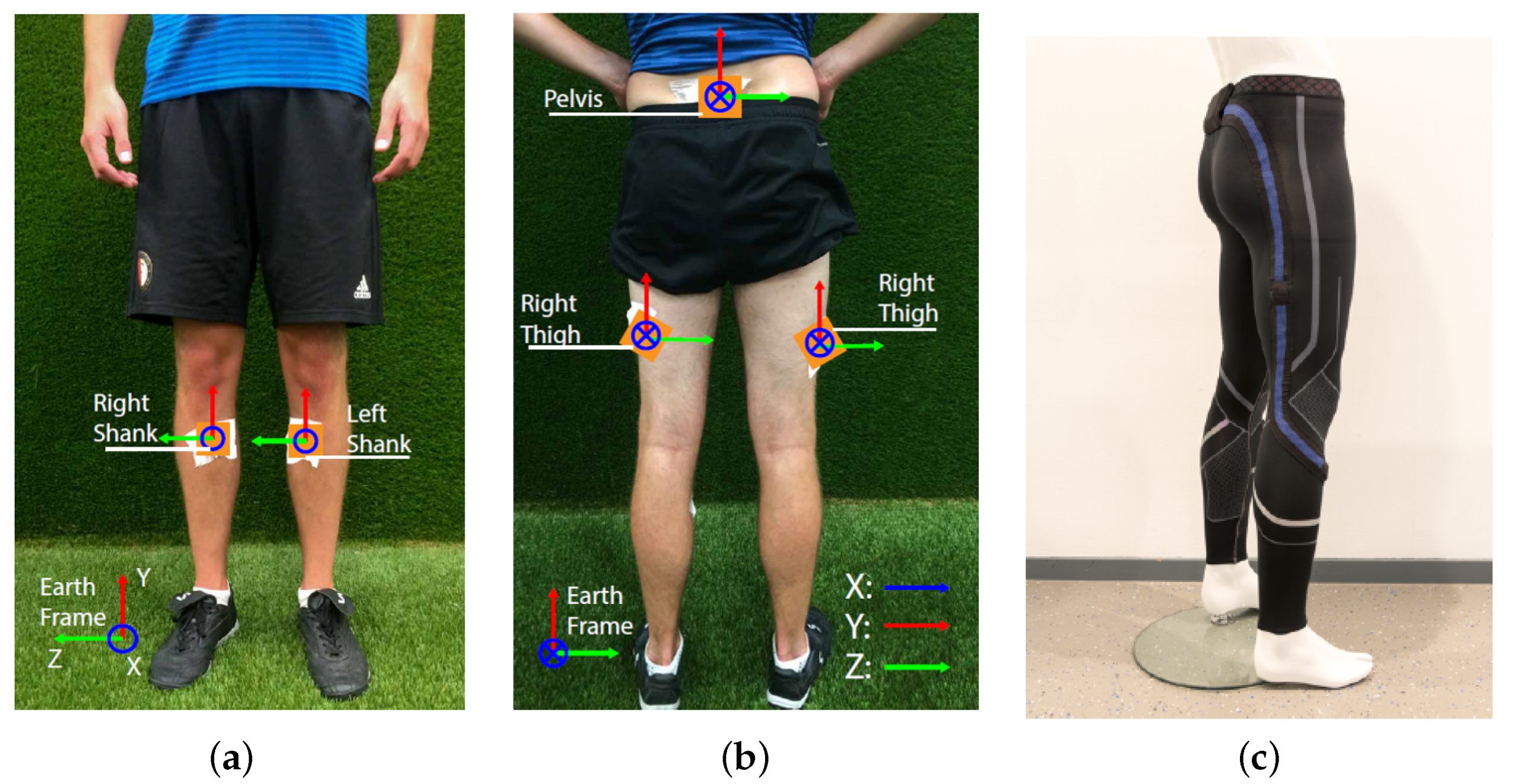
3.1.1. Data Collection Procedure
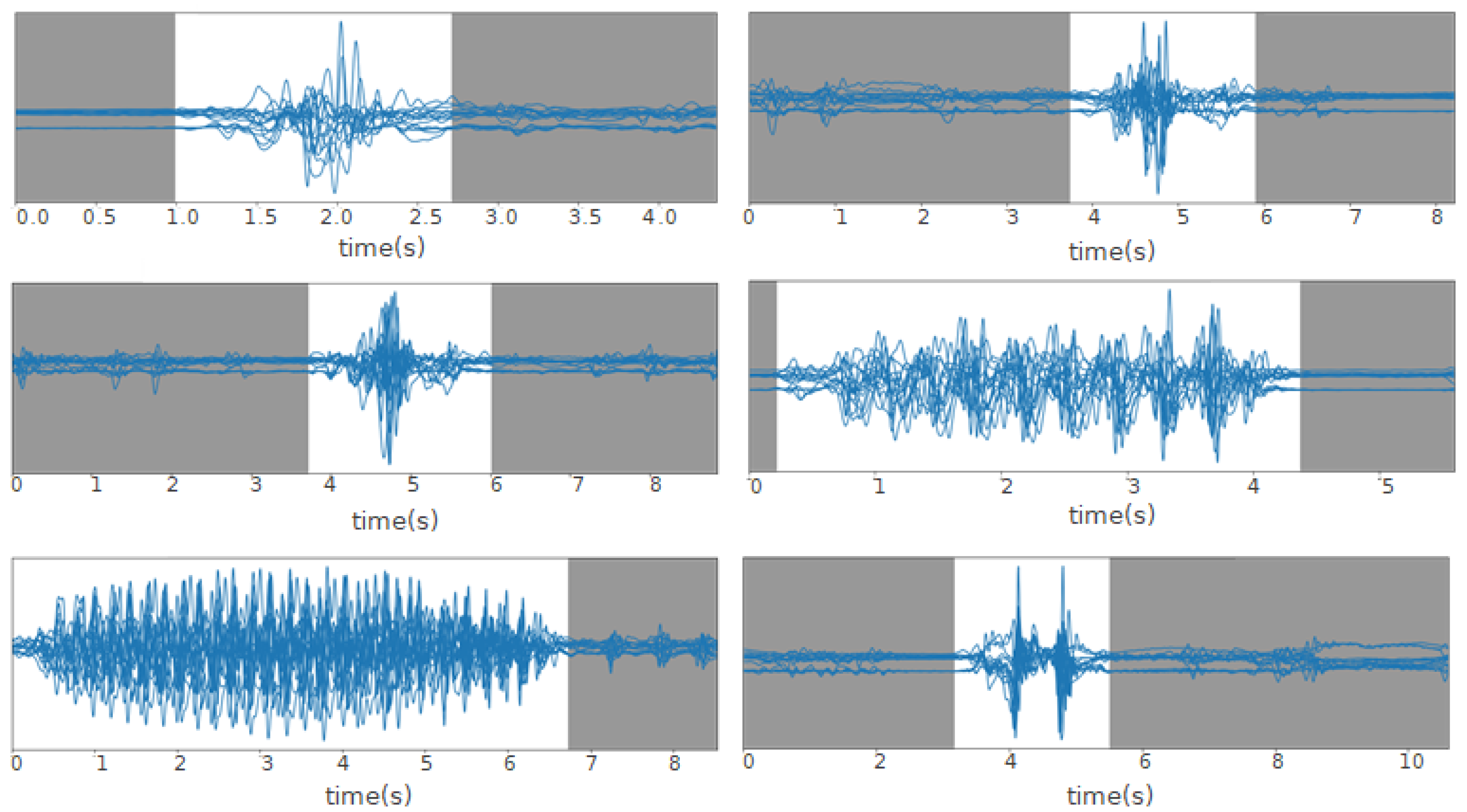
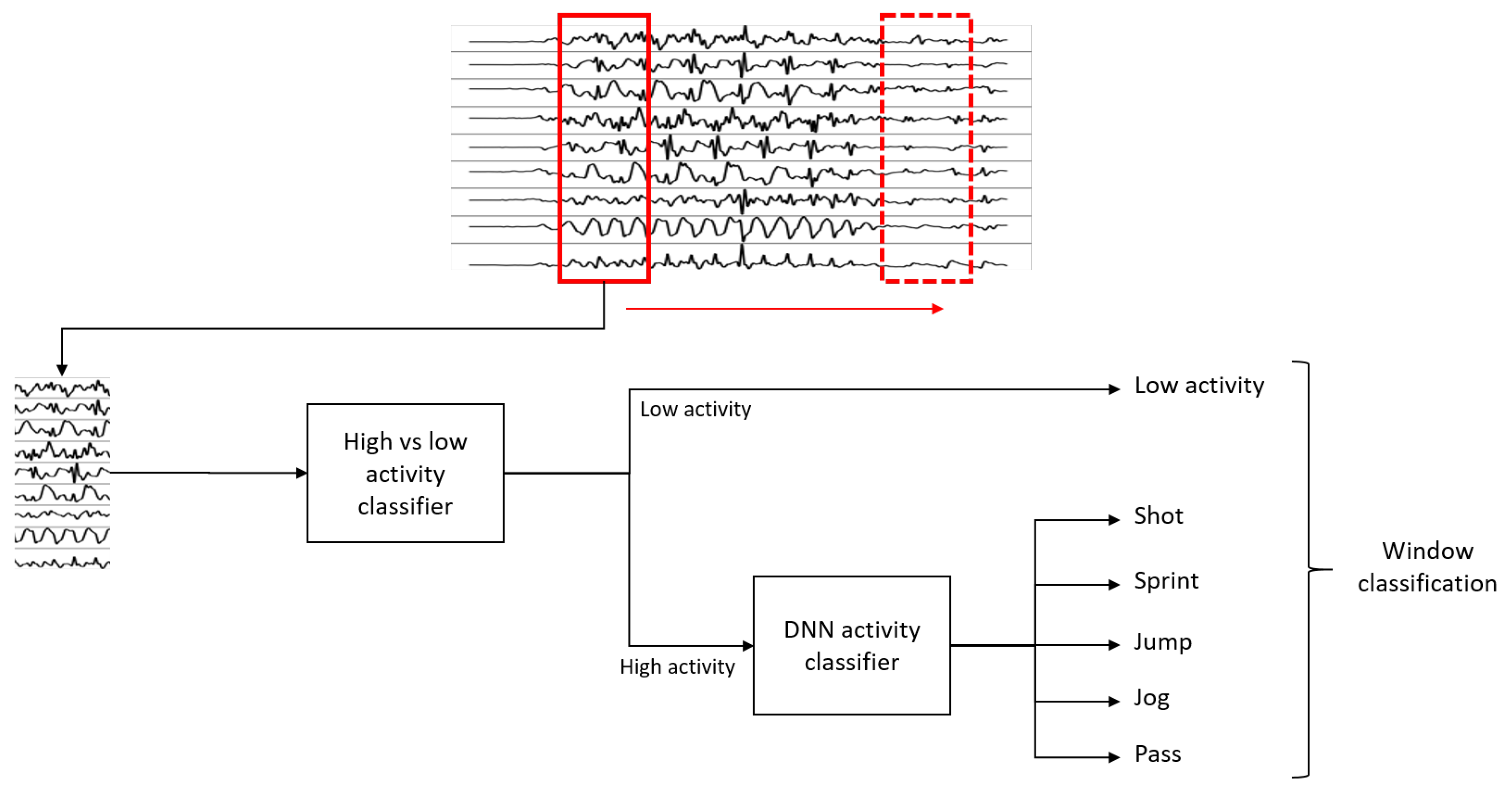
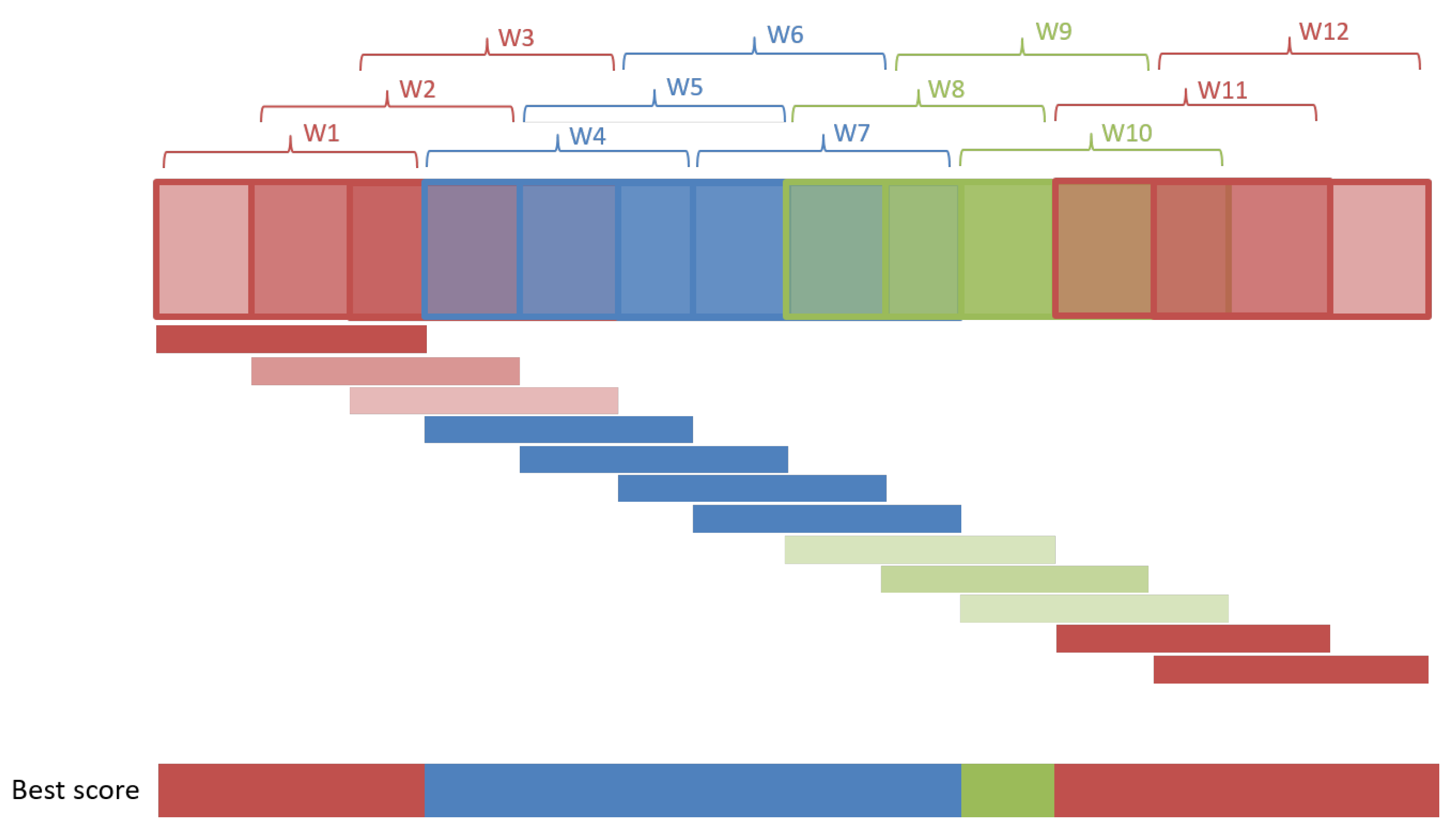
3.1.2. Activity Isolation
| Algorithm 1:Threshold-based activity isolation |
 |
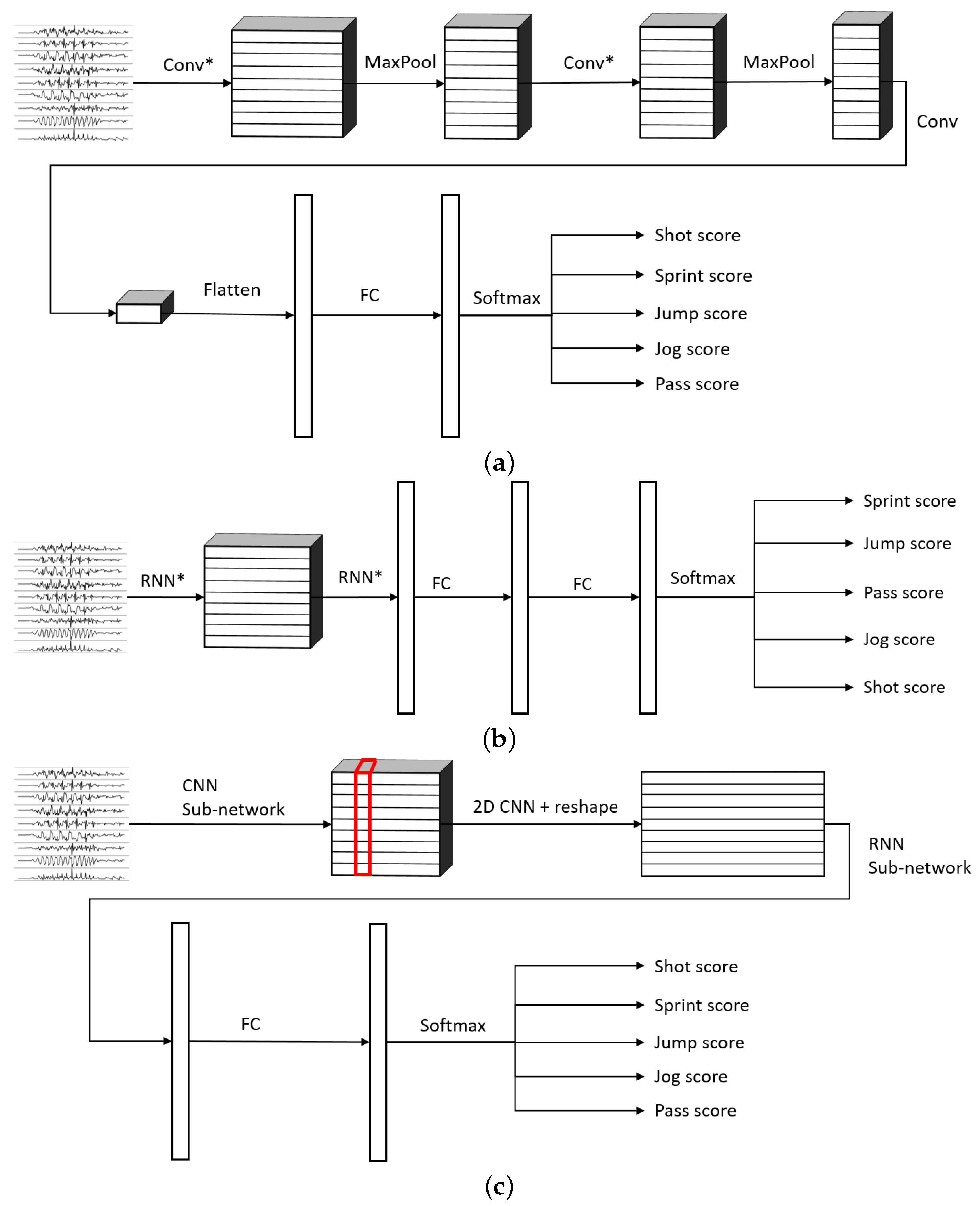
3.2. Neural Network Architecture
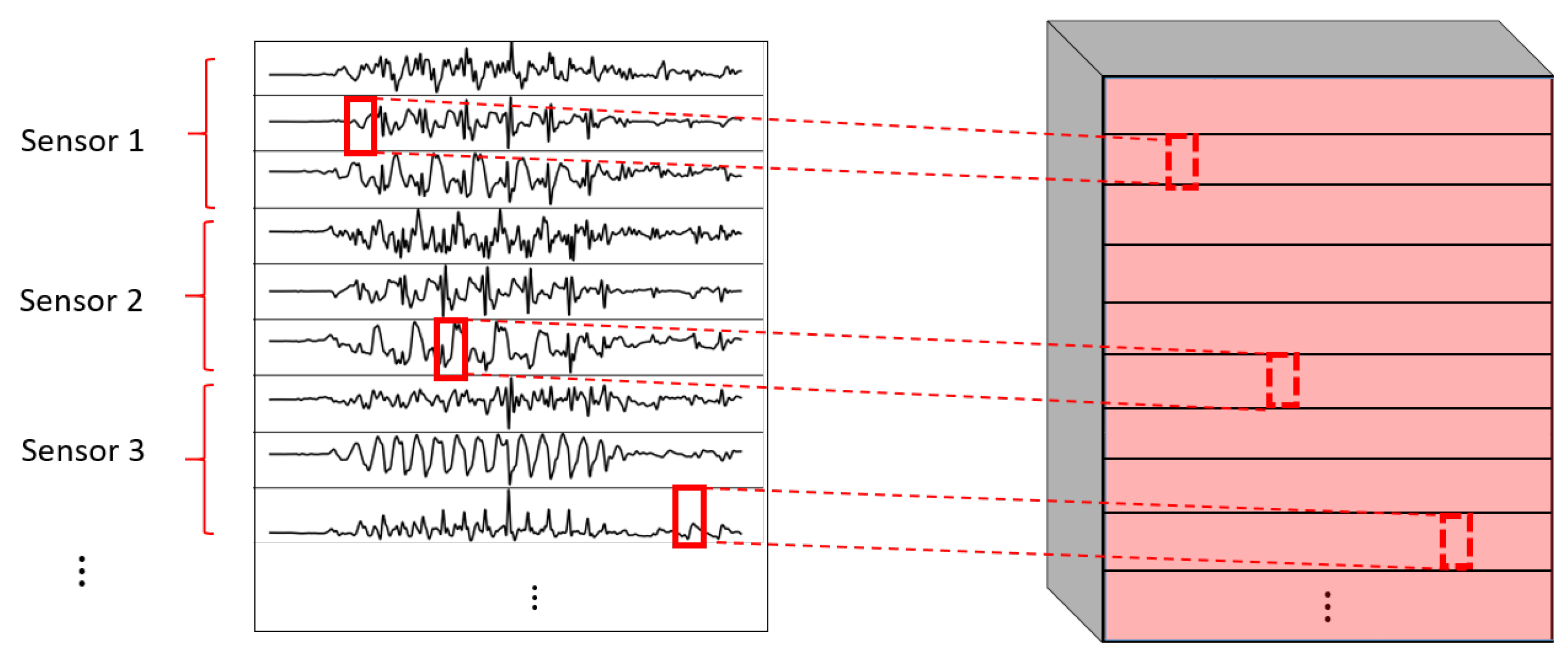
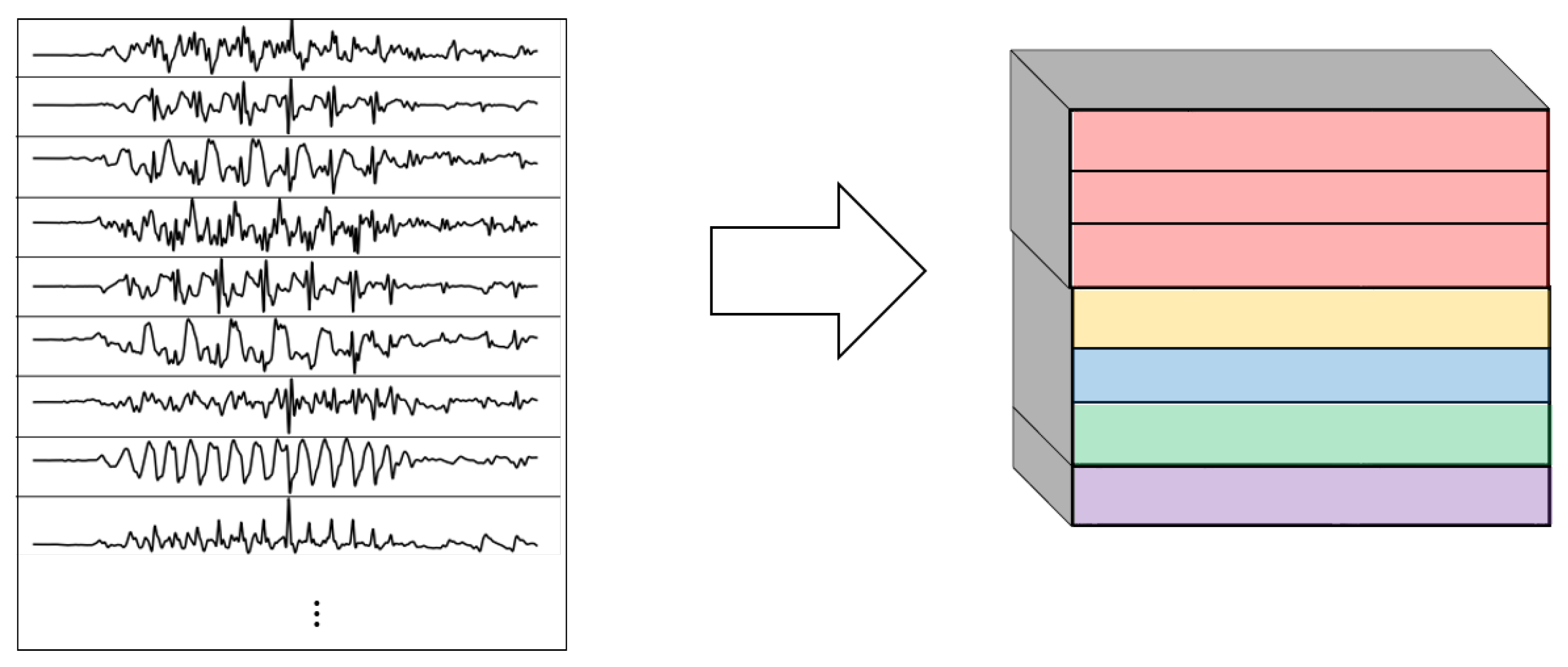
- 1DCNN weight sharing:One-dimensional convolutions with the same filters for all the signals. In this type of convolution, filters of size are used, where m is a hyperparameter that determines the timesteps used in the convolution. The 1 implies that each signal is convolved alone. Additionally, weight sharing means that the same filters are used for all the signals. Figure 6 explains this logic. Note that each sensor is composed of three signals (X, Y, and Z axis of the sensor). The convolutions are made for each signal using the same set of k filters (represented in red).
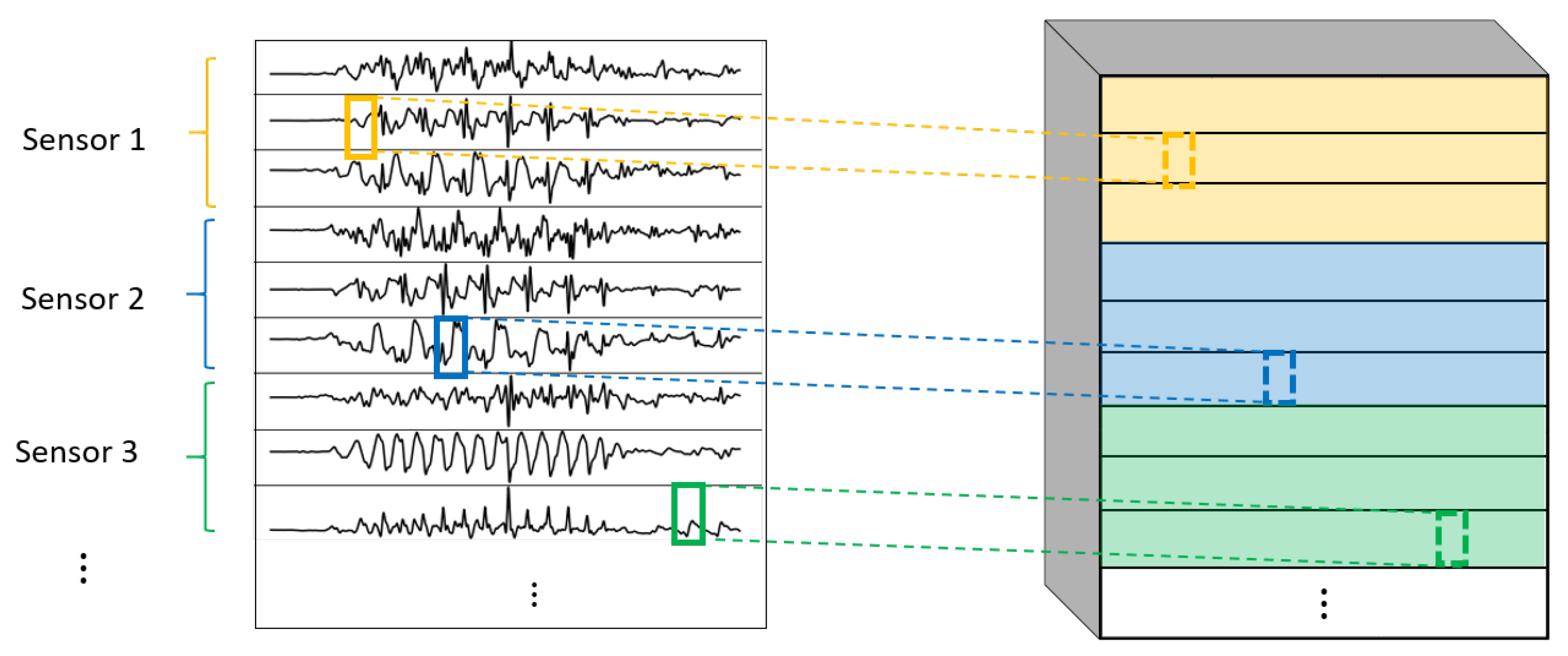
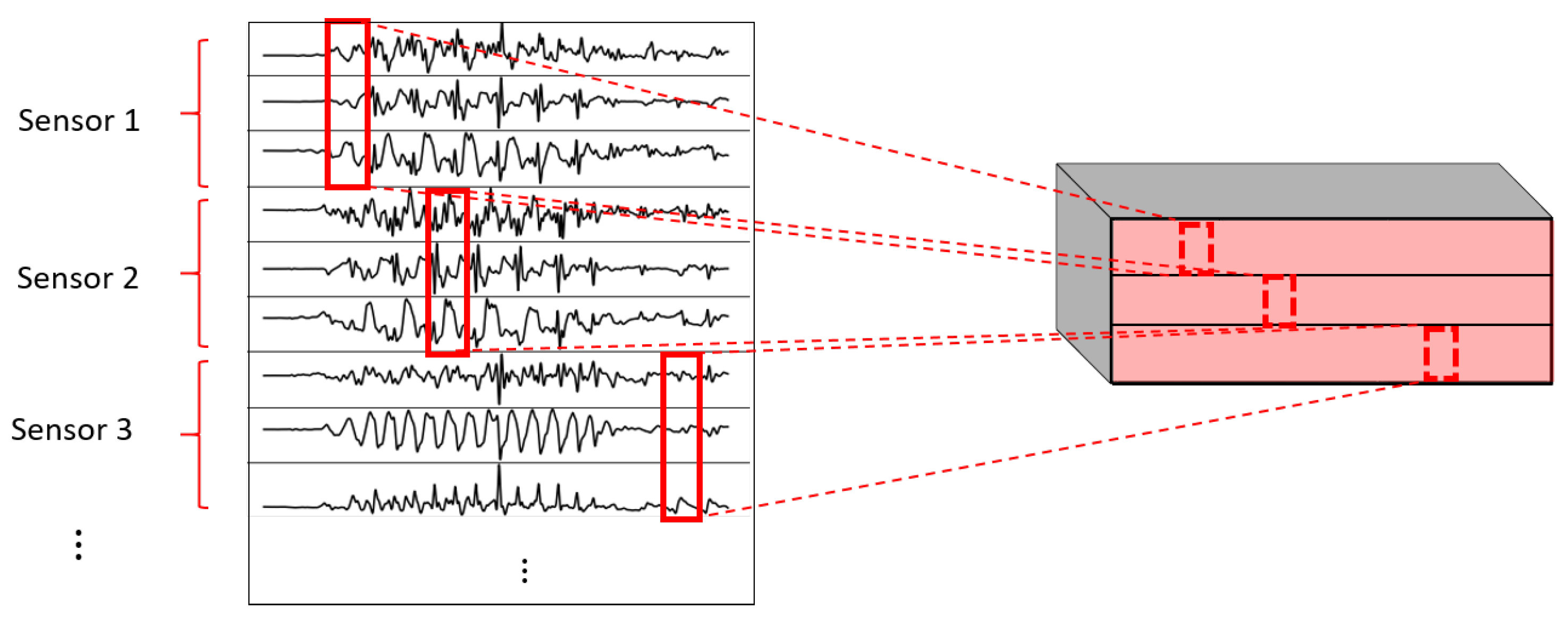
- 1DCNN per sensor:One-dimensional convolutions with the same filters for all the signals of the same sensor, but different filters for each sensor. In this type of convolution, filters of size are used, where m is a hyperparameter that determines the timesteps used in the convolution. The 1 implies that each signal is convolved alone. However, each sensor has its own set of k filters, meaning that the filters are not shared among the sensors. Figure 7 shows this logic. The convolutions are made for each sensor using, for each one of them, a different set of k filters (but the same set of filters are used for the three axis of the same sensor). The different sets of filters are represented with different colors in the figure.
- 1DCNN combined:Combination of 1DCNN weight sharing and 1DCNN per sensor. Both types of convolutions are performed and their results (feature maps) are concatenated one on top of the other. Figure 8 shows this logic.
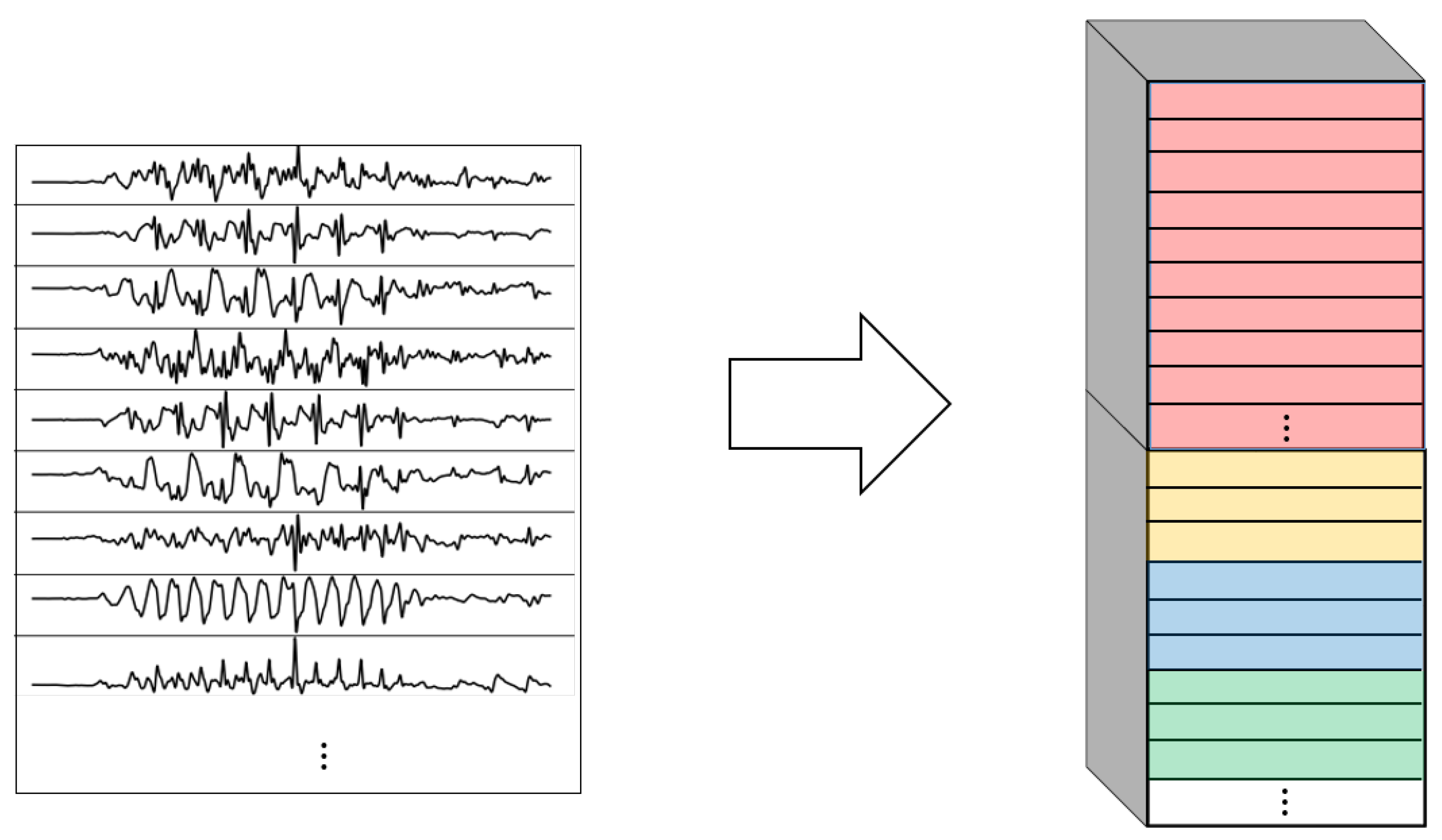
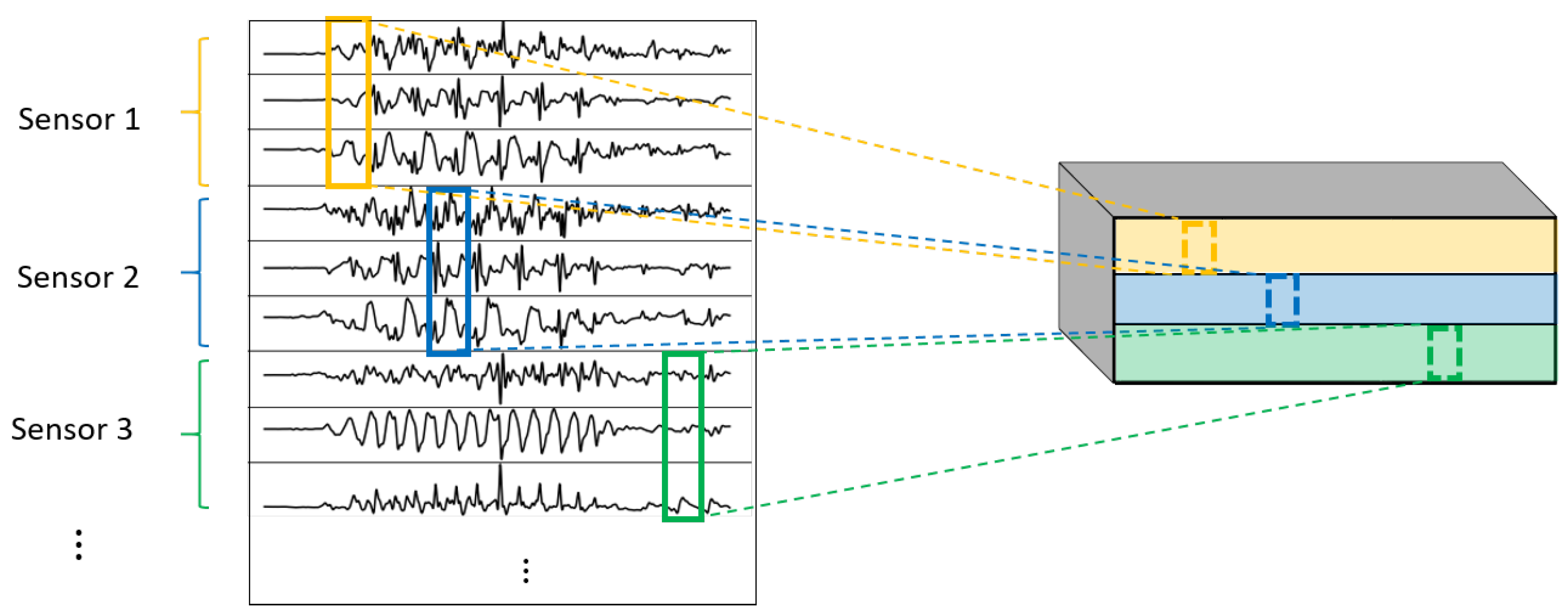
- 2DCNN weight sharing:Two-dimensional convolutions with the same filters for all the sensors. In this type of convolution, filters of size are used, where m is a hyperparameter that determines the timesteps used in the convolution. The 3 means that the 3 axes of the same sensor are used together in the convolution. In order to convolve each sensor by itself so that specific patterns can be extracted by combinations of the X, Y, and Z signals of the same sensor, a spatial stride of 3 is used. Additionally, weight sharing means that the same filters are used for all the sensors. Figure 9 explains this logic.
- 2DCNN per sensor:Two-dimensional convolutions with different filters for each sensor. In this type of convolution, filters of size are used, where m is a hyperparameter that determines the timesteps used in the convolution. The 3 means that the 3 axes of the same sensor are used together in the convolution. In order to convolve each sensor by itself so that specific patterns can be extracted by combinations of the X, Y, and Z signals of the same sensor, a spatial stride of 3 is used. Figure 10 explains this logic. The convolutions are made for each sensor using, for each one of them, a different set of k filters. The different sets of filters are represented with different colors in the figure.
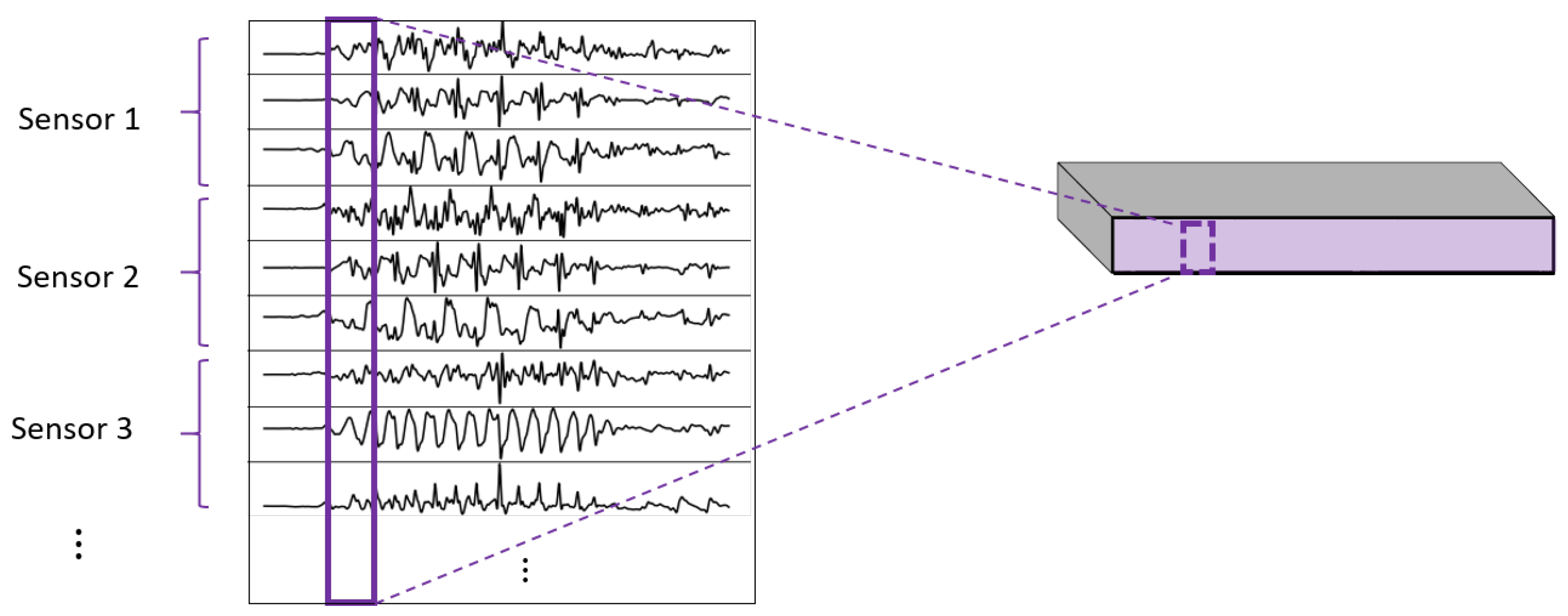
- 2DCNN all sensors:Two-dimensional convolutions made across all the sensors (thus also signals) at once. In this type of convolution, filters of size are used, where m is a hyperparameter that determines the timesteps used in the convolution. Figure 11 explains this logic.
- 2DCNN combined:Combination of 2DCNN weight sharing, 2DCNN per sensor, and 2DCNN all sensors. The three types of convolutions are performed and the resulting feature maps are concatenated one on top of the other. Figure 12 shows this logic.
- For all the models without any LSTM or bLSTM component, the learning rate was initialized at . After every 10 epochs of training, it was reduced to its 75%.
- For all the models with only LSTM or bLSTM (no convolutional part), the learning rate was initialized at . After every 10 epochs of training, it was reduced to its 50%.
- For all the models that combined a CNN part with a LSTM or bLSTM part, the learning rate was initialized at . After every 10 epochs of training, it was reduced to its 75%.
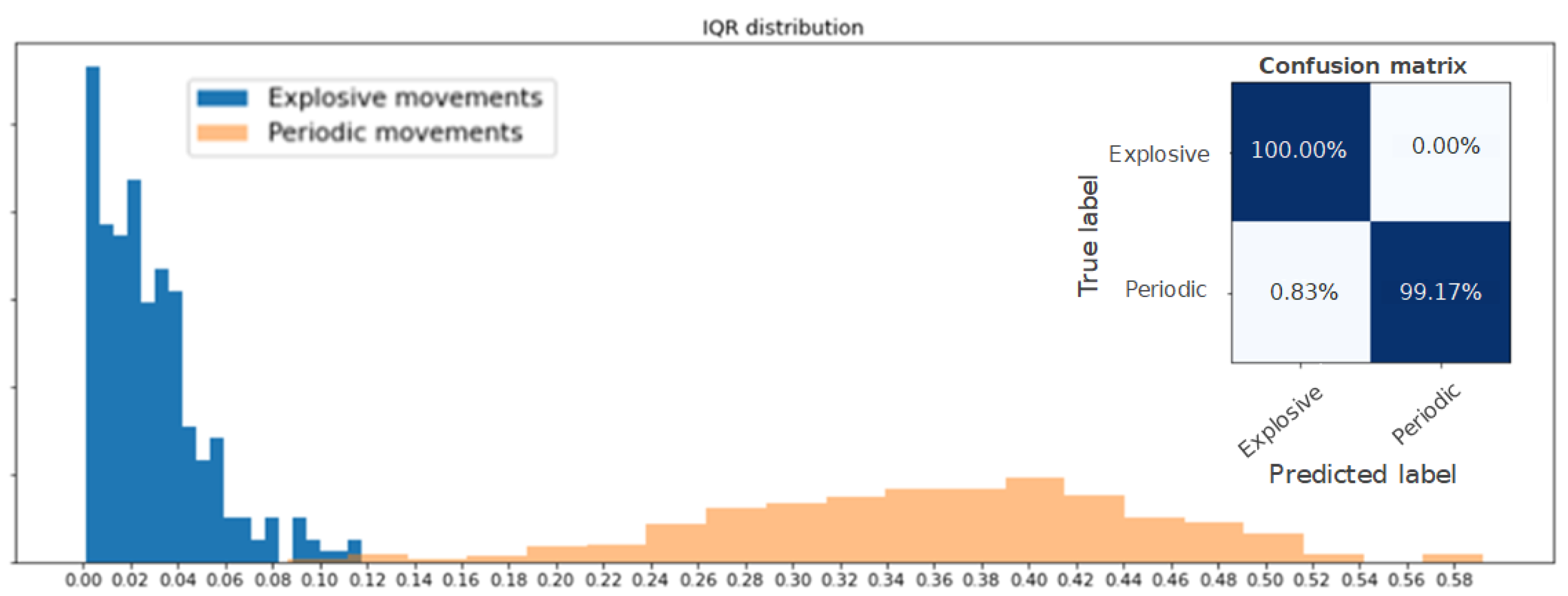
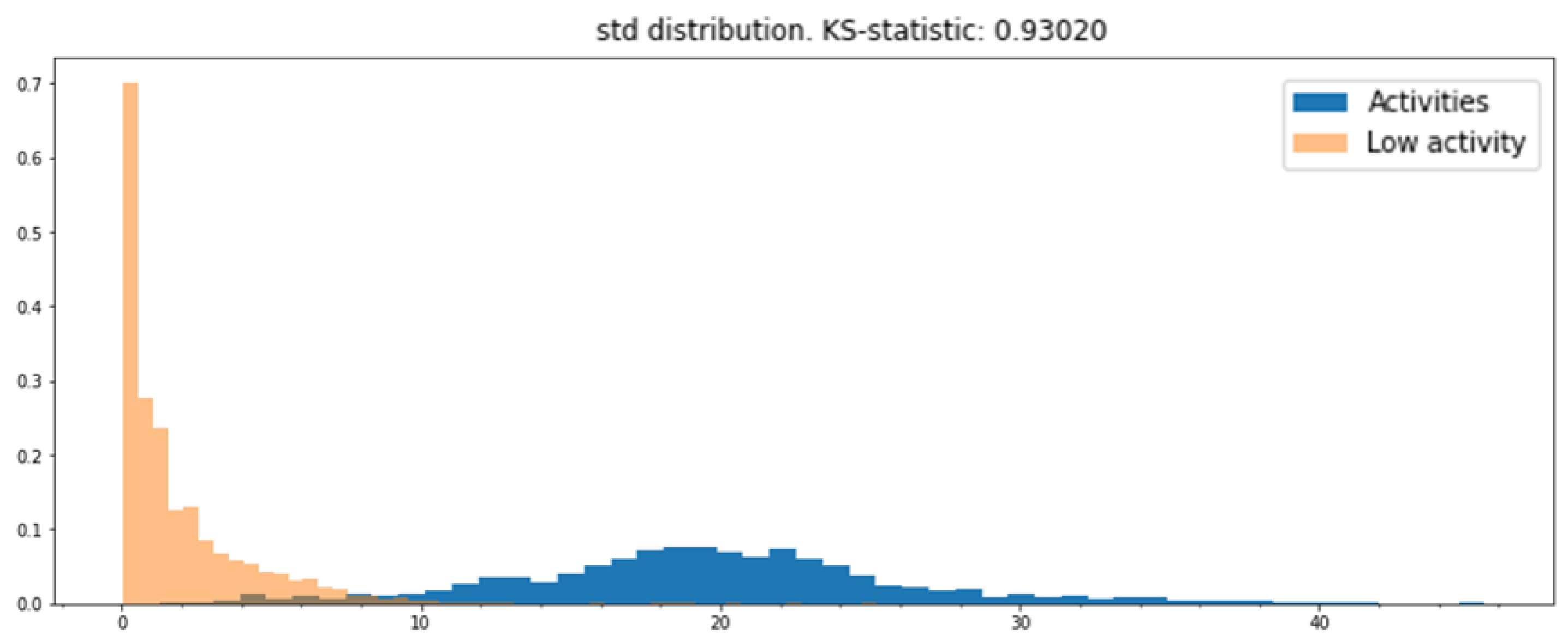
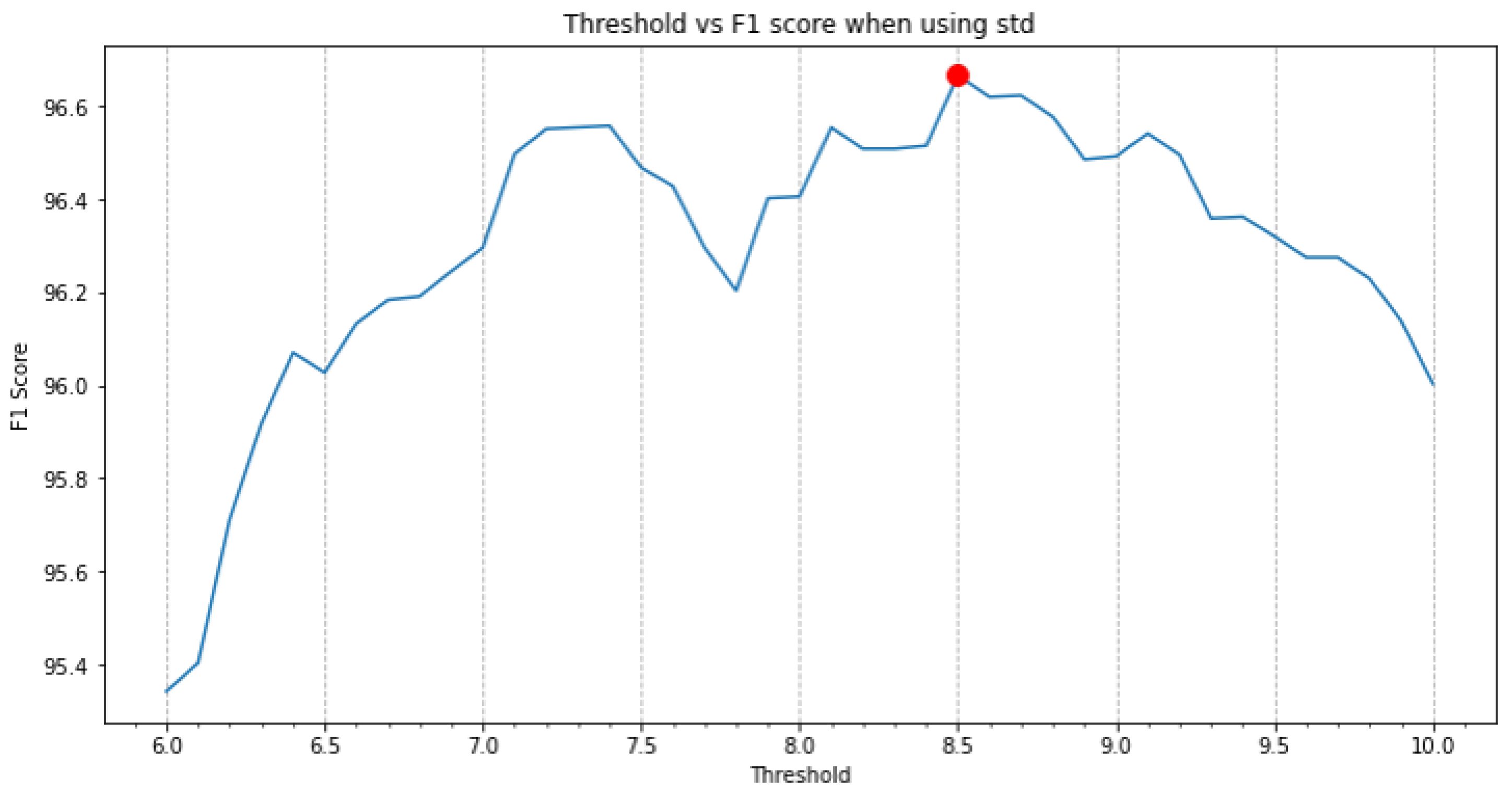
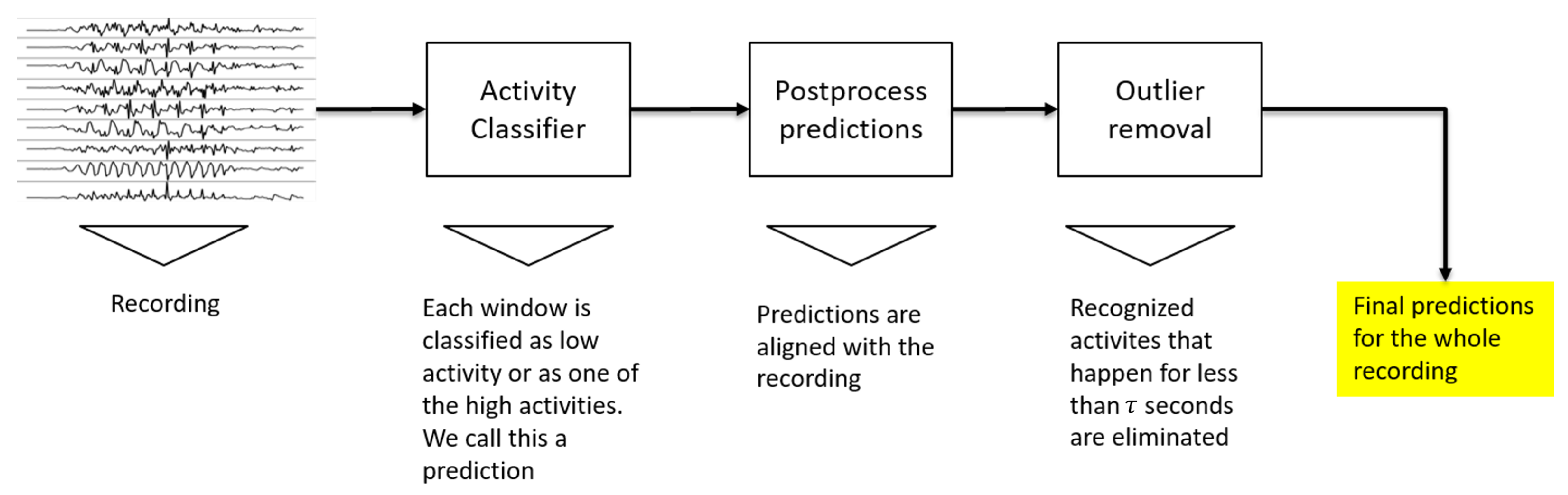
3.3. Postprocessing and Evaluation
- Mean;
- Standard deviation (std);
- Coefficient of variation (CV);
- Interquartile range (IQR);
- Range.
4. Results
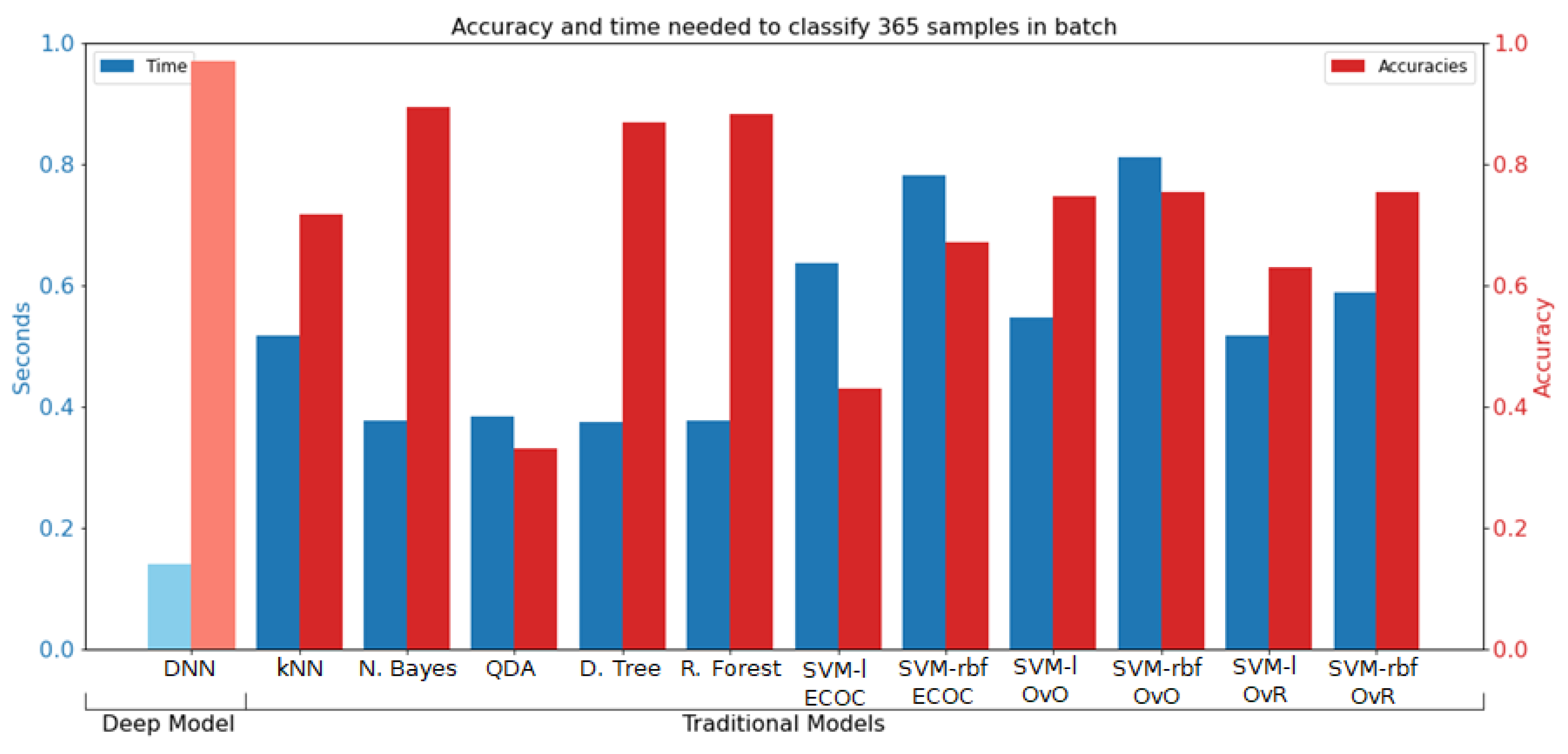
4.1. Training Results
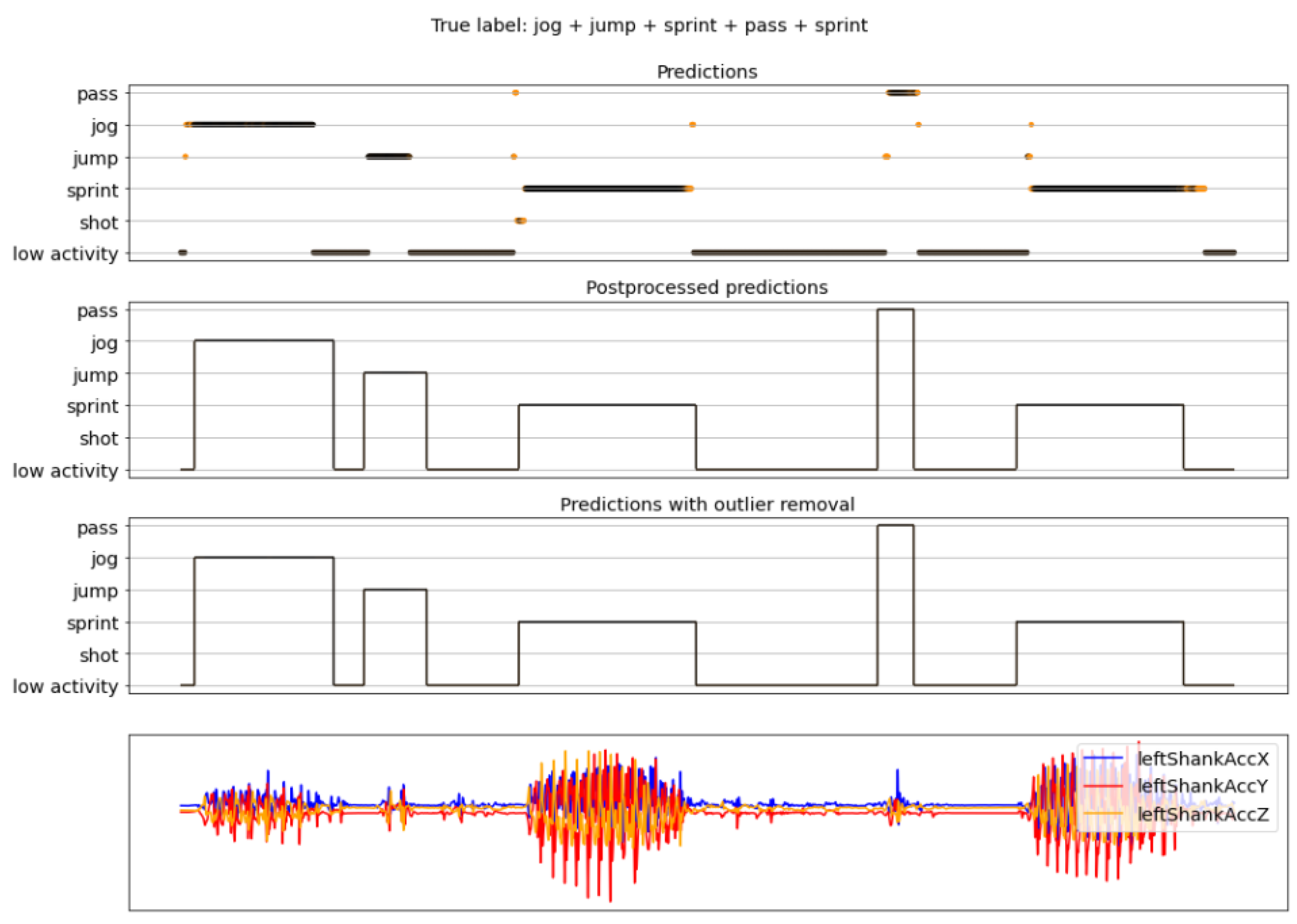
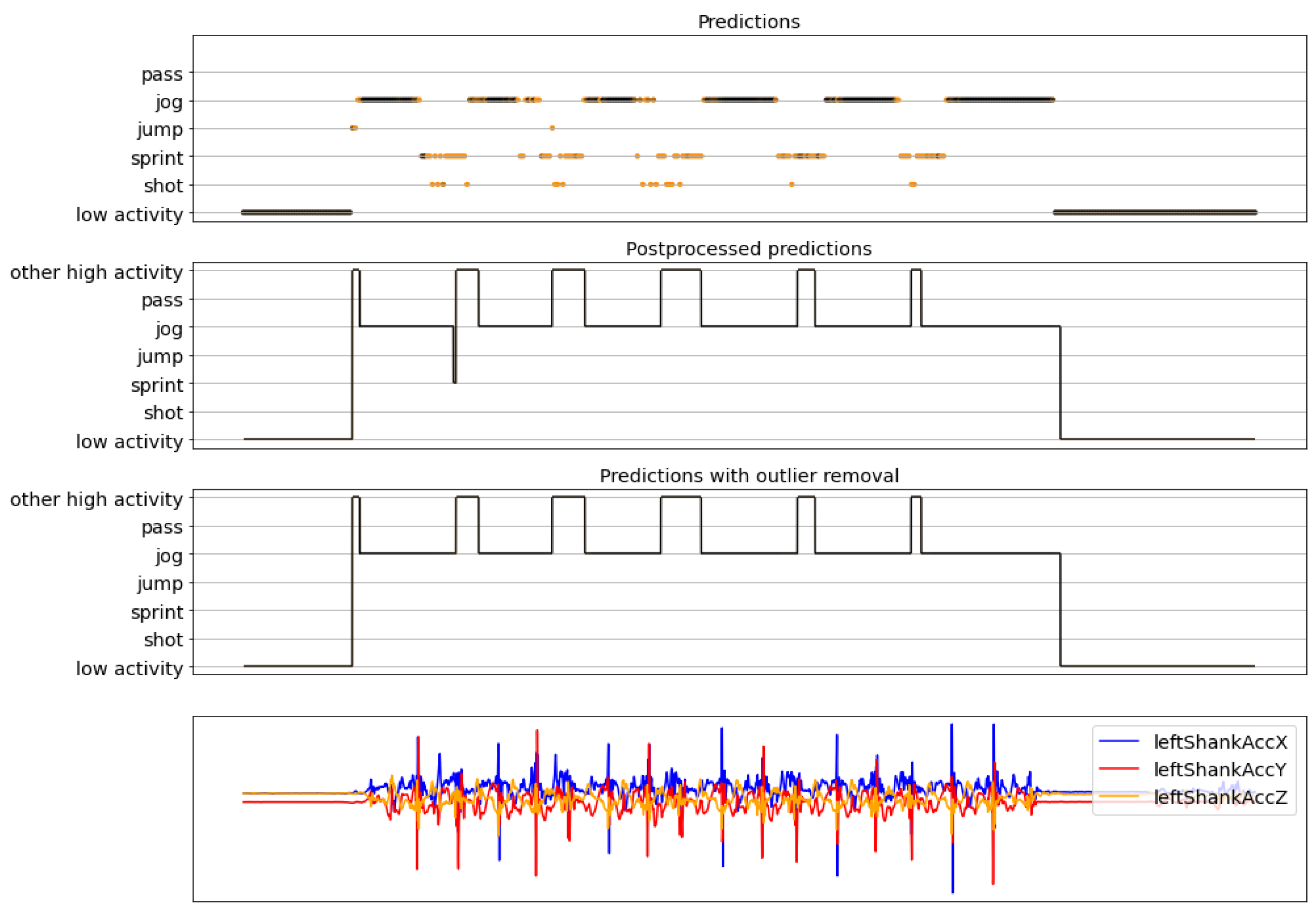
4.2. Complete Pipeline Results
5. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Abd, M.A.; Paul, R.; Aravelli, A.; Bai, O.; Lagos, L.; Lin, M.; Engeberg, E.D. Hierarchical Tactile Sensation Integration from Prosthetic Fingertips Enables Multi-Texture Surface Recognition. Sensors 2021, 21, 4324. [Google Scholar] [CrossRef] [PubMed]
- Slim, S.; Atia, A.; Elfattah, M.; Mostafa, M.S.M. Survey on human activity recognition based on acceleration data. Intl. J. Adv. Comput. Sci. Appl. 2019, 10, 84–98. [Google Scholar] [CrossRef]
- Wang, L.; Liu, R. Human activity recognition based on wearable sensor using hierarchical deep LSTM networks. Circuits Syst. Signal Process. 2020, 39, 837–856. [Google Scholar] [CrossRef]
- Adaskevicius, R. Method for recognition of the physical activity of human being using a wearable accelerometer. Elektron. Elektrotechnika 2014, 20, 127–131. [Google Scholar] [CrossRef]
- Mannini, A.; Sabatini, A.M. Machine learning methods for classifying human physical activity from on-body accelerometers. Sensors 2010, 10, 1154–1175. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- De Vries, S.I.; Engels, M.; Garre, F.G. Identification of children’s activity type with accelerometer-based neural networks. Med. Sci. Sport. Exerc. 2011, 43, 1994–1999. [Google Scholar] [CrossRef] [PubMed]
- Ignatov, A. Real-time human activity recognition from accelerometer data using Convolutional Neural Networks. Appl. Soft Comput. 2018, 62, 915–922. [Google Scholar] [CrossRef]
- Ha, S.; Yun, J.M.; Choi, S. Multi-modal convolutional neural networks for activity recognition. In Proceedings of the 2015 IEEE International Conference on Systems, Man, and Cybernetics, Hong Kong, China, 9–12 October 2015; pp. 3017–3022. [Google Scholar]
- Zebin, T.; Scully, P.J.; Ozanyan, K.B. Evaluation of supervised classification algorithms for human activity recognition with inertial sensors. In Proceedings of the 2017 IEEE SENSORS, Glasgow, UK, 29 October–1 November 2017; pp. 1–3. [Google Scholar]
- Blank, P.; Hoßbach, J.; Schuldhaus, D.; Eskofier, B.M. Sensor-based stroke detection and stroke type classification in table tennis. In Proceedings of the 2015 ACM International Symposium on Wearable Computers, Osaka, Japan, 7–11 September 2015; pp. 93–100. [Google Scholar]
- Connaghan, D.; Kelly, P.; O’Connor, N.E.; Gaffney, M.; Walsh, M.; O’Mathuna, C. Multi-sensor classification of tennis strokes. In Proceedings of the SENSORS, 2011 IEEE, Limerick, Ireland, 28–31 October 2011; pp. 1437–1440. [Google Scholar]
- Groh, B.H.; Kautz, T.; Schuldhaus, D.; Eskofier, B.M. IMU-based trick classification in skateboarding. In Proceedings of the KDD Workshop on Large-Scale Sports Analytics, Sydney, Australia, 10–13 August 2015; Volume 17. [Google Scholar]
- Kautz, T.; Groh, B.H.; Hannink, J.; Jensen, U.; Strubberg, H.; Eskofier, B.M. Activity recognition in beach volleyball using a Deep Convolutional Neural Network. Data Min. Knowl. Discov. 2017, 31, 1678–1705. [Google Scholar] [CrossRef]
- Schuldhaus, D.; Zwick, C.; Körger, H.; Dorschky, E.; Kirk, R.; Eskofier, B.M. Inertial sensor-based approach for shot/pass classification during a soccer match. In Proceedings of the KDD Workshop on Large-Scale Sports Analytics, Sydney, Australia, 10–13 August 2015; pp. 1–4. [Google Scholar]
- Liu, X. Tennis Stroke Recognition: Stroke Classification Using Inertial Measuring Unit and Machine Learning Algorithm in Tennis. Master’s Thesis, Delft University of Technology, Delft, The Netherlands, 2020. [Google Scholar]
- Jiao, L.; Bie, R.; Wu, H.; Wei, Y.; Ma, J.; Umek, A.; Kos, A. Golf swing classification with multiple deep convolutional neural networks. Int. J. Distrib. Sens. Netw. 2018, 14, 1550147718802186. [Google Scholar] [CrossRef] [Green Version]
- Schuldhaus, D. Human Activity Recognition in Daily Life and Sports Using Inertial Sensors; FAU University Press: Boca Raton, FL, USA, 2019. [Google Scholar]
- Xu, C.; Chai, D.; He, J.; Zhang, X.; Duan, S. InnoHAR: A deep neural network for complex human activity recognition. IEEE Access 2019, 7, 9893–9902. [Google Scholar] [CrossRef]
- Xia, K.; Huang, J.; Wang, H. LSTM-CNN architecture for human activity recognition. IEEE Access 2020, 8, 56855–56866. [Google Scholar] [CrossRef]
- Lv, M.; Xu, W.; Chen, T. A hybrid deep convolutional and recurrent neural network for complex activity recognition using multimodal sensors. Neurocomputing 2019, 362, 33–40. [Google Scholar] [CrossRef]
- Ordóñez, F.J.; Roggen, D. Deep convolutional and lstm recurrent neural networks for multimodal wearable activity recognition. Sensors 2016, 16, 115. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Hubel, D.H.; Wiesel, T.N. Receptive fields, binocular interaction and functional architecture in the cat’s visual cortex. J. Physiol. 1962, 160, 106–154. [Google Scholar] [CrossRef] [PubMed]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Pascanu, R.; Mikolov, T.; Bengio, Y. On the difficulty of training recurrent neural networks. In Proceedings of the International Conference on Machine Learning, PMLR, Atlanta, GA, USA, 17–19 June 2013; pp. 1310–1318. [Google Scholar]
- Wilmes, E.; De Ruiter, C.J.; Bastiaansen, B.J.; Van Zon, J.F.; Vegter, R.J.; Brink, M.S.; Goedhart, E.A.; Lemmink, K.A.; Savelsbergh, G.J. Inertial sensor-based motion tracking in football with movement intensity quantification. Sensors 2020, 20, 2527. [Google Scholar] [CrossRef] [PubMed]
- Invensense. Nine-Axis (Gyro + Accelerometer + Compass) MEMS MotionTracking™ Device; Revision 4.3; Invensense: San Jose, CA, USA, 2013. [Google Scholar]
- Wilmes, E. Measuring Changes in Hamstring Contractile Strength and Lower Body Sprinting Kinematics during a Simulated Soccer Match. Master’s Thesis, Delft University of Technology, Delft, The Netherlands, 2019. [Google Scholar]
- Steijlen, A.; Bastemeijer, J.; Plaude, L.; French, P.; Bossche, A.; Jansen, K. Development of Sensor Tights with Integrated Inertial Measurement Units for Injury Prevention in Football. In Proceedings of the 6th International Conference on Design4Health, Amsterdam, The Netherlands, 1–3 July 2020; Volume 1, p. 3. [Google Scholar]
- Berrar, D. Cross-Validation. In Encyclopedia of Bioinformatics and Computational Biology; Elsevier: Amsterdam, The Netherlands, 2019. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- LeCun, Y.A.; Bottou, L.; Orr, G.B.; Müller, K.R. Efficient backprop. In Neural Networks: Tricks of the Trade; Springer: Berlin/Heidelberg, Germany, 2012; pp. 9–48. [Google Scholar]
- Roggen, D.; Calatroni, A.; Rossi, M.; Holleczek, T.; Förster, K.; Tröster, G.; Lukowicz, P.; Bannach, D.; Pirkl, G.; Ferscha, A.; et al. Collecting complex activity datasets in highly rich networked sensor environments. In Proceedings of the 2010 Seventh International Conference on Networked Sensing Systems (INSS), Kassel, Germany, 15–18 June 2010; pp. 233–240. [Google Scholar]
- Kwapisz, J.R.; Weiss, G.M.; Moore, S.A. Activity recognition using cell phone accelerometers. ACM SigKDD Explor. Newsl. 2011, 12, 74–82. [Google Scholar] [CrossRef]
- Anguita, D.; Ghio, A.; Oneto, L.; Parra, X.; Reyes-Ortiz, J.L. A public domain dataset for human activity recognition using smartphones. In Proceedings of the 21th International European Symposium on Artificial Neural Networks, Computational Intelligence and Machine Learning, Bruges, Belgium, 24–26 April 2013; Volume 3, p. 3. [Google Scholar]

| CNN Sub-Network | Layer 1 | Layer 2 | Layer 3 | Layer 4 |
|---|---|---|---|---|
| 1DCNN weight sharing | Conv(16, (1, 5), 1) | MaxP(1, 4) | Conv(32, (1, 5), 1) | MaxP(1, 4) |
| 1DCNN per sensor | Conv(16, (1, 5), 1) | MaxP(1, 4) | Conv(32, (1, 5), 1) | MaxP(1, 4) |
| 1DCNN combined | Concatenation of 1DCNN variations | |||
| 2DCNN weight sharing | Conv(32, (3, 5), 3) | MaxP(1, 4) | Conv(64, (1, 5), 1) | MaxP(1, 4) |
| 2DCNN per sensor | Conv(32, (3, 5), 1) | MaxP(1, 4) | Conv(64, (1, 5), 1) | MaxP(1, 4) |
| 2DCNN all sensors | Conv(32, (d, 5), 1) | MaxP(1, 4) | Conv(64, (1, 5), 1) | MaxP(1, 4) |
| 2DCNN combined | Concatenation of 2DCNN variations | |||
| Metric | KS Value |
|---|---|
| Mean | 0.9185 |
| Std | 0.9302 |
| CV | 0.7997 |
| IQR | 0.9237 |
| Range | 0.9155 |
| Acc + Gyro | ||||
|---|---|---|---|---|
| Normalized | Unnormalized | |||
| Train | Test | Train | Test | |
| 1D CNN weight sharing | 99.93% | 97.53% | 99.13% | 94.36% |
| 1D CNN per sensor | 99.34% | 97.26% | 98.35% | 93.92% |
| 1D CNN combined | 99.46% | 97.21% | 98.66% | 93.97% |
| 2D CNN weight sharing | 99.29% | 96.44% | 98.80% | 93.59% |
| 2D CNN per sensor | 99.44% | 96.55% | 99.32% | 94.79% |
| 2D CNN all signals | 99.76% | 97.81% | 97.58% | 92.88% |
| 2D CNN combined | 99.44% | 98.08% | 99.34% | 95.34% |
| 1D CNN weight sharing + LSTM | 97.81% | 96.11% | 99.01% | 96.05% |
| 1D CNN per sensor + LSTM | 99.20% | 97.10% | 98.31% | 95.95% |
| 1D CNN combined + LSTM | 98.54% | 97.04% | 98.87% | 96.55% |
| 2D CNN weight sharing + LSTM | 98.54% | 96.71% | 98.87% | 96.27% |
| 2D CNN per sensor + LSTM | 98.31% | 96.71% | 99.32% | 96.71% |
| 2D CNN all signals + LSTM | 98.87% | 97.32% | 98.94% | 95.45% |
| 2D CNN combined + LSTM | 99.08% | 97.53% | 99.32% | 96.71% |
| 1D CNN weight sharing + bLSTM | 99.39% | 98.03% | 99.08% | 96.55% |
| 1D CNN per sensor + bLSTM | 99.51% | 97.86% | 98.66% | 96.38% |
| 1D CNN combined + bLSTM | 99.44% | 98.25% | 99.22% | 96.71% |
| 2D CNN weight sharing + bLSTM | 99.39% | 97.48% | 99.20% | 96.22% |
| 2D CNN per sensor + bLSTM | 99.48% | 97.04% | 98.99% | 96.11% |
| 2D CNN all signals + bLSTM | 99.13% | 97.26% | 98.45% | 94.96% |
| 2D CNN combined + bLSTM | 99.46% | 97.32% | 99.29% | 96.00% |
| LSTM | 63.51% | 60.44% | 91.48% | 77.48% |
| bLSTM | 80.49% | 76.71% | 99.65% | 87.07% |
| Acc + Gyro | ||||
|---|---|---|---|---|
| Normalized | Unnormalized | |||
| Train | Test | Train | Test | |
| 1D CNN weight sharing | 0.09% | 0.87% | 0.81% | 1.33% |
| 1D CNN per sensor | 0.41% | 0.74% | 1.68% | 1.78% |
| 1D CNN combined | 0.44% | 0.70% | 0.33% | 1.48% |
| 2D CNN weight sharing | 0.20% | 0.81% | 0.49% | 1.60% |
| 2D CNN per sensor | 0.29% | 0.37% | 0.46% | 1.42% |
| 2D CNN all signals | 0.15% | 0.67% | 0.87% | 1.38% |
| 2D CNN combined | 0.55% | 0.35% | 0.44% | 1.42% |
| 1D CNN weight sharing + LSTM | 0.79% | 0.56% | 0.52% | 1.21% |
| 1D CNN per sensor + LSTM | 0.58% | 1.44% | 1.22% | 0.87% |
| 1D CNN combined + LSTM | 0.54% | 0.56% | 0.62% | 1.60% |
| 2D CNN weight sharing + LSTM | 0.50% | 0.65% | 0.92% | 1.00% |
| 2D CNN per sensor + LSTM | 0.76% | 1.47% | 0.39% | 1.31% |
| 2D CNN all signals + LSTM | 0.75% | 0.66% | 0.58% | 1.02% |
| 2D CNN combined + LSTM | 0.30% | 0.83% | 0.37% | 1.05% |
| 1D CNN weight sharing + bLSTM | 0.44% | 0.63% | 0.34% | 0.73% |
| 1D CNN per sensor + bLSTM | 0.53% | 0.68% | 0.60% | 0.53% |
| 1D CNN combined + bLSTM | 0.27% | 0.66% | 0.53% | 1.54% |
| 2D CNN weight sharing + bLSTM | 0.65% | 0.97% | 0.41% | 0.96% |
| 2D CNN per sensor + bLSTM | 0.35% | 1.17% | 0.75% | 1.10% |
| 2D CNN all signals + bLSTM | 0.55% | 0.62% | 0.96% | 0.99% |
| 2D CNN combined + bLSTM | 0.92% | 0.82% | 0.36% | 1.50% |
| LSTM | 19.13% | 18.19% | 2.17% | 3.36% |
| bLSTM | 24.22% | 20.14% | 0.24% | 2.25% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cuperman, R.; Jansen, K.M.B.; Ciszewski, M.G. An End-to-End Deep Learning Pipeline for Football Activity Recognition Based on Wearable Acceleration Sensors. Sensors 2022, 22, 1347. https://doi.org/10.3390/s22041347
Cuperman R, Jansen KMB, Ciszewski MG. An End-to-End Deep Learning Pipeline for Football Activity Recognition Based on Wearable Acceleration Sensors. Sensors. 2022; 22(4):1347. https://doi.org/10.3390/s22041347
Chicago/Turabian StyleCuperman, Rafael, Kaspar M. B. Jansen, and Michał G. Ciszewski. 2022. "An End-to-End Deep Learning Pipeline for Football Activity Recognition Based on Wearable Acceleration Sensors" Sensors 22, no. 4: 1347. https://doi.org/10.3390/s22041347
APA StyleCuperman, R., Jansen, K. M. B., & Ciszewski, M. G. (2022). An End-to-End Deep Learning Pipeline for Football Activity Recognition Based on Wearable Acceleration Sensors. Sensors, 22(4), 1347. https://doi.org/10.3390/s22041347








