On Minimum Parking Space Required by Automatic Parallel Parking
Abstract
:1. Introduction
1.1. Related Works
1.2. Contributions of This Paper
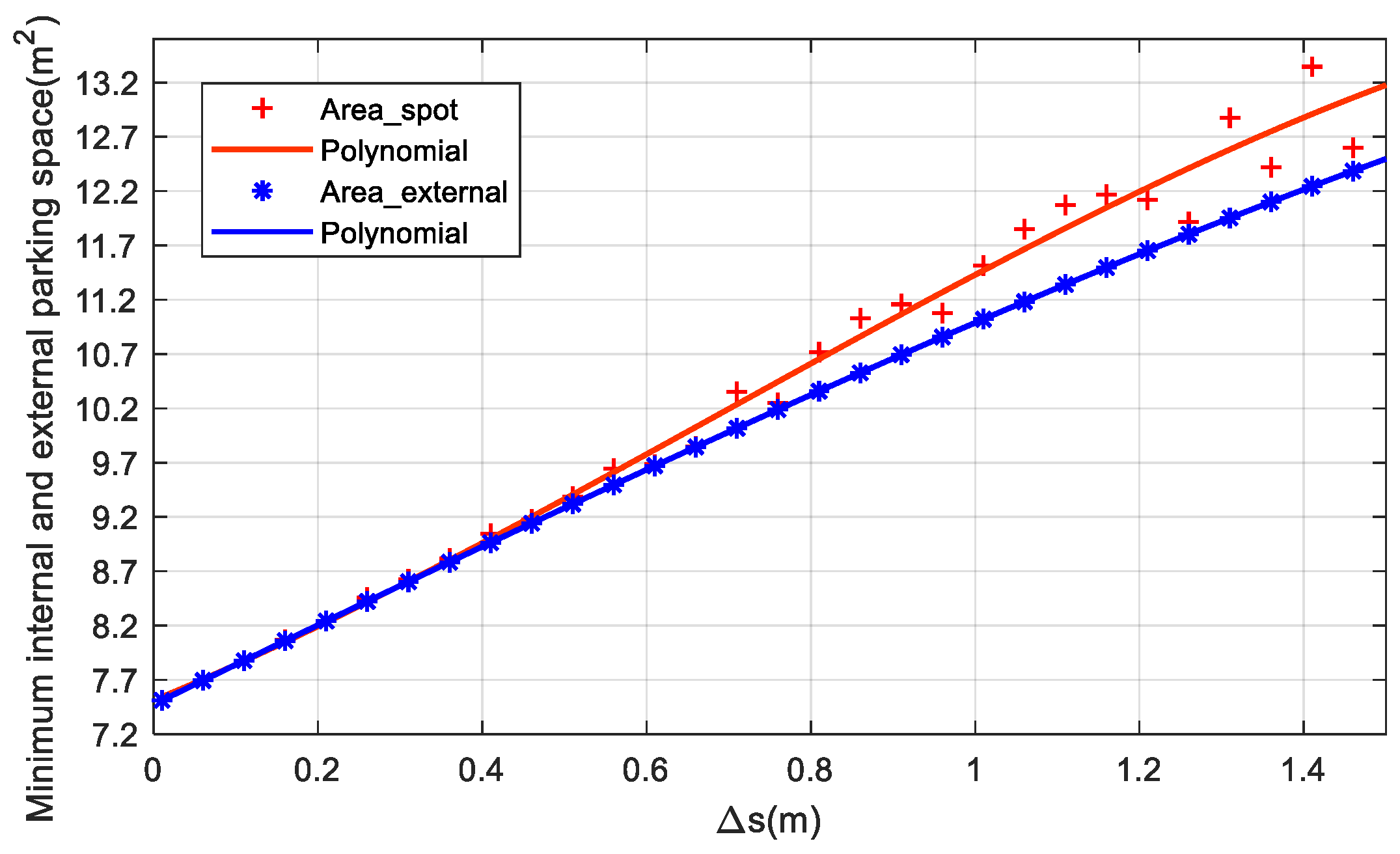
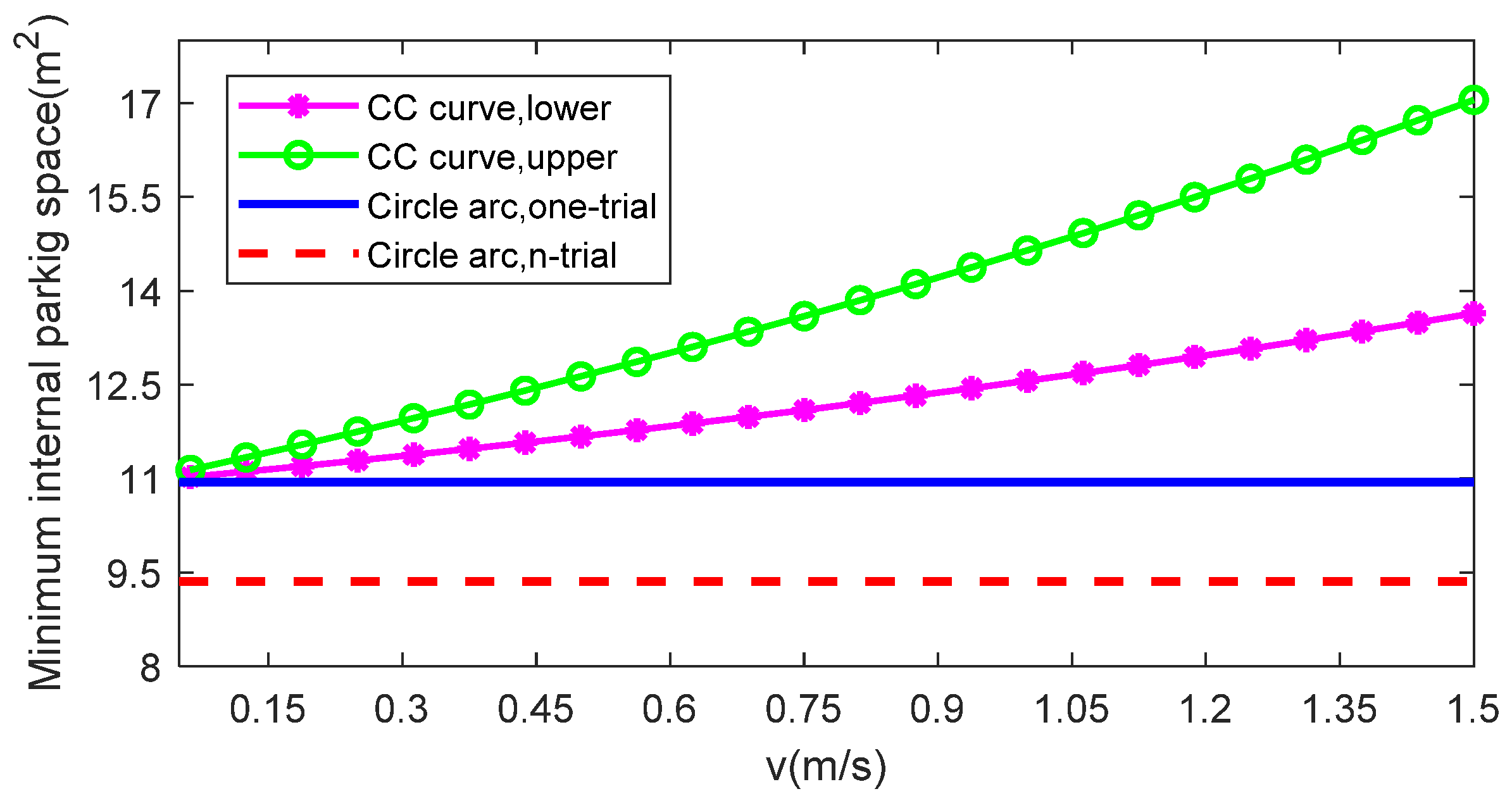
- Considering the extreme case that the number of trials is unbounded, we derive the minimum internal and external space required for n-trial automatic parallel parking based on circular arcs with closed form. The optimal n is given, and it is shown that the lower limits of the minimum internal and external space both approximate the size of the vehicle.
- Considering the extreme case that only one trial is allowed, we give the minimum internal and external space required for automatic parallel parking based on circular arcs and continuous-curvature curves, respectively. It is shown that although the continuous-curvature curve has more smooth transition for path than circular arc, it requires larger space for parking.
- The minimum internal and external spaces that are derived can be the guidelines for urban planners to design right-sized parking slots, and for vehicles to estimate whether a certain piece of space is sufficient for automatic parking with its preferred parking methods.
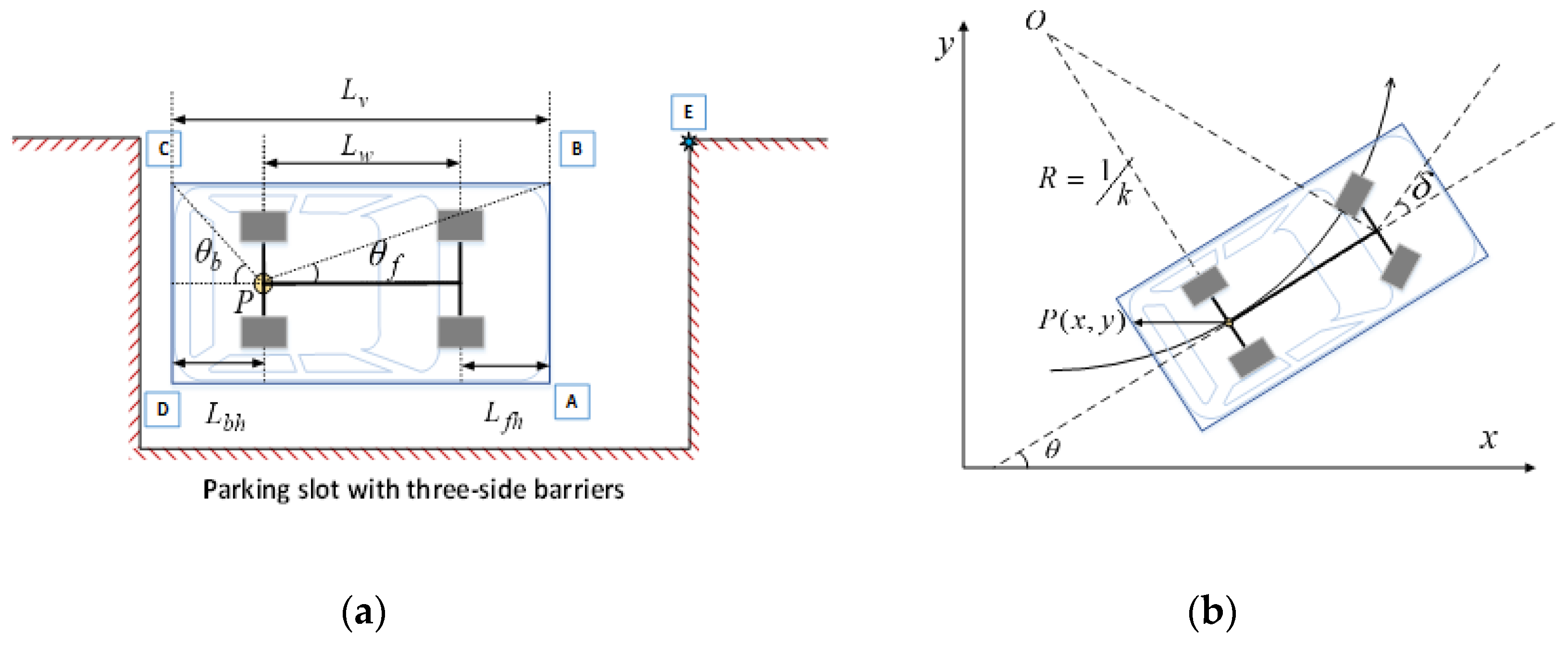
2. Preliminary Modeling
2.1. Simplified Model of Vehicle and Parking Slot
2.2. Kinematic Model of Vehicle
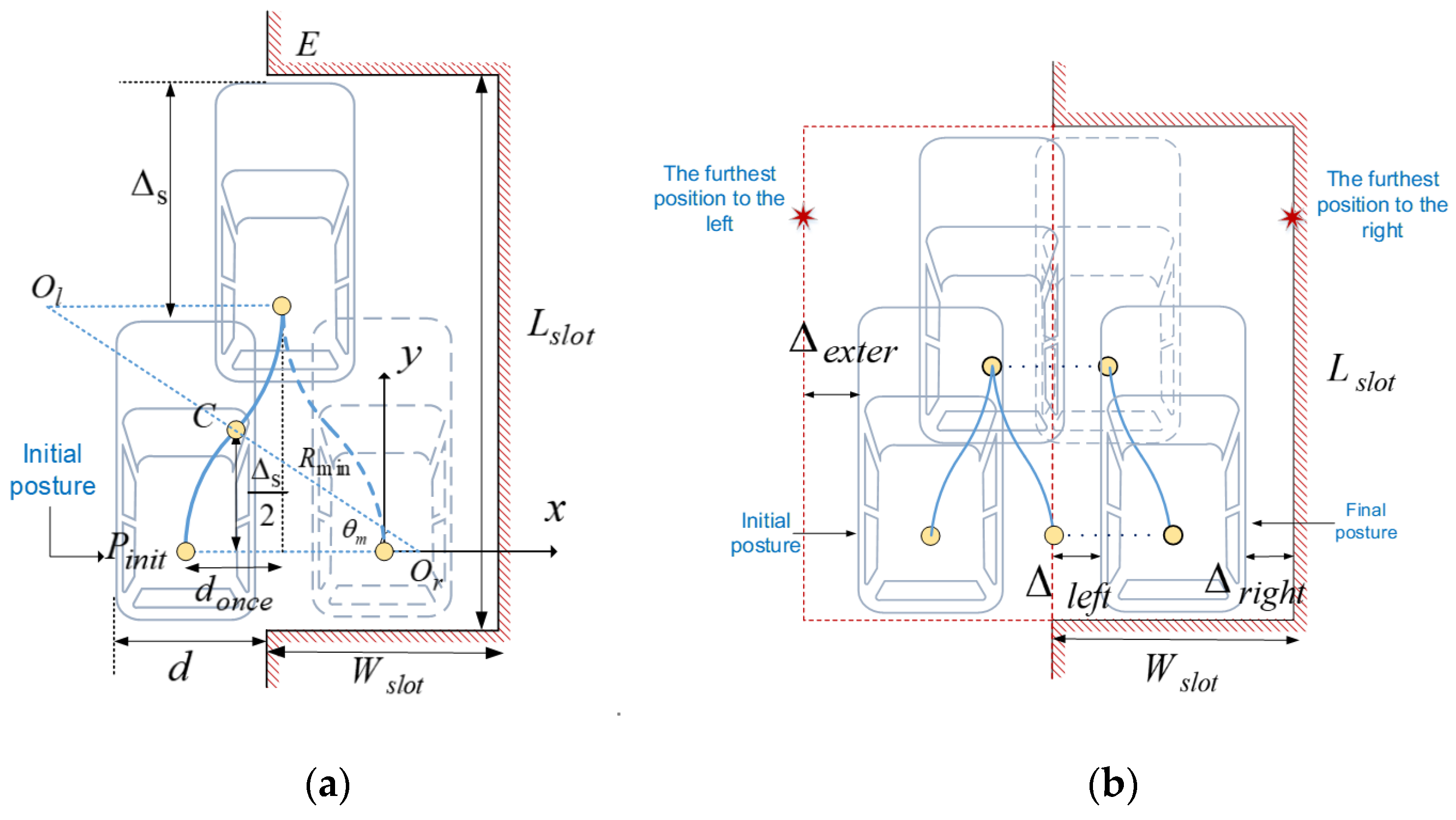
3. Minimum Space for N-Trial Parking Based on Circle Arcs
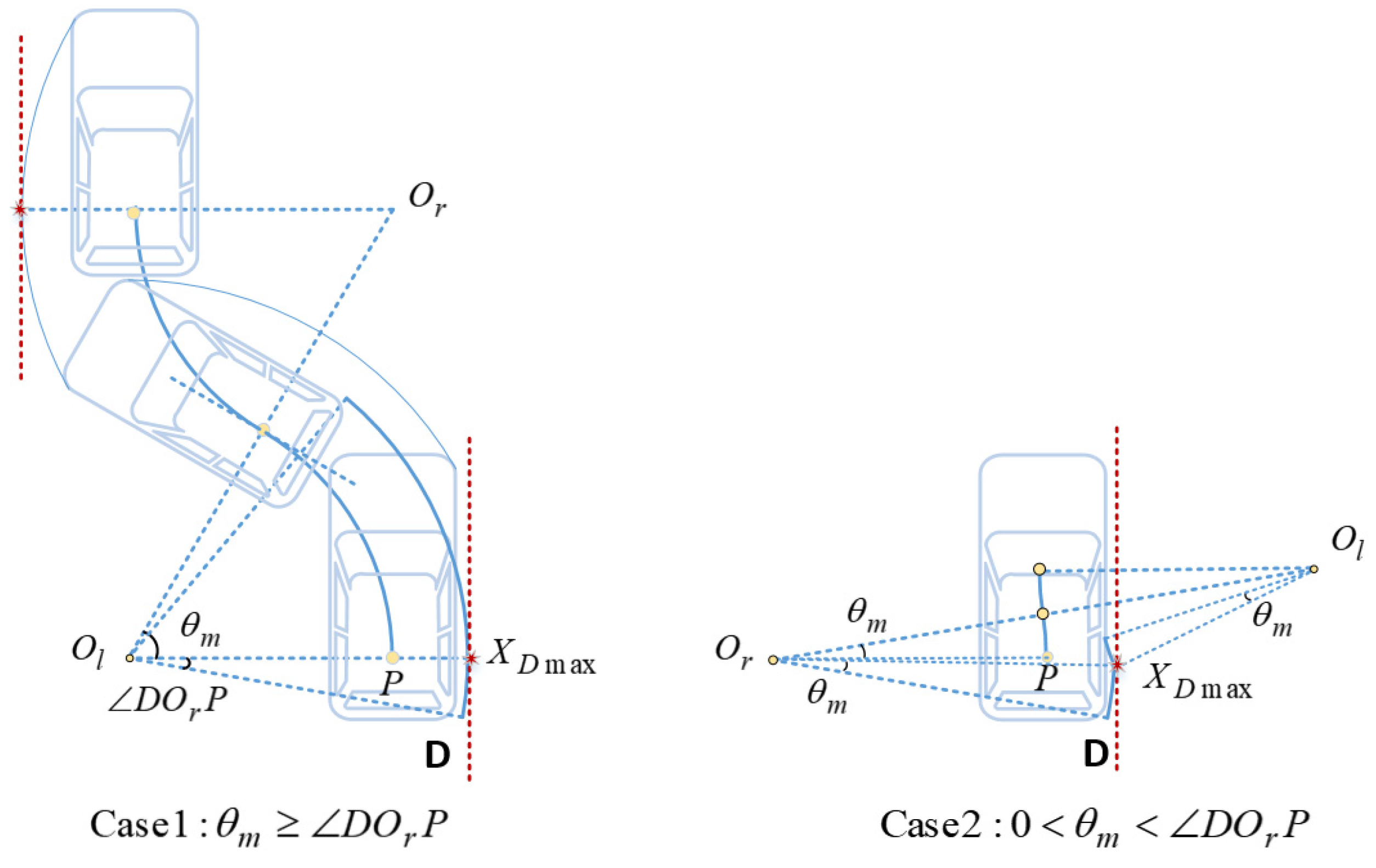
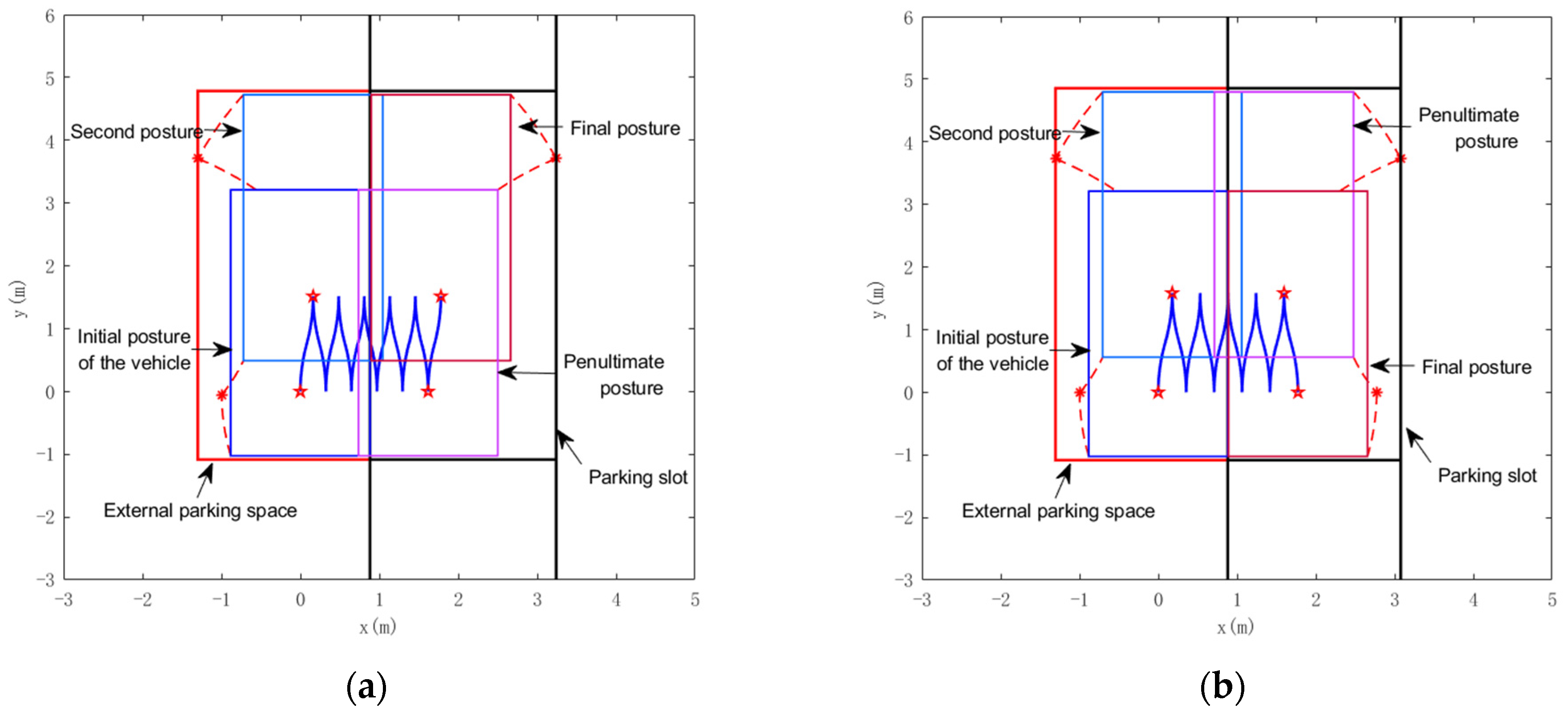
- Situation 1: The vehicle is parked at the top of the slot. In this case, the trajectory of the vehicle shows that is only related to the furthest position reached by the last S-shaped forward movement. It can be concluded from the analytical geometry and Equation (13) that
- Situation 2: The vehicle is parked at the bottom of the slot. In this case, is determined by the farther position that can be reached by the penultimate S-shaped forward movement and the last backward movement. From Equations (13) and (16), there is
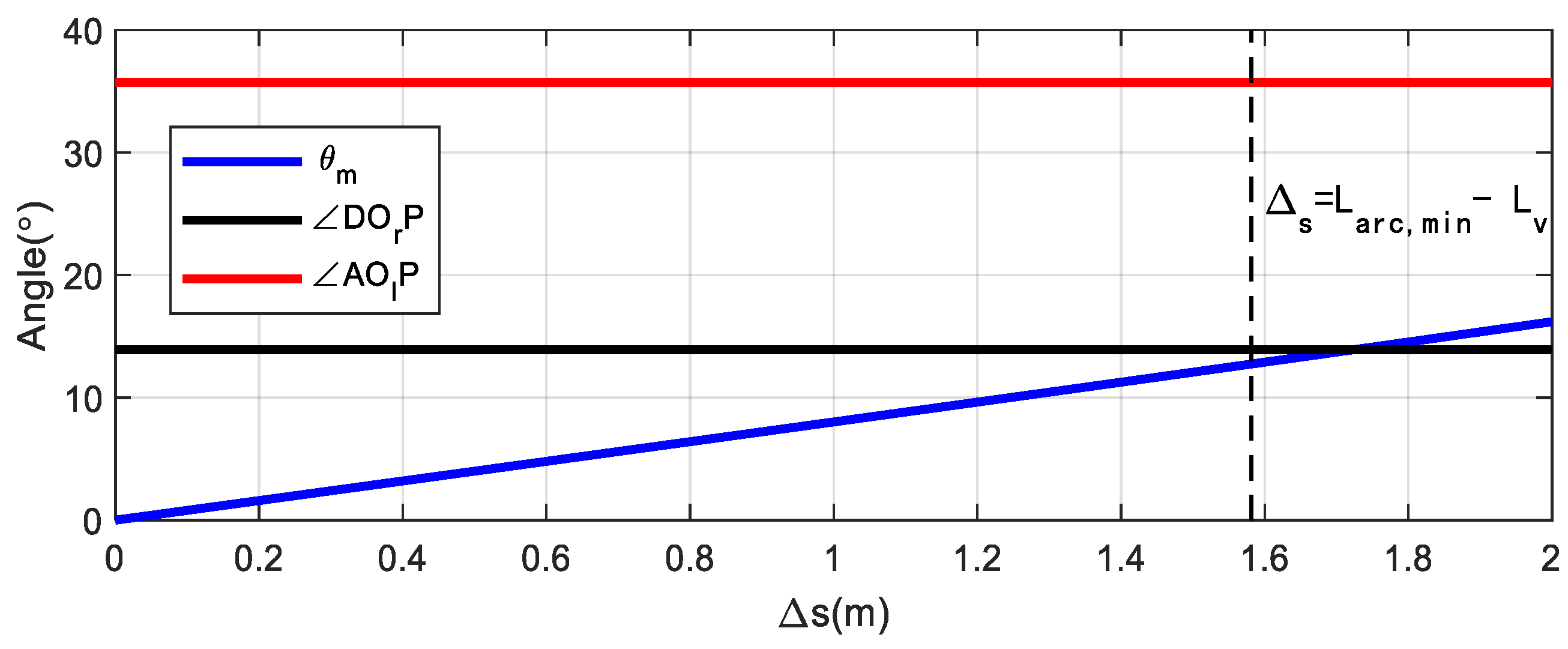
Discussions
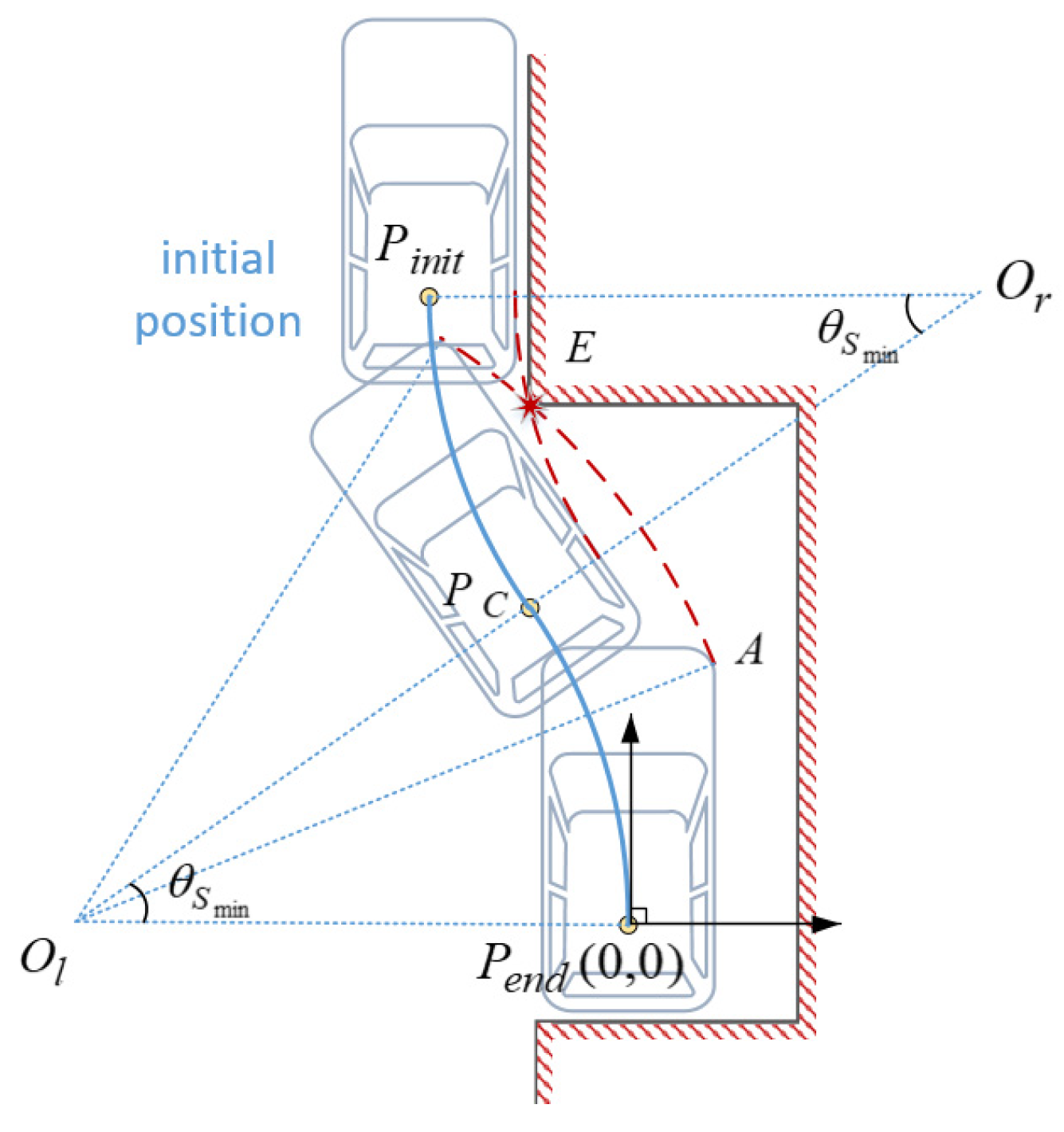
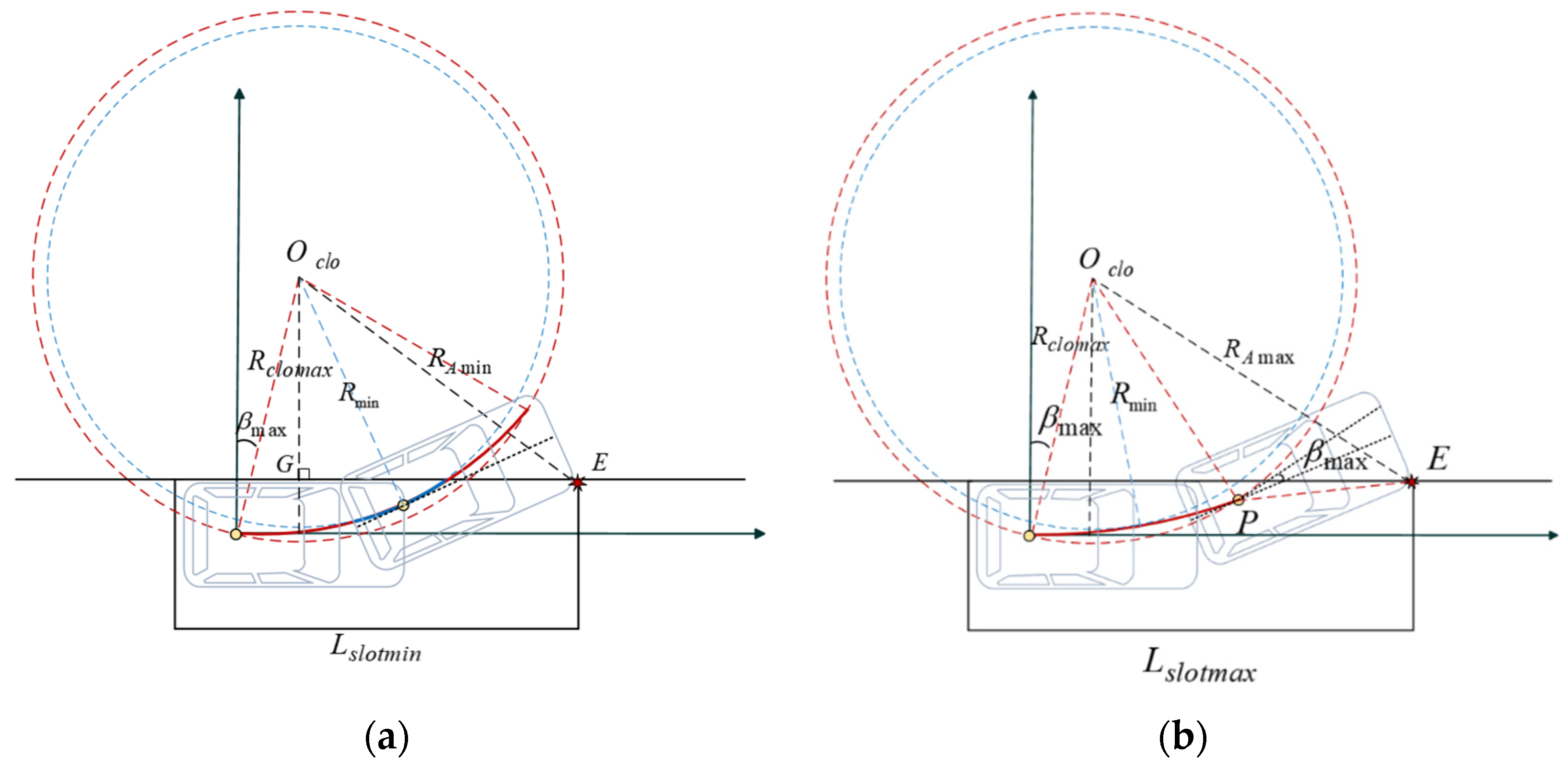
4. Minimum Space for One-Trial Parking Based on Circle Arcs
Discussions
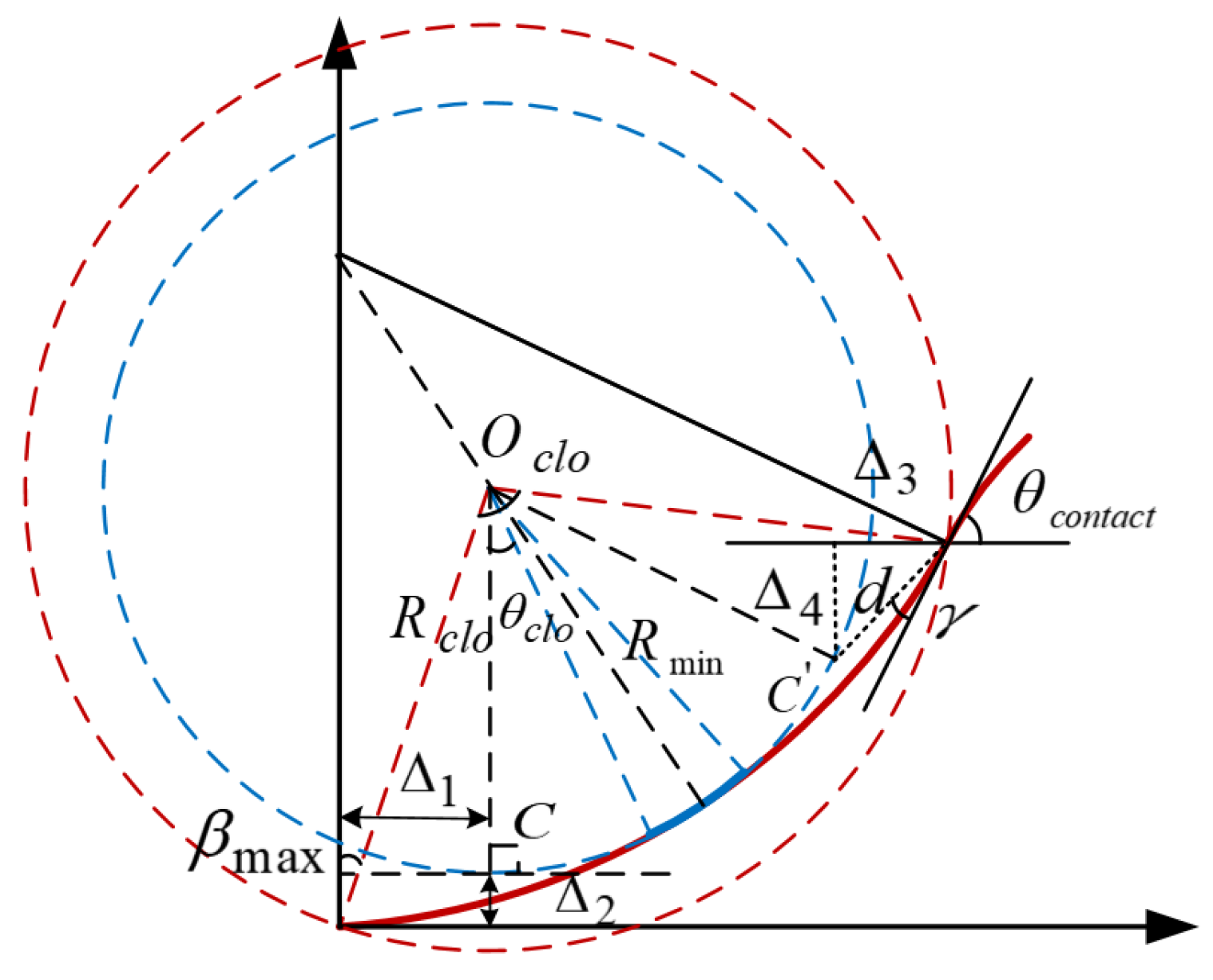
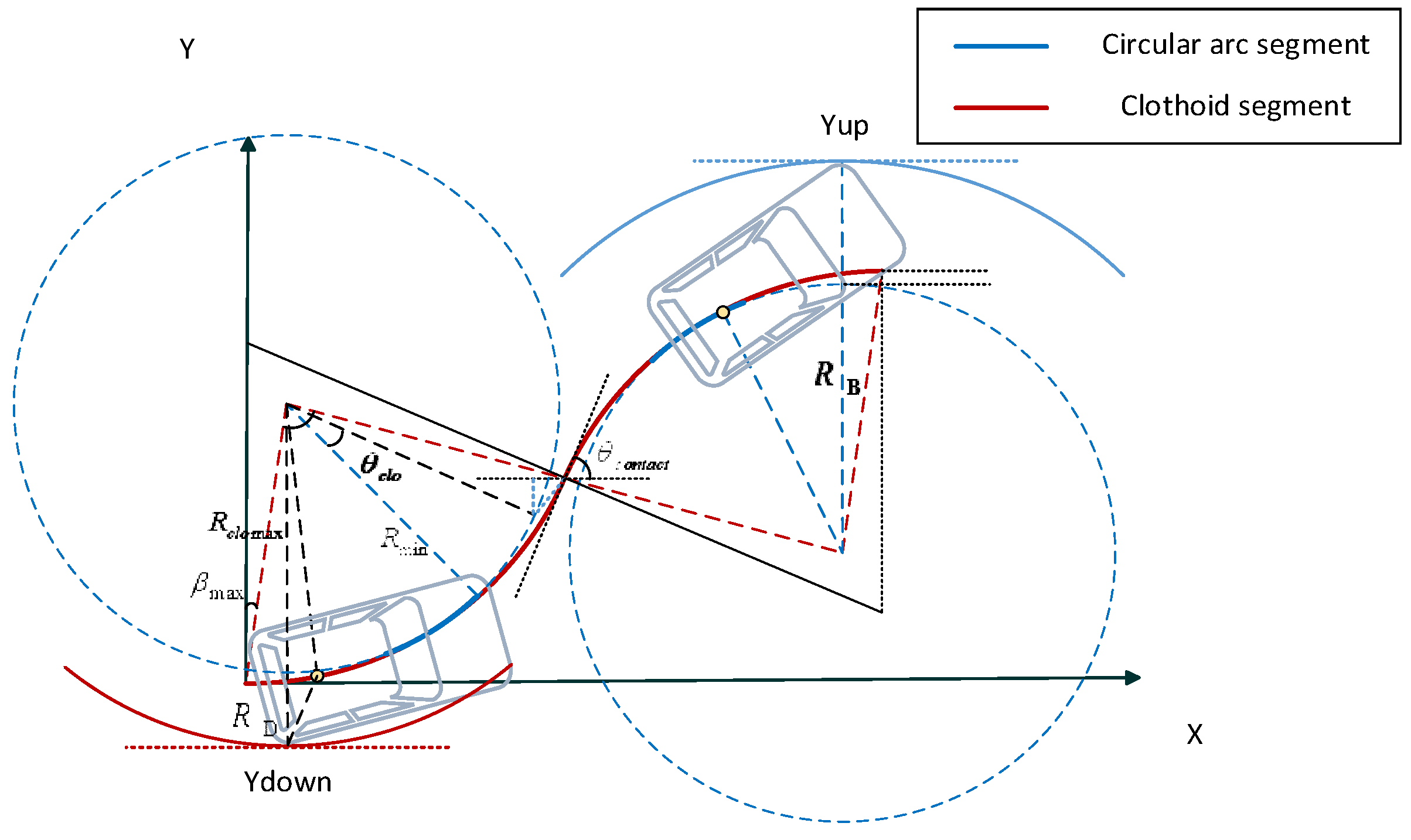
5. Minimum Space for One-Trial Parking Based on Continues-Curvature Curve
5.1. General Properties of Clothoid
5.2. Spatial Increments Relative to Circular Arc Path
5.3. Discussions
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ma, S.; Jiang, H.; Han, M.; Xie, J.; Li, C. Research on automatic parking systems based on parking scene recognition. IEEE Access 2017, 5, 21901–21917. [Google Scholar] [CrossRef]
- Roca-Riu, A.B.; Fernández, E.; Estrada, M. Parking slot assignment for urban distribution: Models and formulations. Omega 2015, 57, 157–175. [Google Scholar] [CrossRef]
- Miller, A. Automated Driving: The Technology and Implications for Insurance. Thatcham Research. 2016. Available online: http://www.brakepro.org/assets/docs/eventresources/invehicle-tech-Dec16/Thatcham_Research_Webinar.pdf (accessed on 12 January 2022).
- Banzhaf, H.; Nienhuser, D.; Knoop, S. The Future of Parking: A Survey on Automated Valet Parking with an Outlook on High Density Parking. In Proceedings of the 2017 IEEE Intelligent Vehicles Symposium (IV), Los Angeles, CA, USA, 11–14 June 2017; pp. 1827–1834. [Google Scholar]
- Yurtsever, E.; Lambert, J.; Carballo, A.; Takeda, K. A survey of autonomous driving: Common practices and emerging technologies. IEEE Access 2020, 8, 58443–58469. [Google Scholar] [CrossRef]
- Jang, C.; Kim, C.; Lee, S.; Kim, S.; Lee, S.; Sunwoo, M. Re-Plannable Automated Parking System with a Standalone around View Monitor for Narrow Parking Lots. IEEE Trans. Intell. Transp. Syst. 2020, 21, 777–790. [Google Scholar] [CrossRef]
- Suhr, J.K.; Jung, H.G. Automatic Parking Space Detection and Tracking for Underground and Indoor Environments. IEEE Trans. Ind. Electron. 2016, 63, 5687–5698. [Google Scholar] [CrossRef]
- Qazi, S.; Sabir, F.; Khawaja, B.A.; Atif, S.M.; Mustaqim, M. Why is internet of autonomous vehicles not as plug and play as we think? Lessons to be learnt from present internet and future directions. IEEE Access 2020, 8, 133015–133033. [Google Scholar] [CrossRef]
- Yang, Y.; Hua, K. Emerging technologies for 5G-enabled vehicular networks. IEEE Access 2019, 7, 181117–181141. [Google Scholar] [CrossRef]
- Hao, Z.; Yuen, K.V.; Mihaylova, L.; Leung, H. Overview of Environment Perception for Intelligent Vehicles. IEEE Trans. Intell. Transp. Syst. 2017, 18, 2584–2601. [Google Scholar] [CrossRef] [Green Version]
- Kim, I.Y.; Yang, K.S.; Jin, J.B.; Hwang, S.-H. Development of Intelligent Electric Vehicle for Study of Unmanned Autonomous Driving Algorithm. In Proceedings of the 2013 World Electric Vehicle Symposium and Exhibition (EVS27), Barcelona, Spain, 17–20 November 2013; pp. 1–6. [Google Scholar] [CrossRef] [Green Version]
- Reeds, J.A.; Shepp, R.A. Optimal paths for a car that goes both forward and backward. Pac. J. Math. 1991, 145, 367–393. [Google Scholar] [CrossRef] [Green Version]
- Dubins, L.E. On curves of minimal length with a constraint on average curvature, and with prescribed initial and terminal positions and tangents. Am. J. Math. 1957, 79, 497–516. [Google Scholar] [CrossRef]
- Boissonnat, J.D.; Cérézo, A.; Leblond, J. Shortest path of bounded curvature in the plane. J. Intell. Robot. Syst. 1994, 11, 5–20. [Google Scholar] [CrossRef]
- Fraichard, T.; Scheuer, A. From Reeds and Shepp’s to Continuous-Curvature Paths. IEEE Trans. Robot. 2004, 20, 1025–1035. [Google Scholar] [CrossRef] [Green Version]
- Gupta, A.; Divekar, R. Autonomous parallel parking methodology for Ackerman configured vehicles. Int. J. Commun. 2013, 1, 1–6. [Google Scholar]
- Choi, S.; Boussard, C. Easy path planning and robust control for automatic parallel parking. IFAC Proc. Vol. 2011, 44, 656–661. [Google Scholar] [CrossRef] [Green Version]
- Lo, Y.K.; Rad, A.B.; Wong, C.W.; Ho, M.L. Automatic Parallel Parking. In Proceedings of the 2003 IEEE International Conference on Intelligent Transportation Systems, Shanghai, China, 12–15 October 2003; IEEE: New York, NY, USA, 2003. [Google Scholar]
- Vorobieva, H.; Glaser, S.; Minoiu-Enache, N.; Mammar, S. Automatic parallel parking in tiny spots: Path planning and control. IEEE Trans. Intell. Transp. Syst. 2015, 16, 396–410. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.; Guo, L.; He, Y. Path Planning Algorithm for Automatic Parallel Parking from Arbitrary Initial Angle. In Proceedings of the 2017 10th International Symposium on Computational Intelligence and Design (ISCID), Hangzhou, China, 9–10 December 2017; pp. 55–58. [Google Scholar] [CrossRef]
- Muller, B.; Deutscher, J.; Grodde, S. Continuous curvature trajectory design and feedforward control for parking a car. IEEE Trans. Control Syst. Technol. 2007, 15, 541–553. [Google Scholar] [CrossRef]
- Kanayama, Y.; Hartman, B.I. Smooth Local Path Planning for Autonomous Vehicles. In Proceedings of the 1989 IEEE International Conference on Robotics and Automation, Scottsdale, AZ, USA, 14–19 May 1989; IEEE: New York, NY, USA, 1989. [Google Scholar]
- Ghilardelli, F.; Lini, G.; Piazzi, A. Path generation using η4-spine for a truck and trailer vehicle. IEEE Trans. Autom. Sci. Eng. 2014, 11, 187–203. [Google Scholar] [CrossRef]
- Eilers, P.; Rijnmond, D.M.; Marx, B.D. Flexible smoothing with B-splines and penalties. Stat. Sci. 1996, 11, 89–121. [Google Scholar] [CrossRef]
- Ammoun, S.; Nashashibi, F. Design and efficiency measurement of cooperative driver assistance system based on wireless communication devices. Transp. Res. Part C Emerg. Technol. 2010, 18, 408–428. [Google Scholar] [CrossRef]
- Nelson, W.L. Continuous-Curvature Paths for Autonomous Vehicles. In Proceedings of the 1989 IEEE International Conference on Robotics and Automation, Scottsdale, AZ, USA, 14–19 May 1989; IEEE: New York, NY, USA, 1989. [Google Scholar]
- Fraichard, T.; Scheuer, A. Continuous-Curvature Path Planning for Car-Like Vehicles. In Proceedings of the 1997 IEEE/RSJ International Conference on Intelligent Robots & Systems. Innovative Robotics for Real-World Applications. IROS ’97, Grenoble, France, 11 September 1997. [Google Scholar]
- Vorobieva, H.; Enache, N.M.; Glaser, S.; Mammar, S. Geometric Continuous-Curvature Path Planning for Automatic Parallel Parking. In Proceedings of the 2013 10th IEEE International Conference on Networking, Sensing and Control, Evry, France, 10–12 April 2013. [Google Scholar]
- Yi, Y.; Lu, Z.; Xin, Q.; Lei, J.; Wang, J. Smooth Path Planning for Autonomous Parking System. In Proceedings of the 2017 IEEE Intelligent Vehicles Symposium (IV), Los Angeles, CA, USA, 11–14 June 2017; pp. 167–173. [Google Scholar] [CrossRef]
- Vorobieva, H.; Glaser, S.; Minoiu-Enache, N.; Mammar, S. Geometric path planning for automatic parallel parking in tiny spots. IFAC Proc. Vol. 2012, 45, 36–42. [Google Scholar] [CrossRef] [Green Version]
- Scheuer, A.; Laugier, C. Planning Sub-Optimal and Continuous-Curvature Paths for Car-Like Robots. In Proceedings of the 1998 IEEE/RSJ International Conference on Intelligent Robots & Systems. Innovations in Theory, Practice and Applications (Cat. No.98CH36190), Victoria, BC, Canada, 17 October 1998. [Google Scholar]




| Notation | |||||||
|---|---|---|---|---|---|---|---|
| Value | 4235 (mm) | 1765 (mm) | 2510 (mm) | 700 (mm) | 1025 (mm) | 35 (°) | 25 (°/s) |
| 0 | 0.100 | 0.250 | 0.500 | 0.750 | 1.000 | |
| 2531 | 405 | 102 | 45 | 26 | ||
| , | 4.235 | 4.335 | 4.485 | 4.735 | 4.985 | 5.235 |
| 1.765 | 1.8094 | 1.8749 | 1.9759 | 2.0813 | 2.1560 | |
| 1.765 | 1.8086 | 1.8698 | 1.9605 | 2.0369 | 2.0990 |
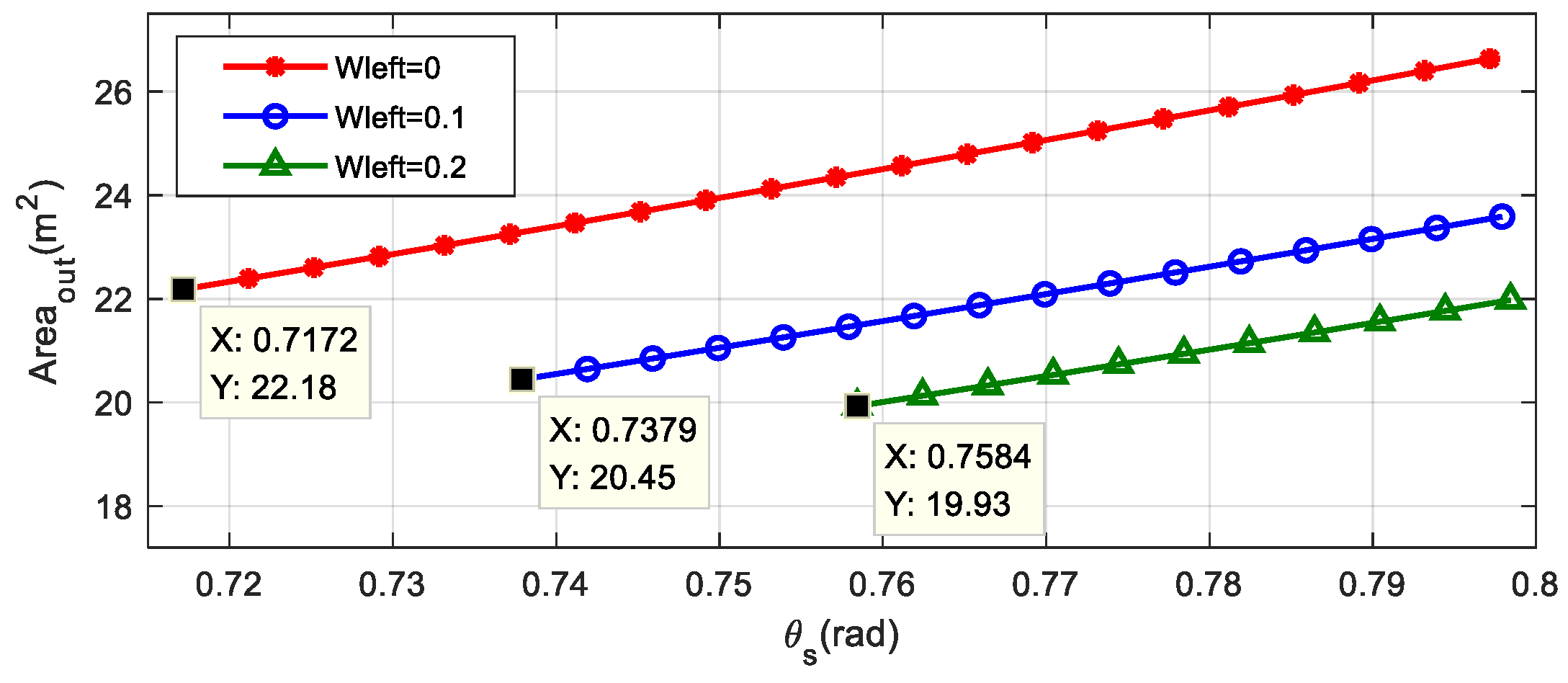
| 0 | 41.081 | 2.799 | 7.922 | 22.181 | 5.817 |
| 0.1 | 42.284 | 2.800 | 7.306 | 20.457 | 5.872 |
| 0.2 | 43.430 | 2.799 | 7.121 | 19.931 | 5.924 |
| 0.3 | 44.633 | 2.801 | 7.010 | 19.637 | 5.974 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Zhou, M.; Liu, Z.; Ding, Z. On Minimum Parking Space Required by Automatic Parallel Parking. Sensors 2022, 22, 795. https://doi.org/10.3390/s22030795
Wang X, Zhou M, Liu Z, Ding Z. On Minimum Parking Space Required by Automatic Parallel Parking. Sensors. 2022; 22(3):795. https://doi.org/10.3390/s22030795
Chicago/Turabian StyleWang, Xuan, Momiao Zhou, Zhengqiong Liu, and Zhizhong Ding. 2022. "On Minimum Parking Space Required by Automatic Parallel Parking" Sensors 22, no. 3: 795. https://doi.org/10.3390/s22030795
APA StyleWang, X., Zhou, M., Liu, Z., & Ding, Z. (2022). On Minimum Parking Space Required by Automatic Parallel Parking. Sensors, 22(3), 795. https://doi.org/10.3390/s22030795






