Deep Learning Approaches for Robust Time of Arrival Estimation in Acoustic Emission Monitoring
Abstract
:1. Introduction
1.1. Acoustic Emissions in Waveguides
1.2. ToA Estimation: From Statistical Methods to Machine Learning
2. Deep Learning Models for ToA Estimation
2.1. Convolutional Neural Network
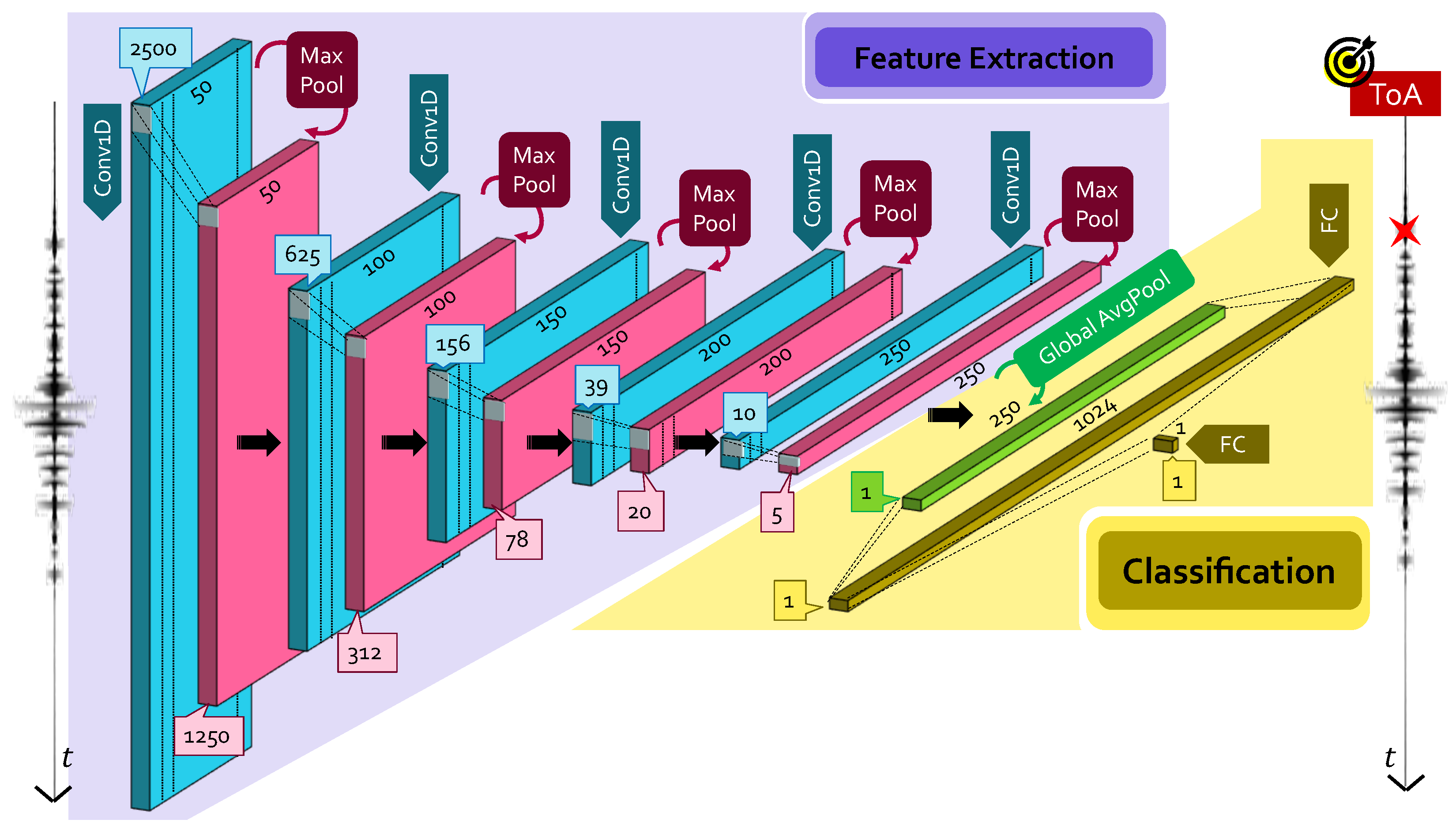
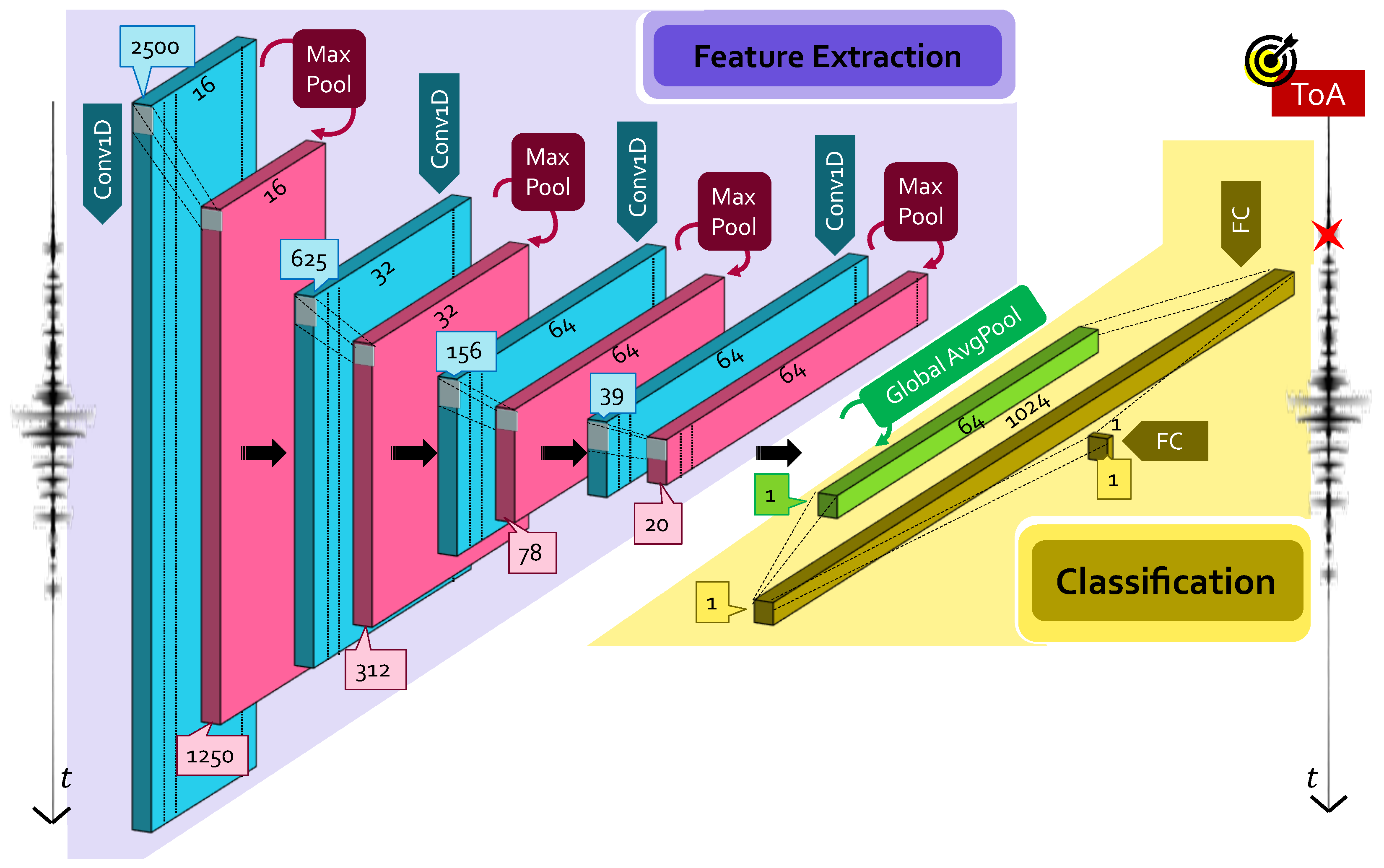
- Convolutional layers: it is in charge of feature extraction from input data, which are passed in a tensor form of dimensions . A convolutional layer runs dot products between the input data and a specific set of weights (or mask), which are stored as taps of a corresponding filter, also known as kernel, of dimension . This filter is recursively applied to subsequent portions, or patches, of the input data by means of a sliding filter mask, which is shifted by a constant quantity called stride ().To increase the learning capability of the network, more than one filter is employed in a single convolutional layer: if is the number of total different kernels per layer, different maps of the the same input data are provided in the output via a proper activation function. A convolutional layer is, thus, completely determined by the tuple of values: .Multiple convolutional layers are usually stacked one after the other, whose typology is dictated, in turn, by the dimensions of the manipulated data. In the case of ToA estimation, where the problem is intrinsically mono-dimensional and thought to be performed on a sensor-wise basis, 1D convolutional (Conv1D) layers are necessary.
- Pooling layers: this layer provides a distilled version of each feature map to shrink the computational complexity and the spatial size of the convolved features. Indeed, since the number of points in each feature map returned at the end of a single convolutional block might be extremely large, and also since many of them only capture minor details, they can be neglected. Different pooling strategies have been proposed: max pooling (MaxPool), which only preserves the maximum value in a specific patch of the feature map; and average pooling (AvgPool), which extracts a single scalar as the average of the points falling in the same feature patch.
- Dense layers: once manifold representations are obtained, the sought pattern hidden within them is learned via dense fully connected (FC) layers, i.e., feed-forward layers with neurons that have full connections to all activations delivered by the previous layer. Firstly, a flattening operation is performed to unroll the feature maps provided by the last pooling layer in a uni-dimensional vector of appropriate dimension; then, these values are used as input of a standard artificial neural network, which acts either as a classifier or a regressor, depending on the desired task.
2.1.1. Large CNN Model
2.1.2. Small CNN Model
2.2. Capsule Neural Network
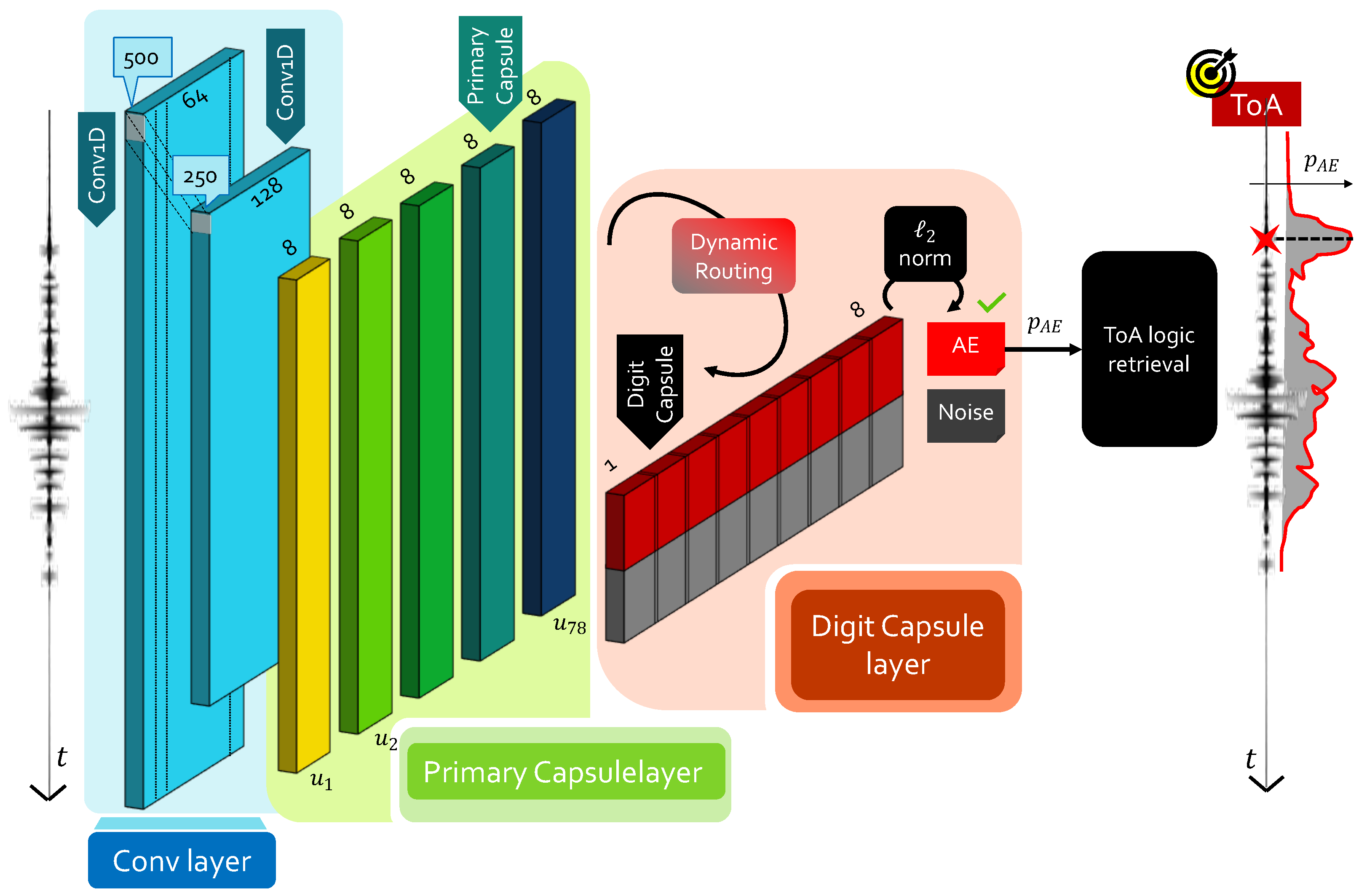
- Primary capsule: this layer performs convolution aggregation via the so-called capsule unit ( being the capsule index), corresponding to multiple combinations of the feature maps retrieved at the end of the convolution process. In their working principles, primary capsules provide an alternative form of convolutional layers: the main difference is that, in this case, a vector-based output is computed rather than working with unitary depth. As such, convolution-based processing is performed by each capsule, which is driven by an appropriate set of kernels and relative stride.
- Digit capsule: at this point, the agreement among different capsules has to be estimated so that it is possible to preserve the spatial dependency between those block representations with highest relevance. This concept is mathematically encoded via the weight opinion matrix , with being the number of classes, each with vector-based output of dimension . Hence, every capsule is judged by means of opinions , also called local digit capsules, to be computed asFrom these local representations, a further level of feature combination is added in a spatially dependent manner, by following the routing-by-agreement protocol [29]. This procedure, also called dynamic routing, introduces the concept of agreement, i.e., how much the individual digit capsules agree with the combined one. The level of agreement is numerically quantified by the weight routing matrix via the coupling coefficientAs such, the final digit capsule is given by . As in traditional convolutional layers, activation is required to ensure that digit capsules with low opinions shrunk to zero, since they do not convey meaningful information. However, the vector-based output of the capsules requires ad hoc functions to fulfill this task: the squashing functionwas purposely proposed in [28] to address it, where and are the input and output of the j-th convolutionally operated capsule. The quantity finally yields the actual measure of agreement, i.e., the higher this product, the more preference is awarded to the corresponding primary capsule . At this point, an iterative algorithm can be called to update the routing matrix, until the desired level of agreement is reached and the sought digit capsule block can be derived, which serves as the output layer for the entire neural network. Finally, it is sufficient to calculate the norm of each of the rows to obtain a corresponding value of the output probability associated to each single class.
ToA Retrieval from CapsNet: The CapsNetToA Architecture
3. Experimental Validation: A Numerical Framework
3.1. Dataset Generation
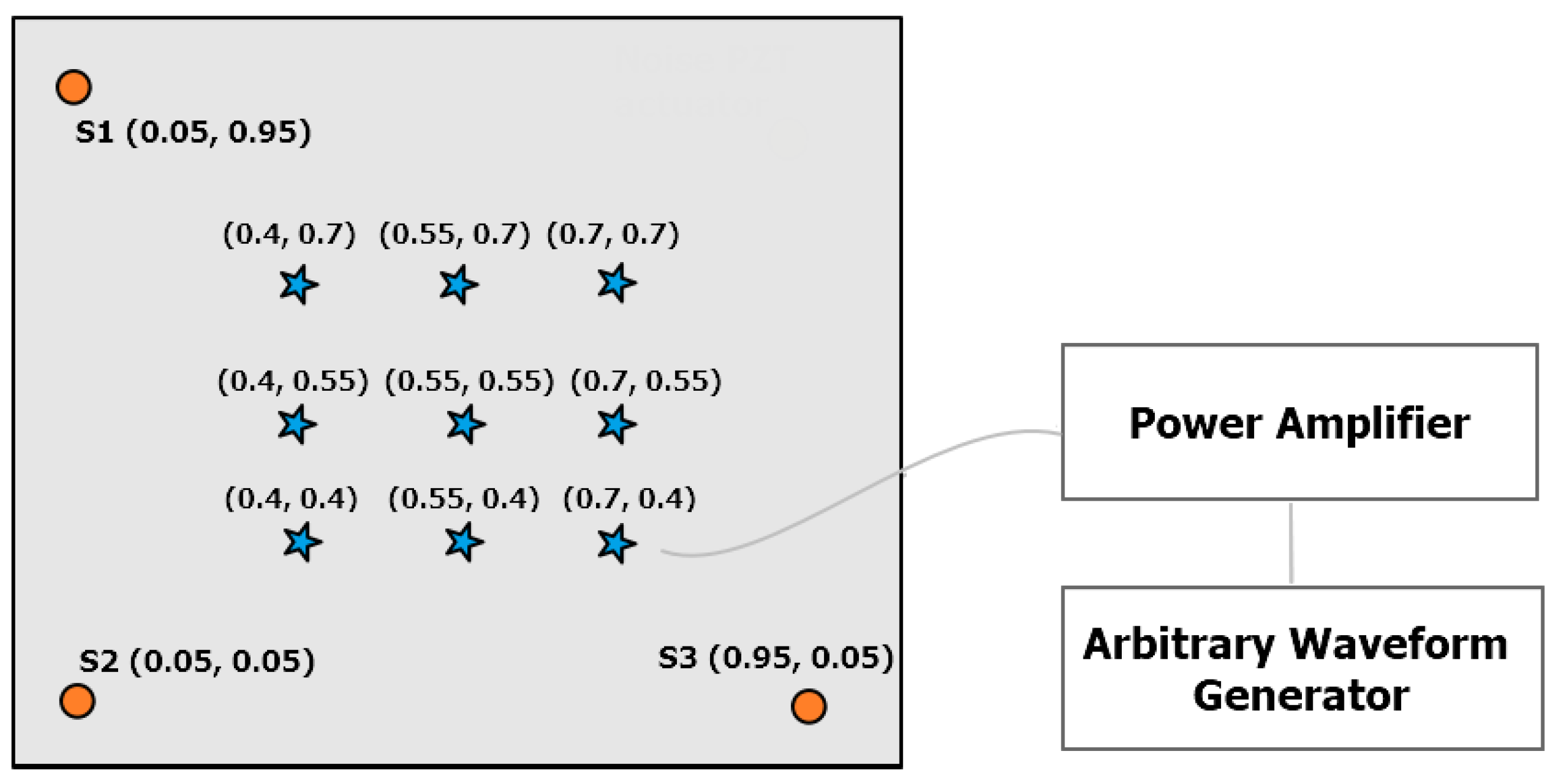
- Traveling distance selection: theoretically, the number of possible propagation distances to be explored between the AE location and the receiving point is infinite. However, by exploiting the symmetry of the structure ensured by its isotropic nature, the number of useful configurations can be reduced by a large extent. A square area of 5 × 5 positions circumscribed to the top east corner of the plate was allocated to AE receivers, while a total amount of 10 × 5 AE actuation points were uniformly distributed in the left half of the plate.
- Noise level variation: since the primary objective of the proposed NN alternatives is to surpass the poor estimation capabilities of reference statistical methods in the presence of noise, Gaussian noise of increasing magnitude was progressively added to the acoustic wave by sweeping the SNR from 30 dB down to 1 dB, in steps of almost 1 dB. Despite the fact that the nature of the background noise of real AE signals can indeed differ [30], additive white stationary noise (such as the one generated by electronic components) can be assumed to be the main source of SNR degradation and, consequently, was used to simulate noisy AE scenarios in this study.
- Pre-trigger window variation: in real AE equipment, the starting time for data logging is triggered by the incoming wave, e.g., once it exceeds a predefined energetic threshold. However, being capable of acquiring also the moments leading up to the acoustic event is of vital importance for appropriate AE signal characterization. As such, sensors are programmed to preserve memory of the pre-trigger signal history, known as the pre-trigger window. This quantity might change widely, from hundreds to thousands of samples, depending on both the application scenario and the employed electronics.Although representing a deterministic parameter that does not strictly depend on the physical phenomenon at the basis of acoustic wave propagation, the pre-trigger time actually plays a crucial role during the learning stage. This observation means that, theoretically, a one-to-one correspondence should exist between one model and one pre-trigger window. This aspect not only requires time and extra computing effort, due to the fact that a new training phase must be entailed whenever a change in the network configuration occurs, but it is also not viable in practical scenarios. Therefore, a data augmentation procedure was encompassed to favor the generalization capability of the neural network models.To this end, acoustic signals were initially generated with a fixed pre–trigger window of 500 samples, that represents a reasonable choice for typical scenarios. Then, one time-lagged version of each signal was derived by adding randomly from 500 to 2000 samples to the initial pre-trigger window. Since the total number of samples in the time history is limited to 5000, these forward shifts required additional samples to be concatenated with the initial portion of the signal, while disregarding the final : to avoid both discontinuities and alterations in the statistical properties, the extra portion of the signal to be added was generated in form of a white noise term drawn from a Gaussian distribution, whose variance was taken to be coincident with the one estimated for the first 400 samples in the original pre-trigger window.Another batch of data was also generated, comprising signals with an increased pre-trigger time beyond 2500 samples, and was entirely used during the testing phase in order to probe how the neural networks could behave with respect to unforeseen delays in the signal.
- Label generation: when Lamb waves are to be characterized, it is difficult to give an unambiguous definition of their time of arrival due to dispersion and multi-modality. For this reason, rather than adopting a labeling approach based on the propagation theory, a different strategy was undertaken in this work. In particular, we exploited the fact that AIC inherently provides very accurate ToA estimations when the SNR is high. As such, the label attached to each time series was taken from the output yielded by AIC when applied to noise-free signals.
3.2. Performance Metrics
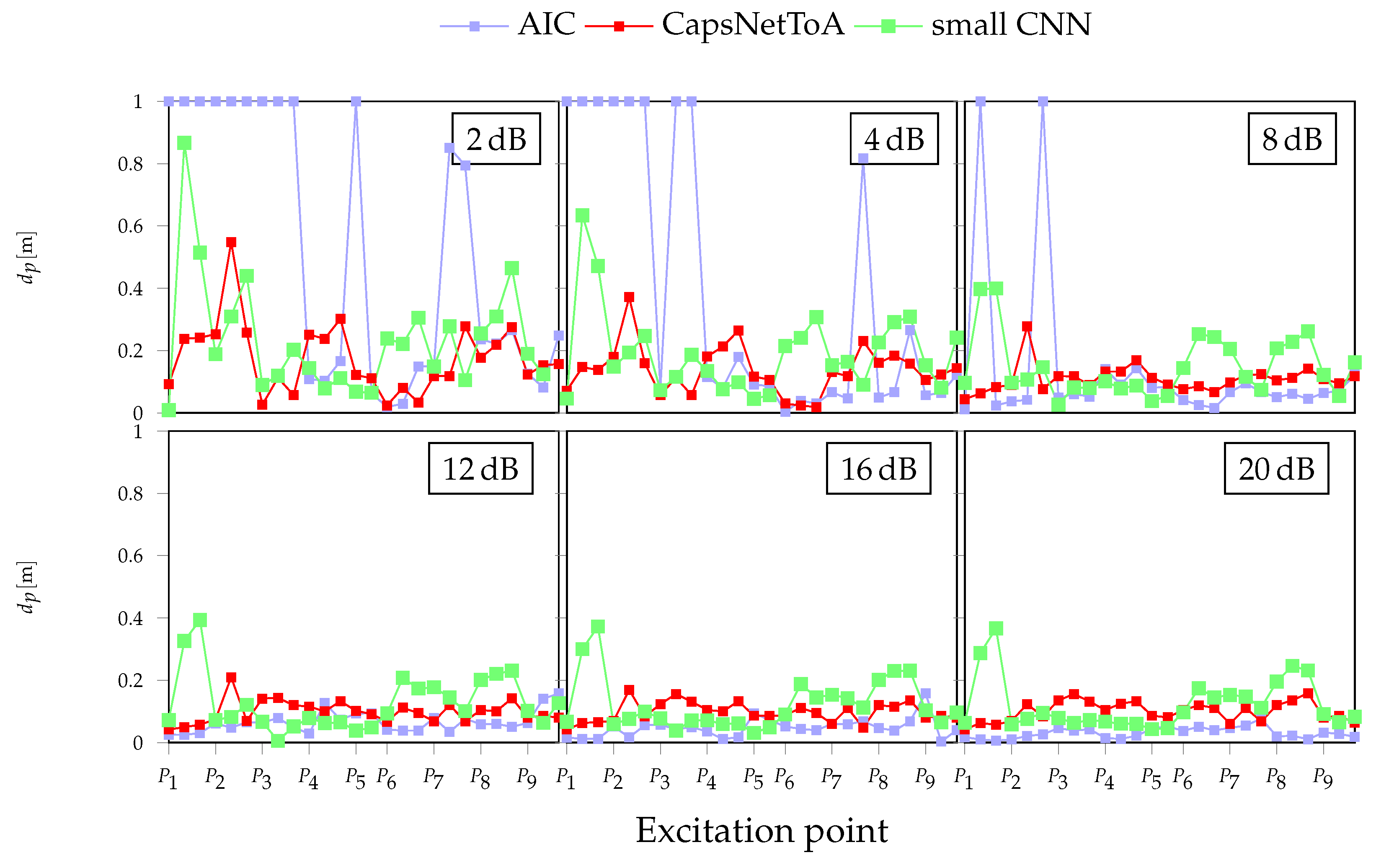
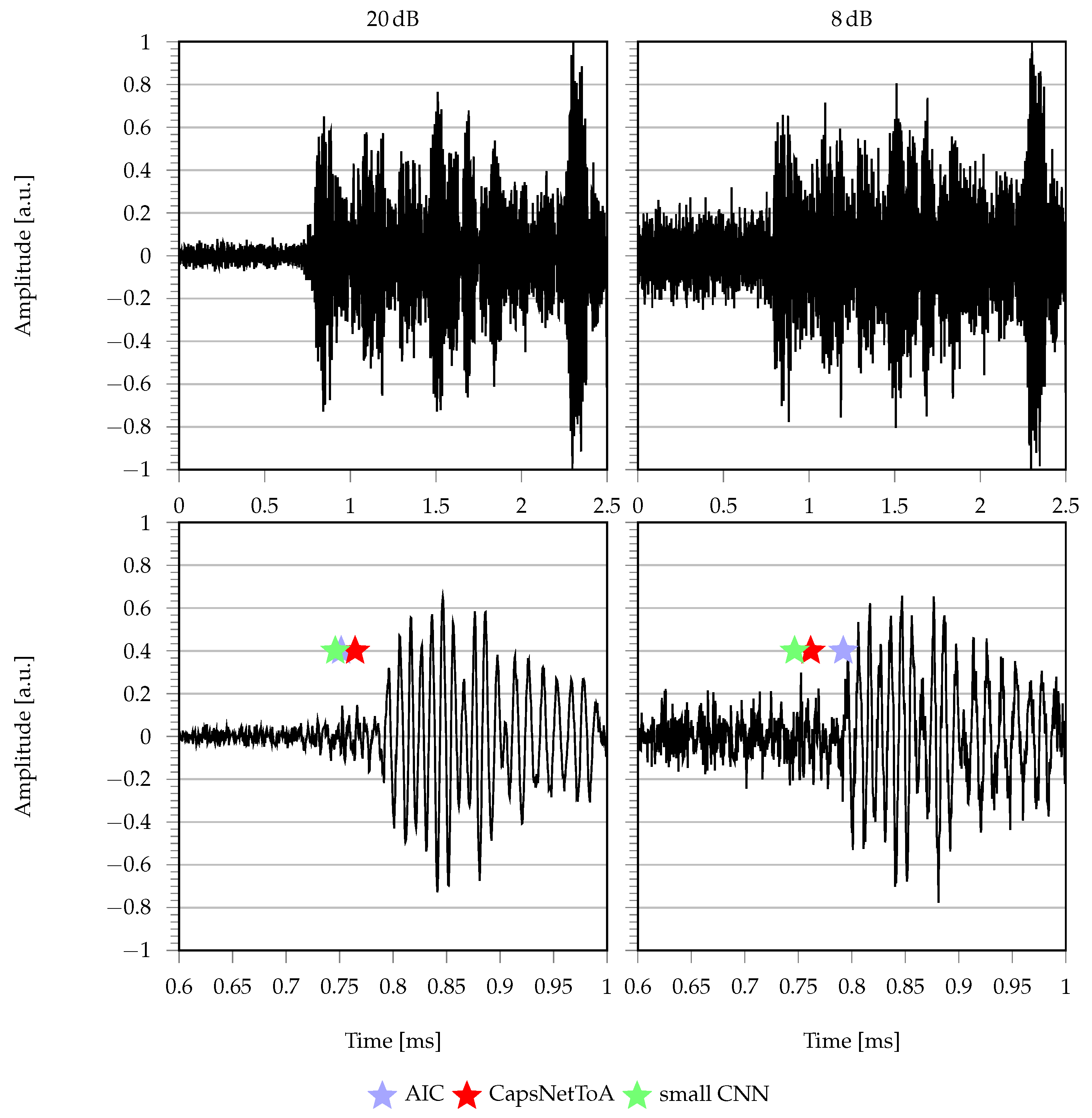
3.3. Results
4. Experimental Validation: ToA for Acoustic Source Localization
4.1. Materials: The AE Equipment
4.2. Methods
4.2.1. Objectives and Testing Procedures
4.2.2. Localization Algorithm
4.2.3. Performance Evaluation Procedure
4.3. Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gholizadeh, S.; Leman, Z.; Baharudin, B.H.T. A review of the application of acoustic emission technique in engineering. Struct. Eng. Mech. 2015, 54, 1075–1095. [Google Scholar] [CrossRef]
- Berkovits, A.; Fang, D. Study of fatigue crack characteristics by acoustic emission. Eng. Fract. Mech. 1995, 51, 401–416. [Google Scholar] [CrossRef]
- Chesné, S.; Deraemaeker, A. Damage localization using transmissibility functions: A critical review. Mech. Syst. Signal Process. 2013, 38, 569–584. [Google Scholar] [CrossRef] [Green Version]
- Ainsleigh, P.L. Acoustic echo detection and arrival-time estimation using spectral tail energy. J. Acoust. Soc. Am. 2001, 110, 967–972. [Google Scholar] [CrossRef]
- Vallen, H. AE testing fundamentals, equipment, applications. J. Nondestruct. Test. 2002, 7, 1–30. [Google Scholar]
- Wirtz, S.F.; Söffker, D. Improved signal processing of acoustic emission for structural health monitoring using a data-driven approach. In Proceedings of the 9th European Workshop on Structural Health Monitoring, Manchester, UK, 10–13 July 2018. [Google Scholar]
- Sikorska, J.; Mba, D. Challenges and obstacles in the application of acoustic emission to process machinery. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2008, 222, 1–19. [Google Scholar] [CrossRef]
- Ramesh, S. The Applied Welding Engineering. Processes, Codes, and Standards; Elsevier: Amsterdam, The Netherlands, 2012; pp. 307–319. [Google Scholar]
- Karbhari, V.M. Non-Destructive Evaluation (NDE) of Polymer Matrix Composites; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Rose, J.L. Guided Wave Studies for Enhanced Acoustic Emission Inspection. Res. Nondestruct. Eval. 2021, 32, 192–209. [Google Scholar] [CrossRef]
- Faisal, H.M.; Giurgiutiu, V. Theoretical and numerical analysis of acoustic emission guided waves released during crack propagation. J. Intell. Mater. Syst. Struct. 2019, 30, 1318–1338. [Google Scholar] [CrossRef]
- Lowe, M.J.S. Wave Propagation|Guided Waves in Structures; Encyclopedia of Vibration; Elsevier: Amsterdam, The Netherlands, 2001; pp. 1551–1559. [Google Scholar]
- Carotenuto, R.; Merenda, M.; Iero, D.; Della Corte, F.G. An indoor ultrasonic system for autonomous 3-D positioning. IEEE Trans. Instrum. Meas. 2018, 68, 2507–2518. [Google Scholar] [CrossRef]
- Adrián-Martínez, S.; Bou-Cabo, M.; Felis, I.; Llorens, C.D.; Martínez-Mora, J.A.; Saldaña, M.; Ardid, M. Acoustic signal detection through the cross-correlation method in experiments with different signal to noise ratio and reverberation conditions. In International Conference on Ad-Hoc Networks and Wireless; Springer: Berlin/Heidelberg, Germany, 2014; pp. 66–79. [Google Scholar]
- Perelli, A.; De Marchi, L.; Marzani, A.; Speciale, N. Frequency warped cross-wavelet multiresolution analysis of guided waves for impact localization. Signal Process. 2014, 96, 51–62. [Google Scholar] [CrossRef]
- St-Onge, A. Akaike information criterion applied to detecting first arrival times on microseismic data. In SEG Technical Program Expanded Abstracts 2011; Society of Exploration Geophysicists: Tulsa, OK, USA, 2011; pp. 1658–1662. [Google Scholar]
- Pearson, M.R.; Eaton, M.; Featherston, C.; Pullin, R.; Holford, K. Improved acoustic emission source location during fatigue and impact events in metallic and composite structures. Struct. Health Monit. 2017, 16, 382–399. [Google Scholar] [CrossRef]
- Li, X.; Shang, X.; Morales-Esteban, A.; Wang, Z. Identifying P phase arrival of weak events: The Akaike Information Criterion picking application based on the Empirical Mode Decomposition. Comput. Geosci. 2017, 100, 57–66. [Google Scholar] [CrossRef]
- Ross, Z.E.; Rollins, C.; Cochran, E.S.; Hauksson, E.; Avouac, J.P.; Ben-Zion, Y. Aftershocks driven by afterslip and fluid pressure sweeping through a fault-fracture mesh. Geophys. Res. Lett. 2017, 44, 8260–8267. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y. Automatic microseismic event picking via unsupervised machine learning. Geophys. J. Int. 2020, 222, 1750–1764. [Google Scholar] [CrossRef]
- Ross, Z.E.; Meier, M.A.; Hauksson, E. P wave arrival picking and first-motion polarity determination with deep learning. J. Geophys. Res. Solid Earth 2018, 123, 5120–5129. [Google Scholar] [CrossRef]
- Zhu, W.; Beroza, G.C. PhaseNet: A deep-neural-network-based seismic arrival-time picking method. Geophys. J. Int. 2019, 216, 261–273. [Google Scholar] [CrossRef] [Green Version]
- Rojas, O.; Otero, B.; Alvarado, L.; Mus, S.; Tous, R. Artificial neural networks as emerging tools for earthquake detection. Comput. Sist. 2019, 23, 335–350. [Google Scholar] [CrossRef]
- Tabian, I.; Fu, H.; Sharif Khodaei, Z. A convolutional neural network for impact detection and characterization of complex composite structures. Sensors 2019, 19, 4933. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z. Improved adam optimizer for deep neural networks. In Proceedings of the 2018 IEEE/ACM 26th International Symposium on Quality of Service (IWQoS), Banff, AB, Canada, 4–6 June 2018; pp. 1–2. [Google Scholar]
- Lin, J.; Rao, Y.; Lu, J.; Zhou, J. Runtime neural pruning. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 2178–2188. [Google Scholar]
- Saad, O.M.; Chen, Y. CapsPhase: Capsule Neural Network for Seismic Phase Classification and Picking. IEEE Trans. Geosci. Remote Sens. 2021. [Google Scholar] [CrossRef]
- Sabour, S.; Frosst, N.; Hinton, G.E. Dynamic routing between capsules. arXiv 2017, arXiv:1710.09829. [Google Scholar]
- Mandal, B.; Dubey, S.; Ghosh, S.; Sarkhel, R.; Das, N. Handwritten indic character recognition using capsule networks. In Proceedings of the 2018 IEEE Applied Signal Processing Conference (ASPCON), Kolkata, India, 7–9 December 2018; pp. 304–308. [Google Scholar]
- Barat, V.; Borodin, Y.; Kuzmin, A. Intelligent AE signal filtering methods. J. Acoust. Emiss. 2010, 28, 109–119. [Google Scholar]
- Testoni, N.; De Marchi, L.; Marzani, A. A stamp size, 40 mA, 5 grams sensor node for impact detection and location. In Proceedings of the European Workshop on SHM, Bilbao, Spain, 5–8 July 2016. [Google Scholar]
- Bogomolov, D.; Testoni, N.; Zonzini, F.; Malatesta, M.; de Marchi, L.; Marzani, A. Acoustic emission structural monitoring through low-cost sensor nodes. In Proceedings of the 10th International Conference on Structural Health Monitoring of Intelligent Infrastructure, Porto, Portugal, 30 June–2 July 2021. [Google Scholar]
- Jiang, Y.; Xu, F. Research on source location from acoustic emission tomography. In Proceedings of the 30th European Conference on Acoustic Emission Testing & 7th International Conference on Acoustic Emission, Granada, Spain, 12–15 September 2012. [Google Scholar]






Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zonzini, F.; Bogomolov, D.; Dhamija, T.; Testoni, N.; De Marchi, L.; Marzani, A. Deep Learning Approaches for Robust Time of Arrival Estimation in Acoustic Emission Monitoring. Sensors 2022, 22, 1091. https://doi.org/10.3390/s22031091
Zonzini F, Bogomolov D, Dhamija T, Testoni N, De Marchi L, Marzani A. Deep Learning Approaches for Robust Time of Arrival Estimation in Acoustic Emission Monitoring. Sensors. 2022; 22(3):1091. https://doi.org/10.3390/s22031091
Chicago/Turabian StyleZonzini, Federica, Denis Bogomolov, Tanush Dhamija, Nicola Testoni, Luca De Marchi, and Alessandro Marzani. 2022. "Deep Learning Approaches for Robust Time of Arrival Estimation in Acoustic Emission Monitoring" Sensors 22, no. 3: 1091. https://doi.org/10.3390/s22031091
APA StyleZonzini, F., Bogomolov, D., Dhamija, T., Testoni, N., De Marchi, L., & Marzani, A. (2022). Deep Learning Approaches for Robust Time of Arrival Estimation in Acoustic Emission Monitoring. Sensors, 22(3), 1091. https://doi.org/10.3390/s22031091









