A Novel Reconstruction Algorithm with High Performance for Compressed Ultrafast Imaging
Abstract
1. Introduction
2. Forward Model of CUP
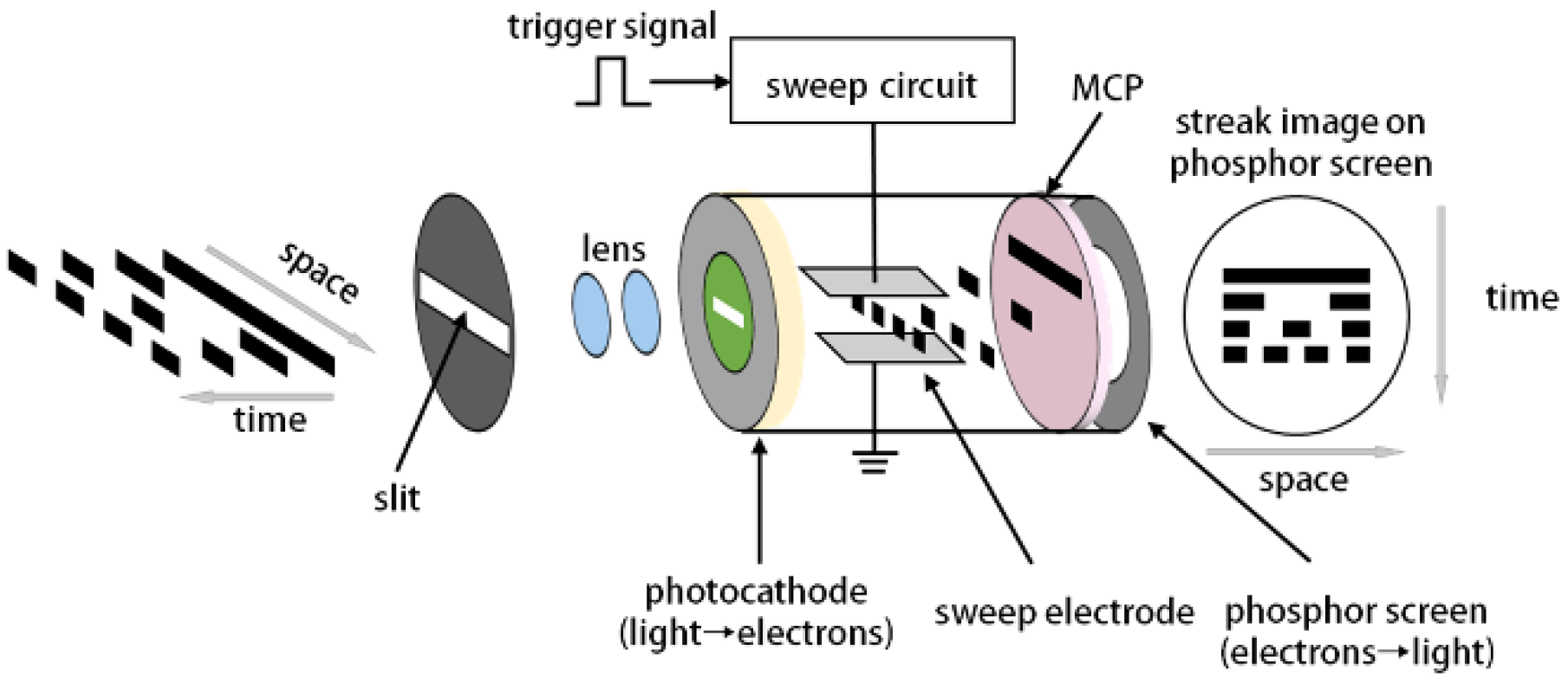
2.1. Principle of Streak Camera
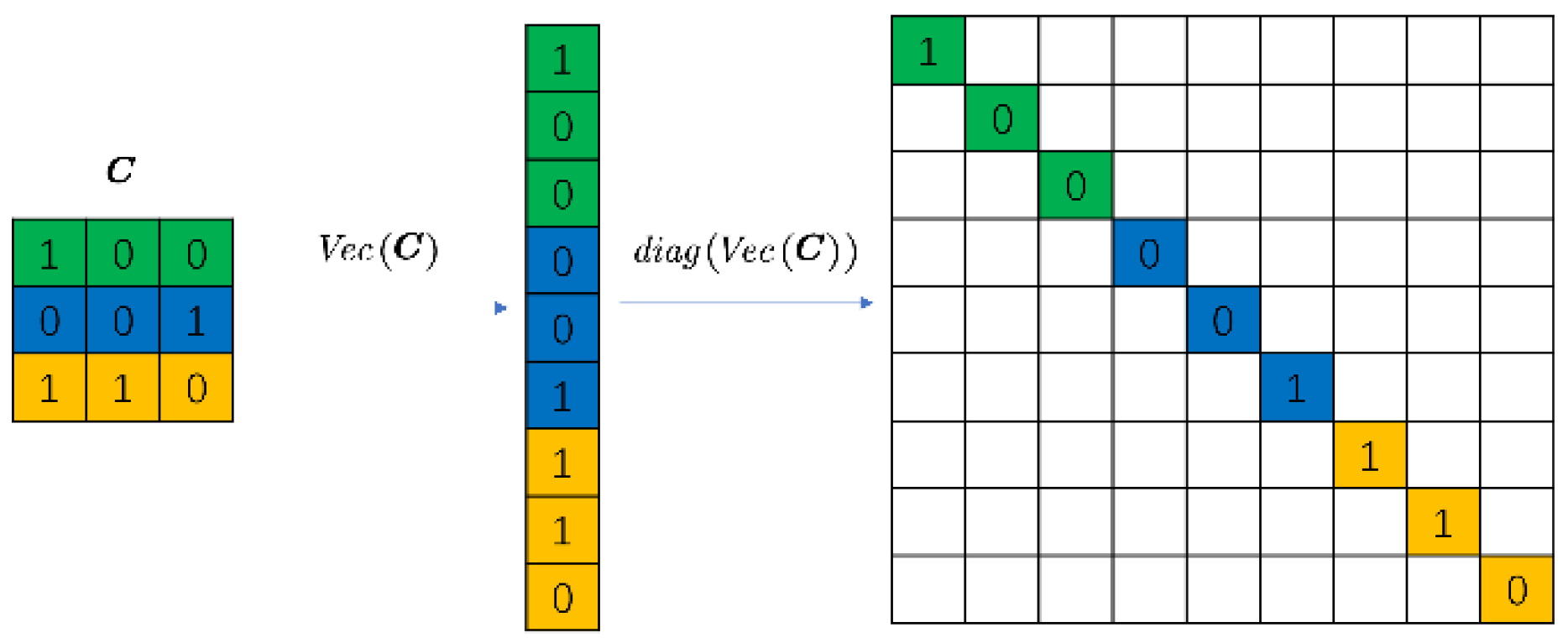
2.2. Design of Compressed Ultrafast Photography
3. Novel Reconstruction Method for CUP
3.1. Algorithm Framework of PnP-ADMM for CUP
3.2. The Architecture of FFDNet
3.3. PnP-ADMM Fixed-Point Convergence for CUP Reconstruction
4. Experiment Results
4.1. PSNR and SSIM on Simulation Datasets
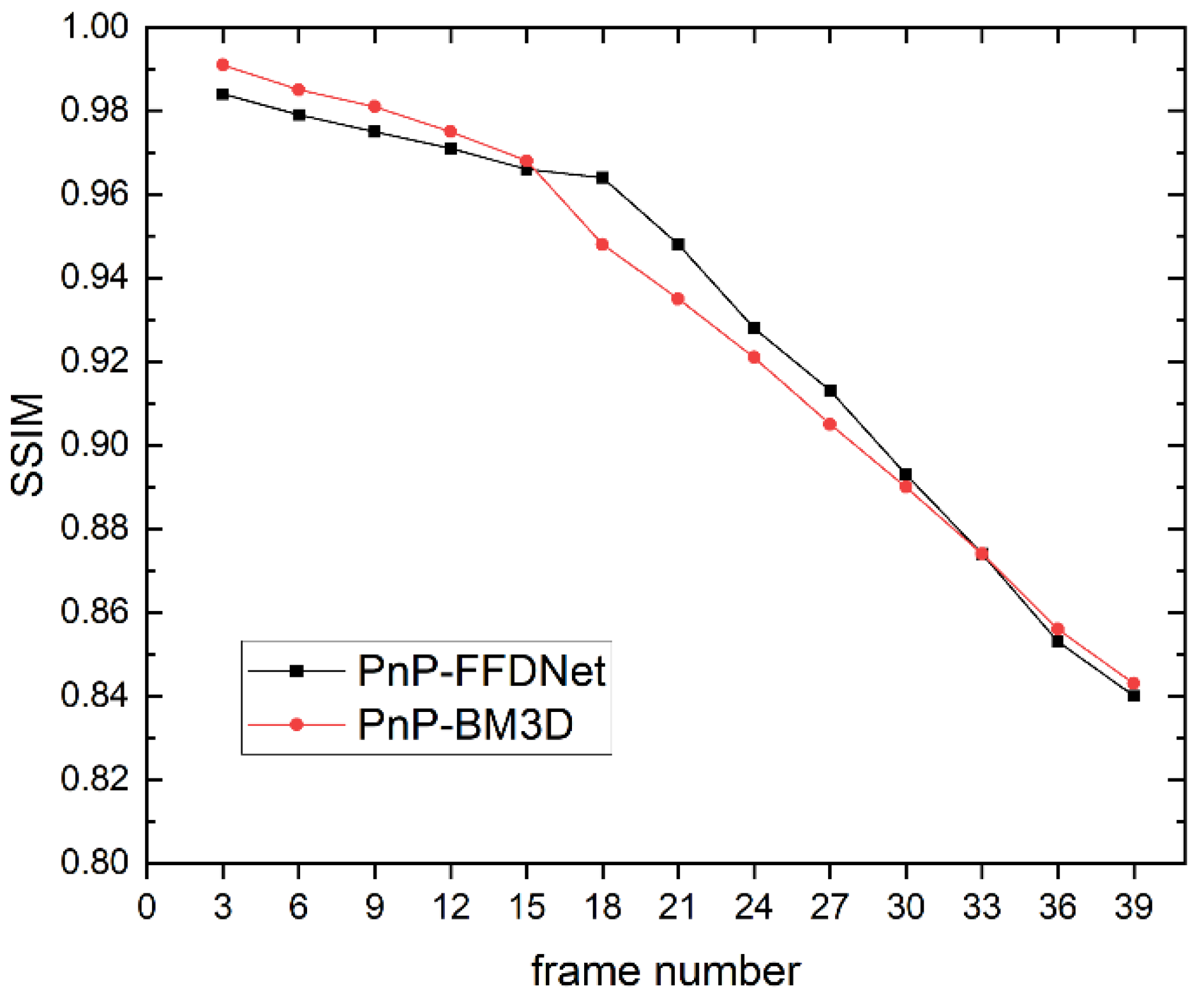
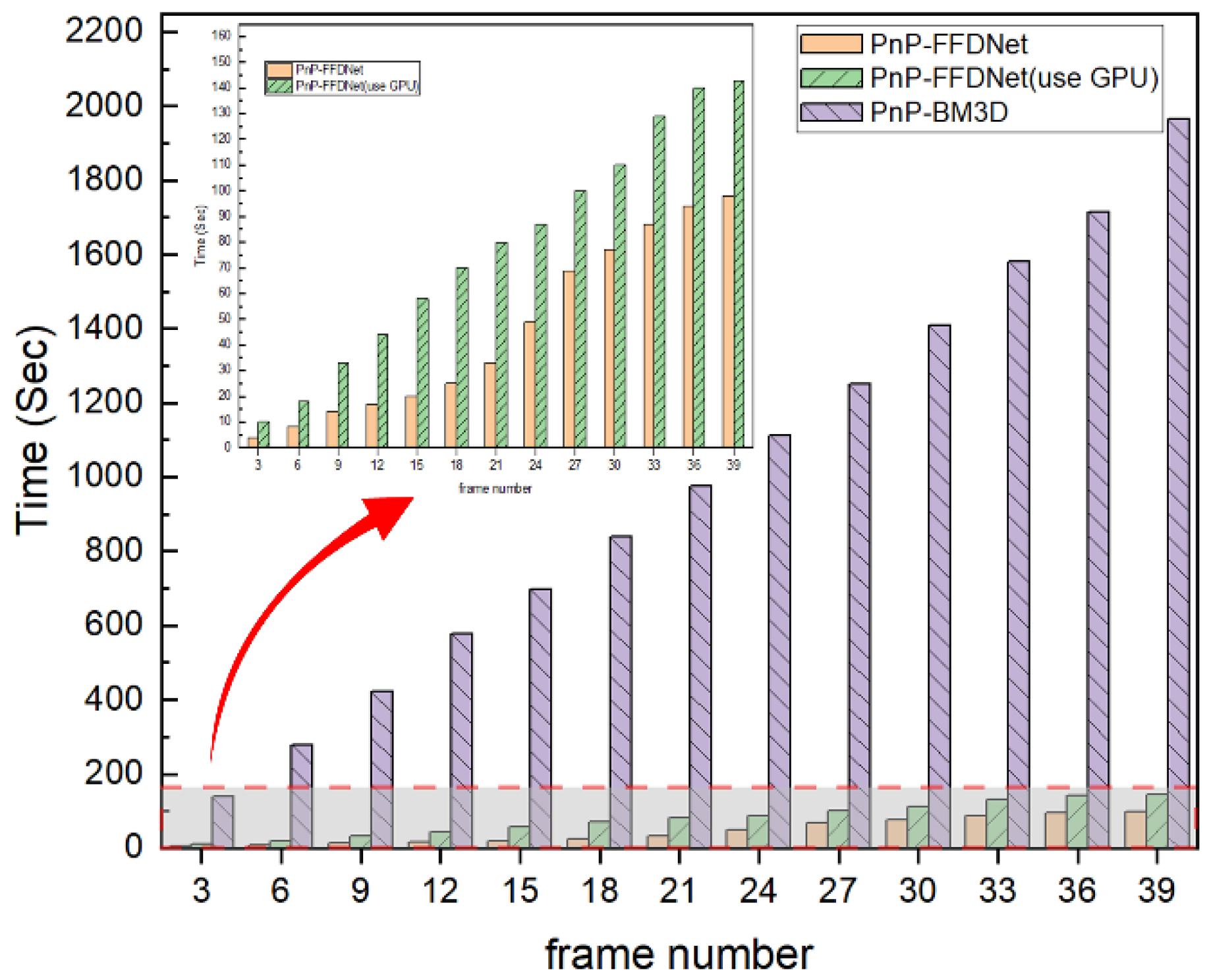
4.2. The Performance of PnP-FFDNet on Data with Different Compression Ratios
4.3. Performance of PnP-FFDNet on Real Data
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Eldar, Y.C.; Kutyniok, G. Compressed Sensing: Theory and Applications; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Liang, J.; Wang, L.V. Single-shot ultrafast optical imaging. Optica 2018, 5, 1113–1127. [Google Scholar] [CrossRef] [PubMed]
- Tsia, K.K.; Goda, K.; Thompson, J.V.; Mason, J.D.; Beier, H.T.; Bixler, J.N. High speed fluorescence imaging with compressed ultrafast photography. In Proceedings of the Society of Photo-Optical Instrumentation Engineers (SPIE), San Francisco, CA, USA, 28 January–2 February 2017; p. 1007613. [Google Scholar]
- Gao, L.; Liang, J.; Li, C.; Wang, L.V. Single-shot compressed ultrafast photography at one hundred billion frames per second. Nature 2014, 516, 74–77. [Google Scholar] [CrossRef] [PubMed]
- Liang, J.; Ma, C.; Zhu, L.; Chen, Y.; Gao, L.; Wang, L.V. Single-shot real-time video recording of a photonic Mach cone induced by a scattered light pulse. Sci. Adv. 2017, 3, e1601814. [Google Scholar] [CrossRef] [PubMed]
- Liang, J.; Gao, L.; Hai, P.; Li, C.; Wang, L. Encrypted three-dimensional dynamic imaging using snapshot time-of-flight compressed ultrafast photography. Sci. Rep. 2015, 5, 15504. [Google Scholar] [CrossRef] [PubMed]
- Bioucas-Dias, J.M.; Figueiredo, M.A.T. A new TwIST: Two-step iterative shrinkage/thresholding algorithms for image restoration. IEEE Trans. Image Process. 2007, 16, 2992–3004. [Google Scholar] [CrossRef] [PubMed]
- Rudin, L.I.; Osher, S.; Fatemi, E. Nonlinear total variation based noise removal algorithms. Phys. D Nonlinear Phenom. 1992, 60, 259–268. [Google Scholar] [CrossRef]
- Zhu, L.; Chen, Y.; Liang, J.; Xu, Q.; Gao, L.; Ma, C.; Wang, L.V. Space- and intensity-constrained reconstruction for compressed ultrafast photography. Optica 2016, 3, 694–697. [Google Scholar] [CrossRef] [PubMed]
- Lai, Y.; Xue, Y.; Cté, C.; Liu, X.; Laramée, A.; Jaouen, N.; Légaré, F.; Tian, L.; Liang, J. Compressed ultrafast photography: Single-shot ultraviolet compressed ultrafast photography (laser photonics rev. 14(10)/2020). Laser Photonics Rev. 2020, 14, 2070055. [Google Scholar] [CrossRef]
- Venkatakrishnan, S.V.; Bouman, C.A.; Wohlberg, B. Plug-and-play priors for model based reconstruction. In Proceedings of the 2013 IEEE Global Conference on Signal and Information Processing, Austin, TX, USA, 3–5 December 2013. [Google Scholar]
- Dabov, K.; Foi, A.; Katkovnik, V.; Egiazarian, K. Image denoising by sparse 3-D transform-domain collaborative filtering. IEEE Trans. Image Process. 2007, 16, 2080–2095. [Google Scholar] [CrossRef] [PubMed]
- Jia, R.; Zhao, H. A fast algorithm for the total variation model of image denoising. Adv. Comput. Math. 2010, 33, 231–241. [Google Scholar] [CrossRef]
- Gu, S.; Lei, Z.; Zuo, W.; Feng, X. Weighted nuclear norm minimization with application to image denoising. In Proceedings of the 2014 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Columbus, OH, USA, 23–28 June 2014. [Google Scholar]
- Mairal, J.; Elad, M.; Sapiro, G. Sparse representation for color image restoration. IEEE Trans. Image Process. 2007, 17, 53–69. [Google Scholar] [CrossRef] [PubMed]
- Elad, M.; Aharon, M. Image denoising via sparse and redundant representations over learned dictionaries. IEEE Trans. Image Process. 2006, 15, 3736–3745. [Google Scholar] [CrossRef] [PubMed]
- Dong, W.; Lei, Z.; Shi, G. Nonlocally centralized sparse representation for image restoration. IEEE Trans. Image Process. 2013, 22, 1620–1630. [Google Scholar] [CrossRef] [PubMed]
- Mairal, J.; Bach, F.; Ponce, J.; Sapiro, G.; Zisserman, A. Non-local sparse models for image restoration. In Proceedings of the 2009 IEEE 12th International Conference on Computer Vision (ICCV), Kyoto, Japan, 29 September–2 October 2010. [Google Scholar]
- Buades, A.; Coll, B.; Morel, J.M. A non-local algorithm for image denoising. In Proceedings of the 2005 IEEE computer society conference on computer vision and pattern recognition (CVPR’05), San Diego, CA, USA, 20–25 June 2005. [Google Scholar]
- Kai, Z.; Zuo, W.; Gu, S.; Lei, Z. Learning deep CNN denoiser prior for image restoration. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Zhang, K.; Zuo, W.; Chen, Y.; Meng, D.; Zhang, L. Beyond a gaussian denoiser: Residual learning of deep CNN for image denoising. IEEE Trans. Image Process. 2017, 26, 3142–3155. [Google Scholar] [CrossRef] [PubMed]
- Zhang, K.; Zuo, W.; Zhang, L. FFDNet: Toward a fast and flexible solution for CNN-based image denoising. IEEE Trans. Image Process. 2018, 27, 4608–4622. [Google Scholar] [CrossRef] [PubMed]
- Tassano, M.; Delon, J.; Veit, T. An Analysis and Implementation of the FFDNet Image Denoising Method. Image Processing On Line 2019, 9, 1–25. [Google Scholar] [CrossRef]
- Chan, S.H.; Wang, X.; Elgendy, O.A. Plug-and-play ADMM for image restoration: Fixed-point convergence and applications. IEEE Trans. Comput. Imaging 2016, 3, 84–98. [Google Scholar] [CrossRef]
- Yuan, X.; Liu, Y.; Suo, J.; Dai, Q. Plug-and-play algorithms for large-scale snapshot compressive imaging. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 14–19 June 2020. [Google Scholar]
- Sreehari, S.; Venkatakrishnan, S.V.; Wohlberg, B.; Buzzard, G.T.; Drummy, L.F.; Simmons, J.P.; Bouman, C.A. Plug-and-play priors for bright field electron tomography and sparse interpolation. IEEE Trans. Comput. Imaging 2016, 2, 408–423. [Google Scholar] [CrossRef]
- Rond, A.; Giryes, R.; Elad, M. Poisson inverse problems by the plug-and-play scheme. J. Vis. Commun. Image Represent. 2016, 41, 96–108. [Google Scholar] [CrossRef]
- Dar, Y.; Bruckstein, A.M.; Elad, M.; Giryes, R. Postprocessing of compressed images via sequential denoising. IEEE Trans. Image Process. 2016, 25, 3044–3058. [Google Scholar] [CrossRef] [PubMed]
- Brifman, A.; Romano, Y.; Elad, M. Turning a denoiser into a super-resolver using plug and play priors. In Proceedings of the 2016 IEEE International Conference on Image Processing (ICIP), Phoenix, AZ, USA, 25–28 September 2016; pp. 1404–1408. [Google Scholar] [CrossRef]








| Algorithm | Runner | Kobe | Traffic | Drop | Crash | Average |
|---|---|---|---|---|---|---|
| TwIST | 24.52 | 25.42 | 19.16 | 29.39 | 24.54 | 24.70 |
| PnP-TV | 23.29 | 23.89 | 19.55 | 29.72 | 24.57 | 24.20 |
| PnP-BM3D | 30.59 | 29.15 | 23.77 | 36.40 | 26.01 | 29.18 |
| PnP-IRCnn | 25.86 | 24.83 | 21.13 | 29.90 | 24.56 | 25.24 |
| PnP-DnCnn | 28.12 | 27.54 | 22.27 | 32.60 | 24.94 | 27.09 |
| PnP-FFDNet | 29.68 | 28.86 | 23.19 | 34.89 | 25.21 | 28.37 |
| Algorithm | Runner | Kobe | Traffic | Drop | Crash | Average |
|---|---|---|---|---|---|---|
| TwIST | 0.82 | 0.82 | 0.58 | 0.92 | 0.82 | 0.79 |
| PnP-TV | 0.82 | 0.84 | 0.68 | 0.95 | 0.87 | 0.83 |
| PnP-BM3D | 0.95 | 0.92 | 0.84 | 0.98 | 0.90 | 0.92 |
| PnP-IRCnn | 0.87 | 0.82 | 0.73 | 0.94 | 0.85 | 0.84 |
| PnP-DnCnn | 0.91 | 0.85 | 0.80 | 0.96 | 0.87 | 0.88 |
| PnP-FFDNet | 0.93 | 0.92 | 0.82 | 0.98 | 0.88 | 0.91 |
| Algorithm | Runner | Kobe | Traffic | Drop | Crash | Average |
|---|---|---|---|---|---|---|
| TwIST | 41 | 67 | 47 | 177 | 104 | 87 |
| PnP-TV | 10 | 7 | 9 | 6 | 8 | 8 |
| PnP-BM3D | 378 | 402 | 387 | 436 | 379 | 396 |
| PnP-IRCnn | 33 | 35 | 36 | 34 | 35 | 35 |
| PnP-IRCnn (use GPU) | 10 | 11 | 12 | 10 | 11 | 11 |
| PnP-DnCnn | 75 | 79 | 80 | 78 | 82 | 79 |
| PnP-DnCnn (use GPU) | 14 | 14 | 15 | 14 | 14 | 14 |
| PnP-FFDNet | 27 | 27 | 27 | 26 | 27 | 27 |
| PnP-FFDNet (use GPU) | 12 | 13 | 12 | 12 | 10 | 12 |
| Algorithm | PSNR | SSIM | Execution Time (s) | Execution Time (s) (Use GPU) |
|---|---|---|---|---|
| TwIST | 21.17 | 0.88 | 270 | - |
| PnP-TV | 21.04 | 0.85 | 33 | - |
| PnP-BM3D | 23.80 | 0.93 | 1124 | - |
| PnP-IRCnn | 25.67 | 0.91 | 103 | 26 |
| PnP-DnCnn | 25.27 | 0.87 | 230 | 40 |
| PnP-FFDNet | 25.65 | 0.95 | 85 | 43 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, Q.; Tian, J.; Pei, C. A Novel Reconstruction Algorithm with High Performance for Compressed Ultrafast Imaging. Sensors 2022, 22, 7372. https://doi.org/10.3390/s22197372
Shen Q, Tian J, Pei C. A Novel Reconstruction Algorithm with High Performance for Compressed Ultrafast Imaging. Sensors. 2022; 22(19):7372. https://doi.org/10.3390/s22197372
Chicago/Turabian StyleShen, Qian, Jinshou Tian, and Chengquan Pei. 2022. "A Novel Reconstruction Algorithm with High Performance for Compressed Ultrafast Imaging" Sensors 22, no. 19: 7372. https://doi.org/10.3390/s22197372
APA StyleShen, Q., Tian, J., & Pei, C. (2022). A Novel Reconstruction Algorithm with High Performance for Compressed Ultrafast Imaging. Sensors, 22(19), 7372. https://doi.org/10.3390/s22197372





