EL-SLE: Efficient Learning Based Stride-Length Estimation Using a Smartphone
Abstract
:1. Introduction
- We cast the stride-length estimation problem as an adaptive learning problem with multiple feature representations using CNN and LSTM modules. We leverage data preprocessing on the IMU measurements with autoencoders and preintegration to eliminate white noise and improve the efficiency of the network.
- We propose a convenient training data obtaining method based on visual-inertial odometry, determining accurate labels of IMU training data for the SLE model using a smartphone’s built-in camera.
- We proposed an online learning module that recognizes the current motion characters to update the network, automatically adjusting the mapping function for the user’s stride-length model using the aid of visual-inertial odometry.
- We conduct extensive experiments with various scenarios, motion modes, gaits, and devices/users, and the results show that the EL-SLE model outperforms the state-of-the-art methods.
2. Related Work
3. Algorithm Description
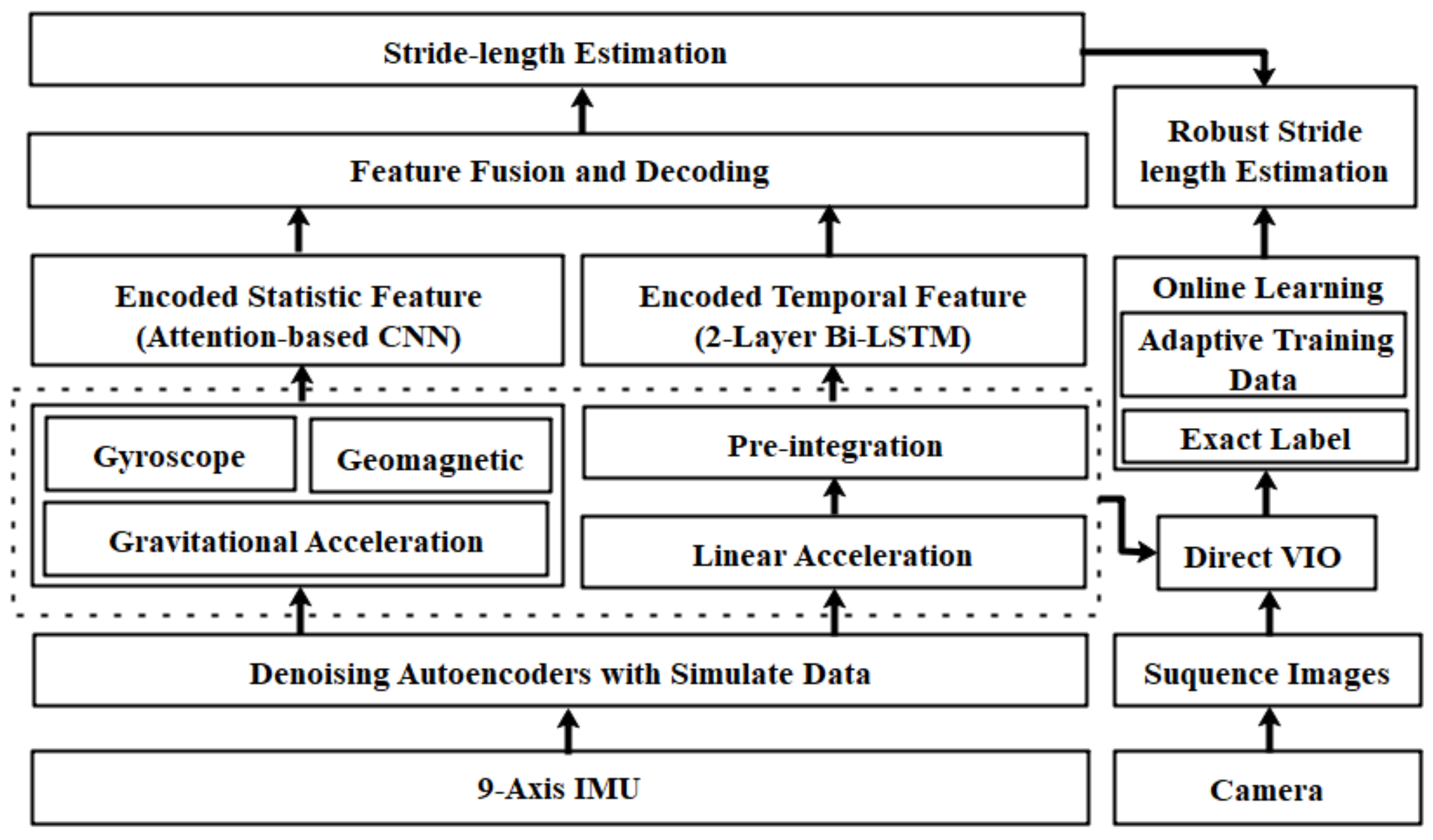
3.1. System Architecture
3.2. Stride Length Estimation Based on Adaptive Learning
3.2.1. Data Preprocessing with Denoising Autoencoders and Preintegration
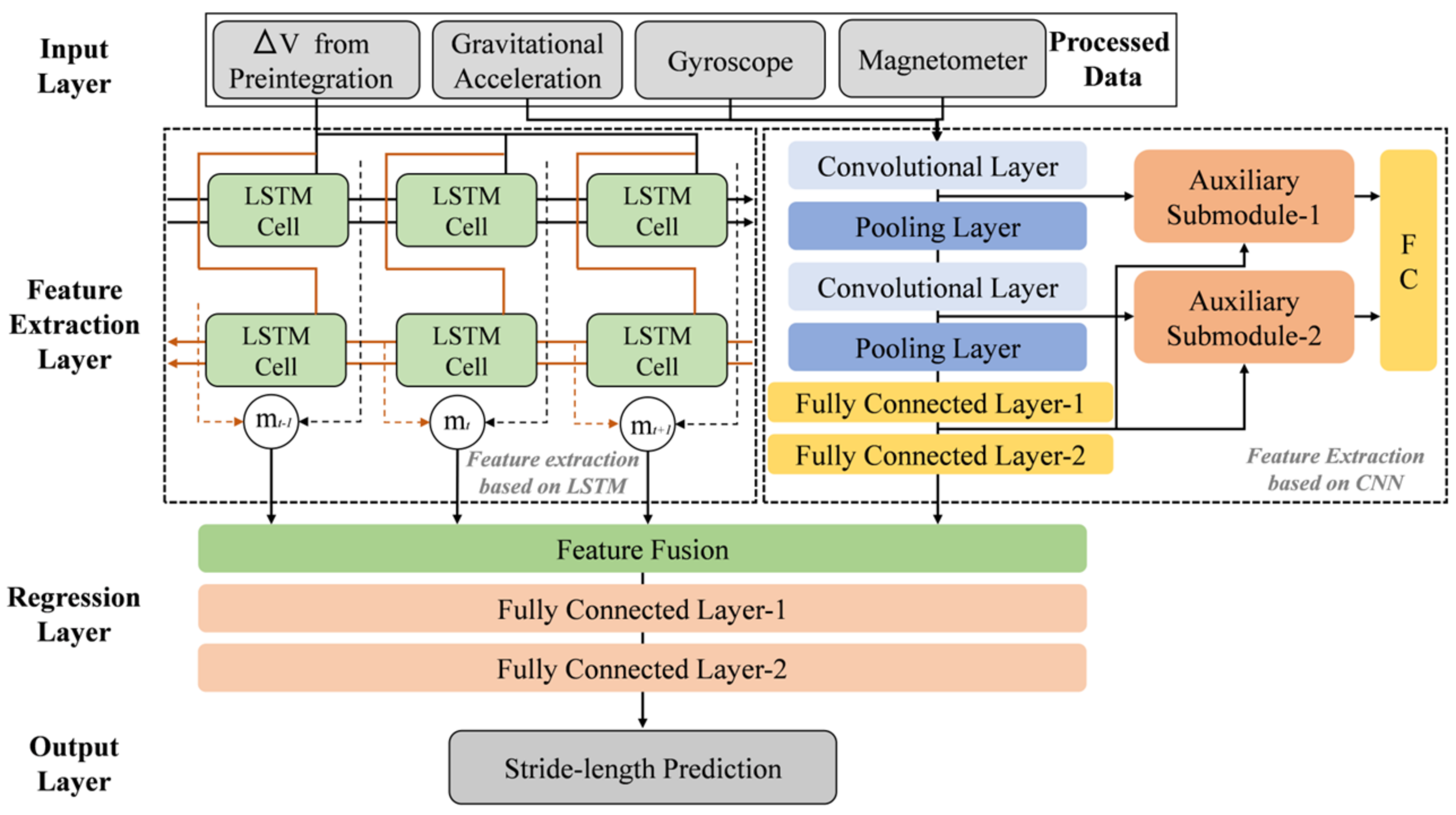
3.2.2. Recognition Feature Extraction with CNN Network
3.2.3. Temporal Features Extraction with LSTM Network
3.2.4. Regression Based on the Fusion Features
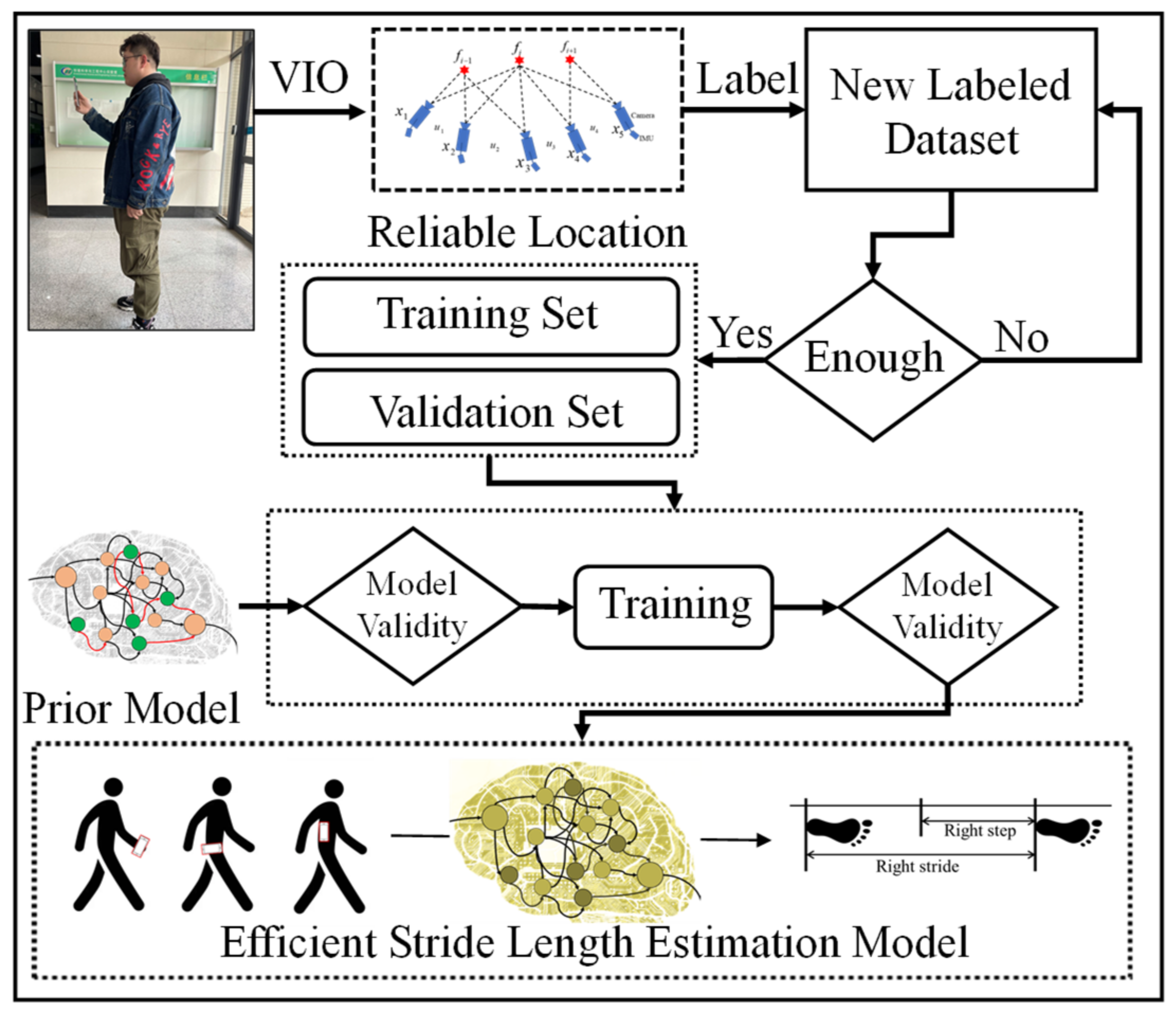
3.3. Vision-Aided Training Data Collection
3.4. Online Learning Module for Model Updating
| Algorithm 1: The updating model procedure based on online learning |
| 1: Input: IMU data, VIO-based locations, and offline SLE model |
| 2: Output: a robust model for stride-length estimation |
| 3: //Online test data obtained from a smartphone |
| 4: IMU data segment according to the step detection algorithm, and remove the first segments |
| 5: For each test segment do |
| 6: Calculating the ground truth of stride length from the statements based on VIO in Equation (16) |
| 7: End for |
| 8: Constructing the label data of each online segment as the form in Section 3.3 |
| 9: //Offline model verfication or updating |
| 10: If the size of the online test data is enough then |
| 11: Evaluate the validity of the offline model according to Equation (18) by using online IMU data |
| 12: If difference ≥ threshold (low reliability of offline model) then |
| 13: Input the online test data as training data for the online learning framework and update the current SLE model |
| 14: Obtain the new online test data when keep walking and evaluate the validity of the updating model according to Equation (18) |
| 15: if difference < threshold (high reliability of offline model) then |
| 16: Return the updating model from the online learning |
| 17: Else |
| 18: Return the offline SLE model after validity with new test data |
| 19: End if |
| 20: End if |
| 21: End if |
4. Experimentation and Evaluation
4.1. Implementation
4.2. Experimental Setup
4.3. Evaluation Metrics
4.4. Performance of Stride-Length Estimation Model
4.4.1. Effect of Denoising Autoencoders and Preintegration
4.4.2. Effect of the Adaptive Learning
4.4.3. Comparison between Normal and Updated Models
4.5. Walking-Distance Estimation
4.6. Comparison with Other Methods
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Harwahyu, R.; Cheng, R.-G.; Wei, C.-H.; Sari, R.F. Optimization of Random Access Channel in NB-IoT. IEEE Internet Things J. 2018, 5, 391–402. [Google Scholar] [CrossRef]
- Jylhä, M.; Guralnik, J.M.; Balfour, J.L.; Fried, L.P. Walking difficulty, walking speed, and age as predictors of self-rated health: The women’s health and aging study. J. Gerontol. Ser. A Biol. Sci. Med Sci. 2001, 56, M609–M617. [Google Scholar] [CrossRef] [PubMed]
- Woo, J.; Ho, S.C.; Yu, A.L. Walking Speed and Stride Length Predicts 36 Months Dependency, Mortality, and Institutionalization in Chinese Aged 70 and Older. J. Am. Geriatr. Soc. 1999, 47, 1257–1260. [Google Scholar] [CrossRef] [PubMed]
- Yu, N.; Zhan, X.; Zhao, S.; Wu, Y.; Feng, R. A Precise Dead Reckoning Algorithm Based on Bluetooth and Multiple Sensors. IEEE Internet Things J. 2018, 5, 336–351. [Google Scholar] [CrossRef]
- Kuang, J.; Niu, X.; Chen, X. Robust Pedestrian Dead Reckoning Based on MEMS-IMU for Smartphones. Sensors 2018, 18, 1391. [Google Scholar] [CrossRef]
- Hostettler, R.; Särkkä, S. IMU and magnetometer modeling for smartphone-based PDR. In Proceedings of the 2016 International Conference on Indoor Positioning and Indoor Navigation (IPIN), Alcala de Henares, Spain, 4–7 October 2016; pp. 1–8. [Google Scholar]
- Weinberg, H. Using the ADXL202 in pedometer and personal navigation applications. Analog Devices AN-602 Appl. Note 2002, 2, 1–6. [Google Scholar]
- Kim, J.W.; Jang, H.J.; Hwang, D.-H.; Park, C. A Step, Stride and Heading Determination for the Pedestrian Navigation System. J. Glob. Position. Syst. 2004, 3, 273–279. [Google Scholar] [CrossRef]
- Yao, Y.; Pan, L.; Fen, W.; Xu, X.; Liang, X.; Xu, X. A Robust Step Detection and Stride Length Estimation for Pedestrian Dead Reckoning Using a Smartphone. IEEE Sens. J. 2020, 20, 9685–9697. [Google Scholar] [CrossRef]
- Shavit, Y.; Ferens, R.; Keller, Y. Paying Attention to Activation Maps in Camera Pose Regression. arXiv 2021, arXiv:2103.11477. [Google Scholar]
- Nigg, B.M.; Bahlsen, H.A.; Luethi, S.M.; Stokes, S. The influence of running velocity and midsole hardness on external impact forces in heel-toe running. J. Biomech. 1987, 20, 951–959. [Google Scholar] [CrossRef]
- Brughelli, M.E.; Cronin, J.B.; Chaouachi, A. Effects of Running Velocity on Running Kinetics and Kinematics. J. Strength Cond. Res. 2011, 25, 933–939. [Google Scholar] [CrossRef]
- Lee, S.-W.; Mase, K.; Kogure, K. Detection of Spatio-Temporal Gait Parameters by Using Wearable Motion Sensors. In Proceedings of the 2005 IEEE Engineering in Medicine and Biology 27th Annual Conference, Shanghai, China, 17–18 January 2006; pp. 6836–6839. [Google Scholar]
- Clark, R.A.; Bower, K.J.; Mentiplay, B.F.; Paterson, K.L.; Pua, Y.-H. Concurrent validity of the Microsoft Kinect for assessment of spatiotemporal gait variables. J. Biomech. 2013, 46, 2722–2725. [Google Scholar] [CrossRef]
- Albert, J.A.; Owolabi, V.; Gebel, A.; Brahms, C.M.; Granacher, U.; Arnrich, B. Evaluation of the Pose Tracking Performance of the Azure Kinect and Kinect v2 for Gait Analysis in Comparison with a Gold Standard: A Pilot Study. Sensors 2020, 20, 5104. [Google Scholar] [CrossRef]
- Webster, K.E.; Wittwer, J.E.; Feller, J.A. Validity of the GAITRite walkway system for the measurement of averaged and individual step parameters of gait. Gait Posture 2005, 22, 317–321. [Google Scholar] [CrossRef]
- Díez, L.E.; Bahillo, A.; Otegui, J.; Otim, T. Step Length Estimation Methods Based on Inertial Sensors: A Review. IEEE Sens. J. 2018, 18, 6908–6926. [Google Scholar] [CrossRef]
- Foxlin, E. Pedestrian tracking with shoe-mounted inertial sensors. IEEE Comput. Graph. Appl. 2005, 25, 38–46. [Google Scholar] [CrossRef]
- Qiu, S.; Wang, Z.; Zhao, H.; Qin, K.; Li, Z.; Hu, H. Inertial/magnetic sensors based pedestrian dead reckoning by means of multi-sensor fusion. Inf. Fusion 2018, 39, 108–119. [Google Scholar] [CrossRef]
- Zhang, W.; Wei, D.; Yuan, H. The Improved Constraint Methods for Foot-Mounted PDR System. IEEE Access 2020, 8, 31764–31779. [Google Scholar] [CrossRef]
- Lan, K.-C.; Shih, W.-Y. On Calibrating the Sensor Errors of a PDR-Based Indoor Localization System. Sensors 2013, 13, 4781–4810. [Google Scholar] [CrossRef]
- Do, T.-N.; Liu, R.; Yuen, C.; Zhang, M.; Tan, U.-X. Personal Dead Reckoning Using IMU Mounted on Upper Torso and Inverted Pendulum Model. IEEE Sens. J. 2016, 16, 7600–7608. [Google Scholar] [CrossRef]
- Guo, Y.; Li, Y.; Sun, Y.L. Accurate indoor localization based on crowd sensing. In Proceedings of the 2016 International Wireless Communications and Mobile Computing Conference (IWCMC), Paphos, Cyprus, 5–9 September 2016; pp. 708–713. [Google Scholar]
- Wang, A.; Ou, X.; Wang, B. Improved Step Detection and Step Length Estimation Based on Pedestrian Dead Reckoning. In Proceedings of the 2019 IEEE 6th International Symposium on Electromagnetic Compatibility (ISEMC), Nanjing, China, 1–4 November 2019; pp. 1–4. [Google Scholar]
- Álvarez, D.; González, R.C.; López, A.M.; Álvarez, J.C. Comparison of Step Length Estimators from Weareable Accelerometer Devices. In Proceedings of the 2006 International Conference of the IEEE Engineering in Medicine and Biology Society, New York, NY, USA, 30 August–3 September 2006; pp. 5964–5967. [Google Scholar]
- Zhang, P.; Chen, X.; Ma, X.; Wu, Y.; Jiang, H.; Fang, D.; Tang, Z.; Ma, Y. SmartMTra: Robust Indoor Trajectory Tracing Using Smartphones. IEEE Sens. J. 2017, 17, 3613–3624. [Google Scholar] [CrossRef]
- Xu, S.; Chen, R.; Yu, Y.; Guo, G.; Huang, L. Locating Smartphones Indoors Using Built-In Sensors and Wi-Fi Ranging with an Enhanced Particle Filter. IEEE Access 2019, 7, 95140–95153. [Google Scholar] [CrossRef]
- Diaz, E.M.; Gonzalez, A.L.M. Step detector and step length estimator for an inertial pocket navigation system. In Proceedings of the 2014 International Conference on Indoor Positioning and Indoor Navigation (IPIN), Busan, Korea, 27–30 October 2014; pp. 105–110. [Google Scholar]
- Bousdar Ahmed, D.; Munoz Diaz, E.; García Domínguez, J.J. Automatic Calibration of the Step Length Model of a Pocket INS by Means of a Foot Inertial Sensor. Sensors 2020, 20, 2083. [Google Scholar] [CrossRef]
- Martinelli, A.; Gao, H.; Groves, P.D.; Morosi, S. Probabilistic Context-Aware Step Length Estimation for Pedestrian Dead Reckoning. IEEE Sens. J. 2018, 18, 1600–1611. [Google Scholar] [CrossRef]
- Ju, H.; Park, S.Y.; Park, C.G. A Smartphone-Based Pedestrian Dead Reckoning System with Multiple Virtual Tracking for Indoor Navigation. IEEE Sens. J. 2018, 18, 6756–6764. [Google Scholar] [CrossRef]
- Huang, B.; Qi, G.; Yang, X.; Zhao, L.; Zou, H. Exploiting cyclic features of walking for pedestrian dead reckoning with unconstrained smartphones. In Proceedings of the 2016 ACM International Joint Conference on Pervasive and Ubiquitous Computing, Heidelberg, Germany, 12–16 September 2016; pp. 374–385. [Google Scholar]
- Gao, H.; Groves, P.D. Context Determination for Adaptive Navigation using Multiple Sensors on a Smartphone. In Proceedings of the 29th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2016), Portland, OR, USA, 12–16 September 2016. [Google Scholar]
- Wang, Q.; Ye, L.; Luo, H.; Men, A.; Zhao, F.; Ou, C. Pedestrian Walking Distance Estimation Based on Smartphone Mode Recognition. Remote. Sens. 2019, 11, 1140. [Google Scholar] [CrossRef]
- Diaz, E.M. Inertial Pocket Navigation System: Unaided 3D Positioning. Sensors 2015, 15, 9156–9178. [Google Scholar] [CrossRef]
- Hannink, J.; Kautz, T.; Pasluosta, C.F.; Barth, J.; Schülein, S.; Gaßmann, K.-G.; Klucken, J.; Eskofier, B.M. Mobile Stride Length Estimation with Deep Convolutional Neural Networks. IEEE J. Biomed. Health Inform. 2018, 22, 354–362. [Google Scholar] [CrossRef]
- Pham, T.T.; Suh, Y.S. Walking Step Length Estimation Using Waist-Mounted Inertial Sensors with Known Total Walking Distance. IEEE Access 2021, 9, 85476–85487. [Google Scholar] [CrossRef]
- Chen, C.; Zhao, P.; Lu, C.X.; Wang, W.; Markham, A.; Trigoni, A. Deep-Learning-Based Pedestrian Inertial Navigation: Methods, Data Set, and On-Device Inference. IEEE Internet Things J. 2020, 7, 4431–4441. [Google Scholar] [CrossRef]
- Sui, J.-D.; Chang, T.-S. IMU Based Deep Stride Length Estimation with Self-Supervised Learning. IEEE Sens. J. 2021, 21, 7380–7387. [Google Scholar] [CrossRef]
- Wang, Q.; Luo, H.; Ye, L.; Men, A.; Zhao, F.; Huang, Y.; Ou, C. Personalized Stride-Length Estimation Based on Active Online Learning. IEEE Internet Things J. 2020, 7, 4885–4897. [Google Scholar] [CrossRef]
- Fusco, G.; Coughlan, J.M. Indoor Localization Using Computer Vision and Visual-Inertial Odometry. In Computers Helping People with Special Needs. ICCHP 2018. Lecture Notes in Computer Science 2018. Comput. Help. People Spec. Needs 2018, 10897, 86–93. [Google Scholar]
- Qin, T.; Li, P.; Shen, S. VINS-Mono: A Robust and Versatile Monocular Visual-Inertial State Estimator. IEEE Trans. Robot. 2018, 34, 1004–1020. [Google Scholar] [CrossRef]
- Abolfazli Esfahani, M.; Wang, H.; Wu, K.; Yuan, S. AbolDeepIO: A Novel Deep Inertial Odometry Network for Autonomous Vehicles. IEEE Trans. Intell. Transp. Syst. 2020, 21, 1941–1950. [Google Scholar] [CrossRef]
- Abadi, M.J.; Luceri, L.; Hassan, M.; Chou, C.T.; Nicoli, M. A collaborative approach to heading estimation for smartphone-based PDR indoor localisation. In Proceedings of the 2014 International Conference on Indoor Positioning and Indoor Navigation (IPIN), Busan, Korea, 27–30 October 2014; pp. 554–563. [Google Scholar]
- Mohammed, S.; Tashev, I. Unsupervised deep representation learning to remove motion artifacts in free-mode body sensor networks. In Proceedings of the 2017 IEEE 14th International Conference on Wearable and Implantable Body Sensor Networks (BSN), Eindhoven, The Netherlands, 9–12 May 2017; pp. 183–188. [Google Scholar]
- Liolios, C.; Doukas, C.; Fourlas, G.K.; Maglogiannis, I. An overview of body sensor networks in enabling pervasive healthcare and assistive environments. In Proceedings of the PETRA ’10 the 3rd International Conference on PErvasive Technologies Related to Assistive Environments, Samos, Greece, 23–25 June 2010. [Google Scholar]
- Qian, W.; Zhu, Y.; Jin, Y.; Yang, J.; Qi, P.; Wang, Y.; Ma, Y.; Ji, H. A Pedestrian Navigation Method Based on Construction of Adapted Virtual Inertial Measurement Unit Assisted by Gait Type Classification. IEEE Sens. J. 2021, 21, 15258–15268. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Schuster, M.; Paliwal, K.K. Bidirectional recurrent neural networks. IEEE Trans. Signal Process. 1997, 45, 2673–2681. [Google Scholar] [CrossRef]
- Ping, Z.; Zhidong, M.; Pengyu, W.; Zhi-hong, D. Pedestrian Stride-Length Estimation Based on Bidirectional LSTM Network. In Proceedings of the 2020 Chinese Automation Congress (CAC), Shanghai, China, 6–8 November 2020; pp. 3358–3363. [Google Scholar]
- Chen, C.; Rosa, S.; Lu, C.X.; Trigoni, A.; Markham, A. SelectFusion: A Generic Framework to Selectively Learn Multisensory Fusion. arXiv 2019, arXiv:1912.13077. [Google Scholar]
- Han, Y.C.; Wong, K.I.; Murray, I. Stride Length Estimation Based on a Single Shank’s Gyroscope. IEEE Sens. Lett. 2019, 3, 1–4. [Google Scholar] [CrossRef]
- Yan, H.; Herath, S.; Furukawa, Y. RoNIN: Robust Neural Inertial Navigation in the Wild: Benchmark, Evaluations, & New Methods. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; pp. 3146–3152. [Google Scholar]
- Herath, S. Robust Neural Inertial Navigation in the Wild. Master’s Thesis, University of Moratuwa, Applied Sciences, School of Computing Science, Moratuwa, Sri Lanka, 2019. [Google Scholar]
- Jin, Y.; Toh, H.-S.; Soh, W.-S.; Wong, L.W.-C. A robust dead-reckoning pedestrian tracking system with low cost sensors. In Proceedings of the 2011 IEEE International Conference on Pervasive Computing and Communications (PerCom), Seattle, WA, USA, 21–25 March 2011; pp. 222–230. [Google Scholar]
- Parodi, B.B.; Lenz, H.; Szabo, A.; Wang, H.; Horn, J.; Bamberger, J.; Obradovic, D. Initialization and Online-Learning of RSS Maps for Indoor/Campus Localization. In Proceedings of the 2006 IEEE/ION Position, Location, and Navigation Symposium, San Diego, CA, USA, 25–27 April 2006; pp. 164–172. [Google Scholar]
- Ketkar, N. Introduction to keras. In Deep Learning with Python; Springer: Berlin/Heidelberg, Germany, 2017; pp. 97–111. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2015, arXiv:1412.6980. [Google Scholar]
- Srivastava, N.; Hinton, G.E.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Klein, I.; Asraf, O. “StepNe” Deep Learning Approaches for Step Length Estimation. IEEE Access 2020, 8, 85706–85713. [Google Scholar] [CrossRef]












| Testers | Abbreviation | Gender | Age | Height (cm) |
| T1 | Male | 26 | 178 | |
| T2 | Male | 27 | 174 | |
| T3 | Female | 23 | 162 | |
| T4 | Female | 25 | 165 | |
| T5 | Male | 29 | 181 | |
| Devices | Abbreviation | Model | Version | Inertial sensor |
| D1 | Google Pixel XL 3 | 9.0 | BMI160 | |
| D2 | Samsung S8 | 8.0 | LSM6DSL | |
| D3 | Huawei Mate 30 | 11.5 | ICM-20690 | |
| D4 | OPPO Reno 6 | 11.3 | ICM-40607 | |
| D5 | Xiaomi 12 | 12.0 | AK09918 |
| Sequence | User (Gender) | Device | Attachments | Time (s) | Distance (m) |
|---|---|---|---|---|---|
| # 1 | # 1/M | Samsung S8 | Handheld | 1495 | 1578 |
| # 7 | # 2/M | Huawei Mate 30 | Handbag | 1497 | 1573 |
| # 11 | # 3/F | OPPO Reno 6 | Handbag | 1450 | 1570 |
| # 14 | # 4/F | Xiaomi 12 | 1462 | 1586 | |
| # 17 | # 5/M | Samsung S8 | Handheld | 1457 | 1583 |
| Test Seq. | L-SLE | L-SLE + DA | L-SLE + DA + PI | |||
|---|---|---|---|---|---|---|
| Mean Error (m) | Error Rate | Mean Error (m) | Error Rate | Mean Error (m) | Error Rate | |
| # 1 | 0.067 | 4.32% | 0.063 | 4.30% | 0.063 | 4.29% |
| # 7 | 0.065 | 4.30% | 0.062 | 4.29% | 0.060 | 4.28% |
| # 11 | 0.059 | 4.28% | 0.057 | 4.25% | 0.054 | 4.24% |
| # 14 | 0.054 | 4.26% | 0.053 | 4.23% | 0.052 | 4.22% |
| # 17 | 0.062 | 4.29% | 0.057 | 4.26% | 0.058 | 4.26% |
| Ave. | 0.061 | 4.29% | 0.058 | 4.27% | 0.057 | 4.23% |
| Test Seq. | LSTM | CNN | LSTM + CNN | |||
|---|---|---|---|---|---|---|
| MAX Error (m) | Error Rate | MAX Error (m) | Error Rate | MAX Error (m) | Error Rate | |
| # 1 | 0.334 | 4.47% | 0.428 | 4.76% | 0.326 | 4.29% |
| # 7 | 0.327 | 4.46% | 0.426 | 4.74% | 0.320 | 4.28% |
| # 11 | 0.328 | 4.43% | 0.419 | 4.71% | 0.314 | 4.24% |
| # 14 | 0.327 | 4.47% | 0.422 | 4.68% | 0.309 | 4.22% |
| # 17 | 0.331 | 4.51% | 0.431 | 4.75% | 0.316 | 4.26% |
| Ave. | 0.329 | 4.47% | 0.425 | 4.73% | 0.317 | 4.26% |
| Test Seq. | Tester | Device (IMU) | Offline Model | Updated Model | ||
|---|---|---|---|---|---|---|
| Mean Error (m) | Error Rate | Mean Error (m) | Error Rate | |||
| # 21 | T #6 | Vivo X70 (LSM6DSO) | 0.068 | 4.33% | 0.057 | 4.25% |
| # 22 | T #6 | Xiaomi 10 (LSM6DS0) | 0.066 | 4.31% | 0.055 | 4.24% |
| # 23 | T #6 | Galaxy F52 (MMC5603) | 0.072 | 4.37% | 0.064 | 4.29% |
| Ave. | 0.068 | 4.34% | 0.059 | 4.26% | ||
| Model | Attributes | Seq#1 | Seq#7 | Seq#11 | Seq#14 | Seq#17 | Seq#21 | Seq#22 | Seq#23 | Ave. |
|---|---|---|---|---|---|---|---|---|---|---|
| Adaptive learning | Error (m) | 45.62 | 42.37 | 39.31 | 37.97 | 42.68 | 50.97 | 51.36 | 51.08 | 45.17 |
| Error rate (%) | 2.9 | 2.7 | 2.5 | 2.4 | 2.7 | 3.2 | 3.3 | 3.1 | 2.9 | |
| Adaptive learning + PP | Error (m) | 43.75 | 40.55 | 39.15 | 36.51 | 40.09 | 48.28 | 49.96 | 50.77 | 43.63 |
| Error rate (%) | 2.8 | 2.6 | 2.5 | 2.3 | 2.5 | 3.1 | 3.1 | 3.2 | 2.8 | |
| Adaptive learning + PP + OL | Error (m) | 43.63 | 39.43 | 39.24 | 35.94 | 39.81 | 45.57 | 44.38 | 45.59 | 41.70 |
| Error rate (%) | 2.8 | 2.5 | 2.5 | 2.3 | 2.5 | 2.8 | 2.8 | 2.9 | 2.6 |
| Methods | Attributes | Seq #1 | Seq #7 | Seq #11 | Seq #14 | Seq #17 | Seq #21 | Seq #22 | Seq #23 | Ave. |
|---|---|---|---|---|---|---|---|---|---|---|
| Kim [8] | Error rate (%) | 5.35 | 5.34 | 4.74 | 4.70 | 5.29 | 5.33 | 5.31 | 5.38 | 5.18 |
| Positioning error (m) | 17.80 | 17.62 | 16.68 | 16.92 | 17.35 | 18.16 | 17.07 | 17.83 | 17.43 | |
| Weinberg [7] | Error rate (%) | 5.03 | 4.96 | 4.77 | 4.70 | 5.16 | 5.09 | 5.17 | 5.11 | 5.00 |
| Positioning error (m) | 16.33 | 15.75 | 14.97 | 14.81 | 16.56 | 16.38 | 16.75 | 17.92 | 16.18 | |
| Zhang [50] | Error rate (%) | 5.36 | 5.23 | 5.16 | 5.08 | 5.54 | 5.78 | 5.72 | 5.83 | 5.46 |
| Positioning error (m) | 17.82 | 17.14 | 17.09 | 16.97 | 18.42 | 18.89 | 18.75 | 19.01 | 18.01 | |
| Wang [34] | Error rate (%) | 4.57 | 4.42 | 4.39 | 4.36 | 4.53 | 4.52 | 4.56 | 4.49 | 4.48 |
| Positioning error (m) | 13.14 | 12.79 | 12.37 | 12.27 | 13.05 | 13.10 | 13.22 | 13.08 | 12.88 | |
| EL-SLE (ours) | Error rate (%) | 4.31 | 4.28 | 4.25 | 4.21 | 4.26 | 4.25 | 4.24 | 4.29 | 4.26 |
| Positioning error (m) | 8.54 | 8.37 | 7.92 | 7.63 | 8.83 | 8.97 | 7.80 | 9.03 | 8.39 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shu, M.; Chen, G.; Zhang, Z. EL-SLE: Efficient Learning Based Stride-Length Estimation Using a Smartphone. Sensors 2022, 22, 6864. https://doi.org/10.3390/s22186864
Shu M, Chen G, Zhang Z. EL-SLE: Efficient Learning Based Stride-Length Estimation Using a Smartphone. Sensors. 2022; 22(18):6864. https://doi.org/10.3390/s22186864
Chicago/Turabian StyleShu, Mingcong, Guoliang Chen, and Zhenghua Zhang. 2022. "EL-SLE: Efficient Learning Based Stride-Length Estimation Using a Smartphone" Sensors 22, no. 18: 6864. https://doi.org/10.3390/s22186864
APA StyleShu, M., Chen, G., & Zhang, Z. (2022). EL-SLE: Efficient Learning Based Stride-Length Estimation Using a Smartphone. Sensors, 22(18), 6864. https://doi.org/10.3390/s22186864






