Accelerated Deconvolved Imaging Algorithm for 2D Multibeam Synthetic Aperture Sonar
Abstract
:1. Introduction
2. Echo Model and Imaging Theory of MBSAS
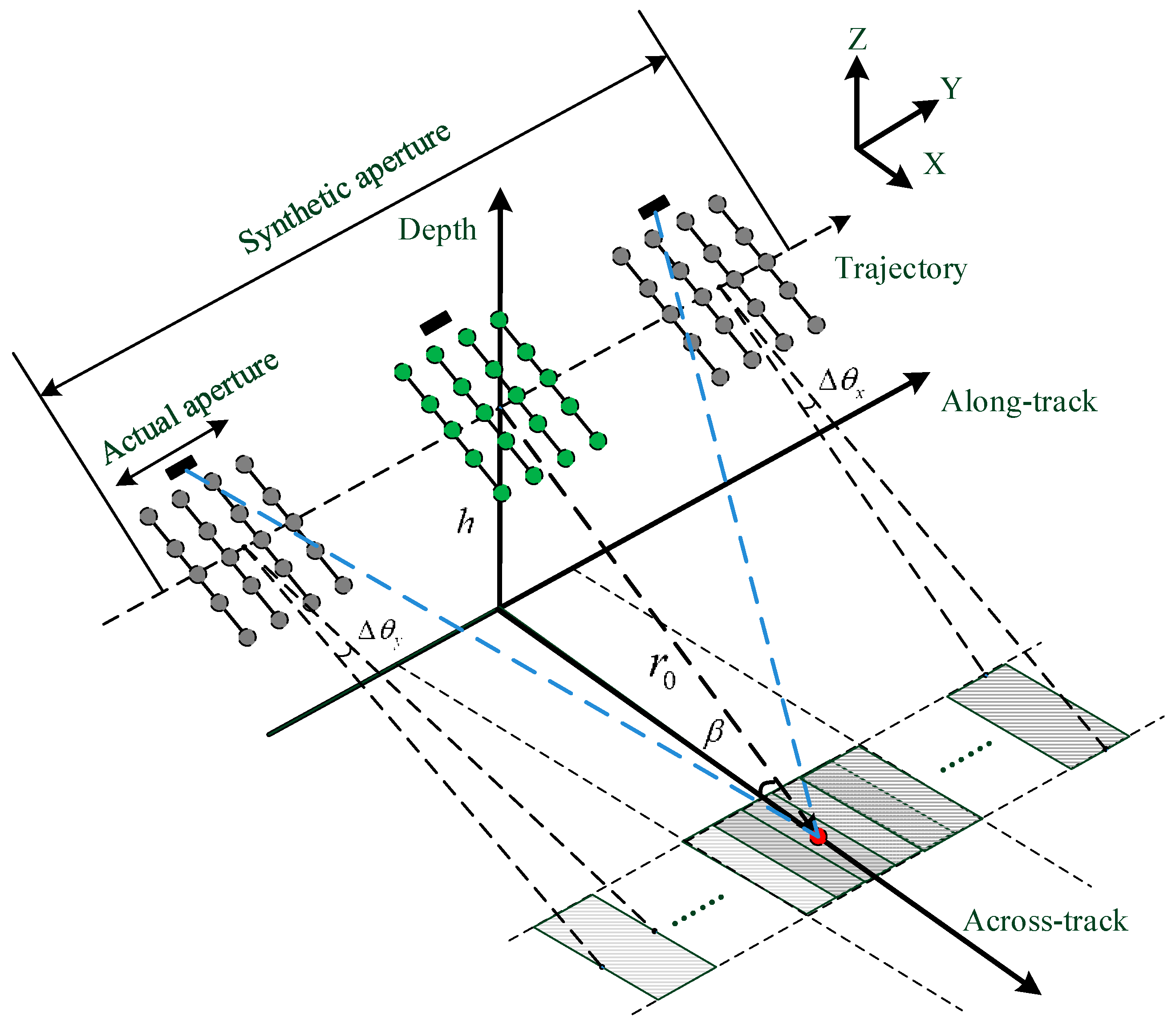
2.1. D Transducer Array and Echo Model of MBSAS
2.2. Basic Imaging Algorithm of MBSAS
3. Deconvolved Beamforming and Accelerated R–L Algorithm
3.1. Directivity and CBF of a ULA
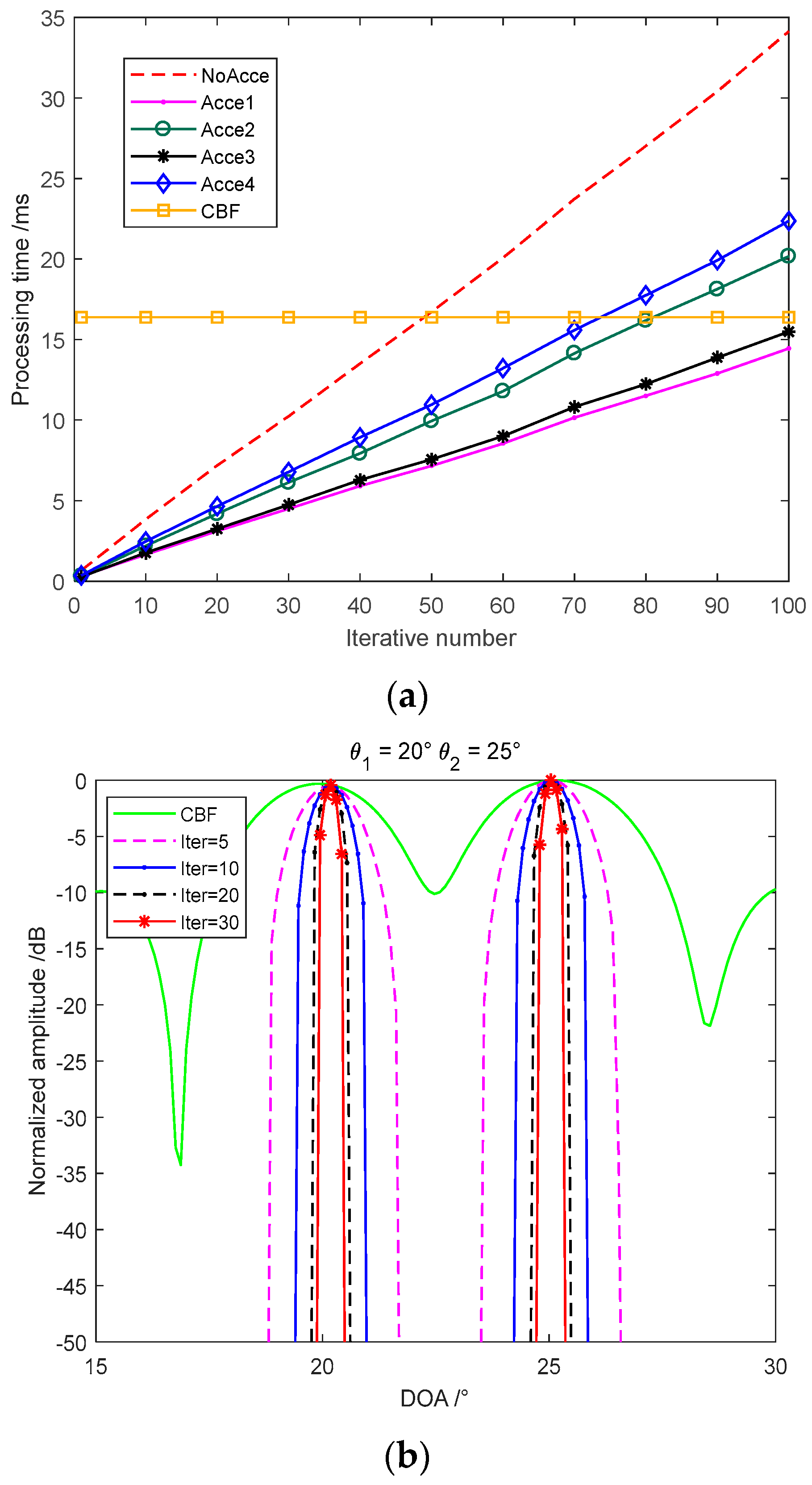
3.2. Deconvolved Beamforming and Accelerated R–L Algorithm
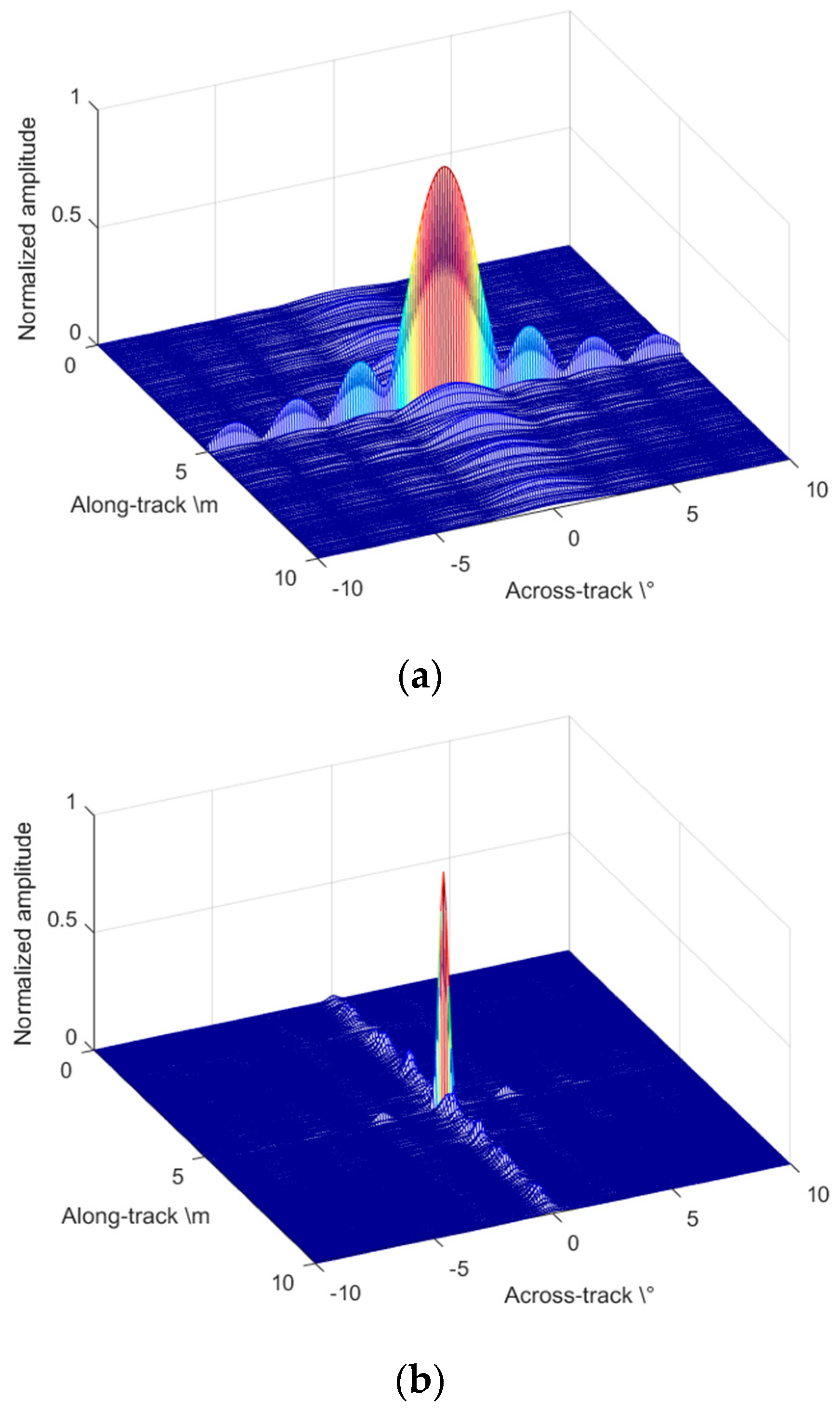
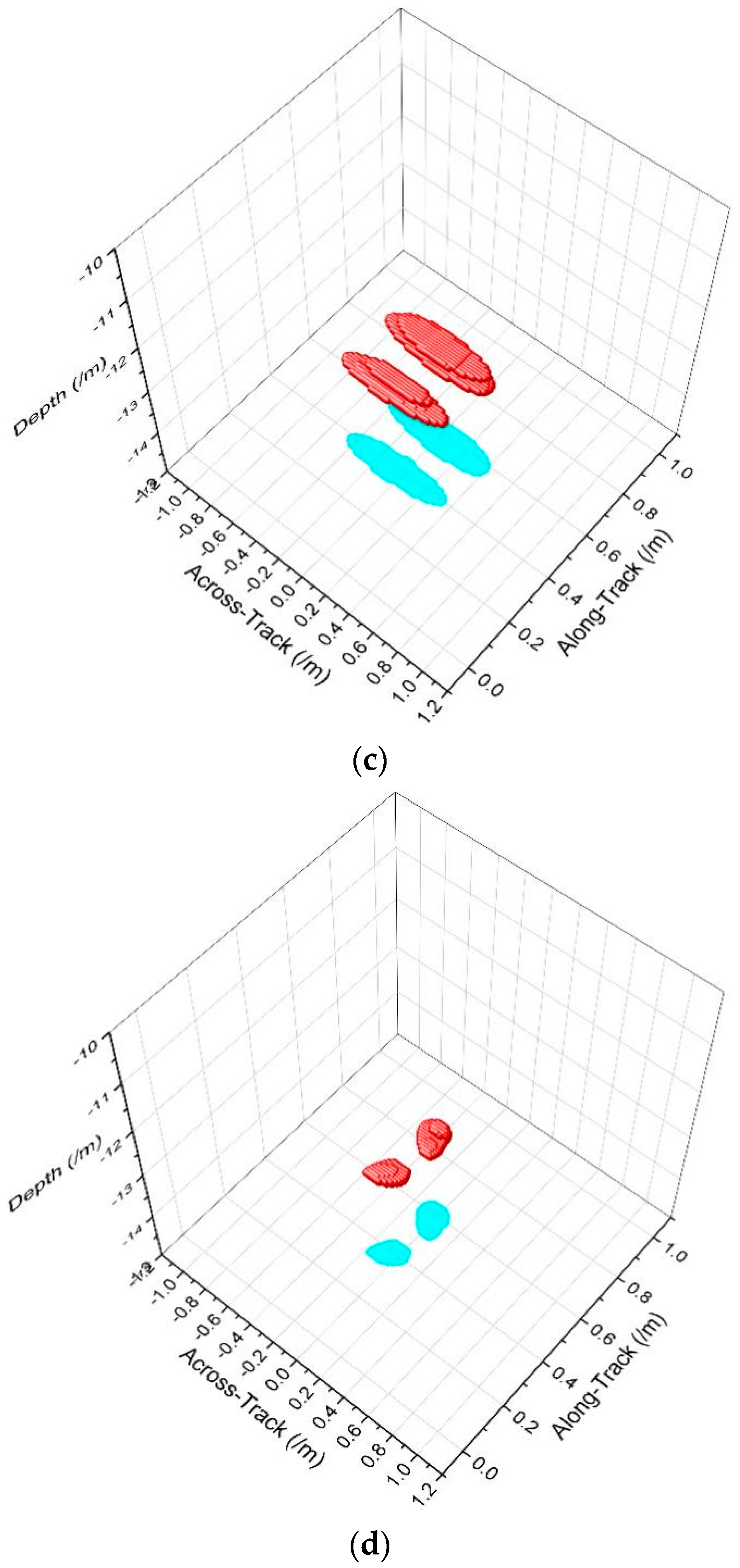
4. Imaging Algorithms Simulations
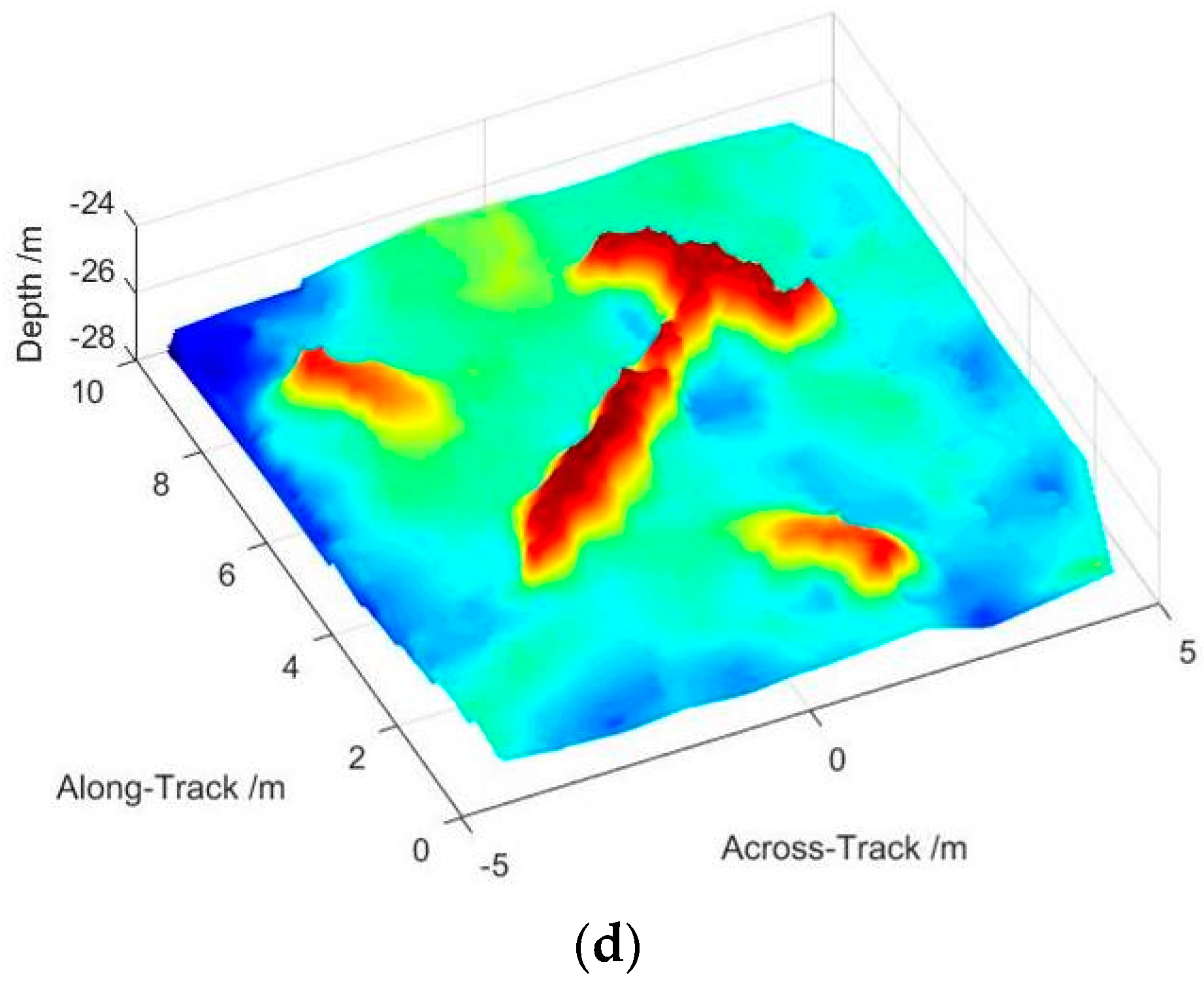
5. Experiment and Results
5.1. Field Experiment of Deconvolved Beamforming Applied on MBES
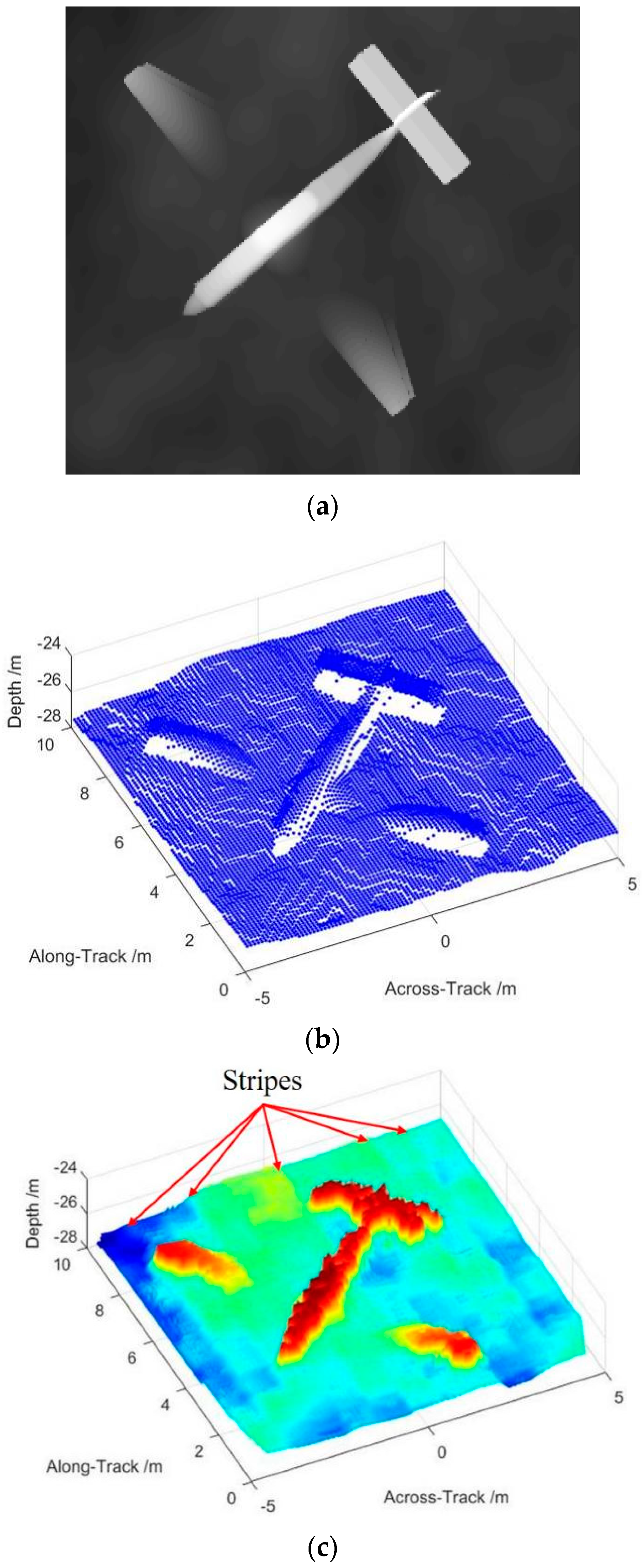
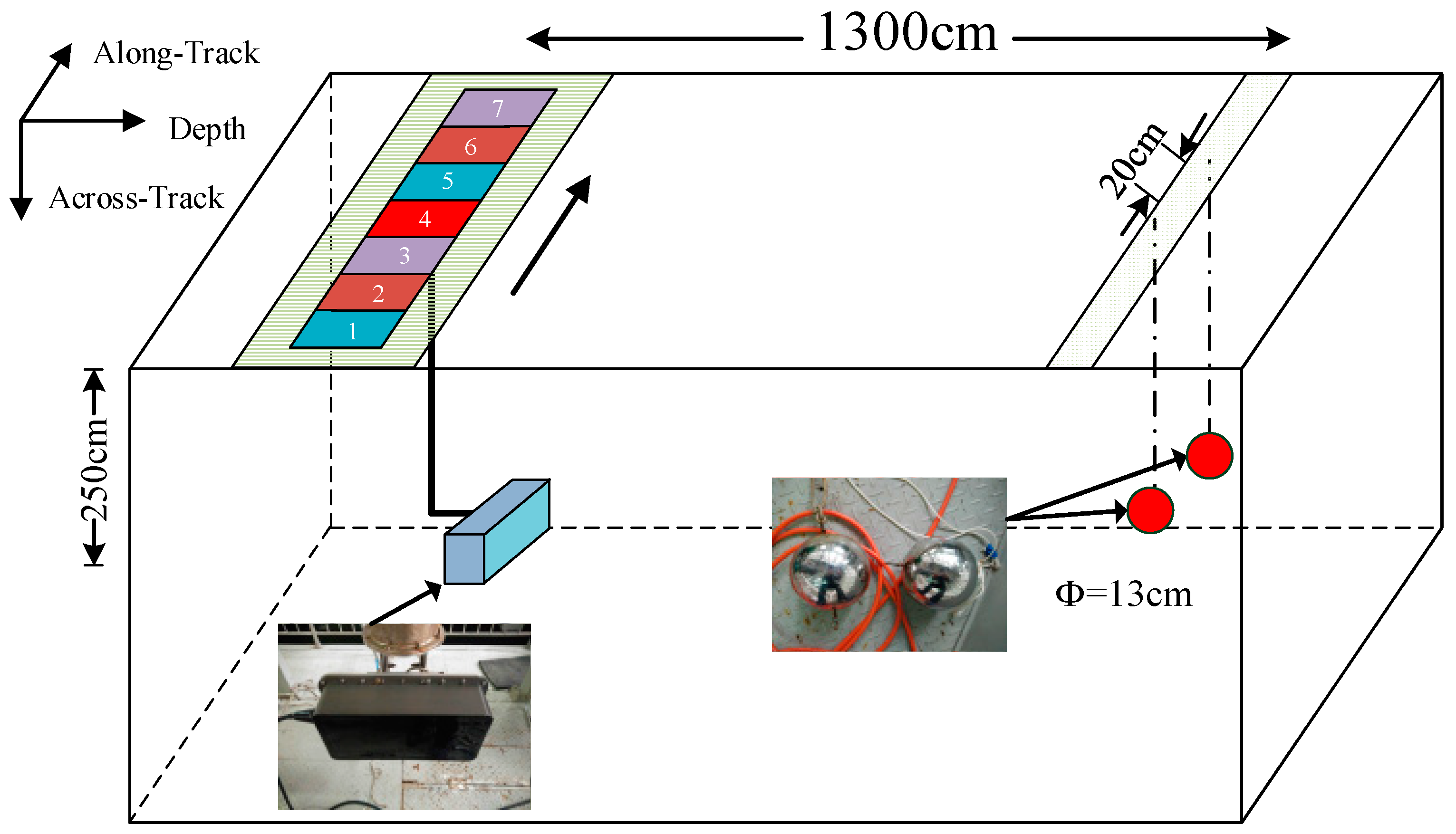
5.2. Tank Experiment of Deconvolved Beamforming Applied on MBSAS
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Petrich, J.; Brown, M.F.; Pentzer, J.L.; Sustersic, J.P. Side scan sonar based self-localization for small Autonomous Underwater Vehicles. Ocean Eng. 2018, 161, 221–226. [Google Scholar] [CrossRef]
- Shang, X.; Zhao, J.; Zhang, H. Obtaining High-Resolution Seabed Topography and Surface Details by Co-Registration of Side-Scan Sonar and Multibeam Echo Sounder Images. Remote Sens. 2019, 11, 1496. [Google Scholar] [CrossRef]
- Varghese, S.; Kumar, A.A.; Nagendran, G.; Balachandrudu, V.; Sheikh, N.; Mohan, K.G.; Singh, N.; Gopakumar, B.; Joshi, R.; Rajasekhar, R. Synthetic Aperture Sonar image of seafloor. Curr. Sci. 2017, 113, 385. [Google Scholar]
- Hagen, P.E.; Callow, H.; Reinertsen, E.; Sabo, T.O. Cassandra: An integrated, scalable, SAS based system for acoustic imaging and bathymetry. In Proceedings of the OCEANS 2018 MTS/IEEE Charleston, Charleston, SC, USA, 22–25 October 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Nagahashi, K.; Asada, A.; Mizuno, K.; Kojima, M.; Katase, F.; Saito, Y.; Ura, T. Autonomous Underwater Vehicle equipped with Interferometric Real and Synthetic Aperture Sonar. In Proceedings of the 2016 Techno-Ocean (Techno-Ocean), Kobe, Japan, 6–8 October 2016; pp. 304–308. [Google Scholar] [CrossRef]
- Marchand, B.; G-Michael, T. Multi-band Synthetic Aperture Sonar Mosaicing. Proc. SPIE 2017, 10182, 101820J. [Google Scholar] [CrossRef]
- Ehrhardt, M.; Degel, C.; Becker, F.J.; Peter, L.; Hewener, H.; Fonfara, H.; Fournelle, M.; Tretbar, S. Comparison of different short-range sonar systems on real structures and objects. In Proceedings of the OCEANS 2017—Aberdeen, Aberdeen, UK, 19–22 June 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Wei, B.; Zhou, T.; Li, H.; Xing, T.; Li, Y. Theoretical and experimental study on multibeam synthetic aperture sonar. J. Acoust. Soc. Am. 2019, 145, 3177–3189. [Google Scholar] [CrossRef]
- Zou, B.; Zhai, J.; Jian, X.; Gao, S. A Method for Estimating Dominant Acoustic Backscatter Mechanism of Water-Seabed Interface via Relative Entropy Estimation. Math. Probl. Eng. 2018, 2018. [Google Scholar] [CrossRef]
- Llort-Pujol, G.; Sintes, C.; Chonavel, T.; Morrison, A.T.; Daniel, S. Advanced Interferometric Techniques for High-Resolution Bathymetry. Mar. Technol. Soc. J. 2012, 46, 9–31. [Google Scholar] [CrossRef]
- Xu, C.; Wu, M.; Zhou, T.; Li, J.; Du, W.; Zhang, W.; White, P.R. Optical Flow-Based Detection of Gas Leaks from Pipelines Using Multibeam Water Column Images. Remote Sens. 2020, 12, 119. [Google Scholar] [CrossRef]
- Sun, X.; Li, R.W. Robust adaptive beamforming method for active sonar in single snapshot. MATEC Web Conf. 2019, 283, 03006. [Google Scholar] [CrossRef]
- Yang, T.C. Deconvolved Conventional Beamforming for a Horizontal Line Array. IEEE J. Ocean. Eng. 2018, 43, 160–172. [Google Scholar] [CrossRef]
- Yang, T.C. On conventional beamforming and deconvolution. In Proceedings of the OCEANS 2016—Shanghai, Shanghai, China, 10–13 April 2016. [Google Scholar]
- Blahut, R. Theory of Remote Image Formation; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Richardson, W.H. Bayesian-Based Iterative Method of Image Restoration. J. Opt. Soc. Am. 1972, 62, 55–59. [Google Scholar] [CrossRef]
- Li, H.; Wei, B.; Du, W. Technical Progress in Research of Multibeam Synthetic Aperture Sonar. Acta Geod. Cartogr. Sin. 2017, 46, 1760–1769. [Google Scholar] [CrossRef]
- Wu, H.; Tang, J.; Zhong, H. A correction approach for the inclined array of hydrophones in synthetic aperturesonar. Sensors 2018, 18, 2000. [Google Scholar] [CrossRef] [PubMed]
- Xenaki, A.; Jacobsen, F.; Grande, E.F. Improving the resolution of three-dimensional acoustic imaging with planar phased arrays. J. Sound Vib. 2012, 331, 1939–1950. [Google Scholar] [CrossRef]
- Dougherty, R. Extensions of DAMAS and Benefits and Limitations of Deconvolution in Beamforming. In Proceedings of the 11th AIAA/CEAS Aeroacoustics Conference, (26th AIAA Aeroacoustics Conference), Monterey, CA, USA, 23–25 May 2005. [Google Scholar] [CrossRef]
- Bai, H. Comparative analysis of convergence between Jacobi iterative method and Gauss Seidel iterative method. J. Hulunbeier Coll. 2019, 17, 55–58. [Google Scholar]
- Guo, X.; Jiang, Z. Criteria of Convergence of Jacobi and Gauss Seidel Iteration methods. J. Comput. Math. Coll. Univ. 1989, 296–304. [Google Scholar]
- Ehrenfried, K.; Koop, L. A Comparison of Iterative Deconvolution Algorithms for the Mapping of Acoustic Sources. In Proceedings of the 12th AIAA/CEAS Aeroacoustics Conference (27th AIAA Aeroacoustics Conference), Cambridge, MA, USA, 8–10 May 2006. [Google Scholar] [CrossRef]
- Beck, A.; Teboulle, M. A Fast Iterative Shrinkage-Thresholding Algorithm for Linear Inverse Problems. SIAM J. Imaging Sci. 2009, 2, 183–202. [Google Scholar] [CrossRef]
- Lylloff, O.; Fernández-Grande, E.; Agerkvist, F.; Hald, J.; Roig, E.T.; Andersen, M.S. Improving the efficiency of deconvolution algorithms for sound source localization. J. Acoust. Soc. Am. 2015, 138, 172–180. [Google Scholar] [CrossRef]
- Li, H.; Lu, D.; Zhou, T. Multi-beam real-time dynamic focused beam-forming method based on FPGA. J. Vib. Shock. 2014, 33, 83–88. [Google Scholar]
- Singh, M.K.; Tiwary, U.S.; Kim, Y.-H. An Adaptively Accelerated Lucy-Richardson Method for Image Deblurring. EURASIP J. Adv. Signal Process. 2007, 2008, 365021. [Google Scholar] [CrossRef]
- Biggs, D.S.C.; Andrews, M. Acceleration of iterative image restoration algorithms. Appl. Opt. 1997, 36, 1766–1775. [Google Scholar] [CrossRef] [PubMed]
- Vallet, P.; Loubaton, P. On the Performance of MUSIC with Toeplitz Rectification in the Context of Large Arrays. IEEE Trans. Signal Process. 2017, 65, 5848–5859. [Google Scholar] [CrossRef]
- Xiao, Y.; Yin, J.; Qi, H.; Yin, H.; Hua, G. MVDR Algorithm Based on Estimated Diagonal Loading for Beamforming. Math. Probl. Eng. 2017, 2017, 7904356. [Google Scholar] [CrossRef]
- Chu, N.; Picheral, J.; Mohammad-Djafari, A.; Gac, N. A robust super-resolution approach with sparsity constraint in acoustic imaging. Appl. Acoust. 2014, 76, 197–208. [Google Scholar] [CrossRef]
- Tan, H.P.; Ramanathan, U. Extraction of height information from target shadow for applications in ATC. In Proceedings of the IEEE 1999 International Geoscience and Remote Sensing Symposium. IGARSS’99, Hamburg, Germany, 28 June–2 July 1999; pp. 351–353. [Google Scholar]
- Wang, A.; Zhao, J.; Shang, X.; Zhang, H. Recovery of seabed 3D micro-topography from side-scan sonar image constrained by single-beam soundings. J. Harbin Eng. Univ. 2017, 38, 739–745. [Google Scholar] [CrossRef]










| Parameters | Values | Parameters | Values |
|---|---|---|---|
| Echo frequency | 150 kHz | Signal bandwidth | 20 kHz |
| Elements on the across-track | 32 | Element spacing on the across-track | 5 mm |
| Elements on the along-track | 4 | Element spacing on the along-track | 110 mm |
| Transmitter aperture size | 160 mm | Synthetized aperture | 4 m |
| Cubical target size | Highlight spacing | 100 mm |
| Parameters | Values | Parameters | Values |
|---|---|---|---|
| Echo frequency | 200 kHz | Waveform | CW |
| Beamwidth | 1.0° | Pulse width | 250 μs |
| Number of elements | 100 | Element spacing | 3.75 mm |
| Swath width | 160° | Depth | 60 m |
| Parameters | Values | Parameters | Values |
|---|---|---|---|
| Echo frequency | 150 kHz | Signal bandwidth | 20 kHz |
| Elements on the across-track | 32 | Elements on the along-track | 4 |
| Transmitter aperture size | 160 mm | Sampling positions | 7 |
| Interval on the along-track | 15 cm | Synthetized aperture | 1.05 m |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, B.; He, C.; Xing, S.; Zheng, Y. Accelerated Deconvolved Imaging Algorithm for 2D Multibeam Synthetic Aperture Sonar. Sensors 2022, 22, 6016. https://doi.org/10.3390/s22166016
Wei B, He C, Xing S, Zheng Y. Accelerated Deconvolved Imaging Algorithm for 2D Multibeam Synthetic Aperture Sonar. Sensors. 2022; 22(16):6016. https://doi.org/10.3390/s22166016
Chicago/Turabian StyleWei, Bo, Chuanlin He, Siyu Xing, and Yi Zheng. 2022. "Accelerated Deconvolved Imaging Algorithm for 2D Multibeam Synthetic Aperture Sonar" Sensors 22, no. 16: 6016. https://doi.org/10.3390/s22166016
APA StyleWei, B., He, C., Xing, S., & Zheng, Y. (2022). Accelerated Deconvolved Imaging Algorithm for 2D Multibeam Synthetic Aperture Sonar. Sensors, 22(16), 6016. https://doi.org/10.3390/s22166016






